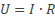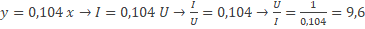Het arrangement Modeldidactiek (modulair) is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 09-11-2024 18:11:28
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Op deze pagina staan alle docentenhandleidingen die zijn ontwikkeld door de docenten van de PLG Modeldidactiek, georganiseerd door Bètapartners en NVON en mogelijk gemaakt door het project Impuls Open Leermateriaal. Alle handleidingen zijn te gebruiken onder Creative Commons Licentie CC-BY-SA.
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
- Trefwoorden
- modeldidactiek, nvon
Gebruikte Wikiwijs Arrangementen
Modeldidactiek. (z.d.).
Artikelen over lessen met de simulaties over straling
https://maken.wikiwijs.nl/207506/Artikelen_over_lessen_met_de_simulaties_over_straling
Modeldidactiek. (z.d.).
Demoles Optica: introductie licht
https://maken.wikiwijs.nl/207489/Demoles_Optica__introductie_licht
Modeldidactiek. (z.d.).
Demoles soorten krachten
Modeldidactiek. (z.d.).
Docentenhandleiding elektriciteit
https://maken.wikiwijs.nl/207483/Docentenhandleiding_elektriciteit
Modeldidactiek. (z.d.).
Docentenhandleiding straling
https://maken.wikiwijs.nl/207486/Docentenhandleiding_straling
Modeldidactiek. (z.d.).
Docenthandleiding golven
Modeldidactiek. (z.d.).
Docenthandleiding: Trillingen
https://maken.wikiwijs.nl/207507/Docenthandleiding__Trillingen
Modeldidactiek. (z.d.).
Doordringend vermogen van radioactieve straling
https://maken.wikiwijs.nl/207504/Doordringend_vermogen_van_radioactieve_straling
Modeldidactiek. (z.d.).
Elektrostatica: ontwikkeling van lading en veld begrip
https://maken.wikiwijs.nl/207485/Elektrostatica__ontwikkeling_van_lading_en_veld_begrip
Modeldidactiek. (z.d.).
Leerlijn onderzoek en practicum
https://maken.wikiwijs.nl/207491/Leerlijn_onderzoek_en_practicum
Modeldidactiek. (z.d.).
Oefenblad 1 trillingen: Formules en berekeningen aan trillend blokje
Modeldidactiek. (z.d.).
Oefening krachten tekenen met snelle feedback
https://maken.wikiwijs.nl/207479/Oefening_krachten_tekenen_met_snelle_feedback
Modeldidactiek. (z.d.).
Oefenles Optica: stralendiagrammen
https://maken.wikiwijs.nl/207522/Oefenles_Optica__stralendiagrammen
Modeldidactiek. (z.d.).
PO1 Consumentenbondartikel
Modeldidactiek. (z.d.).
PO2 Soortelijke weerstand van een draad
https://maken.wikiwijs.nl/207500/PO2_Soortelijke_weerstand_van_een_draad
Modeldidactiek. (z.d.).
Practica vaardigheden en trillingen / golven
https://maken.wikiwijs.nl/207530/Practica_vaardigheden_en_trillingen___golven
Modeldidactiek. (z.d.).
Practicum 1 - spanning van zonnecellen
https://maken.wikiwijs.nl/207493/Practicum_1___spanning_van_zonnecellen
Modeldidactiek. (z.d.).
Practicum 1 Golven: Gekoppelde trillende massa's demo
https://maken.wikiwijs.nl/207516/Practicum_1_Golven__Gekoppelde_trillende_massa_s_demo
Modeldidactiek. (z.d.).
Practicum 1 Trillingen: Relatie trillingstijd, massa en veerconstante
Modeldidactiek. (z.d.).
Practicum 2 Combineren van spanningsbronnen
https://maken.wikiwijs.nl/207494/Practicum_2_Combineren_van_spanningsbronnen
Modeldidactiek. (z.d.).
Practicum 2 Golven: voortplantingssnelheid van een golf
https://maken.wikiwijs.nl/207517/Practicum_2_Golven__voortplantingssnelheid_van_een_golf
Modeldidactiek. (z.d.).
Practicum 2 Trillingen: Massa veersysteem
https://maken.wikiwijs.nl/207511/Practicum_2_Trillingen__Massa_veersysteem
Modeldidactiek. (z.d.).
Practicum 3 Golven: terugkaatsing van pulsen en golven bij het uiteinde
Modeldidactiek. (z.d.).
Practicum 3 Trillingen: Energiehuishouding massa-veersysteem
https://maken.wikiwijs.nl/207514/Practicum_3_Trillingen__Energiehuishouding_massa_veersysteem
Modeldidactiek. (z.d.).
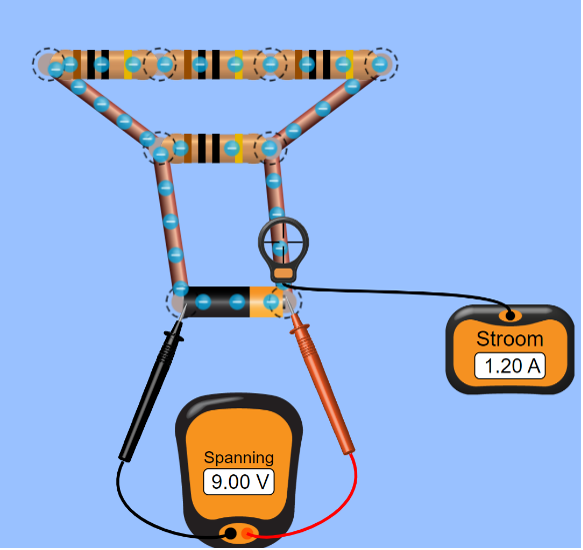
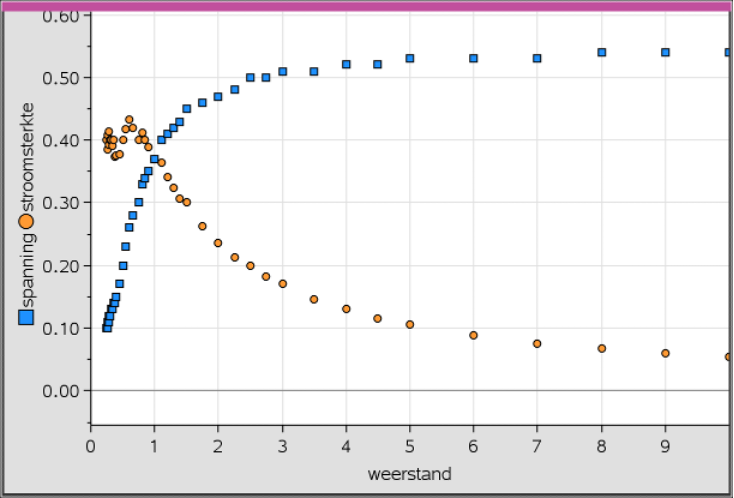
Practicum 3 Wet van Ohm
Modeldidactiek. (z.d.).
Practicum 4 Combineren van weerstanden
https://maken.wikiwijs.nl/207496/Practicum_4_Combineren_van_weerstanden
Modeldidactiek. (z.d.).
Practicum 4 Golven: Staande golven
https://maken.wikiwijs.nl/207519/Practicum_4_Golven__Staande_golven
Modeldidactiek. (z.d.).
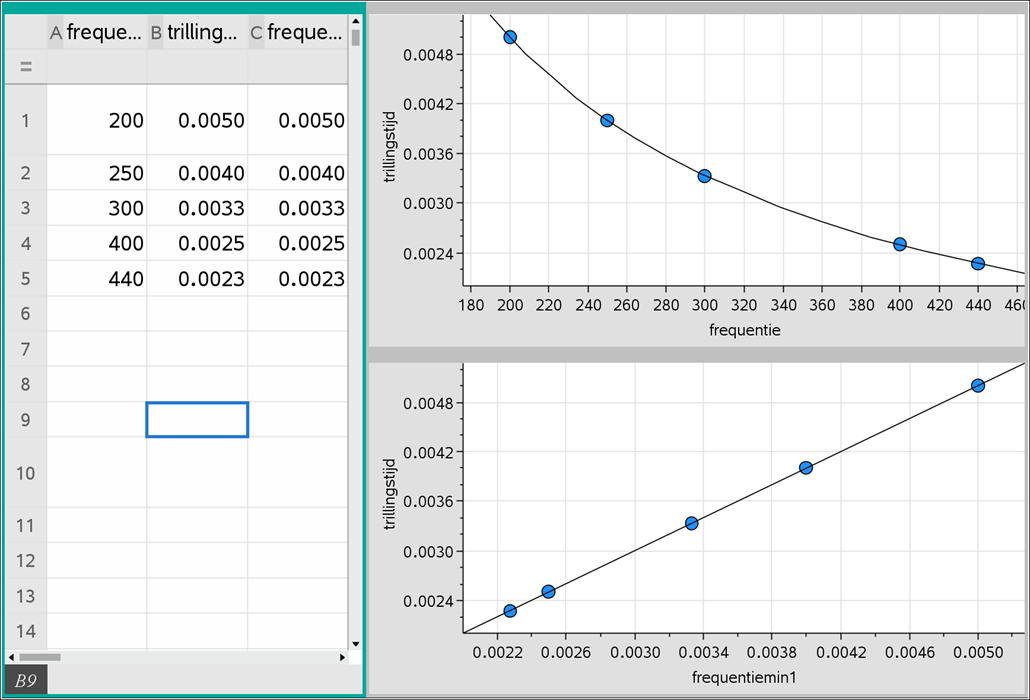
Practicum 4 Trillingen: Relatie trillingstijd en frequentie
https://maken.wikiwijs.nl/207515/Practicum_4_Trillingen__Relatie_trillingstijd_en_frequentie
Modeldidactiek. (z.d.).
Practicum 5 Golven: bepaling geluidssnelheid
https://maken.wikiwijs.nl/207520/Practicum_5_Golven__bepaling_geluidssnelheid
Modeldidactiek. (z.d.).
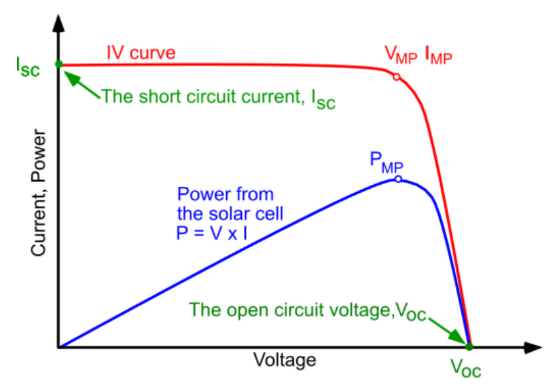
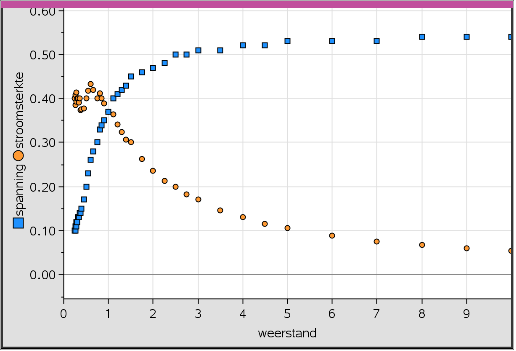
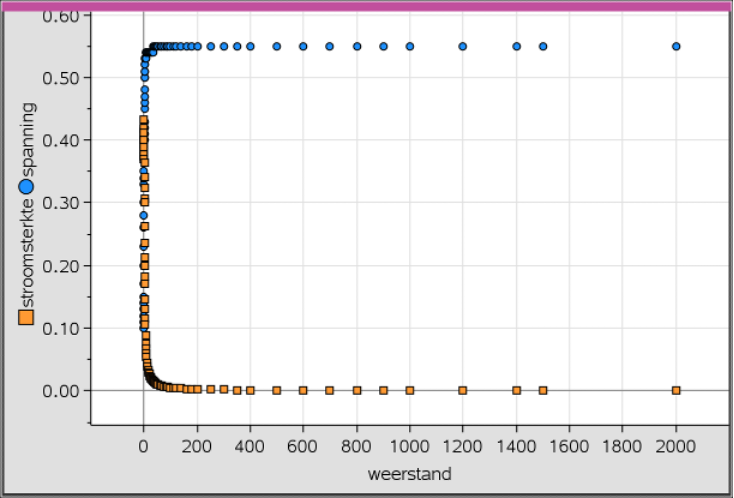
Practicum 5 Maximaal vermogen van een zonnecel
https://maken.wikiwijs.nl/207497/Practicum_5_Maximaal_vermogen_van_een_zonnecel
Modeldidactiek. (z.d.).
Practicum 5 Trillingen: Bouw je eigen klok
https://maken.wikiwijs.nl/207487/Practicum_5_Trillingen__Bouw_je_eigen_klok
Modeldidactiek. (z.d.).
Practicum 6 Golven: Staande golven in een staaf
https://maken.wikiwijs.nl/207521/Practicum_6_Golven__Staande_golven_in_een_staaf
Modeldidactiek. (z.d.).
Practicum botsende treintjes
https://maken.wikiwijs.nl/207469/Practicum_botsende_treintjes
Modeldidactiek. (z.d.).
Practicum cirkelbeweging en vaardigheden: Ronddraaiende stop
https://maken.wikiwijs.nl/207528/Practicum_cirkelbeweging_en_vaardigheden__Ronddraaiende_stop
Modeldidactiek. (z.d.).
Practicum massa en gewicht
Modeldidactiek. (z.d.).
Practicum Optica: lenzenformule
https://maken.wikiwijs.nl/207523/Practicum_Optica__lenzenformule
Modeldidactiek. (z.d.).
Practicum soortelijke warmte (deel 1)
https://maken.wikiwijs.nl/207490/Practicum_soortelijke_warmte__deel_1_
Modeldidactiek. (z.d.).
Practicum soortelijke warmte (deel 2)
https://maken.wikiwijs.nl/207524/Practicum_soortelijke_warmte__deel_2_
Modeldidactiek. (z.d.).
Practicum vaardigheden en mechanica: Horizontale worp
https://maken.wikiwijs.nl/207527/Practicum_vaardigheden_en_mechanica__Horizontale_worp
Modeldidactiek. (2024).
Practicum Vaardigheden: Ohmse weerstand
https://maken.wikiwijs.nl/207526/Practicum_Vaardigheden__Ohmse_weerstand
Modeldidactiek. (z.d.).
Practicum vallende bakjes
Modeldidactiek. (z.d.).
Practicum Verdamping en Condensatie met Concept Cartoon
https://maken.wikiwijs.nl/207492/Practicum_Verdamping_en_Condensatie_met_Concept_Cartoon
Modeldidactiek. (z.d.).
Practicum videometen kar van helling
https://maken.wikiwijs.nl/207470/Practicum_videometen_kar_van_helling
Modeldidactiek. (z.d.).
Practicum videometen treintje
https://maken.wikiwijs.nl/207461/Practicum_videometen_treintje
Modeldidactiek. (z.d.).
Practicum Warmtetransport
Modeldidactiek. (z.d.).
Remediatieoefening elektrische schakelingen
https://maken.wikiwijs.nl/207498/Remediatieoefening_elektrische_schakelingen
Modeldidactiek. (z.d.).
Stralingsbelasting, dosis en dosisequivalent
https://maken.wikiwijs.nl/207505/Stralingsbelasting__dosis_en_dosisequivalent
Modeldidactiek. (z.d.).
Theorie 1 Trillingen: Afleiding verband u(t), v(t) en a(t)
https://maken.wikiwijs.nl/209766/Theorie_1_Trillingen__Afleiding_verband_u_t___v_t__en_a_t_
Modeldidactiek. (z.d.).
Wat is Modeldidactiek
Modeldidactiek. (z.d.).
Werkblad 1 Trillingen: (u,t), (v,t) en (a,t) diagrammen bij een horizontaal trillend blokje
Modeldidactiek. (z.d.).
Werkblad 1B Trillingen: Beweging en krachten op een hangend blokje
https://maken.wikiwijs.nl/207510/Werkblad_1B_Trillingen__Beweging_en_krachten_op_een_hangend_blokje
Modeldidactiek. (z.d.).
Werkblad 2 Trillingen: Energiehuishouding
https://maken.wikiwijs.nl/207512/Werkblad_2_Trillingen__Energiehuishouding
Modeldidactiek. (z.d.).
Werkblad 3: Energieschema's massa-veersysteem
https://maken.wikiwijs.nl/207513/Werkblad_3__Energieschema_s_massa_veersysteem
Modeldidactiek. (z.d.).
Werkblad 4 Trillingen: Begripsvragen over een massa-veersysteem
https://maken.wikiwijs.nl/209765/Werkblad_4_Trillingen__Begripsvragen_over_een_massa_veersysteem
Modeldidactiek. (z.d.).
Werkblad Inductiespanning

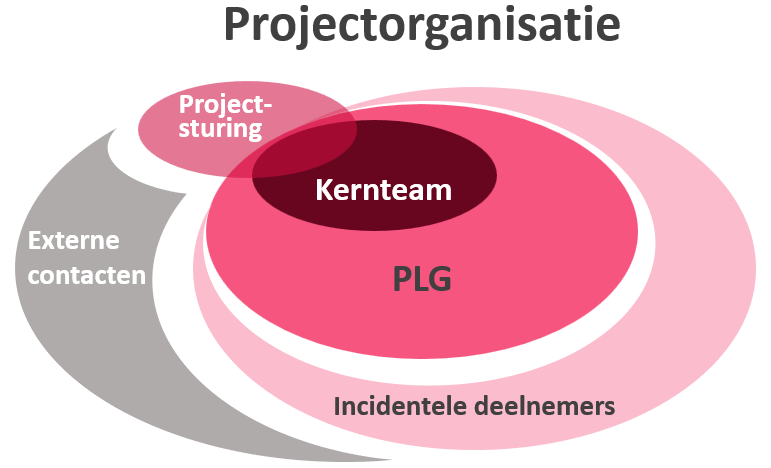
 op whiteboards. Bij de klassikale bespreking van de resultaten van de groepen vallen verschillen in aanpak en presentatie op. Via de whiteboards ziet de docent tijdens de les de ontwikkeling van (groepjes) leerlingen en kan hij/zij daarop direct reageren (formative assessment). Zie ook het
op whiteboards. Bij de klassikale bespreking van de resultaten van de groepen vallen verschillen in aanpak en presentatie op. Via de whiteboards ziet de docent tijdens de les de ontwikkeling van (groepjes) leerlingen en kan hij/zij daarop direct reageren (formative assessment). Zie ook het 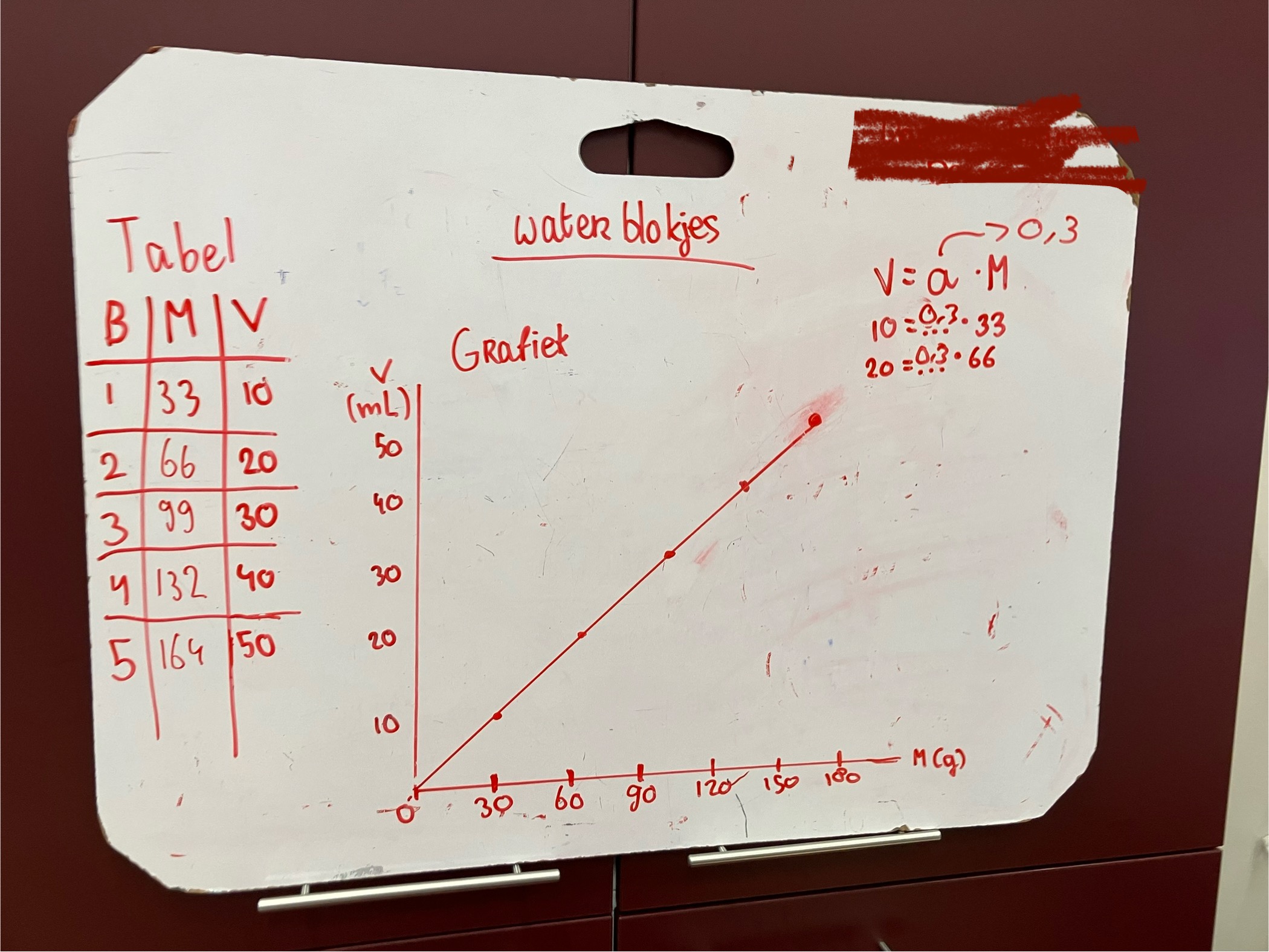
 verkennende workshop over Modeling Instruction™ plaatsgevonden, als professionaliseringsactiviteit vanuit het vo-ho netwerk Bètapartners. Deze workshop werd verzorgd door Dan MacIsaac en Kathleen Falconer van de AMTA (American Modeling Teachers Association), zie de
verkennende workshop over Modeling Instruction™ plaatsgevonden, als professionaliseringsactiviteit vanuit het vo-ho netwerk Bètapartners. Deze workshop werd verzorgd door Dan MacIsaac en Kathleen Falconer van de AMTA (American Modeling Teachers Association), zie de



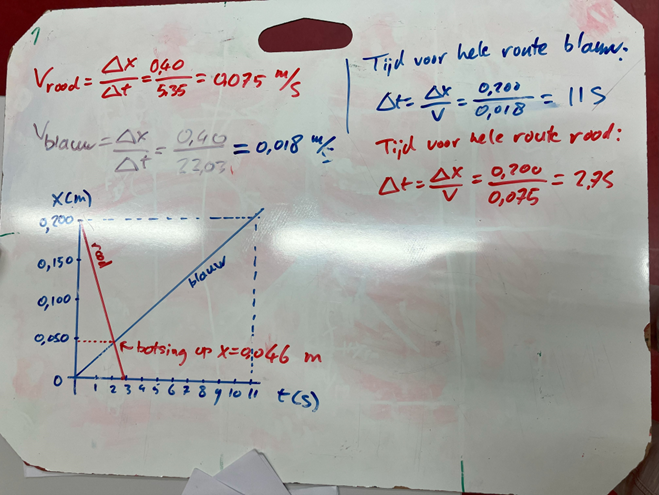
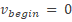 ?
?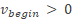 ?
?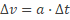 of
of 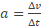


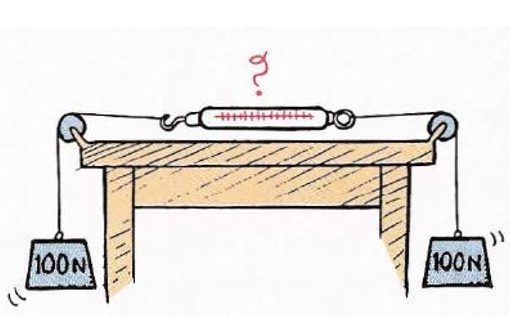



 komt A dan boven of onder de deelstreep? En m? Dat wordt een eerste ruwe benadering van de formule, wie weet moet er A2 staan i.p.v. A
komt A dan boven of onder de deelstreep? En m? Dat wordt een eerste ruwe benadering van de formule, wie weet moet er A2 staan i.p.v. A




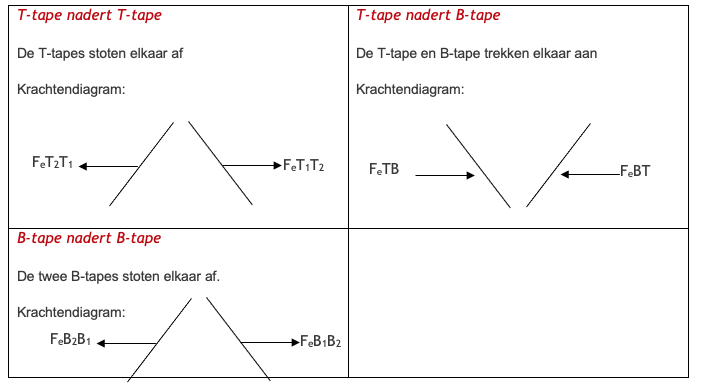
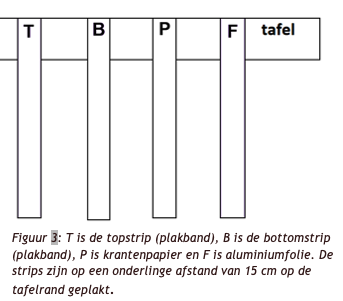 Knip twee stukjes krantenpapier uit, met dezelfde afmeting als de tapes, en hang er één 15 cm links van het folie aan de rand van een tafel. Label het hangende krantenpapier “P”. Benader het hangende papier met het andere stuk papier.
Knip twee stukjes krantenpapier uit, met dezelfde afmeting als de tapes, en hang er één 15 cm links van het folie aan de rand van een tafel. Label het hangende krantenpapier “P”. Benader het hangende papier met het andere stuk papier.  plakkerige kant om eventuele lading te verwijderen. Trek daarna de B- en T-tapes snel uit elkaar. Plak beide strips aan de rand van de tafel, naast het aluminiumfolie en krantenpapier, met minimaal 15 cm ertussen. Zie figuur 3.
plakkerige kant om eventuele lading te verwijderen. Trek daarna de B- en T-tapes snel uit elkaar. Plak beide strips aan de rand van de tafel, naast het aluminiumfolie en krantenpapier, met minimaal 15 cm ertussen. Zie figuur 3.
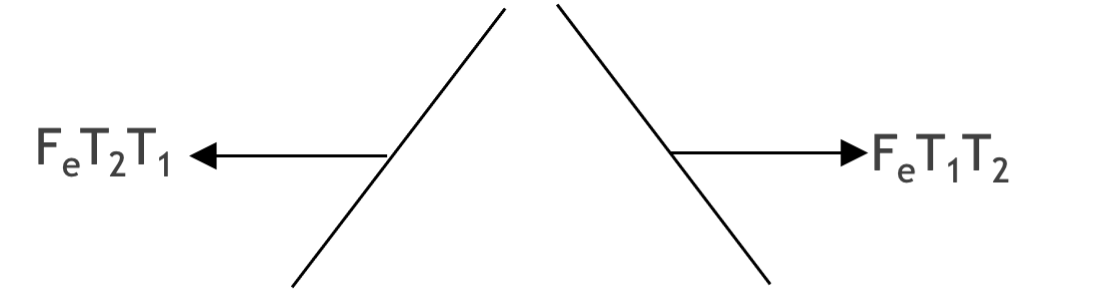
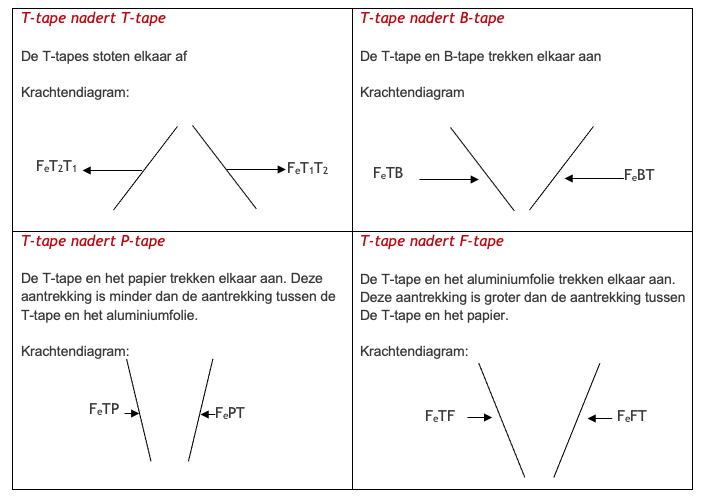
 Werkblad sticky tape
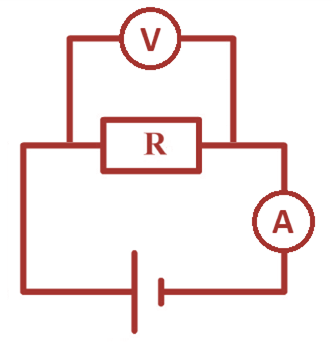
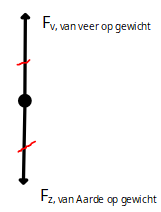
Werkblad sticky tape Michael Faraday en Joseph Henry toonden rond 1830 aan dat een veranderd magnetisch veld een geïnduceerde spanning in een spoel kan veroorzaken. Wanneer de spoel een gesloten stroomkring betreft kan er zelfs een stroom in de spoel gaan lopen (ondanks dat er geen fysieke spanningsbron is aangesloten op de spoel). Met de opstelling in de figuur hiernaast kan een inductiespanning over de spoel worden gemeten. Van welke factoren is de geïnduceerde spanning afhankelijk?
Michael Faraday en Joseph Henry toonden rond 1830 aan dat een veranderd magnetisch veld een geïnduceerde spanning in een spoel kan veroorzaken. Wanneer de spoel een gesloten stroomkring betreft kan er zelfs een stroom in de spoel gaan lopen (ondanks dat er geen fysieke spanningsbron is aangesloten op de spoel). Met de opstelling in de figuur hiernaast kan een inductiespanning over de spoel worden gemeten. Van welke factoren is de geïnduceerde spanning afhankelijk?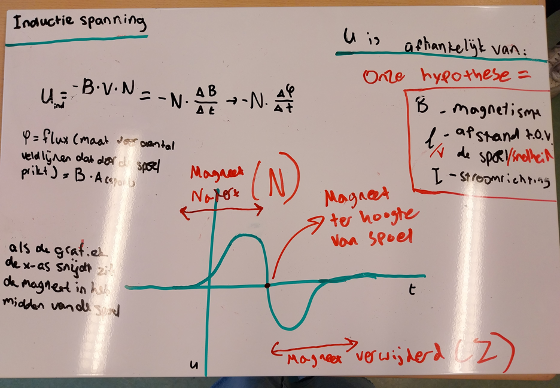

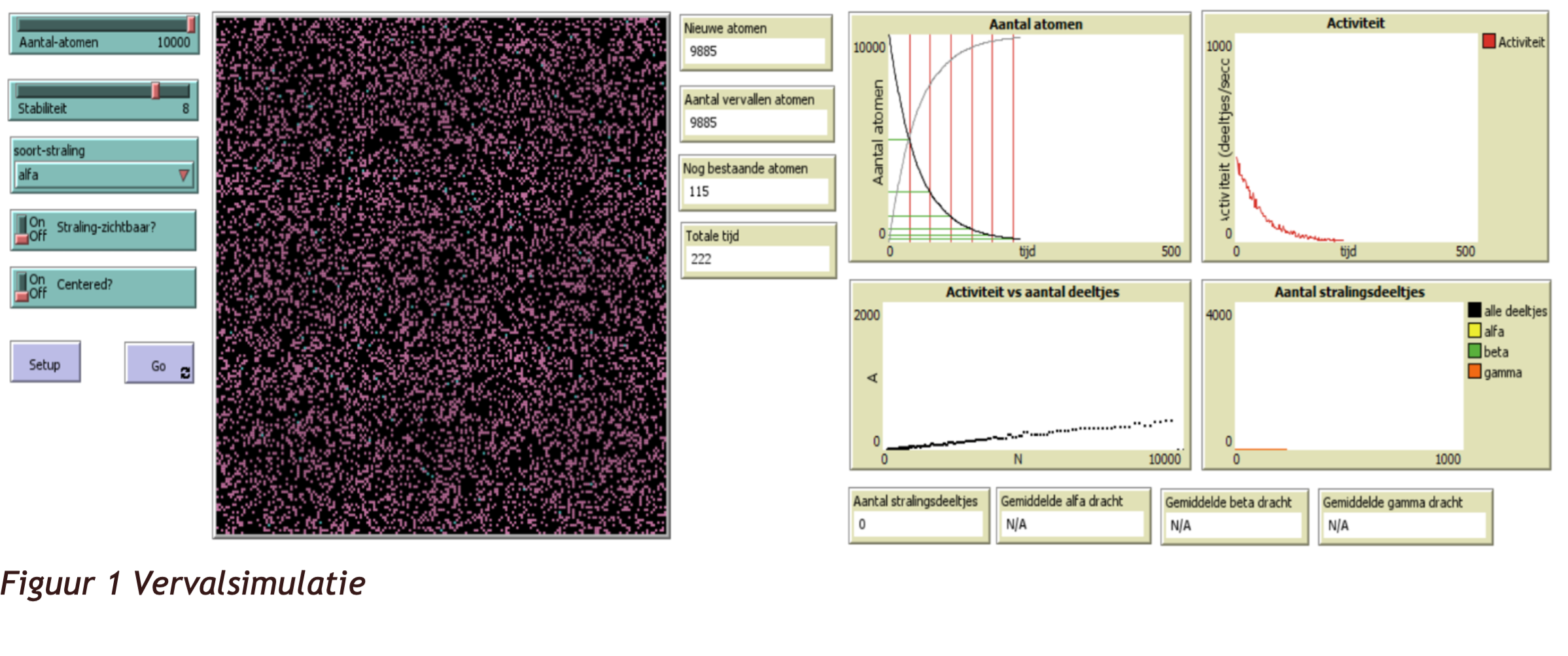
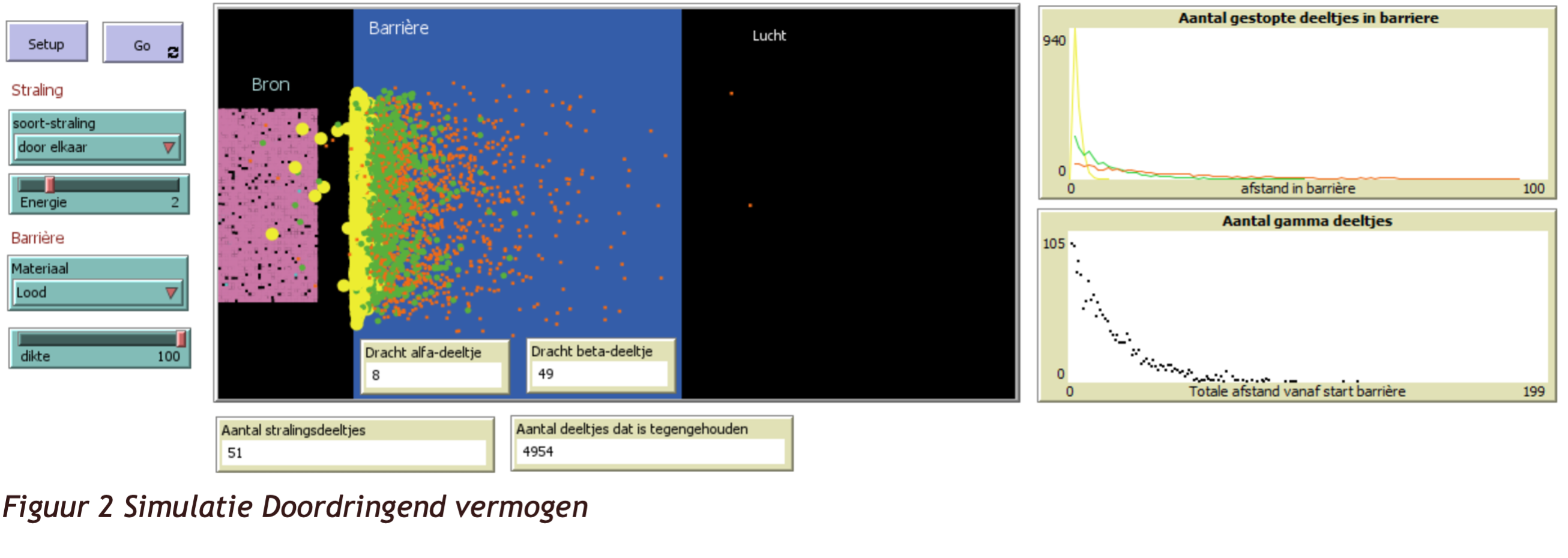


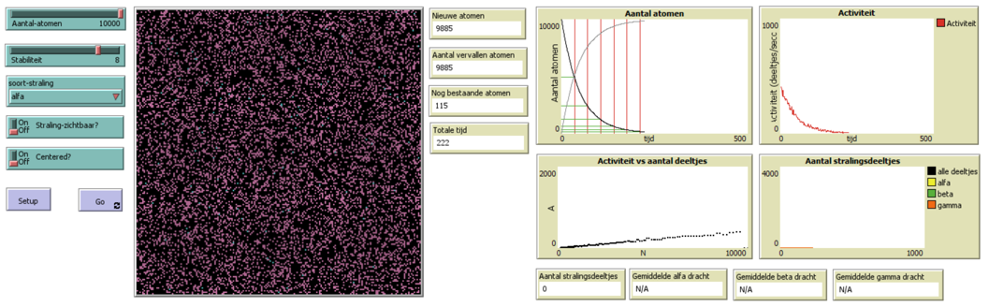


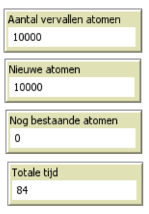 Naast het vierkante vlak staan 4 monitoren (figuur 5) die real-time weergeven wat de waarde is van verschillende variabelen (aantal vervallen atomen, aantal nieuwe atomen (de roze), nog bestaande atomen (de blauwe) en de tijd die is verstreken (in simulatiecycli). Rechts van deze monitoren staan vier diagrammen (figuur 6) die ontstaan tijdens de simulatie. Elk moment kan de simulatie stop gezet worden door op de Go knop te klikken. De diagrammen en monitoren kunnen dan afgelezen worden. Het linker boven paneel geeft het N(t)-diagram voor moederkernen en dochterkernen, het rechter boven paneel het A(t) diagram, links onder het A(N) diagram en rechts onder het aantal stralingsdeeltjes (de grafiek is alleen zichtbaar als de straling zichtbaar is, de deeltjes hebben een levensduur (afhankelijk van de dracht/doordringend vermogen)). Op t=0 s zijn er geen deeltjes, omdat het verval nog moet beginnen.
Naast het vierkante vlak staan 4 monitoren (figuur 5) die real-time weergeven wat de waarde is van verschillende variabelen (aantal vervallen atomen, aantal nieuwe atomen (de roze), nog bestaande atomen (de blauwe) en de tijd die is verstreken (in simulatiecycli). Rechts van deze monitoren staan vier diagrammen (figuur 6) die ontstaan tijdens de simulatie. Elk moment kan de simulatie stop gezet worden door op de Go knop te klikken. De diagrammen en monitoren kunnen dan afgelezen worden. Het linker boven paneel geeft het N(t)-diagram voor moederkernen en dochterkernen, het rechter boven paneel het A(t) diagram, links onder het A(N) diagram en rechts onder het aantal stralingsdeeltjes (de grafiek is alleen zichtbaar als de straling zichtbaar is, de deeltjes hebben een levensduur (afhankelijk van de dracht/doordringend vermogen)). Op t=0 s zijn er geen deeltjes, omdat het verval nog moet beginnen.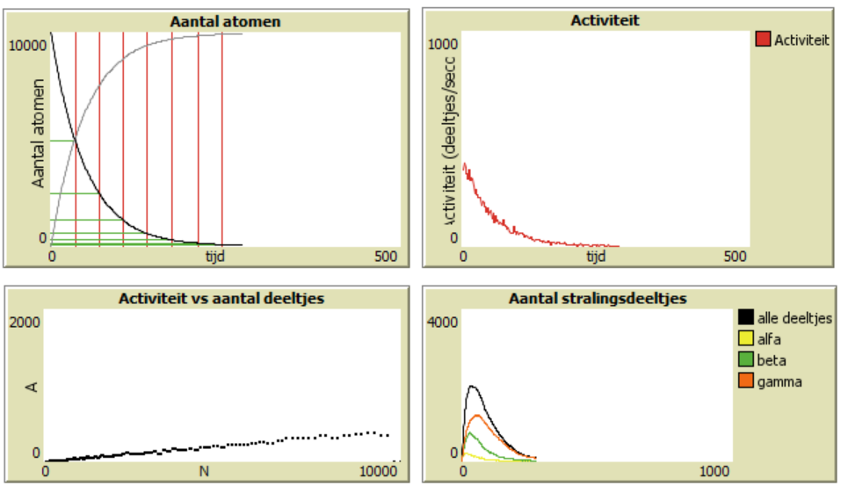

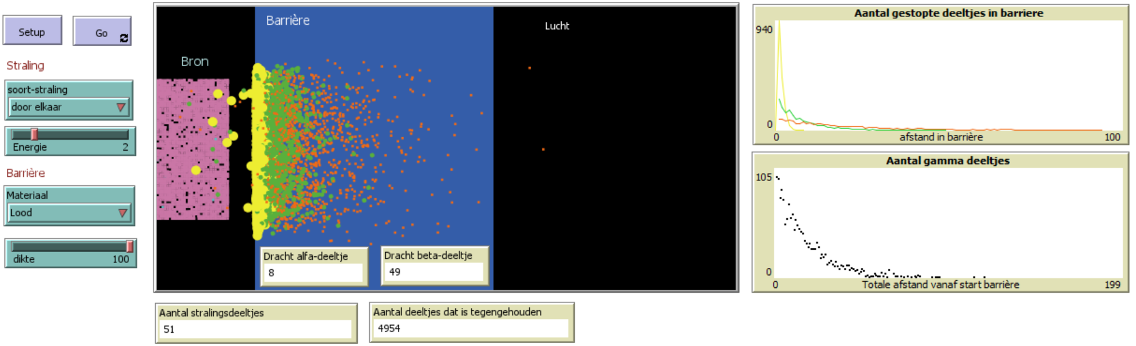

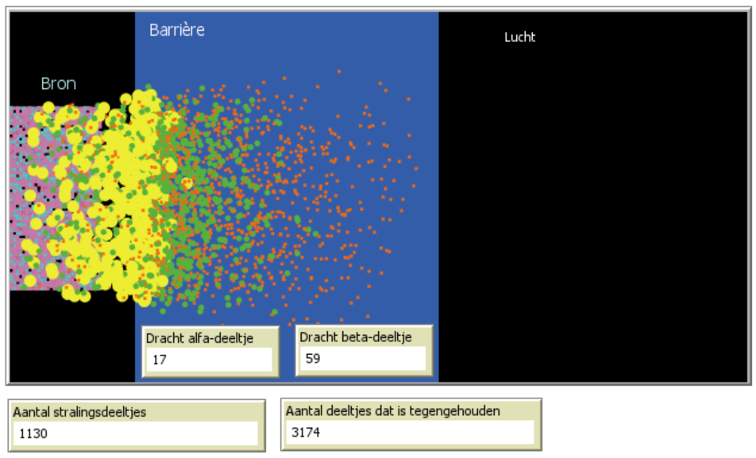

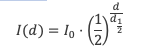

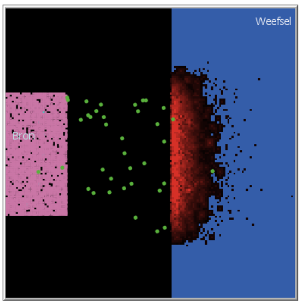
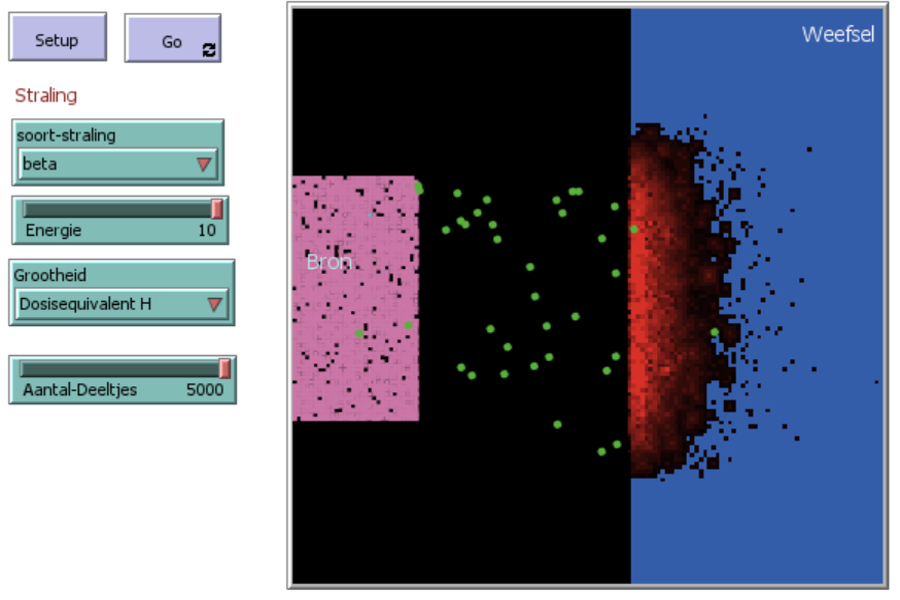
 Het programma initialiseer je met Setup en laat je lopen met Go. Het linker paneel geeft de mogelijkheid om de simulatie in te stellen. Er kan gekozen worden tussen de verschillende soorten straling α, β, en γ. De energie van de deeltjes kan worden aangepast tussen 1 en 10 (kwalitatief, geen eenheden). De verkleuring in het weefsel kan een maat zijn voor dosisequivalent of de dosis. Als laatste kan het aantal deeltjes dat uitgezonden wordt, worden aangepast.
Het programma initialiseer je met Setup en laat je lopen met Go. Het linker paneel geeft de mogelijkheid om de simulatie in te stellen. Er kan gekozen worden tussen de verschillende soorten straling α, β, en γ. De energie van de deeltjes kan worden aangepast tussen 1 en 10 (kwalitatief, geen eenheden). De verkleuring in het weefsel kan een maat zijn voor dosisequivalent of de dosis. Als laatste kan het aantal deeltjes dat uitgezonden wordt, worden aangepast.


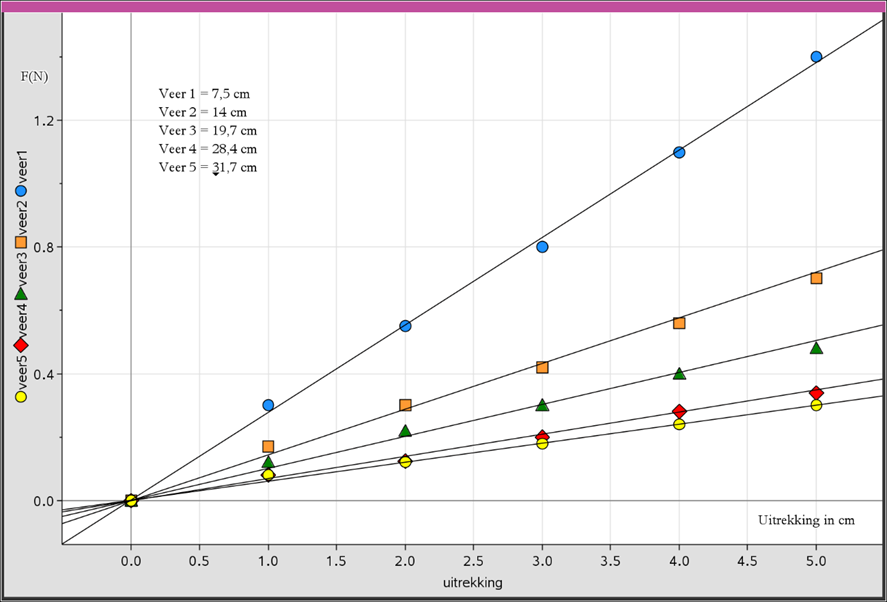
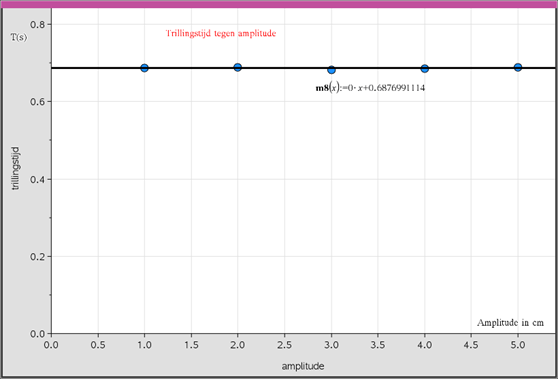
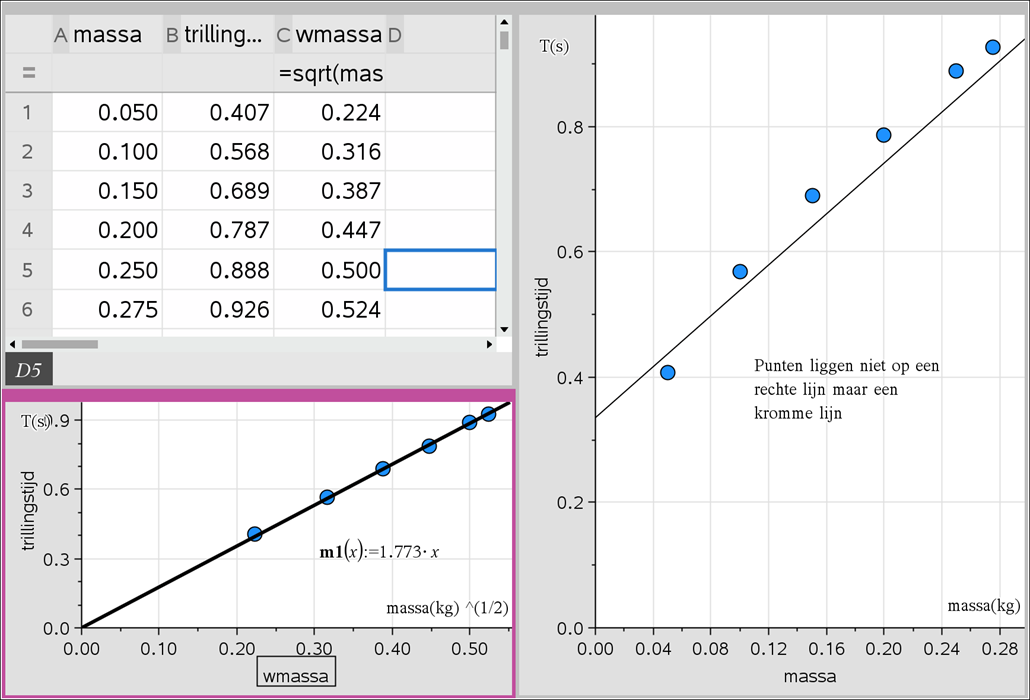
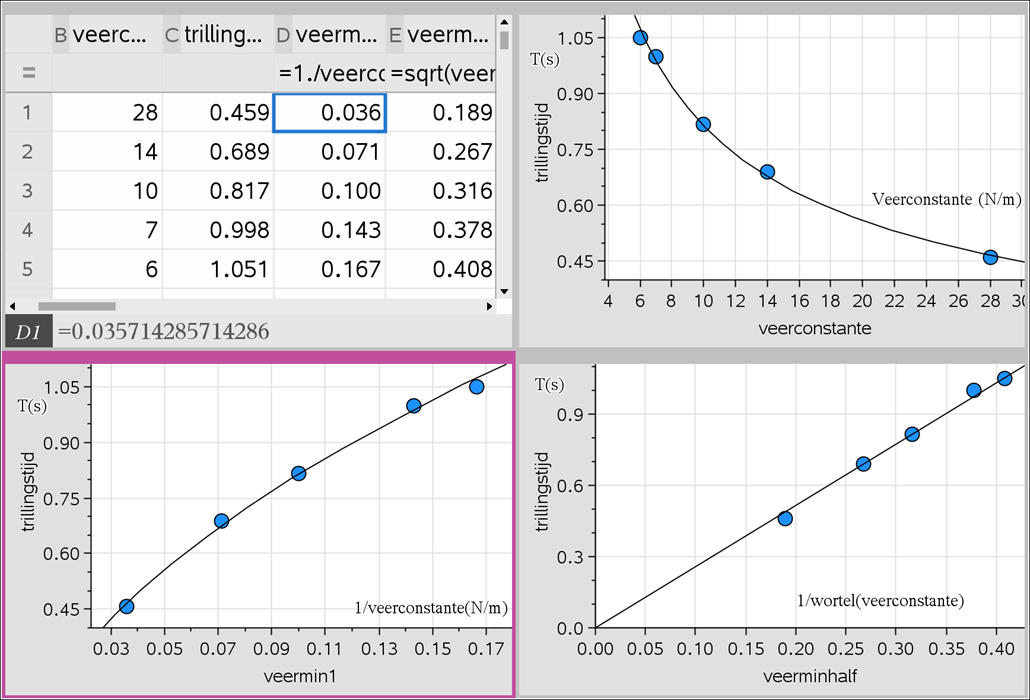
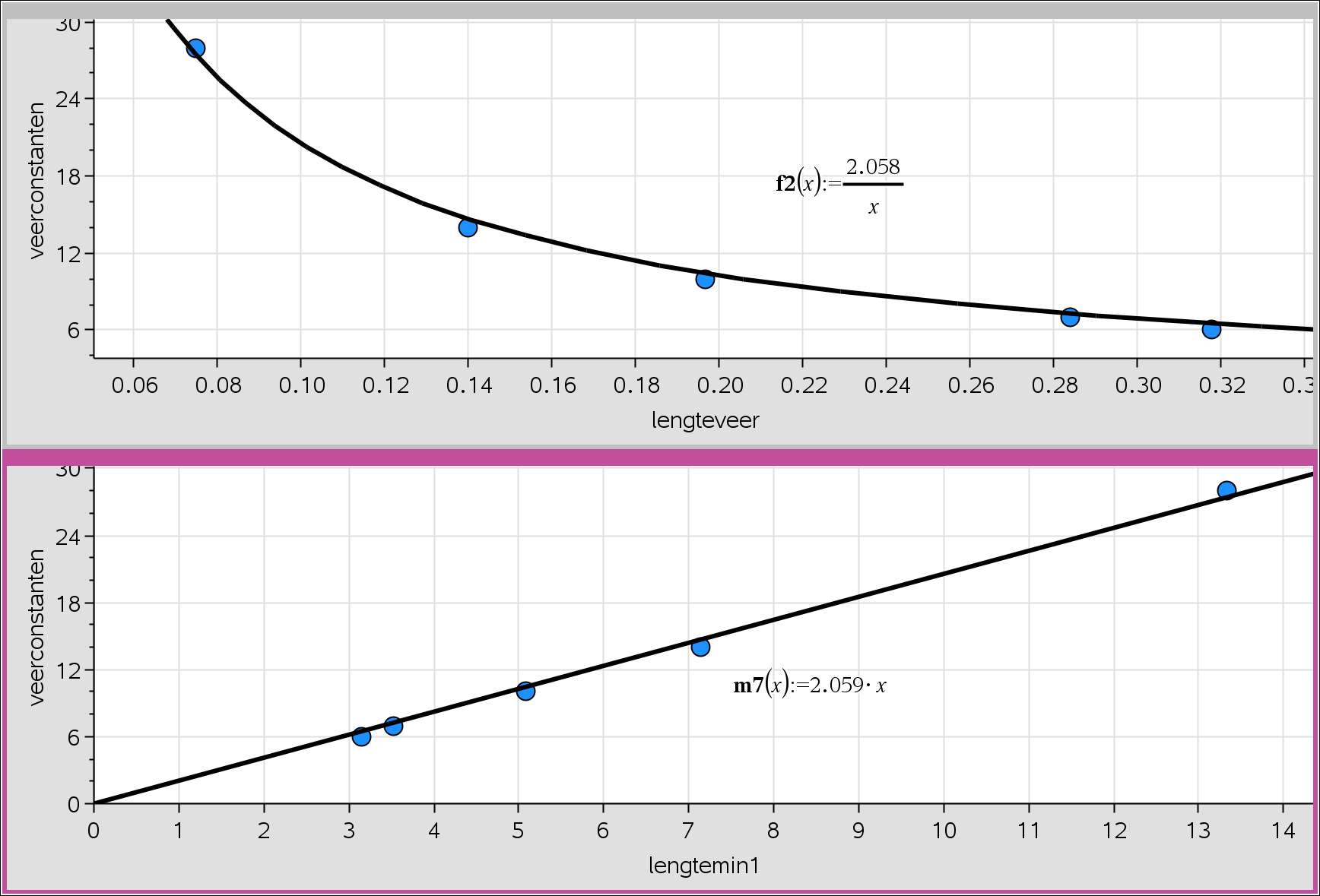
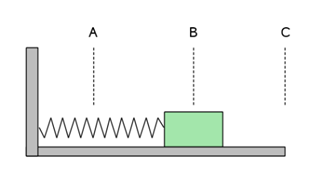
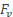
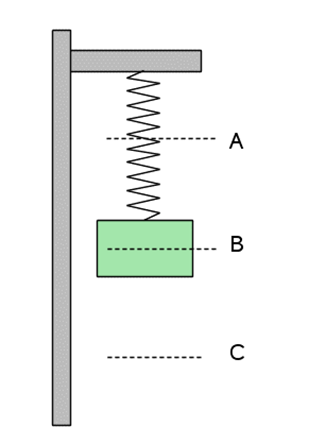



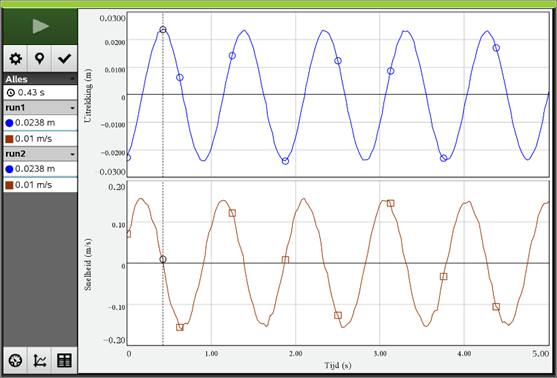
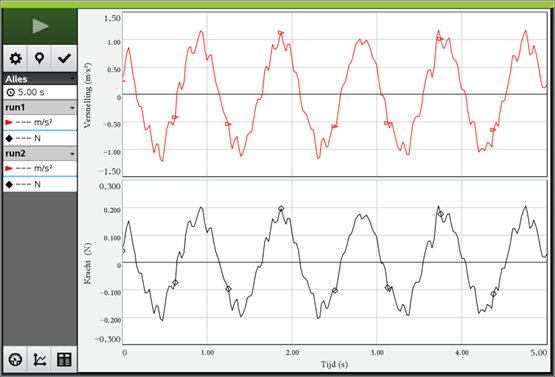
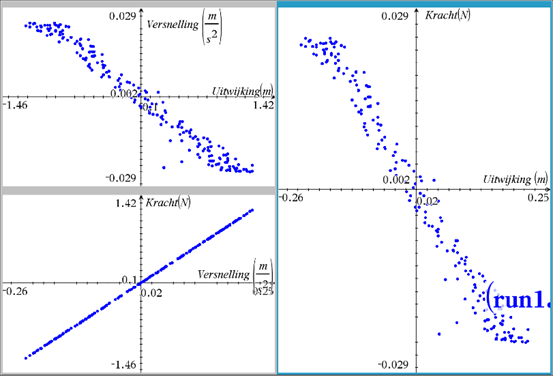
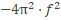
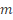
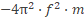
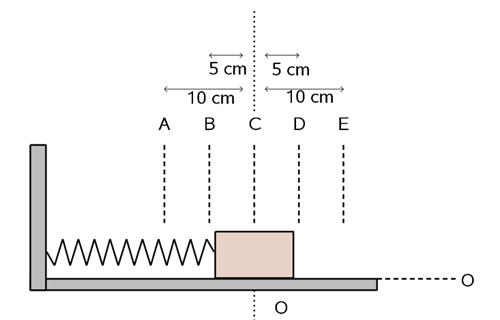

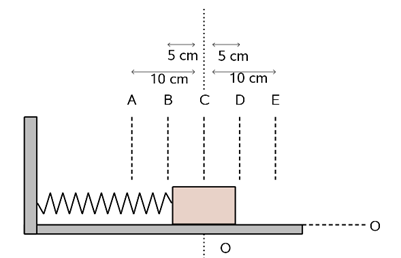

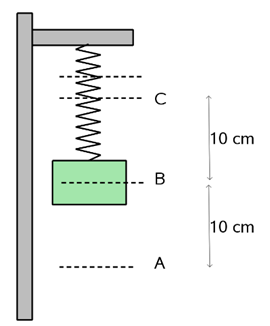









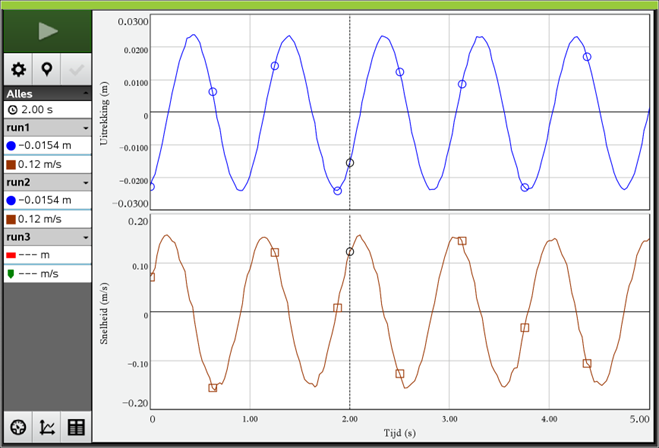
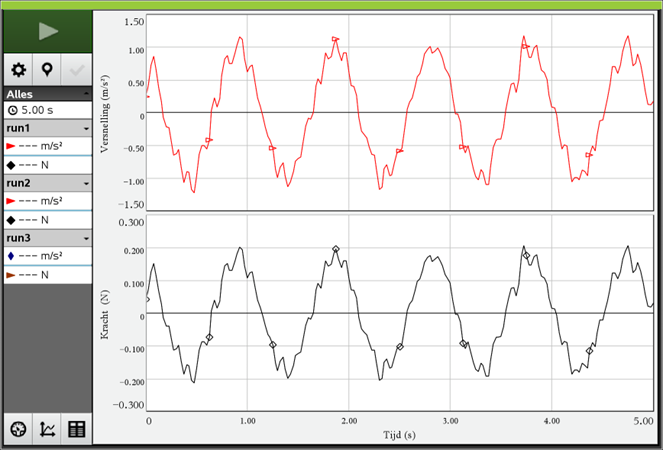

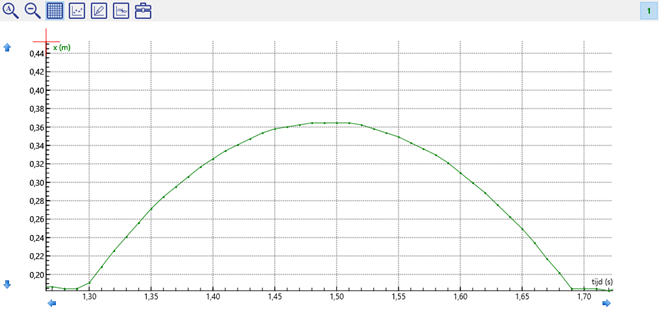
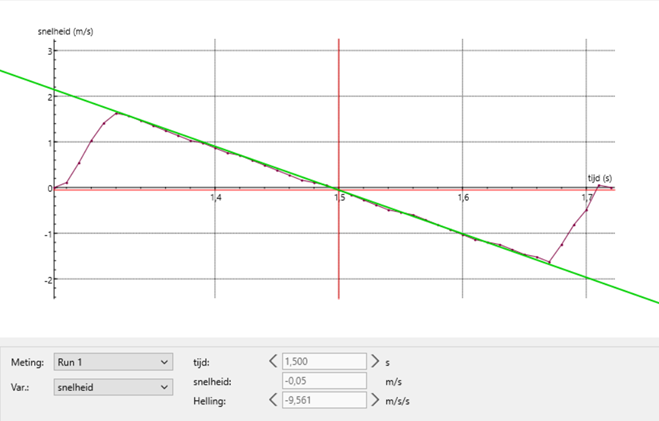
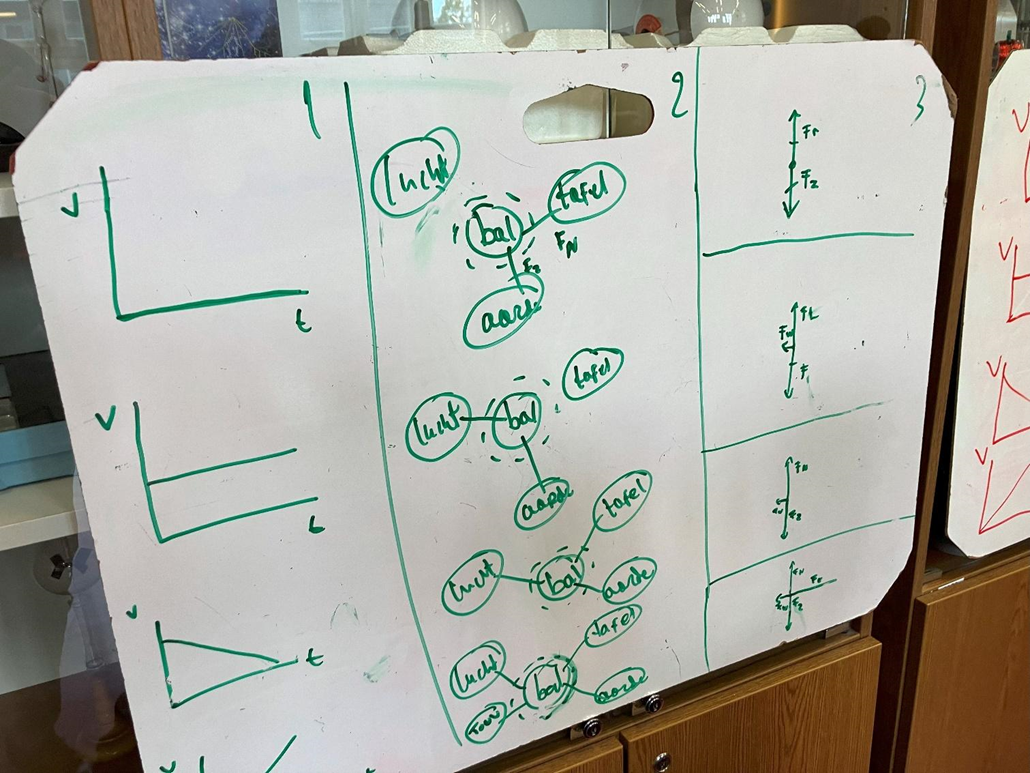
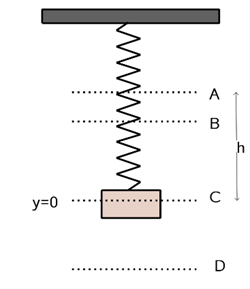
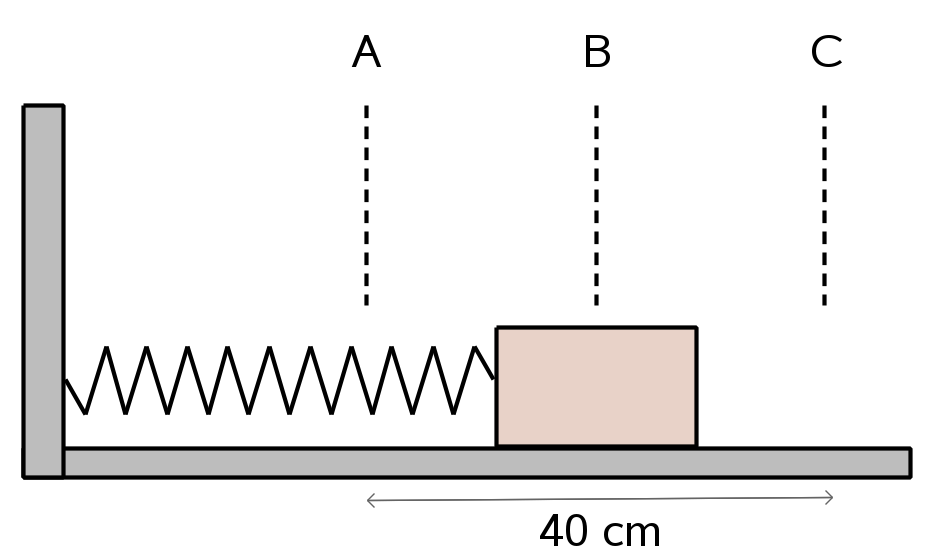
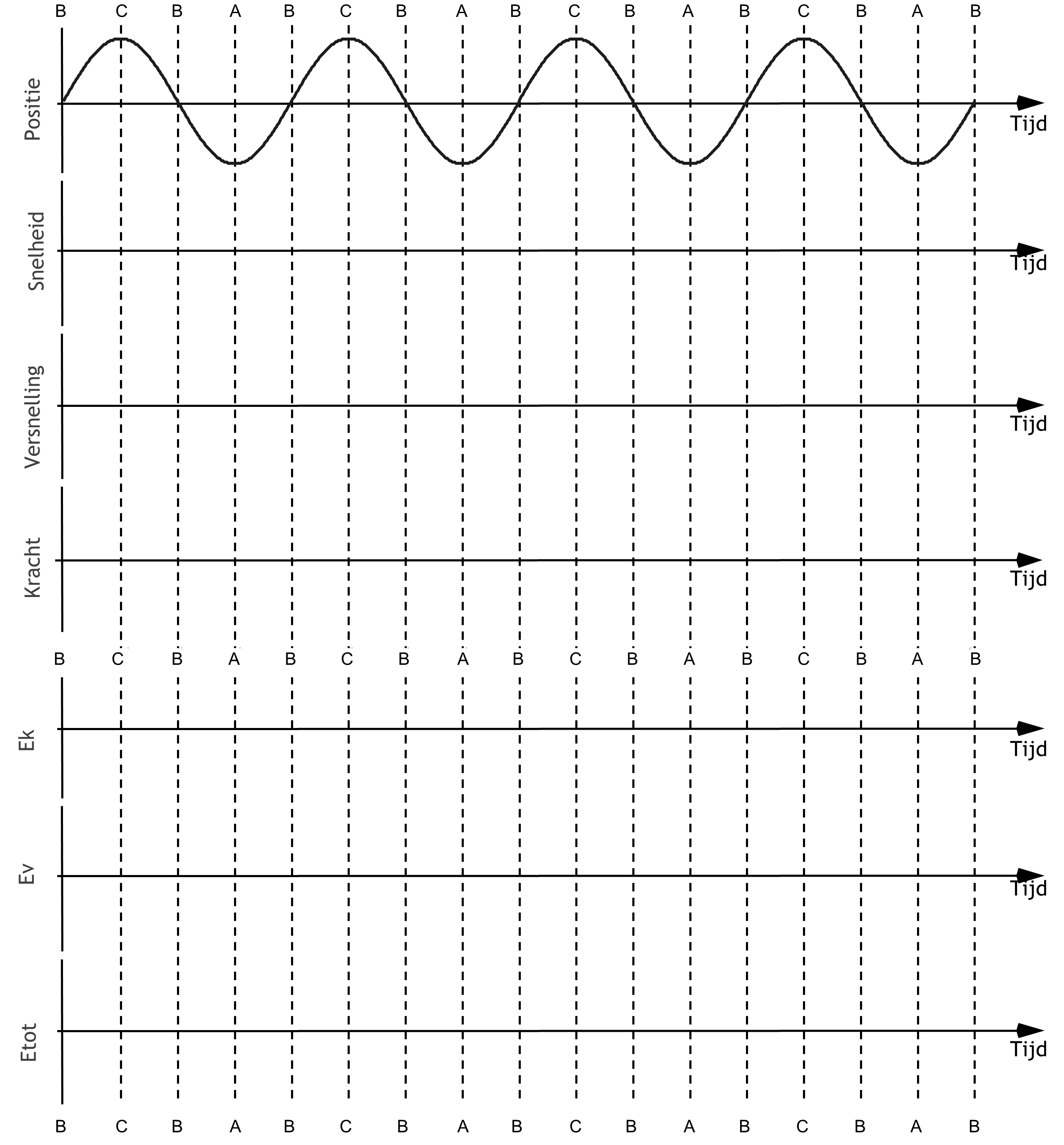
 In het figuur hiernaast zie je een massa aan een veer. Als er geen massa aanhangt dan komt de veer tot A. Met de massa er aan komt de veer in rust tot C. Hij rekt dan h uit. De veer oscilleert tussen B en D.
In het figuur hiernaast zie je een massa aan een veer. Als er geen massa aanhangt dan komt de veer tot A. Met de massa er aan komt de veer in rust tot C. Hij rekt dan h uit. De veer oscilleert tussen B en D.



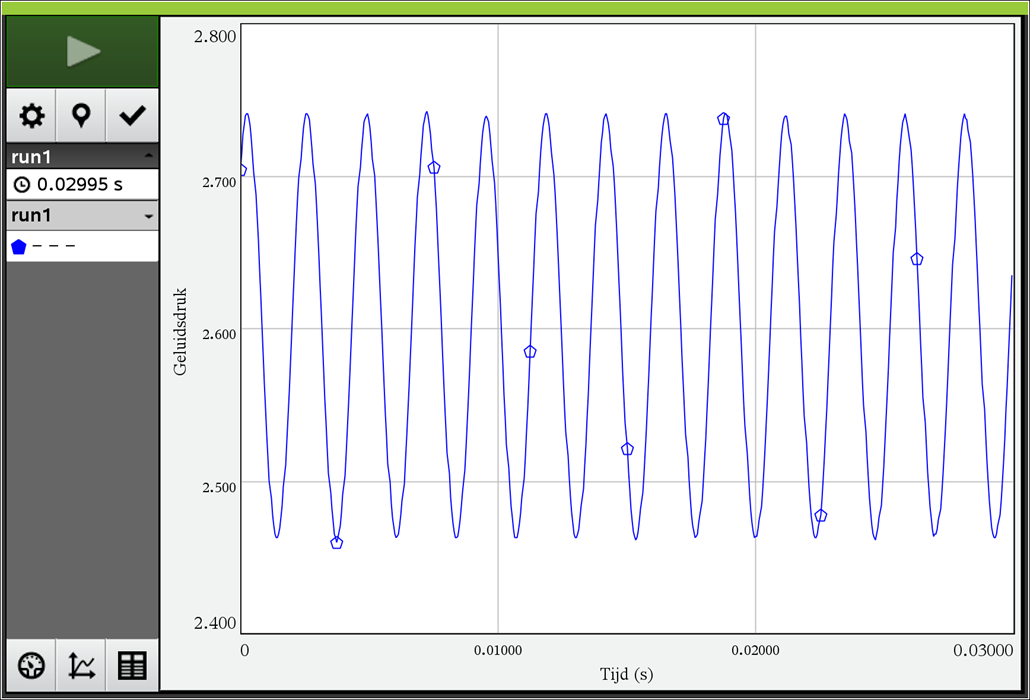
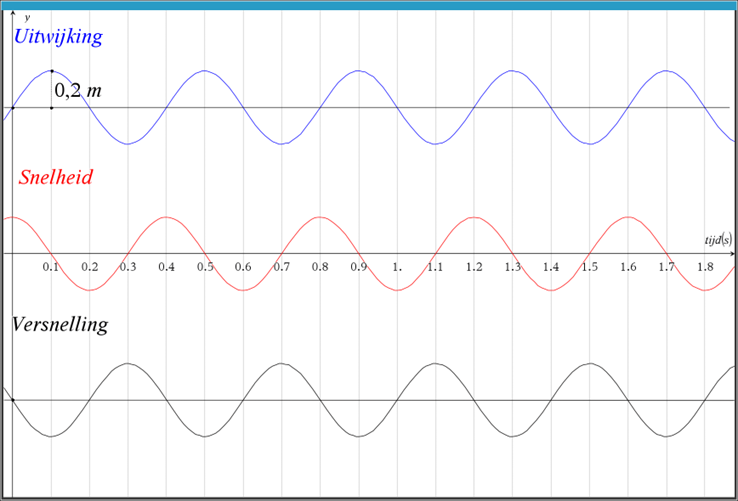




 Verschillende golflengte
Verschillende golflengte


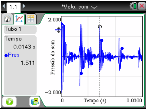

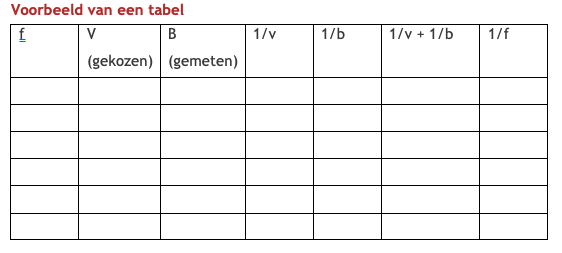
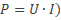
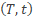
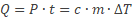
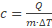
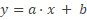
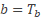
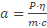
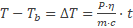
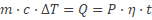
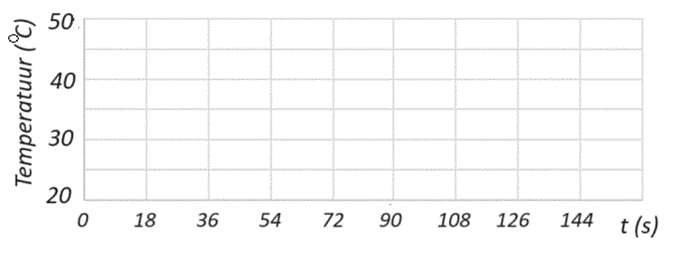
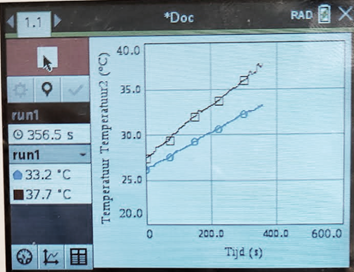
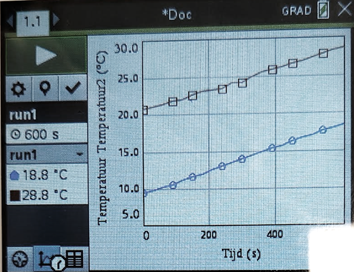
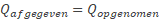
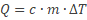
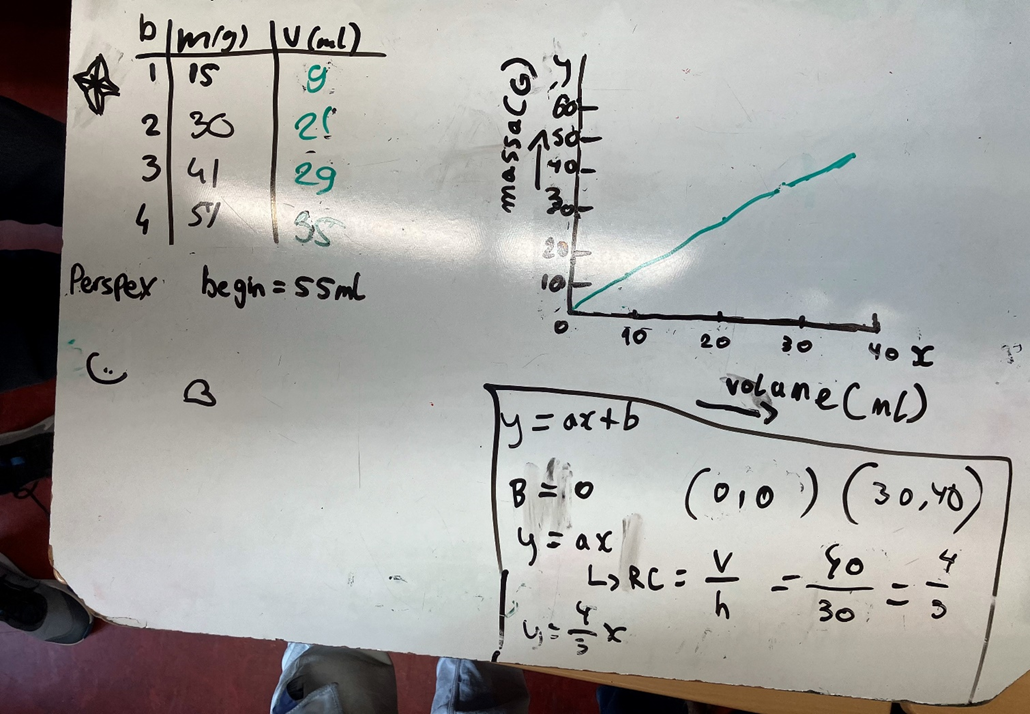
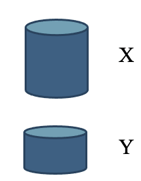 Noteer dichtheid als verhouding:
Noteer dichtheid als verhouding: