In deze paragraaf leer je hoe je het nieuwe bedrag berekent die hoort bij een gegeven percentage.
Voorbeeld:
We willen berekenen hoeveel 12% van 130 is. 130 is het totaal dus 100%. Om 12% hiervan te berekenen is het handig om eerst naar 1% te rekenen. Dit doe je door 130 te delen door 100. Hier komt 1,30 uit. Dus 1,30 is 1% van 130. Om nu naar 12% te rekenen doen we 1,30 vermenigvuldigen met 12. Hier komt 15,6 uit. Dus 15,6 is 12% van 130.
De berekening is dan als volgt:
130 : 100 = 1,30 (1%)
1,30 x 12 = 15,6 (12%)
Deze berekening is heel duidelijk weer te geven in een tabel:
Extra instructievideo percentage gegeven:
Opdrachten:
1. Reken uit
a 6% van 150
b 12% van 150
c 25% van 150
d 45% van 150
2. Reken uit
a 17% van 300
b 17% van 450
c 17% van 750
d 17% van 900
3. Een boekhandelaar verkoopt per week 1800 boeken. 20% van deze boeken zijn thrillers. Hoeveel thrillers verkoopt de boekhandelaar per week?
4. Op het Wellandcollege zitten 1250 leerlingen. 54% van deze leerlingen komt met de fiets naar school.
Hoeveel leerlingen zijn dat?
BTW
BTW (Belasting Toegevoegde Waarde) wordt berekend op alles dat je koopt. Voor eerste levensbehoeften is het percentage 6%, voor luxebehoeften is het
percentage 21% (vroeger 19% dus dat kom je nog vaak tegen in opgaven).
De prijs exclusief BTW is de basis; dit is altijd 100%. De BTW is een percentage van de basis en wordt daarbij opgeteld. De prijs inclusief BTW is dus altijd meer
dan 100% (106%, 119% of 121%, afhankelijk van de opgave).
In een formule:
prijs exclusief BTW + BTW = prijs inclusief BTW
5. De flessen Coca cola zijn in de aanbieding: een sixpack kost nu €2,10 exclusief 6% BTW. Bereken het bedrag aan BTW.
6. Je koopt voor je vriendin bij de Makro een flesje parfum voor haar verjaardag. De prijs exclusief 21% BTW is €14,91. Hoeveel betaal je voor inclusief BTW?
7. Je belt 10 minuten met je oma die in Spanje aan het overwinteren is. Een minuut bellen kost je €0,27 exclusief 21% BTW. Hoeveel kost het hele telefoontje?
8. Je koopt een boek bij de Bruna voor €15 exclusief 21% BTW. Bereken het bedrag aan BTW.
9. Je kat heeft honger dus ga je naar de supermarkt voor een kilo Whiskas. Dat kost je €2,69 exclusief 6% BTW. Bereken hoeveel de prijs inclusief BTW is.
Toets Percentage gegeven Je sluit de paragraaf percentage gegeven af met een toets.
Na het maken van de vragen krijg je een score en kun je de gegeven antwoorden vergelijken met de goede antwoorden.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
In deze paragraaf leer je welk percentage bij een bepaald getal hoort.
Voorbeeld;
23 van de 56 auto's zijn wit. Hoeveel % is dit?
56 auto's is 100%. Hoeveel % is dan 1 auto? 100 : 56 = 1,7857 %
Hoeveel % is dan 23 auto's? 1,7857 x 23 = 41%.
Instructievideo:
Opdrachten:
1. In klas 3B zitten 28 leerlingen. Voor een proefwerk wiskunde hadden 8 leerlingen een onvoldoende. Hoeveel procent van de leerlingen had een onvoldoende? Rond je antwoord af op twee cijfers achter de komma.
2. Isabel heeft € 120,− voor haar verjaardag gekregen. Van dat geld koopt ze een nieuwe broek van € 75,−. De rest van het geld zet ze op haar spaarrekening. Hoeveel procent van het geld zet ze op de spaarrekening?
3. In klas 1q1 zitten 25 leerlingen. Er komen 15 leerlingen op de fiets naar school. Hoeveel procent is dat?
4. Hoeveel procent is:
a 10 van 300
b 30 van 300
c 60 van 300
d 200 van 300
5. Hoeveel procent is:
a 15 van 200?
b 7 van 12?
c 5,2 van 21?
d 8,6 van 20?
6. KLM heeft in totaal 285 vliegtuigen. Daarvan zijn er vier van het type 'Airbus A380'. Hoeveel procent is dat?
7. Jan heeft € 265 op zijn rekening staan. Hij krijgt € 7,40 rente. Hoeveel procent is dat?
1.3 Van deel naar geheel
In deze paragraaf ga je vanuit een bepaald percentage werken naar 100%. Van deel naar geheel noemen we dat.
Instructievideo:
Naast de twee manieren, om het geheel (totaal) te bereken die in de instructievideo staan, is er nog een derde manier. Dit gaat weer met behulp van de verhoudingstabel:
BV. 18% van de leerlingen moet een herexamen maken. Dit zijn 164800 leerlingen. Hoeveel leerlingen hebben examen gemaakt?
In de tabel rekenen we eerst naar 1 procent en daarna naar 100 procent. We delen door 18 om naar 1 procent toe te gaan. Daarna doen we keer 100 om naar 100 procent toe te gaan. Zo weten we het totaal aantal leerlingen dat op het voortgezet onderwijs zat.
Opgaven:
1. Bij deze fabriek werken 42 vrouwen. Dat is 30% van het personeel.
Hoeveel mensen werken er totaal bij deze fabriek?
2. Peter vertelt dat hij 275 euro per week verdient omdat hij 10% loonsverhoging heeft gekregen. Hoeveel verdiende hij
vóór de loonsverhoging?
3. Reken om naar 100%:
a 24% is 214
b 18% is 5,8
c 212% is 200
d 114% is 36,8
4. Op een school is voor het eindexamen een gemiddeld slagingspercentage van 96% behaald. 188 leerlingen zijn geslaagd. Hoeveel leerlingen hebben er in totaal eindexamen gedaan?
5. 28% van de jongens tussen de 13 en 18 jaar doet aan voetbal. Dit zijn 110.000 jongens. Hoeveel jongens zijn er tussen de 13 en 18 jaar?
6. Reken om naar 100%.
a. 33% is 233.
b. 91% is 321.
c. 105% is 23.
d. 0,5% is 2,3.
e. 134% is 269.
7. Jojanne verdient nu 2114,95 euro na een loonsverhoging van 3,5%.Hoeveel verdiende ze voor haar loonsverhoging?
8. Koen verdient nu 1960,90 euro. Hij is minder gaan werken. Hij heeft 5,4% van zijn loon ingeleverd. Wat was zijn loon voordat hij minder ging werken?
1.4 Promille
In deze paragraaf gaan we uitleggen wat promille is en hoe je er mee moet rekenen.
Je hebt eerder gerekend met procenten. Procent betekent letterlijk "per honderd". Promille betekent letterlijk "per duizend".
1 promille is een duizendste deel en geven we aan met het symbool ‰.
5 promille geven we aan als 5‰.
12 promille geven we aan als 12‰.
Voorbeelden:
Enkele voorbeelden met promillen:
- hoeveel promille is 3 van 8?
3 : 8 = 0,375, in promillen is dat dan: 0,375 x 1000‰ = 375‰
- hoeveel promille is 0,2 van 212?
0,2 : 212 = 0,000943, in promillen is dat: 0,000943 x 1000‰ = 0,943‰
- wat is 10‰ van 250?
250 : 1000 = 0,25 (1‰)
0,25 x 10 = 2,5 (10‰)
- wat is 18‰ van 75?
75 : 1000 = 0,075 (1‰)
0,075 x 18 = 1,35 (18‰)
Opdrachten:
1. Reken uit:
a 5‰ van 300
b 12‰ van 120
c 7,5‰ van 28,8
d 20‰ van 20,5
2. Hoeveel promille is:
a 1 van 300
b 3 van 300
c 6 van 300
d 20 van 300
3. Bart heeft thuis 25000 boeken in de kast staan. Hij heeft 120 boeken gelezen. Hoeveel promille is dit? Rond af op 1 decimaal.
4. Gijs drinkt 150 glazen frisdrank per maand. Hiervan zijn 7 glazen cola. Hoeveel promille is dit?
1.5 Exponentiële toename en afname
Om een procentuele toename of afname uit te rekenen, kun je werken
met de groeifactor. Het getal waarmee je de beginhoeveelheid moet
vermenigvuldigen om de nieuwe hoeveelheid te krijgen, noem je de groeifactor.
Instructievideo groeifactor:
Instructievideo formule opstellen en gebruiken:
Algemene formule:
Uitkomst = begingetal x groeifactor tijd
Voorbeeld
Je hebt een spaarrekening met daarop een bedrag van € 400,-.
Je krijgt 5% rente per jaar.
Hoe bereken je hoeveel geld er na één jaar op de rekening staat?
Hoe bereken je hoeveel geld er na twee, drie en vijf jaar op de rekening staat?
bedrag na 2 jaar: € 400,- x 1,052 = € 441,-
bedrag na 3 jaar: € 400,- x 1,053 = € 463,-
bedrag na 5 jaar: € 400,- x 1,055 = € 511,-
Voorbeelden
Een bedrag neemt jaarlijks met 25% toe.
100% + 25% = 125%. De groeifactor is 125/100 = 1,25
Een bedrag neemt jaarlijks met 5% af.
100% – 5% = 95%. De groeifactor is 95/100 = 0,95
Een bedrag groeit met een groeifactor van 1,04.
1,04 = 104% = 100% + 4%.
Het bedrag groeit met 4%
Een bedrag slinkt met een groeifactor van 0,7.
0,7 = 70% = 100% – 30%.
Het bedrag slinkt met 30% (of groeit met -30%)
Opgaven:
1. Je hebt een spaarrekening met daarop een bedrag van € 500,−. Je krijgt 3%rente per jaar.
a. Welke groeifactor hoort bij een jaarlijkse rente van 3%?
b. Bereken het bedrag dat je na één jaar op je rekening hebt staan.
c. Bereken ook het bedrag dat er na twee jaar op je rekening staat.
2. Hoe groot is de groeifactor in de volgende situaties.
a. De prijzen stijgen jaarlijks met 12%.
b. Je hebt een lekke band. Iedere minuut stroomt er 10% van de lucht uit je band.
c. Het aantal vogels in dat gebied neemt ieder jaar met 8% toe.
d. De hoeveelheid zeehonden in de Noordzee daalt jaarlijks met 12%.
3. Welke procentuele verandering hoort bij de volgende situaties.
a. Een bedrag groeit met een groeifactor van 1,06.
b. Bij de jaarlijkse afname van de winst hoort een groeifactor van 0,8.
4. Om een patiënt voor een operatie onder narcose te brengen, wordt 800 mg van een narcosemiddel in het bloed toegediend. De hoeveelheid narcosemiddel neemt per uur 30% af.
a. Welke groeifactor hoort bij afname van 30% per uur?
b. Hoeveel narcosemiddel zit er na 1 uur nog in het bloed?
c. Bereken ook de hoeveelheid narcosemiddel in het bloed na 2 uur.
d. Als de hoeveelheid narcosemiddel in het bloed minder dan 150 mg is, spreek je niet langer van een narcose.
Zoek eens na hoeveel uur de hoeveelheid narcosemiddel in het bloed minder dan 150 mg is.
5. In een bepaald gebied neemt het aantal vogels jaarlijks met 15% toe. Op 1 mei 2012 zijn er 5000 vogels in het gebied geteld.
a. Welke groeifactor hoort bij jaarlijkse groei van 15%?
b. Hoeveel vogels waren op 1 mei 2013 in het gebied aanwezig?
c. En hoeveel vogels op 1 mei 2014?
d. In welk jaar zijn er voor het eerst meer dan 10000 vogels in het gebied?
6. De druk in een fietsband is 4 bar. Je hebt een lekke band waardoor er lucht uit je band stroomt. Per minuut neemt de druk met 10% af.
a. Welke groeifactor hoort bij afname van de druk per minuut met 10%?
b. Bereken de druk nadat de band 1 minuut lek is.
c. Bereken ook de druk nadat de band 2 minuten lek is.
d. Als de druk in je band lager dan 2 bar is, is fietsen op de leeg lopende band eigenlijk niet meer mogelijk.
Zoek eens na hoeveel minuten de druk voor het eerst lager dan 2 bar is.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
a. Bij een groothandel kost een flesje parfum 21,95 exclusief 21% btw. Bereken de prijs inclusief btw.
b. In de winkel kost een fles exclusieve shampoo 14,50 inclusief 21% btw. Bereken de prijs exclusief btw?
3.
a. Bij welke fiets krijg je de grootste korting in euro's?
b. Bij welke fiets krijg je de grootste korting in %?
4. Schrijf met alleen cijfers:
a. 7,4 miljard
b. 307,5 miljoen
5. In 2015 was het tekort van de overheid 2,6% van 251,6 miljard euro. Hoeveel euro is het tekort in 2015? Schrijf je antwoord in cijfers.
6. De bevolkingsomvang van Luxemburg zal tussen 2016 en 2051 toenemen met 0,3 miljoen. Dat is een stijging van 35,4%. Bereken de bevolkingsomvang van Luxemburg in 2016.
7. De prijs van een opel is verhoogd met 3,4%. Dat is een prijsverhoging van 554 euro. Bereken de prijs voor de prijsverhoging.
8. In 2006 waren er 19657000 koeien in Nederland. In 2007 is dat aantal gestegen tot 21899000.
Hoeveel promille is deze stijging?
9. Jo opent een spaarrekening. Zij zet daar 550,00 euro op. De bank geeft 2,3% rente.
a. Wat staat er na 8 jaar op haar rekening?
b. Wat staat er na 15 jaar op haar rekening?
10. Jeggen heeft 6534 inwoners. Men verwacht elk jaar een daling van 2,1%. Hoeveel inwoners verwacht men dan na 10 jaar?
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
In deze paragraaf ga je leren wat koers is en hoe je een koers kan bepalen. Verder ga je rekenen met schaal.
Windroos:
Opgaven
1. a Maak in je schrift een windroos met daarin de richtingen: N, O, Z, W, NO, ZO, NW, ZW, WZW, WNW,
ONO, OZO, NNO, NNW, ZZO, ZZW.
b Zet de koersen in graden bij de windrichtingen.
2. a De wind komt vanuit ZO. Welke richting blaast de wind op?
b De wind komt vanuit NNO. Welke richting blaast de wind op?
3. a Welke koers hoort bij windrichting Oosten?
b Welke koers hoort bij windrichting WNW?
4. Hieronder staat de kaart van Noord-Brabant. Wat is de koers in graden van Eindhoven naar Breda.
Verder ga je in deze paragraaf werken met een schaallijn. Je leert waarom er bij kaarten vaak een schaallijn staat en je leert hoe je met zo'n schaallijn de werkelijke afstand kunt bepalen. Bij de opgaven hoort een werkblad. Deze krijg je van de docent.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Hoogtelijnen zijn lijnen die de hoogteverschillen aangeven. Van bijvoorbeeld een berg kan een hoogtekaart gemaakt worden. Hierop staan de hoogtelijnen weergegeven.
Hieronder zie je een berg met daarnaast de hoogtelijnen weergegeven.
Opgaven
1. Hieronder zie je een hoogtekaart.
a Op welke hoogte ligt punt A?
b Op welke hoogte ligt punt Z?
c Op welke hoogte ligt punt P?
d Op welke hoogte ligt punt Q?
eOp welke hoogte ligt punt C?
Als je een bepaalde route volgt op een hoogtekaart, dan kan je daar een verticale doorsnede van maken.
Video construeren verticale doorsnede:
Hieronder staat nog een voorbeeld van een verticale doorsnede:
2 Maak bij alle drie de hoogtekaarten op het werkblad de verticale doorsnede.
Van een ruimtelijk figuur kun je soms meer te weten
komen als je het figuur doorsnijdt.
Het vlak waarlangs je snijdt, noem je de doorsnede.
Doorsneden van dezelfde ruimtelijke figuur kunnen heel verschillend zijn.
De vorm van de doorsnede zie je als je recht op het snijvlak kijkt.
Van bijvoorbeeld een cilinder kun je verschillende doorsneden maken.
Pythagoras
Bekijk balk ABCD·EFGH met AB = 6, BC = 3 en CG = 4.
Bereken de lengte van lijnstuk BH.
Lijnstuk BH ligt in het vlak ABGH.
Vlak ABGH is een diagonaalvlak.
Bereken nu eerst BG.
Je vindt:
Vlak BGHA is een rechthoek van 6 bij 5.
Bereken BH met de stelling van Pythagoras.
Je vindt:
Video Pythagoras schuine zijde berekenen:
Video Pythagoras rechthoekzijde berekenen:
Opgaven
1 Een ruimtelijk figuur kun je op verschillende manieren doorsnijden.
Het snijvlak dat je krijgt noem je de doorsnede.
Een cilinder wordt op drie verschillende manieren doorgesneden.
Teken van iedere cilinder het snijvlak.
2 Je ziet hieronder balk ABCD·EFGH getekend. Op de ribben liggen de punten P, Q, R en S.
Er geldt PB = QC en ER = HS. De rechthoek wordt doorgesneden langs vlak PQRS. Teken de doorsnede.
Wat voor soort vierhoek is de doorsnede?
3 Je ziet hieronder opnieuw balk ABCD·EFGH getekend. Op ribben liggen de punten P, Q en R.
Er geldt BP = BQ = BR. De rechthoek wordt doorgesneden langs vlak PQR. Teken de doorsnede.
Wat voor soort driehoek is de doorsnede?
4 Je ziet hieronder piramide ABCD·T getekend. Het ondervlak is een vierkant met zijden 4 cm. De opstaande
ribben zijn allemaal 5 cm lang.
a In het grondvlak is de diagonaal AC getekend. De lengte van deze diagonaal is √32 ≈5,66. Leg uit hoe je deze
lengte kunt berekenen.
b De piramide wordt doorgesneden langs vlak ACT. Teken de doorsnede. Wat voor soort driehoek is de
doorsnede?
5 Je ziet hieronder piramide ABCD·T getekend. Op de opstaande punten liggen precies halverwege de
punten P, Q, R en S. De piramide wordt doorgesneden langs vlak PQRST. Teken de doorsnede. Wat voor soort
vierhoek is de doorsnede?
6 Je ziet hiernaast opnieuw piramide ABCD·T met de punten P, Q, R en S getekend.
De punten P en Q liggen op dezelfde hoogte; iets onder het midden van de opstaande ribben.
Ook de punten R en S liggen op dezelfde hoogte, maar juist iets boven het midden van de opstaande ribben.
De piramide wordt doorgesneden langs vlak PQRST. Teken ook nu de doorsnede.
7 In een assenstelsel met drie assen is balk OABC·EFGHgetekend. Gegeven zijn de coördinaten OA = 4, OC = 8 en OH = 3.
a Bereken met de stelling van Pythagoras de lengte van BG.
b Lichaamsdiagonaal AG ligt in diagonaalvlak ABGH.
Wat voor vierhoek is ABGH en wat zijn de afmetingen van deze vierhoek?
8 In een assenstelsel met drie assen is piramide OABC·T getekend.OA = 4 en OC = 4. S is het snijpunt van AC en OB. ST = 4
a Wat zijn de coördinaten van punt S?
b Bereken met de stelling van Pythagoras de lengte van OS.
Laat de wortel in het antwoord staan.
c Bereken nu de lengte van lijnstuk OT.
Rond je antwoord af op één cijfer achter de komma.
2.4 Pythagoras in de ruimte
Verlengde stelling van Pythagoras
In deze paragraaf ga je leren hoe je een lijnstuk berekend die door de ruimte van een ruimtefiguur heen gaat. Dit noemen we een lichaamsdiagonaal.
Hierboven staat de balk ABCD EFGH weergegeven. AG is een lichaamsdiagnonaal. We kunnen de lengte van AG berekenen met de verlengde stelling van Pythagoras.
Eerst ga je zoeken naar 3 bekende zijden die een route maken van A naar G. Bijvoorbeeld AB, BC en CG. Zie afbeelding hieronder.
Nu gaan we de verlengde stelling van Pythagoras gebruiken om AG te berekenen:
Video verlengde stelling van Pythagoras:
opgaven
1 Hieronder staat een kubus met ribben van 4 cm. Bereken de lengte van CE.
2 Hieronder staat balk ABCD EFGH. AB = 5 cm, BC = 4 cm en CG = 5 cm. Bereken de lengte van AG.
3 Hieronder staat balk ABCD EFGH. Bereken de lengte van BH.
4 Hieronder staat kubus ABCD EFGH. Alle ribben zijn 5 cm. Bereken de lengte BH.
2.5 Aanzichten
Om een goed beeld van een ruimtelijk figuur te krijgen, kijk je van verschillende kanten naar het figuur.
Een tekening van wat je ziet, noem je een aanzicht.
Vaak teken je drie aanzichten:
vooraanzicht
zijaanzicht
bovenaanzicht
Van het kubushuisje is een drieaanzicht getekend.
Opgaven
1 Hieronder zie je een bovenaanzicht van een stapel kubusjes met ribben van 1 cm.
De getallen in de vakjes geven het aantal kubusjes aan.
a Teken het vooraanzicht van het kubushuisje
b Teken ook het rechterzijaanzicht van het kubushuisje.
2 Teken van het figuur hieronder het vooraanzicht, bovenaanzicht en zijaanzicht.
3 Teken van het figuur hieronder het vooraanzicht, bovenaanzicht en zijaanzicht.
a. Welke windrichting ligt tussen Oost en ZuidOost?
b. In de tuin van nummer 23 staat een boom. Vul een windrichting in: De boom staat ten ... van het huis.
c. Hoeveel graden hoort bij de winsrichding Noordoost?
2. Op de kaart zie je een stukje van België en Zeeland.
a. Een vissersboot vaart van Westkapelle naar de haven van Knokke. Welke koers vaart het jacht?
b. De kaart is getekend op schaal 1: 400 000. Hoeveel km is het van WestKapelle naar Knokke?
c. Teken de schaallijn bij de kaart.
3.
a. Joost loopt van B naar D. Begint de wandeling ophoog of omlaag?
b. Joost stopt op het laagste punt van de wandeling. Is dat 146 m hoog of 152 m hoog?
c. De schaal is 1: 120 000. In heuvelachtig gebied loop je ongeveer 3,5 km per uur. Hoe lang zal Joost over de wandeling doen?
4.
a. Teken doorsnede BCHE op ware grootte.
b. Teken doorsnede APQE op ware grootte.
5. Bereken de lichaamsdiagonaal van een kubus met ribben van 51 cm.
6. Hieronder zie je een foto van een doosje. De stokje zijn 23 cm lang en passen er niet helemaal in. Hoeveel cm van de stokjes steken er bovenuit?
7. Hieronder is het bovenaanzicht getekend van een blokkenbouwwerk.
a. Teken het vooraanzicht en het rechterzijaanzicht.
b. Sofie haalt 7 blokjes weg. Het vooraanzicht en rechterzijaanzicht veranderen niet. Teken het nieuwe bovenaanzicht met getallen.
8. Welke figuren hieronder is de uitslag van een balk?
9.
a. Hoe heet het bovenvlak?
b. AB = 6 cm.Welke ribben zijn er nog meer 6 cm?
c. Bereken de lengte van AG.
Hoofdstuk 3: Lineaire verbanden
3.1 Van formule naar grafiek
Grafiek maken bij een formule
1) Maak een tabel (bedenk zelf hoe grootte stappen je neemt)
2) Maak een schets van het assenstelsel
3) Zet bij de horizontale as het laagste en hoogste getal, doe hetzelfde bij de verticale as.
4) Bedenk welke stappen je op de assen wil nemen (heb je een kreukellijn nodig?)
5) Teken het assenstelsel, vul de punten in en teken de grafiek
De formule inkomsten in € = 20 + 4t
beschrijft het verband tussen de tijd (t) en inkomsten.
Hoe langer je werkt, hoe meer inkomsten je hebt.
In de formule staan twee variabelen, t en inkomsten.
Bij variabelen horen eenheden.
Hier zijn dat uren en euro’s.
Opdrachten:
1. Gegeven is de formule: Gewicht in kg = 10 + 0,5t t: tijd in maanden
Teken de grafiek bij de formule. Ga op de horizontale as tot 50.
2. Gegeven is de formule: A = 80 - 5t
Teken de grafiek bij de formule.
3. Gegeven is de formule: Inhoud in liters = 10000 - 100t t: tijd in minuten
Teken de grafiek bij de formule.
4. Gegeven is de formule: h = 200 + 2t h: hoogte in meters en t: tijd in seconden
Teken de grafiek bij de formule.
3.2 Gelijkmatige toename of afname
Maak bij elke stap de deling:
Als daar bij elke stap hetzelfde uit komt dan is er gelijkmatige toe- of afname
20 : 2 = 10
10 : 1 = 10
30 : 3 = 10
Het antwoord is overal 10 dus er is hier gelijkmatige toename. Als er bij 1 stap een ander getal uit komt dan is er geen gelijkmatige toename of afname. Het moet dus kloppen voor alle stappen
Opdrachten:
1.
Hidde heeft een folderwijk. Het aantal folders dat rondgebracht moet worden verschilt per week. Hidde krijgt 7,5 cent per folder die hij rondbrengt.
Bekijk de tabel.
aantal folders
100
150
200
250
300
verdiensten (€)
7,5
a
Tussen welke variabelen is in de tabel een verband weergegeven?
b
Neem de tabel over en vul hem verder in.
c
Is er gelijkmatige toename of afname?
2.
Als je van een vierkant de lengte van een zijde weet, kun je de oppervlakte uitrekenen. Bekijk de tabel.
lengte zijde vierkant
1
2
3
4
5
oppervlakte vierkant
1
4
a
Tussen welke variabelen is in de tabel een verband weergegeven?
b
Neem de tabel over en vul hem verder in.
c
Is er gelijkmatige toename of afname?
3.
Een leraar rekent de proefwerkcijfers uit met de volgende formule: cijfer=15×aantal punten+1
a
Denk je dat er sprake is van gelijkmatige toename of afname?
b
Maak een tabel bij de formule en controleer of je antwoord op vraag a klopt.
aantal punten
10
15
20
25
30
cijfer
4. Geef bij de volgende tabellen aan of er sprake is van gelijkmatige toename of afname. Laat dit zien met een berekening.
a
aantal folders
100
150
200
250
275
verdiensten (€)
15
35
55
75
85
b
aantal folders
42
36
28
26
22
verdiensten (€)
60
48
32
26
14
c
aantal folders
50
42
32
22
20
verdiensten (€)
40
48
58
68
70
d
aantal folders
1
3
7
11
15
verdiensten (€)
8
16
32
48
68
3.3 Van tabel naar formule
Titel onderkant = begingetal +/- stapgrootte x titel bovenkant
Begingetal = Het getal onder de 0. Als er geen 0 staat moet je zelf uitrekenen wat er onder had gestaan als die er wel was geweest.
+/- Bij gelijkmatige toename een + Bij gelijkmatige afname een -
Stapgrootte = verschil onder: verschil boven. Het getal dat hier elke keer uit komt is de stapgrootte (ALS het elke keer gelijk is)
Hieronder uitleg met een paar filmpjes.
Opdrachten:
1.
In de tabel is een verband tussen een getal en de uitkomst weergegeven.
getal
0
1
2
3
4
5
uitkomst
5
9
13
17
21
25
a
Vul in:
Als je bij de tabel een grafiek tekent, gaat de grafiek door (0,....).
b
Vul in:
Telkens als het getal met 1 toeneemt, neemt de uitkomst met ..... toe.
c
Maak een formule bij het verband tussen getal en uitkomst.
2.
In de tabel is een verband tussen een getal en de uitkomst weergegeven.
getal
0
1
2
3
4
5
uitkomst
24
21
18
15
12
9
a
Vul in:
Als je bij de tabel een grafiek tekent, gaat de grafiek door (0,....).
b
Vul in:
Telkens als het getal met 1 toeneemt, neemt de uitkomst met ..... af.
c
Maak een formule bij het verband tussen getal en uitkomst.
3.
Een loodgietersbedrijf rekent voor reparaties voorrijkosten + een vast
bedrag per uur.
Voor een klus die twee uur duurt, betaal je € 90,-.
Voor een klus die vier uur duurt, betaal je € 140,-.
a
In de tabel zijn de genoemde klussen ingevuld.
aantal uur
0
1
2
3
4
5
bedrag
..
..
90
..
140
..
Neem de tabel over en probeer hem verder in te vullen.
b
Maak een formule bij het verband tussen het aantal uur en het bedrag.
4.
a
De tabel gaat over een kaars.
aantal uur
0
1
2
3
4
5
lengte in cm
13
11
9
7
5
3
Maak de formule bij deze kaars.
b
Wanneer is de kaars opgebrand?
5.
a
In deze tabel zijn de afstanden gegeven van een vliegtuig.
aantal uur
1
2
3
4
5
afstand in km
250
500
750
1000
1250
Maak een formule bij het verband tussen aantal uur en de afstand.
b
Jan moet een afstand vliegen van 2355 km. Hoeveel uur is hij onderweg?
6
Geef de formules van onderstaande tabellen?
a.
3.4 Van grafiek naar formule
Titel verticale as = begingetal +/- stapgrootte x titel horizontale as
Begingetal = Op welke hoogte snijdt de grafiek de verticale as?
+/- Bij een stijgende grafiek een + Bij een dalende grafiek een -
Stapgrootte = Kies 2 punten op de grafiek die je makkelijk af kan lezen. Doe de deling: verticaal verschi: horizontaal verschil.
Hieronder uitleg met een paar filmpjes:
Opdrachten:
1.
a
Teken een assenstelsel. Zet bij de horizontale as de variabele getal en bij de verticale as de variabele uitkomst.
Teken in het assenstelsel de punten A(2,3) en B(6,5).
Teken een rechte lijn door de punten A en B.
b
In welk punt snijdt de lijn de verticale as?
c
Hoe groot is de stapgrootte?
d
Maak een formule bij het verband tussen getal en uitkomst.
2.
a
Teken een assenstelsel. Zet bij de horizontale as de variabele getal en bij de verticale as de variabele uitkomst.
Teken in het assenstelsel de punten A(2,6) en B(6,4).
Teken een rechte lijn door de punten A en B.
b
In welk punt snijdt de lijn de verticale as?
c
Hoe groot is het stapgrootte?
d
Maak een formule bij het verband tussen getal en uitkomst.
3.
Voor het bepalen van de proefwerkcijfers heeft een leraar de volgende tabel gemaakt.
aantal punten
0
4
8
12
16
20
24
28
32
36
cijfer
1
2
3
4
5
6
7
8
9
10
a
Vul in:
Als je bij de tabel een grafiek tekent, gaat de grafiek door (0,....)
De stapgrootte van de grafiek is ..... .
b
Maak een formule bij het verband tussen het aantal punten en het cijfer.
c
Reken met de formule uit welk cijfer je krijgt als je 30 punten hebt gehaald.
Voor geschiedenis heb je de volgende vier cijfers gehaald: 5,27,37,5 en 6,0
Alle cijfers tellen even zwaar mee.
a
Bereken het gemiddelde. Laat zien hoe je het doet.
b
Voor op het rapport wordt het gemiddelde afgerond op een geheel getal.
Welk cijfer krijg je op je rapport voor geschiedenis?
2.
In de tabel zie je hoeveel boeken een winkelier de afgelopen week heeft verkocht.
dag
maandag
dinsdag
woensdag
donderdag
vrijdag
zaterdag
aantal boeken
280
250
350
275
525
1020
Bereken het gemiddeld aantal verkochte boeken per dag.
3.
Bekijk de rij getallen.
4
5
5
5
6
6
7
7
8
a
Welk getal is de modus van deze rij getallen?
b
Wat is de mediaan van deze rij getallen?
c
Bereken ook het gemiddelde van deze rij getallen.
4.
Bekijk nu ook deze rij getallen.
16
16
17
14
15
16
19
15
17
17
a
Leg uit waarom deze rij getallen geen modus heeft.
b
Wat is de mediaan van deze rij getallen?
c
Bereken ook het gemiddelde van deze rij getallen.
5.
Klas 3B heeft een proefwerk Duits gemaakt. De resultaten zie je in de frequentietabel.
cijfer
frequentie
5
4
6
8
7
6
8
4
9
2
24
a
Welk cijfer is de modus van alle cijfers?
b
Zet de getallen op een rijtje en bepaal de mediaan van deze cijfers.
c
Hoeveel procent van de leerlingen heeft een lager cijfer dan de mediaan?
4.2 Diagrammen lezen
Opdrachten:
1.
a. Wat is het gemiddelde van klas 2A en van klas 2B?
b. Wat is de modus van klas 2A en van klas 2B?
c. Wat is de mediaan van klas 2A en van klas 2B?
2. Bepaal van onderstaande boxplot het maximum, het minimum, de mediaan, de eerste mediaan en de tweede mediaan.
3.
In de frequentietabel zie je verdeling van de gewichten (in kg) van een groep personen.
klasse (kg)
frequentie
45 tot 50
1
50 tot 55
5
55 tot 60
8
60 tot 65
15
65 tot 70
19
70 tot 75
9
75 tot 80
3
a
Wat is het klassenmidden van de klasse '50 tot 55'?
b
Wat is de klassenbreedte van iedere klasse?
c
Welk klasse heeft de hoogste frequentie?
d
Hoeveel procent van deze groep personen weegt minder dan 70 kg?
e
Maak een staafdiagram bij de frequentietabel.
4.3 Boxplot en steel-blad diagram
Steelbladdiagram
Een steelbladdiagram is een schematische weergave van een reeks gegevens.
Je gebruikt een steelbladdiagram als de gegevens zo verschillen van elkaar
dat een frequentietabel veel te lang wordt, omdat er dan alleen maar nullen, enen en tweeën in voor zouden komen.
Dat laatste zou dus niet overzichtelijk zijn.
Voorbeeld steelbladdiagram:
0
1
2
3
4
5 6 6
3 5 7 7 8 8
1 1 3 3 3 5
4 7 7
0 1
steel
blad/bladeren
Zonder enige informatie weet je niet wat de getallen betekenen.
Mogelijkheden:
- Kleinste getal is 0,5 en het grootste getal is 4,1.
- Kleinste getal is 5 en het grootste getal is 41.
Uit de context van de som moet blijken of de steel voor eenheden of tientallen staat.
Noot: De gegevens in het blad (de bladeren) hoeven niet per se op volgorde te staan.
Al is dat natuurlijk wel netjes, als je dit doet.
Steelbladdiagram maken
Uit een reeks gegevens is vrij makkelijk een steelbladdiagram te maken.
Kijk eerst naar de kleinste en grootste waarde in je gegevens.
Besluit aan de hand van die twee wat je als steel neemt en hoe lang je die maakt.
Daarna ga je systematisch alle waarden langs en zet je ze in het 'blad'-gedeelte.
Voorbeeld
Maak een steelbladdiagram bij de volgende gegevens:
21 28 31 30 17 8 22 10 18 43 51 27 20 44 28
16 11 38 30 25 6 17 15 16 39 38 16 15 15 15
Een geschikte steel is 0 t/m 5 voor de tientallen.
De bladeren worden dan de eenheden.
In het beelddiagram zie je van een aantal beroepen het gemiddeld inkomen.
Wat is het gemiddeld jaarinkomen van een arts?
En wat is het gemiddeld inkomen van een fysiotherapeut ongeveer?
De gegevens zouden ook in een tabel gepresenteed kunnen worden.
Wat is een voordeel van een tabel ten opzichte van een beelddiagram?
En wat is een nadeel?
2.
Aan een groep jongeren is gevraagd hoe zij aan hun geld komen.
De antwoorden staan in de tabel.
inkomen uit:
aantal
zakgeld
22
kleedgeld
15
krantenwijk
10
oppassen
8
vakkenvullen
6
anders
13
Kun je uit de gegevens opmaken aan hoeveel jongeren de vraag gesteld is?
Hieronder zie je het begin van een beelddiagram bij de tabel.
Neem het beelddiagram over en maak het af.
3
In het nationale scholieren onderzoek van NIBUD (2008) staat hoeveel middelbare scholieren gemiddeld per maand uitgeven. Uit het onderzoek blijkt dat jongens gemiddeld iets meer geld uitgeven dan meisjes.
Leeftijd
Jongens €
Meisjes €
12 jaar
73
67
13 jaar
81
82
14 jaar
102
101
15 jaar
139
127
16 jaar
190
167
17 jaar
212
193
18 jaar
307
225
Hieronder zie je het begin van een staafdiagram bij de gegevens.
Neem het figuur over en maak het diagram verder af.
4
Een bedrijf hoopt dat haar website per maand 40.000 keer wordt bezocht.
In het diagram hieronder zie je hoeveel het bezoek het eerste half jaar afweek van dit aantal.
Hoeveel bezoekers trok de website ongeveer in januari?
En hoeveel ongeveer in maart?
Was het gemiddeld aantal bezoekers in de eerste zes maanden hoger of lager dan 40.000?
5
Bekijk de afbeelding over de verdeling van het water op de aarde.
Uit het figuur kun je aflezen dat van al het water op aarde 3% zoet water is.
Van het zoete water is 0,3% oppervlaktewater en van oppervlaktewater bevindt zich 2% in rivieren.
De totale watervoorraad op aarde is 1400 miljoen km³.
Hoeveel km³ zoet water is er op aarde?
Bereken de hoeveelheid oppervlaktewater op aarde.
Bereken de hoeveelheid water in de rivieren.
Hoeveel liter is dat? Schrijf je antwoord voluit.
4.4 Grafen
In een graaf kun je zien welke plaatsen verbonden zijn.
Voorbeeld:
We zien hier dat er een directe weg tussen A en B ligt, maar geen directe weg tussen B en C. Om van B in C te komen, ga je bijvoorbeeld langs A en E.
Soms staan er één of meerdere pijlen in een graaf. Het heet dan een gerichte graaf.
Dit betekent dat je over die weg alleen in de richting van de pijl kunt gaan. Je kunt dus direct van R naar Q, maar van Q naar R zul je via P moeten.
Er kunnen ook nog getallen in een graaf staan. Dan noemen we het een gewogen graaf.
Wanneer er meerdere wegen mogelijk zijn om van een punt in een ander punt te komen, moet je altijd de kortste weg nemen. Van L naar N kan via M (8+7=15), maar direct is korter (11). Van K naar N is 6, maar van N naar K is 11+5=16.
Opdrachten:
1
Van vier leerlingen is het volgende bekend:
Joep zit op hockey en op tennis. Suzanne zit op voetbal en op tennis. Joset zit alleen op hockey en voetbal. Anke zit op waterpolo en tennis.
Teken een graaf waarin de knooppunten de vier personen zijn. Je tekent een weg tussen twee personen als de twee personen aan dezelfde sport doen.
2.
Bekijk de graaf. De graaf geeft de afstanden in km weer tussen een vijftal steden. De graaf is een gerichte en gewogen graaf: je kunt wel rechtstreeks van A naar C, maar niet rechtstreeks van C naar A.
Hoe groot is de afstand van A naar C?
En hoe groot is de afstand van C naar A?
Hoe groot is de afstand van D naar C?
En hoe groot is de afstand van C naar D?
3.
In deze graaf wordt het aantal verhuizingen tussen vier dorpen in het afgelopen jaar weergegeven. Je ziet bijvoorbeeld dat er vanuit Paaldorp 6 mensen naar Randdorp zijn verhuisd.
a
Hoeveel mensen zijn er van Randdorp naar Uitdorp verhuisd?
En hoeveel van Uitdorp naar Randdorp?
b
Als je kijkt naar de verhuizingen tussen Randdorp en Uitdorp dan zie je dat Randdorp een 'verhuisoverschot' van 2 mensen heeft: door de verhuizingen tussen Randdorp en Uitdorp is het aantal inwoners van Randdorp met 2 toegenomen.
Kijk naar de verhuizingen tussen Middendorp en Paaldorp.
Welke stad heeft een verhuisoverschot?
Hoe groot is dat verhuisoverschot?
c
Laat met een berekening zien dat het aantal inwoners van Middendorp door alle verhuizingen met 2 mensen is toegenomen.
d
Met hoeveel mensen is het aantal inwoners van Uitdorp veranderd?
4.5 cirkeldiagram
- Cirkeldiagram lezen
Aan 200 mensen is gevraagd wat hun favoriete sport is.
Hun antwoorden zijn verwerkt in een cirkeldiagram.
Je ziet dat 60% van de ondervraagden gekozen heeft voor voetbal.
60% = 0.6
60% van 200 mensen is 0,6 × 200 = 120
Dus van 120 mensen is voetbal de favoriete sport.
- Cirkeldiagram tekenen
Stap 1: bereken de percentages
Stap 2: bereken de hoeken
Stap 3: teken het cirkeldiagram.
Voorbeeld
25 personen doen aan sport. 10 personen doen voetbal, 8 personen doen tennis, 6 personen doen hockey en 1 persoon doet handbal. De sporten zijn de Sectoren.
In de tabel hieronder staat het weergegeven.
Sport
Voetbal
Tennis
Hockey
Handbal
Totaal
Aantal
10
8
6
1
25
Procenten
Hoek
Stap 1: bereken de percentages.
10 : 25 x 100 = 40%
8 : 25 x 100 = 32%
6 : 25 x 100 = 24%
1 : 25 x 100 = 4%
Dit zetten we in de tabel:
Sport
Voetbal
Tennis
Hockey
Handbal
Totaal
Aantal
10
8
6
1
25
Procenten
40
32
24
4
100
Hoek
Stap 2: bereken de hoeken.
De hoeken kan je berekenen door de percentages x 3,6 te doen.
Stap 3: teken het cirkeldiagram.
Teken een straal omhoog in de cirkel.
Teken de hoek van 144° en zet het percentage er in. Dit is de eerste sector.
Teken de andere hoeken.
Het cirkeldiagram is nu klaar!
opgaven
1.
Aan 50 mensen is gevraagd wat hun favoriete sport is.
Ze mochten kiezen uit voetbal, tennis, volleybal en hockey.
De resultaten vind je in de tabel.
Sport
Aantal
Percentage
Voetbal
30
30 / 50 = 0,6 = 60 %
Tennis
12
......
Volleybal
5
......
Hockey
3
......
Totaal
50
......
Vul de kolom ''Percentage'' op het werkblad verder in.
Bij de tabel van vraag 1a is een cirkeldiagram gemaakt.
Zet de juiste namen bij de sectoren.
Doe dit op het werkblad.
2. Er zitten 20 leerlingen in de klas die een mobiele telefoon hebben. 8 leerlingen hebben een Iphone, 5 leerlingen een samsung, 3 leerlingen een LG en 4 leerlingen een Huawei. Vul de tabel verder in en teken het cirkeldiagram op het werkblad.
3. Boer Jansen heeft in totaal 320 dieren op zijn boerderij. Hij heeft 280 koeien, 5 honden, 25 kippen en 10 konijnen . Vul de tabel verder in en teken het cirkeldiagram op het werkblad.
4. Boer de Vries heeft in totaal 120 dieren rondlopen. Hij heeft 85 varkens, 20 kippen, 10 konijnen en 5 honden. Vul de tabel verder in en teken het cirkeldiagram op het werkblad.
Neem over en vul in.
Rond je antwoorden af op drie cijfers achter de komma.
tan 77° ≈ ....
tan 26° ≈ ....
tan 40° ≈ ....
tan 45° = ....
b
Bereken de bijbehorende hoek. Rond af op hele graden.
tan∠A =0,5 geeft ∠A ≈ ...°
tan∠B =1,5 geeft ∠B ≈ ...°
tan∠C =0,9 geeft ∠C ≈ ...°
tan∠D =1 geeft ∠D = ...°
2
Bekijk de figuur hieronder.
Van driehoek ABC is ∠B =90°, AB =10 en BC =7.
a
Bereken tan∠A.
b
Bereken de grootte van ∠A in een geheel aantal graden.
3 Bekijk de figuur hieronder.
Van driehoek PQR is ∠P =90°, PQ =6 en PR =10.
a
Bereken tan∠Q.
b
Bereken de grootte van ∠Q in een geheel aantal graden.
4 Bekijk de figuur.
Van driehoek KLM is ∠K =90°, KL =10 en KM =8.
a
Bereken tan∠L en bereken de grootte van ∠L in een geheel aantal graden.
b
Bereken tan∠M en bereken de grootte van ∠M in een geheel aantal graden.
c
Tel de som van de drie hoeken van de driehoek bij elkaar op. Klopt de uitkomst?
5
Bekijk de rechthoekige driehoeken.
a
Bereken tan∠Q en bereken de grootte van ∠Q in een geheel aantal graden.
b
Bereken ook de grootte van ∠R.
c
Bereken tan∠L en bereken de grootte van ∠L in een geheel aantal graden.
d
Bereken ook de grootte van ∠K.
6
Bekijk de rechthoekige driehoeken. De rechter driehoek is een vergroting van de linker driehoek. De vergrotingsfactor is 1,5
a
Bereken tan∠A en bereken de grootte van ∠A in een geheel aantal graden.
b
Bereken tan∠D en bereken de grootte van ∠D in een geheel aantal graden.
c
Wat valt je op?
7 Bekijk de rechthoekige driehoeken.
a
Bereken tan∠P en bereken de grootte van ∠P in een geheel aantal graden.
b
Bereken ook de grootte van ∠Q.
c
Bereken tan∠K en bereken de grootte van ∠K in een geheel aantal graden.
d
Bereken ook de grootte van ∠M.
8 Bereken van de volgende driehoeken het hellingspercentage.
9 Welke hellingsgetal hoort bij de volgende hellingspercentages?
a 15%
b 22%
c
5.3 Zijden berekenen met tangens
Met de tangens kan je niet alleen een hoek berekenen van een rechthoekige driehoek, maar ook een zijde.
Voorbeeld
Bekijk de rechthoekige driehoek ABC
met ∠B = 90°, ∠A = 30° en AB = 4.
Bereken zijde BC.
Instructievideo:
Opgaven
1 Bekijk de figuur.
Van driehoek ABC is ∠B =90°, AB =10 en ∠A =35°.
Bereken de lengte van BC.
2 Bekijk de figuur.
Van driehoek PQR is ∠P =90°, PR =10 en ∠Q =63°.
Bereken lengte PQ. Rond af op een decimaal.
3 Bekijk de rechthoekige driehoeken.
Bereken PQ en LM. Rond af op een decimaal.
4 Bereken AC. Rond af op een decimaal.
5 Bereken AB. Rond af op een decimaal.
5.4 Tangens en rechthoekige driehoeken
Soms moet je een schuine zijde van een rechthoekige driehoek berekenen. Dit kan met Pythagoras. Dit kan alleen als je de twee rechthoekszijden weet.
Hieronder staat een rechthoekige driehoek met hoek B = 40º en AC = 8.
Bereken BC.
BC kan je berekenen als je AB weet. Dit is net als AC een rechthoekzijde.
Zijde AB kunnen we berekenen met de tangens.
tan 40 = \({AC \over AB} = {8 \over AB}\)
AB = 8 : tan 40 = 9,53
Nu kunnen we BC berekenen met Pythagoras.
Het kan ook voorkomen dat je een hoek moet berekenen. Daarvoor moet je ook de rechthoekzijden weten. Daarvoor kan je ook Pythagoras gebruiken. Hieronder staat uitgelegd hoe je dat doet.
Bereken hoek R.
Allereerst gaan we met Pythagoras PQ berekenen.
Nu kunnen we ∠R berekenen.
tan ∠R = \({PQ \over QR} = {10,6 \over 3}=3,53\)
∠R = tan-1 3,53 = 74º
Opgaven
1 Bereken DF.
2 Bereken AC.
3 Bereken hoek I.
4 Bereken hoek D.
5.5 Tangens in de ruimte
Als je in een ruimtelijk figuur een hoek moet
uitrekenen, kijk dan goed in welk vlak de hoek ligt.
Voorbeeld
Bekijk balk ABCD·EFGH met AB = 6, AD = 3 en AE = 4.
Bij hoekpunt B is de hoek ∠CBG aangegeven.
Bereken de grootte van ∠CBG in graden nauwkeurig.
- ∠CBG ligt in zijvlak BCGF.
Zijvlak BCGF is een rechthoek van 3 bij 4.
- Vanuit ∠CBG weet je de lengte van de overstaande rhz
en aanliggende rhz.
Gebruik de tangens.
Opgaven
1 Bekijk balk ABCD·EFGH met AB =6, BC =3 en CG =4
In de balk is hoek ∠BAG aangegeven.
Je moet de grootte van deze hoek berekenen.
a Bereken met de stelling van Pythagoras de lengte van zijde BG.
b Wat voor soort driehoek is driehoek ABG?
Maak een schets van deze driehoek.
Zet de bekende afmetingen bij de zijden.
c Bereken ∠GAB.
2 Bekijk balk ABCD·EFGH met AB =6, BC =3 en CG =4
In de balk is hoek ∠BHF aangegeven.
Je moet de grootte van deze hoek berekenen.
a Bereken met de stelling van Pythagoras de lengte van zijde FH.
Rond je antwoord af op twee cijfers achter de komma.
b Bereken ∠BHF.
3 In een assenstelsel met drie assen is piramide OABC·T getekend. De coördinaten van de punten A, C en T zijn: A(5,0,0), C(0,5,0) en T(0,0,5).
Je moet de grootte van ∠OBT berekenen.
a Bereken met de stelling van Pythagoras lengte OB.
Rond je antwoord af op twee cijfers achter de komma.
b Bereken ∠OBT.
4 Bekijk balk ABCD·EFGH met AB =6, BC =3 en CG =4
Op ribbe AB ligt punt P, zo dat AP =4.
In de balk is diagonaalvlak ABGH getekend.
Je moet de grootte van de hoeken APH, BPG en GPH berekenen.
a Bereken met de stelling van Pythagoras de lengte van zijde BG.
b Bereken ∠APH.
c Bereken ∠BPG.
5 De schoorsteen hiernaast is van bovenaf gezien een vierkant van 80 cm bij 80 cm.
a Laat met een berekening zien dat de aangegeven hoek bij punt A ongeveer 63° is.
b De schoorsteen gaat door een gat in het dak. Bereken de afmetingen van dat gat in mm nauwkeurig.
5.6 D-toets
Diagnostische toets
1.
Link extra oefenopgaven tangens hoek berekenen + antwoorden op het einde
Soms herhaalt een beweging zich na een bepaalde tijd.
Je hebt dan te maken met een periodiek verband.
Je ziet hier een grafiek van een periodiek verband tussen
de hoogte (h in m) en de tijd (t in min).
In de grafiek is de periode aangegeven. De periode geeft aan
om de hoeveel tijd de beweging zich herhaalt. De periode is 4 min.
De evenwichtsstand ligt bij een hoogte h = 3 m.
De uitwijking (of amplitude) is het maximale verschil tussen de
hoogte en de evenwichtsstand. Je ziet dat de uitwijking 2 m is.
Opgaven
1.
In de grafiek hieronder is een periodiek verband weergegeven.
a
Op welke hoogte ligt de evenwichtslijn.
b
Hoelang is de periode? Geef de periode aan in de figuur.
c
De frequentie is het aantal perioden per tijdseenheid. Bereken de frequentie per uur.
d
Hoe groot is de amplitude? Geef de amplitude aan in de figuur.
2.
In de grafiek hieronder is een periodiek verband weergegeven.
a
Op welke hoogte ligt de evenwichtslijn.
b
Hoelang is de periode? Geef de periode aan in de figuur.
c
De frequentie is het aantal perioden per tijdseenheid. Bereken de frequentie per uur.
d
Hoe groot is de amplitude? Geef de amplitude aan in de figuur.
3.
De grafiek hieronder laat het temperatuurverloop in een aquarium zien.
a
Hoeveel graden schommelt de temperatuur?
b
Wat is de gemiddelde temperatuur in het aquarium?
c
Hoelang is de periode?
d
Om 12.40 uur en 15.20 uur is de temperatuur 20°C.
Op welke tijdstippen voor 24.00 uur is de temperatuur weer 20°C?
4.
Je ziet een schematisch reuzenrad. Het rad draait heel langzaam rond.
Tijdens het instappen draait het rad gewoon door.
Herman draait rond in het reuzenrad. In de tabel zie je op verschillende tijdstippen (t in sec) op welke hoogte (h in m) hij zich bevindt.
t (sec)
0
20
40
60
80
100
120
140
160
180
200
220
h (m)
5
8
13
18
21
18
13
8
5
8
13
18
a
Neem het assenstelsel over en teken de grafiek bij de tabel.
b
Wat voor soort verband herken je?
c
Hoe lang duurt één keer rond draaien? De periode is .... sec.
d
Op welke hoogte bevindt zich het instapplatform?
e
Hoe groot is de diameter van het reuzenrad?
f
Op welke hoogte bevindt Herman zich op 320 sec na het instappen?
En op 400 sec na het instappen?
g
Herman draait in het totaal zes rondjes in het rad.
Hoelang zit Herman in het rad? Geef je antwoord ook in minuten.
5.
Op een kerktoren zit een torenklok. De grote wijzer van de torenklok is van het midden van de klok tot het topje 0,6 meter lang. Het midden van de klok bevindt zich precies 50 meter boven de grond.
a
Op welke hoogte is het topje van de grote wijzer om 12 uur?
En om 12.15 uur en om 12.30 uur?
b
Er is een periodiek verbandt tussen de hoogte en het aantal minuten.
Geef van dit periodiek verband de periode, de evenwichtsstand en de amplitude.
6.2 Kwadratische verbanden
In een formule kan een variabele in het kwadraat voorkomen.
Je spreekt dan van een kwadratisch verband.
Voorbeeld
Een vierkant heeft zijden van a cm.
De oppervlakte van het vierkant is a · a = a²
Met de formule opp = a² kun je de volgende tabel invullen:
Omdat er in de formule een variabele in het kwadraat
voorkomt, spreek je van een kwadratisch verband.
Een kwadratisch verband is geen lineair verband.
De grafiek van een kwadratisch verband is geen
rechte lijn.
De grafiek wordt een parabool genoemd.
Voorbeeld
Bekijk de formule: u = g² – 4·g + 5
Bij de formule kun je de volgende tabel maken.
Bij de tabel is een grafiek getekend.
De grafiek is een een dalparabool.
Voorbeeld
Bekijk de formule: u = – (g – 2)² + 8
Bij de formule kun je de volgende tabel maken.
Bij de tabel is een grafiek getekend.
De grafiek is een een bergpabool.
Voorbeeld
Bij de formule u = –(g – 2)² + 8 is een grafiek getekend.
De grafiek is een bergparabool.
Links van de lijn g = 2 is de grafiek stijgend.
Rechts van de lijn g = 2 is de grafiek dalend.
Het punt (2, 8) is het hoogste punt.
Je noemt dat punt de top van de parabool.
In de top heeft u de grootste waarde u = 8.
Je zegt het maximum van de grafiek is 8.
Een parabool is symmetrisch.
De symmetrie-as is een verticale as door de top van de parabool.
Je kan aan de formule zien of de parabool een dalparabool of een bergparabool is.
Kijk naar het getal dat voor de variabele die in het kwadraat staat. Is deze negatief, dan is het een bergparabool. Is deze positief, dan is het een dalparabool.
Opgaven
1.
Je ziet een rij stippenfiguren.
a
Neem de tabel over en vul hem in.
nummer figuur n
1
2
3
4
aantal stippen a
1
b
Bekijk de formules hieronder. Welke formule past bij het verband tussen het figuurnummer n en het aantal stippen a?
a =2 × n
a = n²
2.
In de tabel hieronder is een verband tussen de variabelen getal en uitkomst weergegeven.
getal
0
1
2
3
4
uitkomst
3
5
11
21
35
a
Teken met behulp van de gegevens uit de tabel een grafiek.
b
Is het verband tussen getal en uitkomst een lineair verband? Leg je antwoord uit.
c
Het verband is een kwadratisch verband. Probeer uit te zoeken welke formule bij de tabel en de grafiek hoort. Kies uit:
uitkomst = getal² + 3
uitkomst = 2 · getal²
uitkomst = 2 · getal² + 3
3.
De tabel hieronder past bij de formule: uitkomst = getal² + 3
getalg
−2
−1
0
1
2
uitkomstu
7
4
3
4
7
Bij de tabel is ook een grafiek getekend.
a
Hoe noem je de grafiek bij een kwadratisch verband?
b
Is de grafiek bij deze formule een bergparabool of een dalparabool?
c
Geef de coördinaten van de 'top'.
d
Is er sprake van een minimum of van een maximum?
e
Neem over en vul 'stijgend' of 'dalend' in.
Links van de lijn g =0 is de grafiek ........
Rechts van de lijn g =0 is de grafiek ........
Teken de grafiek bij de tabel.
Maak gebruik van de symmetrie om uit te zoeken waar de top ligt.
c
Welke lijn is de symmetrieas?
5. Bij de baan van een tennisbal hoort de formule: h = −0,01 · (a - 10)² + 1,5.
In de formule is h de hoogte van de bal in meters en a de horizontale afstand in meters nadat de tennisbal
het racket van de tennisser verlaat.
a
Laat met een berekening zien dat de bal het racket van de tennisser verlaat (a =0) op een hoogte van 0,5 meter.
b
Bereken ook de hoogte als a =20
6. Geef bij de volgende formules aan of het een bergparabool is of een dalparabool.
a H = -0,02a2 + 3
b K = 3a - 0,5a2
c g = 3b2 - 4b
d W = -8c + 4c2
7.
Een rechthoek heeft een omtrek van 15 cm.
a
Als je de lengte van de rechthoek weet, kun je de breedte uitrekenen.
Hoe groot is de breedte van de rechthoek als de lengte 4 cm is?
b
Het verband tussen lengte en de breedte kun je weergeven in en formule.
Welke van onderstaande formules geeft het verband goed weer.
breedte==7,5+lengte
breedte==7,5−lengte
breedte==15+lengte
breedte==15−lengte
c
De oppervlakte van de rechthoek kun je berekenen met de formule: opp=7,5×lengte−lengte²
Neem onderstaande tabel over en vul hem verder in.
lengte
0
1
2
3
4
5
6
7
7,5
oppervlakte
0
6,5
d
Waarom loopt de lengte in de tabel van 0 tot 7,5?
e
Teken de grafiek bij de tabel.
f
De grafiek is een parabool.
Marianne denkt dat de top van de parabool (4,14) is. Heeft Marianne gelijk?
6.3 Top van een parabool
De algemene formule voor een kwadratische formules is y = ax2 + bx + c
a = het getal voor x2
b = het getal voor x
c = een los getal
Voorbeeld 1
Stel je hebt de volgende formule:
y = -2x2 +2x - 3
a = -2
b = 2
c = -3
Voorbeeld 2
Stel je hebt de volgende formule:
y = 4x2 - 5x +2
a = 4
b = -5
c = 2
Met a en b kan je de coördinaten van de top van een parabool uitrekenen.
De top bestaat uit een x-coördinaat en een y-coördinaat.
De 'top' van de parabool is (-3,6).
De formule die bij de parabool hoort is: y = -0,5x2 - 3x + 1,5
a = -0,5
b = -3
c = 1,5
De x-coördinaat kan je berekenen met de formule: \(-b \over 2a\)
De x-coördinaat = \(--3\over2*-0,5\)= \(3 \over -1\) = -3
De y-coördinaat kan je nu berekenen door -3 in te vullen in de formule.
y = -0,5x2 - 3x + 1,5
y = -0,5 * (-3)2 - 3 * (-3) + 1,5 = 6
De coördinaten van de top is (-3,6).
Opgaven
1. Bereken de coördinaten van de top:
a y= -15 + 4,5x2b y = -41 - 9x2 c y= -4x2 + 2x + 7 d y = 5x² + 6x - 8
e y = 2x2 - 3x + 5 f y= x2 + x + 1 g y = 3x + x2 h y= -2x\(^2\) + 10 i y = 1,2x² +8,4x + 1 j y = -0,25x2 + 4x - 7
6.4 Wortelverbanden
Je spreekt van een wortelverband als in de formule een wortelteken voorkomt.
Voorbeeld
Om de gemiddelde lengte jongens van 0 tot en
met 20 jaar uit te rekenen, kun je een vuistregel gebruiken. Bij die vuistregel kun je een formule maken:
Bij de formule kun je een tabel maken en een grafiek tekenen.
In de tabel en de grafiek zie je een afnemende stijging.
Opgaven
1.
Gegeven is de formule:
Het verband tussen getal en uitkomst is een wortelverband.
a
Neem de tabel over en vul hem verder in.
getal
0
1
4
9
16
uitkomst
b
Neem het assenstelsel over en teken de grafiek bij de tabel.
c
Bereken met de formule de uitkomst als getal = 6.
Rond je antwoord af op één cijfer achter de komma.
d
Gebruik de grafiek om te bepalen bij welk getal
de uitkomst ongeveer 7 is.
2.
Gegeven is de formule:
Het verband tussen getal en uitkomst is een wortelverband.
a
Neem de tabel over en vul hem verder in.
getal
0
1
4
9
16
uitkomst
b
Neem het assenstelsel over en teken de grafiek bij de tabel.
c
Bereken met de formule de uitkomst als getal = 6.
Rond je antwoord af op één cijfer achter de komma.
d
Gebruik de grafiek om te bepalen bij welk getal
de uitkomst ongeveer 4,5 is.
3.
Om de gemiddelde lengte van meisjes tussen de 0 en 20 jaar uit te rekenen, kun je de volgende formule gebruiken:
a
Neem de tabel over en vul hem verder in.
Rond de lengte steeds af op een geheel aantal cm.
leeftijd (jaar)
0
5
10
15
20
gem. lengte(cm)
b
In de tabel zie je afnemende stijging.
Leg uit wat daarmee wordt bedoeld.
c
Neem het assenstelsel over en teken de grafiek bij de tabel.
4.
Een econoom van een groot winkelbedrijf heeft een model opgesteld van de dagelijkse aspergeverkoop. De verkoop (V) in kg hangt af van de prijs (p) in euro volgens de formule:
Let op:
de formule is alleen geldig bij prijzen tussen de 3 en 15 euro.
a
Neem de tabel over en vul hem verder in.
Rond de verkoop steeds af op een heel aantal kg.
p (euro)
3
6
9
12
15
V (kg)
b
Neem het assenstelsel over en teken de grafiek bij de tabel.
c
De omzet aan asperges kun je uitrekenen door de prijs p met de verkochte hoeveelheid V te vermenigvuldigen.
Bereken de omzet bij een prijs van 3 euro. Bereken ook de omzet bij een prijs van 6 euro, een prijs van 9 euro en een prijs van 12 euro.
6.5 Machtsverbanden
Hogere machten
Een kwadratisch verband is een voorbeeld van een machtsverband.
In een kwadratisch verband komt een variabele in kwadraat (tweede macht) voor.
Naast tweedegraads verbanden heb je ook verbanden met hogere machten.
Voorbeeld
De inhoud (I) van een bol hangt af van de grootte van de straal (r).
De inhoud kun je benaderen met de formule: I = 4,2 × r3
Bij dit verband kun je een tabel en grafiek maken.
Opgaven
1.
Gegeven is de formule:
uitkomst = \(1 \over 4\) × getal3
Het verband tussen getal en uitkomst is een machtsverband.
a
Neem de tabel over en vul hem verder in.
getal
0
1
2
3
4
uitkomst
b
Neem het assenstelsel over en teken de grafiek bij de tabel.
c
Bereken met de formule de uitkomst als getal = 2,5.
Rond je antwoord af op één cijfer achter de komma.
d
Gebruik de grafiek om te bepalen bij welk getal
de uitkomst ongeveer 10 is.
2.
Gegeven is de formule:
uitkomst = \(1 \over 2 \) × (getal − 2) 4
Het verband tussen getal en uitkomst is een machtsverband.
a
Neem de tabel over en vul hem verder in.
getal
0
1
2
3
4
uitkomst
b
Neem het assenstelsel over en teken de grafiek bij de tabel.
c
Bereken met de formule de uitkomst als getal = 0,5.
Rond je antwoord af op één cijfer achter de komma.
d
Bereken met de formule ook de uitkomst als getal = 3,5.
Rond je antwoord af op één cijfer achter de komma.
e
Vergelijk de antwoorden op vraag c en vraag d. Wat valt je op?
3
Op sommige plaatsen in Nederland zie je windmolens die worden gebruikt om elektriciteit op te wekken. Het vermogen dat zo'n windmolen levert hangt af van de wieklengte en van de windsnelheid. Voor een windmolen met een wieken van 10 m geldt de formule:
vermogen = 0,052 × windsnelheid3
Het verband tussen de windsnelheid in m/s (meter per seconde) en het vermogen in kW (kiloWatt) is een machtsverband.
a
Bij een windsnelheid van 2 m/s spreek je van een zwakke wind.
Bereken het vermogen dat de windmolen levert bij 2 m/s.
b
Bij een windsnelheid van 10 m/s spreek je van een vrij krachtige wind.
Bereken ook het vermogen dat de windmolen levert bij 10 m/s.
c
De windmolen levert een vermogen van 100 kW.
Zoek uit, door te proberen, hoe groot de windsnelheid is.
4
In een fabriek worden de scooters hiernaast gemaakt. De totale kosten voor het maken van de scooters worden productiekosten genoemd.
De productiekosten in euro's hangen af van het aantal scooters (s) dat gemaakt wordt en kun je berekenen met de formule:
productiekosten = 0,5 × s3 − 50 × s2 + 3200 × s
a
Bereken met behulp van de formule de productiekosten voor 58 scooters. Schrijf de berekening op.
b
De fabrikant verkoopt de scooters voor 2500 euro per stuk.
Maak een formule waarme je de opbrengst kunt berekenen.
c
De fabrikant berekente de winst met de formule:
winst = opbrengst − productiekosten
Bij welk aantal scooters in de winst het hoogst, bij 40 of bij 80 scooters?
Laat zien hoe je aan je antwoord komt.
6.6 Andere verbanden
Hieronder zie je een aantal voorbeelden van andere verbanden.
opdrachten:
1.
2.
3.
6.7 D-toets
Diagnostische toets
1
De tabel hieronder past bij de formule: uitkomst=getal² +3
getalg
−2
−1
0
1
2
uitkomstu
7
4
3
4
7
Bij de tabel is ook een grafiek getekend.
a
Hoe noem je de grafiek bij een kwadratisch verband?
b
Is de grafiek bij deze formule een bergparabool of een dalparabool?
c
Geef de coördinaten van de 'top'.
d
Is er sprake van een minimum of van een maximum?
e
Neem over en vul 'stijgend' of 'dalend' in.
Links van de lijn g=0 is de grafiek ........
Rechts van de lijn g=0 is de grafiek ........
f
Welke lijn is de symmetrieas?
2
Bekijk de formule: uitkomst = getal² −3 · getal .
a
Neem de tabel over en vul hem verder in.
getalg
−1
0
1
2
3
4
uitkomstu
b
Teken de grafiek bij de tabel.
Maak gebruik van de symmetrie om uit te zoeken waar de top ligt.
Een lengte-eenheid staat voor een bepaalde lengte of afstand. Bij het omrekenen van eenheden, reken je met de stapgrootte. De standaardmaat is de meter.
Van groot naar klein: km hm dam m dm cm mm
De stapgrootte tussen de eenheden van lengte op de trap is steeds een factor 10.
Elke stap van 'groot naar klein' is keer 10 en van 'klein naar groot' is delen door 10.
Zo is 15 m gelijk aan 1500 cm,
want 15 x 10 x 10 = 1500 (2 stappen).
En zo is 12 dm gelijk aan 1,2 m,
want 12 : 10 = 1,2 (1 stap).
Tabel
Eenheden van lengte
km = kilometer
1 km = 1000 m
hm = hectometer
1 hm = 100 m
dam = decameter
1 dam = 10 m
m = meter (standaardmaat)
1 m = 10 dm = 100 cm = 1000 mm
dm = decimeter
1 dm = 1/10 m = 0,1 m = 10 cm
cm = centimeter
1 cm = 1/100 m = 0,01 m = 10 mm
mm = millimeter
1 mm = 1/1000 m = 0,001 m
Oppervlakte eenheid
Een oppervlakte-eenheid staat voor een bepaalde oppervlakte of grootte. Bij het omrekenen van eenheden, reken je met de stapgrootte. De standaardmaat is de vierkante meter.
De stapgrootte tussen de eenheden van oppervlakte op de trap is steeds een factor 100.
Elke stap van 'groot naar klein' is keer 100 en van 'klein naar groot' is delen door 100.
Zo is 6 m2 gelijk aan 60 000 cm2,
want 6 x 100 x 100 = 60 000 (2 stappen).
En zo is 3 dm2 gelijk aan 0,03 m2,
want 3 : 100 = 0,03 (1 stap).
Tabel
Eenheden van oppervlakte
km2 = vierkante kilometer
1 km2 = 1 000 000 m2 = 100 hm2
hm2 = vierkante hectometer
ha = hectare
1 hm2 = 10 000 m2 = 1 ha
dam2 = vierkante decameter
1 dam2 = 100 m2 = 1 are
m2 = vierkante meter (standaardmaat)
ca = centiare
Een inhouds-eenheid staat voor een bepaalde inhoud of volume. Bij het omrekenen van eenheden, reken je met de stapgrootte. De standaardmaat is de liter.
De stapgrootte tussen de eenheden van inhoud op de trap is steeds een factor 10.
Elke stap van 'groot naar klein' is keer 10 en van 'klein naar groot' is delen door 10.
Zo is 2 l gelijk aan 2000 ml,
want 2 x 10 x 10 x 10 = 2000 (3 stappen).
1 ml = 1 cc
Tabel
Eenheden van inhoud
hl = hectoliter
1 hl = 100 l
l = liter (standaardmaat)
dm3 = kubieke decimeter
1 l = 10 dl = 100 cl = 1000 ml = 1 dm3
dl = deciliter
1 dl = 1/10 l = 0,1 l
cl = centiliter
1 cl = 1/100 l = 0,01 l
ml = milliliter
cm3 = kubieke centimeter
1 ml = 1/1000 l = 0,001 l = 1 cm3
Opgaven
1.
a
3,6 km = ..... m
b
0,13 dam = ..... m
c
0,15 dm = ..... mm
d
13 dm = ..... cm
e
7,5 hm = ..... m
f
0,15 dam = ..... dm
2.
a
130 cm = ..... m
b
450 m = ..... hm
c
12 mm = ..... dm
d
73 cm = ..... m
e
7,5 hm = ..... km
f
0,15 dam = ..... km
3.
a
3,6 km² = ..... m²
b
0,13 dam² = ..... m²
c
0,15 dm² = ..... mm²
d
13 dm² = ..... cm²
e
7,5 hm² = ..... m²
f
0,15 dam² = ..... dm²
4.
a
130 cm² = ..... m²
b
450 m² = ..... hm²
c
12000 mm² = ..... dm²
d
73000 cm² = ..... m²
e
7,5 hm² = ..... km²
f
0,15 dam² = ..... km²
5.
a
24 m³ = ..... dm³
b
4,8 dm³ = ..... mm³
c
0,98 m³ = ..... cm³
d
24000 cm³ = ..... m³
e
5400 dm³ = ..... m³
f
24000 mm³ = ..... dm³
6.
a
3,6 L = ..... dm³
b
13 cL = ..... dm³
c
40000 mL = ..... dm³
7.2 Oppervlakte en omtrek
Oppervlakte driehoek
Voor de oppervlakte van een driehoek geldt:
oppervlakte driehoek = ½ × zijde × hoogte
Let op: de hoogte staat altijd loodrecht op de zijde.
Hieronder zie je driehoek KLM met LM = 10.
In de driehoek is een hoogtelijn KN op LM getekend; KN = 4,6.
Bereken de oppervlakte van de driehoek KLM.
oppervlakte Δ KLM = ½ × zijde × hoogte
oppervlakte Δ KLM = ½ × 10 × 4,6
oppervlakte Δ KLM = 23
Oppervlakte parallellogram
Voor de oppervlakte van een parallellogram geldt:
oppervlakte parallellogram = zijde × hoogte
Let op: de hoogte staat altijd loodrecht op de zijde.
Voorbeeld
Hieronder zie je parallellogram KLMN met LM = 5.
In KLMN is een hoogtelijn PQ op LM getekend. PQ = 4,6
Bereken de oppervlakte van parallellogram KLMN.
π is een Griekse letter. Spreek uit: pie
π is ongeveer 3,14
Voorbeeld
Van een cirkel met middelpunt M is de straal 3 cm.
Bereken de omtrek van cirkel.
omtrek cirkel = 2 × π × straal
omtrek cirkel = 2 × π × 3 cm
omtrek cirkel ≈ 2 × 3,14 × 3 cm
omtrek cirkel ≈ 18,84 cm
Oppervlakte cirkel
Voor de oppervlakte van een cirkel geldt:
oppervlakte cirkel = π × straal2 of oppervlakte cirkel = ¼ × π × diameter2
Voorbeeld
Van een cirkel met middelpunt M is de straal 3 cm.
Bereken de oppervlakte van de cirkel.
oppervlakte cirkel = π × straal2
oppervlakte cirkel = π × 32
oppervlakte cirkel ≈ 3,14 × 9
oppervlakte cirkel ≈ 28,26 cm2
Opgaven
1.
Bekijk het figuur.
Lijnstuk RS is de hoogtelijn van driehoek PQR. PS=6, SQ=4 en RS=5
Bereken de oppervlakte van driehoek PQR.
2.
Bekijk het figuur.
Op roosterpapier is een driehoek getekend.
Ieder hokje is 1 bij 1.
Hoe groot is de oppervlakte van de driehoek?
3.
Bekijk het figuur.
Bereken de oppervlakte van parallellogram ABCD.
4.
Bekijk het figuur.
Op roosterpapier is een parallellogram getekend.
Ieder hokje is 1 bij 1.
Hoe groot is de oppervlakte van het parallellogram?
5. Bekijk vierhoek ABCD.
Bereken de omtrek van deze vierhoek.
6.
Van een 1-euromunt is de straal ongeveer 12 mm. Bereken de omtrek van een 1-euromunt. Rond je antwoord af op één decimaal achter de komma.
7.
Van het 1-euromunt is de straal ongeveer 12 mm.
Bereken de oppervlakte van een 1-euromunt. Rond je antwoord af op één decimaal achter de komma.
7.3 Oppervlakte van ruimtefiguren
Oppervlakte balk
De oppervlakte van een rechthoek bereken je met de formule: lengte · breedte.
Als de rechthoek ook een hoogte heeft, noemen we dit een balk. Deze heeft dus de afmetingen lengte, breedte en hoogte. Van zo'n balk kan je ook de oppervlakte berekenen. Je kunt ook de inhoud van een balk bepalen.
Uitwerking:
De oppervlakte van een balk kun je berekenen door de oppervlaktes van alle zijvlakken te berekenen en bij elkaar op te tellen. Een balk heeft altijd van elk zijvlak 2 dezelfde, zoals je kan zien in de afbeelding. Dit gegeven kun je gebruiken om het rekenwerk wat te verkorten. Hieronder staat welke afmetingen je met elkaar moet vermenigvuldigen om de oppervlakte te berekenen van het betreffende zijvlak:
Bekijk de volgende ruimtelijke figuren.
Voor deze ruimtelijke figuren geldt dat alle doorsneden evenwijdig
aan het grondvlak dezelfde vorm en grootte hebben.
Voor deze ruimtelijke figuren geldt:
Inhoud = oppervlakte grondvlak × hoogte
Inhoud piramide en kegel
- inhoud piramide = oppervlakte grondvlak × hoogte: 3
- inhoud kegel = oppervlakte grondvlak × hoogte : 3
Instructievideo inhoud balk,kubus en prisma:
Instructievideo inhoud piramide en kegel:
Opgaven
1 Het grondvlak van dit prisma heeft een oppervlakte van 25 cm². De hoogte is 5 cm.
Bereken de inhoud van dit prisma.
2
Dit prisma is een halve kubus. De ribben van de kubus zijn 4 cm.
a
De oppervlakte van het grondvlak ABC= 8 cm².
Leg uit waarom.
b
Bereken de inhoud van dit prisma.
3 De voorkant van deze 'tent' is een gelijkzijdige driehoek. De basis is 1,4 m, de hoogte is 2 m. De diepte van de tent is 2,5 m.
a
Bereken de oppervlakte van de voorkant van de tent.
b
Bereken de inhoud van de tent.
4 Het grondvlak van een cilinder heeft een oppervlakte van 16 cm². De hoogte is 5 cm.
Bereken de inhoud van de cilinder.
5 De bodem van een cilinder heeft een diameter van 8 cm. De hoogte van de cilinder is 5 cm.
a
Hoe bereken je de oppervlakte van een cirkel?
Bereken de oppervlakte van het grondvlak.
Rond af op één cijfer achter de komma.
b
Bereken de inhoud van de cilinder.
6 Een soepblik heeft een inhoud van 0,6L (=0,6 dm³). Het blik is 12 cm hoog.
a
Bereken de oppervlakte van het grondvlak van het blik.
b
Volgens Erik is de diameter van het grondvlak van het blik ongeveer 8 cm.
Ga na of dat klopt.
7 Het grondvlak van de piramide hieronder is een gelijkbenige rechthoekige driehoek, met AC=BC=6 cm. De hoogte van de piramide is 6 cm.
Bereken eerst de oppervlakte van het grondvlak.
Bereken vervolgens de inhoud van de piramide.
8 grondvlak van de kegel hieronder is een cirkel met een straal van 3 cm.
De hoogte van de kegel is 8 cm.
Bereken eerst de oppervlakte van het grondvlak.
Bereken vervolgens de inhoud van de piramide.
9 Een piramide heeft een inhoud van 300 cm³. Het grondvlak heeft een oppervlakte van 25 cm².
Bereken de hoogte van de piramide.
10 Joost heeft dit potje hiernaast gemaakt. Hij is begonnen met het maken van een kegel met een hoogte van 8 cm en met een grondvlak met een diameter van 8 cm. Daar heeft hij een kegel met een hoogte van 4 cm en een diameter van 4 cm vanaf gehaald.
Bereken de inhoud van het potje.
7.5 Oppervlakte en inhoud vergroten
Vergrotingsfactor
Een origineel kan je vergroten. Het beeld wat ontstaat is vergroot of verkleint met een vergrotingsfactor.
De vergrotingsfactor is 2,5. Dit kan je berekenen door de lengte van het beeld te delen door de lengte van het origineel.
10 : 4 = 2,5
Oppervlakte vergroten
Oppervlakte beeld = oppervlakte origineel x vergrotingsfactor2
Oppervlakte beeld = 12 x 1,52 = 27 cm2
Vergrotingsfactor berekenen
Berekenen vergrotingsfactor:\(\sqrt{oppervlakte beeld \over oppervlakte origineel}\)= \(\sqrt{30 \over10} \)= 1,73
Inhoud vergroten
Samenvattend
Wanneer van een ruimtelijke figuur alle lengtes met eenzelfde factor k worden vermenigvuldigd, dan geldt:
de lengtevergrotingsfactor is k;
de oppervlaktevergrotingsfactor is k2;
de inhoudvergrotingsfactor is k3;
Bij twee gelijkvormige figuren kan de éne figuur uit de andere ontstaan door zo'n vermenigvuldiging met een vaste vergrotingsfactor (of verkleiningsfactor).
Opgaven
1 Het figuur hieronder wordt vergroot met een vergrotingsfactor van 4. Bereken de nieuwe oppervlakte.
2 Bereken de vergrotingsfactor.
3 Olievat 1 wordt vergroot met een vergrotingsfactor van 1,8. De inhoud is 45 liter. Bereken de inhoud van olievat 2.
4 Bereken oppervlakte 2.
5. Het kleine poppetje heeft een inhoud van 0,8 cm3 . Het grotere poppetje is 1,5 keer zo groot. Bereken de inhoud van het grote poppetje.
7.6 Gewicht
Opgaven
1.Reken om
a
4 kg =..... g
b
2,4 g =..... mg
c
0,05 kg =..... mg
2. Vul in.
a
4 ton = ..... kg
b
24000 g = ..... ton
c
7 kg = ..... mg
3 Vul in
a
0,4 kg + 30 g = ..... g
b
24 kg + 0,9 ton = ..... ton
c
0,5 kg - 200 gram = ..... g
7.7 D-toets
Diagnostische toets
1.
2.
3.
4.
5.
6.
7.
a. Bereken de omtrek van deze vlieger op 1 decimaal nauwkeurig.
b. Bereken de oppervlakte van deze vlieger.
Oppervlakte en inhoud ruimtefiguren:
8. Bereken de oppervlakte en de inhoud van deze balk.
9. Bereken de oppervlakte en de inhoud van deze cilinder.
10. Bereken de inhoud van deze prisma's.
11. Bereken de inhoud van deze piramide.
12. Bereken de inhoud van deze kegel.
Oppervlakte en inhoud vergroten:
13.
Joan maait grasvelden om wat bij te verdienen. Fam de Wit heeft een grasveld van 20 m2. Fam de Zwart heeft een grasveld van dezelfde vorm. De vergrotingsfactor van 4. Bereken de oppervlakte van het rgasveld van fam de Zwart.
14.
Een terras van 12 m2 wordt 3 keer zo groot gemaakt. Wat is de oppervlakte van de vergrootte terras?
15.
Ronde spiegels worden in verschillende maten gemaakt. De oppervlakte van een kleine spiegel is 50 cm2. De oppervlakte van de grote spiegel is 2500 cm2. Bereken de vergrotingsfactor.
16.
Bianca ontwerpt een vijver. Op de schaal is de vijver 25 cm2, in werkelijkheid is de vijver 25 m2. Bereken de vergrotingsfactor. En op welke schaal is de tekening gemaakt?
17.
Een doos heeft de inhoud van 35 m3. De andere doos is 3 keer zo groot.
Wat is zijn inhoud?
18.
De inhoud van een melkkannetje is 1,2 dl. Er bestaan grotere melkkannetjes met dezelfde vorm. Daarvan zijn alle maten 2,5 keer zo groot. Bereken de inhoud van dit grotere melkkannetje.
19.
Bij snackbar "het frietje' verkopen ze milkshakes. De kleine beker heeft een inhoud van 0,2 liter. De grote van 0,8 liter. De bekers hebben dezelfde vorm. Bereken de vergrotingsfactor.
20.
2 blikken zijn gelijkvormig. De ene heeft een inhoud van 150 ml, de andere 900 ml.
Duizend is een 1 met 3 nullen. Duizend x duizend is een miljoen. Dat is een 1 met 6 nullen. Zo is er voor elke stap van drie nullen een naam, althans voor de eerste paar stappen.
Na duizend en miljoen komen miljard, biljoen en biljard, triljoen en triljard. Daarna komen nog meer termen, maar Beter Rekenen zal daar geen vragen over stellen.
duizend
1.000
(1 met 3 nullen)
miljoen
1.000.000
(1 met 6 nullen)
miljard
1.000.000.000
(1 met 9 nullen)
biljoen
1.000.000.000.000
(1 met 12 nullen)
biljard
1.000.000.000.000.000
(1 met 15 nullen)
triljoen
1.000.000.000.000.000.000
(1 met 18 nullen)
triljard
1.000.000.000.000.000.000.000
(1 met 21 nullen)
Grote gewichten:
1 ton = 1000 kilogram
Geld:
1 ton = 100.000 euro
Capaciteit op de computer
De opslagruimte op de computer wordt uitgedrukt in bytes. Hieronder staat een omrekenschema:
Opgaven
1
Schrijf de volgende woordgetallen in cijfers:
driehonderdduizend zevenenveertig =
300047
vierhonderdduizend vierhonderdnegentig =
vierhonderdnegentigduizend negenhonderd =
zesduizend =
zeshonderdvierduizend twintig =
2
Het cijfer 207500 wordt geschreven als het woordgetal:
A tweehonderdzevenduizend vijf
B tweehonderdzevenduizend vijftig
C tweehonderdzevenduizend vijfhonderd
D zevenduizend vijfhonderdtwee
3
Het cijfer 6000 wordt geschreven als het woordgetal:
A zesduizend tien
B zesduizend vijf
C zesduizend twintig
D zesduizend
4
Het cijfer 988000 wordt geschreven als het woordgetal:
A negenhonderdtachtigduizend acht
B achtentachtigduizend negenhonderd
C negenhonderdtachtigduizend achthonderd
D negenhonderdachtentachtigduizend
5
Het cijfer 410007 wordt geschreven als het woordgetal:
A vierhonderdtienduizend zeven
B tienduizend vierhonderdzeven
C vierhonderdtienduizend zevenhonderd
D vierhonderdtienduizend zeventig
6
Koppel onderstaande cijfers aan de juiste woordgetallen
13 Mehdi heeft 83 CD's. Iedere CD heeft een capaciteit van 80 MB. Wat is de totale capaciteit in GB?
14 Julian krijgt iedere dag 2 euro zakgeld. Dit spaar hij op. Hoeveel geld heeft Julian na 60 jaar gespaard? Geef je antwoord in tonnen.
8.2 Wetenschappelijke notatie
Opgaven
1
a Schrijf 100000 als macht van 10.
Het getal 304586 bestaat uit 3 honderdduizendtallen, 0 tienduizendtallen, 4 duizendtallen, 5honderdtallen, 8 tientallen en 6 eenheden.
b Laat zien, hoe je dit kunt schrijven met machten van 10.
c Schrijf 0,00001 als macht van 10.
d Schrijf 204000 in de wetenschappelijke notatie.
2
Schrijf als macht van 10:
a 1000
b 100000000
c 10 miljard
d 0,001
e 1100000
f 10 miljardste
3
Schrijf in de wetenschappelijke notatie:
a 123 miljoen
b 614000000000
c 0,00001496
d 0,00000000000042
4
Gebruik bij de volgende berekeningen de wetenschappelijke notatie. Geef je antwoord ook in die vorm.
a In Nederland wonen ongeveer 16 miljoen mensen. Het gemiddeld inkomen van een Nederlander is ongeveer € 18.000,=. Bereken het nationaal inkomen (het inkomen van alle Nederlanders samen).
b In Nederland zijn er jaarlijks ongeveer 1,5 miljoen middelbare scholieren. Zo'n scholier kost de overheid gemiddeld € 4500,=. Hoeveel geeft de overheid jaarlijks ongeveer uit aan middelbaar onderwijs?
5
Bacteriën zijn micro-organismen. Een bepaald soort bacterie heeft een gewicht van 2,4⋅10-8 kg.
a Op een plant bevinden zich 3,2 miljoen van deze bacteriën. Hoeveel wegen deze bacteriën samen?
b Hoeveel van deze bacteriën wegen samen 1 kg?
8.3 Kleine getallen
Naast grote getallen heb je ook kleine getallen.
een tiende
0,1
10-1
een honderdste
0,01
10-2
een duizendste
0,001
10-3
een tienduizendste
0,0001
10-4
een honderdduizendste
0,00001
10-5
Opgaven
1 Schrijf de volgende getallen in de wetenschappelijke notatie.
a 0,000000137
b 0,000342
c 0,0056
d 0,00019
e 0,000000865
f 0,0082
g 0,00000000467
2 Schrijf zonder een macht van 10.
a 5,5 × 10-3
b 2,51 × 10-7
c 1,03 × 10-4
d 34, 61 x 10-6
e 501,6 x 10-3
f 62,15 x 10-6
8.4 Eenheden van tijd
Een tijd-eenheid staat voor een bepaalde hoeveelheid tijd. Met eenheden van tijd kun je rekenen.
Voorbeelden:
1 jaar = 52 weken
52 weken = 12 maanden
1 week = 7 dagen
1 dag = 24 uur
1 uur = 60 minuten
1 minuut = 60 seconde
1 uur = 60 x 60 = 3600 seconden
1 dag = 24 x 3600 = 86 400 seconden
792 uren = 792 : 24 = 33 dagen
54 jaren = 54 x 12 = 648 maanden
Tabel
Eenheden van tijd
1 millennium = 1000 jaren
het meervoud van millennium is millennia
1 eeuw = 100 jaren
1 jaar = 4 kwartalen
1 jaar = 12 maanden
1 jaar is 365 dagen, of 366 dagen in een schrikkeljaar *
1 jaar is 52 weken + 1 dag, of + 2 dagen in een schrikkeljaar *
1 kwartaal = 3 maanden = 1/4 jaar
1 maand = 1/12 jaar
1 maand is 30 of 31 dagen, en in de maand
februari 28 dagen of 29 dagen in een schrikkeljaar *
1 week = 7 dagen
1 dag (etmaal) = 24 uur
1 uur = 60 minuten
1 minuut = 60 seconden
* Een schrikkeljaar komt om de vier jaar voor. Een 'gewoon' jaar heeft 365 (= 52 x 7 + 1) dagen, een schrikkeljaar heeft 366 dagen.
2,45 uur is niet 2 uur en 45 minuten, maar 2 uur en 0,45 x 60 = 27 minuten.
3,6 jaar = 3 jaar en 0,6 x 365 = 219 dagen.
Opgaven
1
a Kees vliegt naar Spanje. De vliegreis duurt 165 minuten. De reistijd is
............. uur en ................. minuten.
b Loes gaat met de auto op vakantie. Ze zit 5 uur en 45 minuten in de auto.
Hoeveel minuten zijn dat?
2
a 86 uur = ............. dagen en ....... uur
b 27 maanden = ................. jaar en ................. maanden
c 626 jaar = ..................... eeuwen en ............. jaar
3
a 5 minuten = ...seconden
b 12 uur = ...minuten
c 3 dagen = ...uren
d 2 kwartalen = ...weken
e 3 eeuwen = ...jaar
f 2 uur = ...seconden
4
a Hoeveel jaar en hoeveel dagen is 5,8 jaar?
b Hoeveel uur en hoeveel minuten is 3,2 uur?
c Hoeveel dagen en hoeveel uur is 6,5 dagen?
d Hoeveel minuten en hoeveel seconden is 520 seconden?
8.5 Eenheden van snelheid
De snelheid wordt uitgedrukt in twee verschillende eenheden. Namelijk in een eenheid van lengte en een eenheid van tijd. Dit wordt een samengestelde eenheid genoemd.
\(snelheid ={afstand \over tijd}\)
Toelichting:
De (gemiddelde) snelheid is te berekenen door de afgelegde weg te delen door de tijd.
Stel dat een fietser een afstand aflegt van 9 km in 30 minuten. Wat is dan de snelheid per minuut en per uur?
De snelheid is dan 9 : 30 = 0,3 km/minuut. Lees 0,3 km per minuut.
De snelheid is dan 0,3 x 60 = 18 km/uur. Lees 18 km per uur.
Voorbeelden:
1 km = 1000 m en 1 m = 100 cm
1 uur = 60 minuten = 3600 seconden
16 m/uur = 16 x 100 = 1 600 cm/uur
15 000 m/sec = 15000 : 1000 = 15 km/sec
80 m/sec = 80 x 60 = 4800 m/minuut
4 200 m/uur = 4200 : 60 = 70 m/minuut
7 100 cm/sec = 7100 : 100 x 3600 = 255 600 m/uur
10 m/sec = 10 : 1000 x 3600 = 36 km/uur
Let goed op wanneer je bij het omrekenen moet vermenigvuldigen of delen.
De eenheden van snelheid zijn km/uur (kilometer per uur) en m/s (meter per seconde). Met een verhoudingstabel kun je de eenheden van snelheid omrekenen.
Nathan loopt 100 meter in 25 seconden.
Aanpak:
: 25 x 60 x 60
Tijd
25 sec.
1 sec.
1 min.
1 uur
Afstand
100 m
4 m
240 m
14400 m
: 25 x 60 x 60
Trucje:
x 3,6
---------------->
m/s km/uur
<-------------------
: 3,6
Opgaven
1
a Karel loop 2,5 km in 1 kwartier. Hoeveel kilometer is dat per uur?
b Jaap fietst 5 meter per seconde. Met een verhoudingstabel kun je zijn
snelheid in km per uur berekenen. Vul de tabel in.
Tijd
1 sec.
1 min.
1 uur
Afstand
5 m
Hoeveel km per uur fietst Jaap?
2 Een hardloper loopt 300 meter in 42 seconde.
a Hoeveel m/s is zijn snelheid?
b Hoeveel km/uur is dat?
3 Een auto rijdt 110 m/s. Hoeveel km/uur is dit?
4
a 40 m/s = ...km/uur
b 56 km/uur = ...m/s
c 50 km/uur = ...m/s
d 2 m/s = ...km/uur
8.6 Verhoudingen
Een verhouding geeft een evenredig verband tussen twee variabelen weer.
In het dagelijks spraakgebruik kom je regelmatig verhoudingen tegen.
Voorbeelden
Vier van de vijf jongens zijn gek op voetbal.
Er zijn drie keer zoveel meisjes als jongens.
De verhouding van limonadesiroop en water is 1 : 6 (1 staat tot 6).
Eén centimeter op de kaart is in werkelijkheid 10 km.
Je hebt een kans van één op tien dat je gekozen wordt.
Een verhouding kun je weergeven in een verhoudingstabel.
Voorbeeld
Angelique heeft een kralenketting die bestaat uit witte en rode kralen. De verhouding tussen de witte en rode kralen is 2 : 3.
In de verhoudingtabel is het onderste getal steeds 1,5 keer
zo groot als het bovenste getal.
In een verhoudingstabel kun je getallen in de onderste en
de bovenste rij met hetzelfde getal vermenigvuldigen of door hetzelfde getal delen.
De verhouding blijft 2 : 3.
Opgaven
1
Vier van de vijf jongens zijn gek op voetbal.
In een klas zitten 20 jongens. Hoeveel zijn er gek op voetbal?
2
Er zijn drie keer zoveel meisjes als jongens op dat feestje.
Op het feestje zijn 15 meisjes. Hoeveel jongens zijn er?
3
De verhouding van limonadesiroop en water is 1:6.
Je wilt één liter (= 1000 ml) limonade maken.
Hoeveel ml limonadesiroop heb je ongeveer nodig?
Rond af op een geheel aantal ml.
4
Angelique heeft een kralenketting die bestaat uit witte en rode kralen.
De verhouding tussen de witte en rode kralen is 2 : 5.
Neem de tabel over en vul hem verder in. Vul ook de kolom totaal in.
witte kralen
2
8
20
10
50
60
rode kralen
5
......
......
......
......
......
totaal
7
......
......
......
......
......
5
Voor veel televisietoestellen geldt dat de verhouding hoogte : breedte van de beeldbuis 9:16 is. Joost heeft een televisietoestel van 45cm hoog.
Hoe breed is het televisietoestel?
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bij grafiek I hoort de formule: uitkomst = - 4 + 3 x getal
Bij grafiek II hoort de formule: uitkomst = 6 - 2 x getal
Opgaven
1 Welke formule hoort bij welke grafiek?
formule I: y = 7
formule II: y = 6 - x
formule III: y = 0,5x
formule IV: x = -2
formule V: y = -1
2 Schrijf bij iedere grafiek de formule op.
9.3 Som- en verschilgrafieken
Somgrafiek
In een dorp is een aantal jaar het aantal mannen en vrouwen geteld.
De aantallen staan in een grafiek.
Je kunt het aantal mannen en vrouwen bij elkaar optellen.
Dat geeft het totaal aantal inwoners van het dorp.
De grafiek van het totaal heet de somgrafiek.
Verschilgrafiek
Een dorp heeft een aantal jaar bijgehouden hoeveel mensen naar het dorp verhuisd zijn (vestiging) en hoeveel mensen vanuit het dorp verhuisd zijn naar ergens anders (vertrek).
Bij de tabel is een grafiek getekend.
In 2002 is het aantal inwoners door de verhuizingen met 10 toegenomen.
In 2004 is het aantal inwoners door de verhuizingen gelijk gebleven.
In 2005 is het aantal inwoners door de verhuizingen met 8 afgenomen.
Instructievideo somgrafiek en verschilgrafiek:
somformule en verschil formules:
Er zijn 2 formules gegeven over de inkomsten van Jan en Tara..
Inkomsten Jan = 15 + 8,50t
Inkomsten Tara = 40 +8t.
Hieronder zie je hoe je hier een somformule van kan maken en een verschilformule.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
a Stel dat ze hun inkomsten bij elkaar willen leggen. Welke somformule hoort hierbij?
b Ze willen graag het verschil weten. Welke verschilformule Lara - Jochem hoort hierbij?
6 Joep en daantje hebben beide een bijbaantje.
Inkomsten joep = 3 + 3,50t
Inkomsten Daantje = 5 + 2,50t
t is tijd in uren.
a Stel dat ze hun inkomsten bij elkaar willen leggen. Welke somformule hoort hierbij?
b Ze willen graag het verschil weten. Welke verschilformule Daantje - Joep hoort hierbij?
9.4 Vergelijkingen oplossen met de balansmethode
Balansmethode
Soms kun een vergelijking oplossen door aan een balans te denken.
Bekijk de vergelijking 4·g + 3 = 2·g + 9
Bij de vergelijking kun je aan de balans hiernaast denken. Op de balans liggen links 4 rode blokjes van g gram en 3 blokjes van 1 gram en rechts 2 rode blokjes van g gram en 9 blokjes van 1 gram.
- Haal eerst links en rechts twee rode blokjes van g gram
weg. Je krijgt de vergelijking: 2·g + 3 = 9
- Haal nu links en rechts drie blokjes van 1 gram weg.
Je krijgt de vergelijking: 2·g = 6
- Twee blokjes wegen samen 6 gram, dus één blokje weegt 3 gram.
Je krijgt als oplossing: g = 3
In een vergelijking kunnen ook negatieve getallen voorkomen.
Dan is het lastig om aan een balans te denken.
Je kunt de vergelijking dan wel oplossen met de balansmethode.
Bekijk de vergelijking:
Controle: 4 × 6 – 3 = 21 en 2 × 6 + 9 = 21 Klopt!
Opgaven
1
Bekijk de formules:
I u = 15 × g
II u = 12 × g + 18
a
Je wilt weten voor welk getal g de formules dezelfde uitkomst u hebben.
Welke vergelijking moet je oplossen?
b
Los de vergelijking op met behulp van de balansmethode:
15 · g
=
12 · g + 18
c Controleer de oplossing.
2
Twee verschillende klusbedrijven gebruiken verschillende formules voor het berekenen van de kosten voor een reparatie:
I k = 27,5 × t + 25
II k = 25 × t + 40
In de formules staat t voor het aantal uur dat een reparatie duurt en k voor de kostprijs in euro.
a
Je wilt weten bij welk aantal uren de bedrijven even duur zijn.
Welke vergelijking moet je oplossen?
b
Los de vergelijking op met behulp van de balansmethode:
27,5 · t + 25
=
25 · t + 40
c
Controleer de oplossing.
3
Los de volgende vergelijkingen op met de balansmethode.
a
7g +6 = 5g +15
b
11g + 4 = 6g + 39
c
7g + 7 = 4g + 15
4
Los de volgende vergelijkingen op met de balansmethode.
a
7g − 6 = 5g + 15
b
11g − 18 = 6g − 3
c
7g + 11 = 4g + 2
5
Los de volgende vergelijkingen op met de balansmethode.
a
8a + 9 = 2a + 63
b
4k − 20 = k + 13
c
6p − 12 = 78 − 4p
9.5 Oplossen met inklemmen
Instructievideo inklemmen:
Opgaven
1
Een auto rijdt 1 op 15.
De formule is: afstand =15 × hoeveelheid benzine
a
Je wilt weten hoeveel benzine je verbruikt als je 200 km rijdt.
Welke vergelijking moet je oplossen?
b
Wat is de oplossing van de vergelijking?
Rond je antwoord af op één cijfer achter de komma.
2
Een taxibedrijf gebruikt bij het berekenen van de ritprijs de volgende formule:
prijs = 2,5 x afstand +3
prijs in euro, afstand in km.
a
Meneer De Vries moet € 19,25 afrekenen.
Je wilt weten hoeveel km de rit was.
Welke vergelijking moet je oplossen?
b
Los de vergelijking op met inklemmen.
3
Een leraar rekent de proefwerkcijfers uit met de volgende formule:
cijfer == (aantal punten +3) :3
a
Je wilt weten hoeveel punten je moet halen voor een 6.
Welke vergelijking moet je oplossen?
b
Los de vergelijking op.
4 Met lucifers kun je driehoeken maken, kijk maar naar het figuur.
De formule is:
aantal lucifers = 2× aantal driehoeken +1
a
Je wilt weten hoeveel driehoeken je kunt maken met 60 lucifers.
Welke vergelijking moet je oplossen?
b
Los de vergelijking op. Wat vind je van de oplossing?
5 Bekijk de vergelijking: 2,5 g +3 =16,75
Los de vergelijking op met inklemmen.
6 Bekijk de vergelijking (g +3) : 3 = 8
Los de vergelijking op met inklemmen.
9.6 D- toets
Diagnostische toets
1 Schrijf van elk assenstelsel op wat fout is.
2 Kim plant een struik in haar tuin. De struik wordt maximaal 1,5 meter hoog.
Bij de groei van de struik hoort de formule: Hoogte in cm = 18 + 7t
t = tijd in maanden. Teken de grafiek in een assenstelsel.
3 Bij elke grafiek hoort een formule. Schrijf deze formule op.
4
a Teken de grafiek y = 5
b Teken de grafiek x = -1
5 Twee boers willen samen een spelcomputer kopen. Ze zijn aan het sparen. Dit doen ze met de formules:
spaarbedrag Jan = 50 + 5t
spaarbedrag Wim = 35 + 6t
t = tijd in weken.
a Schrijf de somformule op.
b Teken de somgrafiek.
c Bereken hoeveel geld de broers hebben gespaard na 4 weken.
6 De broers willen weten wie wat spaart en daarvoor maken ze een verschil grafiek.
a Schrijfde verschilformule op van Jan - Wim.
b Teken de verschilgrafiek.
7 Het verschil tussen invoer en uitvoer heet handelsoverschot.
a Neem de tabel over en vul verder in.
b Teken de verschilgrafiek uitvoer - invoer.
8 Los de vergelijkingen op met de balansmethode.
a 6a + 24 = 4a + 48
b 26 + 2x = 13 + x
c 7b - 40 = 50 + 2b
d 11 - p = 2p + 8
9 Katja zoekt een tuinbedrijf. Ze gaat op zoek op internet om daar de prijzen te vergelijken.
Klusjesbedrijf Jansen: Kosten = 75 + 1,75a
Klusjesbedrijf Bart: Kosten = 40 + 2a
a= de oppervlakte in m2.
a Maak een vergelijking van de formules.
b Los deze vergelijking op met de balansmethode.
c Wanneer zijn de klasjesbedrijven even duur?
d Hoe duur zijn ze dan?
e Katja's tuin is 100 m2. Welk bedrijf kan ze het beste nemen?
10 2 Stadjes Malen en Erde liggen dicht bij elkaar. Ze houden de hoeveelheid inwoners bij.
In Malen : aantal inwoners = 8200 + 180t
In Erde: aantal inwoners = 9500 - 170t
Hierin is t tijd in jaren.
De inwoners van Malen en Erde willen een feest organiseren als het aantal inwoners gelijk is.
a Teken de grafieken.
b Lees af uit de grafieken na hoeveel jaar het inwonersaantal even groot is.
c Controleer dit antwoord met inklemmen.
d In welk jaar wordt het feest gegeven?
11 Bij de groei van bamboe hoort de formule: hoogte in cm = 10 + 35t t: tijd in dagen.
Jos heeft zo’n bamboeplant in zijn tuin gezet. Bij zijn plant hoort de vergelijking: 450 =10 + 35t
a Los deze vergelijking op met inklemmen.
b Hoeveel dagen is de eucalyptus van Jos aan het groeien?
12 Los de vergelijking 241 = 79 - 4,5a op met inklemmen.
Hoofdstuk 10: Goniometrie 2
10.1 Driehoeken
Tangens
Hieronder staat driehoek ABC.
Als je vanuit hoek A kijkt, dan is AB de aanliggende zijde, BC de overstaande zijde en AC de schuine zijde.
Om de tangens van hoek A te berekenen kan je het ezelsbruggetje TOA gebruiken. Dit betekent:
tan ∠A = \(overstaande zijde\over aanliggende zijde\)
Voorbeeld
Bereken de tangens van hoek A. Zie figuur hieronder.
tan ∠A = \(BC\over AB\)= \(5\over 12\)= 0,42
Hoek berekenen
Instructievideo hoek berekenen met de tangens:
Zijde berekenen
Instructievideo zijde berekenen met de tangens:
Tangens en Pythagoras
Soms moet je een schuine zijde van een rechthoekige driehoek berekenen. Dit kan met Pythagoras. Dit kan alleen als je de twee rechthoekszijden weet.
Hieronder staat een rechthoekige driehoek met hoek B = 40º en AC = 8.
Bereken BC.
BC kan je berekenen als je AB weet. Dit is net als AC een rechthoekzijde.
Zijde AB kunnen we berekenen met de tangens.
tan 40 = \({AC \over AB} = {8 \over AB}\)
AB = 8 : tan 40 = 9,53
Nu kunnen we BC berekenen met Pythagoras.
Het kan ook voorkomen dat je een hoek moet berekenen. Daarvoor moet je ook de rechthoekzijden weten. Daarvoor kan je ook Pythagoras gebruiken. Hieronder staat uitgelegd hoe je dat doet.
Bereken hoek R.
Allereerst gaan we met Pythagoras PQ berekenen.
Nu kunnen we ∠R berekenen.
tan ∠R = \({PQ \over QR} = {10,6 \over 3}=3,53\)
∠R = tan-1 3,53 = 74º
Berekenen hellingsgetal en hellingspercentage
Instructievideo berekenen hellingsgetal en hellingspercentage:
Het arrangement 3mavo is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteurs
Marleen Everhardus
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2018-05-24 16:14:14
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 3.0 Nederlands licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
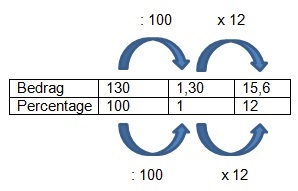
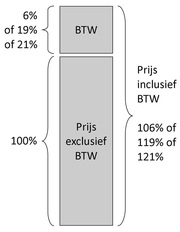
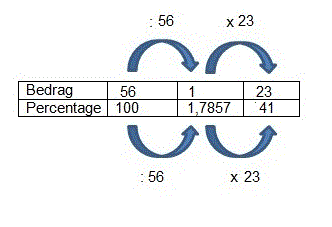
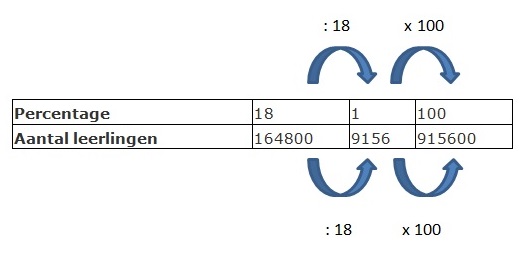
Extra opgaven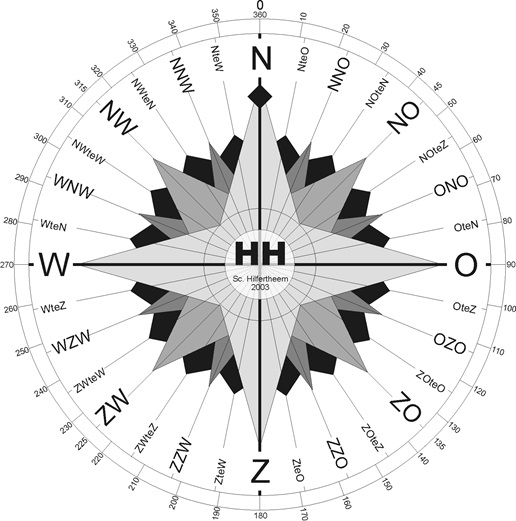
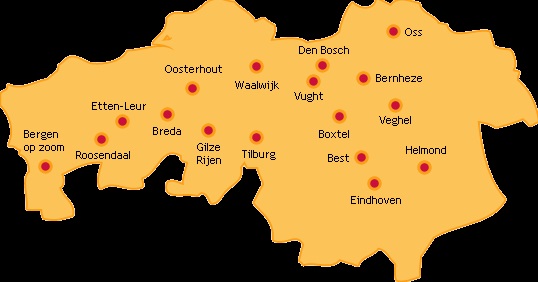
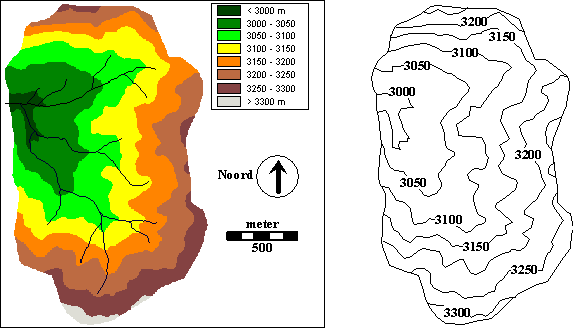
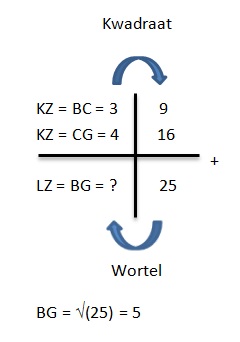
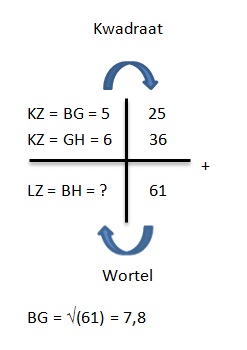
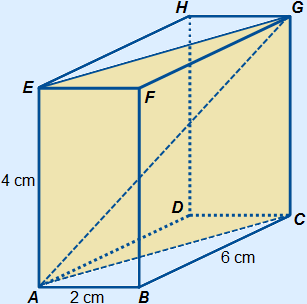
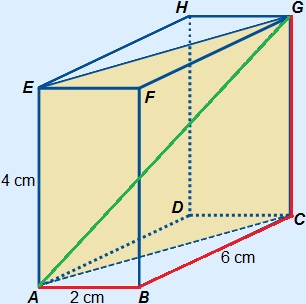
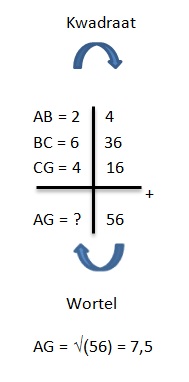
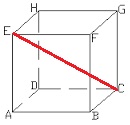
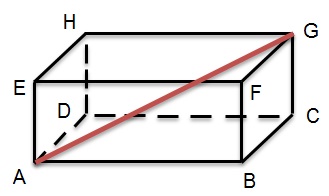
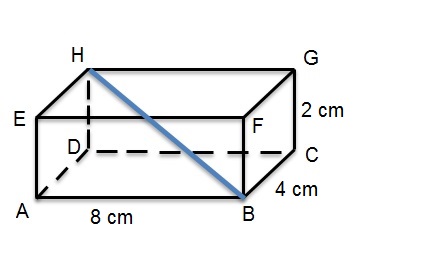
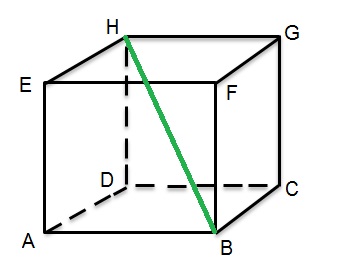
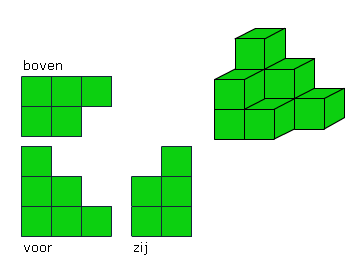
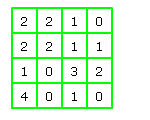
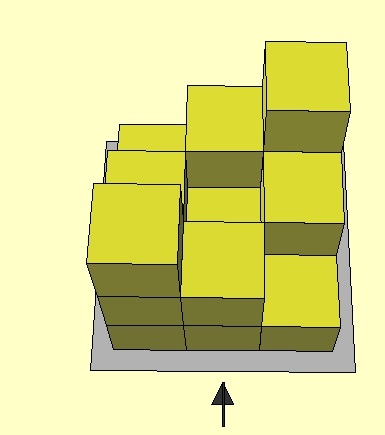
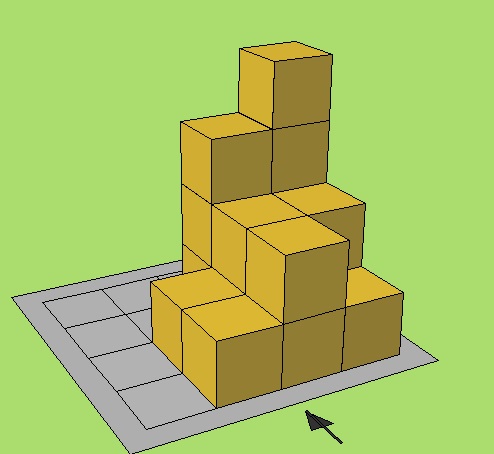
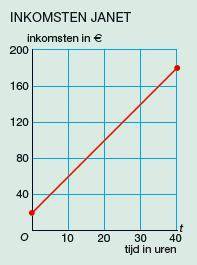
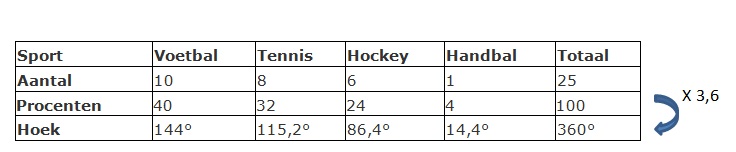
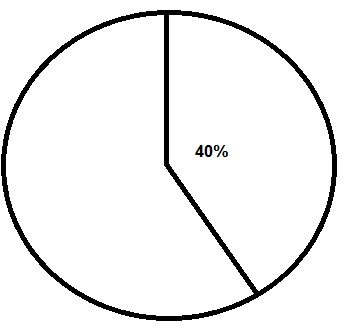
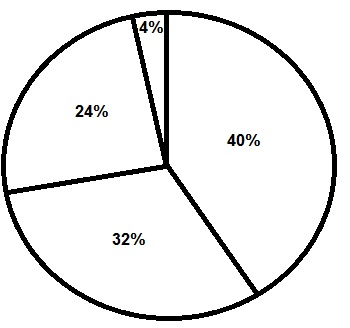
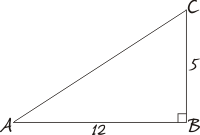
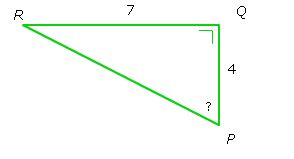
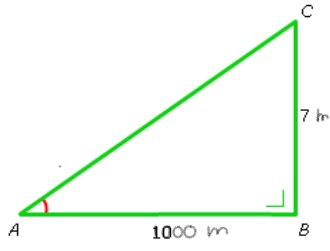
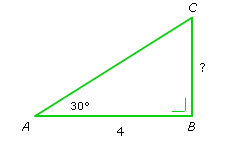
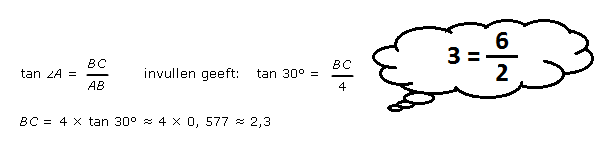
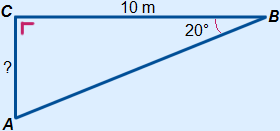
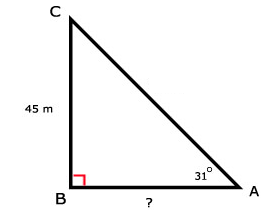
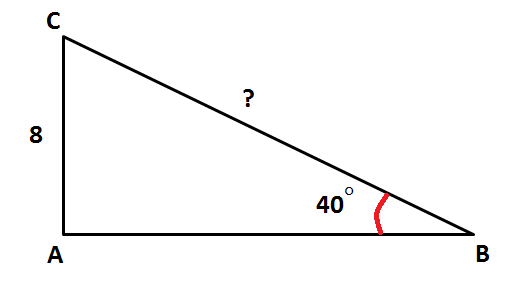
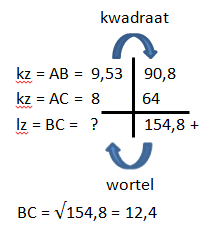
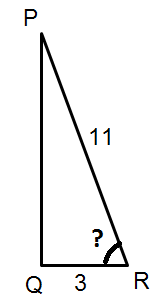
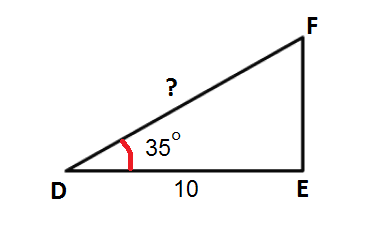
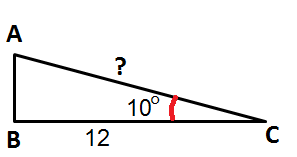
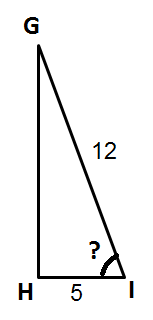
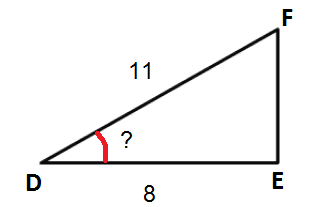
deel van 430.
Werkblad schaallijnen
Voorbeeld
