Op deze website vind je alle informatie voor het vak wiskunde voor de klas 4 mavo (gemengd)theoretische leerweg) voor leerlingen van 't Rijks.
Deze onlinemethode is gebaseerd op de stercolletie* van VO content, maar aangepast en verrijkt door de docenten van 't Rijks. Voor vragen of opmerkingen kunt u contact opnemen met Dhr. van der Giessen
* De stercollectie is ontwikkeld op basis van de kerndoelen basisvorming en de door de SLO ontwikkelde inhoud- en leerdoelspecificaties voor het vak wiskunde.
‘t Rijks is een middelbare school in Bergen op zoom voor mavo+, havo en vwo onderwijs.
Naast reguliere mavo- havo- en vwo opleidingen bieden wij ook een tto-profiel, loot-profiel, technasium en mavo+ route.
Ik klas 4 Mavo krijg je wiskunde gedurende 4 lesuren per week. Naast wiskunde worden ook onderdelen van rekenen behandeld. Voor wiskunde werken we deels uit de methode Getal&Ruimte en deels via deze website.
Een webpagina vastzetten op je plank. Als je vaak naar dezelfde webpagina gaat, kun je die vastzetten op je plank. Volg de stappen hieronder om wiskunde vast te maken als snelkoppeling.
Selecteer Meer Meer hulpprogramma'sSnelkoppeling maken.
Selecteer in de hoek van je scherm de Launcher .
Klik met de rechtermuisknop op het gewenste snelkoppelingsicoon in een lijst met apps en snelkoppelingen.
Selecteer Vastzetten op plank.
Tip: Als je het gewenste snelkoppelingsicoon niet kunt vinden, gebruik je de zoektoets of de Launcher-toets om het icoon te vinden door zoekwoorden te gebruiken.
Opdracht 2
Deze vragen gaan over de site waar je nu bent.
UIt hoeveel 'hoofdstukken' bestaat deze website?
Wat is het onderwerk van 'hoofdstuk 4'?
Hoeveel paragrafen heeft 'hoofdstuk 2'?
Over welk hoofdstuk weet jij al heel veel?
Opdracht 3
De website van wiskunde wordt gemaakt en onderhouden door de docenten van 't Rijks. De vragen kun je terug vinden op de website.
De vragen werk je uit in een A4-ruitjesschrift met kantlijn. Heeft jou schrift geen kantlijn, teken deze dan zelf (2 á 3 hoekjes)
Controleren van je werk doe je aan het eind van de paragraaf. Onderaan de pagina staat een link naar de antwoorden.
Scroll naar het eind van deze webpagina en bekijk de antwoorden maar eens.
Kennisbank
Wiskunde spullen.
Bij wiskunde heb je natuurlijk ook bepaalde spullen nodig. Hieronder staat wat je elke wiskundeles bij je moet hebben:
Schrift/ van A4 formaat met ruitjespapier van 1 cm bij 1 cm.
Pennen, blauw en rood, grijspotlood, gum en puntenslijper.
Geodriehoek.
Rekenmachine casio FX-82EX
Passer en 3 kleurpotlode (rood, groen en blauw)
Hoe kun je wiskunde leren?
Wiskunde is een doe vak. Dat houdt in dat alleen uit je hoofdleren (zoals je woordjes leert) niet genoeg is. Wiskunde leer je door oefenen.
Let goed op in de wiskunde lessen. Houdt je aandacht bij wat de docent vertelt en maak aantekeningen. Na de uitleg probeer je eerst zelf de opdrachten uit te werken. Kijk bijvoorbeeld nog eens goed naar je aantekeningen, lees de kennisbankjes en kijk met name naar de (aangeboden) stappenplannen die je gebruikt om de opdrachten uit te werken.
Lukt het niet zelfstandig, vraag dan (fluisterend) je buur eens om hulp, samen kom je er vaak al wel uit. Lukt het samen niet? Steek dan je vinger op en vraag je docent om hulp.
Thuis kun je de aangeboden youtubefilmpje nog eens gebruiken als uitleg moment.
Heb jij je werk af, kijk het daarna na. Wees streng voor jezelf. Ben je klaar met nakijken, probeer opgaven die je fout had nog eens op nieuw, of noteer de opgaven die je fout had en vraag dit nog eens na in de lessen. De foute opdrachten moet je zo ie zo herhalen voordat je gaat toetsen.
Veel succes!
Opdracht 4
Lees het kennisbankje hierboven maar eens door.
Noteer in je schrift welke tip jij het handigst vindt.
Opdracht 5
Kijk nog eens naar de afbeelding naast opdracht 3.
In deze afbeelding wordt vertelt wat wij als docenten van jou verwachten ten aanzien van het werken in je schrift.
Teken nu als jouw schrift geen kantlijn heeft op de komende vijf pagina's alvast kantlijnen.
Heb je tot nu toe tussen jou antwoorden nog geen regel overgeslagen in je schrift. Doe dit dan vanaf dit punt. Zo wordt je werk overzichtelijker.
Tot slot, ga je straks je werk nakijken, kijk dan na met een andere kleur pen of potlood. Houdt bij wat je fout doet zodat je dit kunt navragen in de volgende les en je beter kunt voorbereiden op toetsmomenten.
Klik op deze link om de antwoorden van deze paragraaf te openen.
Het PTA
H1 Lineair, exponentieel en omgekeerd evenredig
§1 Werken met verbanden
§2 Lineaire verbanden
§3 Groeifactoren
§4 Exponentiële verbanden
§5 Omgekeerd evenredig
§6 Gemengde opgaven
D-toets
Herhaling
H2 Goniometrie en Pythagoras
§1 Pythagoras
§2 Hellingsgetal en hellingspercentage
§3 Zijden berekenen met goniometrie
§4 Hoeken berekenen met goniometrie
§5 Werken in ruimtefiguren
§6 Gemengde opgaven
D-toets
Herhaling
H3 Verhoudingen en procenten
Verhoudingen in een tabel
Snelheid
Schaal
Percentage gevraagd
Percentage gegeven
Gemengde opgaven
D-toets
Herhaling
H4 Statistieken
Centrum maten
Frequentie, turfen en beelddiagram
Staafdiagram en histogram
Cirkeldiagram en steel-bladdiagram
Boxplot
Gemengde opgaven
D-toets
Herhaling
H5 Vlakke meetkunde
Eigenschappen vierhoeken
Hoeken meten en tekenen
Eigenschappen van driehoeken
Oppervlakte
Omtrek
Gemengde opgaven
D-toets
Herhaling
H6 Rekenen, meten en schatten
Metriekstelsel en vuistregels
Kaart en schaal
Symmetrie
Vergrotingsfactoren
Gemengde opgaven
D-toets
Herhaling
H7 Omgaan met verbanden
Wortel en machtsverbanden
Periodieke grafieken
Evenredig en omgekeerd evenredig
Lineaire en exponentieel
Gemengde opgaven
D-toets
Herhaling
H8 Ruimtemeetkunde
Uitslag
Inhoud balk, kubus en cilinder
Inhoud kegel en piramide
Samengestelde figuren
In de ruimte
Gemengde opgaven
D-toets
Herhaling
Voorbereiden SE
SE 3
SE 4
SE 4, het tweede SE in mavo 4 gaat over de hoofdstukken 4, 5 en 7.
De onderwerpen zijn:
Omgaan met verbanden
Goniometrie en Pythagoras
Meetkunde
Rekenen
Opdracht 1.
Amir heeft een nieuw huis gekocht. Hij gaat radiatoren kopen om de kamers in zijn huis te verwarmen.
De maximale warmte die een radiator kan afgeven is de warmtecapaciteit. De benodigde warmtecapaciteit van de radiator hangt af van de aanbevolen temperatuur en van de inhoud van de kamer. Op een internetpagina van een bedrijf dat radiatoren verkoopt, ziet Amir de volgende tabel:
Amir wil in zijn woonkamer twee radiatoren ophangen die samen minstens 6053 watt aan warmtecapaciteit leveren. Bereken hoeveel euro Amir minimaal moet betalen voor detwee radiatoren. Schrijf je berekening op. (3pnt)
Opdracht 2.
In onderstaande tabel staat de aanbevolen temperatuur per kamer.
Om de benodigde warmtecapaciteit te berekenen, gebruikt Amir de volgende woordformule:
warmtecapaciteit = temperatuur x 3,86 x inhoud ruimte.
Hierbij is warmtecapaciteit in watt, temperatuur is de aanbevolen temperatuur in °C en inhoud is de inhoud ruimte in m3
De woonkamer van Amir is 4 m bij 6,6 m en 2,7 m hoog. Laat met een berekening zien dat de benodigde warmtecapaciteit voorAmirs woonkamer afgerond 6053 watt is. (2pnt)
Opdracht 3.
Amir heeft een designradiator gezien die hij voor zijn badkamer wil kopen.
De inhoud van de badkamer is 32 m3 en de designradiator levert 2988 watt aan warmtecapaciteit.
Bereken hoeveel °C de temperatuur in de badkamer van Amir is met deze designradiator. Schrijf je berekening op en geef je antwoord in één decimaal.(3pnt)
Opdracht 4.
Marnix kookt een ei en zet het in een eierdopje in de keuken. De temperatuur van het gekookte ei neemt langzaam af volgens de woordformule:
temperatuur = 21 + 79 x 0,85tijd
Hierin is temperatuur de temperatuur van het gekookte ei in °C entijd de tijd in minuten na het koken.
Laat met een berekening zien dat het gekookte ei 5 minuten na het koken ongeveer 56 °C is.(1pnt)
Opdracht 5.
Als het gekookte ei lange tijd afkoelt, wordt de temperatuur van het gekookte ei gelijk aan de temperatuur in de keuken.
Hoeveel °C is de temperatuur in deze keuken? (1pnt)
Opdracht 6.
Neem onderstaande tabel over in je schrift. Vul de tabel in en teken daarna de bijbehorende grafiek. (4pnt)
Opdracht 7.
Marnix wil het gekookte ei pellen als de temperatuur van het gekookte ei net onder de 30 °C is. Na hoeveel hele minuten is de temperatuur van het gekookte ei voor het eerst onder de 30 °C? Schrijf je berekening op. (3 pnt)
Kennisbank.
Goniometrie en pythagoras.
Werk je binnen een rechthoekige driehoek, moet je een zijde of de grote van een hoek in graden berekenen, dan maak je vaak gebruik van de stelling van Pythagoras of de goniometrische verhouding.
Pythagoras
Goniometrie
Je werkt alleen met de lengte van de zijden.
Je weet 2 zijden en wil de 3e zijde berekenen
Je werkt met graden en zijden.
Je weet twee zijde en moet een hoek berekenen.
Je weet een zijde en een hoek, en moet een andere zijde berekenen.
Uitlegfilmpje
Uilegfilmpje
Opdracht 8.
De Alpe d’Huez is een berg in de Franse Alpen. Elk jaar wordt de actie Alpe d’HuZes gehouden: deelnemers beklimmen deze berg om zo veel mogelijk geld in te zamelen voor het goede doel. Dit kan hardlopend, wandelend of fietsend zijn. In 2017 werd bij deze actie 10,4 miljoen euro ingezameld.
In 2017 waren er 4200 deelnemers. Bereken het gemiddelde bedrag in euro dat per deelnemer werd ingezameld. Schrijf je berekening op. Rond je antwoord af op honderdtallen. (3pnt)
Opdracht 9
Het startpunt van de klim ligt in Le Bourg-d’Oisans op 799 m hoogte. Het eindpunt ligt op de Alpe d’Huez op 1860 m hoogte. De weg van Le Bourg-d’Oisans naar Alpe d’Huez is 13800 m. Zie de schets hieronder.
Bereken de aangegeven hellingshoek. Schrijf je berekening op.(4pnt)
Opdracht 10.
Bij het steilste deel van de weg heeft de helling over een afstand van 1 km een hellingshoek van 11,5o.
Bereken, zonder te meten, hoeveel meter het hoogteverschil tussen het begin en het eind van dit deel van de klim is. Schrijf je berekening op. (4pnt)
Opdracht 11.
Je ziet een dartbord en ernaast het middelste gedeelte van het dartbord. Dit middelste deel heet de bull’s eye en bestaat uit een cirkel met daaromheen een ring.
De buitenste ring van de bull’s eye heeft een buitendiameter van 31,8 mm en een binnendiameter van 12,7 mm.
Bereken hoeveel mm de oppervlakte van de buitenste ring van de bull’s eye is. Schrijf je berekening op. (4pnt)
Opdracht 12.
De omtrek van het hele dartbord is 142 cm.
Bereken hoeveel cm de diameter van het dartbord is. Schrijf je berekening op.
Opdracht 13.
Het dartbord bestaat uit meerdere sectoren. Alle sectoren zijn even groot. Je ziet een tekening van de sector van het getal 6 van dit dartbord.
MC = 170 mm, MA = 107 mm en AC = 63 mm. De lengte van de boog CD = 53 mm.
Bereken hoeveel mm de lengte van de boog AB is. Schrijf je berekening op. (3 pnt)
Yusef gaat darten en gooit de dartpijl in een rechte lijn in de bull’s eye. Hij laat precies boven punt B zijn dartpijl los
Opdracht 14.
Bereken, zonder te meten, hoeveel cm de dartpijl aflegt. Schrijf je berekening op. (3pnt)
Opdracht 15.
Bereken hoeveel graden hoek Y is. Schrijf je berekening op. (3pnt)
Opdracht 16.
Hierboven zie je een foto en een schematische tekening van een wip. Punt A en punt B zijn de uiteinden van de wip. De lengte AB is 405 cm. Het draaipunt T is het midden van AB en zit op een hoogte van 62,5 cm. Punt M ligt recht onder punt T
Bereken, zonder te meten, hoeveel cm de lengte van AM is. Schrijf je berekening op.(4pnt)
Opdracht 17.
Anniek (A) en Bente (B) zitten op de uiteinden van de wip. Ze gaan regelmatig omhoog en omlaag. Op de uitwerkbijlage is in een assenstelsel de grafiek getekend die de hoogte van Anniek boven de grond weergeeft.
Na het omhoog gaan, staat de wip even stil. Hoeveel seconden staat de wip dan even stil? (1 pnt)
Hoeveel keer gaat Anniek omhoog in één minuut? Laat zien hoe je aan je antwoord komt. (2pnt)
Opdracht 19.
Teken in hetzelfde assenstelsel op de uitwerkbijlage de grafiek die de hoogte van Bente boven de grond weergeeft. Teken de grafiek van 0 tot 10 seconden. (3pnt)
Opdracht 20.
Bereken de amplitude van de grafiek van Bente. Schrijf je berekening op. (3pnt)
Opdracht 21.
Een selfie is een foto waar degene die hem maakt ook zelf op staat. In het jaar 2014 waren er meerdere wereldrecords die te maken hadden met selfies.
Microsoft had het wereldrecord ‘meeste mensen op een selfie’, zie de foto. In totaal stonden 1151 mensen op deze selfie. Deze selfie wordt afgedrukt op een foto van 10 bij 15 cm.
Bereken hoeveel mensen er gemiddeld op 1 cm staan. Schrijf je berekening op. (2pnt)
Opdracht 22.
Het wereldrecord ‘meeste selfies in één uur’ stond op naam van de Britse Lee Goodfellow, die 657 selfies maakte in één uur. Bereken hoeveel seconden Lee gemiddeld nodig had om één selfie te maken. Schrijf je berekening op. (2pnt)
Opdracht 23.
De Turkse Atasun Optik had met 103690 ‘grootste collectie selfies’. Atasun maakte elke dag 50 selfies.
Bereken hoeveel jaar hij nodig had om dit wereldrecord te halen. Schrijf je berekening op. (2pnt)
Opdracht 24.
Makati City in de Filipijnen had de meeste mensen die weleens een selfie maakten, namelijk 258 selfiemakers per 100000 mensen. In totaal had Makati City 610000 inwoners in het jaar 2014. Bereken hoeveel selfiemakers er in totaal in Makati City woonden in het jaar 2014. Schrijf je berekening op. (3pnt)
Opdracht 25.
Biologen hebben ontdekt dat bossalamanders steeds kleiner worden. Vanaf het jaar 1980 wordt voor het berekenen van de lengte van een gemiddelde bossalamander de volgende formule gebruikt:
L = 9,75 x 0,99t
Hierin is L de lengte in cm en t het aantal jaren met t = 0 op 1 januari 1980.
Hoeveel cm was de lengte van de bossalamander op 1 januari 1980? (1pnt)
Opdracht 26.
Een bioloog beweert dat de lengte van de bossalamander in het jaar 2000 met 25% is afgenomen ten opzichte van het jaar 1980. Laat met een berekening zien of de bewering van de bioloog klopt met de formule. (4pnt)
Opdracht 27.
Met hoeveel procent neemt de lengte van de bossalamander per jaar af? (1pnt)
Opdracht 28.
Bereken op 1 januari van welk jaar de bossalamander volgens de formule voor het eerst kleiner is dan 7,5 cm. Schrijf je berekening op. (4 pnt)
Opdracht 29.
Een groep van 10 leerlingen en 2 docenten gaat met de trein van Amsterdam naar Kopenhagen. De trein vertrekt om 19.01 uur. De treinreis duurt 15 uur en 6 minuten. Hoe laat komt de trein de volgende dag aan in Kopenhagen? (2pnt)
Opdracht 30.
De enkele treinreis van Amsterdam naar Kopenhagen kost € 59 per persoon. In de nachttrein zijn wagons met slaapruimtes, waarvoor je extra moet betalen. De leerlingen slapen in een couchette 6 en een couchette 4. De docenten slapen in een sleeper 2. In de tabel staan de extra kosten. Voor de hele groep moet eenmalig € 37 reserveringskosten betaald worden..
Bereken hoeveel euro de totale kosten van de hele groep zijn voor de enkele treinreis van Amsterdam naar Kopenhagen. Schrijf je berekening op. (3pnt)
Opdracht 31.
De trein terug vertrekt om 18.10 uur uit Kopenhagen en komt de volgende dag om 09.59 uur aan in Amsterdam. Hoeveel minuten duurt de treinreis terug langer of korter dan de heenreis? Laat zien hoe je aan je antwoord komt. (3pnt)
Opdracht 32.
Kopenhagen ligt in Denemarken en daar wordt betaald met Deense kronen. 1 euro is 7,4352 Deense kronen. De terugreis kost in totaal 9426,70 Deense kronen. Bereken hoeveel euro dit is. Schrijf je berekening op. (2pnt)
Opdracht 33.
Op de foto staan verschillende drinkpakjes in de vorm van een prisma. Hieronder is het voorvlak getekend met de maten in cm. Het voorvlak is symmetrisch. De hoogte van het voorvlak is 6,5 cm. Op de uitwerkbijlage staat het voorvlak op ware grootte.
In een van de drinkpakjes zit sinaasappelsap. Op het voorvlak van het pakje is een sinaasappelschijf getekend.
Teken in het voorvlak op de uitwerkbijlage een zo groot mogelijke halve cirkel en verdeel deze halve cirkel in vier gelijke delen. (3pnt)
Opdracht 34.
Bereken, zonder te meten, hoeveel cm de omtrek van het voorvlak is. Schrijf je berekening op. (5pnt)
Opdracht 35.
Bereken hoeveel cm2 de oppervlakte van het voorvlak is. Schrijf je berekening op. (3 pnt)
Opdracht 36.
De inhoud van het drinkpakje is 170 ml. Bereken hoeveel cm de diepte van het drinkpakje is. Schrijf jeberekening op en geef je antwoord in één decimaal. (2 pnt)
*Als je geen antwoord hebt gevonden bij vraag 35, neem dan voor de oppervlakte van het voorvlak 63 cm.
Opdracht 37.
In een speeltuin staat een kabelbaan. Lune gaat van de kabelbaan af. In25 meter afgelegd. Bereken haar gemiddelde snelheid in km per uur. Schrijf je berekening op. (3pnt)
Opdracht 38.
Vanaf startpunt S rolt een katrol K langs een kabel naar beneden. Als Lune van de kabelbaan gaat, is de hoogte van de katrol K te berekenen met de formule:
Hoogte = 3,6 - \(\sqrt{(0,31 \times tijd)} \)
Hierin is hoogte in meters en tijd in seconden na de start.
Laat met een berekening zien dat de katrol zich na 3 seconden op een hoogte van afgerond 2,6 meter bevindt. (1pnt)
Opdracht 39.
Neem onderstaande tabel over in je schrift. Vul de tabel in met behulp van de formule bij vraag 38.
Teken daarna de bijbehorende grafiek. (4pnt)
Opdracht 40.
Aan de katrol zit een stang met onderaan een zitje. De afstand tussen het zitje en de katrol is 1,75 meter. Bereken na hoeveel seconden het z itje 1 meter boven de grond is. Geef je antwoord in één decimaal. Schrijf je berekening op.
Het arrangement 4 Vmbo-tl Wiskunde is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2022-02-08 12:06:36
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
‘t Rijks is een middelbare school in Bergen op zoom voor mavo+, havo en vwo onderwijs.
Meer hulpprogramma's 
.
of de Launcher-toets 
om het icoon te vinden door zoekwoorden te gebruiken.
De website van wiskunde wordt gemaakt en onderhouden door de docenten van 't Rijks. De vragen kun je terug vinden op de website.
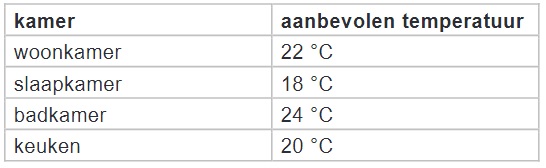
Marnix kookt een ei en zet het in een eierdopje in de keuken. De temperatuur van het gekookte ei neemt langzaam af volgens de woordformule:
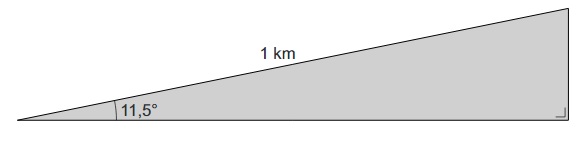
De Alpe d’Huez is een berg in de Franse Alpen. Elk jaar wordt de actie Alpe d’HuZes gehouden: deelnemers beklimmen deze berg om zo veel mogelijk geld in te zamelen voor het goede doel. Dit kan hardlopend, wandelend of fietsend zijn. In 2017 werd bij deze actie 10,4 miljoen euro ingezameld.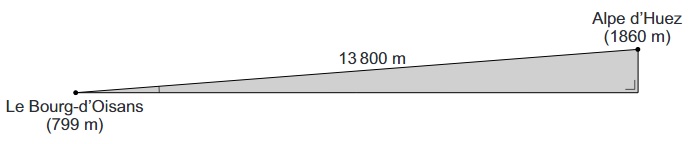
Een selfie is een foto waar degene die hem maakt ook zelf op staat. In het jaar 2014 waren er meerdere wereldrecords die te maken hadden met selfies.
Biologen hebben ontdekt dat bossalamanders steeds kleiner worden. Vanaf het jaar 1980 wordt voor het berekenen van de lengte van een gemiddelde bossalamander de volgende formule gebruikt:
Een groep van 10 leerlingen en 2 docenten gaat met de trein van Amsterdam naar Kopenhagen. De trein vertrekt om 19.01 uur. De treinreis duurt 15 uur en 6 minuten. Hoe laat komt de trein de volgende dag aan in Kopenhagen? 
