Je hebt hele getallen: bijvoorbeeld 7 of 23 of 100. Je hebt ook getallen met een komma:
bijvoorbeeld 0,4 of 12,5 of 23,75. 0,4 spreek je uit als 0 komma 4.
Op een rekenmachine type je in een punt in plaats van een komma.
Je ziet dan 0.4 of 12.5 of 23.75 op je scherm.
De cijfers achter de komma heten decimalen.
0,4 en 12,5 hebben één decimaal.
23,75 heeft twee decimalen.
0,4 en 12,5 en 23,75 heten decimale getallen.
Het getal 2,1 is hetzelfde als 2,10 en 2,100 enz. Een extra nul achteraan de decimalen verandert de waarde van het getal niet. Het is soms wel handig om zo'n extra nul erbij te zetten, zodat het getal kunt vergelijken met andere getallen.
Zo is het getal 1,21 groter dan het getal 1,2, want 1,2 is hetzelfde als 1,20. Nu kun je duidelijk zien dat 1,21 > 1,20.
Neem bijvoorbeeld het getal 1,18. Dit is weer kleiner dan 1,2, want 1,18 < 1,20.
Je kan dus altijd nullen achter een decimaal getal zetten om erachter te komen of een getal groter of kleiner is dan een ander decimaal getal.
Er bestaan tekens voor groter dan, kleiner dan en gelijk aan.
Het teken < betekent is kleiner dan
Het teken > betekent is groter dan
Het teken = betekent is gelijk aan
4 < 7 betekent 4 is kleiner dan 7
18 > 17 betekent 18 is groter dan 17
2 + 4 = 6 betekent 2 + 4 is gelijk aan 6.
Vuistregels
De cijfers achter de komma noem je decimalen.
Je kunt nullen achter een decimaal getal zetten om erachter te komen of een getal groter of kleiner is dan een ander decimaal getal.
Voorbeeld vraag
a. Is 10,93 groter of kleiner dan 10,9298?
b. Is 104,0528 groter of kleiner dan 104,08?
Uitwerking:
a. Groter. 10,93 kan je ook schrijven als 10,9300. Nu weet je 10,9300 > 10,9298. 10,93 is dus groter dan 10,9298.
b. Kleiner. 104,08 kan je ook schrijven als 104,0800. Nu weet je dat 104,0528 < 104,0800. 104,0528 is dus kleiner dan 104,08.
Uitleg en opgaven Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De cijfers in een getal hebben een waarde, die afhangt van de plaats in het getal. Een voorbeeld:
In het getal 537 vijfhonderdzevenendertig hebben de cijfers de volgende waarde:
de 5 is 5 x 100 = 500 waard
de 3 is 3 x 10 = 30 waard
de 7 is 7 x 1 = 7 waard
Voor de waarde van een cijfer in een getal hebben we namen:
de 7 is 7 waard, dit zijn de EENHEDEN
de 3 is 30 waard, dit zijn de TIENTALLEN
de 5 is 500 waard, dit zijn de HONDERDTALLEN
In het getal 2345,67 hebben de cijfers de volgende waarde:
de 2 is 2 x 1000 = 2000
de 3 is 3 x 100 = 300
de 4 is 4 x 10 = 40
de 5 is 5 x 1 = 5
de 6 is 6 x 100 = 0,6
de 7 is 7 x 10 = 0,07
Maak opdracht 5 en 6 van stencil H1
1.3 Breuken
Breuken vereenvoudigen:
Schrijf breuken altijd zo eenvoudig mogelijk op. Je rekenmachientje doet dit automatisch.
Om breuken te vergelijken, op te tellen of af te trekken moeten die breuken dezelfde noemer hebben.
Het gelijk maken van de noemers heet gelijknamig maken.
Voorbeeld: welke breuk is groter? 1/5 of 2/9?
Uitwerking:
Maak de breuken eerst gelijknamig. 1/5=9/45 en 2/9=10/45.
Nu zie je dat 9/45 kleiner is dan 10/45. In wiskundetaal noteer je: 9/45 < 10/45.
Breuken optellen en aftrekken:
Op je rekenmachine zit een speciale toets om breuken in te voeren.
Bij vermenigvuldigen moet je de tellers en de noemers van breuken met elkaar vermenigvuldigen. Een gemengde breuk moet je eerst als gewone breuk herschrijven. Als je eenmaal kunt vermenigvuldigen is het delen met breuken makkelijk.
Voorbeeld: 1 1/3x1/5=4/3x1/5=4/15
Breuken vermenigvuldigen:
In de instructievideo wordt uitgelegd dat je teller met teller en noemer met noemer vermenigvuldigt.
Voorbeeld:
3/4x2/7=
twee gewone breuken vermenigvuldigen
Stap 1
3x2/4x7=
teller maal teller en noemer maal noemer
Stap 2
6/28=3/14
vereenvoudig als nodig
SOM: 2/3 van alle leerlingen heeft vandaag een korte broek aan. Hoe bereken je 2/3 van 159?
Je kunt dit op 2 manieren uitrekenen. 159:3 x 2 = 106 leerlingen of 2/3 x 159 = 106 leerlingen.
Dus 4/5 van de 206 is: 4/5 x 206 = 164,8 of 206:5 x 4 = 164,8.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Maak opdracht 8 t/m 13 van stencil H1. Je mag je rekenmachine gebruiken.
1.4 Afronden
In veel van de sommen die je gaat maken zal je gevraagd worden om je antwoord af te ronden.
Hiervoor is het belangrijk dat je de regels voor het afronden van een getal goed begrijpt.
Afronden
Als je afrondt op een 2 decimalen kijk je naar het derde decimaal. Wil je afronden op 3 decimalen, dan kijk je naar het vierde decimaal. Je kijk dus altijd naar het eerstvolgende decimaal. Is dit decimaal een 4 of lager, dan hoef je niet te doen. Is dit decimaal een 5 of hoger dan wordt het cijfer ervoor 1 hoger.
Bij het afronden van getallen, kun je dus de volgende stappen aanhouden:
Ga na waarop je moet afronden.
Kijk naar het eerstvolgende getal/decimaal.
Bij een getal van 4 of lager: hoef je niets te doen.
Bij een getal van 5 of hoger: wordt het cijfer ervoor 1 hoger.
Bijvoorbeeld.
a. Rond 6,53489 af op 3 decimalen. Antwoord: 6,535
b. Rond 6,53489 af op 2 decimalen. Antwoord: 6,53
c. Rond 6,53489 af op 1 decimalen. Antwoord: 6.5
d. Rond 6,53489 af op een geheel getal. Antwoord: 7.
Uitleg en opgaven afronden
Uitleg en opgaven
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Om te rekenen met verhoudingen maak je gebruik maken van een verhoudingstabel.
In een verhoudingstabel blijft de verhouding gelijk als je boven én onder met hetzelfde getal vermenigvuldigt of deelt.
Bijvoorbeeld:
Wel of geen verhoudingstabel:
In een verhoudingstabel wordt boven en onder met hetzelfde getal vermenigvuldigd of door hetzelfde getal gedeeld.
Voorbeeld:
De bovenste is wel een verhoudingstabel, want 3×4=12 en 7×4=28. Naar 18 is het makkelijkst vanuit 3. 3×6=18 en 7×6=42
De onderste is geen verhoudingstabel. De achterste getallen kloppen wel (2×10=20 en 5×10=50), maar de middelste getallen kloppen niet. Want:
2×3=6, maar 5×3=15 en er staat 9 ipv 15. Je kunt dus niet zeggen:
2+4=6 en 5+4=9, want je mag alleen x of : gebruiken.
Prijs berekenen:
*Let op: geldbedragen rond je af op 2 decimalen.
In de winkel kost 150 gram gerookte worst € 0,99.
Met behulp van een verhoudingstabel kun je uitrekenen wat 100 gram kost.
Stappenplan:
Stap 1
Vul in wat je weet en waar je naar toe wilt.
...
...
gewicht in gram
150
100
prijs in €
0,99
?
...
...
Stap 2
Zet tussen twee getallen op dezelfde rij een 1.
In dit geval kan het alleen tussen 150 gram en 100 gram.
...
...
gewicht in gram
150
1
100
prijs in €
0,99
?
...
...
Stap 3
Bepaal een route van 150 naar 100 gram.
Vul bij de pijlen in wat je moet doen.
÷ 150
× 100
gewicht in gram
150
1
100
prijs in €
0,99
?
...
...
Stap 4
Neem de rekenstappen over bij de onderste pijlen en bereken het antwoord.
÷ 150
× 100
gewicht in gram
150
1
100
prijs in €
0,99
0,66
÷ 150
× 100
Als 150 gram worst € 0,99 kost, dan betaal je voor 100 gram worst € 0,66.
De tussenuitkomst onder de 1 schrijven we niet op, we berekenen in één keer 0,99 : 150 × 100 = 0,66.
Prijzen vergelijken:
Een verhoudingstabel kun je goed gebruiken om prijzen met elkaar te vergelijken.
Voorbeeld:
Bij koffiewinkel Het zwarte bakkie betaal je € 3,90 voor een pond Arabica koffie.
Bij de koffiewinkel De koffieboon kost anderhalf pond Arabica koffie € 5,80.
Bij welke winkel is de Arabica het voordeligst?
Uitwerking:
Maak twee verhoudingstabellen en reken de prijs uit voor een gelijk gewicht, bijvoorbeeld per ons.
Het zwarte bakkie
De koffieboon
÷ 500
× 100
gram
500
1
100
prijs
3,90
?
÷ 500
× 100
÷ 750
× 10
gram
750
1
100
prijs
5,80
?
÷ 750
× 10
Bij Het zwarte bakkie betaal je voor 1 ons Arabica 3,90 : 500 × 100 = € 0,78.
Bij De koffieboon betaal je voor 1 ons Arabica 5,80 : 750 × 100 = € 0,77.
De Arabica is goedkoper bij De koffieboon.
Uitleg en opgaven Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Er zijn veel verschillende soorten figuren. Sommigen zijn plat, zoals een cirkel, vierkant, rechthoek, driehoek, etc. en anderen zijn ruimtelijk. Deze figuren zijn de ruimtefiguren. Een aantal daarvan moeten we kennen.
Bij het tekenen van deze figuren stippelen we normaal gesproken alle lijnen die we niet echt kunnen zien omdat ze aan de achter- of onderkant zitten.
Een kubus heeft 6 platte vlakken.
Een balk heeft ook 6 platte vlakken.
Een bol heeft 1 gebogen vlak.
Een kegel heeft 1 plat vlak en 1 gebogen vlak.
Een cilinder heeft 2 platte vlakken en 1 gebogen vlak.
Uitleg en opgaven ruimtefiguren
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Een uitslag is een bouwplaat. Je kunt een figuur op verschillende manieren openknippen, en dus verschillende uitslagen krijgen. Zo zijn in de onderstaande figuur 8 uitslagen weergegeven. Echter, ze kloppen niet allemaal! Je kunt de bouwplaten uitknippen en in elkaar zetten. Dan zie je dat bij de linkse uitslagen er wél een kubus wordt gevormd en bij de rechtse twee niet. De twee rechtse zijn dan ook fout. Er zijn overigens nog meer goede (en foute) uitslagen mogelijk!
Uitleg en opgaven uitslagen
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De kubus is een ruimtefiguur die bestaat uit 6 precies even grote vierkanten.
Ribben, vlakken, hoekpunten
Figuren hebben verschillende kanten. Een voorkant, achterkant, zijkanten… Deze kanten zijn ook wel vlakken. Een vlak van een ruimtefiguur wordt omgeven door ribben. Hoekpunten hebben altijd een letter als naam.
In een kubus of rechthoek begint die belettering altijd bij de hoekpunt die het meeste linksonder vooraan ligt. Dat is hoekpunt A. Het volgende hoekpunt (B) ligt daar naast, tegen de klok in. Je blijft tegen de klok in doorgaan met nummeren tot je weer bij A bent. Dan komt er recht boven A het volgende hoekpunt te liggen, en weer tegen de klok in doorgaan.
Een ribbe krijgt de naam van de hoekpunten waar hij tussen in ligt. Zo heet de ribbe die tussen A en B ligt ribbe AB, of ribbe BA, dat is ook goed.
Een grensvlak heeft ook een naam. Bij een grensvlak moet je vaak vier of meer hoekpunten opgeven. Die hoekpunten liggen wel vast in een bepaalde volgorde. De rechterzijkant van een kubus heet bijvoorbeeld BCGF. Je begint bij één hoekpunt (B) en gaat dan rond en schrijft op welke hoekpunten je tegen komt. BFGC is dan dus ook goed. Je mag NIET kriskras door de figuur gaan. BGFC is bijvoorbeeld dus niet goed.
Overzichtstabel
Hieronder kun je zien hoeveel vlakken, hoekpunten en ribben elke ruimtefiguur heeft.
Wiskundige naam
Aantal platte vlakken
Aantal gebogen vlakken
Ribben
Hoekpunten
Vorm grensvlakken
Balk
6
0
12
8
Rechthoek
Kubus
6
0
12
8
Vierkant
Bol
0
1
0
0
-
Cilinder
2
1
2
0
Cirkel / Rechthoek
Kegel
1
1
1
1
Cirkel
Piramide
Verschilt
0
Minstens 6
Minstens 4
Driehoeken / grondvlak verschilt
Prisma
Verschilt
0
Minstens 9
Minstens 6
Rechthoeken / grondvlak verschilt
Uitleg en opgaven grensvlakken en ribben
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Een piramide lijkt op een kegel maar dan niet met een rond grondvlak maar met een grondvlak met hoeken zoals een vierkant of een driehoek. Een piramide hoeft echter niet altijd 4 zijvlakken te hebben! Dit kunnen er ook 3 zijn, of meer dan vier!
PRISMA
Een prisma is de lastigste vorm. Een prisma bestaat uit een grondvlak en een bovenvlak die recht boven elkaar liggen. Tussen die vlakken liggen alleen maar rechthoeken. Er zitten dus geen uitsteeksels aan de figuur. Een prisma bestaat alleen maar uit rechte vlakken. Een prisma kan dus ook veel verschillende vormen hebben. Denk aan een tentje of een huis.
Driehoek tekenen:
Zo teken je ∆ABC met AB = 2,5 cm, AC = 1 cm en BC = 2 cm1.
1 Teken een lijn AB van 2,5 cm
2. Neem tussen de passerpoten een afstand van 1 cm. Zet de passerpunt in A en teken een cirkel.
3. Neem tussen de passerpoten een afstand van 2 cm. Zet de passerpunt in B en teken een deel van de cirkel.
4. Het punt waar de cirkels elkaar snijden, daar ligt punt C. Zet daar een stip en verbind punt A met C en verbind punt B met C.
Maak opdracht 25 tot en met 30 + 32 + 33 van stencil H2.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Een lijn is recht en heeft geen eindpunten. Een lijn kan dus oneindig lang doorlopen.
Lijnen worden aangegeven met een kleine letter.
Een lijnstuk heeft wel eindpunten. Er zijn 2 eindpunten en tussen deze 2 punten bevindt zich het lijnstuk. Eindpunten van een lijnstuk worden aangegeven met hoofdletters.
Lijnen die elkaar nooit snijden worden evenwijdige lijnen genoemd.
Evenwijdige lijnen snijden elkaar niet, zelfs al worden ze tot in het oneindige verlengd.
Deze lijnen zijn parallel aan elkaar.
Evenwijdige lijnen noteer je met het teken //.
Als 2 lijnen een rechte hoek met elkaar maken zeggen we dat de lijnen loodrecht op elkaar staan.
Het tekenen van loodrechte lijnen en evenwijdige lijnen kun je vinden in de powerpoint.
Uitleg en opgaven
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Het maakt voor de oplossing veel uit of je begint met optellen of vermenigvuldigen.
Afgesproken is dat vermenigvuldigen en delen voor optellen en aftrekken gaan.
De voorrangsregel op een rij:
1. Tussen de haakjes;
2. Vermenigvuldigen of delen van links naar rechts;
3. Optellen of aftrekken van links naar rechts.
Schrijf alle tussenstappen onder elkaar op, onderstreep steeds de bewerking die voorrang heeft en zet het antwoord na het laatste '='-teken.
Voorbeeld 1
Bereken met behulp van tussenstappen (5 - 3) × 3 =
Stap 1
(5 - 3) × 3 =
Stap 2
2 × 3 = 6
Voorbeeld 2
Bereken met behulp van tussenstappen 6 × (3 + 4) : 2 - 8 =
Stap 1
6 × (3 + 4) : 2 - 8 =
Stap 2
6 × 7 : 2 - 8 =
(let op: haakjes vallen weg)
Stap 3
42 : 2 - 8 =
Stap 4
21 - 8 = 13
Maak opdracht 3 tot en met 5 van stencil H5.
Uitleg en opgaven voorrangsregels
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leren: 50% = 1/2 20% = 1/5 Tip: gebruik je rekenmachine!
33,3% = 1/3 12,5% = 1/8
25% = 1/4 10% = 1/10
Van breuk naar percentage (procenten):
Doe -> breuk x 100%
Vb: 7/20 x 100% = 35%
Van percentage naar breuk:
Schrijf 30% als een breuk:
30% = 30 : 100 = 3/100 = 3/10 = 0,3
Vereenvoudig met rekenmachine:
30/100 -> 30 [ab/c] 100 = 3/10
Aantal procenten van iets:
40% van €120,00
40% = 40 : 100 = 0,4
0,4 x 120 = € 48,00
Maak opdracht 1 tot en met 4 van stencil H7.
7.2 Rekenen met procenten
* Voorbeeld 1:
Hoe bereken je het aantal jongens in een klas als je weet dat er ongeveer 30% jongens zitten in een klas van 26.
In dit voorbeeld zijn de jongens het deel en is de klas het geheel. Te berekenen is het aantal jongens. Maak gebruik van een verhoudingstabel.
De jongens vormen ongeveer 30% van het geheel. De hele klas is 100%.
Stap 1
Zet de jongens als deel boven de klas als geheel in de tabel.
We zoeken de waarde van "?". heeft.
%
100
?
aantal
26
Stap 2
Zet het aantal van de klas in de tabel en de 1 er tussen in de bovenste rij.
%
100
1
30
aantal
26
Stap 3
Bepaal de route van 100 via 1 naar 26.
:100 x30
%
100
1
30
aantal
26
:100 x30
Stap 4
Bereken het aantal jongens, gebruik zonodig je rekenmachine.
:100 x30
%
100
1
30
aantal
26
0,26
7,8
:100 x30
Het aantal jongens is afgerond 8.
In feite heb je die 8 als volgt uitgerekend: 30: 100 × 26 = 7,8, dus 8 jongens.
* Voorbeeld 2:
Tijdens een concert zijn er 34000 plaatsen in het Gelredome. Bij het concert van Rihanna was 93,5% van de kaarten verkocht.
Hoeveel kaarten zijn dat?
%
100
1
93,5
aantal
34000
????
Je krijgt dan de berekening: 34000 : 100 x 93,5 = 31790 zitplaatsen.
Opgaven procenten
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
9% betekent 9 op de 100. In een klas met 100 leerlingen vormen 9 jongens ook precies 9% van de klas. Maar wat nu als je een klas hebt van 38 leerlingen?
Hoe bereken je het percentage jongens als er 9 jongens is een klas van 38 leerlingen zitten?
Stap 1
Maak de verhoudingstabel en zet de getallen in de tabel.
%
100
aantal
38
1
9
Stap 2
Bepaal de route van 38, via 1 naar 9.
:38 x9
%
100
?
aantal
38
1
9
:38 x9
Stap 3
Bereken ?
:38 x9
%
100
2,63...
23,7
aantal
38
1
9
Het percentage jongens is 24%.
In feite heb je die 24% als volgt uitgerekend: 9 : 38 × 100 ≈23,7%
* Voorbeeld 2:
In Nederland kennen we 21 soorten vleermuizen. Hiervan zijn 9 soorten zeldzaam. Mart wil weten goeveel procent dat is.
%
100
???
aantal
21
1
9
Berekening: 100 : 21 x 9 = 42,9%
Nog een voorbeeldfilmpje:
Maak opdracht 15 tot en met 19 van stencil H7.
7.5 Afname en toename in procenten
* Toename in procenten:
In 2010 had een volleybalvereniging 69 leden. In 2011 is het aantal leden gestegen tot 87. Met hoeveel procent is het aantal leden toegenomen?
87 -69 = 18
%
100
26,1
aantal
69
1
18
100: 69 x 18 = 26,1%
* Afname in procenten:
Een jas is afgeprijsd van €152,- naar €75,-. Hoeveel procent is de jas goedkoper geworden?
Een grootheid is iets wat je kunt meten.
Voorbeelden zijn lengte, oppervlakte, tijd, inhoud en snelheid.
Eenheid
Een eenheid is waar je grootheden in meet.
Voorbeelden zijn meter, vierkante meter, jaar, liter en km/u.
Maak van het stencil H8 opdracht 1 tot en met 3.
8.2 Eenheden van lengte
Een lengte-eenheid staat voor een bepaalde lengte of afstand. Bij het omrekenen van eenheden, reken je met de stapgrootte. De standaardmaat is de meter.
Van groot naar klein: km hm dam m dm cm mm
De stapgrootte tussen de eenheden van lengte op de trap is steeds een factor 10.
Elke stap van 'groot naar klein' is keer 10 en van 'klein naar groot' is delen door 10.
Zo is 15 m gelijk aan 1500 cm,
want 15 x 10 x 10 = 1500 (2 stappen).
En zo is 12 dm gelijk aan 1,2 m,
want 12 : 10 = 1,2 (1 stap).
Kan Het DAmetje Met De Cm Meten.
Tabel
Eenheden van lengte
km = kilometer
1 km = 1000 m
hm = hectometer
1 hm = 100 m
dam = decameter
1 dam = 10 m
m = meter (standaardmaat)
1 m = 10 dm = 100 cm = 1000 mm
dm = decimeter
1 dm = 1/10 m = 0,1 m = 10 cm
cm = centimeter
1 cm = 1/100 m = 0,01 m = 10 mm
mm = millimeter
1 mm = 1/1000 m = 0,001 m
Maak daarna de opdrachten 4 t/m 7 van stencil H8.
Uitleg en opgaven lengtematen
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De oppervlakte is eenvoudig voor te stellen als het gebied binnen de gegeven wiskundige figuur. De oppervlakte bereken je met formules.
De oppervlakte wordt uitgedrukt in oppervlakte-eenheden.
Hoe groot is het weiland?
Dit weiland heeft een lengte van 200 meter en een breedte van 100 meter. Hoe groot is het stuk grond? Het is de bedoeling dat je de oppervlakte van het weiland berekent.
Een veelgebruikte maat voor oppervlakte is de vierkante meter. Dat is de grootte van een vierkant van 1 meter breed en 1 meter lang. Je schrijft ook wel 1 m2.
We gaan uitzoeken hoeveel vierkante meter de oppervlakte van het weiland is: om dit te kunnen bereken ga je opzoek naar de lengte en breedte; dus
De oppervlakte van het weiland is 100 x 200 m2 = 20.000 m2.
Eenheden van oppervlakte
Een oppervlakte-eenheid staat voor een bepaalde oppervlakte of grootte. Bij het omrekenen van eenheden, reken je met de stapgrootte. De standaardmaat is de vierkante meter.
De stapgrootte tussen de eenheden van oppervlakte op de trap is steeds een factor 100.
Elke stap van 'groot naar klein' is keer 100 en van 'klein naar groot' is delen door 100.
Zo is 6 m2 gelijk aan 60 000 cm2,
want 6 x 100 x 100 = 60 000 (2 stappen).
En zo is 3 dm2 gelijk aan 0,03 m2,
want 3 : 100 = 0,03 (1 stap).
Tabel
Eenheden van oppervlakte
km2 = vierkante kilometer
1 km2 = 1 000 000 m2 = 100 hm2
hm2 = vierkante hectometer
ha = hectare
1 hm2 = 10 000 m2 = 1 ha
dam2 = vierkante decameter
1 dam2 = 100 m2 = 1 are
m2 = vierkante meter (standaardmaat)
ca = centiare
De tabel laat zien dat een oppervlakte van 1 m2 overeenkomt met de oppervlakte van een vierkant met zijden van 1 m bij 1 m. In 1 are passen dus 100 vierkanten van 1 m2.
Maak opdracht 8 t/m 13 van stencil H8.
Uitleg en opgaven oppervlaktematen
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Een inhouds-eenheid staat voor een bepaalde inhoud of volume. Bij het omrekenen van eenheden, reken je met de stapgrootte. De standaardmaat is de liter.
De stapgrootte tussen de eenheden van inhoud op de trap is steeds een factor 10.
Elke stap van 'groot naar klein' is keer 10 en van 'klein naar groot' is delen door 10.
Zo is 2 l gelijk aan 2000 ml,
want 2 x 10 x 10 x 10 = 2000 (3 stappen).
Tabel
Eenheden van inhoud
hl = hectoliter
1 hl = 100 l
l = liter (standaardmaat)
dm3 = kubieke decimeter
1 l = 10 dl = 100 cl = 1000 ml = 1 dm3
dl = deciliter
1 dl = 1/10 l = 0,1 l
cl = centiliter
1 cl = 1/100 l = 0,01 l
ml = milliliter
cm3 = kubieke centimeter
1 ml = 1/1000 l = 0,001 l = 1 cm3
Voorbeeld 1:
In een zeephouder zit 1 liter vloeibare zeep. Per keer handen wassen wordt er 2,5 ml gebruikt. Na hoeveel keer is de zeephouder leeg?
Een massa-eenheid staat voor een bepaalde massa of een bepaald gewicht. Bij het omrekenen van de ene naar de andere eenheid, reken je met de stapgrootte. De standaardmaat is de gram.
De stapgrootte tussen de eenheden op de trap is steeds een factor 1000.
Elke stap van 'groot naar klein' is keer 1000 en van 'klein naar groot' is delen door 1000.
Zo is 2500 kg gelijk aan 2,5 ton,
want 2500 : 1000 = 2,5 (1 stap).
Tabel
Eenheden van massa of gewicht
ton
1 ton = 1000 kg
kg = kilogram
1 kg = 1/1000 ton = 0,001 ton
g = gram (standaardmaat)
1 g = 1/1000 kg = 0,001 kg
mg = milligram
1 mg = 1/1000 g = 0,001 g
Maak opdracht 18 tot en met 20 van stencil H8.
8.6 Eenheden van tijd
Een tijd-eenheid staat voor een bepaalde hoeveelheid tijd. Met eenheden van tijd kun je rekenen.
Voorbeelden:
1 jaar = 52 weken
52 weken = 12 maanden
1 week = 7 dagen
1 dag = 24 uur
1 uur = 60 minuten
1 minuut = 60 seconde
1 uur = 60 x 60 = 3600 seconden
1 dag = 24 x 3600 = 86 400 seconden
792 uren = 792 : 24 = 33 dagen
54 jaren = 54 x 12 = 648 maanden
Tabel
Eenheden van tijd
1 millennium = 1000 jaren
het meervoud van millennium is millennia
1 eeuw = 100 jaren
1 jaar = 4 kwartalen
1 jaar = 12 maanden
1 jaar is 365 dagen, of 366 dagen in een schrikkeljaar *
1 jaar is 52 weken + 1 dag, of + 2 dagen in een schrikkeljaar *
1 kwartaal = 3 maanden = 1/4 jaar
1 maand = 1/12 jaar
1 maand is 30 of 31 dagen, en in de maand
februari 28 dagen of 29 dagen in een schrikkeljaar *
1 week = 7 dagen
1 dag (etmaal) = 24 uur
1 uur = 60 minuten
1 minuut = 60 seconden
* Een schrikkeljaar komt om de vier jaar voor. Een 'gewoon' jaar heeft 365 (= 52 x 7 + 1) dagen, een schrikkeljaar heeft 366 dagen.
2,45 uur is niet 2 uur en 45 minuten, maar 2 uur en 0,45 x 60 = 27 minuten.
3,6 jaar = 3 jaar en 0,6 x 365 = 219 dagen.
Maak opdracht 21 t/m 24 van de stencils van H8.
8.7 Eenheden van snelheid
De snelheid wordt uitgedrukt in twee verschillende eenheden. Namelijk in een eenheid van lengte en een eenheid van tijd. Dit wordt een samengestelde eenheid genoemd.
afstand
[eenheid van lengte]
snelheid
=
---------
tijd
[eenheid van tijd]
Toelichting:
De (gemiddelde) snelheid is te berekenen door de afgelegde weg te delen door de tijd.
Stel dat een fietser een afstand aflegt van 9 km in 30 minuten. Wat is dan de snelheid per minuut en per uur?
De snelheid is dan 9 : 30 = 0,3 km/minuut. Lees 0,3 km per minuut.
De snelheid is dan 0,3 x 60 = 18 km/uur. Lees 18 km per uur.
Voorbeelden:
1 km = 1000 m en 1 m = 100 cm
1 uur = 60 minuten = 3600 seconden
16 m/uur = 16 x 100 = 1 600 cm/uur
15 000 m/sec = 15000 : 1000 = 15 km/sec
80 m/sec = 80 x 60 = 4800 m/minuut
4 200 m/uur = 4200 : 60 = 70 m/minuut
7 100 cm/sec = 7100 : 100 x 3600 = 255 600 m/uur
10 m/sec = 10 : 1000 x 3600 = 36 km/uur
Let goed op wanneer je bij het omrekenen moet vermenigvuldigen of delen.
De eenheden van snelheid zijn km/uur (kilometer per uur) en m/s (meter per seconde). Met een verhoudingstabel kun je de eenheden van snelheid omrekenen.
Nathan loopt 100 meter in 25 seconden.
Aanpak:
: 25 x 60 x 60
Tijd
25 sec.
1 sec.
1 min.
1 uur
Afstand
100 m
4 m
240 m
14400 m
: 25 x 60 x 60
Trucje:
x 3,6
---------------->
m/s km/uur
<-------------------
: 3,6
Maak opdracht 25 tot en met 28 van stencil H8.
8.8 Eenheden van informatie
Bij een aankoop van een nieuwe computer wil je weten wat de prestaties ervan zijn om een goede keuze te maken. Je kijkt dan onder meer naar het werkgeheugen en de opslagcapaciteit van de harde schijf. Deze worden uitgedrukt in de eenheid byte(s).
De byte is de standaardeenheid waarmee veel wordt gerekend. Voor de byte wordt een voorvoegsel geplaatst. Veel gebruikte voorvoegsels zijn: kilo, mega, giga en de tera. Zie de tabel hieronder
In het dagelijks leven wordt vaak gebruik gemaakt van formules. De meest gebruikte formules zijn woordformules.
Een glazenwasser moet bij een gebouw de ramen wassen. Hij rekent € 25,- voorrijkosten en ieder uur dat hij werkt rekent hij € 35,-.
We kunnen nu een formule maken: bedrag (in €) = 25 + 35 x aantal uren.
Je betaalt € 25 voorrijkosten en ieder uur komt er €35,- bij.
Op het moment dat deze glazenwasser 4 uur werkt krijgen we de volgende formule:
bedrag = 25+35x4
= € 165,00
Op het moment dat deze glazenwasser 8 uur werkt dan krijgen we de volgende formule:
bedrag = 25+35x8
= € 305,00
Wanneer we een woordformule hebben dan kunnen we deze formule korter opschrijven. Wanneer deze formule: bedrag (in €) = 25 + 35 x aantal uur elke keer weer moet opschrijven dan ben je heel lang bezig. We kunnen daarom alles afkorten.
Het aantal uur kunnen we afkorten met u. Het bedrag wordt dan b.
De nieuwe formule wordt dan: b = 25+35u.
Hierbij is b het bedrag en u het aantal uur.
Wanneer de glazenwasser 5 uur gewerkt heeft dan heeft hij verdient:
b = 25+35x5
b = € 200,00
Maak opdracht 4 en 5 van stencil H9.
Opgaven
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Een symmetrie-as is de lijn zó dat links en rechts van die lijn elkaars spiebelbeeld zijn. Dit soort symmetrie heet daarom spiegelsymmetrie, maar wordt ook somslijnsymmetrie genoemd.
Spiegelsymmetrie wordt ook wel vouwsymmetrie genoemd, omdat als je langs de symmetrie-as vouwt links precies op rechts valt. In de afbeelding hierboven zijn de symmetrie-assen in rood aangegeven.
Een gelijkbenige driehoek is een driehoek met twee even lange zijden. Die twee zijden noemen we ook wel de benen van de driehoek. Het hoekpunt waar de benen samenkomen is de top van de driehoek, de twee overige hoeken heten de basishoeken en de zijde tegenover de top noemen we de basis.
* Rechthoekige driehoek
Rechhoekige driehoeken hebben de volgende kenmerken
- Er zit precies één hoek in van 90 graden. Dit is een rechte hoek.
- De andere 2 hoeken zijn samen ook 90 graden. (In een driehoek zijn alle hoeken samen altijd 180 graden)
- Als de andere 2 hoeken allebei 45 graden zijn, is de driehoek ook gelijkbenig. (zie gelijkbenige driehoeken)
* Gelijkbenige driehoek
Een driehoek met twee gelijke zijden. Heeft één symmetrieas. De hoek waar de symmetrieas doorheen gaat is de tophoek. De andere twee hoeken, die gelijk van grootte zijn door de symmetrieas, noem je basishoeken. De twee basishoeken hebben dezelfde grootte.
* Gelijkzijdige driehoek
Een driehoek met drie gelijke zijden. Deze driehoek heeft drie symmetrieassen. De hoeken van deze driehoek zijn altijd alle drie 60°.
Maak opdracht 3 tot en met 5 van stencil H10.
Uitleg en opgaven
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Pak punt Q vast in de afbeelding hier boven. Draai de figuur zó dat hij er weer net zo uit ziet als eerst, maar dan gedraaid.
Als je Q één rondje laat draaien, hoe vaak is de figuur dan weer hetzelfde?
Als in één rondje 360° zit, om de hoeveel graden ziet het figuur er dan weer hetzelfde uit?
Wat je in de opdracht hiervoor hebt benoemd, is dat het figuur dat je daar draaide, draaisymmetrisch is. De kleinste draaihoek is het aantal graden waarna het figuur er weer hetzelfde uit ziet (het antwoord op vraag b).
Stappenplan: Kleinste draaihoek bepalen
1
Zet een punt in het midden van de figuur. Zet er de punt van je potlood op, zodat je blaadje kan draaien om dat punt.
2
Draai de figuur, totdat het voor het eerst er weer precies hetzelfde uit ziet
3
Bedenk hoe vaak dit gebeurt als je de figuur één rondje laat draaien
3 keer
4
Bereken hoeveel graden hoort bij deze kleinste draaihoek
360° ÷ 3 = 120°
Maak opdracht 10 tot en met 14 van stencil H10.
10.5 Schuifsymmetrie
Motief en patroon:
Het figuur wat je steeds terug vindt in schuifsymmetrische figuren noemen we een motief.
bijvoorbeeld het motief is dit:
Als je het figuur gaat schuiven krijg je uiteindelijk een patroon:
* Schuifsymmetrie bij lijnen:
Schuifsymmetrie: Als lijnen evenwijdig (parallel) zijn de hoeken gelijk.
Het arrangement Wiskunde leerjaar 1 kader is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteurs
Marleen Everhardus
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2018-04-03 09:15:24
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 3.0 Nederlands licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Decimale getallen
Decimale getallen
Breuken
Breuken
Breuken vergelijken
Breuken vergelijken
Afronden
Afronden
Verhoudingstabellen
Verhoudingstabellen
Ruimtelijke figuren
Ruimtelijke figuren
Uitslagen
Uitslagen
Grensvlakken en ribben
Grensvlakken en ribben
Cirkel
Cirkel
Plaatsbepalen op de kaart
Plaatsbepaling op de kaart
Codes
Codes
Coördinaten
Coördinaten
Negatief in het assenstelsel
Negatief in het assenstelsel
Lijn, lijnstuk en punt
Lijn, lijnstuk en punt
Hoeken
Hoeken
Hoeken meten
Hoeken meten
Kijklijnen en kijkhoeken
Kijklijnen en kijkhoeken
Hoeken tekenen
Wat is negatief
Wat is negatief?
Optellen met negatieve getallen
Optellen met negatieve getallen
Aftrekken met negatieve getallen
Aftrekken met negatieve getallen
Vermenigvuldigen met negatieve getallen
Vermenigvuldigen met negatieve getallen
Voorrangsregels
Voorrangsregels
Lineair verband
Lineair verband 1
Verhoudingstabellen
Verhoudingstabellen
Procenten
Procenten
Rekenen met procenten
Rekenen met procenten
Rekenen met procenten
Procenten erbij of eraf
Procenten erbij of eraf
Lengtematen
Lengtematen
Omtrek
Omtrek
Oppervlaktematen
Oppervlaktematen
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Uitleg en opgaven
Uitleg en opgaven
extrastof H1 Getallen (6).doc
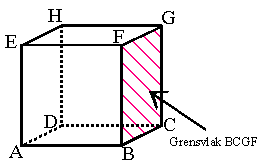
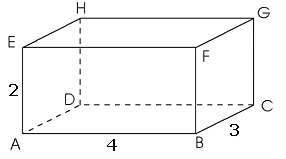
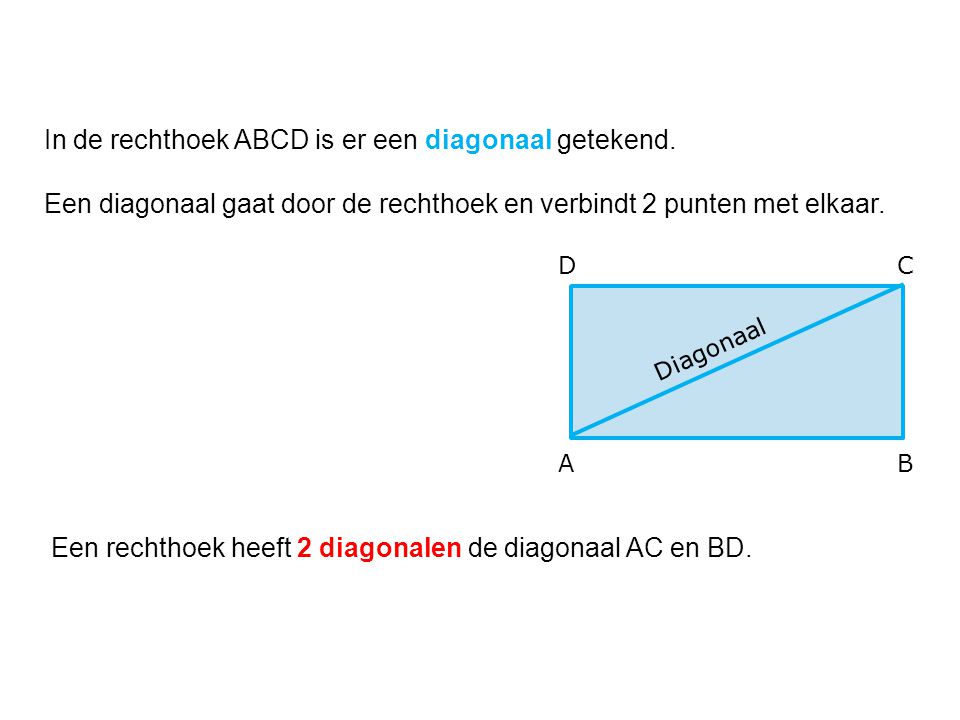
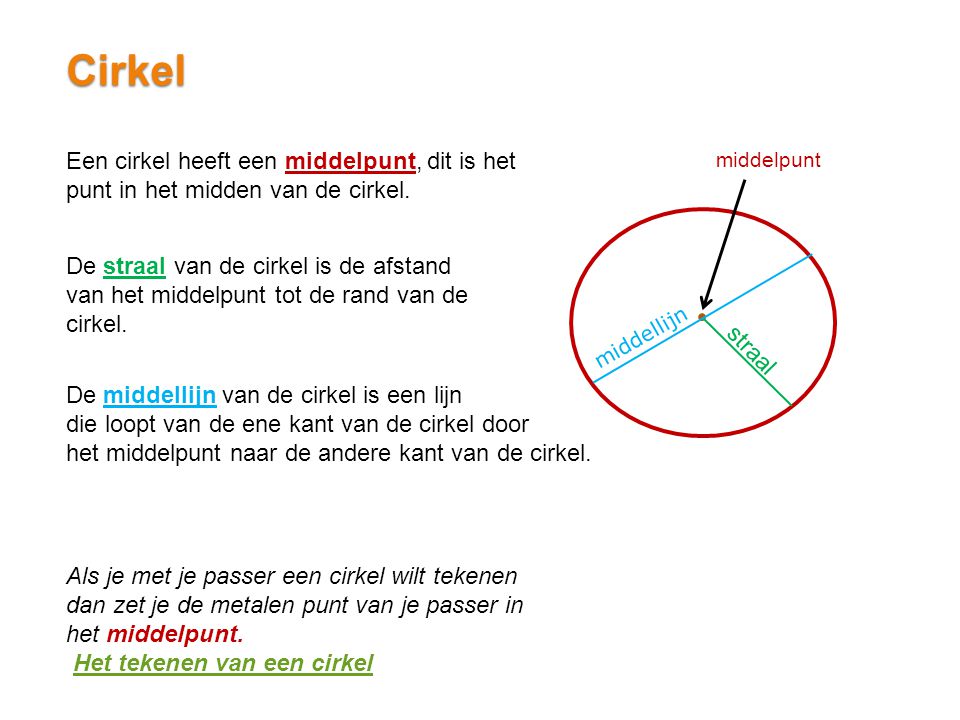
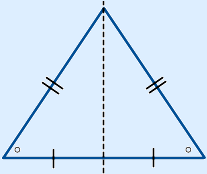
Een middellijn wordt ook wel diameter genoemd.
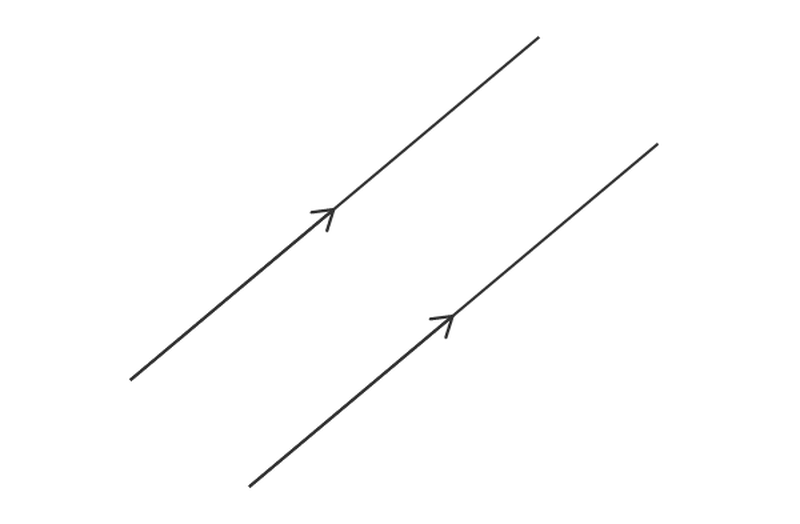
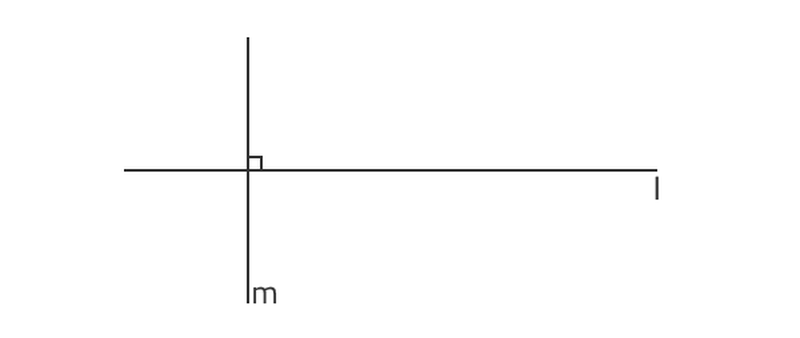
Uitleg en opgaven
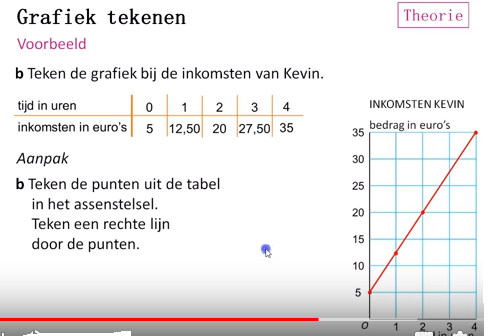
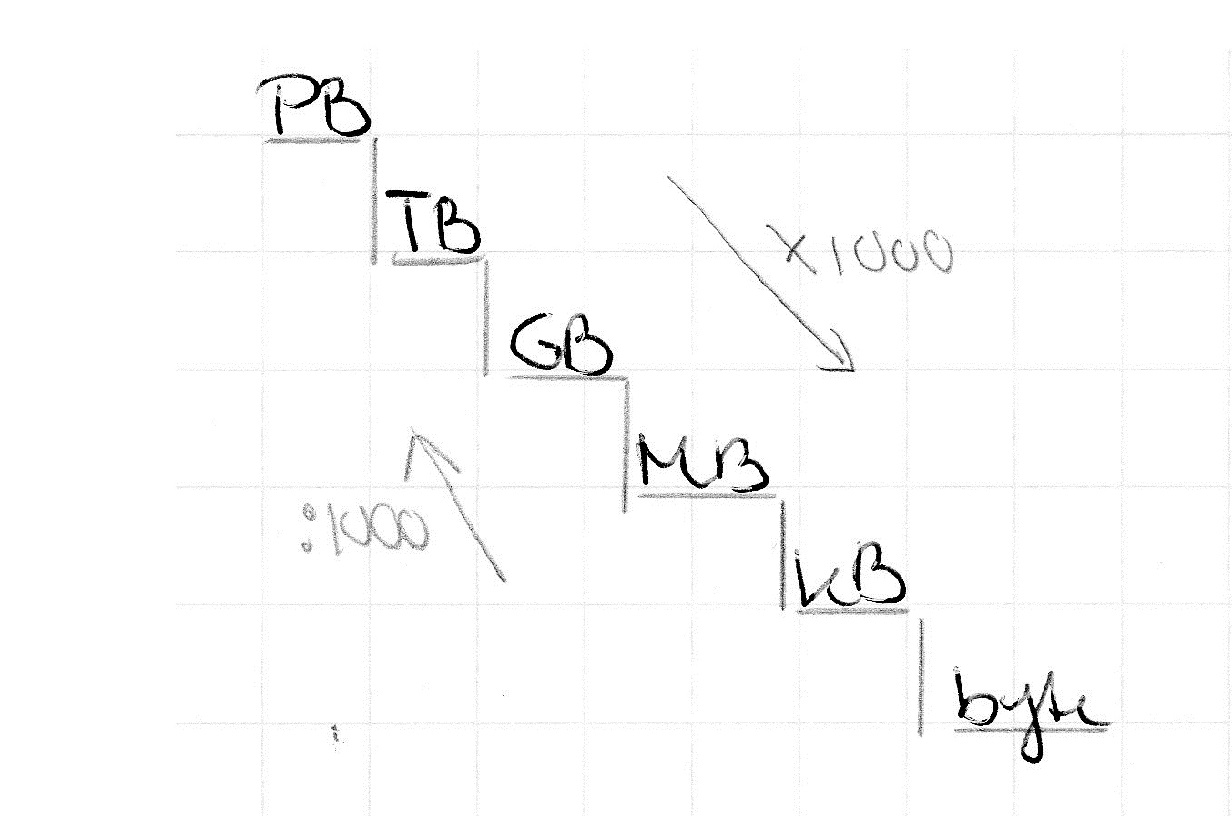
De byte is de standaardeenheid waarmee veel wordt gerekend. Voor de byte wordt een voorvoegsel geplaatst. Veel gebruikte voorvoegsels zijn: kilo, mega, giga en de tera. Zie de tabel hieronder
