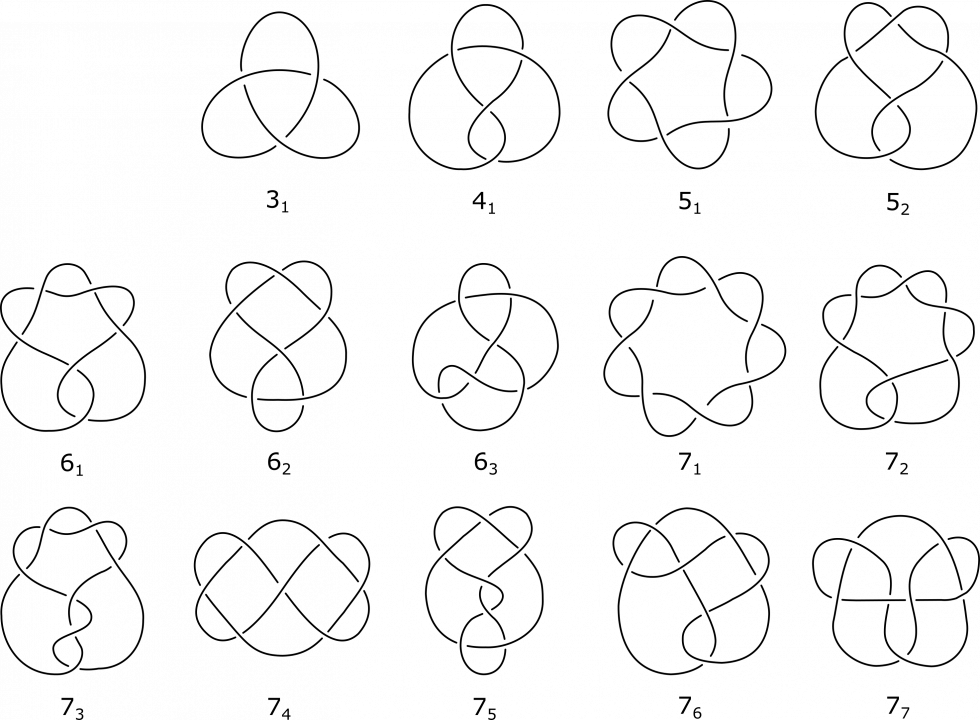
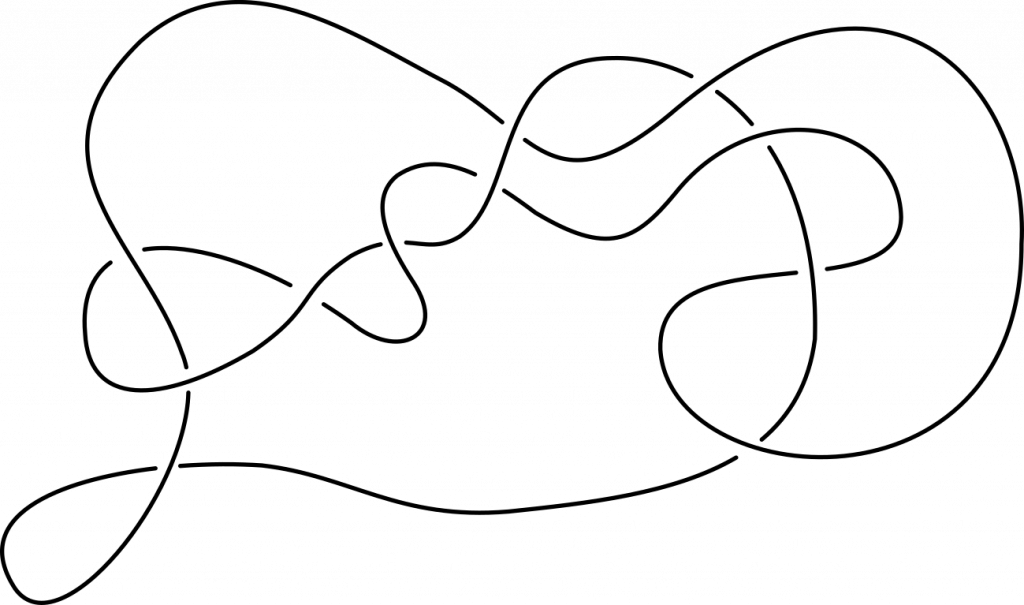
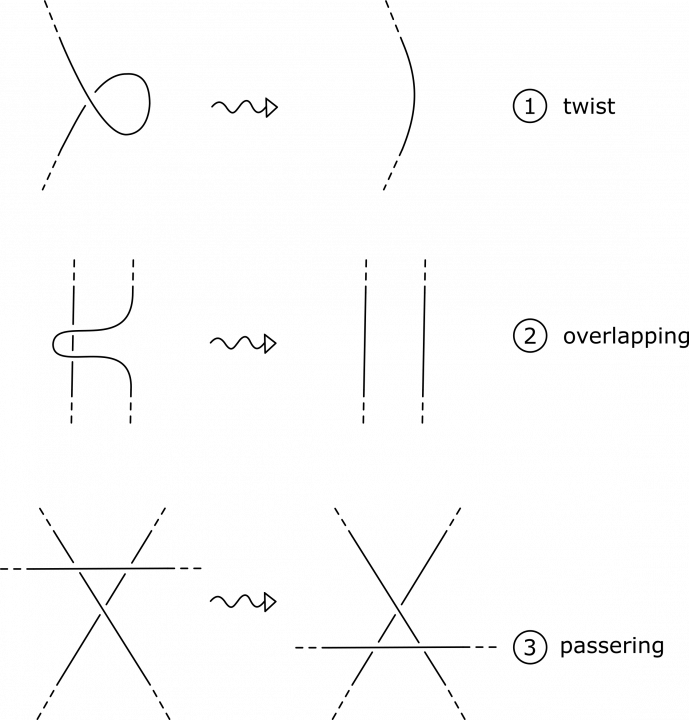
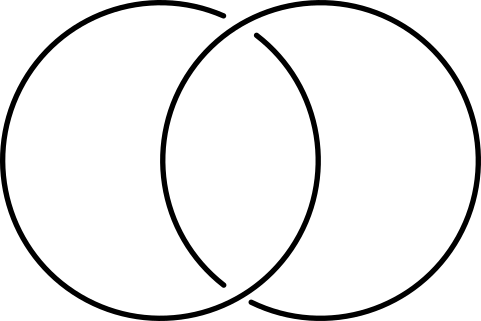
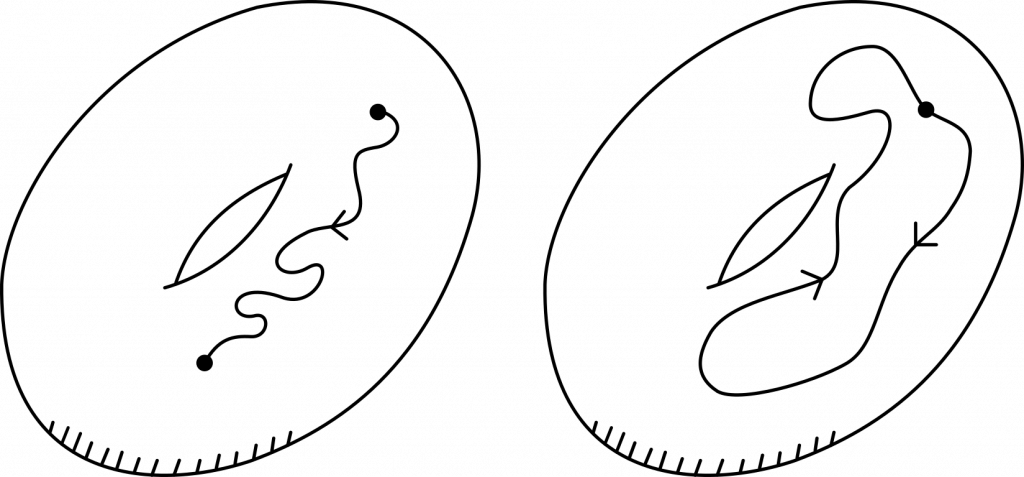
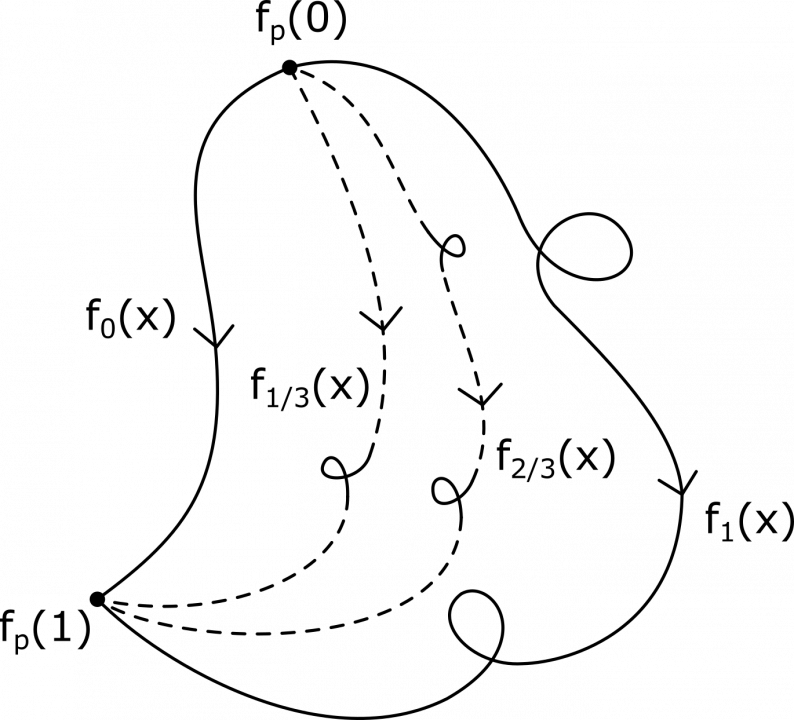
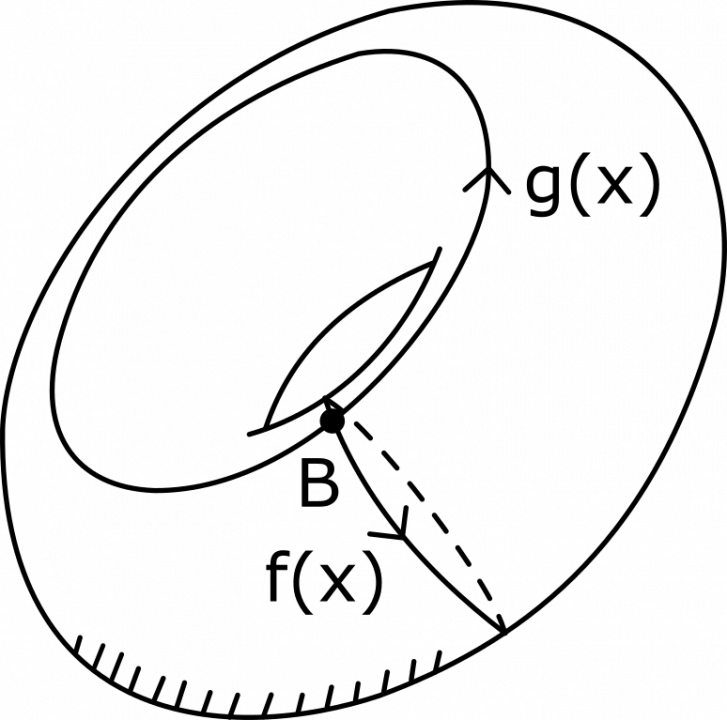
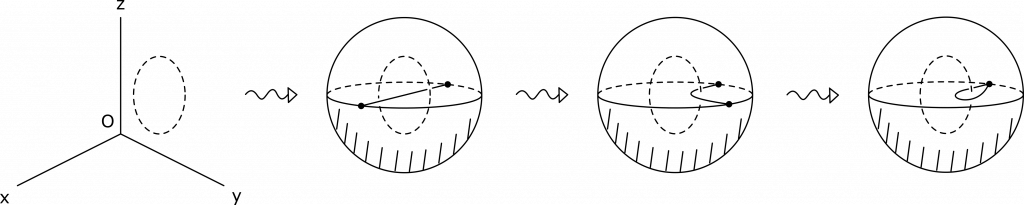
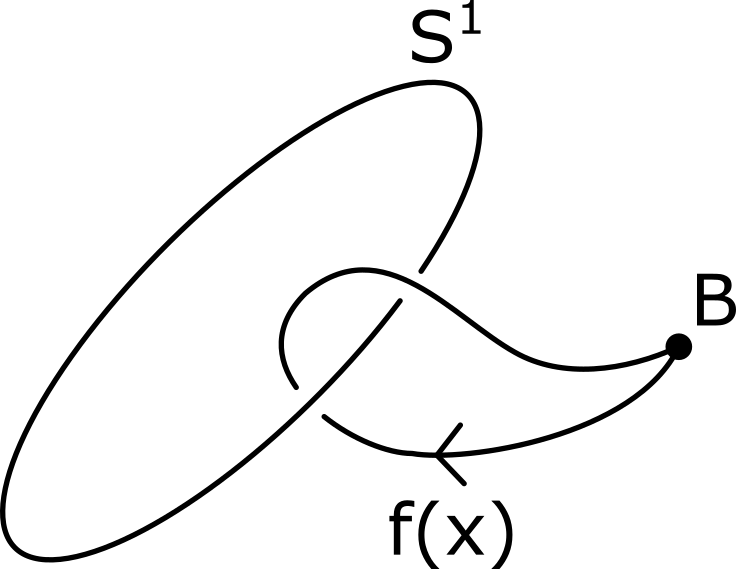
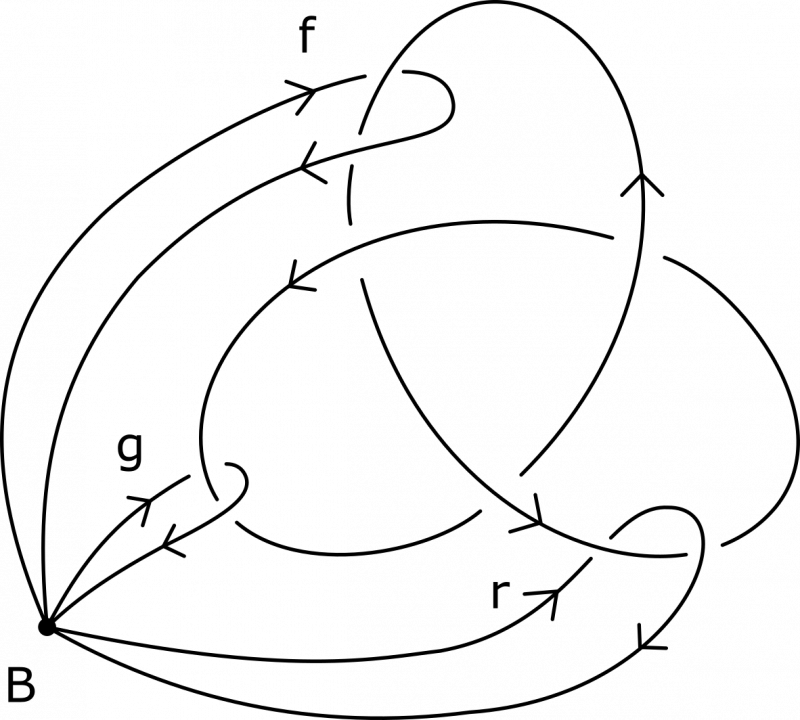
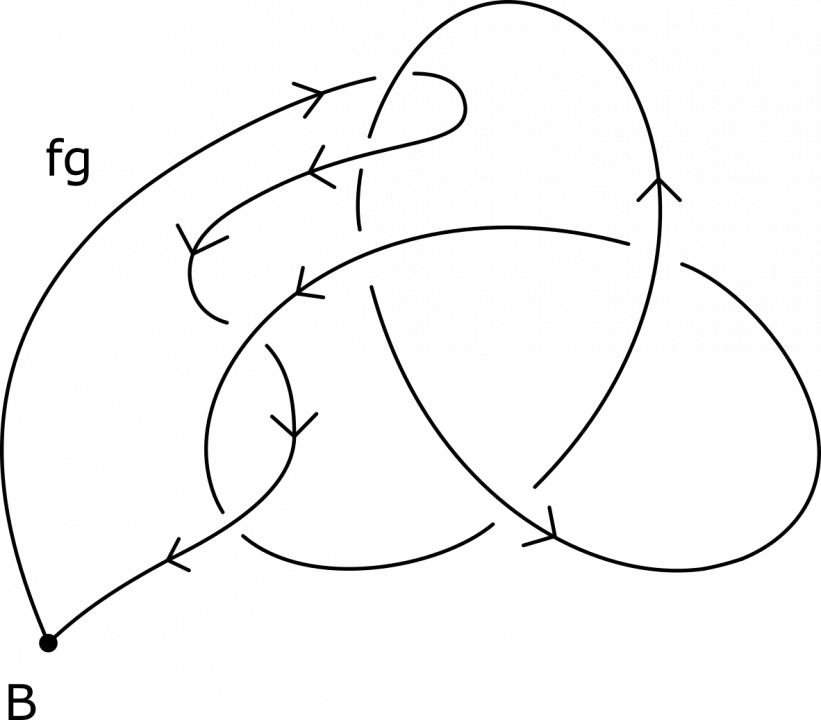
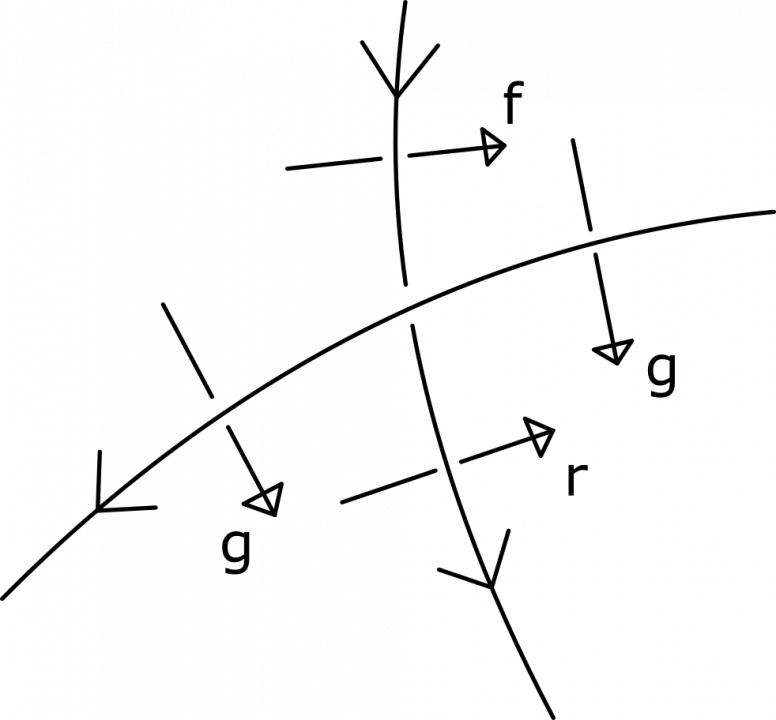
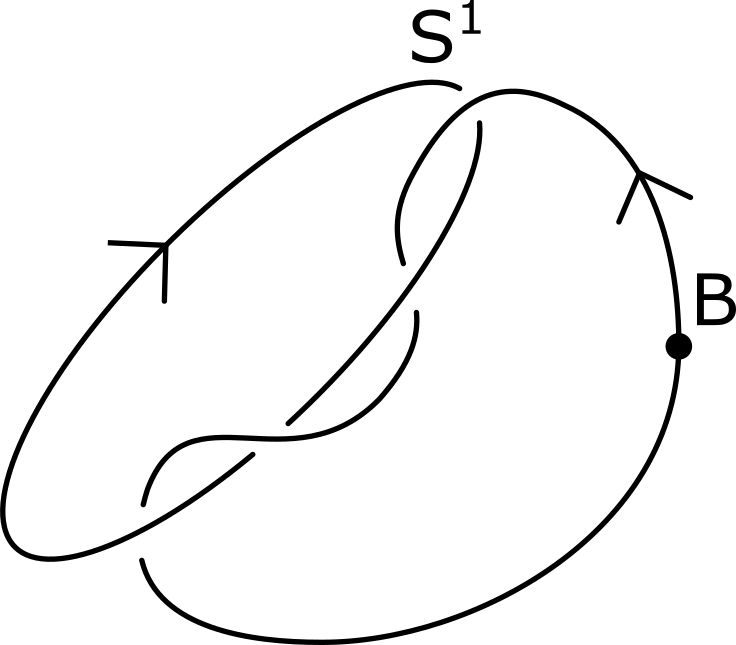
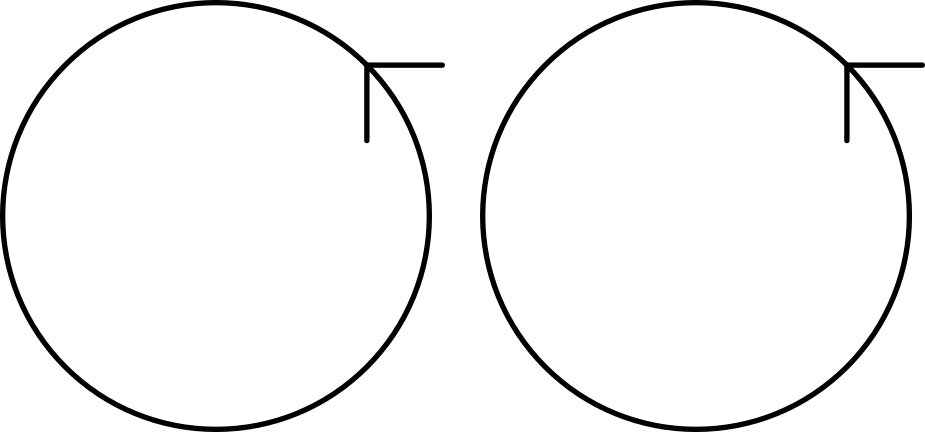
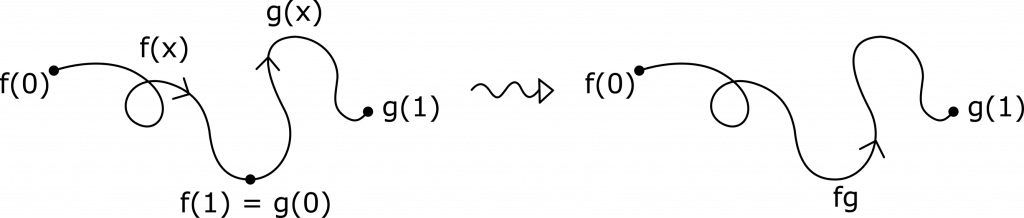Het arrangement Knopen en groepen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 06-06-2022 12:44:59
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- een korte cursus die naar knoopgroepen toewerkt voor degene die bekend is met de belangrijkste concepten van groepentheorie
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- moeilijk
- Studiebelasting
- 0 uur 50 minuten
- Trefwoorden
- algebraische topologie, groepen, groepentheorie, knoopgroep, knopen, knopentheorie, topologie, wiskunde


 R
R