Het arrangement 2H01 Verhoudingen en procenten is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 02-08-2022 09:41:40
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Intro H1 V21-22
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Gebruikte Wikiwijs Arrangementen
Wiskundesectie Juliana. (z.d.).
2H01 Verhoudingen en procenten
https://maken.wikiwijs.nl/178359/2H01__Verhoudingen_en_procenten
Wiskundesectie Juliana. (z.d.).
2H06 Verhoudingen en procenten
https://maken.wikiwijs.nl/116592/2H06__Verhoudingen_en_procenten
Wiskundesectie Juliana. (z.d.).
H6 Verhoudingen en procenten
https://maken.wikiwijs.nl/178049/H6_Verhoudingen_en_procenten


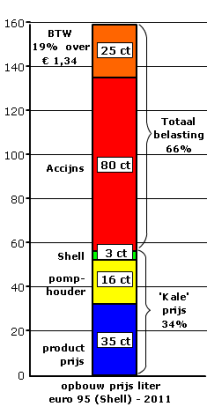






 In een verhoudingstabel mag je het onderste en bovenste getal met hetzelfde getal vermenigvuldigen.
In een verhoudingstabel mag je het onderste en bovenste getal met hetzelfde getal vermenigvuldigen.

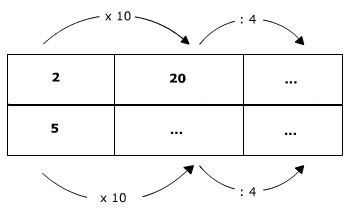





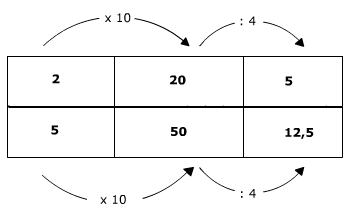


 Voorbeeld 1
Voorbeeld 1



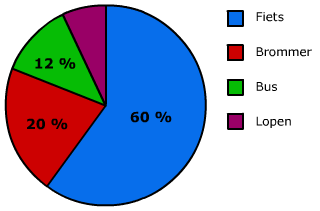






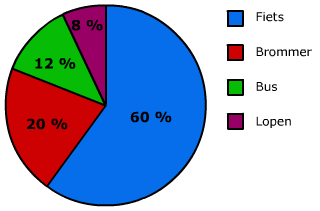






 die door leerlingen voor leerlingen zijn gemaakt.
die door leerlingen voor leerlingen zijn gemaakt.












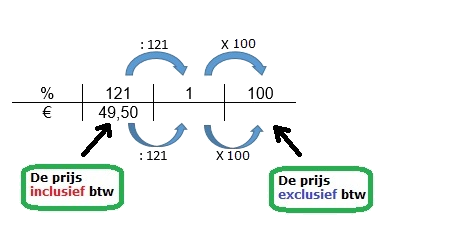
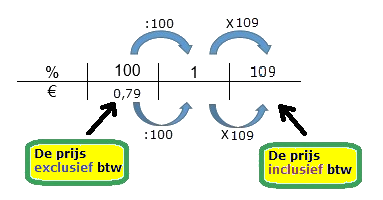





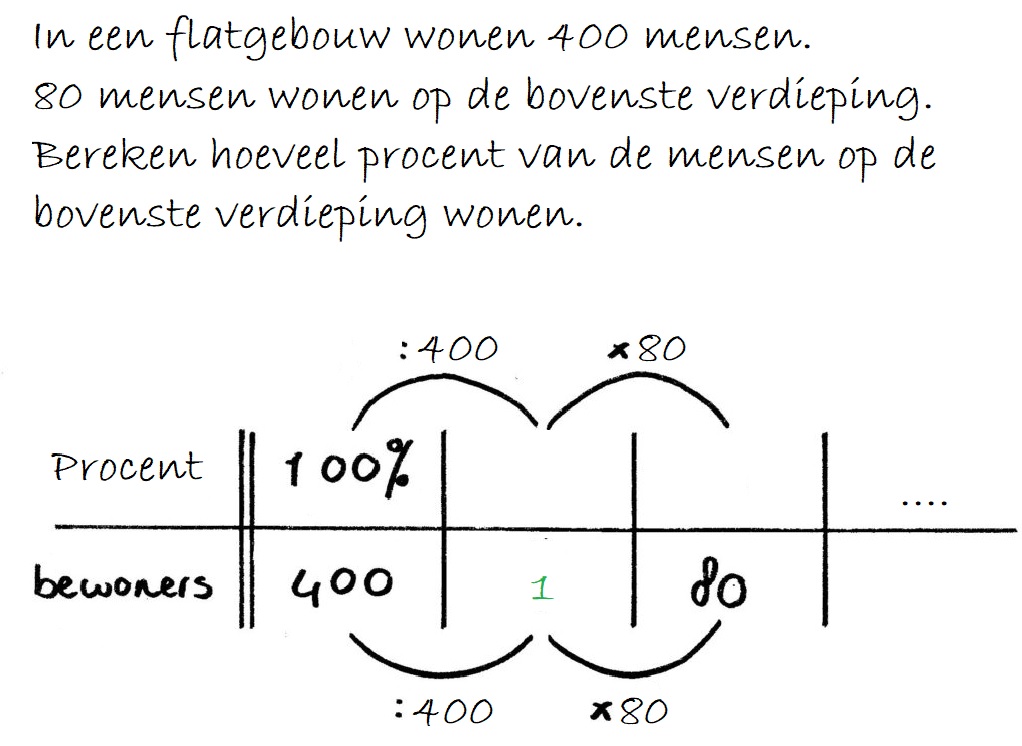 Maak je gebruik van een tabel, teken de lijntjes van je tabel dan met potlood en geodriehoek. Zet ook de boogjes bij je tabel.
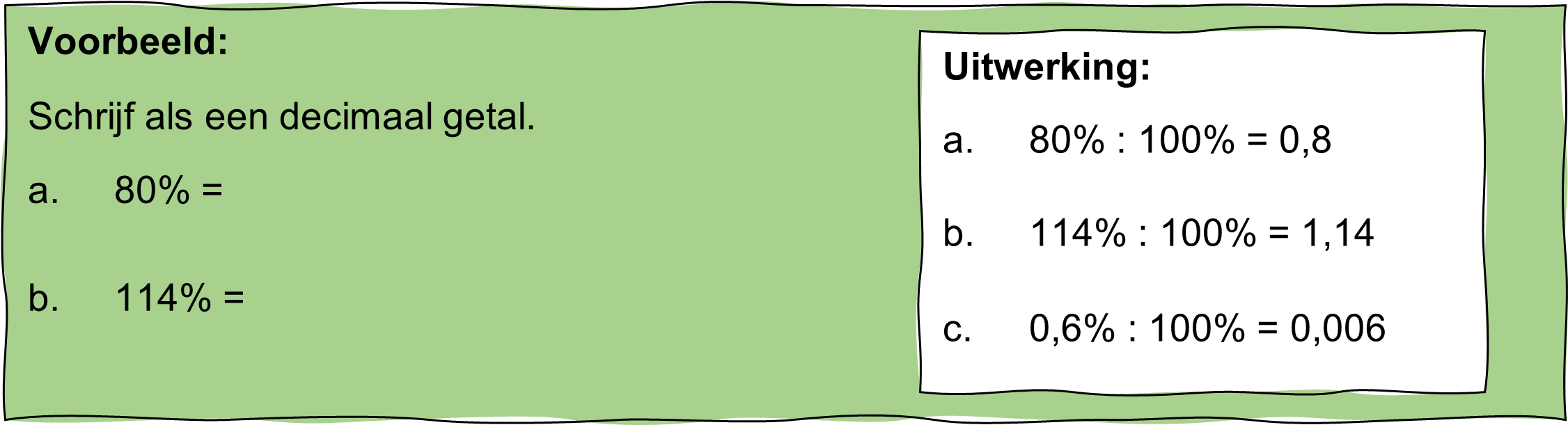
Maak je gebruik van een tabel, teken de lijntjes van je tabel dan met potlood en geodriehoek. Zet ook de boogjes bij je tabel. In een dierentuin worden 22 keizerspinguins gehouden. Dat is 36,84% van alle pinguins die er zijn.
In een dierentuin worden 22 keizerspinguins gehouden. Dat is 36,84% van alle pinguins die er zijn.






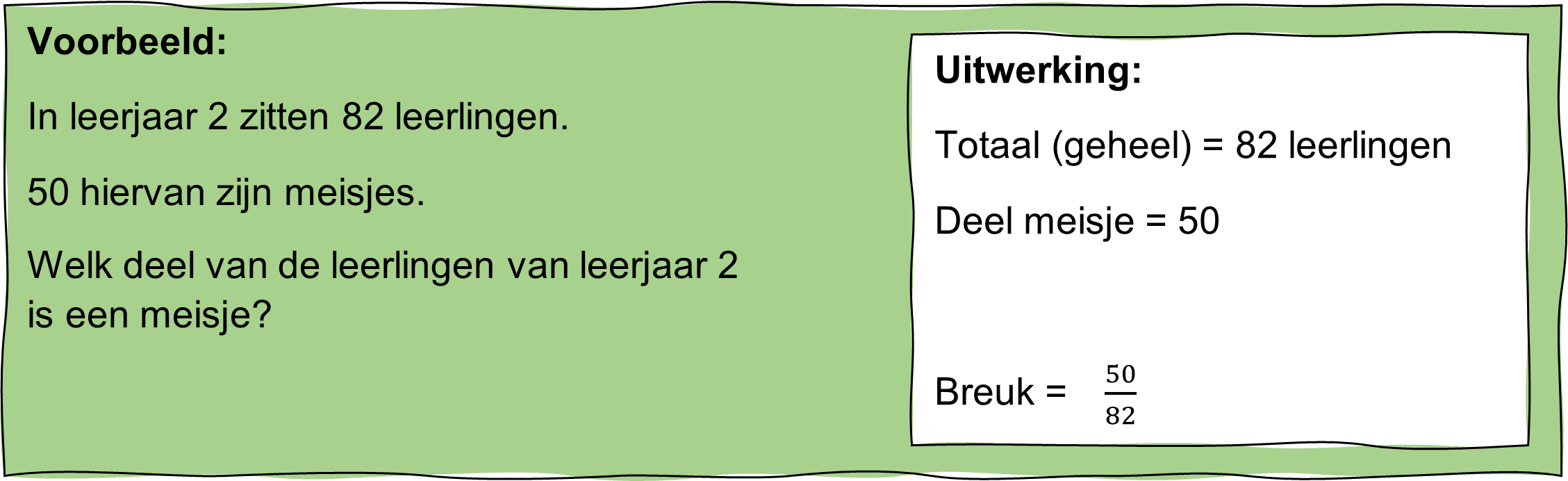






 Op een zaterdag verkoopt een boekhandel 640 boeken.
Op een zaterdag verkoopt een boekhandel 640 boeken.



 In de kantine is er vandaag een aanbieding. Normaal kost een panini €1,50, nu krijg je €0,25 korting.
In de kantine is er vandaag een aanbieding. Normaal kost een panini €1,50, nu krijg je €0,25 korting. Op een school geven in totaal 78 docenten les in verschillende vakken. 14,11% van deze docenten geeft wiskunde.
Op een school geven in totaal 78 docenten les in verschillende vakken. 14,11% van deze docenten geeft wiskunde.
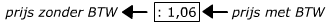
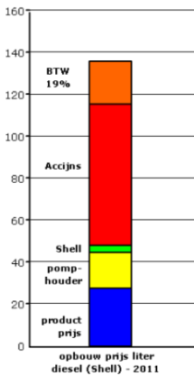

 =…………………………
=………………………… =…………………………
=………………………… =…………………………
=…………………………  =………………………….
=………………………….  =………………………….
=………………………….  =…………………………
=………………………… =…………………………
=………………………… =…………………………
=…………………………
