Het arrangement 1VMBO-TL Wiskunde is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 30-06-2021 13:00:45
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Bronnen
| Bron | Type |
|---|---|
|
https://drive.google.com/open?id=1oCtKWBzdIzrq-4pyk76gxInoJ634NRvU https://drive.google.com/open?id=1oCtKWBzdIzrq-4pyk76gxInoJ634NRvU |
Link |
|
coördinaten math4all http://math4allview.appspot.com/view?repo=m4a2015&comp=hv-me1&subcomp=hv-me16&thread=ma-havovwo-12&parent=www.math4all.nl/overzichten/havo-vwo-1-2/35 |
Link |
|
Nog enkele sommen 3.1 Breuken https://drive.google.com/open?id=0B1IR5xAG9om4QUZ4ajhYRDFjWjQ |
Link |
|
EXTRA MAVO OPDRACHTEN ALLE STOF https://docs.google.com/document/d/1LZbYSCF7yjxaUGxJFfBQ3ogz5Rfcx8UZg7OqVjLWtDI/edit?usp=sharing |
Link |


 ‘t Ravelijn is een middelbare school in Steenbergen voor mavo en voorbereidend MBO
‘t Ravelijn is een middelbare school in Steenbergen voor mavo en voorbereidend MBO










 In het eerste hoofdstuk van het jaar leer jij je weg vinden in de wiskundewereld.
In het eerste hoofdstuk van het jaar leer jij je weg vinden in de wiskundewereld.




















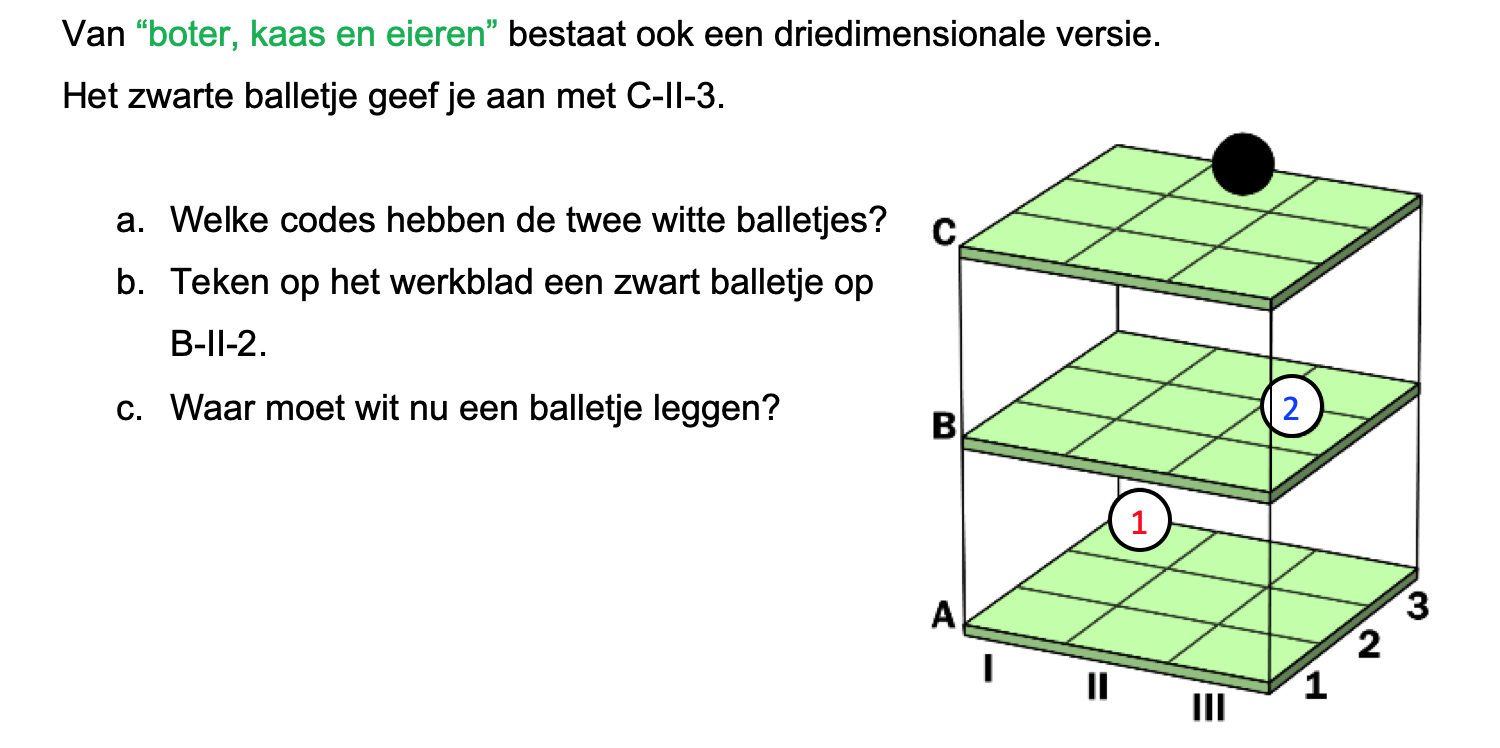





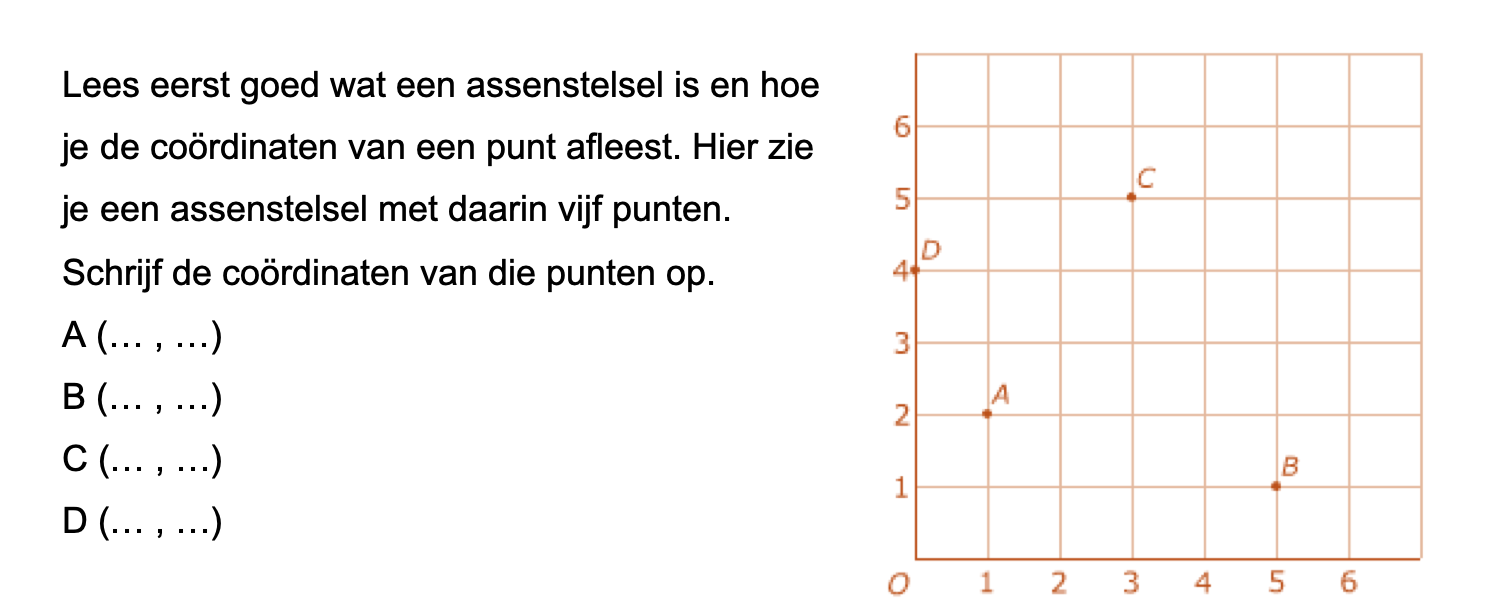





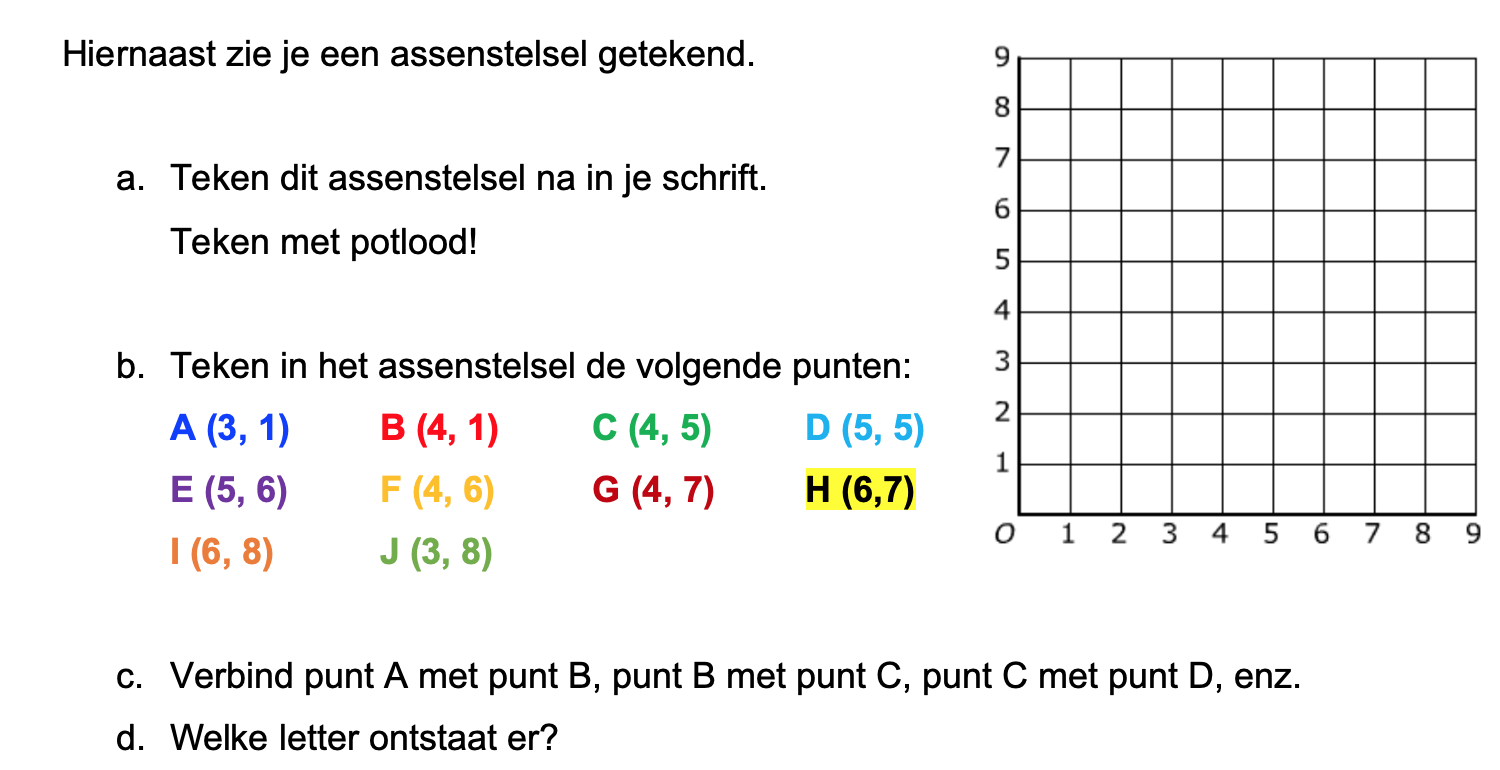










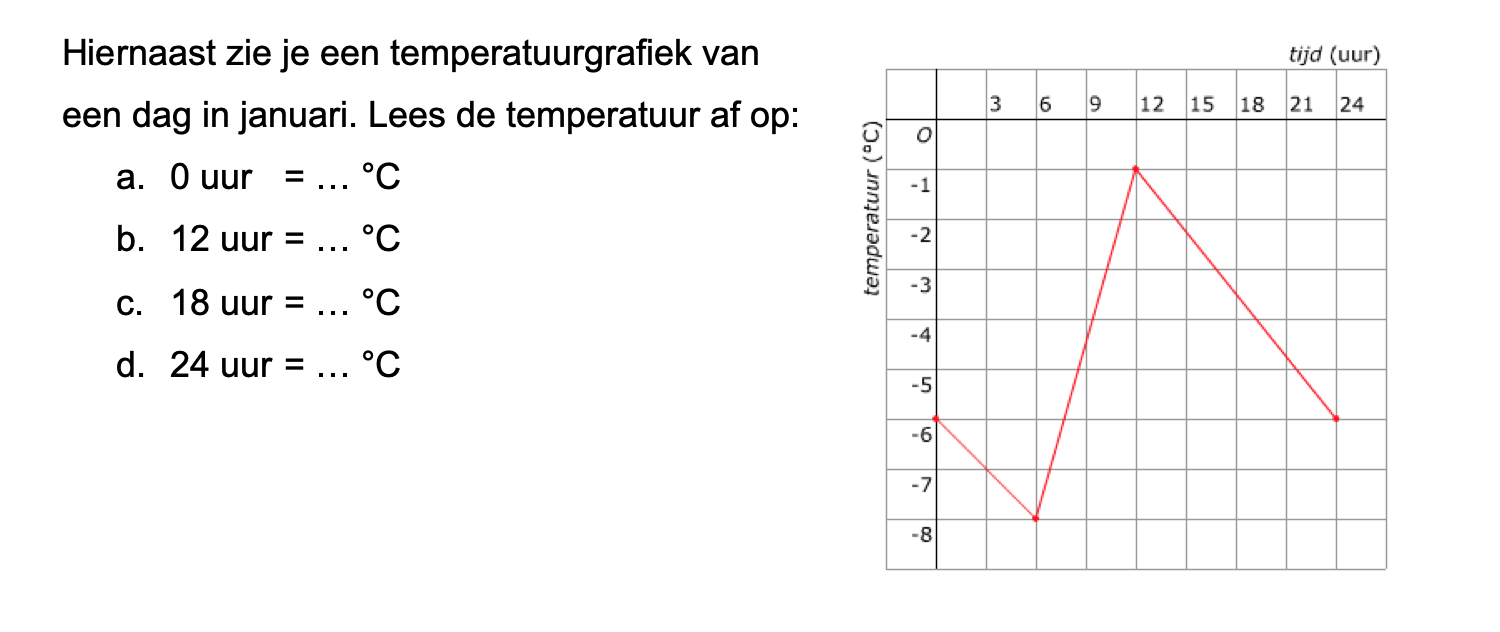



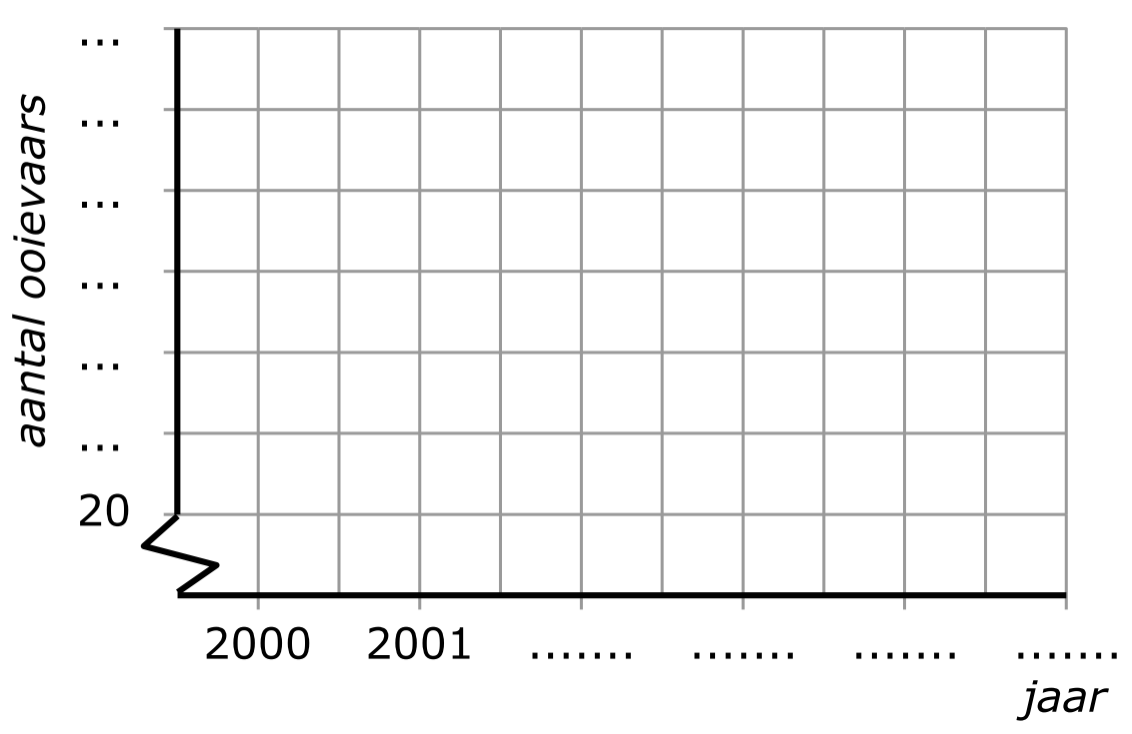
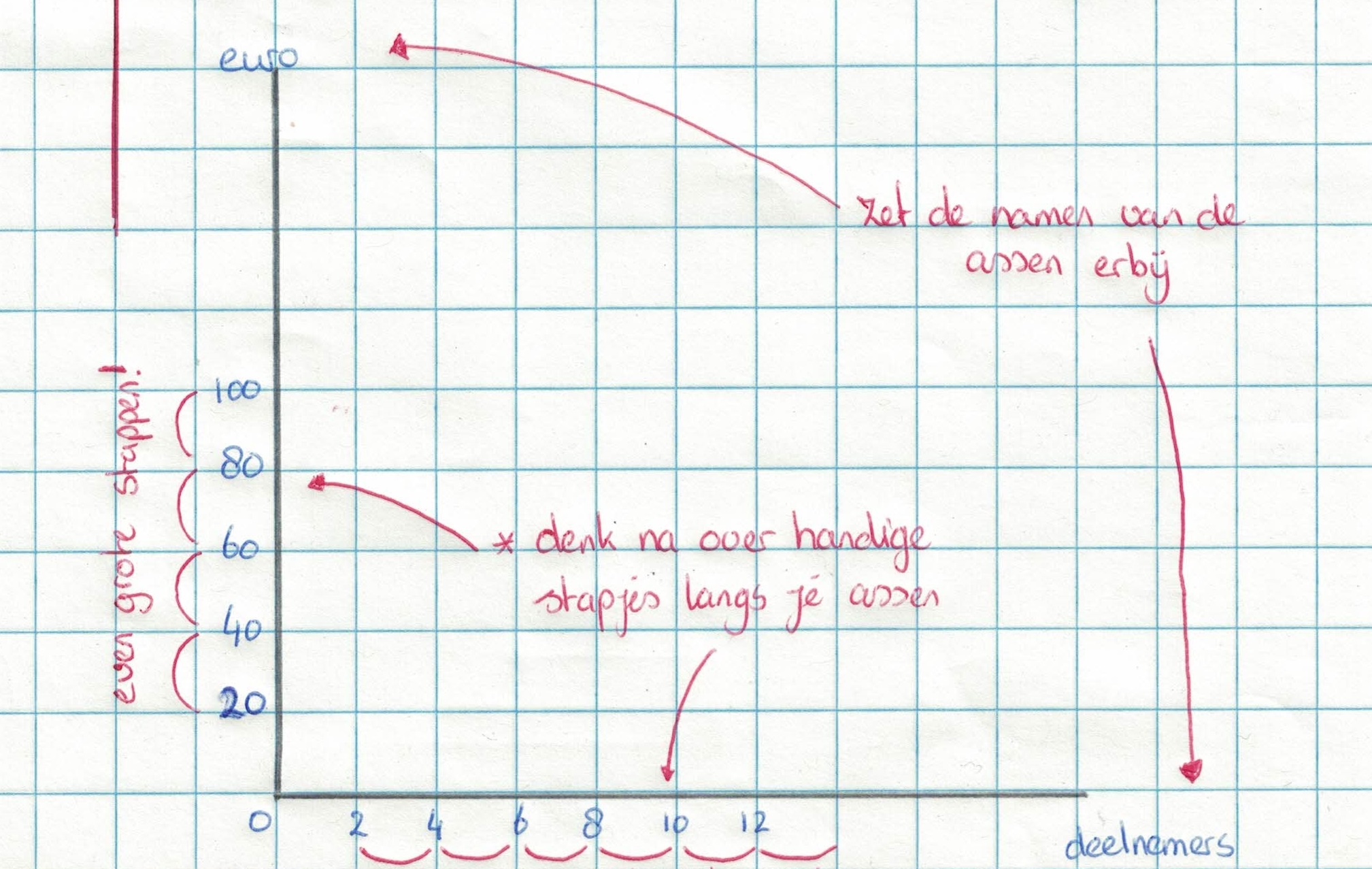
 Een belangrijke vaardigheid bij wiskunde is het kunnen tekenen van een grafiek.
Een belangrijke vaardigheid bij wiskunde is het kunnen tekenen van een grafiek.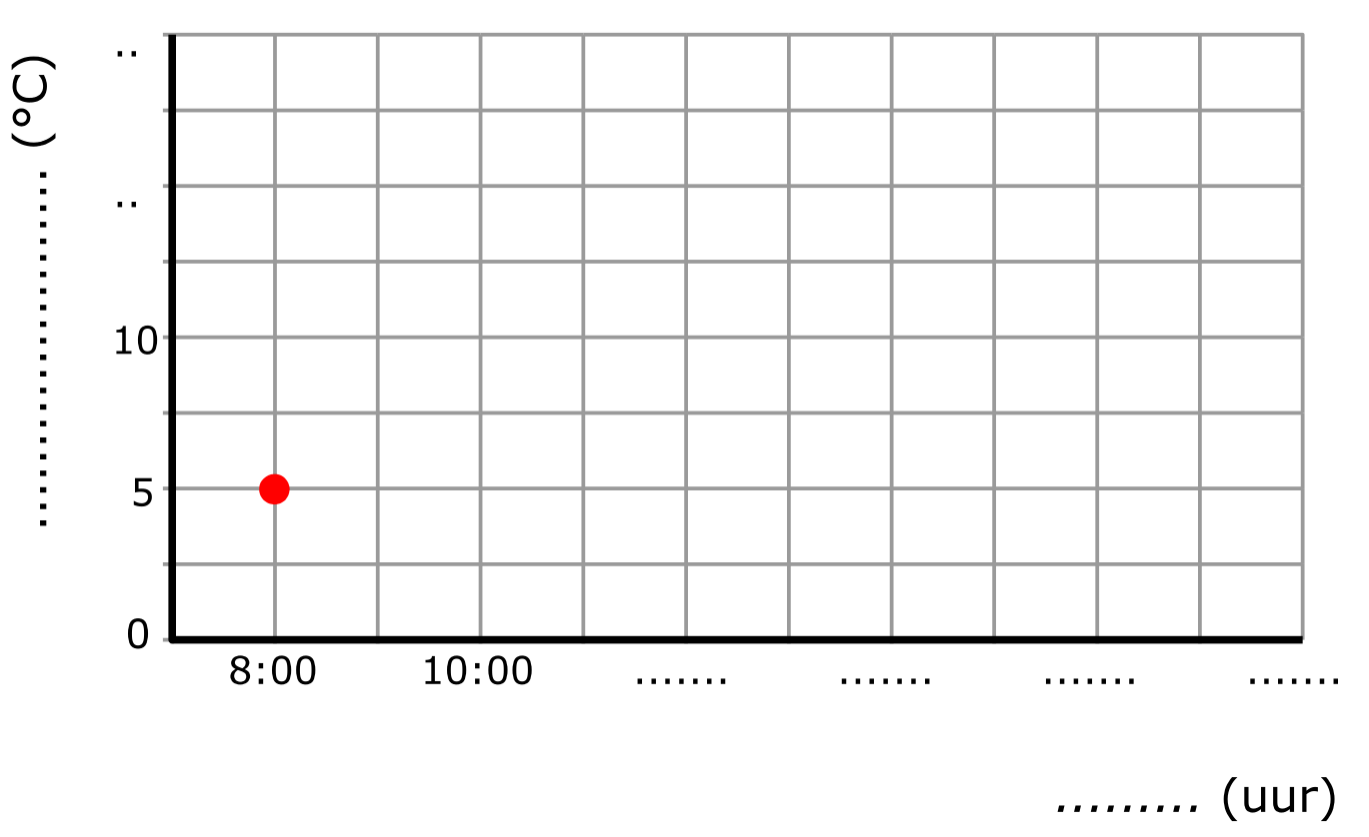 -as komen de woordjes boven uit de tabel, bij de y-as altijd de woordjes onder in de tabel.
-as komen de woordjes boven uit de tabel, bij de y-as altijd de woordjes onder in de tabel.







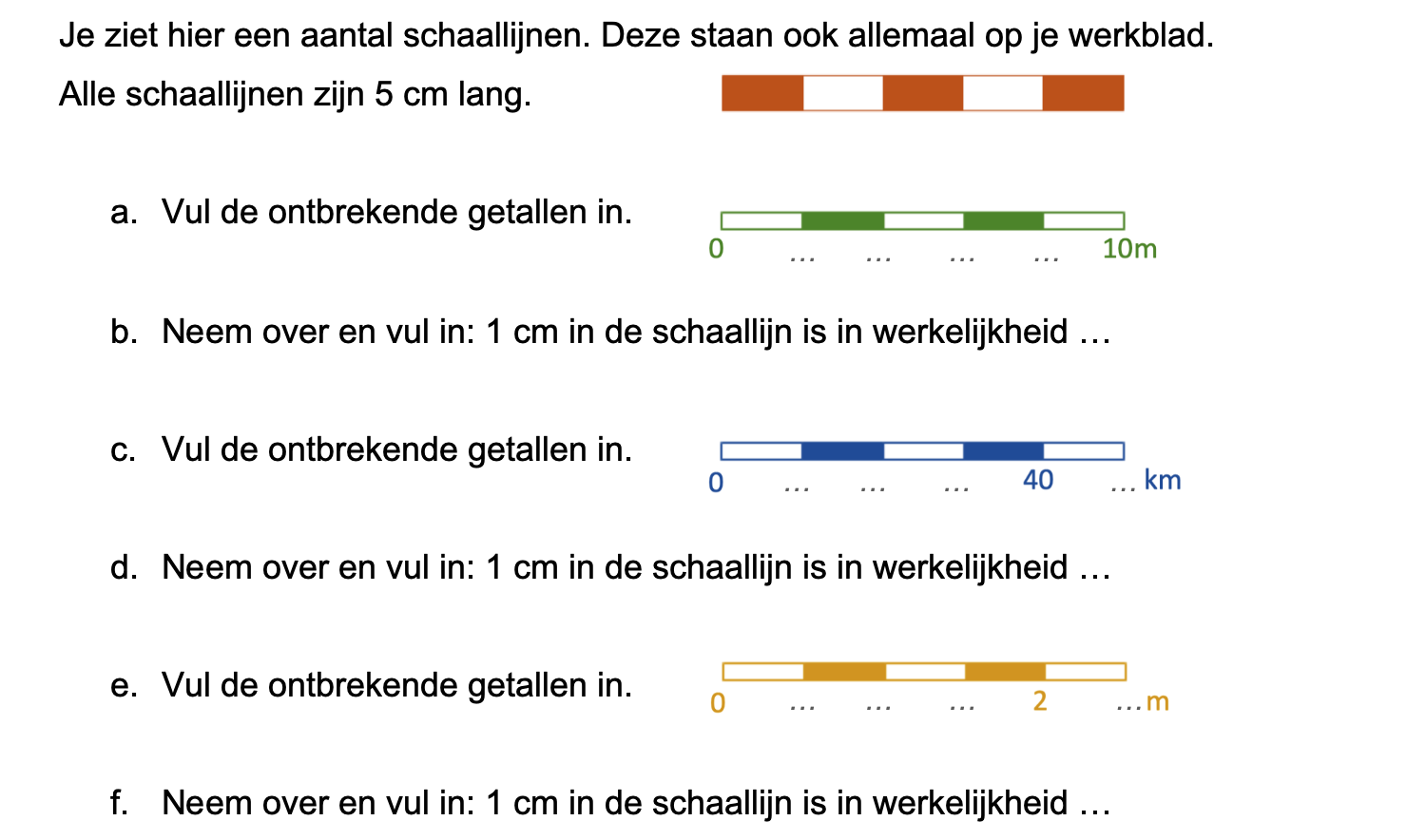



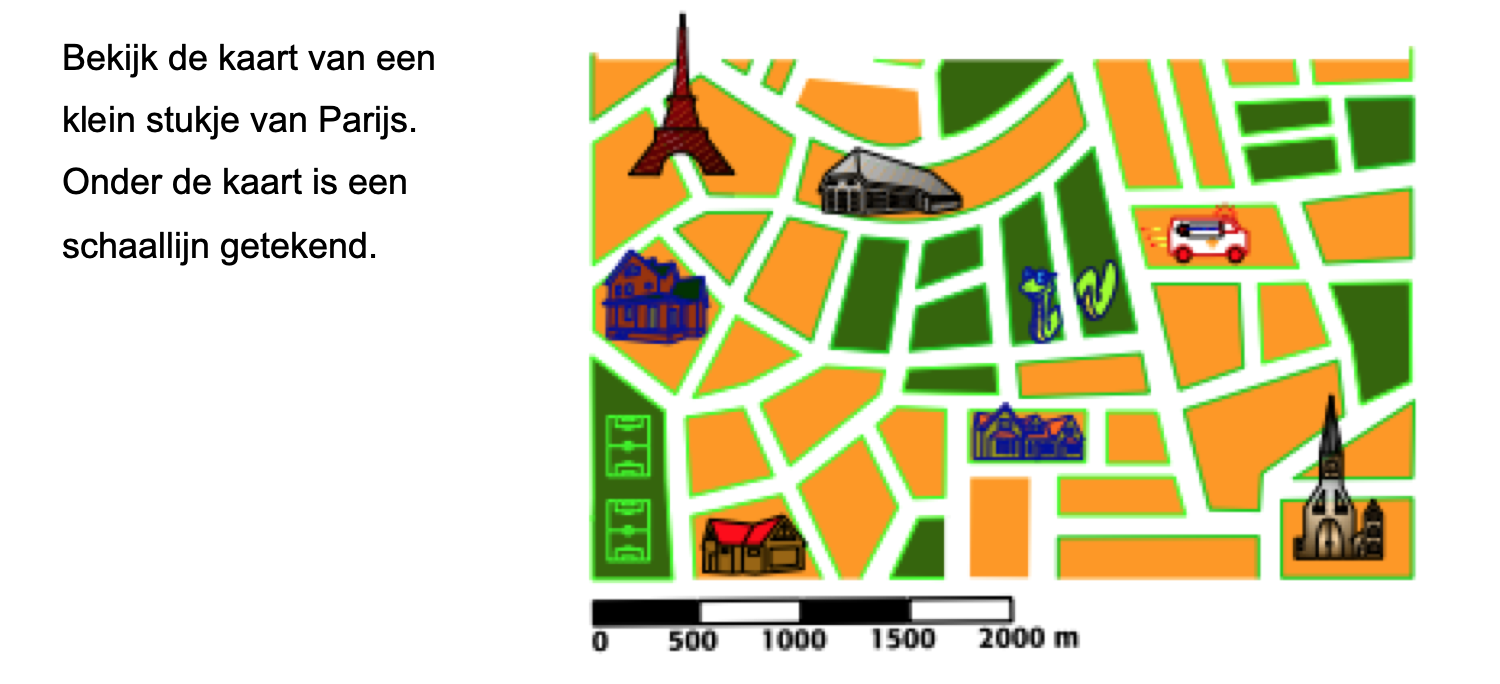




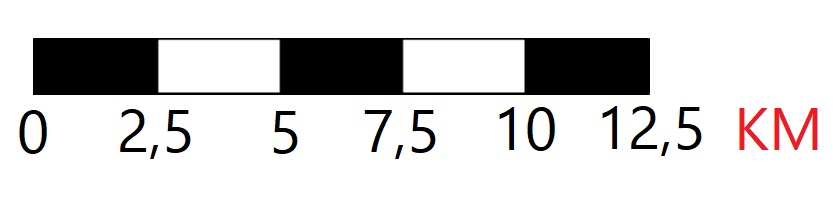
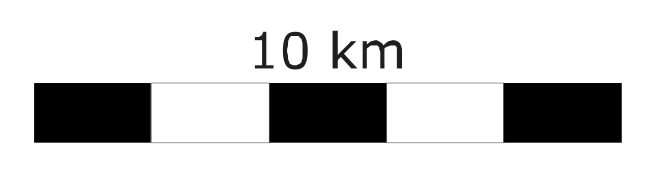 Hiernaast staat een schaallijntje. Het schaallijntje bestaat uit 5 blokjes, de schaallijn is dus 5 cm lang. In werkelijkheid komt dat overeen met een afstand van 10 km.
Hiernaast staat een schaallijntje. Het schaallijntje bestaat uit 5 blokjes, de schaallijn is dus 5 cm lang. In werkelijkheid komt dat overeen met een afstand van 10 km. 
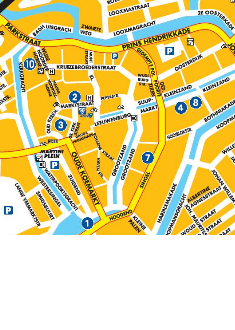
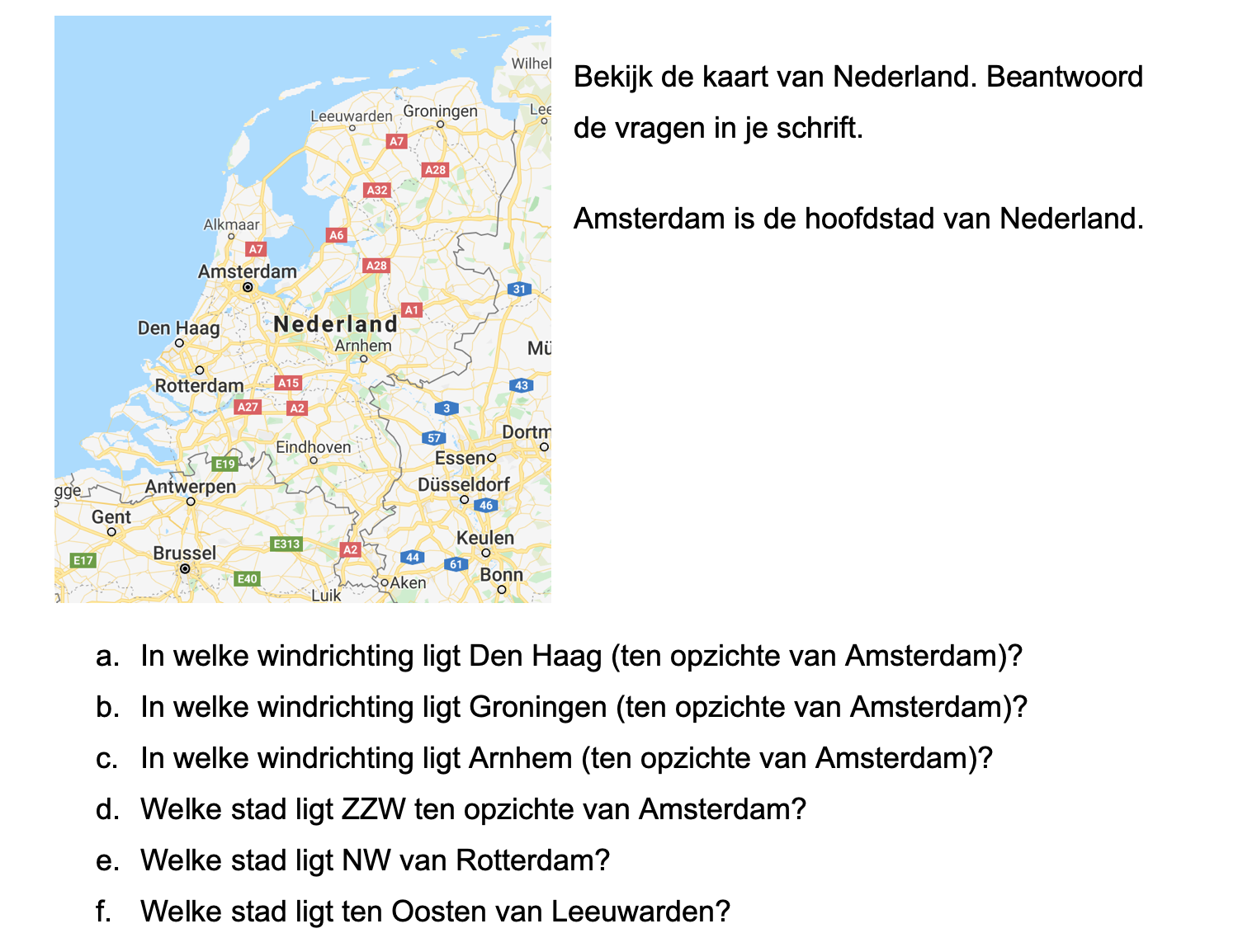
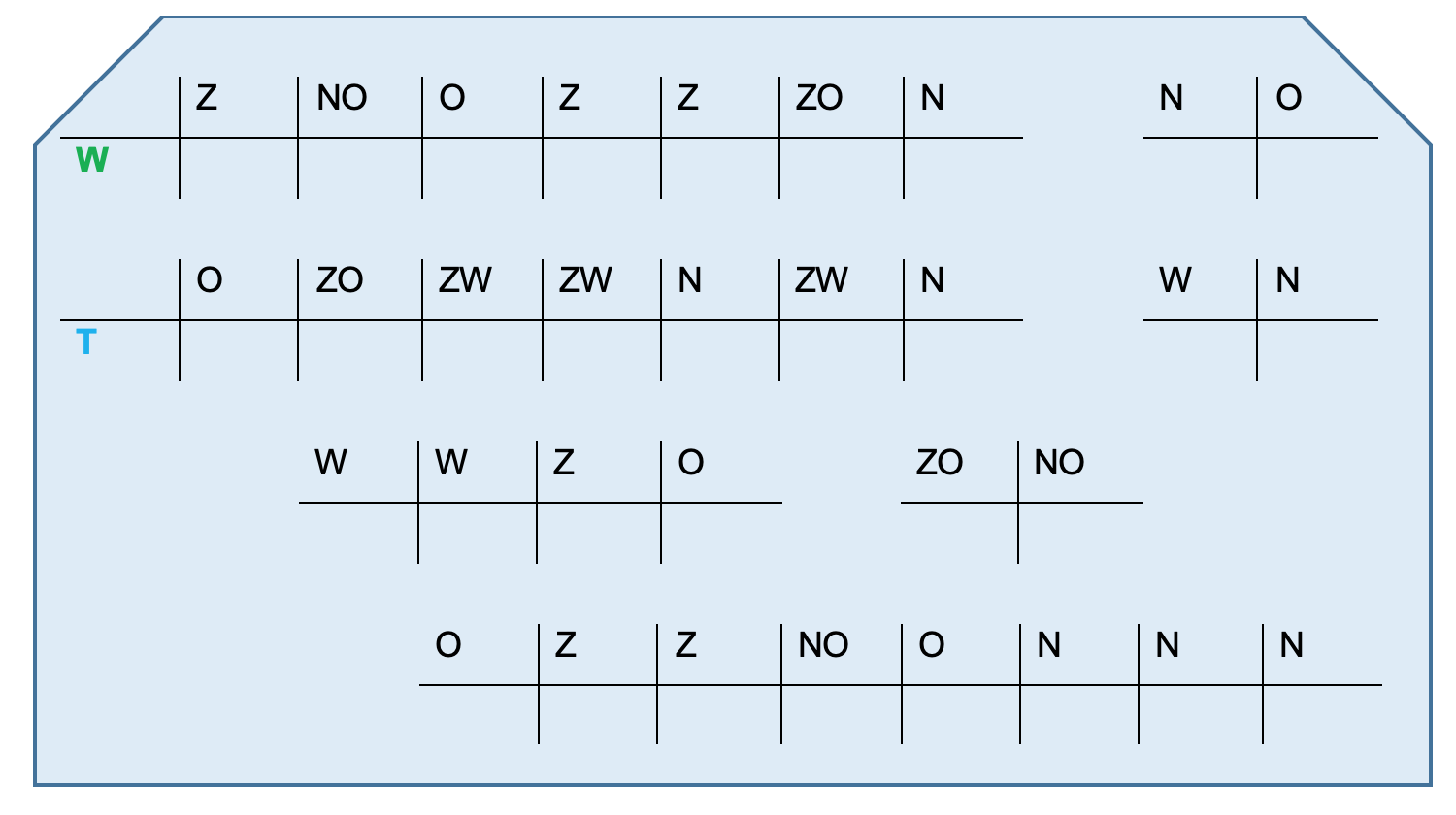
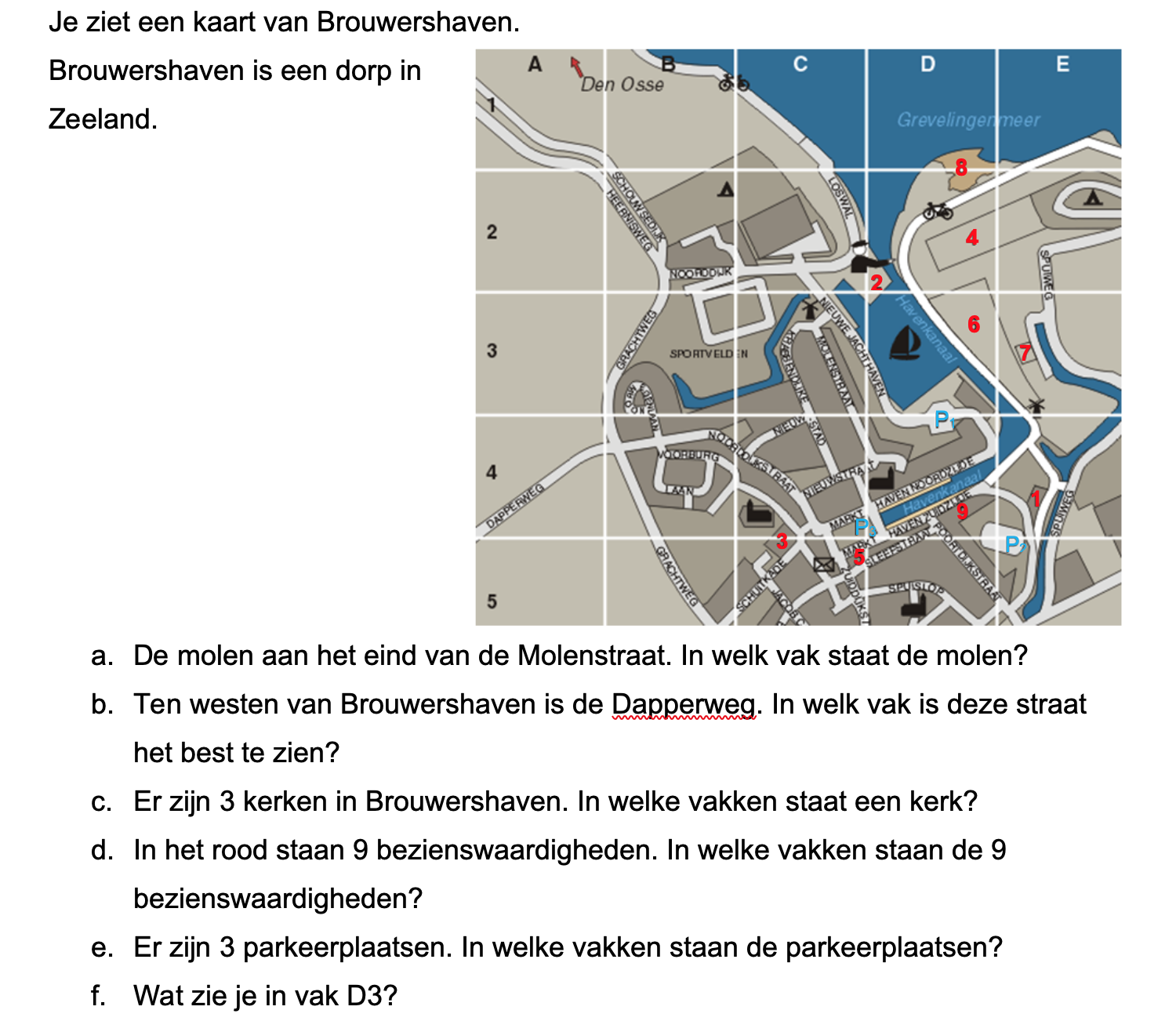
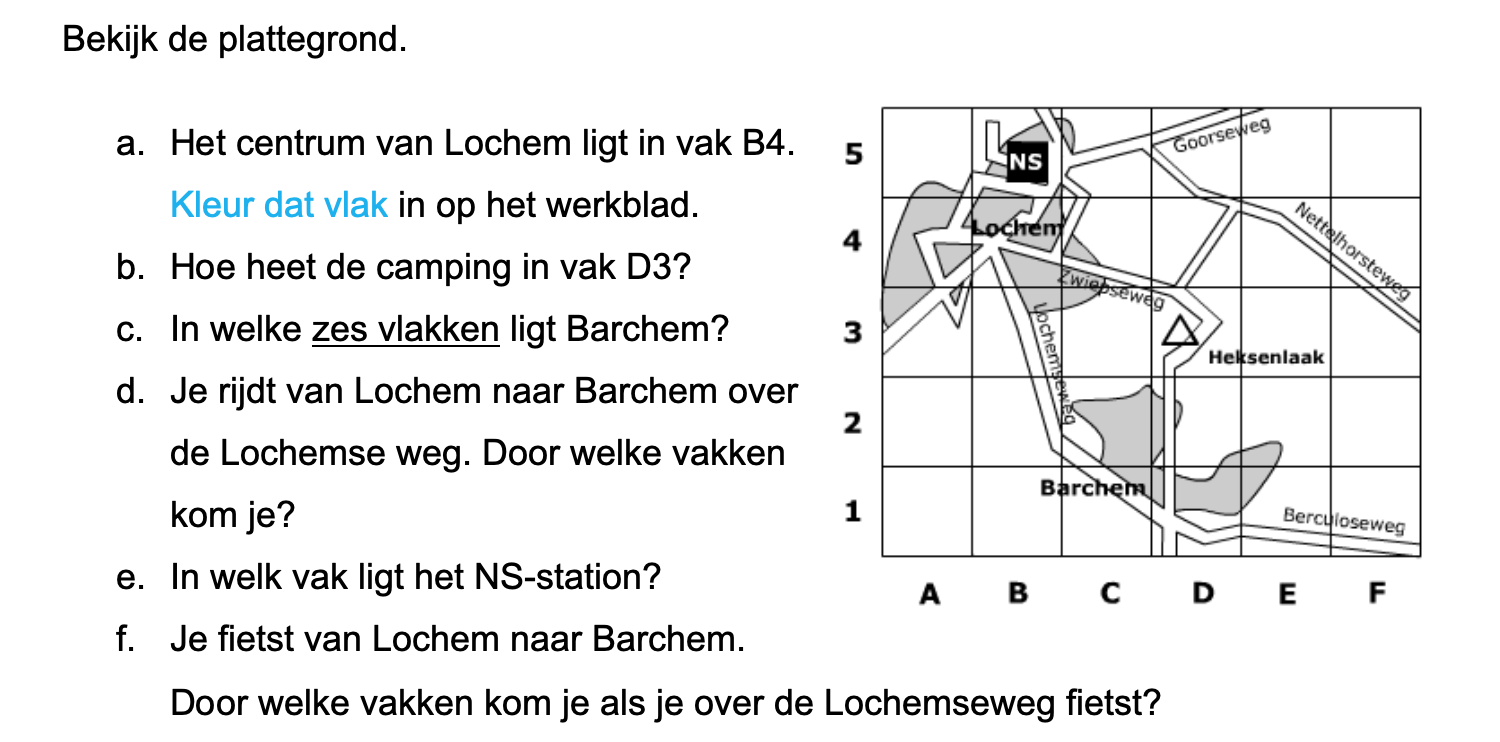
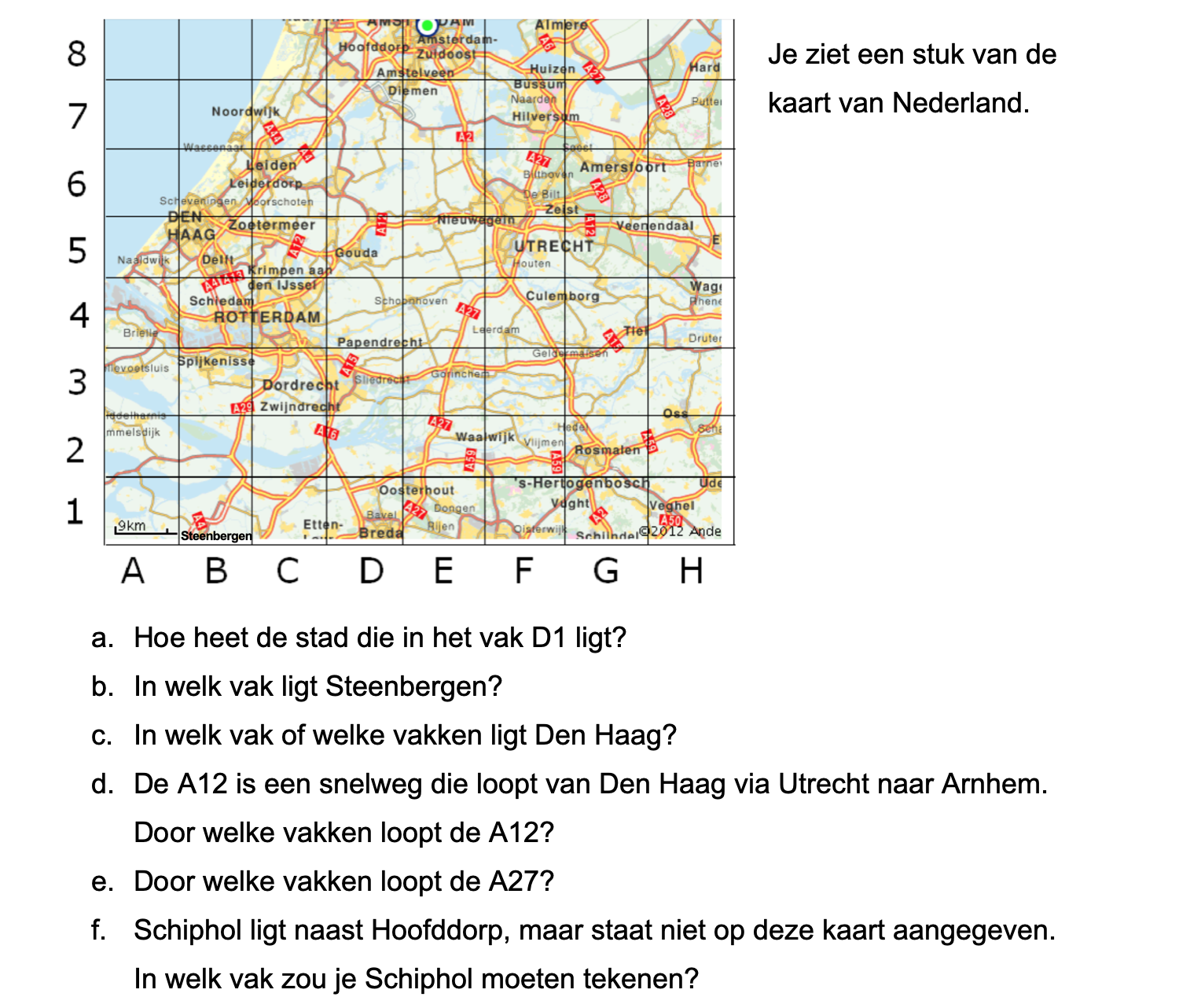
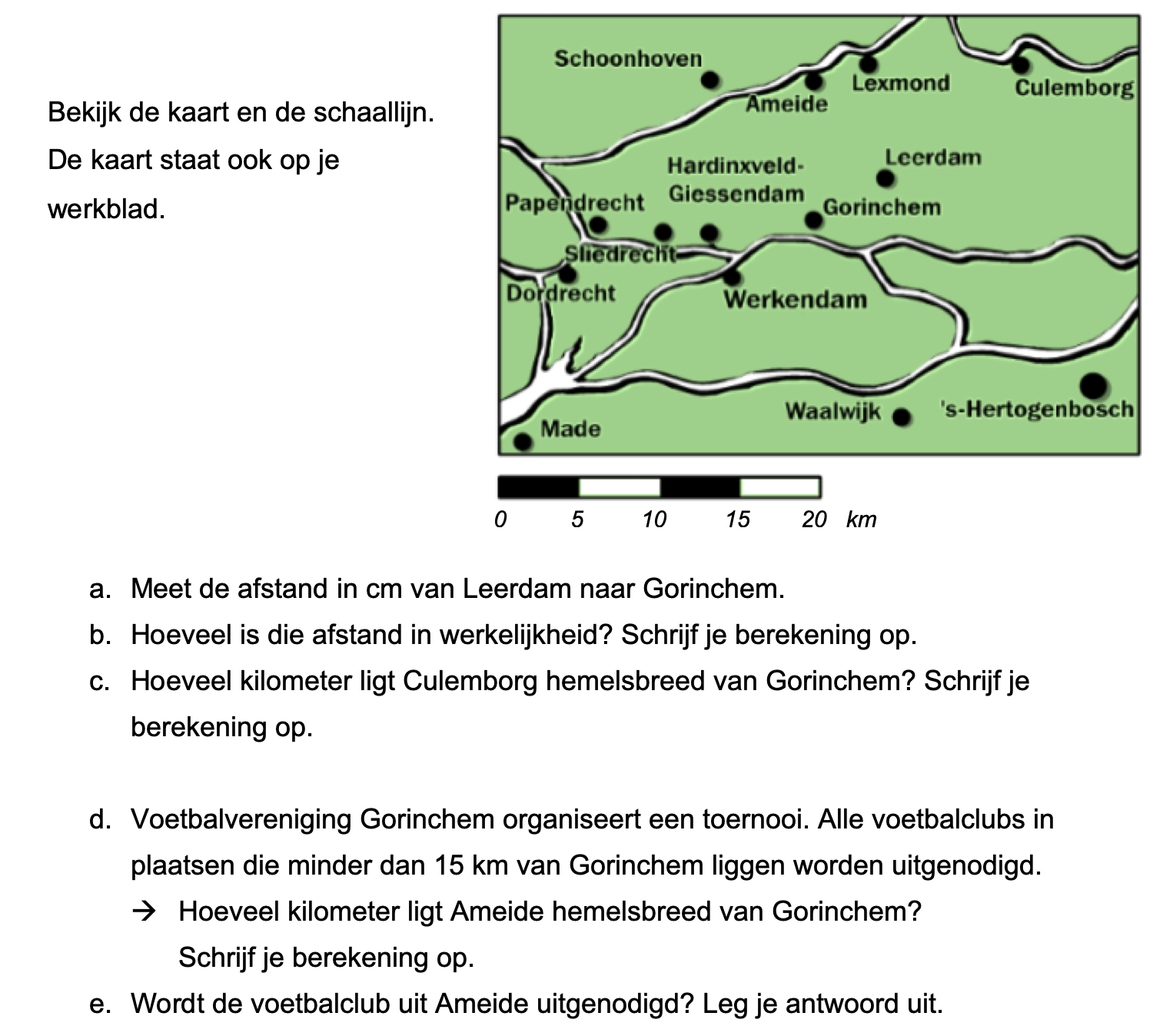
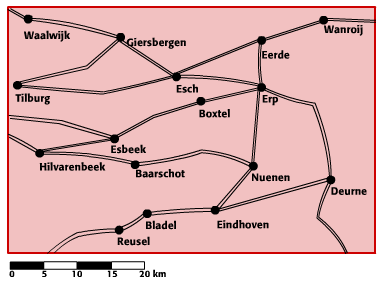 Bekijk het kaartje hiernaast, de kaart staat ook op je werkblad.
Bekijk het kaartje hiernaast, de kaart staat ook op je werkblad.
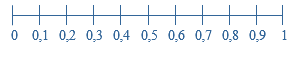 0,5 is groter dan 0,4 en
0,5 is groter dan 0,4 en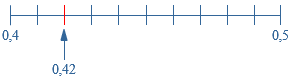 0,42 ligt tussen 0,4 en 0,5 in.
0,42 ligt tussen 0,4 en 0,5 in. 0,125 ligt tussen 0,12 en 0,13.
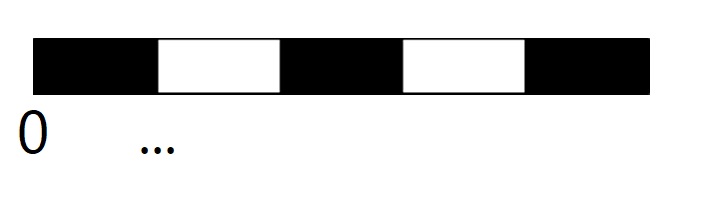
0,125 ligt tussen 0,12 en 0,13. Bekijk de getallenlijn hiernaast.
Bekijk de getallenlijn hiernaast. Bekijk de getallenlijn hiernaast.
Bekijk de getallenlijn hiernaast.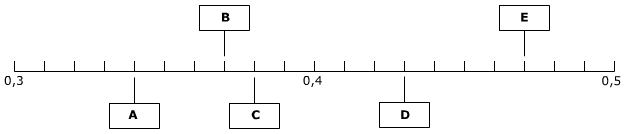


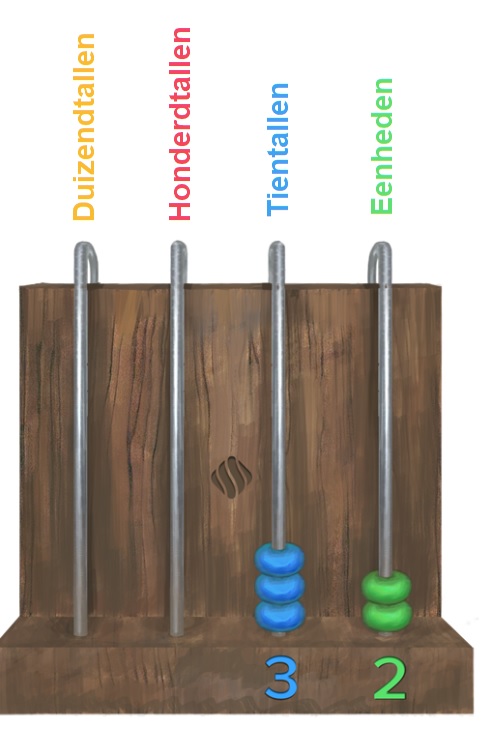
 De teller telt het aantal stukje dat je 'koopt'
De teller telt het aantal stukje dat je 'koopt'
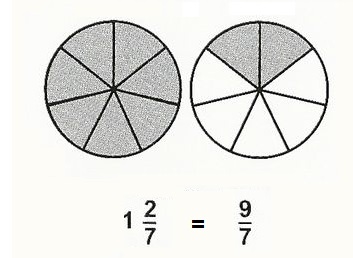 Hiernaast zie je twee cirkels. De cirkels zijn allebei in 7 stukken gesneden. De linkercirkel is helemaal ingekleurd van de tweede cirkel zijn er 2 stukken gekleurd. We zien hier dus
Hiernaast zie je twee cirkels. De cirkels zijn allebei in 7 stukken gesneden. De linkercirkel is helemaal ingekleurd van de tweede cirkel zijn er 2 stukken gekleurd. We zien hier dus 
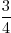 of
of 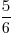 ?
?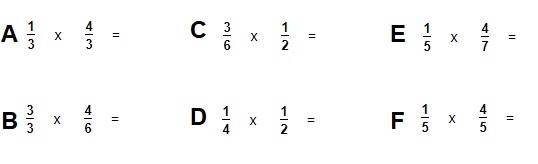
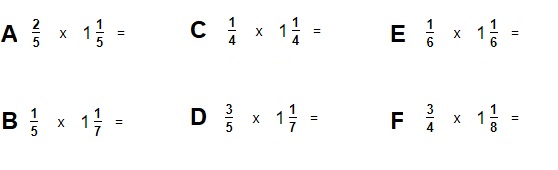

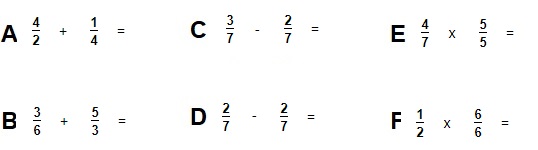
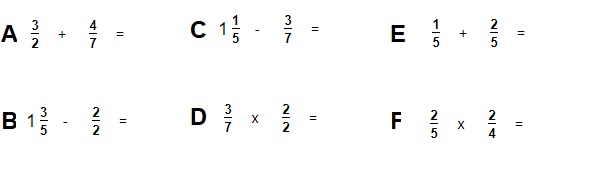
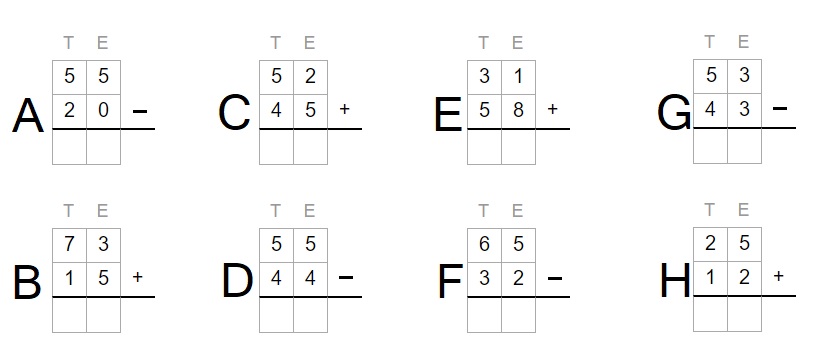
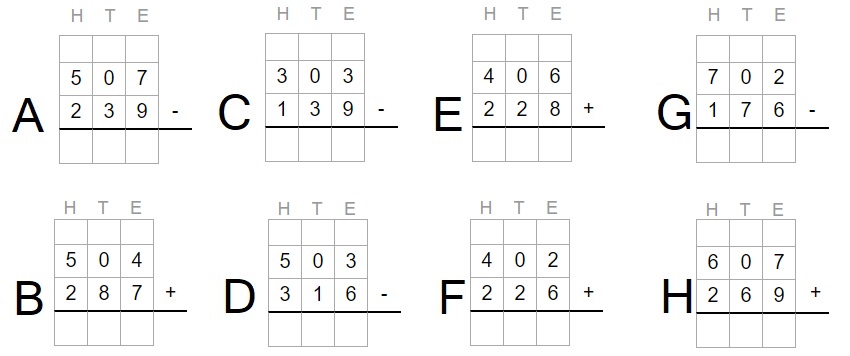



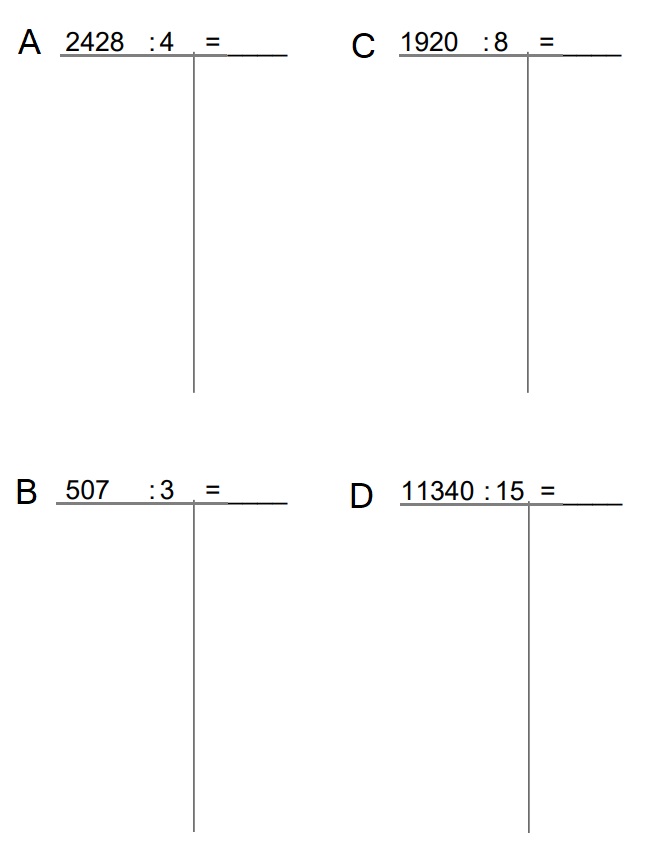
 In deze paragraaf leer je over machten en wortels.
In deze paragraaf leer je over machten en wortels.

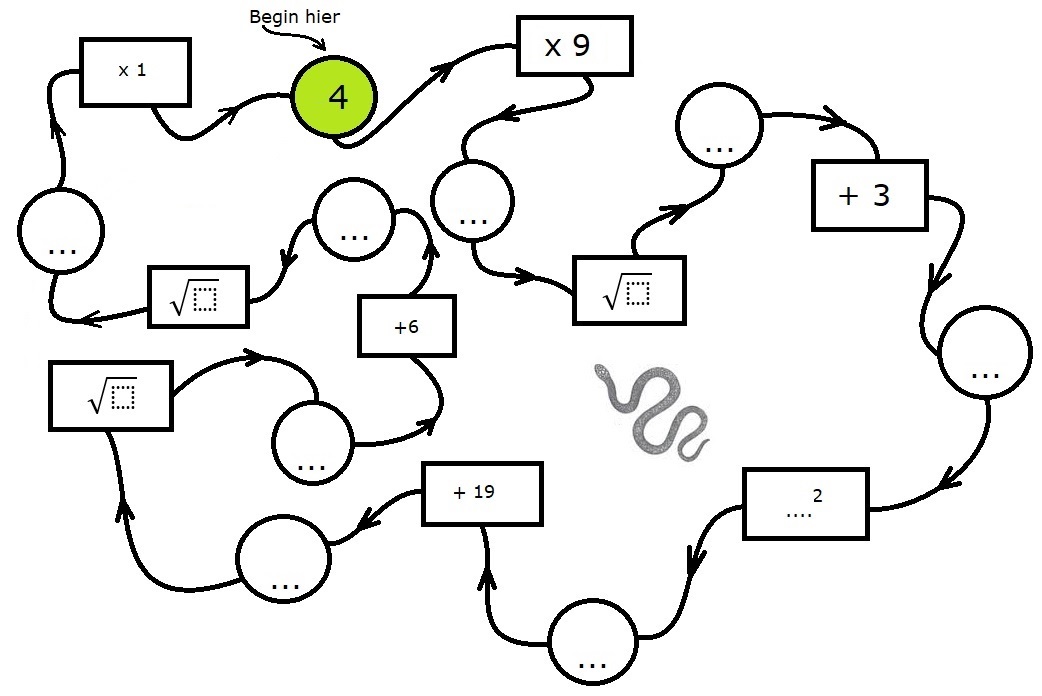
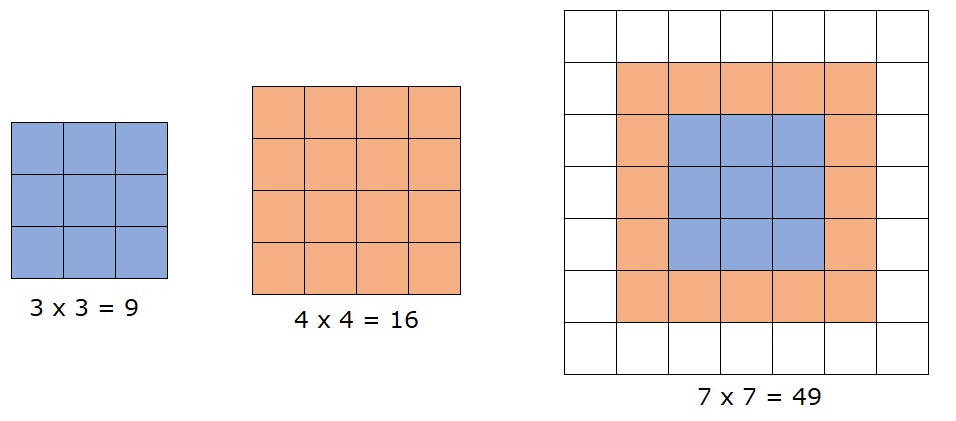
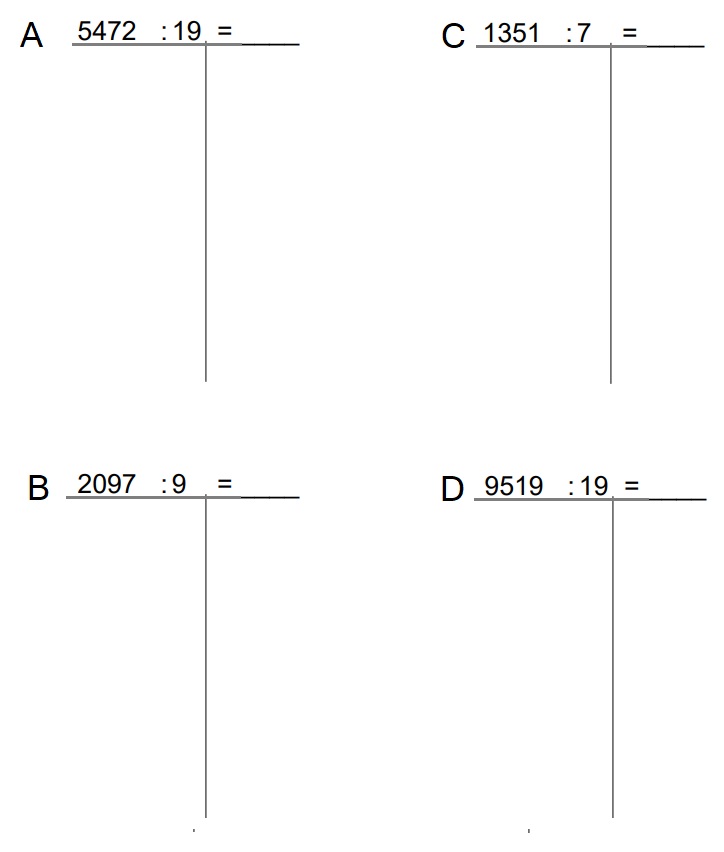
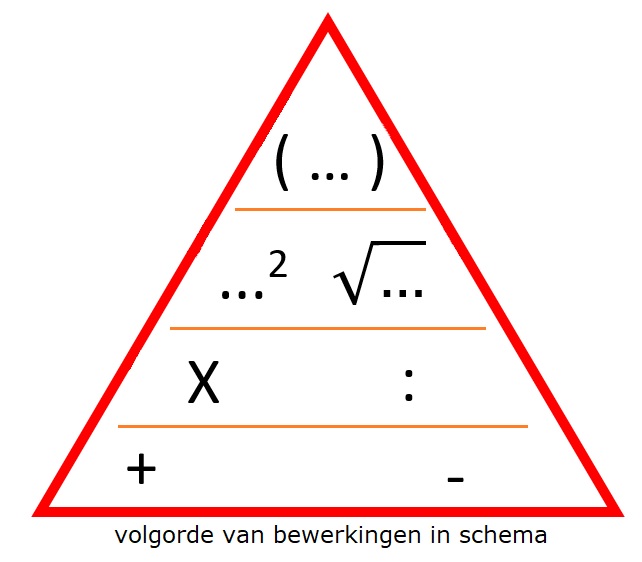
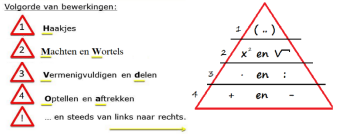 Je wist vast al dat er een bepaalde volgorde bij het berekenen van opgaven wordt gehanteerd.
Je wist vast al dat er een bepaalde volgorde bij het berekenen van opgaven wordt gehanteerd.
 Je gaat bij de patatzaak om de hoek samen met je vrienden wat eten.
Je gaat bij de patatzaak om de hoek samen met je vrienden wat eten.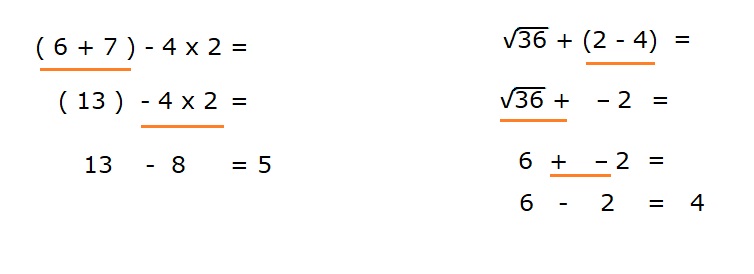
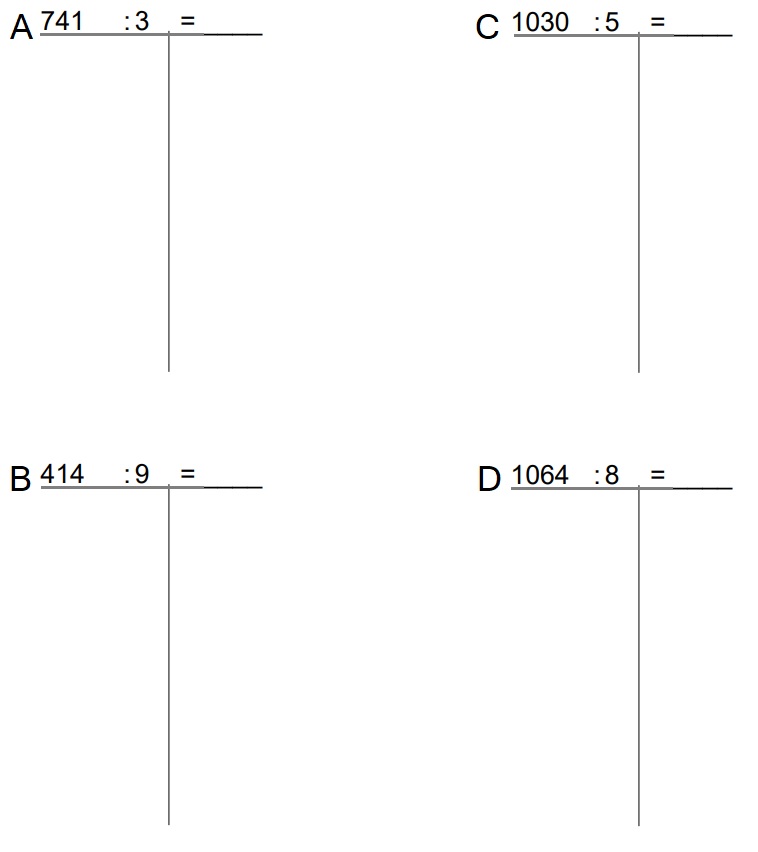
 Nu je alle 'gewone' paragrafen (delen) van het het hoofdstuk rekenen hebt afgerond is het tijd om je te gaan voorbereiden op de repetitie.
Nu je alle 'gewone' paragrafen (delen) van het het hoofdstuk rekenen hebt afgerond is het tijd om je te gaan voorbereiden op de repetitie.
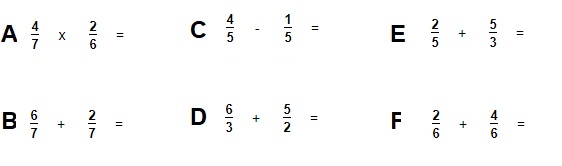
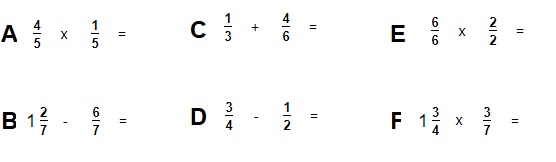
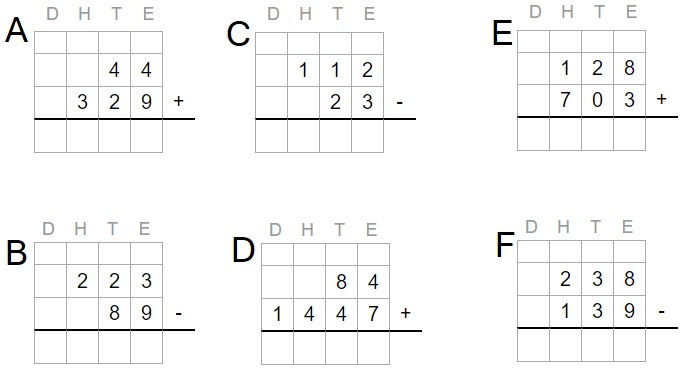

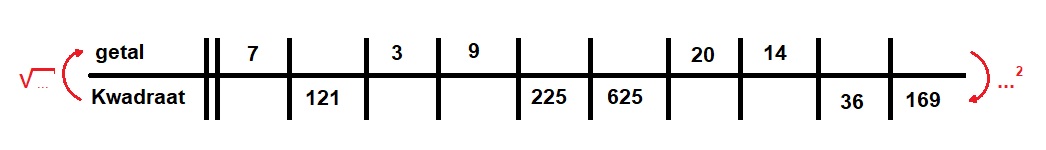

 Op een telraam kun je dit goed duidelijk maken.
Op een telraam kun je dit goed duidelijk maken.




 Aan het eind van dit hoofdstuk:
Aan het eind van dit hoofdstuk:

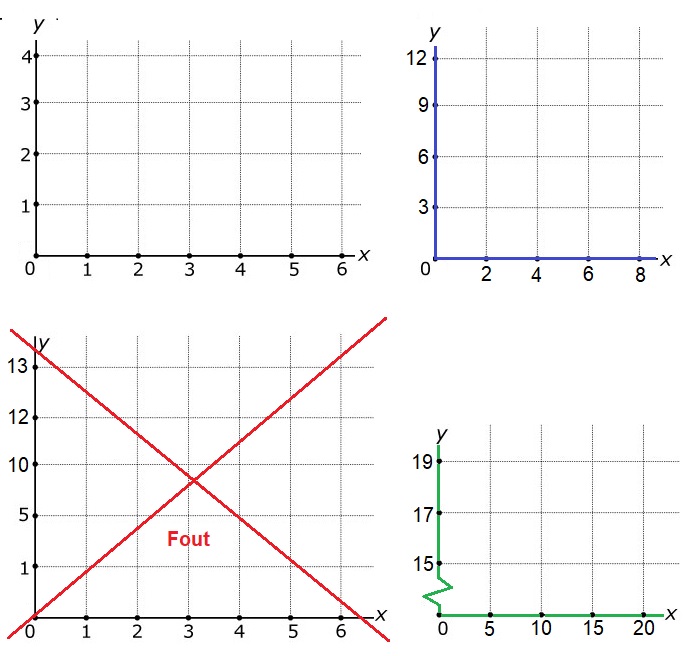
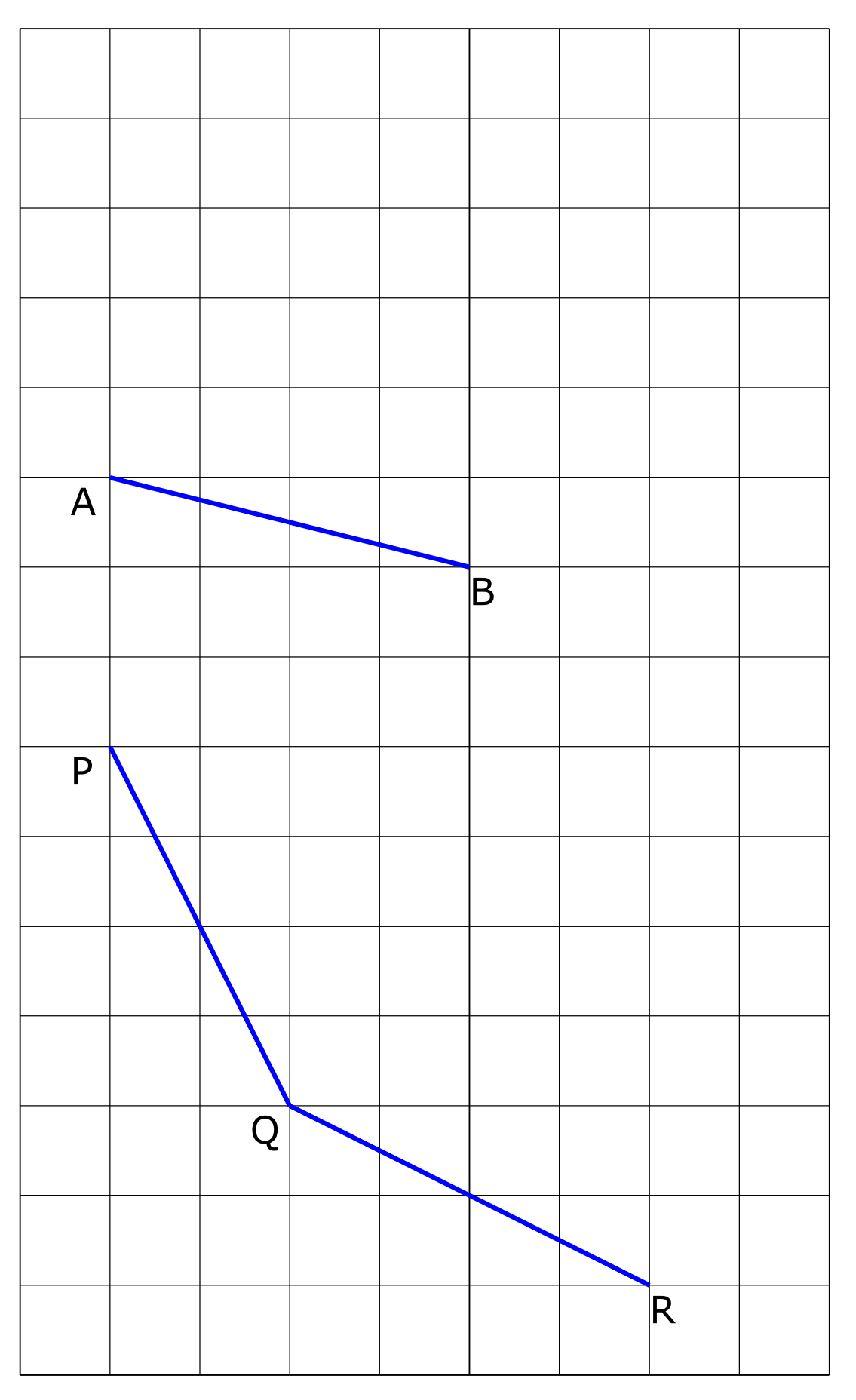
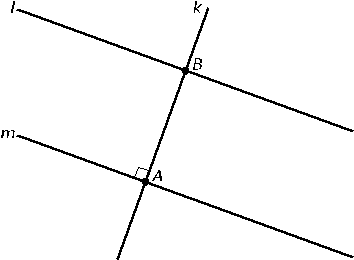 Bekijk de lijnen hiernaast in de afbeelding.
Bekijk de lijnen hiernaast in de afbeelding.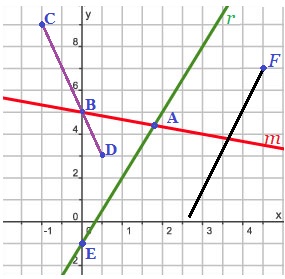 Hiernaast zie je verschillende lijnen, lijnstukken en halve lijnen getekend in een assenstelsel.
Hiernaast zie je verschillende lijnen, lijnstukken en halve lijnen getekend in een assenstelsel. De lijnen
De lijnen 


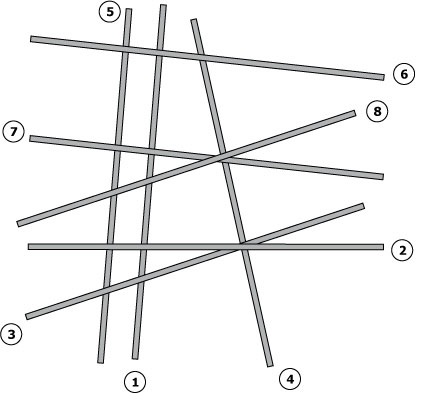 Bekijk de mikadostokjes op de afbeelding.
Bekijk de mikadostokjes op de afbeelding.
 De lijnen
De lijnen 
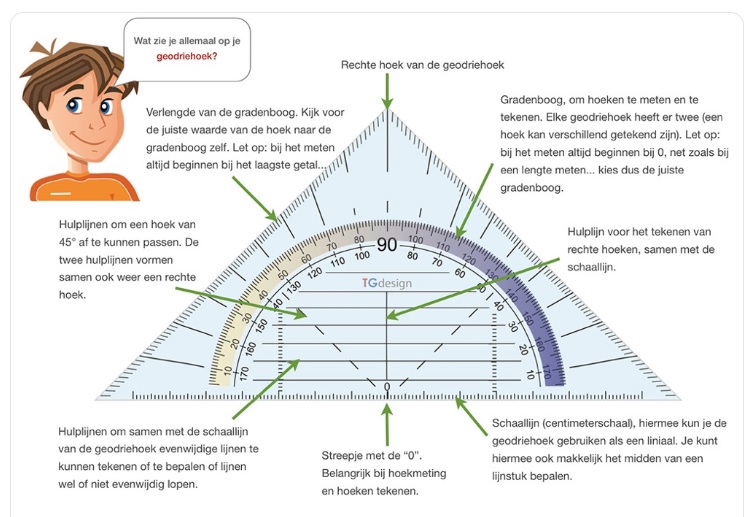
 In de wiskunde is de afstand altijd de lengte van de kortste verbinding. Een afstand is een lengtemaat. Deze meten we met een lineaal. Aan je geodriehoek zit ook een lineaal vast.
In de wiskunde is de afstand altijd de lengte van de kortste verbinding. Een afstand is een lengtemaat. Deze meten we met een lineaal. Aan je geodriehoek zit ook een lineaal vast.
 fstand tussen twee punten meten we dus altijd met een rechte lijn.
fstand tussen twee punten meten we dus altijd met een rechte lijn. De afstand tussen een punt en een lijn meet je altijd loodrecht.
De afstand tussen een punt en een lijn meet je altijd loodrecht. Ook de kortste afstand tussen twee lijnen meet je loodrecht.
Ook de kortste afstand tussen twee lijnen meet je loodrecht.
 Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad.
Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad. Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad.
Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad.
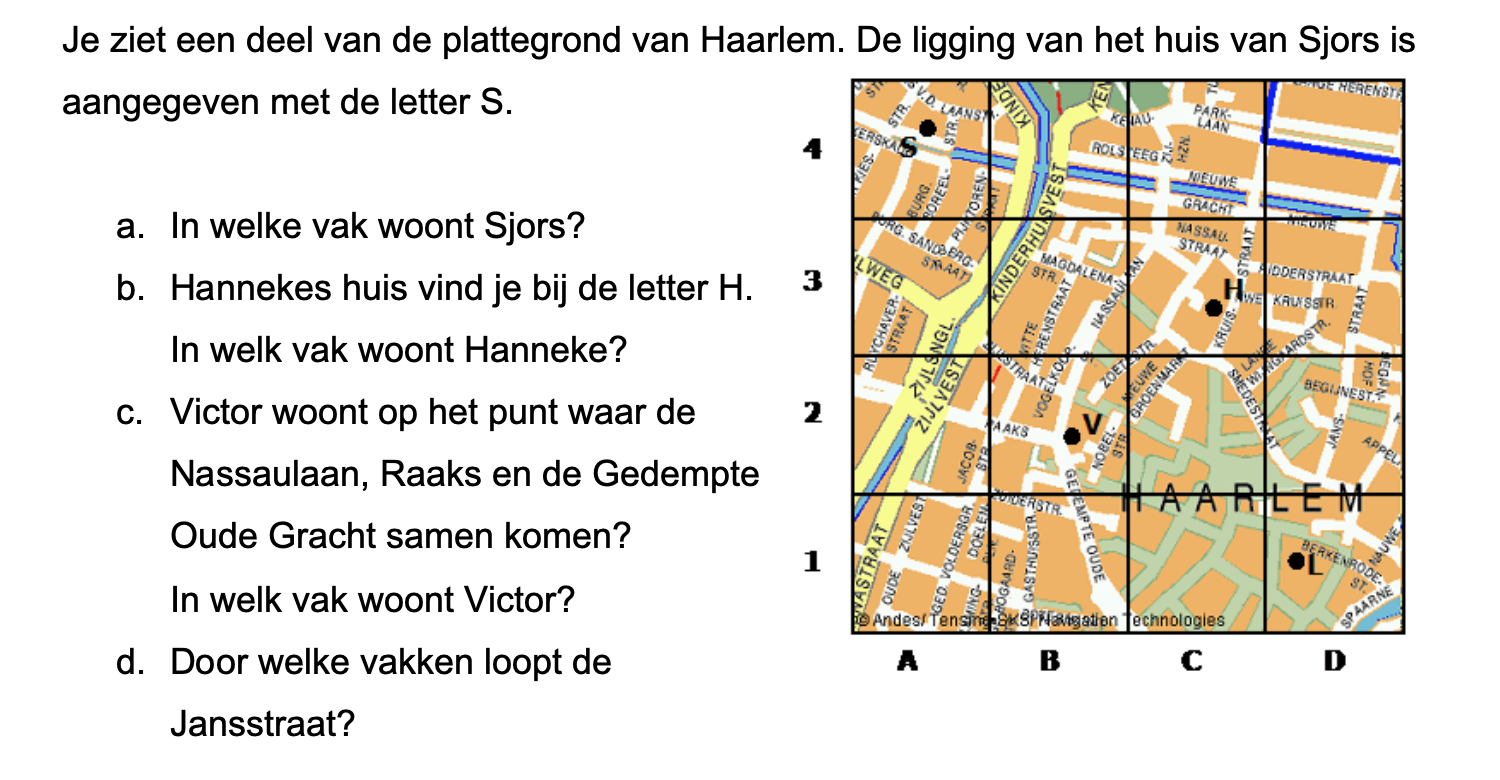
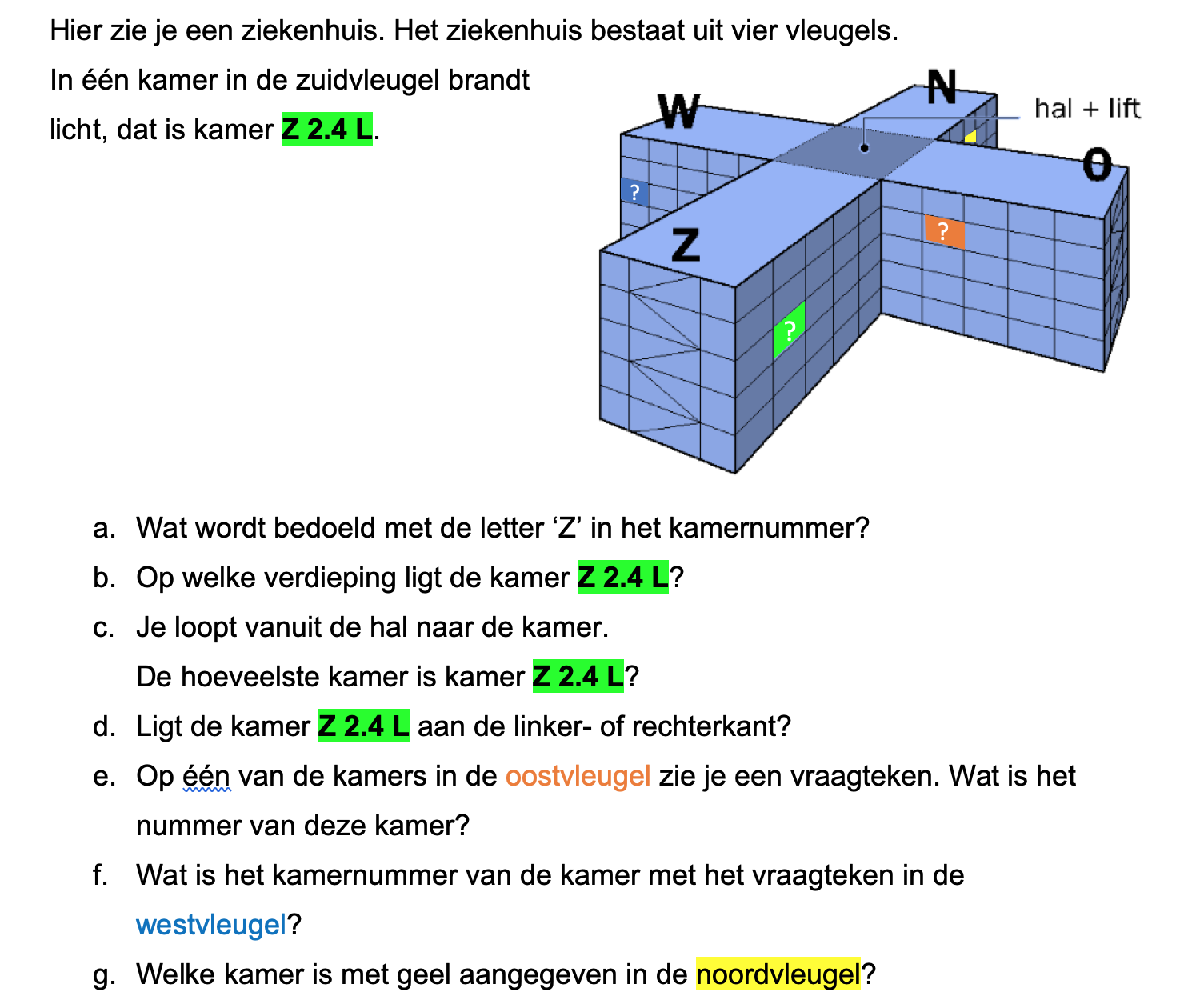
 Je ziet een plattegrond van een school en de fietsenstalling.
Je ziet een plattegrond van een school en de fietsenstalling.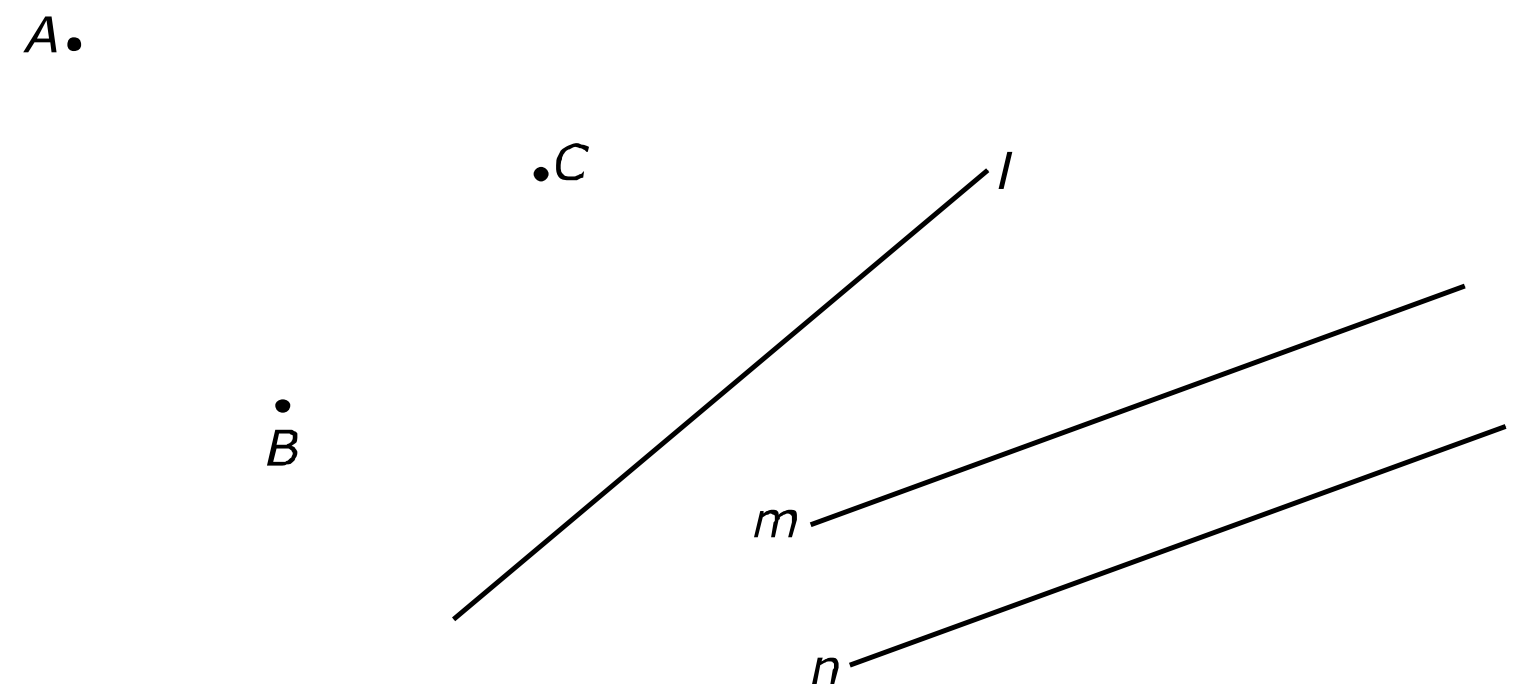
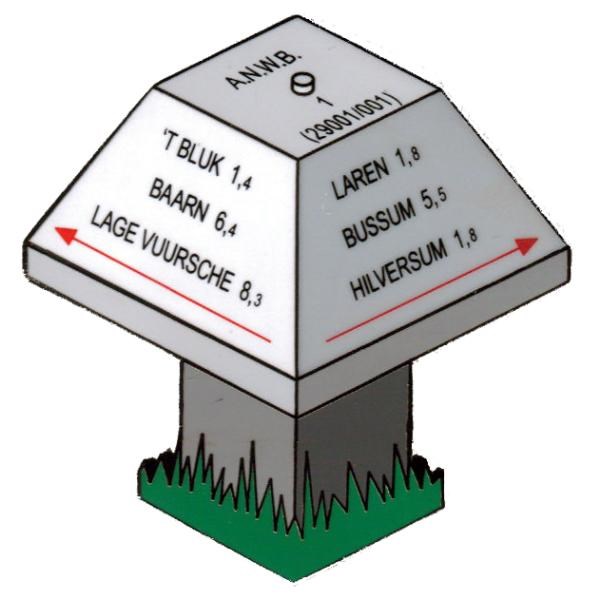
 De afstand naar Harfsen staat op de paddenstoel.
De afstand naar Harfsen staat op de paddenstoel.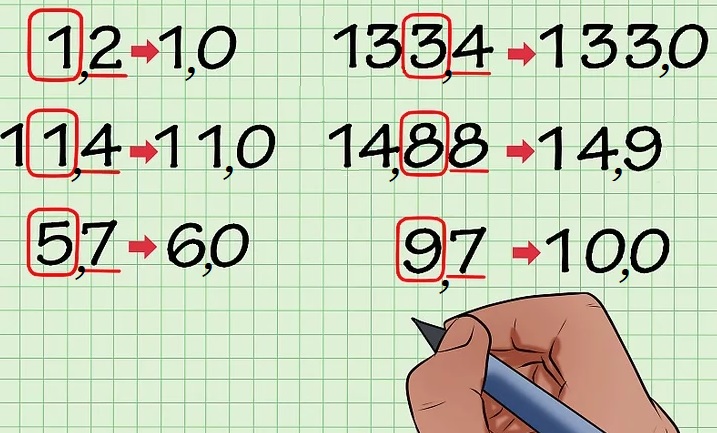

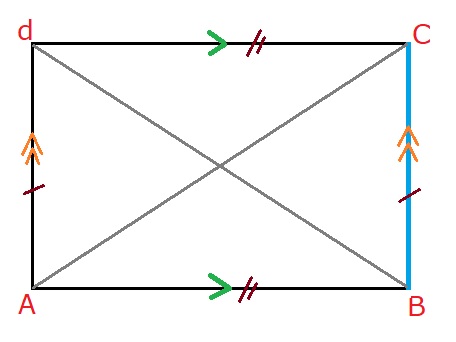
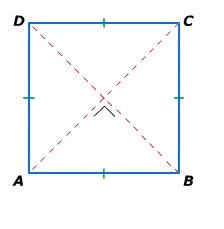 Een vierkant is een vlakke figuur het figuur is 2d, plat.
Een vierkant is een vlakke figuur het figuur is 2d, plat.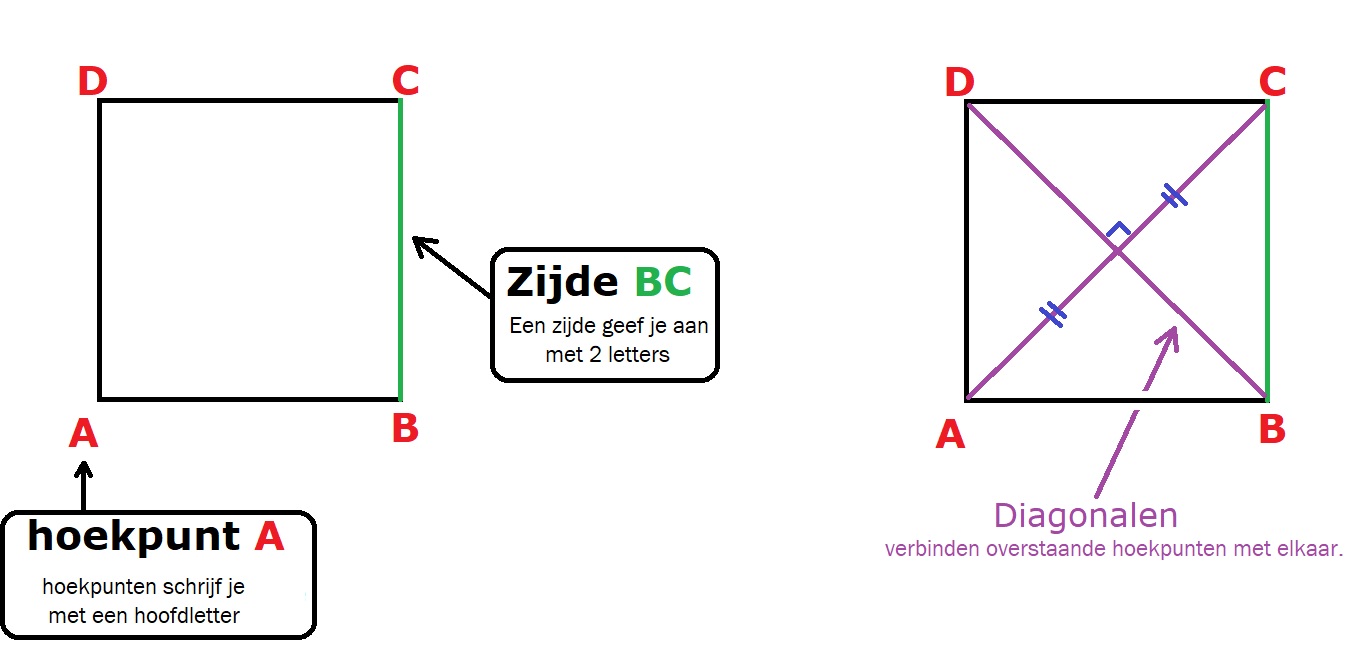
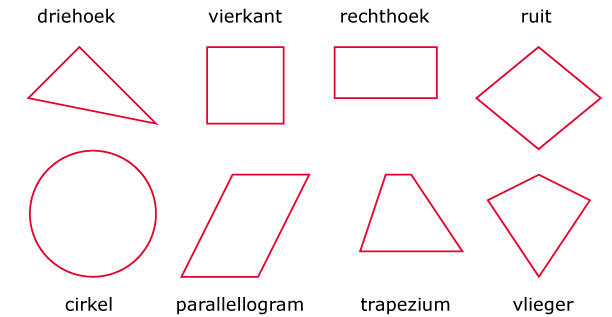
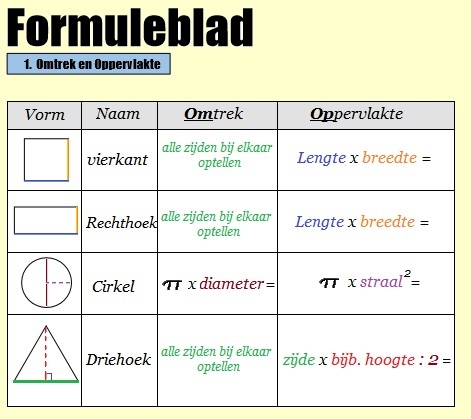
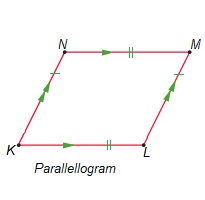
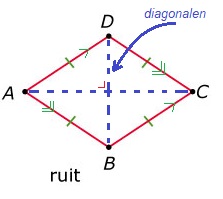
 Bekijk de vlakke figuren hiernaast goed en leer de namen en de kenmerken (eigenschappen) ervan uit je hoofd. Zodat je deze gemakkelijk van elkaar kunt onderscheiden. De eigenschappen (kenmerken) van de verschillende figuren kun je downloaden via deze
Bekijk de vlakke figuren hiernaast goed en leer de namen en de kenmerken (eigenschappen) ervan uit je hoofd. Zodat je deze gemakkelijk van elkaar kunt onderscheiden. De eigenschappen (kenmerken) van de verschillende figuren kun je downloaden via deze  In een vierkant
In een vierkant In een rechthoek
In een rechthoek In een parallellogram
In een parallellogram In een ruit
In een ruit Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.
Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.
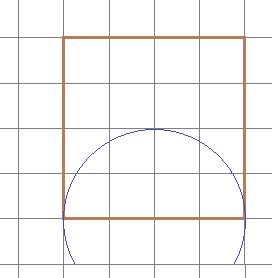 et de metalen punt in het midden van één van de zijde en de potloodpunt op een hoekpunt. Teken nu een halve cirkel. Als je het goed gedaan hebt, krijg je de figuur die je hiernaast ziet in je schrift.
et de metalen punt in het midden van één van de zijde en de potloodpunt op een hoekpunt. Teken nu een halve cirkel. Als je het goed gedaan hebt, krijg je de figuur die je hiernaast ziet in je schrift.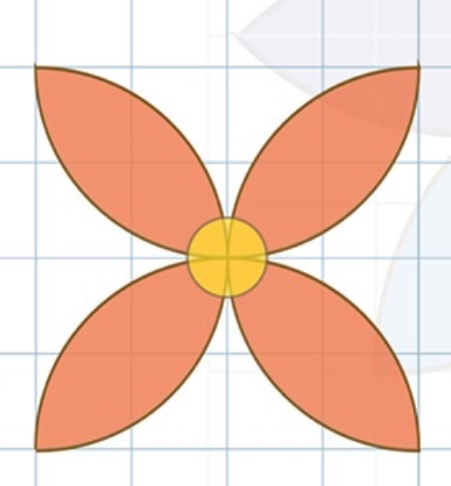
 Hiernaast zie je hoe je met je passer het Genesis patroon kunt tekenen.
Hiernaast zie je hoe je met je passer het Genesis patroon kunt tekenen. Maak de figuur die je hiernaast ziet na in je schrift.
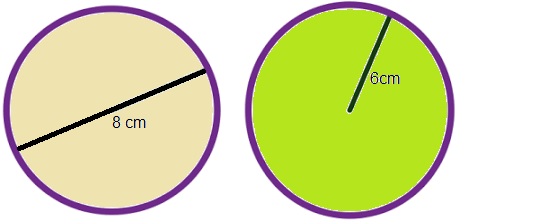
Maak de figuur die je hiernaast ziet na in je schrift.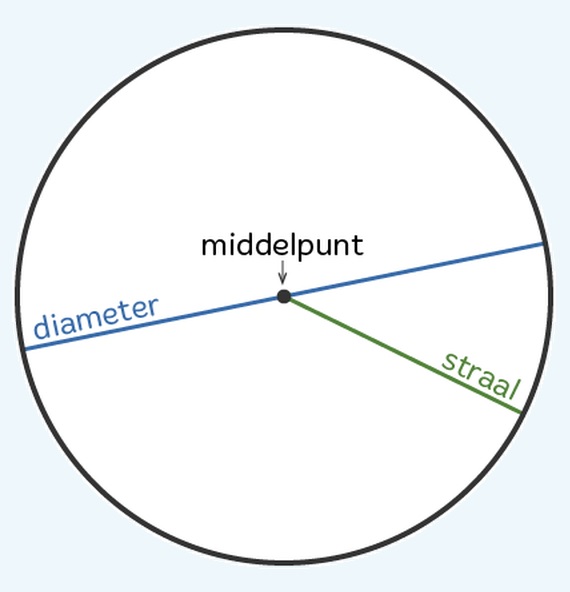 Om de omtrek te kunnen bereken van een cirkel moet je dus wel weten wat een diameter (en wat een straal) is. Kijk maar eens naar de afbeelding hiernaast. Dan wordt dat waarschijnlijk snel duidelijk.
Om de omtrek te kunnen bereken van een cirkel moet je dus wel weten wat een diameter (en wat een straal) is. Kijk maar eens naar de afbeelding hiernaast. Dan wordt dat waarschijnlijk snel duidelijk.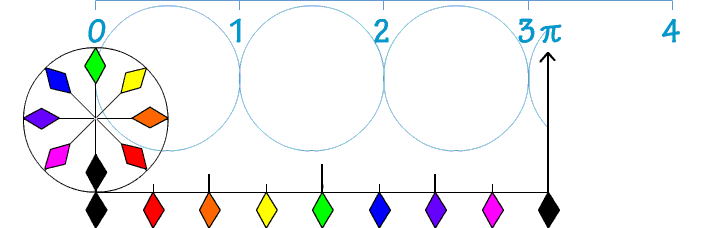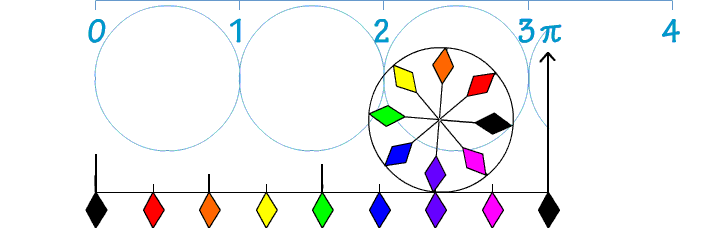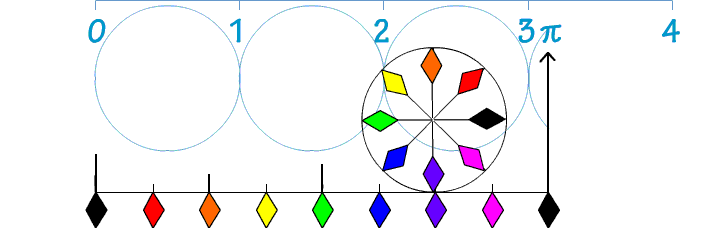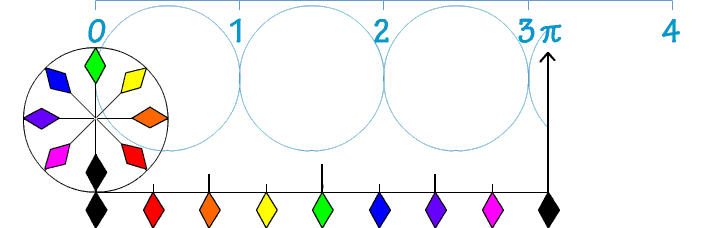

 Een ring is eigenlijk een soort holle cirkel. Er is een grote cirkel waar een kleine cirkel uitgehaald wordt. Hiernaast zie je de schets van een ring. Bereken de oppervlakte van het gele gedeelte. Rond je antwoord af op 2 decimalen.
Een ring is eigenlijk een soort holle cirkel. Er is een grote cirkel waar een kleine cirkel uitgehaald wordt. Hiernaast zie je de schets van een ring. Bereken de oppervlakte van het gele gedeelte. Rond je antwoord af op 2 decimalen.
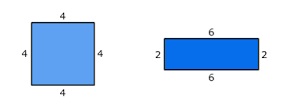 Bekijk het vierkant en de rechthoek hiernaast.
Bekijk het vierkant en de rechthoek hiernaast.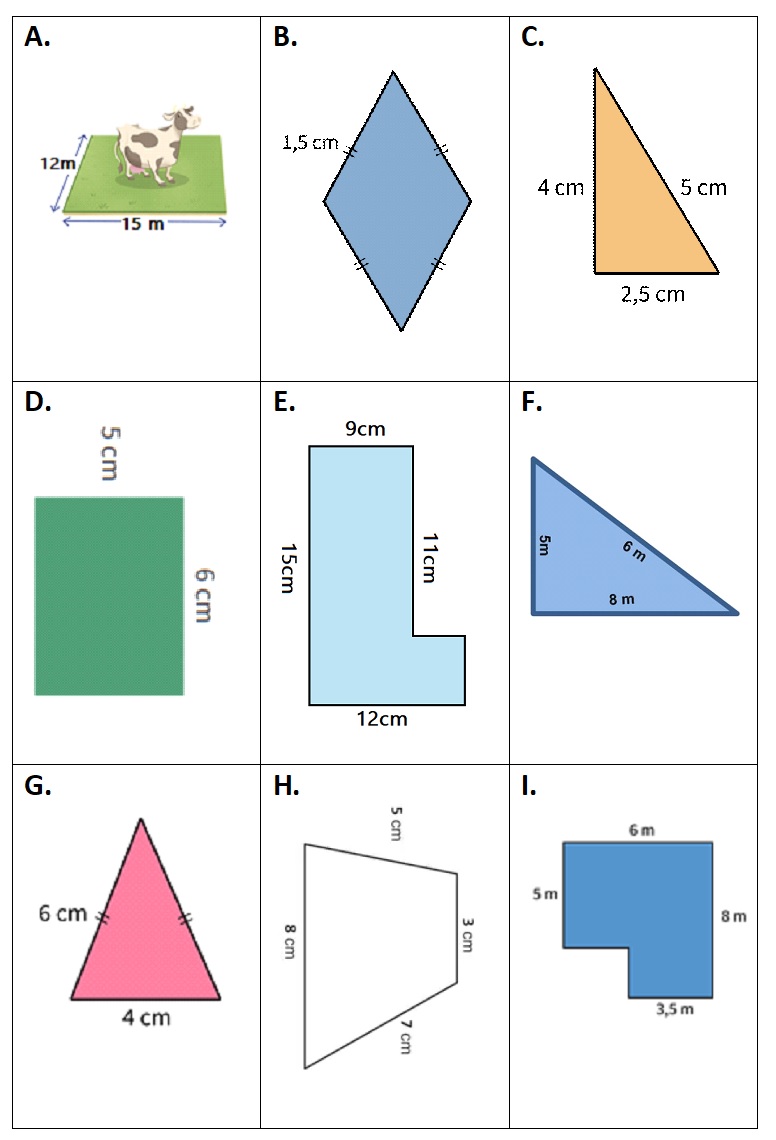




 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.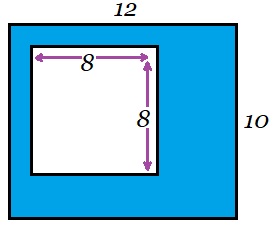 Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.
Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.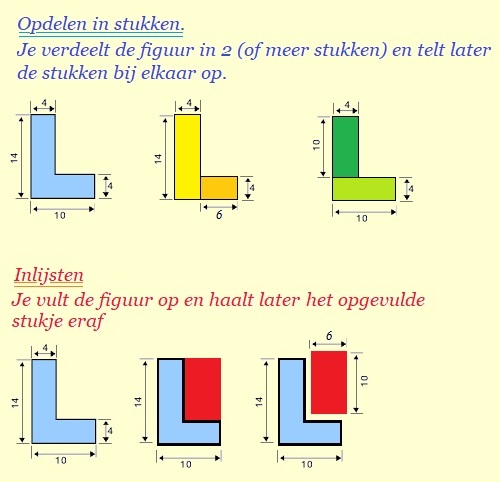
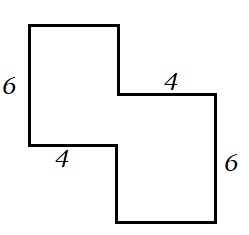
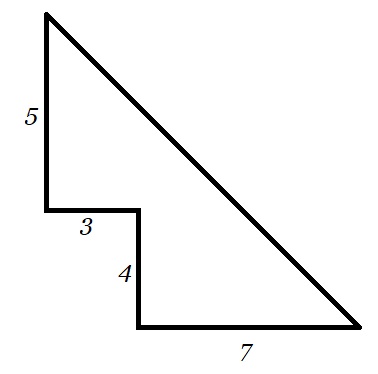 Bekijk de figuur hiernaast. Bereken de oppervlakte van deze figuur.
Bekijk de figuur hiernaast. Bereken de oppervlakte van deze figuur.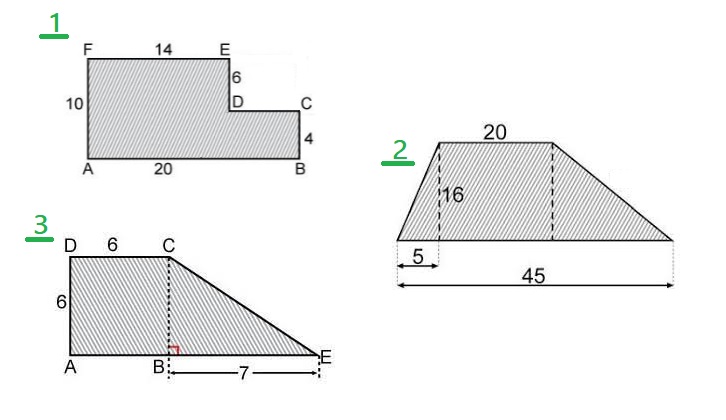
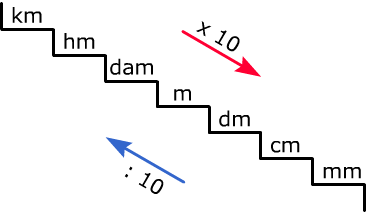
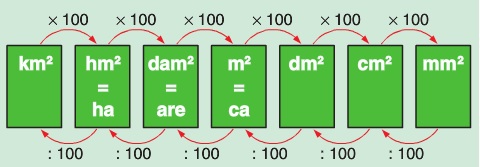
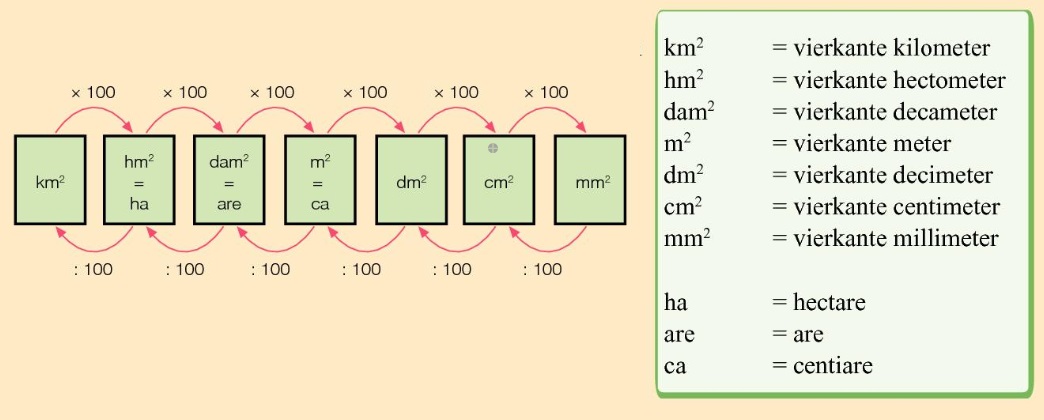
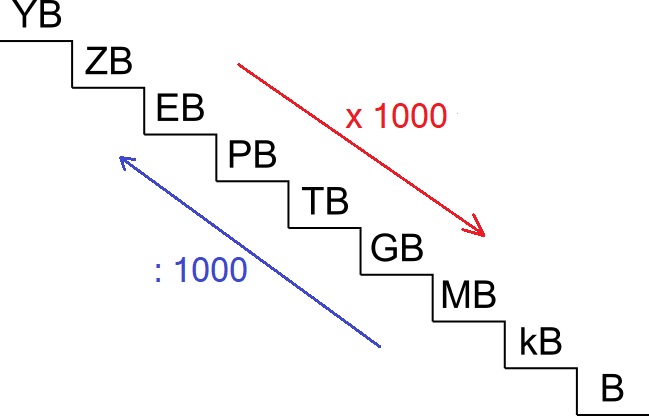
 Een metriek stelsel of metrisch systeem is een systeem van uniforme standaardeenheden voor het meten van bijvoorbeeld afstand, gewicht en temperatuur. Uniform wil zeggen over het zelfde. alle landen die met het metriek stelsel werken houden zich aan dezelfde afspraken.
Een metriek stelsel of metrisch systeem is een systeem van uniforme standaardeenheden voor het meten van bijvoorbeeld afstand, gewicht en temperatuur. Uniform wil zeggen over het zelfde. alle landen die met het metriek stelsel werken houden zich aan dezelfde afspraken.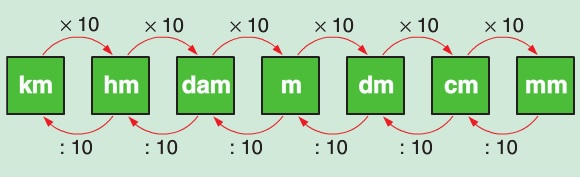
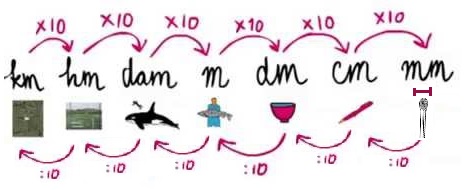
 De lengte van een lesboek is 40 centimeter (cm). Hoeveel decimeter is dat?
De lengte van een lesboek is 40 centimeter (cm). Hoeveel decimeter is dat?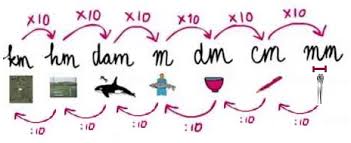



 aat uit twee even grote vakken.
aat uit twee even grote vakken.



 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.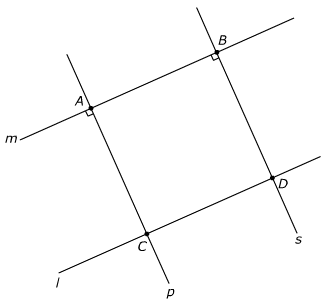
 Bekijk de vier figuur hiernaast.
Bekijk de vier figuur hiernaast.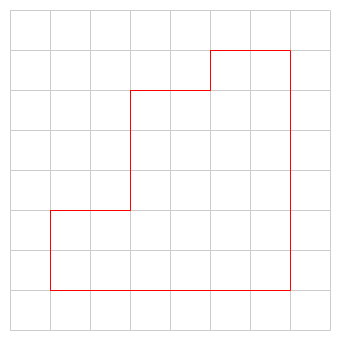


 Aan het eind van dit hoofdstuk kan ik:
Aan het eind van dit hoofdstuk kan ik:
 In de voorkennis herhalen we stukje van de wiskunde die je op de basisschool al geleerd hebt of een stukje van de wiskunde dat al eens in een voorgaand hoofdstuk behandeld is.
In de voorkennis herhalen we stukje van de wiskunde die je op de basisschool al geleerd hebt of een stukje van de wiskunde dat al eens in een voorgaand hoofdstuk behandeld is.
 Liggen stokje 1 en 3 loodrecht op elkaar?
Liggen stokje 1 en 3 loodrecht op elkaar?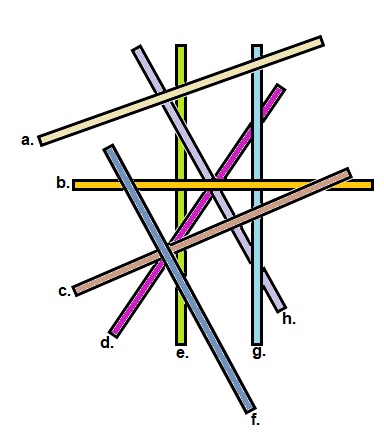
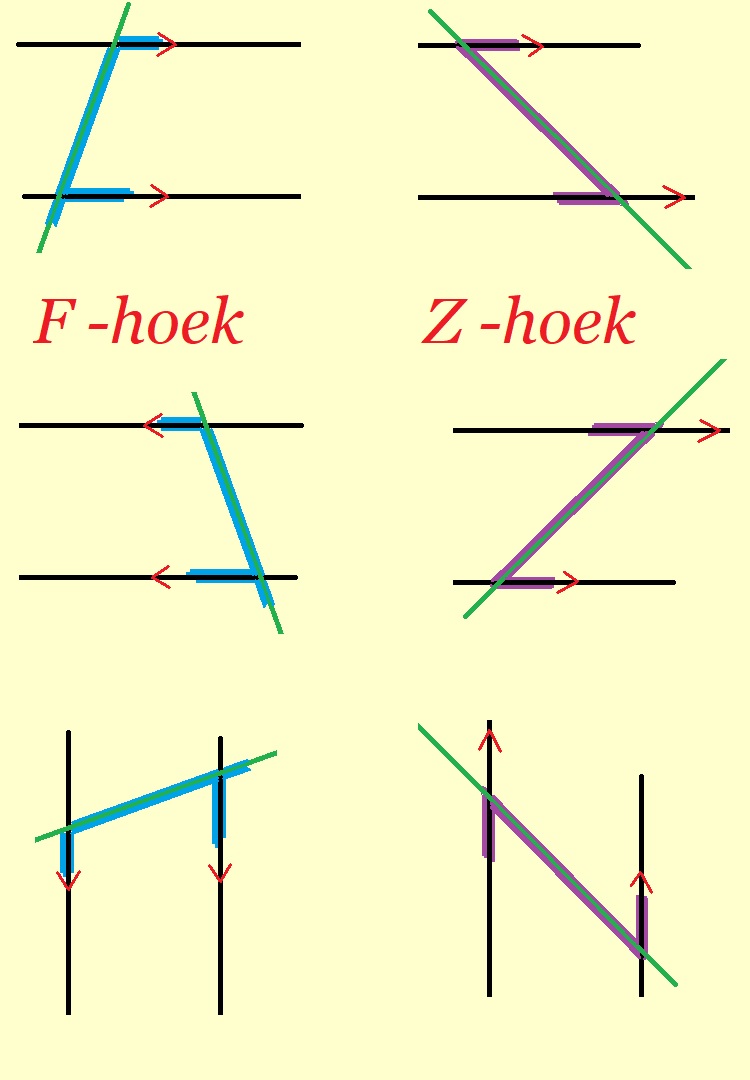
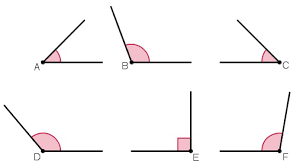 In de tweede paragraaf van dit hoofdstuk gaat het over hoeken.
In de tweede paragraaf van dit hoofdstuk gaat het over hoeken.
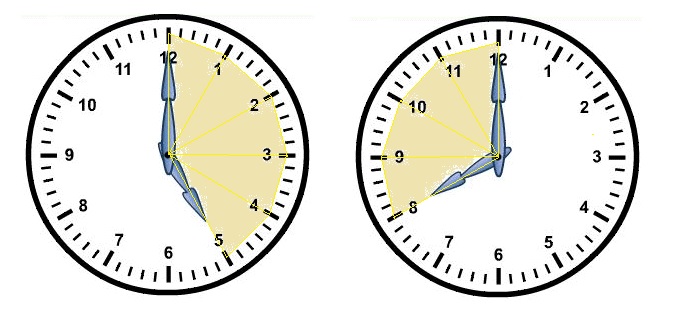
 Over hoeveel graden draait de grote wijzer van een klok in:
Over hoeveel graden draait de grote wijzer van een klok in: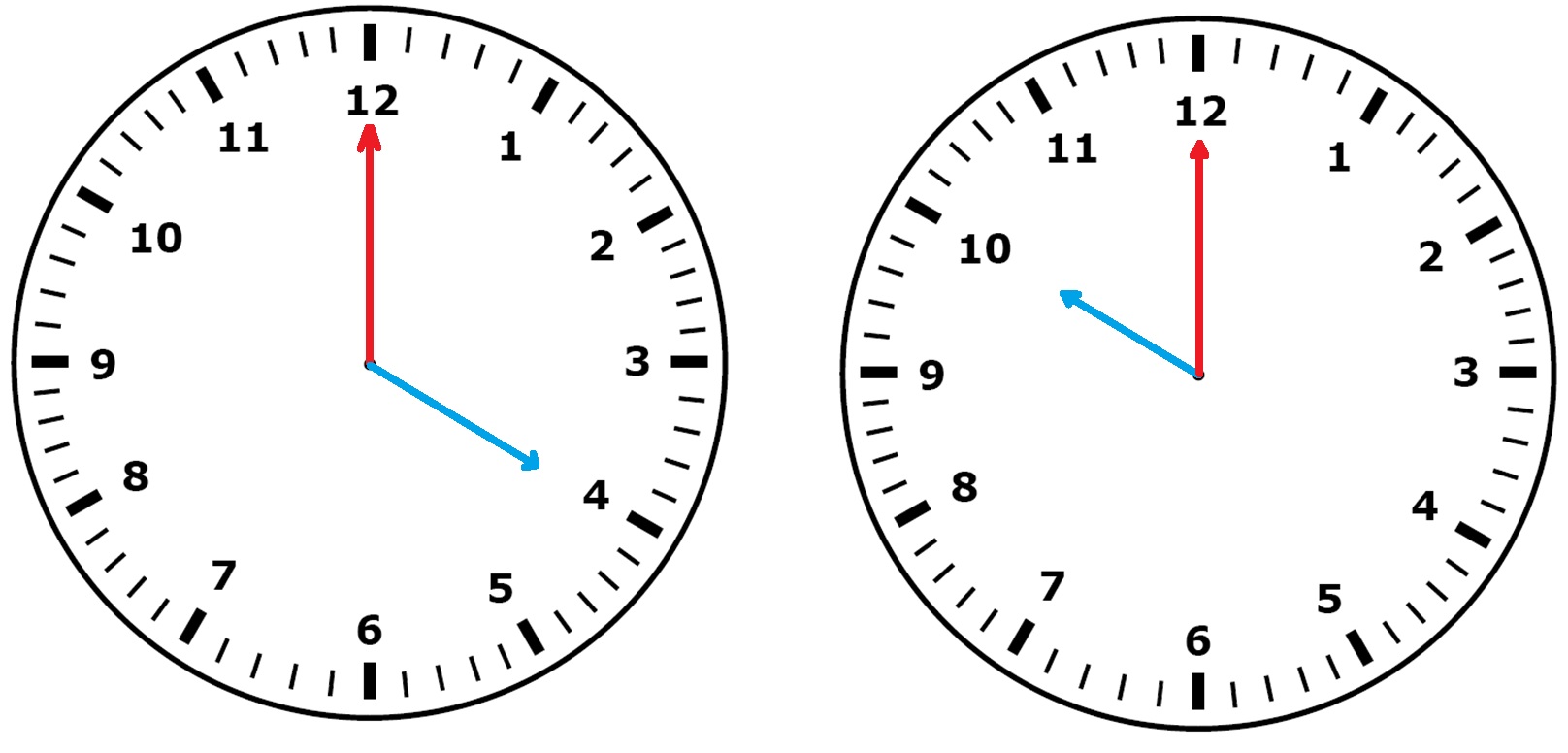 Bereken hoe groot de hoek is tussen de wijzers van een klok om.
Bereken hoe groot de hoek is tussen de wijzers van een klok om.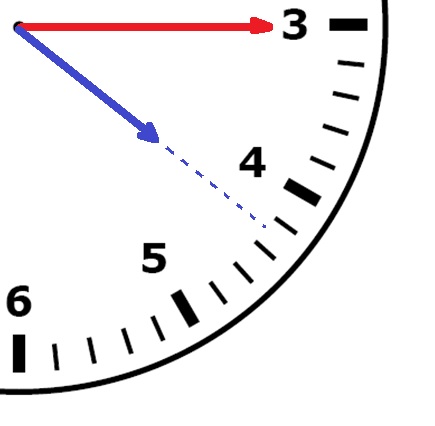 Wanneer de klok niet op een heel uur staat maar bijvoorbeeld op een half uur of op een kwartier (een kwart) dan wijst de kleine wijzer ook niet meer precies het getal aan.
Wanneer de klok niet op een heel uur staat maar bijvoorbeeld op een half uur of op een kwartier (een kwart) dan wijst de kleine wijzer ook niet meer precies het getal aan.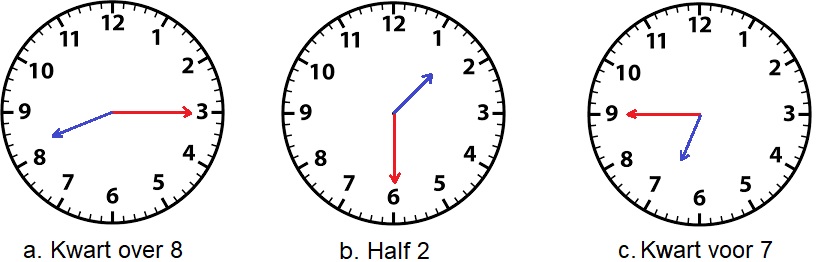

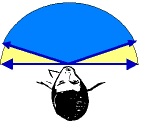 In de voorbeelden hierboven spreken we over je gezichtsveld. Dat is het gebied dat je kunt zien zonder je hoofd of je ogen te bewegen. Wanneer iets of iemand voor je staat dan beneemt deze een deel van je zicht.
In de voorbeelden hierboven spreken we over je gezichtsveld. Dat is het gebied dat je kunt zien zonder je hoofd of je ogen te bewegen. Wanneer iets of iemand voor je staat dan beneemt deze een deel van je zicht.
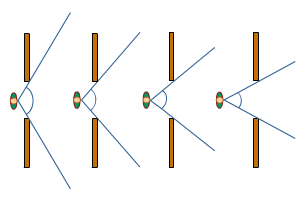

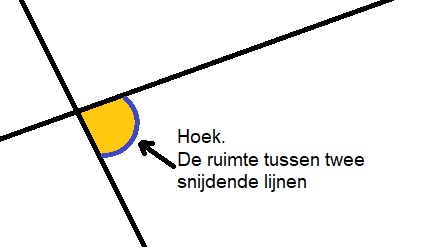
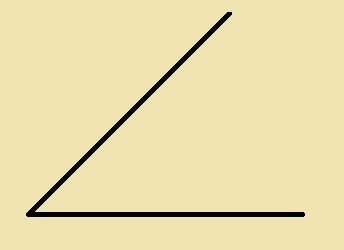
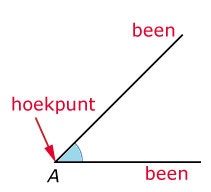 Een hoek bestaat dus uit twee lijnen. Deze lijnen noemen we de benen van de hoek.
Een hoek bestaat dus uit twee lijnen. Deze lijnen noemen we de benen van de hoek.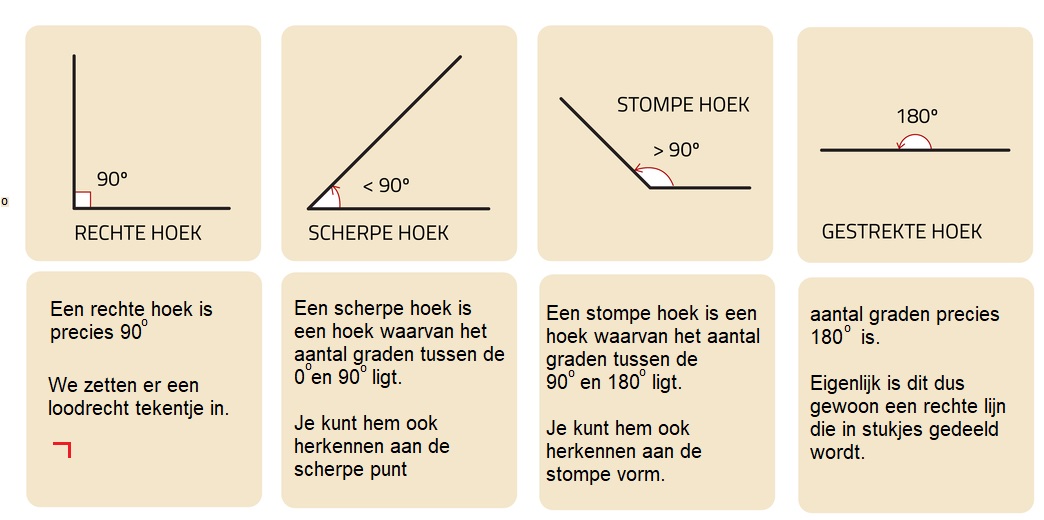
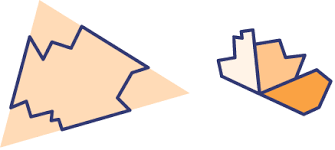
 Hiernaast zie je een bootje. In dit bootje zijn 7 hoeken verstopt. De hoeken hebben allemaal een hoofdletter.
Hiernaast zie je een bootje. In dit bootje zijn 7 hoeken verstopt. De hoeken hebben allemaal een hoofdletter. Als je naar een analoge klok kijkt, een analoge klok is een klok met wijzers, dan maken de wijzers van de klok ook een hoek met elkaar. Bekijk het plaatje van de zes klokken hiernaast.
Als je naar een analoge klok kijkt, een analoge klok is een klok met wijzers, dan maken de wijzers van de klok ook een hoek met elkaar. Bekijk het plaatje van de zes klokken hiernaast. In deze paragraaf leer je hoeken opmeten.
In deze paragraaf leer je hoeken opmeten.
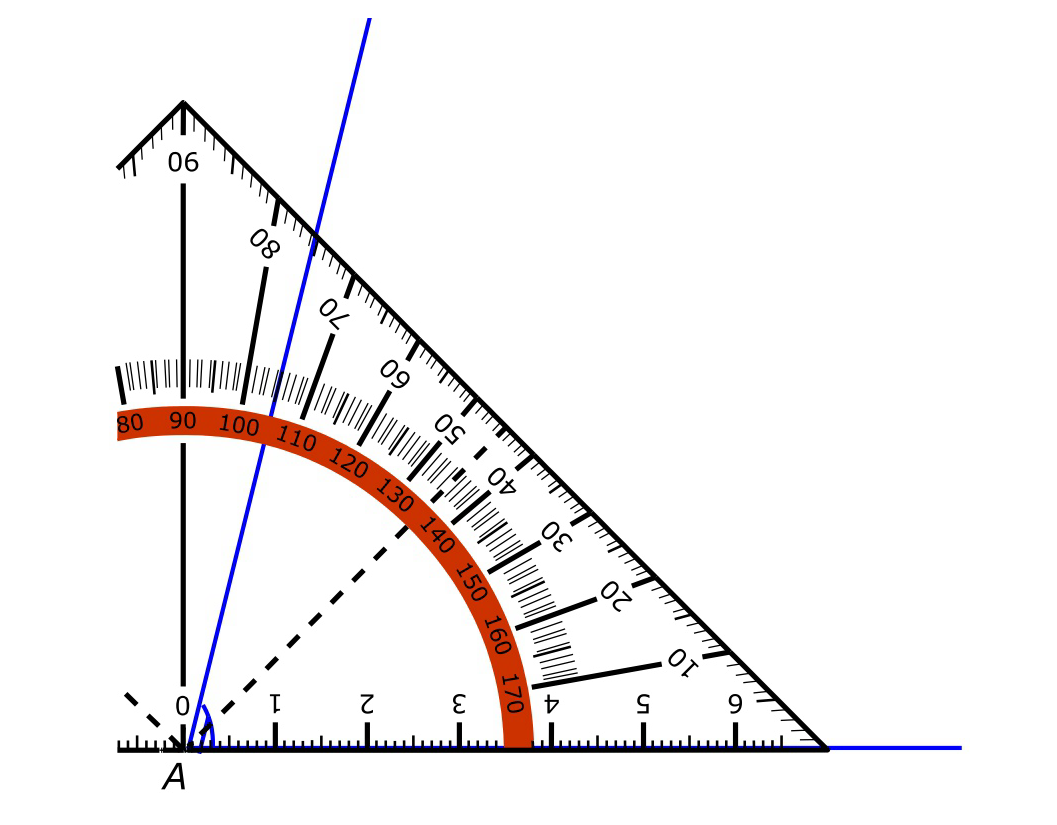
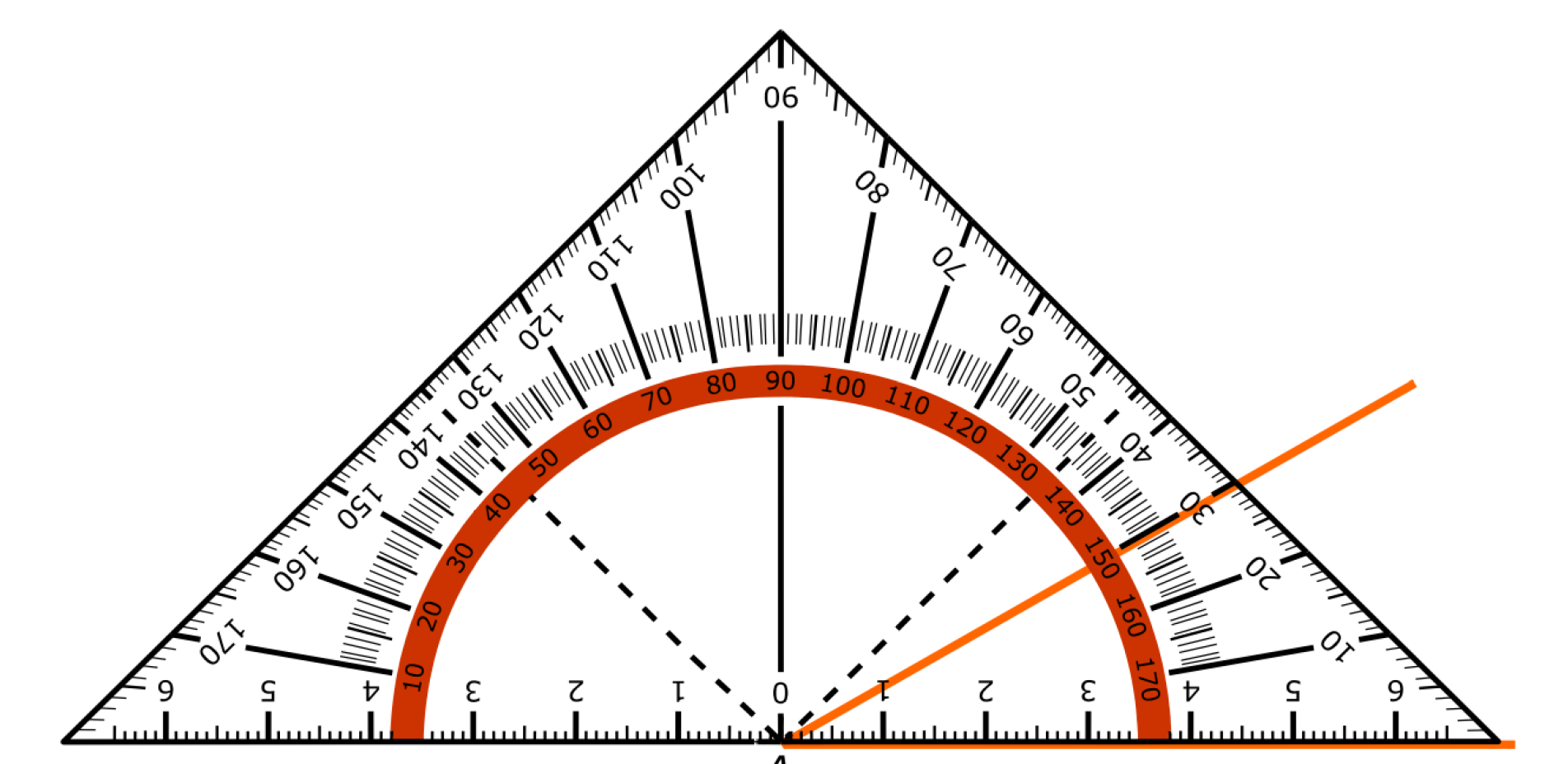
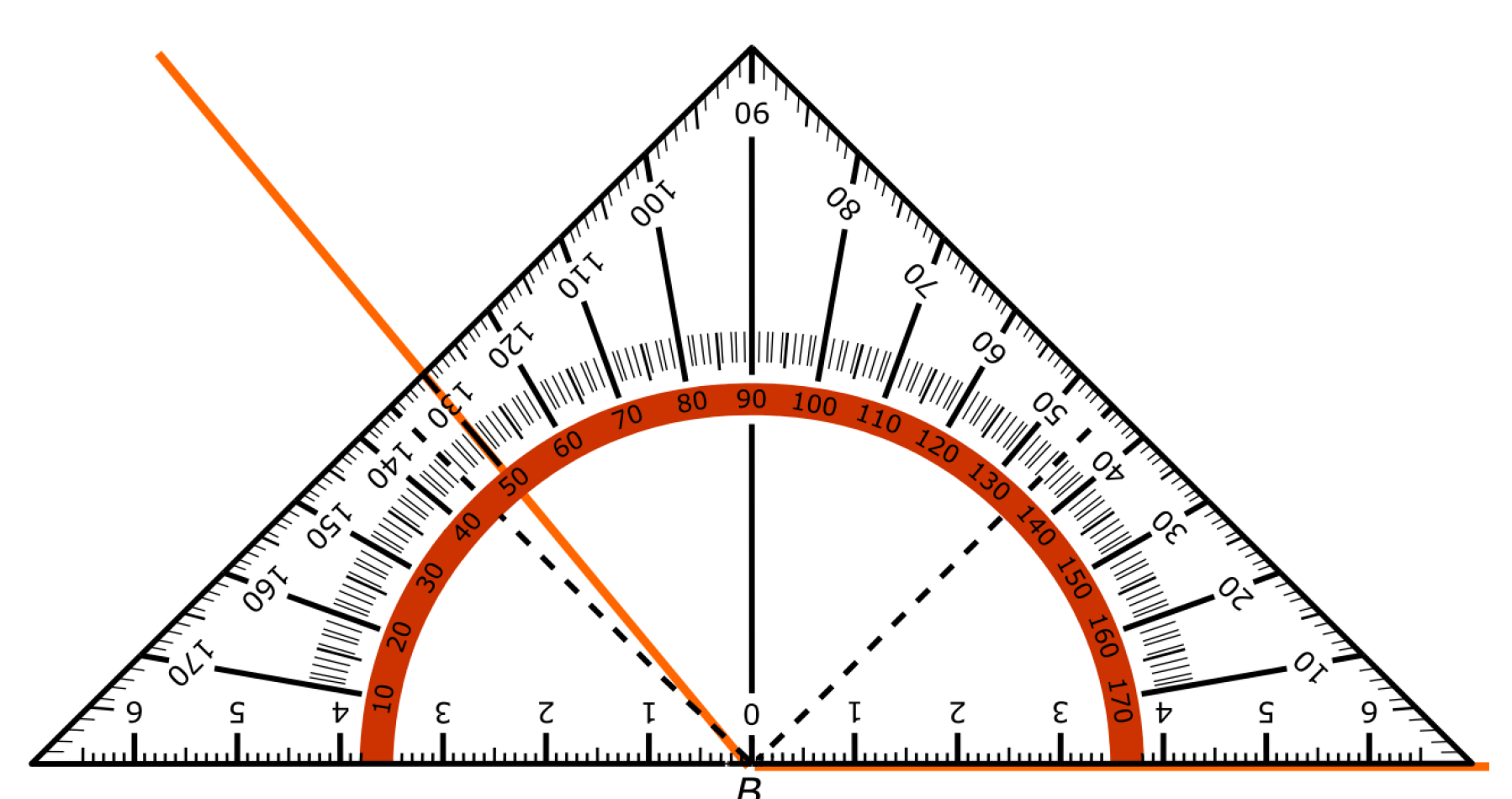
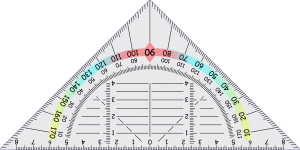
 Het kunnen meten van een hoek is een vaardigheid. Het is dus niet iets wat je uit je hoofd kunt leren, het is iets dat je moet kunnen voordoen net zoals hooghouden met een bal bijvoorbeeld.
Het kunnen meten van een hoek is een vaardigheid. Het is dus niet iets wat je uit je hoofd kunt leren, het is iets dat je moet kunnen voordoen net zoals hooghouden met een bal bijvoorbeeld.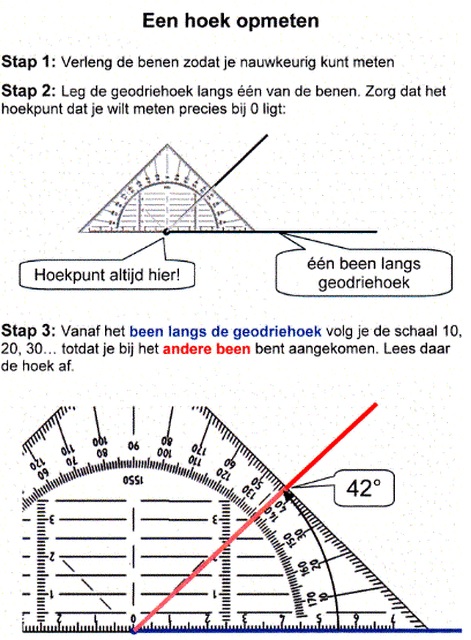
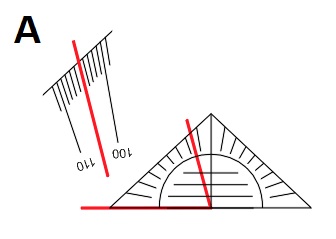
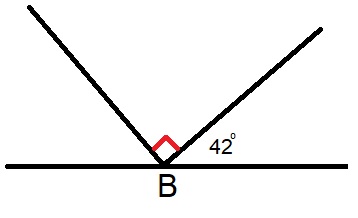
 In de vorige paragraaf heb je geleerd hoe je een hoek kunt opmeten.
In de vorige paragraaf heb je geleerd hoe je een hoek kunt opmeten.
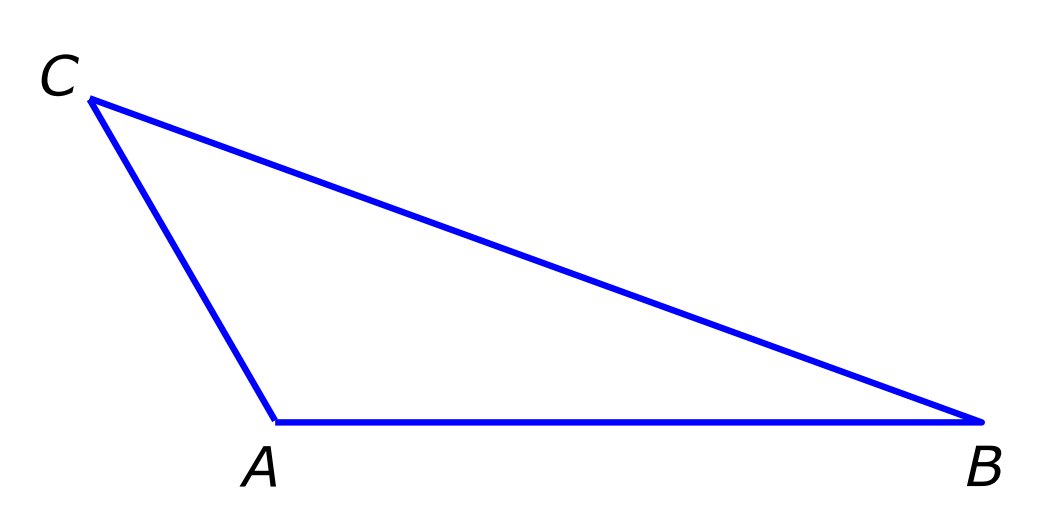
 In paragraaf 5 van dit hoofdstuk leer je hoe je de hoeken binnen een driehoek kunt berekenen.
In paragraaf 5 van dit hoofdstuk leer je hoe je de hoeken binnen een driehoek kunt berekenen. Stap 1. Teken een driehoek. Het maakt niet uit hoe groot deze is, als hij maar netjes drie hoekpunten heeft.
Stap 1. Teken een driehoek. Het maakt niet uit hoe groot deze is, als hij maar netjes drie hoekpunten heeft.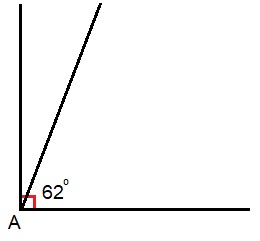
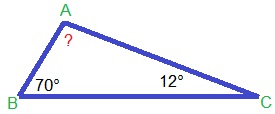
 Nu je geleerd hebt dat de driehoeken van een driehoek samen altijd 180o zijn, kunnen we hier mooi gebruik van maken. Want weet je twee hoekjes van een een driehoek, dan kun je dus de derde berekenen. En dat is veel sneller (en soms preciezer) dan opmeten.
Nu je geleerd hebt dat de driehoeken van een driehoek samen altijd 180o zijn, kunnen we hier mooi gebruik van maken. Want weet je twee hoekjes van een een driehoek, dan kun je dus de derde berekenen. En dat is veel sneller (en soms preciezer) dan opmeten.
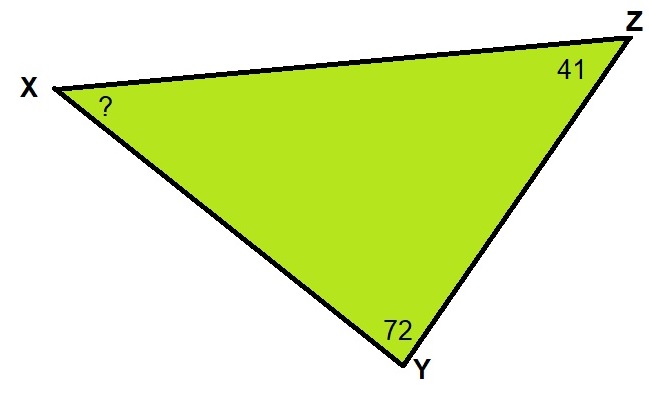
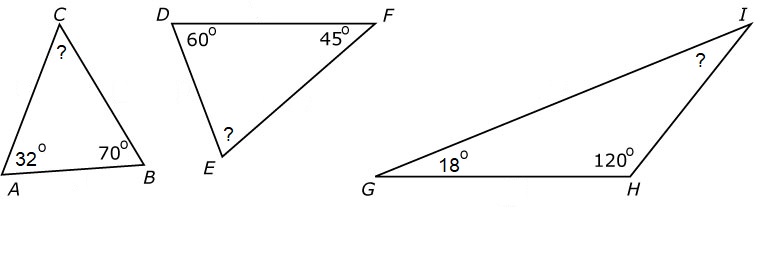
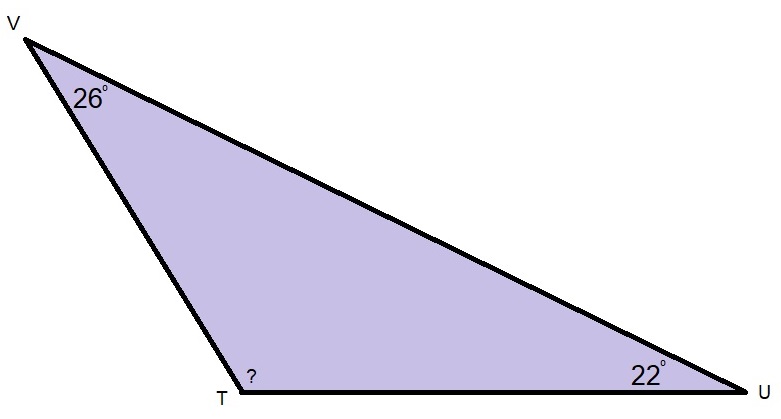
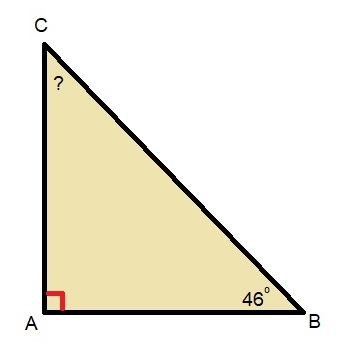 H4.5 opdracht 8
H4.5 opdracht 8 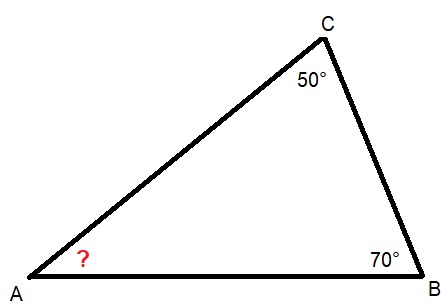
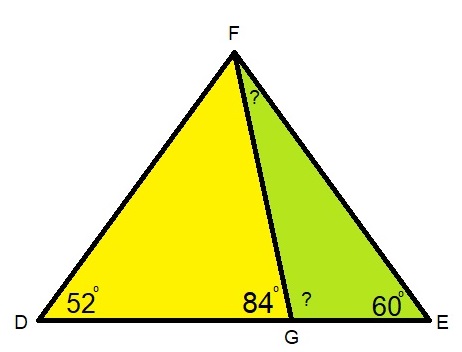

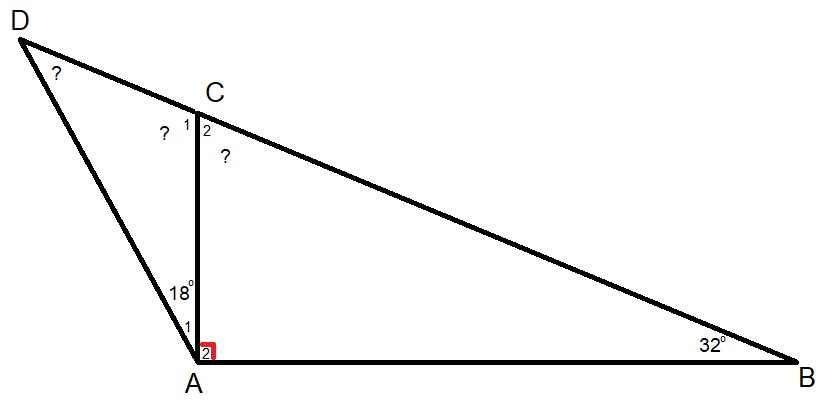 H4.5 opdracht 12
H4.5 opdracht 12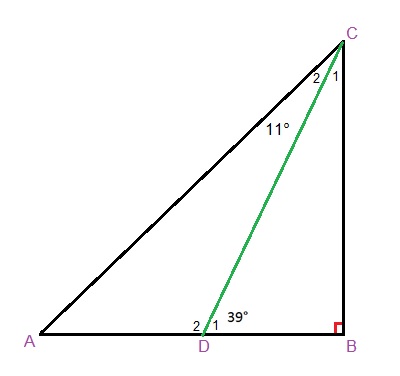 H4.5 opdracht 13
H4.5 opdracht 13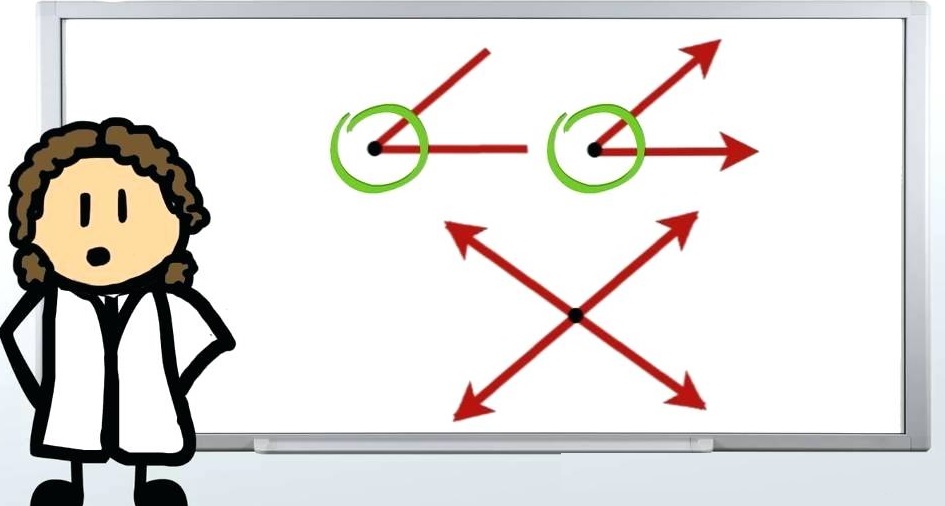 Het is al weer tijd voor de gemengde opgaven.
Het is al weer tijd voor de gemengde opgaven.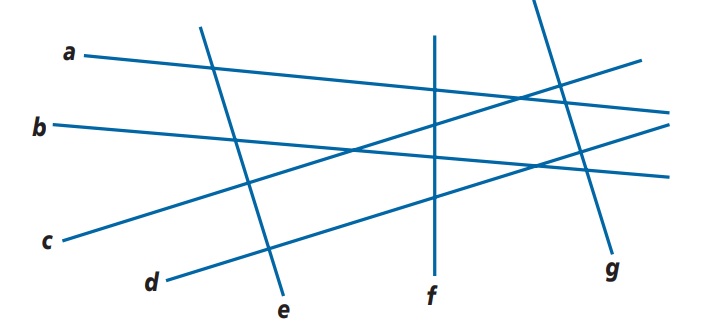

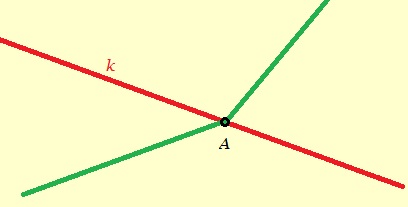
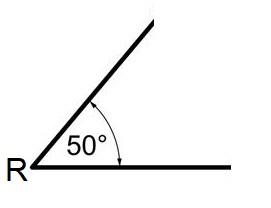 Hiernaast zie je hoek R van 50o.
Hiernaast zie je hoek R van 50o. De herhaling van het hoofdstuk is de laatste oefening voor je toets.
De herhaling van het hoofdstuk is de laatste oefening voor je toets.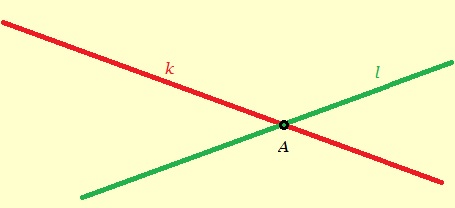

 Algebra is het deel van de wiskunde dat zich bezig houdt met formules, letters en rekenregels.
Algebra is het deel van de wiskunde dat zich bezig houdt met formules, letters en rekenregels. Aan het eind van dit hoofdstuk kan ik:
Aan het eind van dit hoofdstuk kan ik:

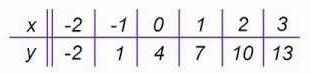


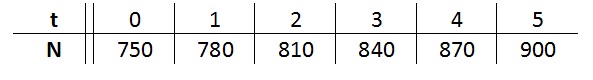
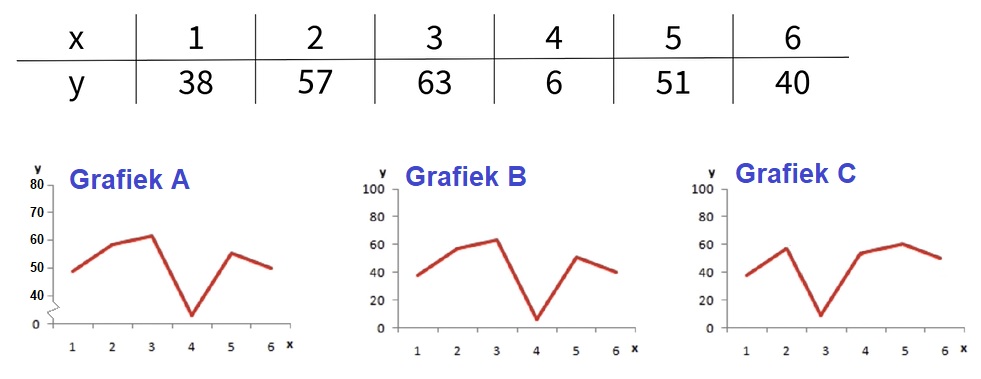
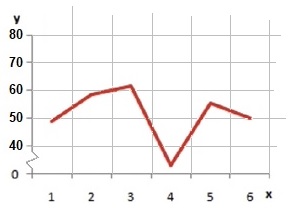
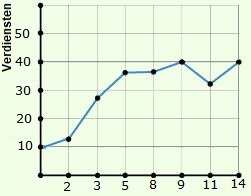


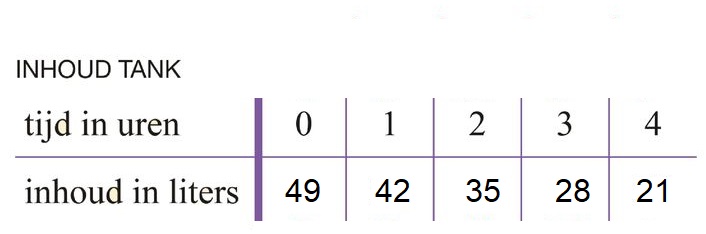



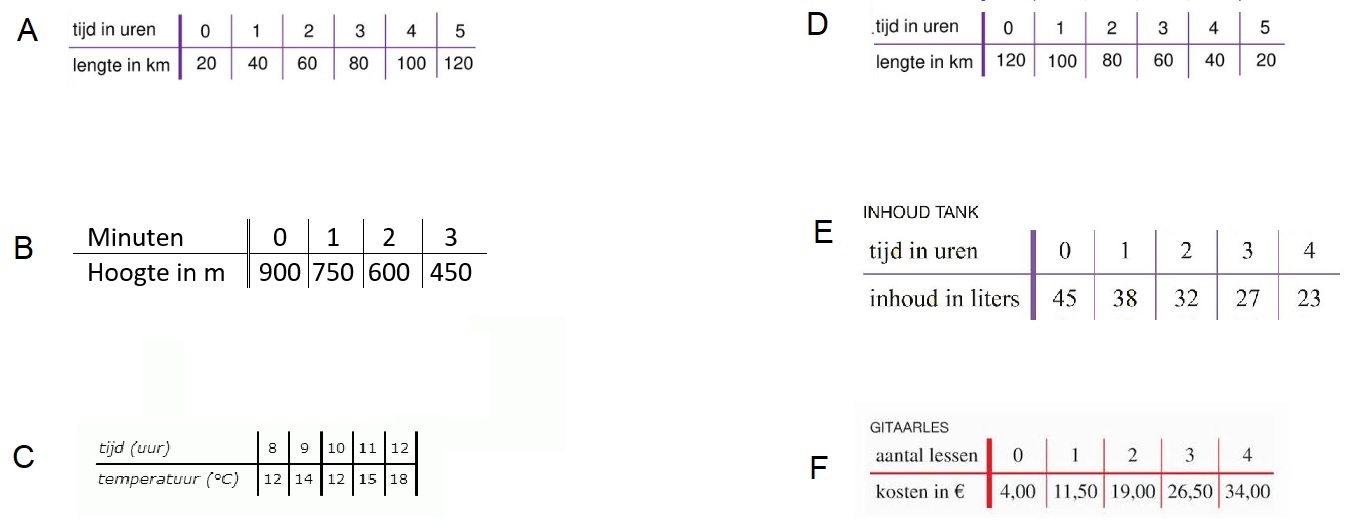
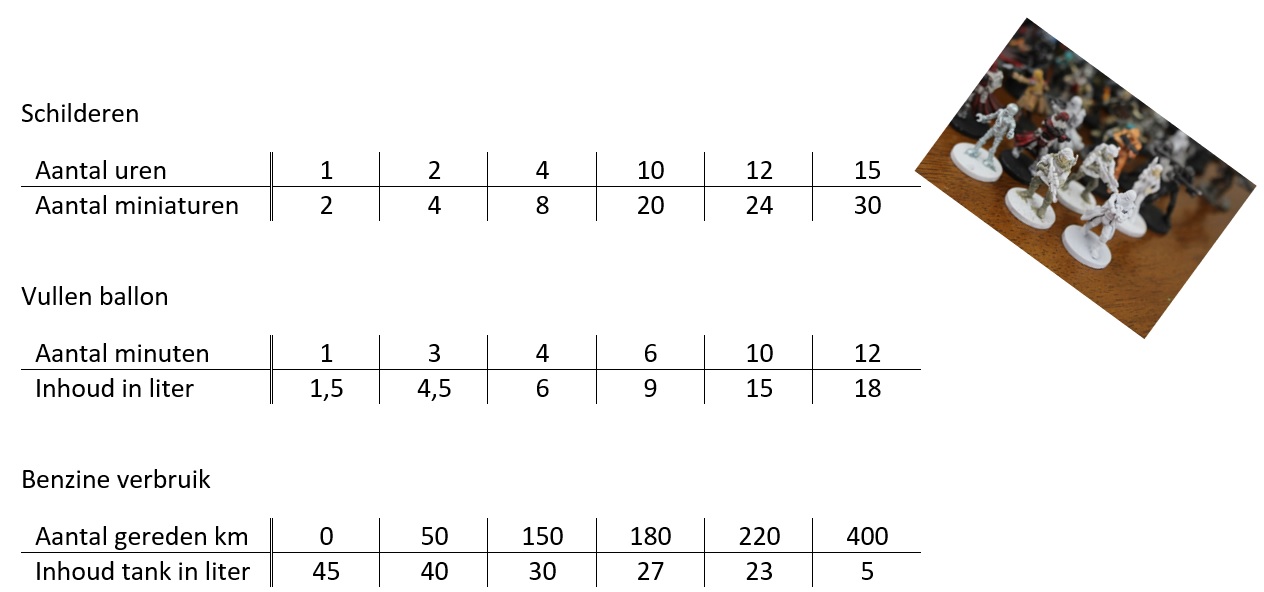


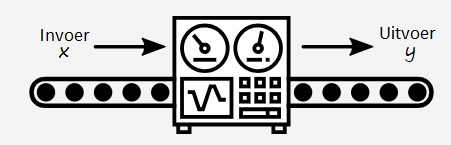
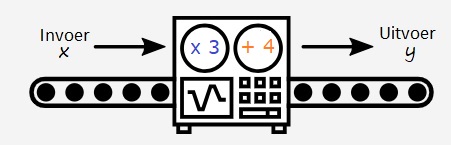
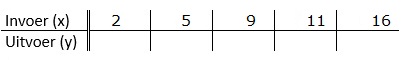
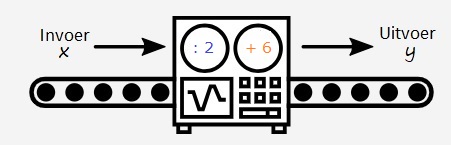

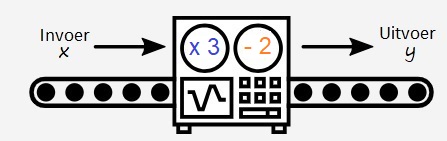

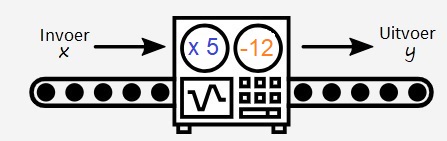

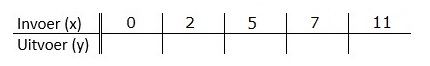
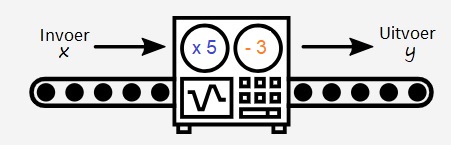


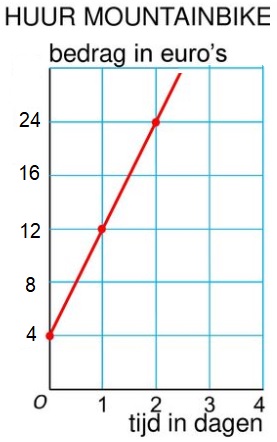
 Gegeven is de formule:
Gegeven is de formule:  Gegeven is de formule:
Gegeven is de formule:  Serena bestelt een taxi. Het instaptarief van deze taxi is €3. Dus wanneer je instapt kost het al €3,-
Serena bestelt een taxi. Het instaptarief van deze taxi is €3. Dus wanneer je instapt kost het al €3,- Kimberley wil graag een goudvis in een aquarium op haar kamer. De verkoper in de dierenwinkel heeft een mooi starters aquarium voor haar. Dit kost €20,- Nu moet Kimberley alleen nog goudvissen komen. Deze kosten €1,50 per stuk
Kimberley wil graag een goudvis in een aquarium op haar kamer. De verkoper in de dierenwinkel heeft een mooi starters aquarium voor haar. Dit kost €20,- Nu moet Kimberley alleen nog goudvissen komen. Deze kosten €1,50 per stuk Joan gaat een dagje winkelen. Ze kiest er voor haar auto te parkeren in een parkeergarage.
Joan gaat een dagje winkelen. Ze kiest er voor haar auto te parkeren in een parkeergarage. Kevin werkt in een restaurant. Hij is daar ober. Iedere maand krijgt hij een vastbedrag van de baas uit de fooien pot. Ook krijgt hij natuurlijk per uur nog salaris.
Kevin werkt in een restaurant. Hij is daar ober. Iedere maand krijgt hij een vastbedrag van de baas uit de fooien pot. Ook krijgt hij natuurlijk per uur nog salaris.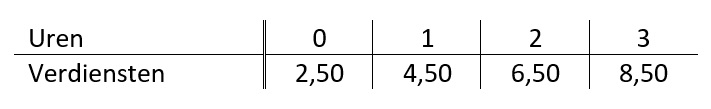
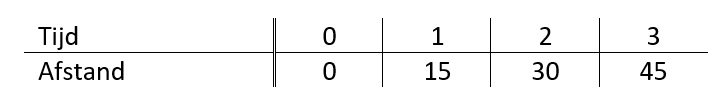
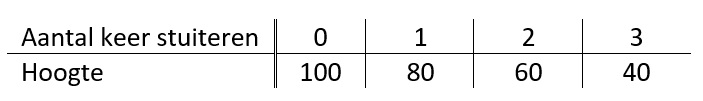
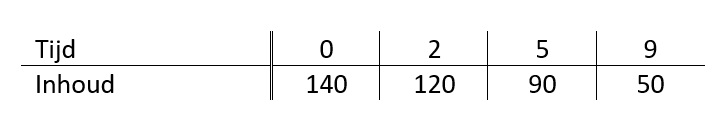


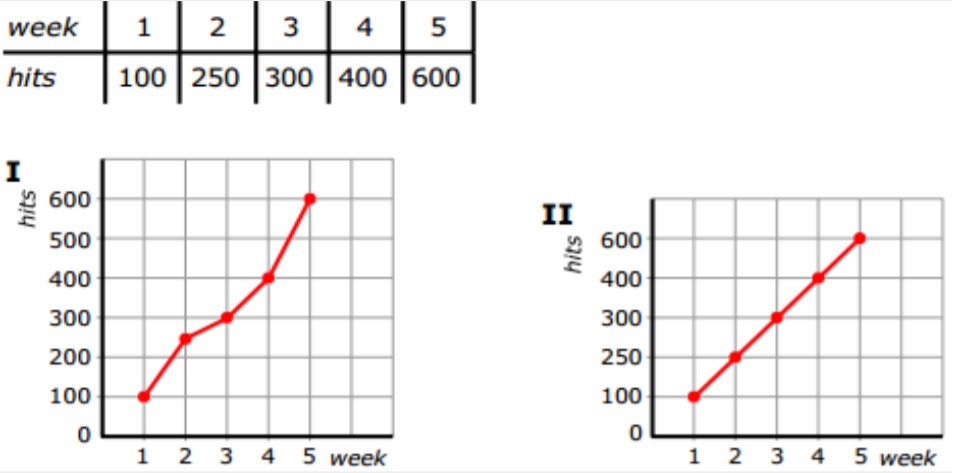
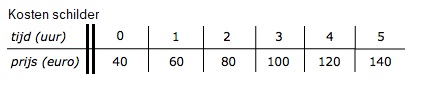
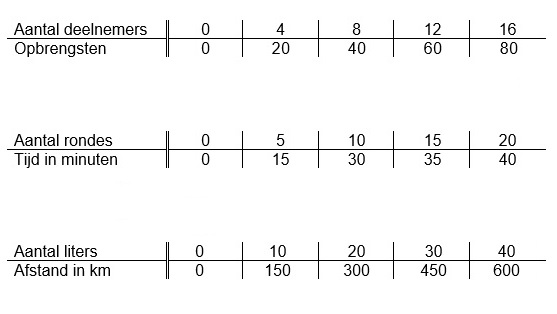
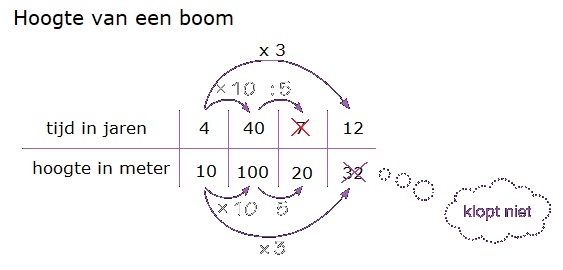
 In de tabel hieronder zie je het verband tussen de inhoud van de bezine tank en de afgelegde afstand.
In de tabel hieronder zie je het verband tussen de inhoud van de bezine tank en de afgelegde afstand.
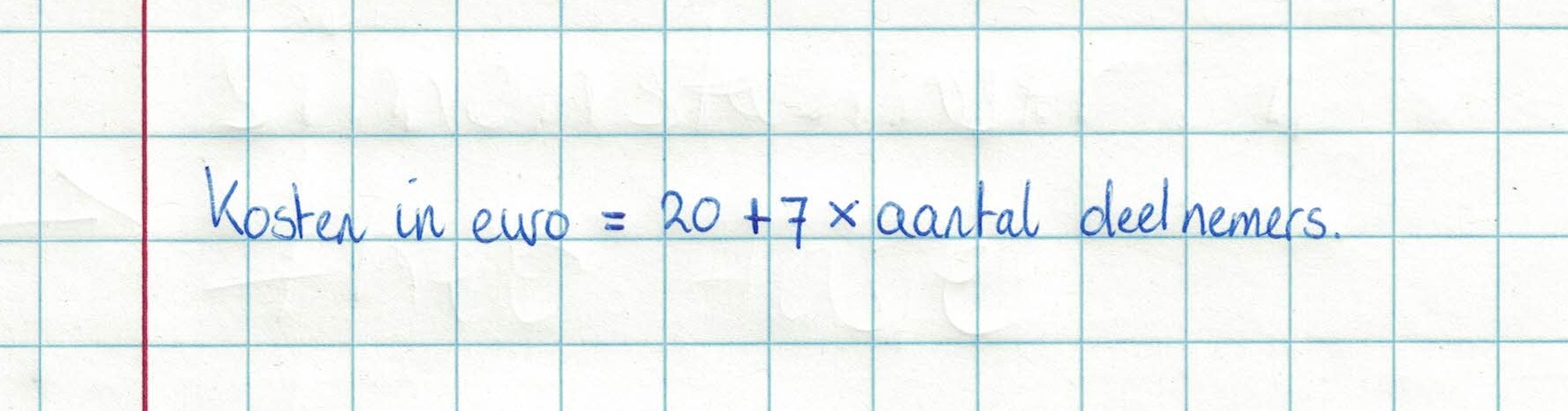


 Op een pak kaarsen van 24 cm lang staat geschreven dat deze elk uur 4 cm korter worden.
Op een pak kaarsen van 24 cm lang staat geschreven dat deze elk uur 4 cm korter worden. Joshua spaart voor een nieuwe spelcomputer. Hij heeft al 100 euro gespaard. Om sneller te kunnen sparen werkt Joshua elke week bij Emre in de kledingzaak. Hier verdient hij €25,- per dag mee.
Joshua spaart voor een nieuwe spelcomputer. Hij heeft al 100 euro gespaard. Om sneller te kunnen sparen werkt Joshua elke week bij Emre in de kledingzaak. Hier verdient hij €25,- per dag mee.

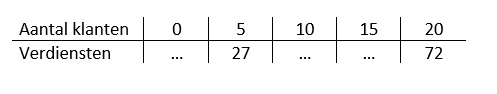


 Een dagje naar de Kermis in Tilburg met de trein
Een dagje naar de Kermis in Tilburg met de trein


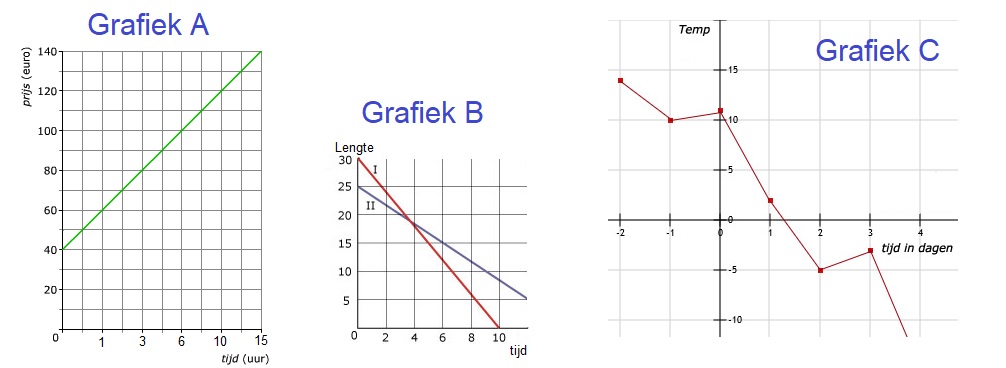
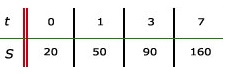
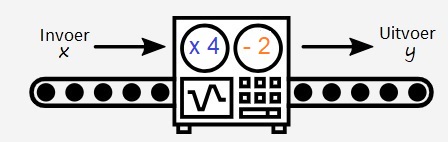
 Nu je iets meer weet over lineaire formules maken we de stap naar algebra. In de algebra worden getallen voorgesteld door letters en bestaan er allerlei regels die zeggen hoe je met die letters moet rekenen.
Nu je iets meer weet over lineaire formules maken we de stap naar algebra. In de algebra worden getallen voorgesteld door letters en bestaan er allerlei regels die zeggen hoe je met die letters moet rekenen. Aanbieding, aanbieding. Alleen vandaag 15% korting. schreeuwt een marktkoopman. Bij een ander kraampje lees je 5 halen 3 betalen. En bij weer een ander kraampje lees je inclusief btw. Al deze zaken hebben met procenten te maken.
Aanbieding, aanbieding. Alleen vandaag 15% korting. schreeuwt een marktkoopman. Bij een ander kraampje lees je 5 halen 3 betalen. En bij weer een ander kraampje lees je inclusief btw. Al deze zaken hebben met procenten te maken. Aan het eind van dit hoofdstuk weet ik:
Aan het eind van dit hoofdstuk weet ik: De eerste paragraaf gaat over verhoudingstabellen.
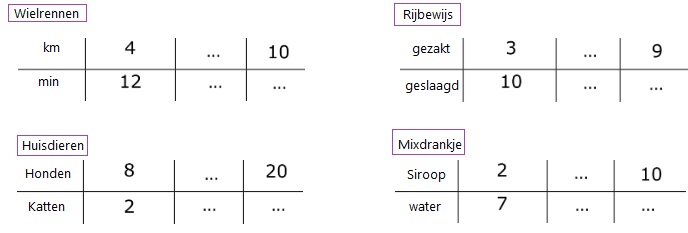
De eerste paragraaf gaat over verhoudingstabellen.
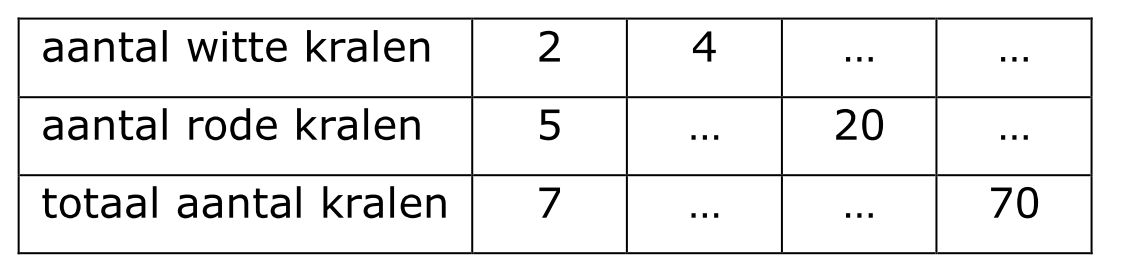
 In een doos met legostenen zitten in totaal 80 stenen.
In een doos met legostenen zitten in totaal 80 stenen.




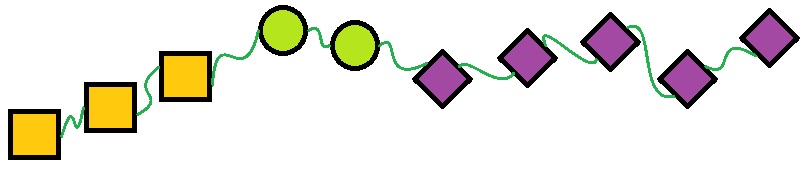 Suzhanna vindt het leuk om in haar vrije tijd kettingen te rijgen. Hiernaast zie je één van haar ontwerpen. De verhouding bij deze ketting is 3:2:5 (3 oranje, 2 groen, 5 paarse kralen.)
Suzhanna vindt het leuk om in haar vrije tijd kettingen te rijgen. Hiernaast zie je één van haar ontwerpen. De verhouding bij deze ketting is 3:2:5 (3 oranje, 2 groen, 5 paarse kralen.)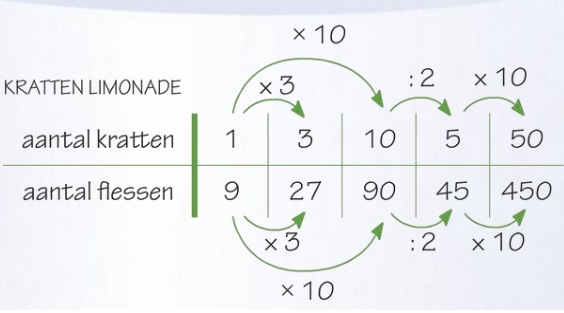

 Bekijk de ketting van Carolien en de ketting van Inge.
Bekijk de ketting van Carolien en de ketting van Inge. Je ziet twee pakken waspoeder.
Je ziet twee pakken waspoeder.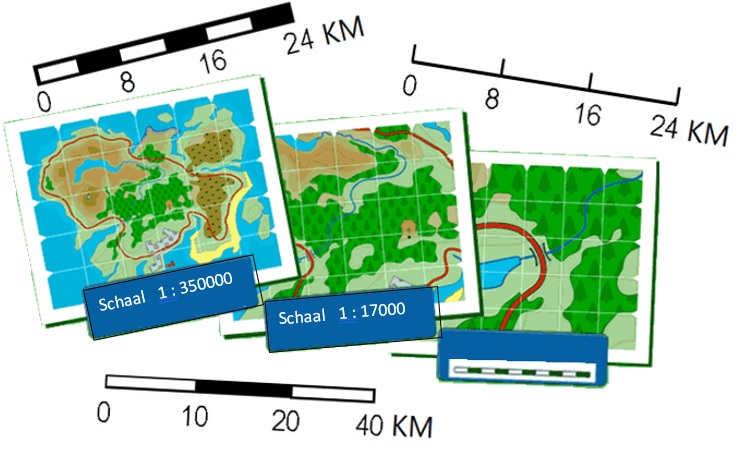 De naam van de paragraaf zegt het al.
De naam van de paragraaf zegt het al.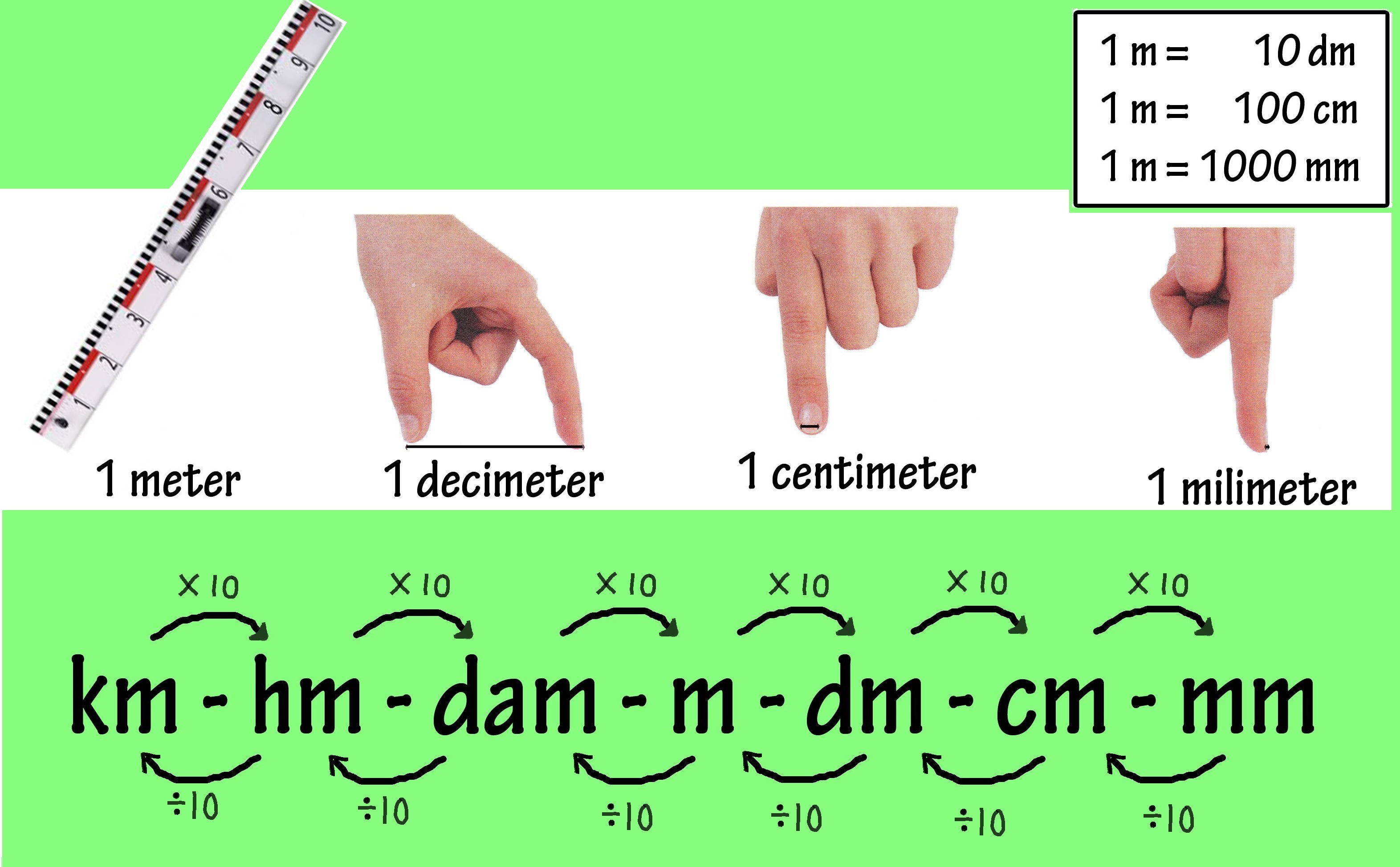
 Op het plaatje hiernaast zie je het Unity.
Op het plaatje hiernaast zie je het Unity.%20-%20kopie-750x750.jpg) Wie later in de mode en ontwerpwereld aan de slag wil krijgt ook te maken met werken op schaal.
Wie later in de mode en ontwerpwereld aan de slag wil krijgt ook te maken met werken op schaal. In de derde paragraaf gaat het over het berekenen van een gemiddelde snelheid.
In de derde paragraaf gaat het over het berekenen van een gemiddelde snelheid.
 Orlando wil graag fit blijven, daarom gaat Orlando vaak een stukje hardlopen in het park.
Orlando wil graag fit blijven, daarom gaat Orlando vaak een stukje hardlopen in het park.
 Op 16 augustus 2009 liep Usain Bolt het wereldrecord op de 100m sprint.
Op 16 augustus 2009 liep Usain Bolt het wereldrecord op de 100m sprint.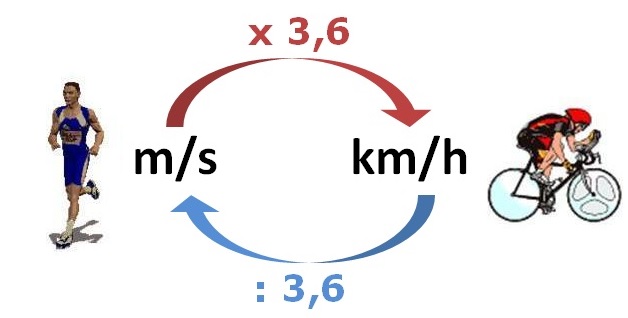


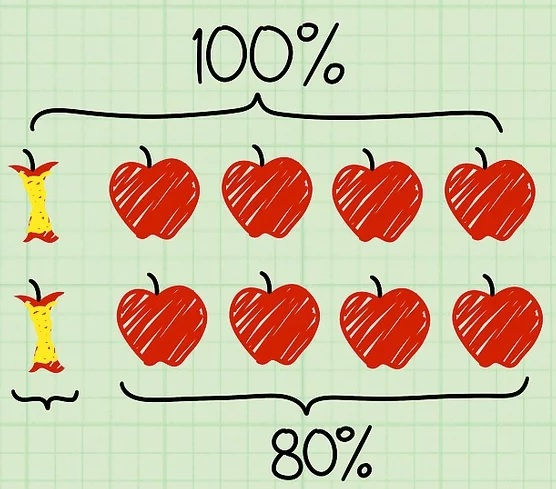 Ieder jaar komt het onderwerp 'werken met percentages '(opgaven met procenten)terug. Je herhaalt je kennis die je de afgelopen jaren hebt opgedaan en krijgt natuurlijk ook weer een klein stukje nieuwe kennis aangeboden.
Ieder jaar komt het onderwerp 'werken met percentages '(opgaven met procenten)terug. Je herhaalt je kennis die je de afgelopen jaren hebt opgedaan en krijgt natuurlijk ook weer een klein stukje nieuwe kennis aangeboden.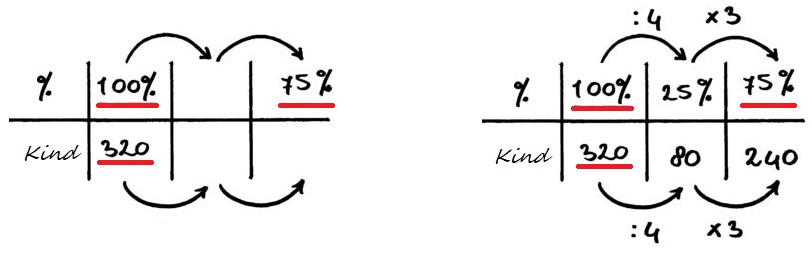

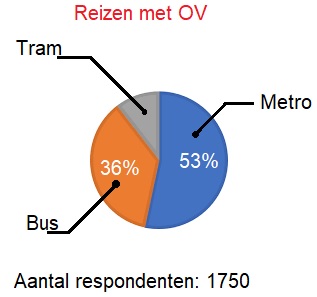 Onder studenten is een enquete gehouden.
Onder studenten is een enquete gehouden.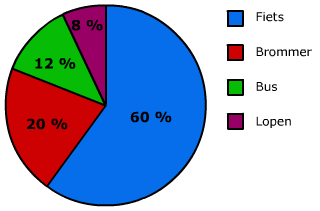 In het cirkeldiagram zie je hoe de leerlingen van het Weilandcollege naar school komen. Op het Weilandcollege zitten
In het cirkeldiagram zie je hoe de leerlingen van het Weilandcollege naar school komen. Op het Weilandcollege zitten 
 Een pizzabakker heeft bij gehouden welke extra ingrediënten mensen op hun pizza bestellen. In het diagram hiernaast zie je welke ingrediënten er zoal extra besteld worden.
Een pizzabakker heeft bij gehouden welke extra ingrediënten mensen op hun pizza bestellen. In het diagram hiernaast zie je welke ingrediënten er zoal extra besteld worden.
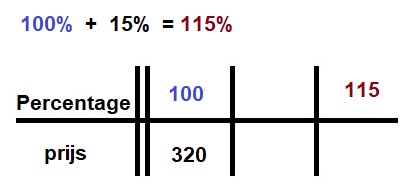
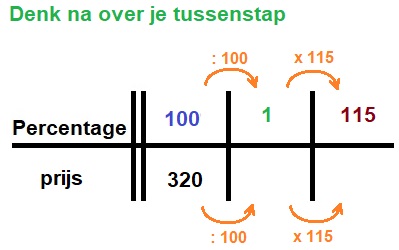 Stap 2
Stap 2 reken uit
reken uit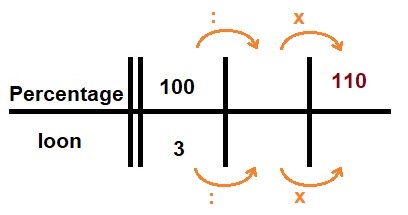
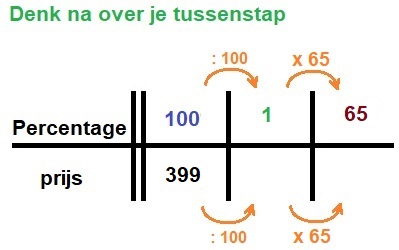
 Een jaarabonnement op het tijdschrift Quest Junior kostte vorig jaar €35,-. Dit jaar is de prijs met 15% gestegen.
Een jaarabonnement op het tijdschrift Quest Junior kostte vorig jaar €35,-. Dit jaar is de prijs met 15% gestegen.
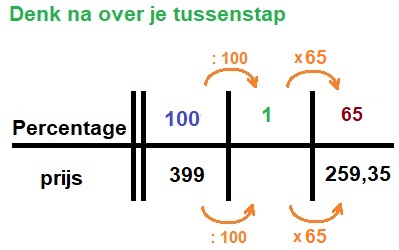

 Wanneer er een nieuwe generatie spelcomputers op de markt komt worden de oude spelcomputers vaak in prijs verlaagd.
Wanneer er een nieuwe generatie spelcomputers op de markt komt worden de oude spelcomputers vaak in prijs verlaagd. De kat van Martijn is op dieet gezet. Begin vorige maand woog de kat 7,8 kg. Inmiddels is de kat al 7% lichter in gewicht.
De kat van Martijn is op dieet gezet. Begin vorige maand woog de kat 7,8 kg. Inmiddels is de kat al 7% lichter in gewicht. Een abonnement op Netflix is door de jaren heen steeds iets duurder geworden.
Een abonnement op Netflix is door de jaren heen steeds iets duurder geworden. Bekijk de producten hiernaast goed.
Bekijk de producten hiernaast goed. Je kunt op dit moment dus al twee type opgave oplossen met behulp van een tabel. Nu kijken we naar een ander type opgave, namelijk wanneer je moet berekenen welk deel (het percentage) er bekend is.
Je kunt op dit moment dus al twee type opgave oplossen met behulp van een tabel. Nu kijken we naar een ander type opgave, namelijk wanneer je moet berekenen welk deel (het percentage) er bekend is.
 In de herfst en wintermaanden regent het vaker dan in de zomermaanden.
In de herfst en wintermaanden regent het vaker dan in de zomermaanden.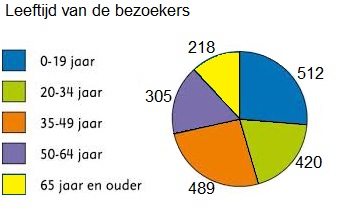
 Hiernaast zie je de top 3 vervoersmiddelen om mee op vakantie te gaan. Er ontbreken er natuurlijk ook nog een aantal, denk bijvoorbeeld aan de boot, fiets of bus.
Hiernaast zie je de top 3 vervoersmiddelen om mee op vakantie te gaan. Er ontbreken er natuurlijk ook nog een aantal, denk bijvoorbeeld aan de boot, fiets of bus. Neem voordat je begint aan de gemengde opgaven even de tijd om na te denken over de paragrafen die je gemaakt hebt. Welke paragraaf vond je lastig? In welke paragraaf heb je de meeste antwoorden niet helemaal goed berekend? Lees de uitleg van die twee paragrafen nog eens door voordat je begint
Neem voordat je begint aan de gemengde opgaven even de tijd om na te denken over de paragrafen die je gemaakt hebt. Welke paragraaf vond je lastig? In welke paragraaf heb je de meeste antwoorden niet helemaal goed berekend? Lees de uitleg van die twee paragrafen nog eens door voordat je begint
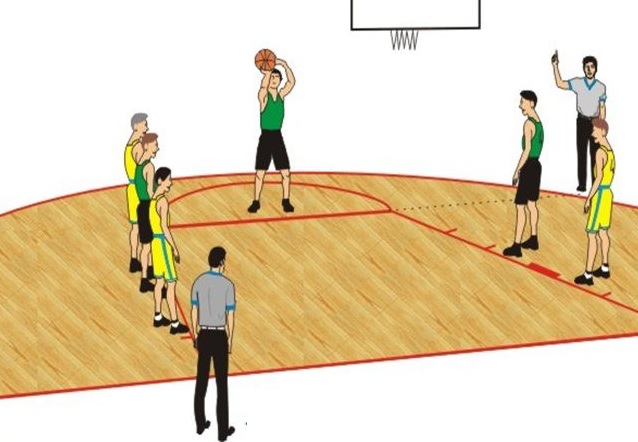 Tijdens het schieten van vrije worpen gooit Mohammed er 7 van de 12 in.
Tijdens het schieten van vrije worpen gooit Mohammed er 7 van de 12 in.
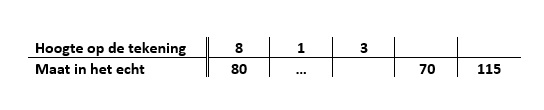
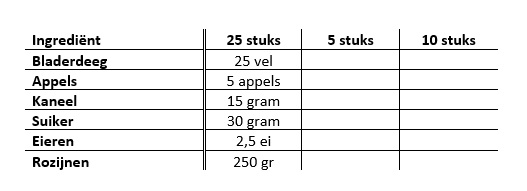
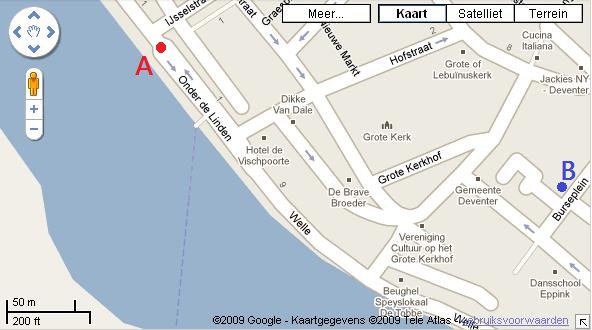









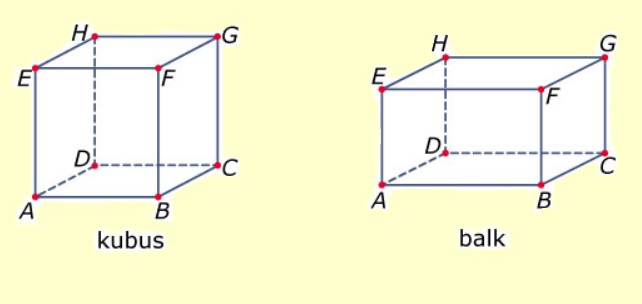
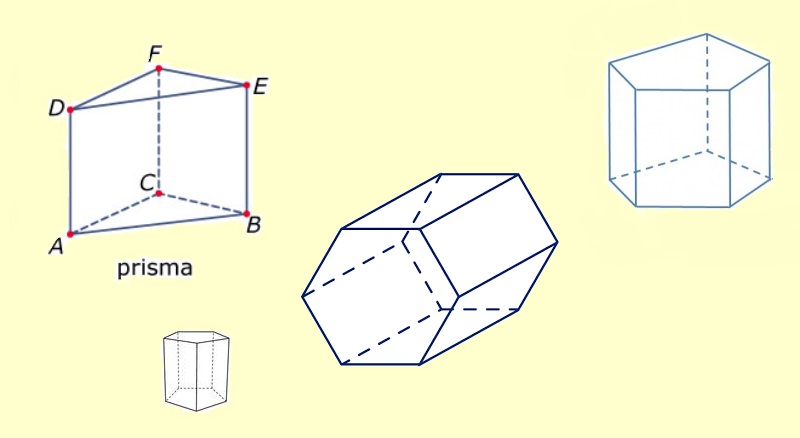
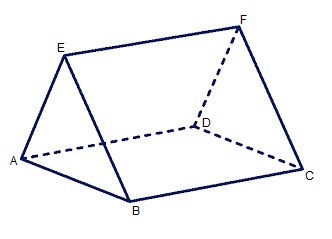
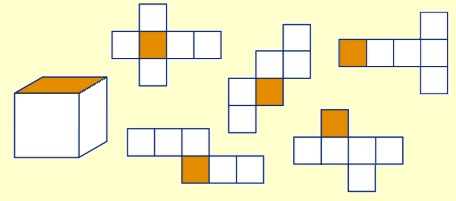
 Aan het begin van dit jaar heb je al kennis gemaakt met de vlakkefiguren. Behalve vlakke figuren bestaat de wereld om ons heen ook uit ruimte figuren. De naam zegt het al, ze nemen ruimte in. Je kunt er iets in stoppen. Denk maar aan een schoenendoos of een klaslokaal.
Aan het begin van dit jaar heb je al kennis gemaakt met de vlakkefiguren. Behalve vlakke figuren bestaat de wereld om ons heen ook uit ruimte figuren. De naam zegt het al, ze nemen ruimte in. Je kunt er iets in stoppen. Denk maar aan een schoenendoos of een klaslokaal. Aan het eind van dit hoofdstuk kan ik:
Aan het eind van dit hoofdstuk kan ik: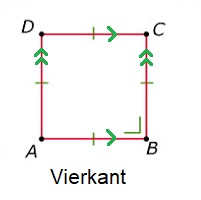
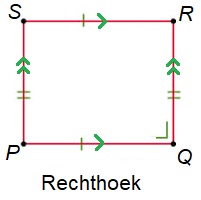


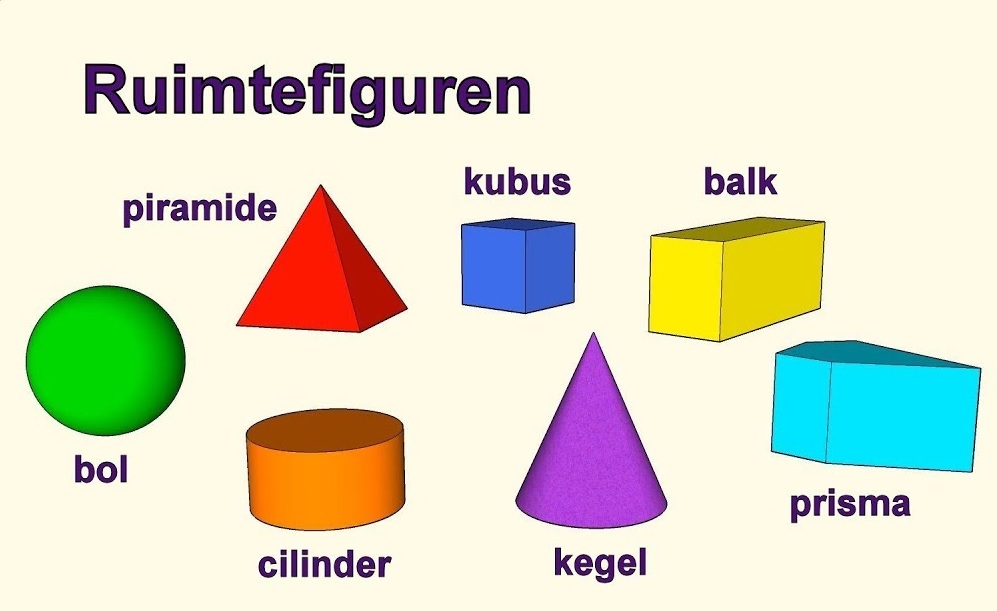
 Ruimtefiguren kunnen bestaan uit gebogen vlakken en uit platte vlakken.
Ruimtefiguren kunnen bestaan uit gebogen vlakken en uit platte vlakken.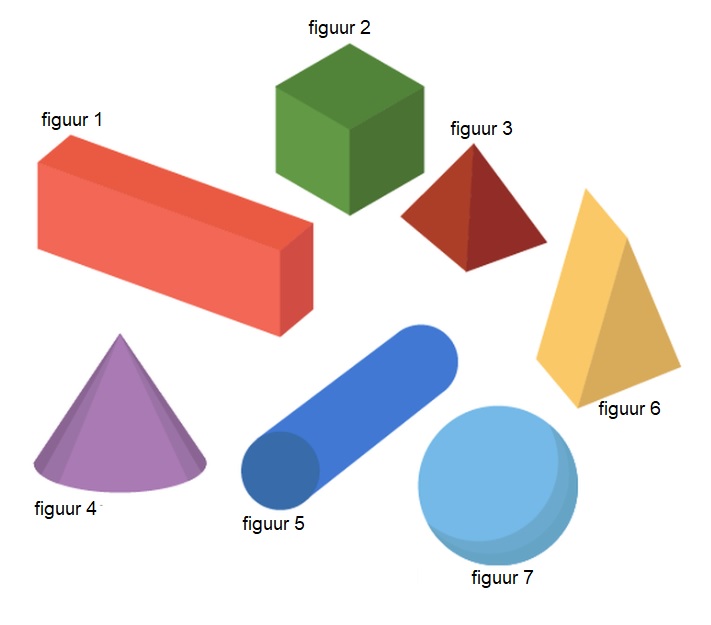

 De lijnen, stokjes waar een figuur uit bestaat noemen we de ribben.
De lijnen, stokjes waar een figuur uit bestaat noemen we de ribben.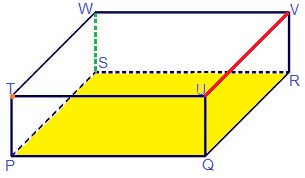
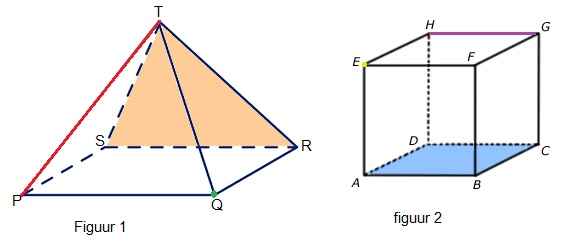

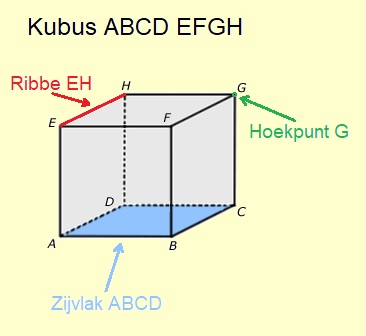
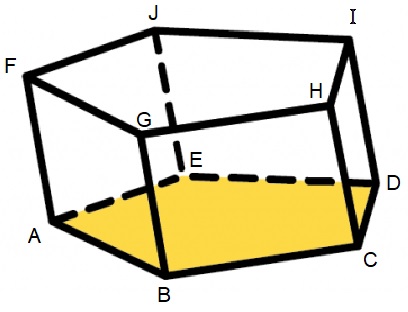
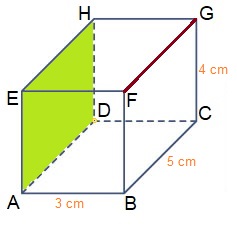
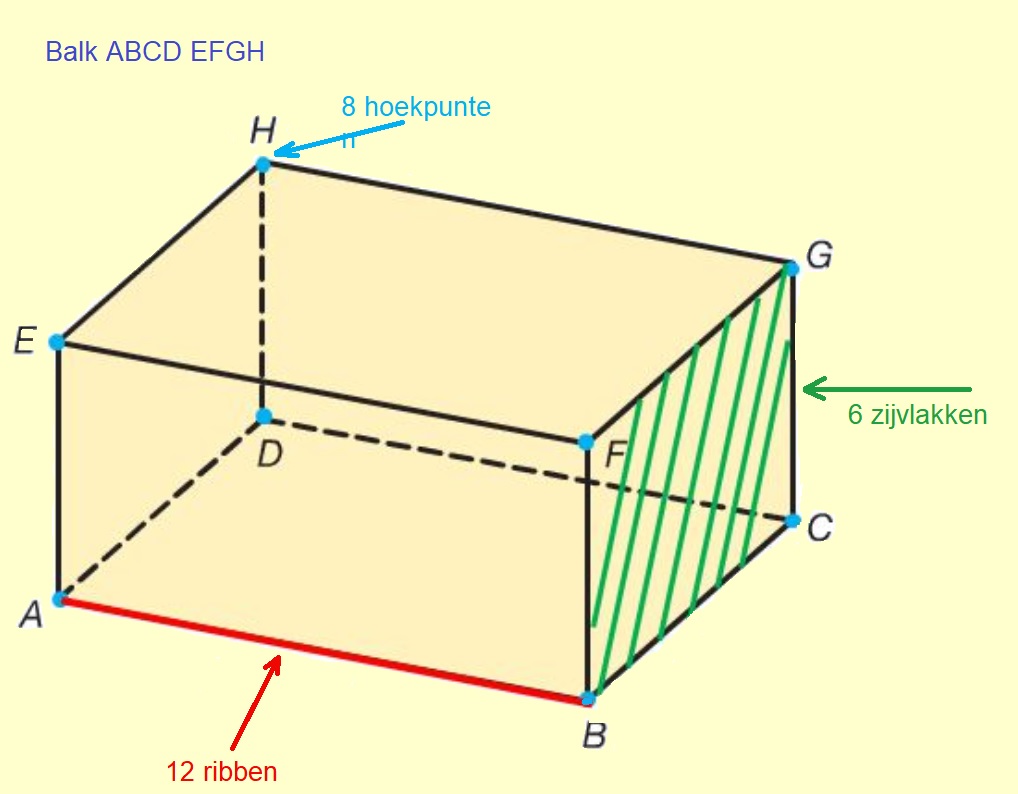 In de opsomming van de eigenschappen worden de begrippen hoekpunt, ribben en zijvlakken genoemd. Maar wat zijn dat nou eigenlijk. Kijk maar eens naar de afbeelding van de balk hiernaast.
In de opsomming van de eigenschappen worden de begrippen hoekpunt, ribben en zijvlakken genoemd. Maar wat zijn dat nou eigenlijk. Kijk maar eens naar de afbeelding van de balk hiernaast.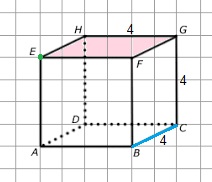
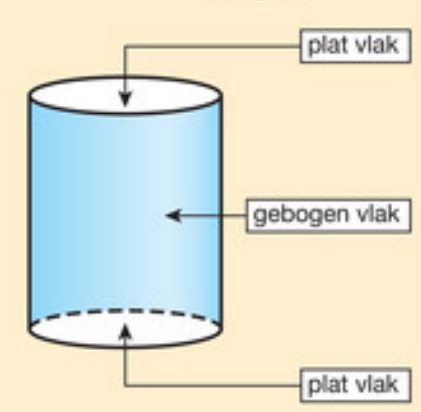
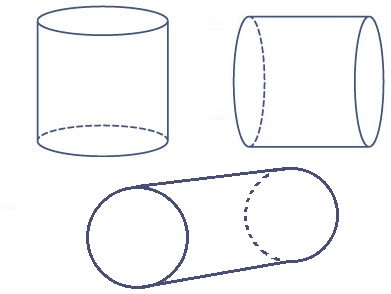
 Hiernaast zie je een afbeelding van een cilinder.
Hiernaast zie je een afbeelding van een cilinder.
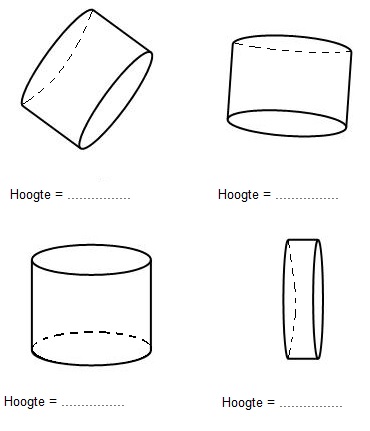






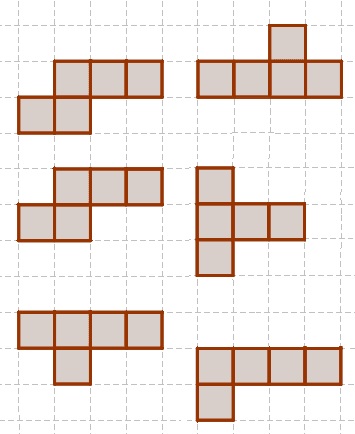
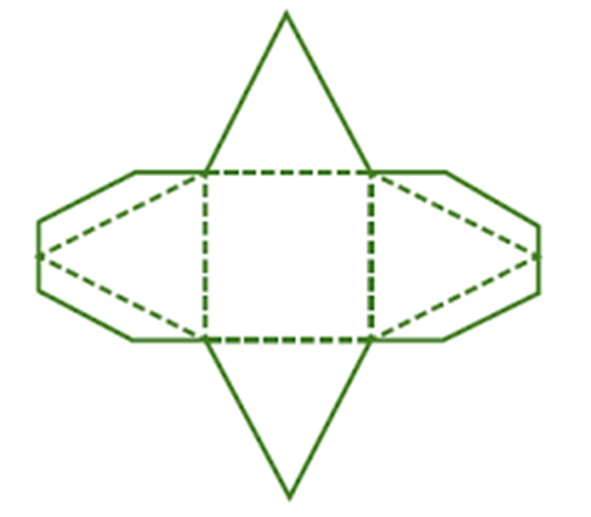
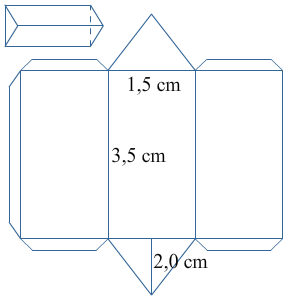
 Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.
Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.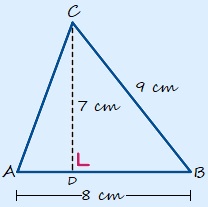
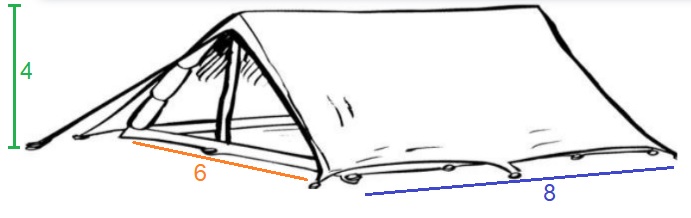
 Bekijk het huisje op de afbeelding hiernaast.
Bekijk het huisje op de afbeelding hiernaast.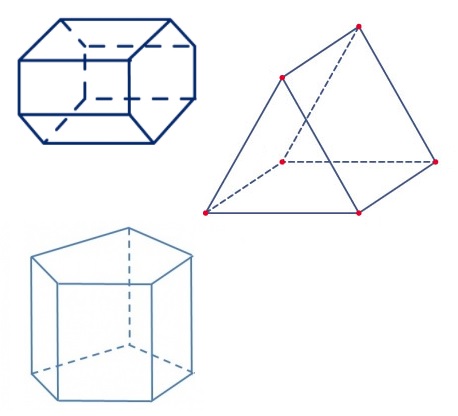 H7.5 opdracht 6
H7.5 opdracht 6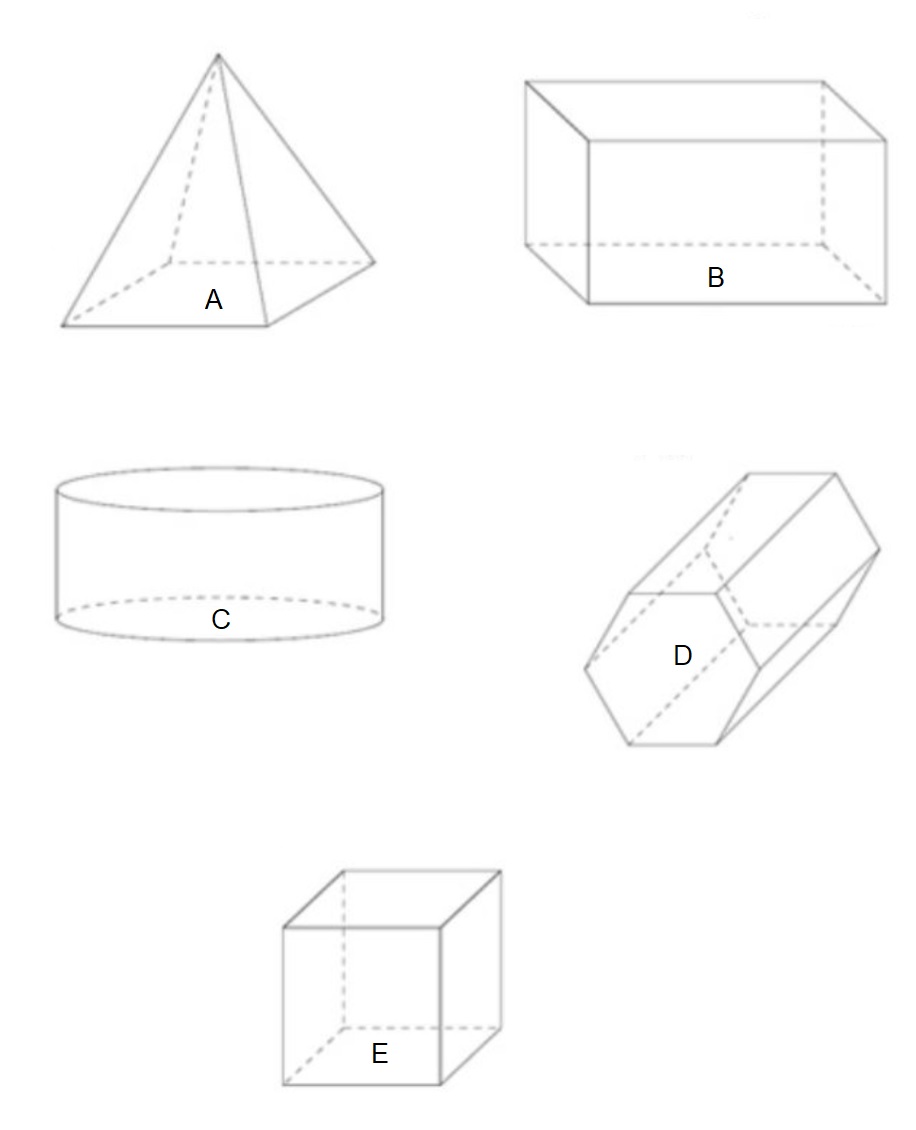
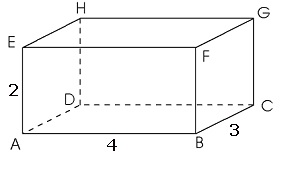
 Bekijk de balk hiernaast.
Bekijk de balk hiernaast.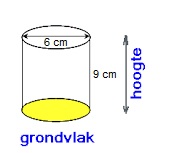 H7.5 opdracht 12
H7.5 opdracht 12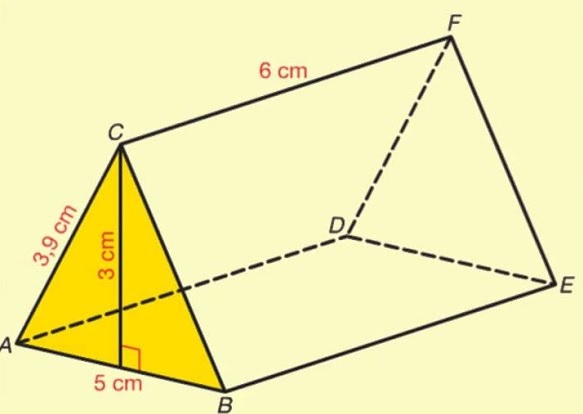 H7.5 opdracht 13
H7.5 opdracht 13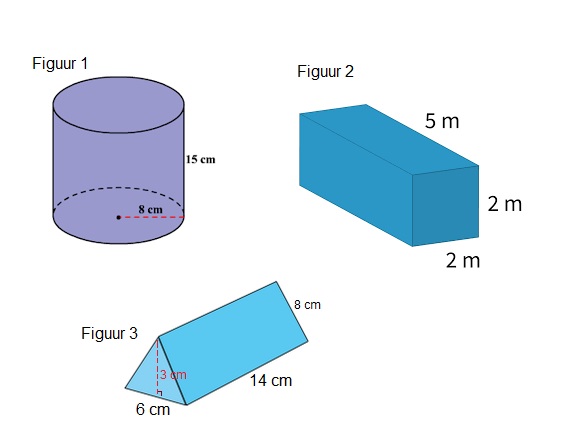 H7.5 opdracht 14
H7.5 opdracht 14 H7.5 opdracht 15
H7.5 opdracht 15 H7.5 opdracht 16
H7.5 opdracht 16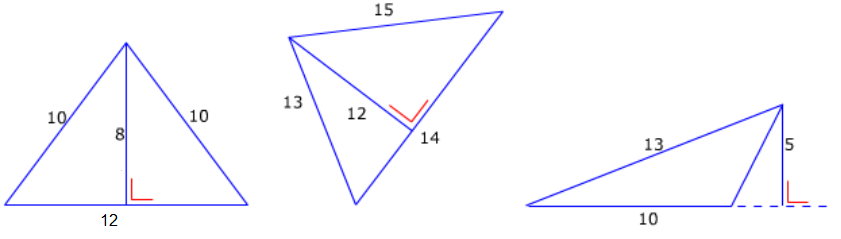
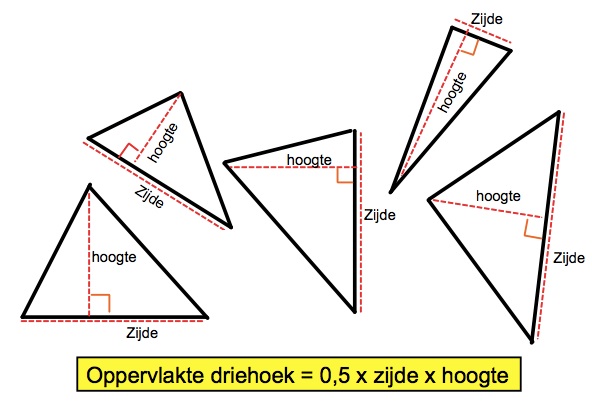
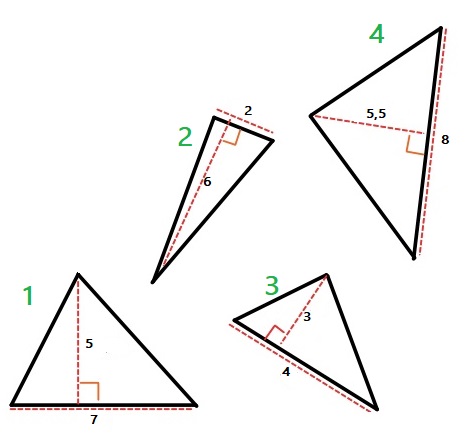
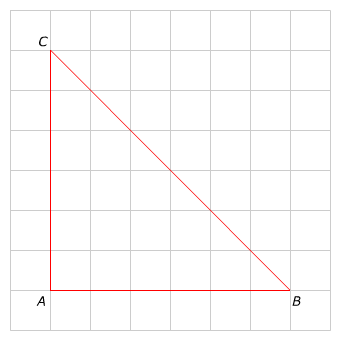
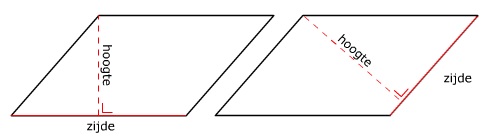
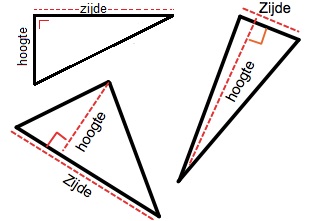
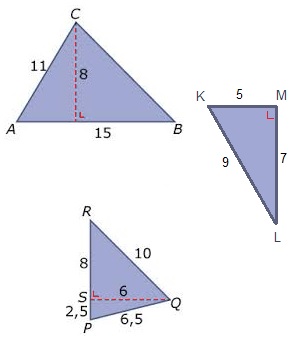
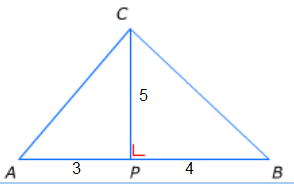
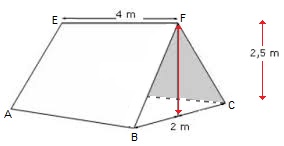
 Bereken van de vier driehoeken hiernaast de oppervlakte.
Bereken van de vier driehoeken hiernaast de oppervlakte. Bereken van deze figuren de oppervlakte.
Bereken van deze figuren de oppervlakte.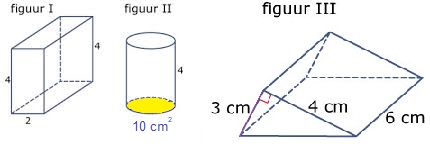
 Heb jij vandaag al eens een complimentje aan iemand gegeven, of heeft iemand misschien iets negatiefs opgemerkt? Wat heeft dat nou met wiskunde te maken? Wanneer je positief en negatief op getallen betrekt dan heeft het heel veel met wiskunde te maken.
Heb jij vandaag al eens een complimentje aan iemand gegeven, of heeft iemand misschien iets negatiefs opgemerkt? Wat heeft dat nou met wiskunde te maken? Wanneer je positief en negatief op getallen betrekt dan heeft het heel veel met wiskunde te maken. Aan het eind van dit thema:
Aan het eind van dit thema: Wat hebben negatieve getallen nou met onze omgeving te maken? Sterker nog het heeft met alle inwoners van Nederland te maken. Want zonder onze dijken zou de helft van Nederland gewoon een stuk zee zijn. Goed voor de vissen maar wat minder goed voor onze economie. Want in het Westelijk deel wordt in ons land heel erg veel geld verdient.
Wat hebben negatieve getallen nou met onze omgeving te maken? Sterker nog het heeft met alle inwoners van Nederland te maken. Want zonder onze dijken zou de helft van Nederland gewoon een stuk zee zijn. Goed voor de vissen maar wat minder goed voor onze economie. Want in het Westelijk deel wordt in ons land heel erg veel geld verdient. In het eerste deel van werken met negatieve getallen leer je wat een negatief getal is,
In het eerste deel van werken met negatieve getallen leer je wat een negatief getal is, Een voorbeeld:
Een voorbeeld: Hiernaast zie je een flatgebouw met 11 verdiepingen.
Hiernaast zie je een flatgebouw met 11 verdiepingen. Temperaturen meet je in graden Celcius. Je schrijft ℃. Hiernaast zie je hoe je temperaturen onder 0 ℃ opschrijft.
Temperaturen meet je in graden Celcius. Je schrijft ℃. Hiernaast zie je hoe je temperaturen onder 0 ℃ opschrijft.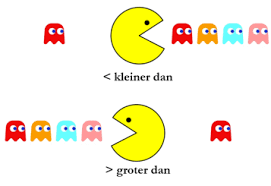
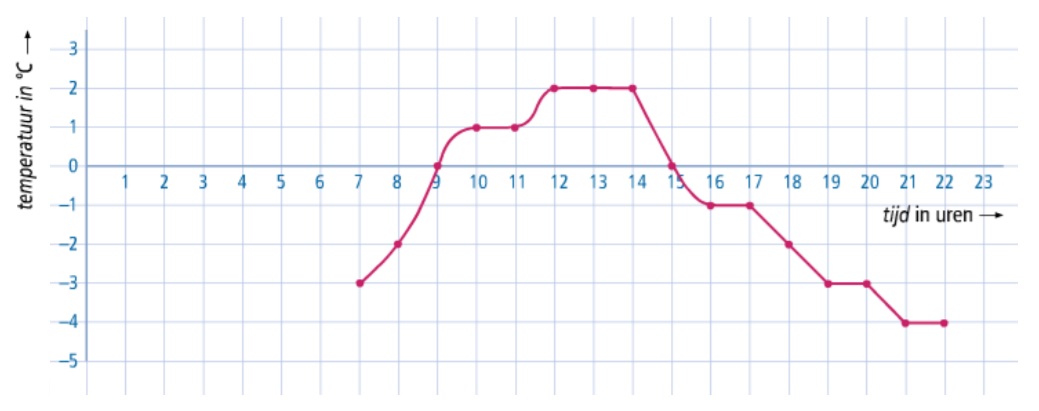


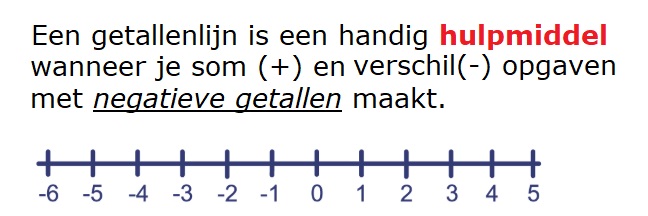
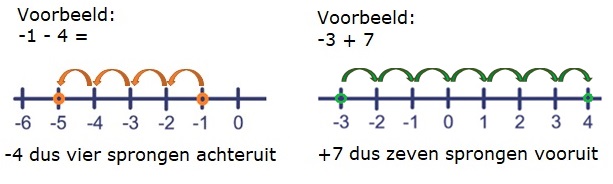
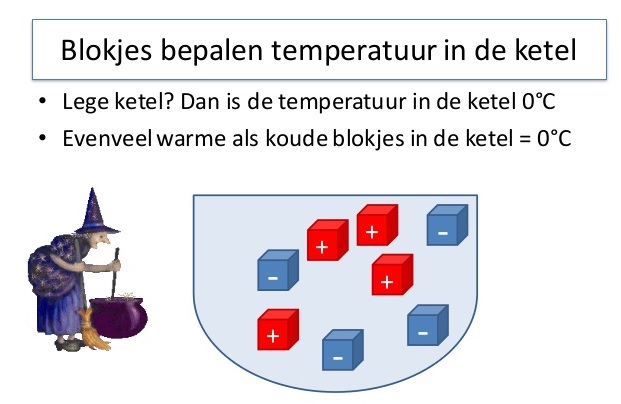
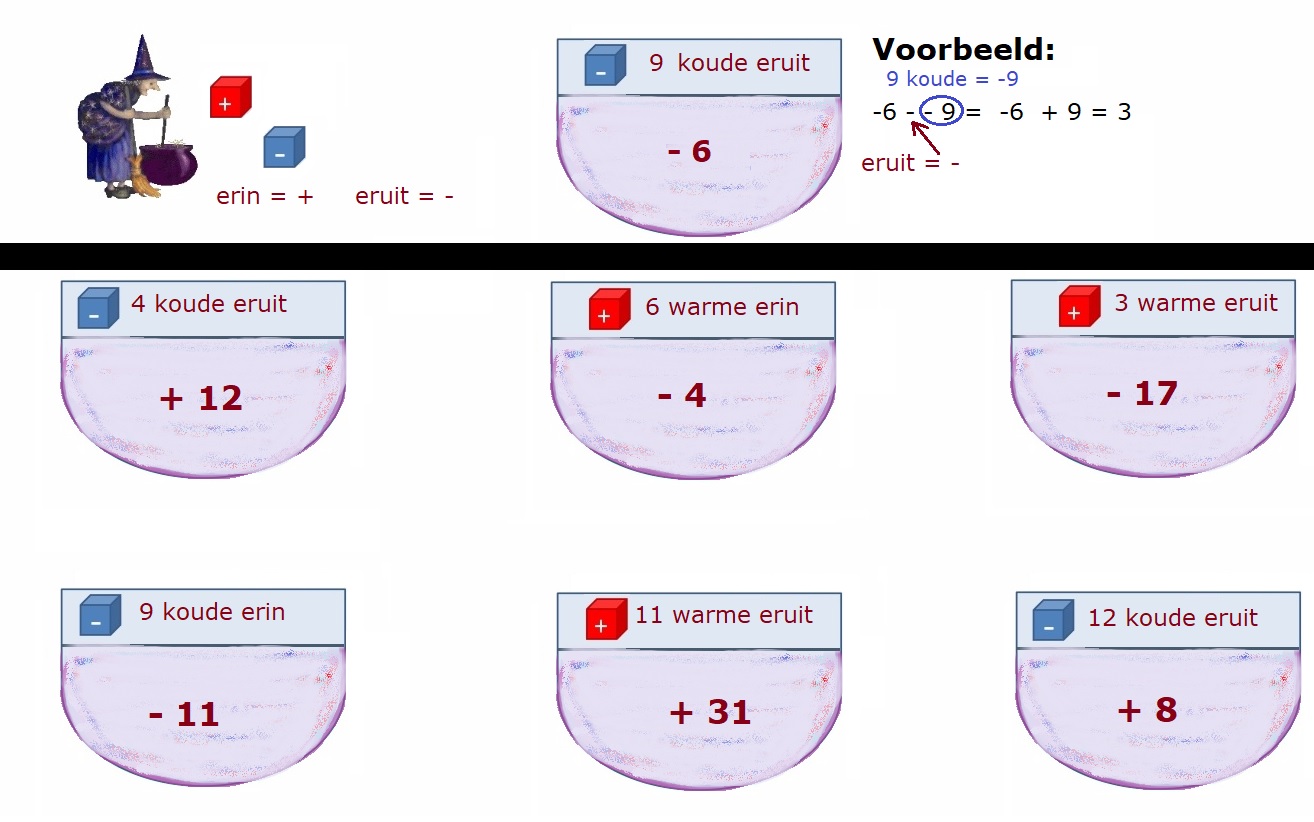
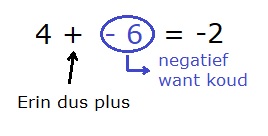

 Denk er aan:
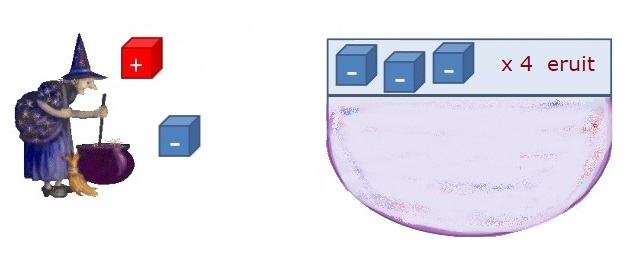
Denk er aan: In het tweede deel van bewerkingen met negatieve getallen leer je negatieve getallen vermenigvuldigen en delen. Je leert een stukje theorie (uitleg) uit het hoofd en oefent met het toepassen hiervan.
In het tweede deel van bewerkingen met negatieve getallen leer je negatieve getallen vermenigvuldigen en delen. Je leert een stukje theorie (uitleg) uit het hoofd en oefent met het toepassen hiervan.


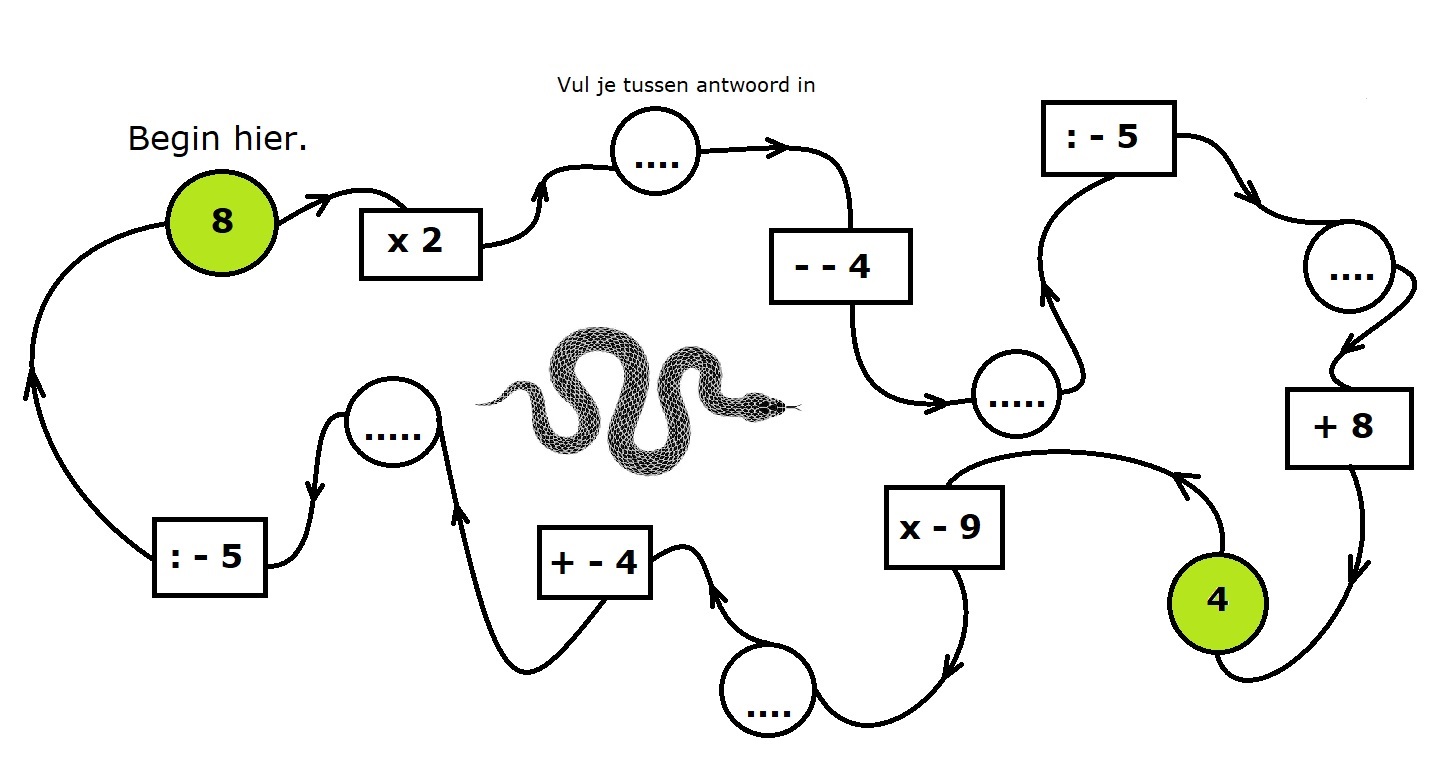
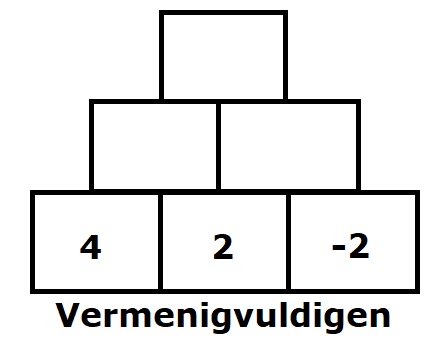
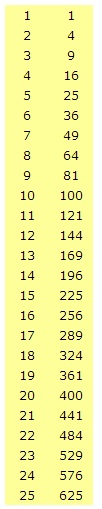

 H8.4 opdracht 4
H8.4 opdracht 4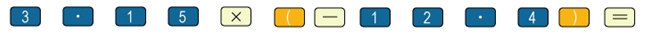
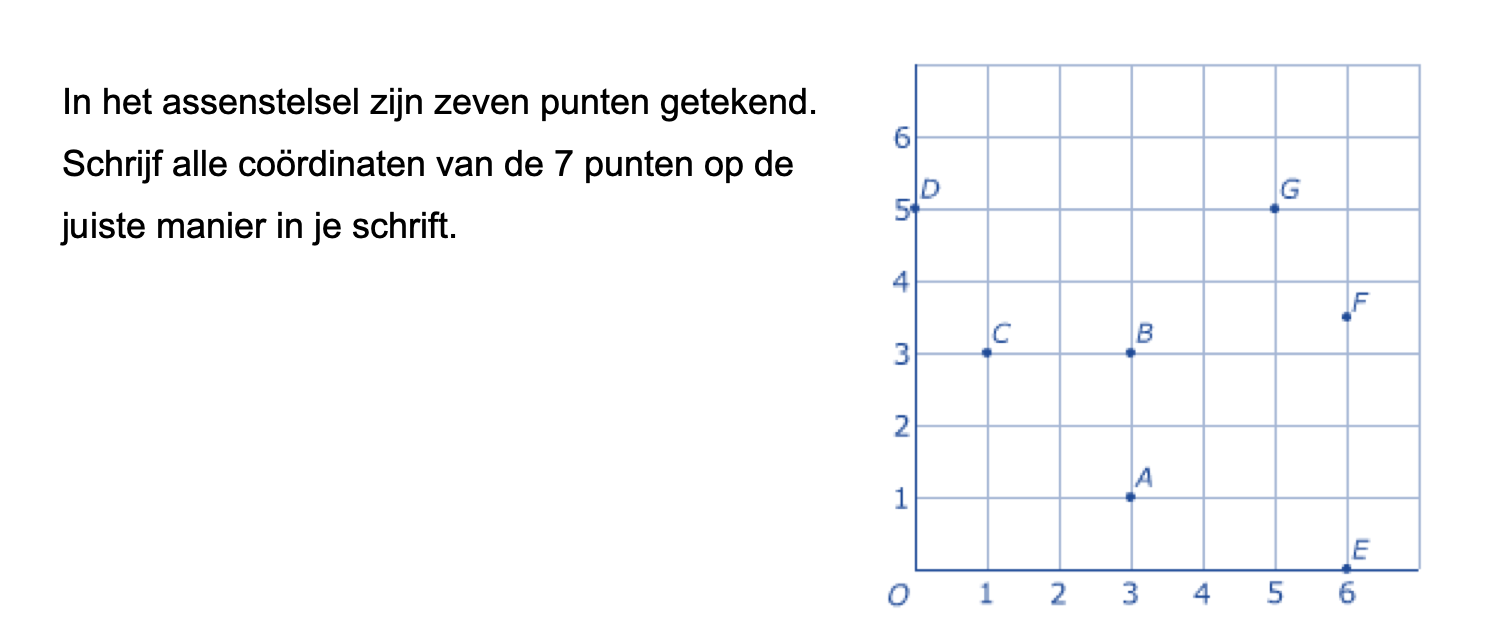
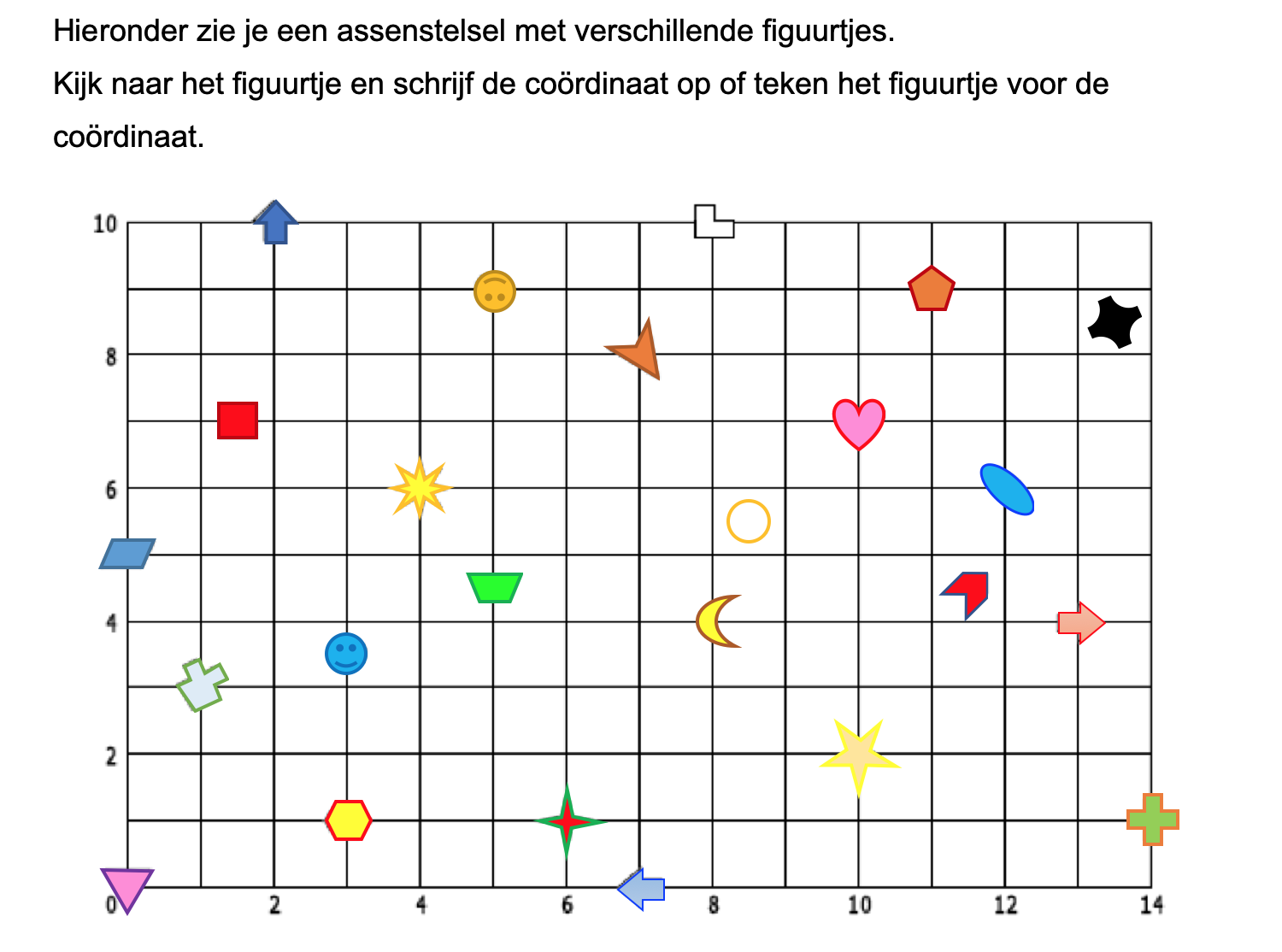
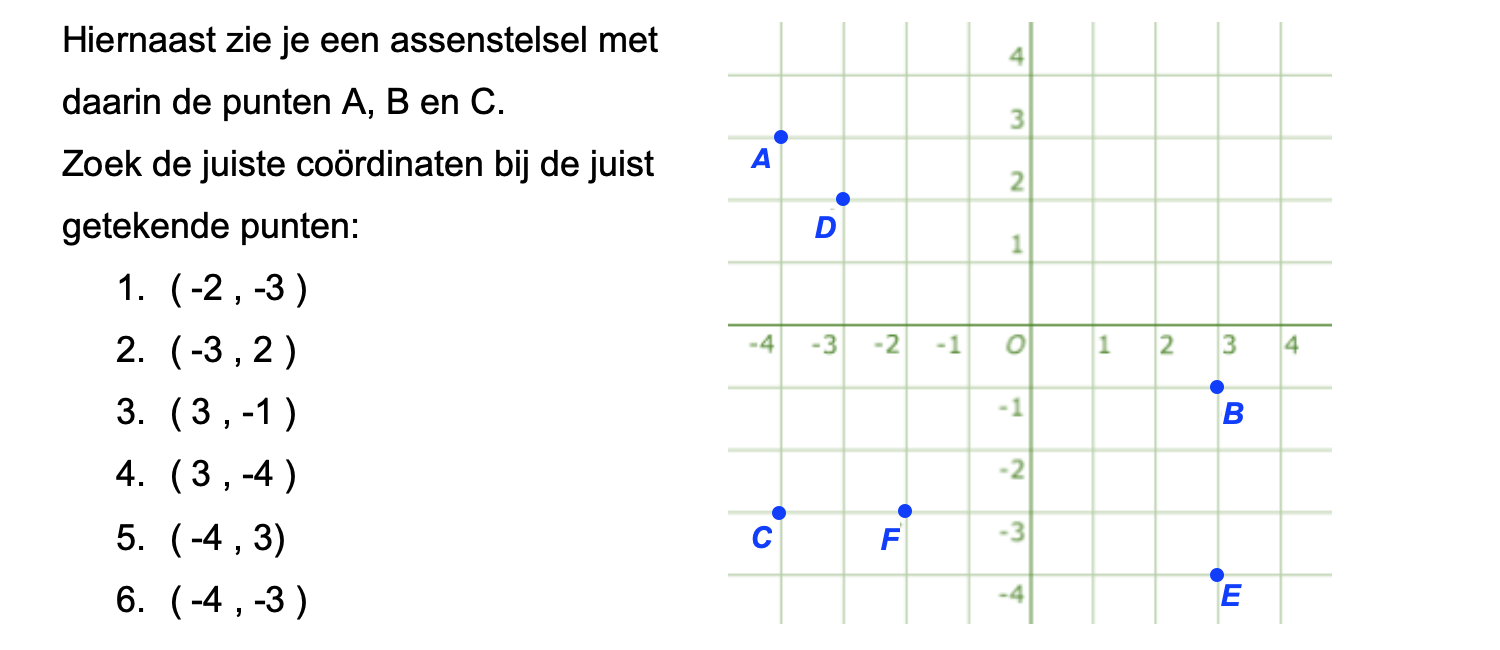
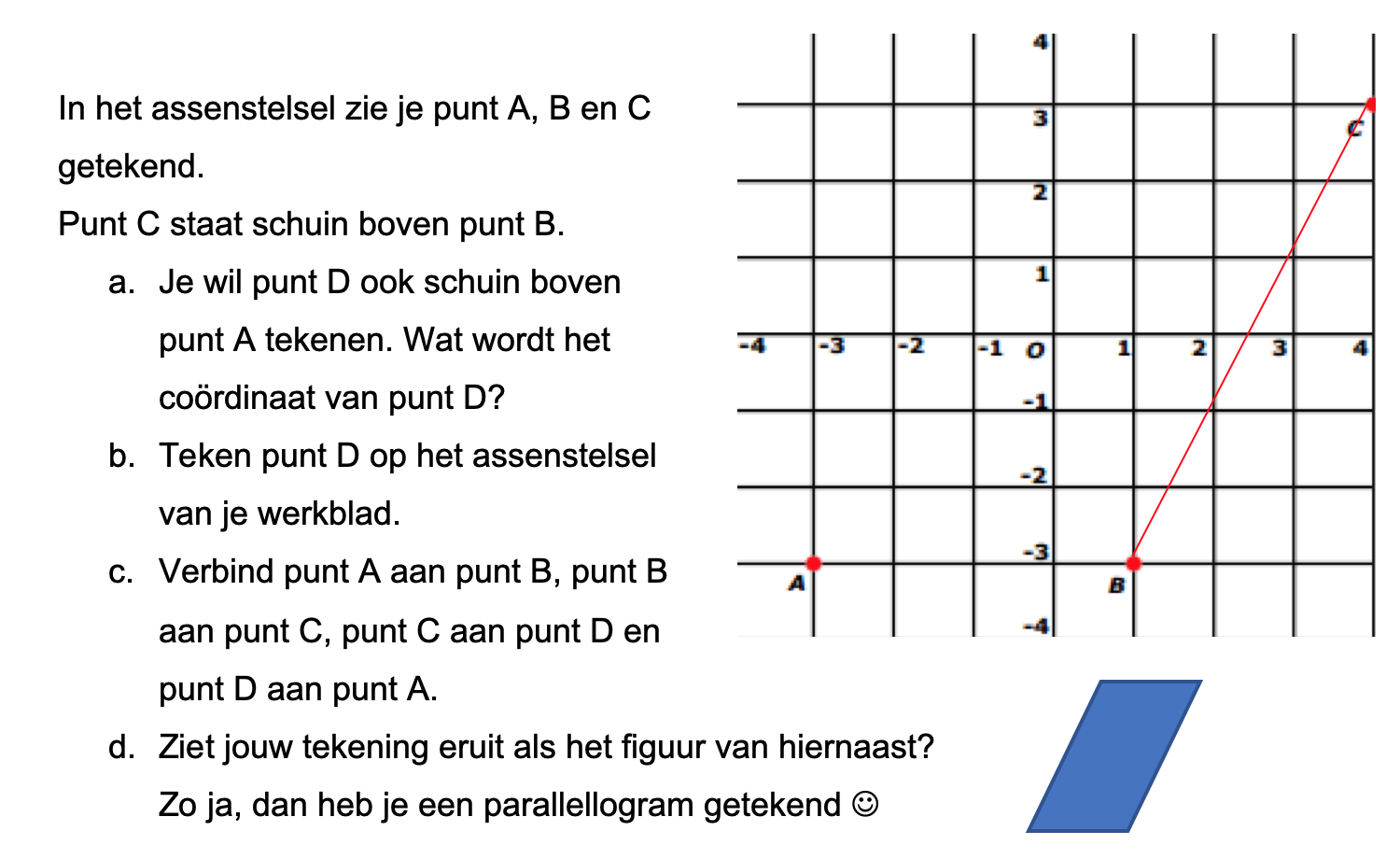
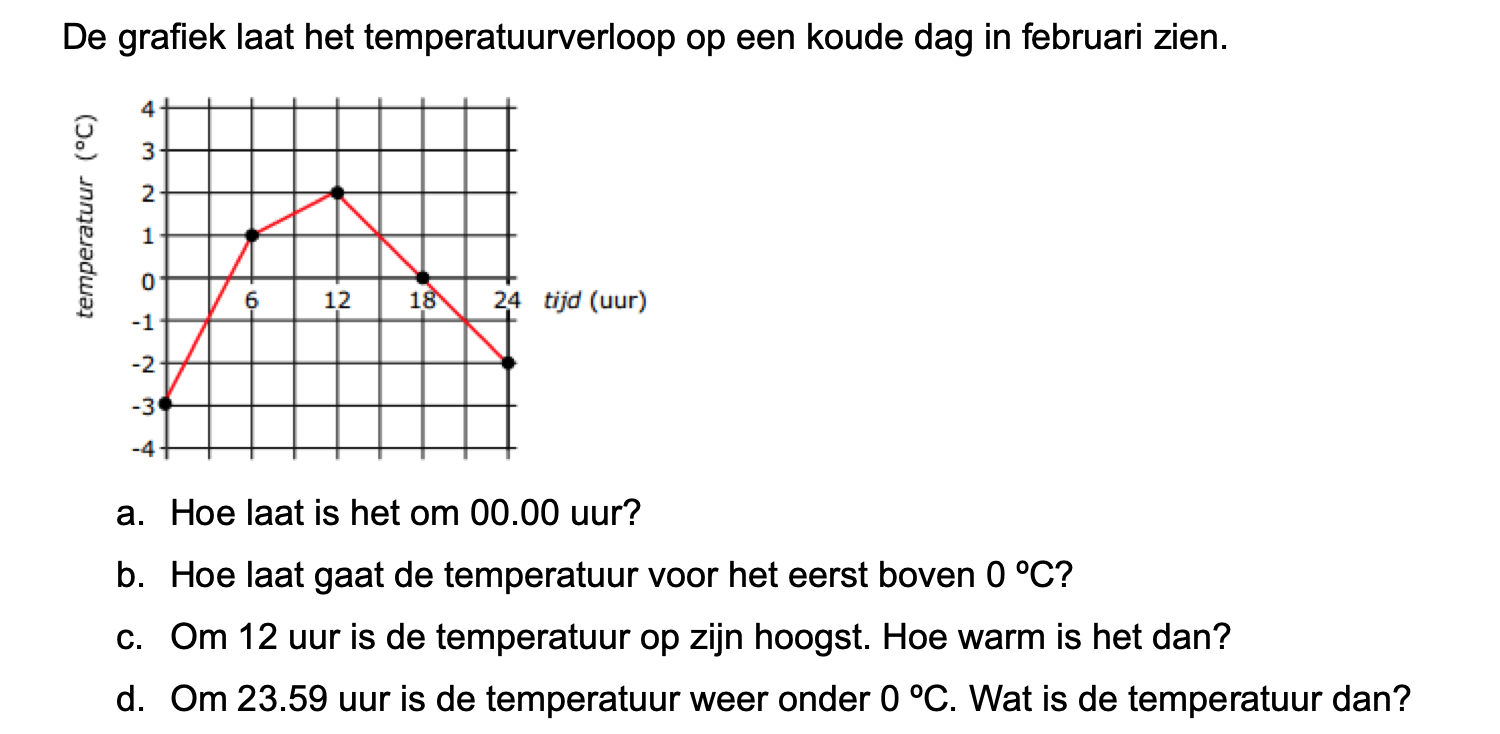
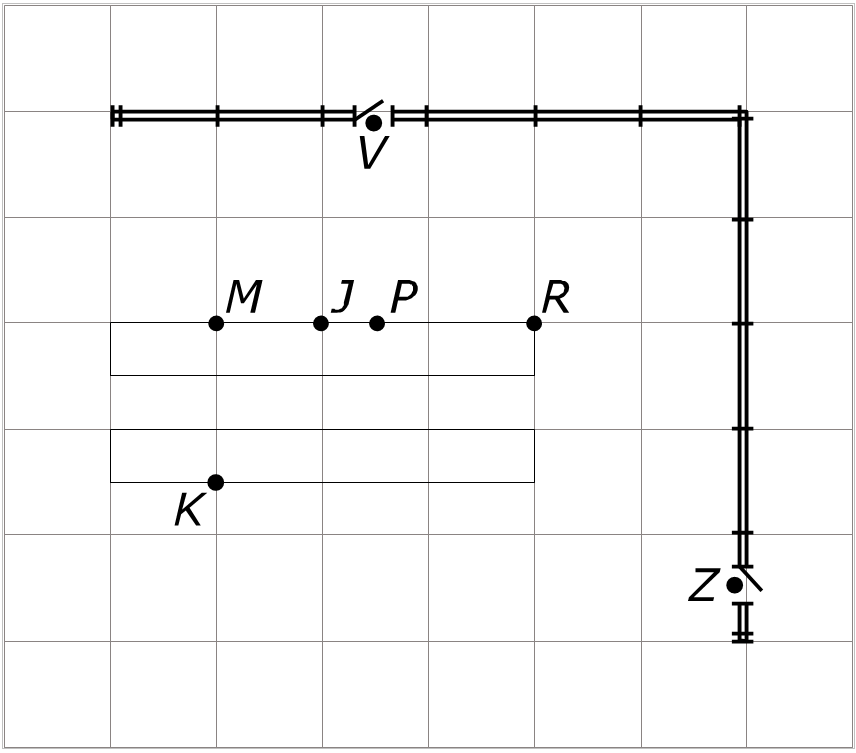
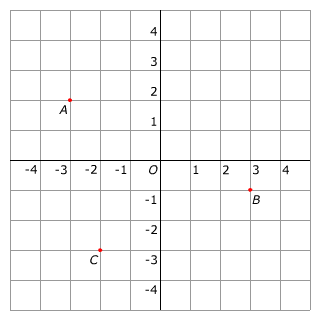
 Geef van elk punt in het assenstelsel hieronde de coördinaten.
Geef van elk punt in het assenstelsel hieronde de coördinaten.