de afgelopen lessen zijn jullie bezig geweest met het hoofdstuk 'Goniometrie'. Via deze website gaan jullie oefenen voor de toets en je eindexamen.
De doelen:
Na het oefenen via deze website...
- ... Weet je wat de tangens, sinus en de cosinus is.
- ... Kun je het hellingspresentage berekenen met behulp van de tangens.
- ... Kun je de tangens, sinus en cosinus berekenen.
- ... Kun je een hoek berekenen met behulp van de tangens, sinus en cosinus.
- ... Kun je een zijden berekenen met behulp van de tangens, sinus en cosinus.
- ... Rekenen met de tangens in een ruimtefiguur.
Figuur 5.1.0
Hoelang?
Je krijgt meerdere lessen de tijd om te werken aan de paragraven.
Wat ga je doen?
Je gaat aan de slag met de paragrafen die hier links worden aangeven.
Om te beginnen klik je op het juiste tabblad. Eerst lees je de theorie en daarna maak je de opdrachten. Hierna ga je verder met de volgende paragraaf.
Als laatste maak je de oefentoets. Dit is een voorbereiding op je toets en je eindexamen.
Hulp?
Als je vragen hebt over een opdracht, lees je eerst nogmaals de theorie of kijk je het filmpje. Heb je hierna toch nog vragen, dan steek je je vinger op en stel je hem aan je docent.
Klaar?
Ben je eerder klaar? Ga kun je de opdrachten uit het boek gaan maken of je vraagt aan je docent wat je kunt doen.
Veel succes!!
Hellingspercentage
In het filmpje hieronder wordt uitlegd hoe je het hellingspercentage moet berekenen.
Hellingspercentage berekenen
Oefenopgaven
Figuur 5.1.1
Figuur 5.1.2
Tangens berekenen
Om de tangens van een hoek te berekenen gebruiken we bijna dezelfde formule als voor het hellingspercentage.
Het enige wat anders is aan deze fomule is dat we geen x 100% gebruiken.
Om het te verduidelijken hieronder een klein voorbeeld.
.
Figuur 5.2.1
Als we vanuit \(\angle P\) kijken, dan zien we dat QR de overstaande zijde is en dat PQ de aanliggende zijde is.
Stap 1: Vul de formule in met letters.
Stap 2: Vul de waardes op de juiste plek in.
Stap 3: Reken uit.
!Let op! Tangens rond je af op 3 decmialen.
\(Tangens\angle P = {QR \over PQ}\)
\(Tangens\angle P = {84 \over 600} \approx0,14\)
Nu komt er precies 0,14 uit, dan mag je gewoon 0,14 opschrijven.
Oefenopgaven
Hoeken berekenen met tangens
In de link hieronder vind je een filmpje over hoeken berekenen met de tangens. Er worden een aantal vragen tussendoor gesteld. Dus let goed op en doe goed mee.
Klik op het vergrotingsknopje van het filmpje. Anders kun je de opdracht niet meer zien als de vraag verschijnt.
Hoeken berekenen met de tangens
Oefenopgaven
Figuur 5.3.1
Figuur 5.3.2
Zijde berekenen met tangens
Bekijk het filmpje hieronder. Hier wordt uitgelegd hoe je een zijde van een rechthoekige driehoek kunt berekenen met de Tangens.
Zijden berekenen met de Tangens
Oefenopgaven
Tangens in de ruimte
Bij het berekenen van hoeken in een ruimtefiguur moeten we steeds dezelfde stappen doorlopen.
Kijk in welke driehoek of vierhoek de hoek ligt die je moet berekenen.Maak een schets. (Let op!: Je hebt een rechthoekige driehoek nodig.)
Zet de waardes die je al weet erbij.
Berekenen de eventuele zijdes die je nog nodig denkt te hebben.
Berekenen de gevraagde hoek aan de hand van de Tangens.
Als je toch merkt dat je eerst stap niet begrijpt, kijk dat terug naar de paragraaf waar het wordt uitgelegd.
Oefenopgaven
Figuur 5.5.1
Figuur 5.5.2
Sinus berekenen
Het berekenen van de sinus is niet veel anders dan het berekenen van de tangens. Het enige verschil is de formule. De formule voor het berekenen van de sinus is:
Als we vanuit \(\angle C\) kijken, dan zien we dat AB de overstaande zijde is en dat AC de schuinezijde is.
Stap 1: Vul de formule in met letters.
Stap 2: Vul de waardes op de juiste plek in.
Stap 3: Reken uit.
!Let op! Sinus rond je af op 3 decmialen.
Oefenopgaven
Hoeken berekenen met sinus
In de link hieronder vind je een filmpje over hoeken berekenen met de sinus. Er worden een aantal vragen tussendoor gesteld. Dus let goed op en doe goed mee.
Klik op het vergrotingsknopje van het filmpje. Anders kun je de opdracht niet meer zien als de vraag verschijnt.
Hoek berekenen met de sinus
Oefenopgaven
Zijde berekenen met sinus
Om de zijde van een rechthoekige driehoeken te berekenen met de sinus hebben we de formule nodig van de sinus. Deze wordt in bovenstaande paragrafen beschreven.
Als we een zijde willen gaan berekenen moeten we minstens één zijde weten en één hoek.
Hieronder wordt een voorbeeld gegeven en een algemeen stappenplan om een zijde te kunnen berekenen met de sinus. Bekijk het filmpje tot 3:38.
Zijde berekenen met de sinus
Oefenopgaven
Figuur 5.8.1
Figuur 5.8.2
Figuur 5.8.3
Cosinus berekenen
Als we de cosinus gaan berekenen gebruiken we weer een andere formule. Deze is alsvolgt:
Als we vanuit \(\angle C\) kijken, dan zien we dat BC de aanliggende zijde is en dat AC de schuinezijde is.
Stap 1: Vul de formule in met letters.
Stap 2: Vul de waardes op de juiste plek in.
Stap 3: Reken uit.
!Let op! Cosinus rond je af op 3 decmialen.
Oefenopgaven
Figuur 5.9.2
Figuur 5.9.3
Figuur 5.9.4
Hoeken berekenen met Cosinus
In de link hieronder vind je een filmpje over hoeken berekenen met de cosinus. Er worden een aantal vragen tussendoor gesteld. Dus let goed op en doe goed mee.
Klik op het vergrotingsknopje van het filmpje. Anders kun je de opdracht niet meer zien als de vraag verschijnt.
Hoek berekenen met de cosinus
Oefenopgaven
Zijde berekenen met cosinus
Ook bij het bereken van een zijde met de cosinus hebben we een aantal factoren nodig. We hebben de fomule van de cosinus nodig en een rechthoekige driehoek. Van deze driehoek moeten we minstens één zijde weten en één hoek.
Hieronder wordt een voorbeeld gegeven en een algemeen stappenplan om een zijde te kunnen berekenen met de cosinus. Bekijk het filmpje tot 2:13
Achter de opgave staat of een I of een II. Dit geeft aan of het tijdvak 1 is of tijdvak 2.
Hieronder staan een aantal voorbeeld vragen. Let wel op! Als je extra wilt oefenen kun je ook naar Examenblad gaan, maar soms worden hier extra vormen gevraagd waar wij het nog niet over gehad hebben.
Het arrangement Goniometrie is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
Mandy de Bes
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2021-02-10 14:41:50
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
In deze lessen reeks kun je oefenen met de tangens, sinus en de cosinus. Hellingspercentages, hoeken, zijdes en in de ruimte komt allemaal terug. Het bevat uitleg, voorbeelden en oefenmateriaal. Ook kun je jezelf toetsen en daarna verder oefenen met lastige onderwerpen.
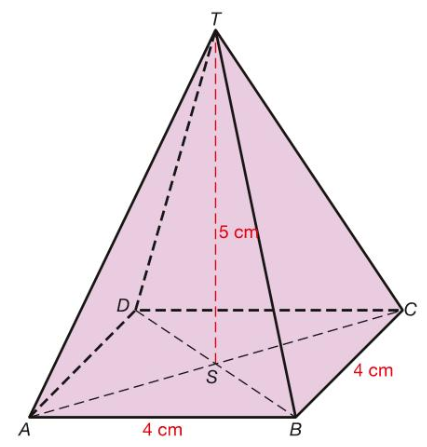
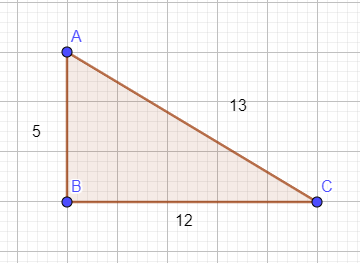
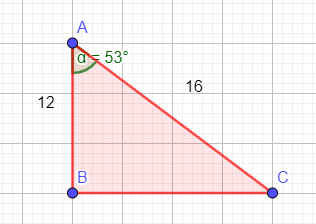
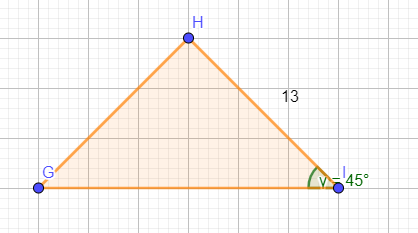
In deze lessen reeks kun je oefenen met de tangens, sinus en de cosinus. Hellingspercentages, hoeken, zijdes en in de ruimte komt allemaal terug. Het bevat uitleg, voorbeelden en oefenmateriaal. Ook kun je jezelf toetsen en daarna verder oefenen met lastige onderwerpen.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Poort Examen 2015-I
