§2 Hoeken
Uitleg
Wijzers van de klok.
Een analoge klok heeft wijzers. Deze wijzers draaien rond. Met behulp van de wijzers kun je de tijd aflezen.
Wanneer een wijzer helemaal ronddraait legt deze 360o af.
Op de klok hiernaast staat de grote wijzer boven aan (op de twaalf) en de kleine wijzer op twee. We kunnen nu de ruimte tussen de wijzers berekenen.
De ruimte tussen de wijzers noemen we de hoek van de wijzers. Deze bereken je in graden. Je weet immers dat wanneer een wijzer helemaal ronddraaid deze 360o aflegt.
Een hele cirkel is 360o.
De cijfers op de klok, dus de 1 en 2 en 3 enzovoorts, verdelen de klok in 12 gelijke stukken.
Om de grootte van 1 zo’n stuk te berekenen, moet je 360o delen door 12. Je komt dan uit op 30o.
Om 2 uur is die hoek 2 keer zo groot, dus 30o x 2 =60o.
En om 5 uur is de hoek 5 keer zo groot, dus 30o x 5 =150o.
Om 8 uur is de hoek KLEINER dan om 5 uur. We gaan namelijk altijd uit van de kleinste hoek tussen de wijzers.
Van 8 naar 12 zijn 4 stukjes van 30o, dus 30o x 4 =120o
Maak nu opgave 1 t/m 4 van de opdrachten.
Kijkhoek en gezichtsveld.
Wanneer je om je heen kijkt heb je ook te maken met hoeken. Je kunt bijvoorbeeld niet om de hoek van het lokaal kijken of door een muur heen. Sommige objecten (spullen, dingen) zorgen er voor dat je delen niet kunt zien. Net als wanneer er een heel groot persoon voor je staat.
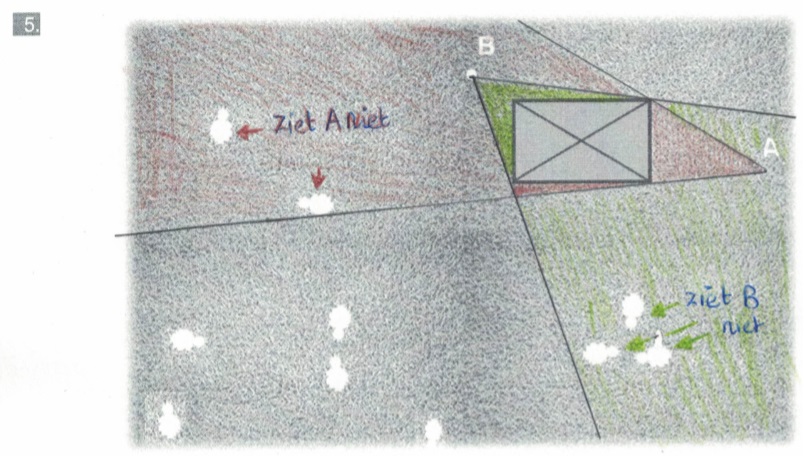
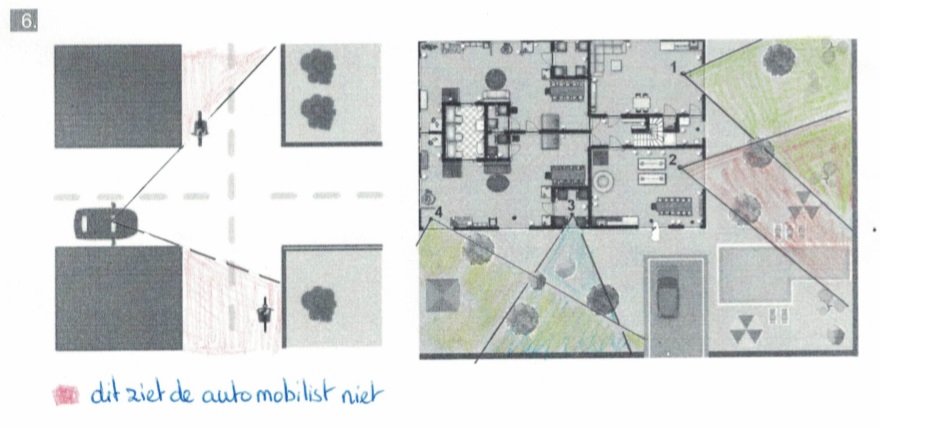
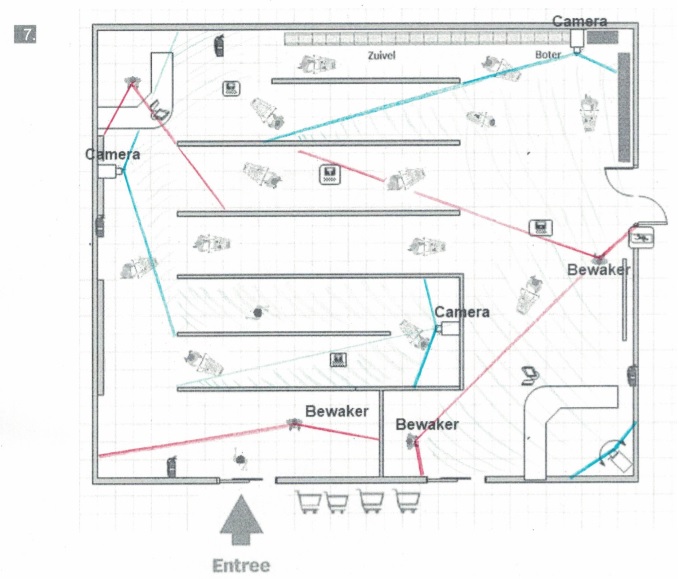
In de voorbeelden hierboven spreken we over je gezichtsveld. Dat is het gebied dat je kunt zien zonder je hoofd of je ogen te bewegen. Wanneer iets of iemand voor je staat dan beneemt deze een deel van je zicht.
Onze ogen zitten voor in ons hoofd. Daarom kunnen we het gebied dat recht voor je neus is goed waarnemen Dit gebied (blauw in het plaatje) wordt door bijde ogen gezien. Nadert er iets van de zijkant dan zie je het minder scherp. Het wordt dan maar waargenomen door 1 oog.
Klik op de link om een uitleg met plaatjes te bekijken
Uitleg kijklijnen kennisbank wiskunde
Wanneer je het gezichtsveld gaat tekenen, teken je dus twee lijnen vanuit het puntje van je neus. Je neus zit namelijk midden tussen je ogen.
Je kunt niet door muren heen kijken dus de kijklijnen teken je langs de puntjes van de muur.
Houdt ook rekening met de plaats waar je staat. Dit bepaald namelijk wat je wel en niet kunt zien en hoe groot je kijkhoek is.
Hoe verder je van de opening in de muur staat, hoe kleiner de hoek wordt die je kunt zien.
Maak nu opgave 5 t/m 8 van de opdrachten.
Een hoek.
Wanneer we spreken over een hoek, dan bedoelen we de ruimte tussen twee snijdende lijnen.
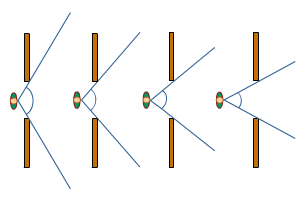
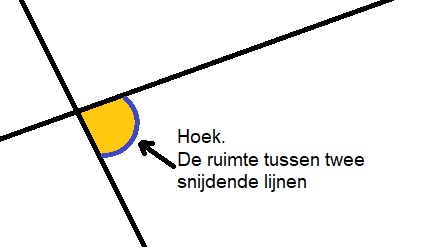
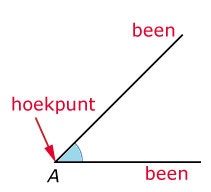Een hoek bestaat dus uit twee lijnen. Deze lijnen noemen we de benen van de hoek.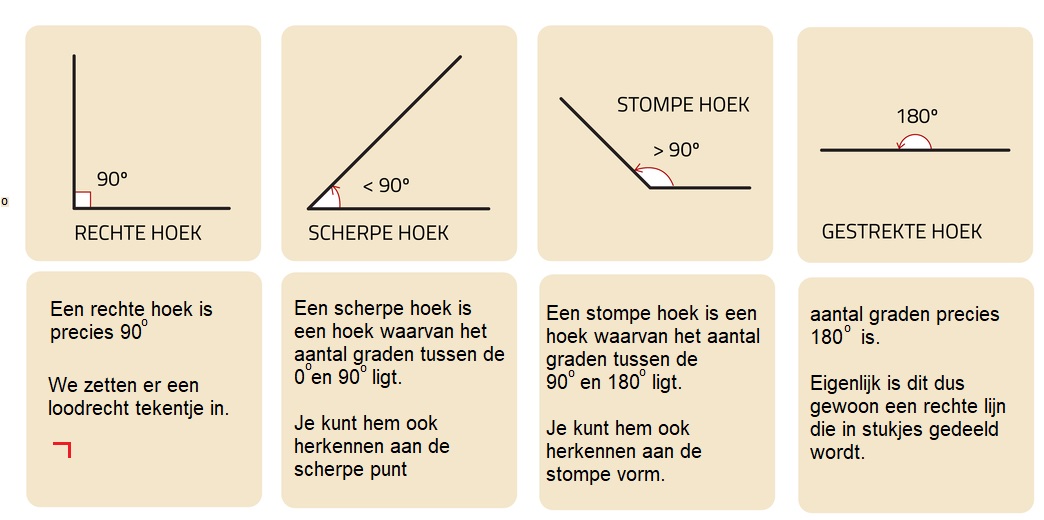
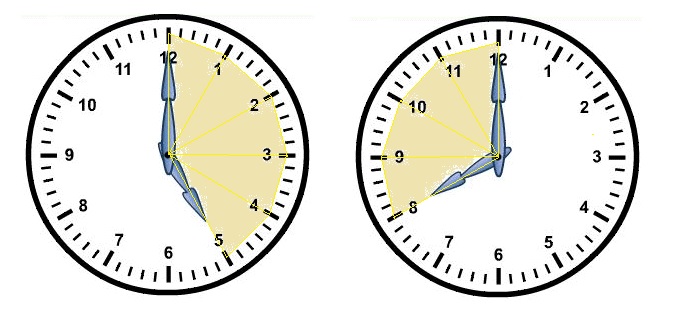
Een hoek meet je in graden. Dit doe je met je geodriehoek.
hoe precies? dat leren we in een andere paragraaf. Voor nu concentreren we ons eerst op de vorm van de hoek.
We kennen verschillende soorten hoeken.
In het filmpje hiernaast wordt dat perfect uitgelegd.
Het plaatje hieronder is een samenvatting van de uitleg uit het filmpje.
Handig om over te nemen in je schrift en te leren.
Maak nu opgave 9 t/m 14 van de opdrachten
Opgaven
Over hoeveel graden draait de grote wijzer van een klok in: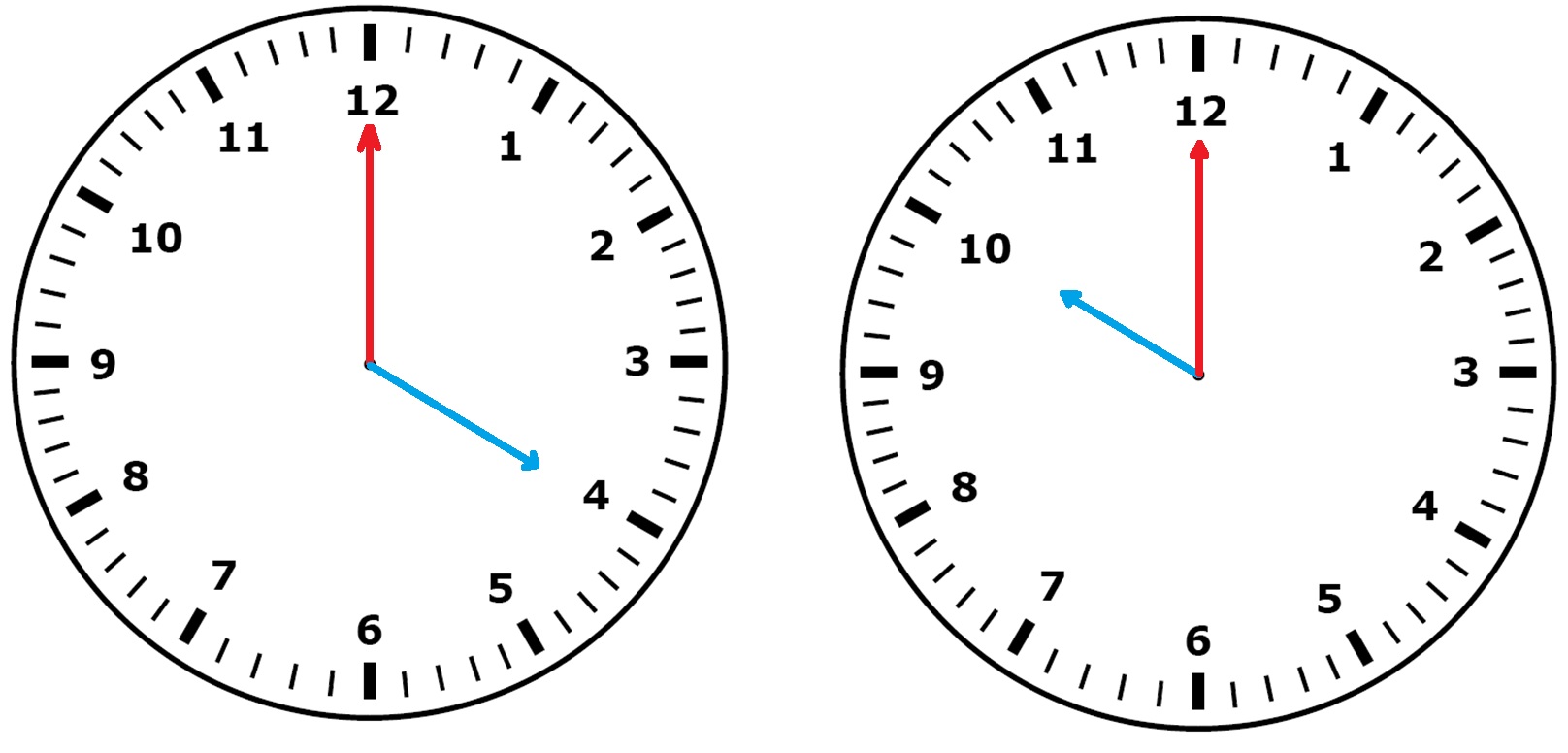
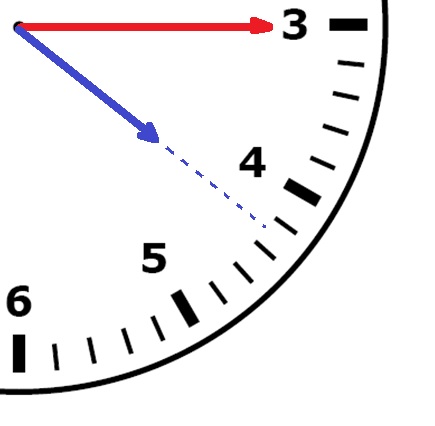- één uur?
- tien minuten?
- één minuut?
| ..2. |
|
Hoek tussen de wijzers |
Bereken hoe groot de hoek is tussen de wijzers van een klok om.
- 4 uur
- 10 uur
Bereken de hoek tussen de wijzers van de klok om
- 5 uur
- 8 uur
Wanneer de klok niet op een heel uur staat maar bijvoorbeeld op een half uur of op een kwartier (een kwart) dan wijst de kleine wijzer ook niet meer precies het getal aan.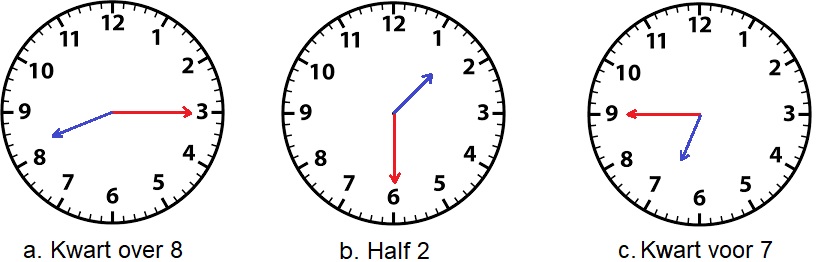
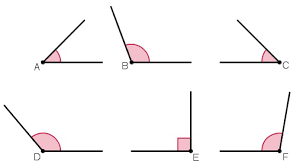
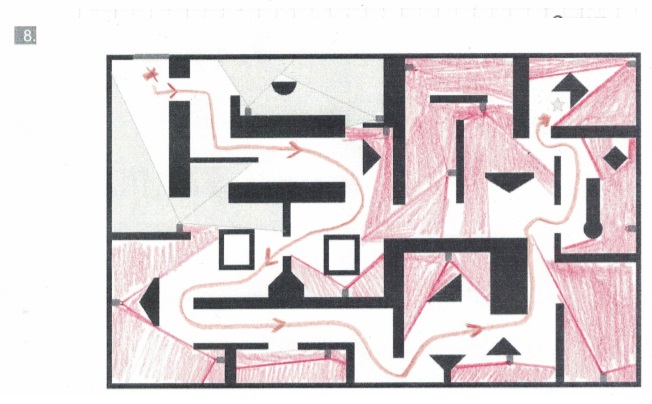
Om kwart over 4 staat de grote wijzer op kwart over (15) en de kleine wijzer is een klein stukje voorbij de vier geschoven. Ook dan kun je berekenen hoeveel graden er tussen de kleine en grote wijzer past.
Tussen de grote en de kleine wijzer zit één heel uurstreepje dat is 360o : 12 = 30o
De kleine wijzer is een kwart van een heel uur streepje verschoven dus:
30o : 4 = 7,5o.
In totaal zit er dus 30o +7,5o = 37,5o tussen de kleine en grote wijzer.
Bereken nu zelf bij de volgende twee klokken hoeveel graden er tussen de wijzers zit.
Lees nu eerst het tweede deel van de uitleg bij deze paragraaf goed door en bekijk het instructiefilmpje. Begin daarna aan vraag 5 t/m 8.
Herhaling uitleg.
Hieronder zie je een voorbeeld van iemand die door twee ramen kijkt. Je kan goed zien wat Jan wel en niet kan zien. Myrthe en Mathijs ziet hij wel staan, Merel ziet hij niet staan.
Probeer nu zelf de volgende opdracht.
| ..5. |
 |
Kijklijnen |
Bekijk de afbeelding. Deze staat ook op je werkblad.
Teken het zichtveld dat je hebt vanuit punt A.
Teken ook het zichtveld uit punt B.
Vanuit welk punt kun je de meeste schapen zien? Noteer de letter in je ruitjesschrift
| ..6. |
|
Kijklijnen |
- Bekijk de afbeelding. De afbeelding staat ook op het werkblad afgedrukt.
Geef met kijklijnen aan welke fietser wel en welke fietser niet gezien wordt door de automobilist.
- Bekijk de afbeelding. De afbeelding staat ook op het werkblad.
Je ziet de plattegrond van een huis. Achter elk raam is een stip getekend. Dat is het punt van waar je door het raam naar buitenkijkt. Vier van deze punten zijn genummerd met de cijfer 1, 2, 3 en 4. Teken vanuit deze punten de kijklijnen die horen bij het van het zichtveld.
| ..7. |
|
Kijklijnen |
Bekijk de afbeelding. Deze staat ook op het werkblad.
Je ziet hier een plattegrond van een supermarkt. De supermarkt wordt beveiligd met camera's en beveiligers. Teken in elke kamer de kijklijnen. Doe hetzelfde met de bewakers.
Welke klanten worden niet door een bewaker of camera gezien? Noteer het aantal in je schrift.
| ..8. |
|
Beveiliging |
Bekijk de afbeelding. Deze is ook afgedrukt op het werkblad.
Op deze plattegrond zie je een museum. In de ruimte rechtboven is een gouden ster tentoongesteld. Het is aan jou de taak om ongezien (door de camera's) bij de gouden ster te komen. Teken in iedere camera de kijklijnen en stippel daarna je route naar de gouden ster uit.
Van twee camera's is het zichtveld al getekend.
Lees tot slot het derde deel van de uitleg over verschillende soorten hoeken.
Maak daarna de laatste opgaven bij deze paragraaf.
Bekijk de afbeelding hiernaast. Schrijf in je wiskunde schrift van ieder hoek op of het een gestrekte hoek, stompe hoek, rechte hoek of scherpe hoek is.
\(\angle \space A =\)
\(\angle \space B=\)
\(\angle \space C=\)
| ..10. |
|
Hoeken in een bootje. |
Hiernaast zie je een bootje. In dit bootje zijn 7 hoeken verstopt. De hoeken hebben allemaal een hoofdletter.
- Welke hoeken zijn scherp, noteer de letters in je schrift.
- Welke hoeken zijn stomp, noteer de letters in je schrift.
- Zijn er ook rechte hoeken? Noteer de letters in je schrift.
- Kun je ook gestrekte hoeken vinden, noteer dan de letters in je schrift.
| ..11. |
|
Hoeken tussen de wijzers van de klok |
Als je naar een analoge klok kijkt, een analoge klok is een klok met wijzers, dan maken de wijzers van de klok ook een hoek met elkaar. Bekijk het plaatje van de zes klokken hiernaast.
Noteer in je schrift van iedere tijd of de wijzers een scherpe, stomp, rechte of gestrekte hoek met elkaar maken.
Bedenk nu zelf, als het je echt niet lukt, schets het dan in je schrift of gebruik het klokje
a. Wat voor soort hoek maken de wijzers van de klok om 2 uur 's middags?
b. Wat voor soort hoek maken de wijzers van de klok om 7 uur 's ochtends?
c. Wat voor soort hoek maken de wijzers van de klok om 9 uur 's avonds?
d. Wat voor soort hoek maken de wijzers van de klok om 5 uur 's middags?
e. Wat voor soort hoek maken de wijzers van de klok om 6 uur 's ochtends?
In de figuur hierboven zijn verschillende hoeken aangegeven. In hoekpunt A komen twee hoeken samen. Als van hoek A wordt gesproken, is niet duidelijk welke hoek bedoeld wordt: de hoek met het ruitje of de hoek met het bolletje. Daarom worden hoeken met drie letters genoteerd.
De hoek met het ruitje noteer je als ∠DAS.
De middelste letter is het hoekpunt. De buitenste letters komen in alfabetische volgorde.
De hoek met het bolletje noteer je als ∠BAS.
- Noteer nu zelf de hoek met het sterretje.
- Noteer ook de hoek met het klavertje.
- Noteer nog één andere hoek, wanneer je buur klaar is laat je hem of haar opzoeken welke hoek jij hebt genoteerd.
Bekijk de figuur hiernaast.
- Noteer drie scherpe hoeken.
- Noteer de letter van de rechte hoek.
- Noteer de letter van de stompe hoek.
Uitwerkingen
Let op, hier vindt je alleen antwoorden. Je kunt dus alleen je eindantwoord nakijken.
In je schrift schrijf je altijd de volledige berekening op!
a. 3600 : 12 x 1 = 300
b. 3600 : 60 x 10 = 600
c. 3600 : 60 x 1 = 60
a. 3600 : 12 x 1 = 1200
b. 3600 : 12 x 2 = 600
a. 3600 : 12 x 5 = 1500
b. 3600 : 12 x 4 = 1200
a. 5 x 300 + 300 : 4 = 157,50
b. 4 x 300 + \(1\over 2\) x 300 = 1350
c. 2 x 300 + \(1 \over 4\) x 300 = 67,50
c. Je ziet de meeste schapen vanuit punt C.
∠ A = scherp ∠ D= stomp
∠ B = stomp ∠ E = recht
∠ C = scherp ∠ F = stomp
a. ∠ A, ∠ D, en ∠ E zijn scherp.
b. ∠ C en ∠ G zijn stomp.
c. ∠ B is een rechte hoek.
d. ∠ F is een gestrekte hoek.
*We meten altijd de kleinste hoek tussen de wijzers!
01:00 uur = scherpe hoek 04:00 uur = stompe hoek
02:00 uur = scherpe hoek 05:00 uur = stompe hoek
03:00 uur = rechte hoek 06:00 uur = gestrekte hoek
*We meten altijd de kleinste hoek tussen de wijzers!
a. Scherpe hoek
b. Stompe hoek
c. Rechte hoek
d. Stompe hoek
e. Gestrekte hoek
a. ∠BSC.
b. ∠DCS.
c. * allerlei hoeken zijn mogelijk, laat diegene die naast je zit dit controleren.
a. ∠ABE, ∠AEB, ∠BED, ∠DBE, ∠CBD of ∠BDC.
b. ∠D is recht. (er staat een loodrechtteken in!)
c. ∠A.
Test jezelf
