Het arrangement Thema 10 Afstanden - havo/vwo1 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 06-08-2025 15:30:05
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Het thema 'Afstanden' is ontwikkeld door auteurs en medewerkers van de Wageningse Methode.
Fair Use
In de Stercollecties van VO-content wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Dit thema valt onder de arrangeerbare leerlijn van de Stercollecties voor wiskunde voor havo/vwo leerjaar 1. Dit is thema ’Afstanden'. De volgende onderdelen worden behandeld: nauwkeurig de gebieden tekenen die op een bepaalde afstand liggen van punten, lijnen of vormen, de gebieden tekenen die op gelijke afstand liggen ten opzichte van twee punten of lijnen, gebieden opdelen in stukken die even ver, dichterbij of verder weg liggen, een cirkel tekenen die precies om een driehoek past, of juist de grootste cirkel tekenen die in een driehoek past, bij al deze bovenstaande tekeningen kun je daarbij loodlijnen, middelloodlijnen, deellijnen (of bissectrices) en evenwijdigheid gebruiken en uitleggen waarom de tekening juist is.
- Leerniveau
- HAVO 1; VWO 1;
- Leerinhoud en doelen
- Lengte, omtrek, oppervlakte en inhoud; Redeneren in de (vlakke) meetkunde; Hoeken;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 7 uur 30 minuten
- Trefwoorden
- afstanden, arrangeerbaar, cirkel, deellijnen, driehoek, gebieden tekenen, havo/vwo 1, loodlijnen, stercollectie, wiskunde

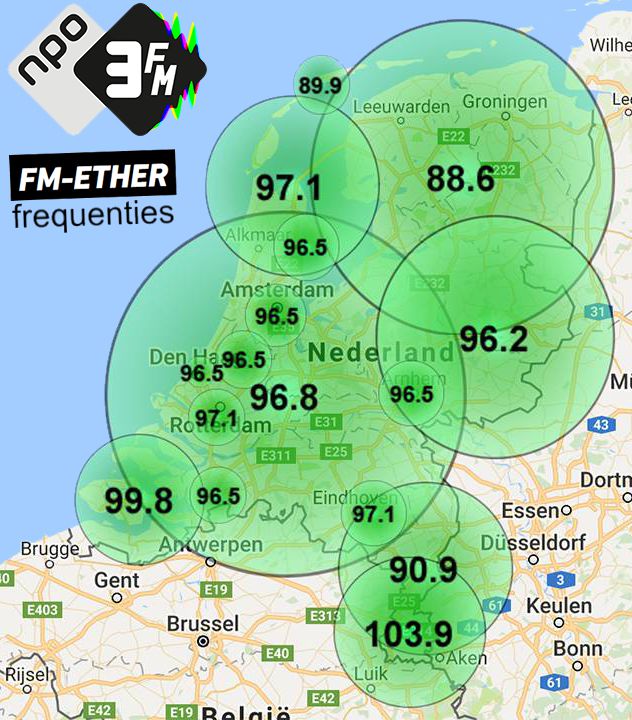
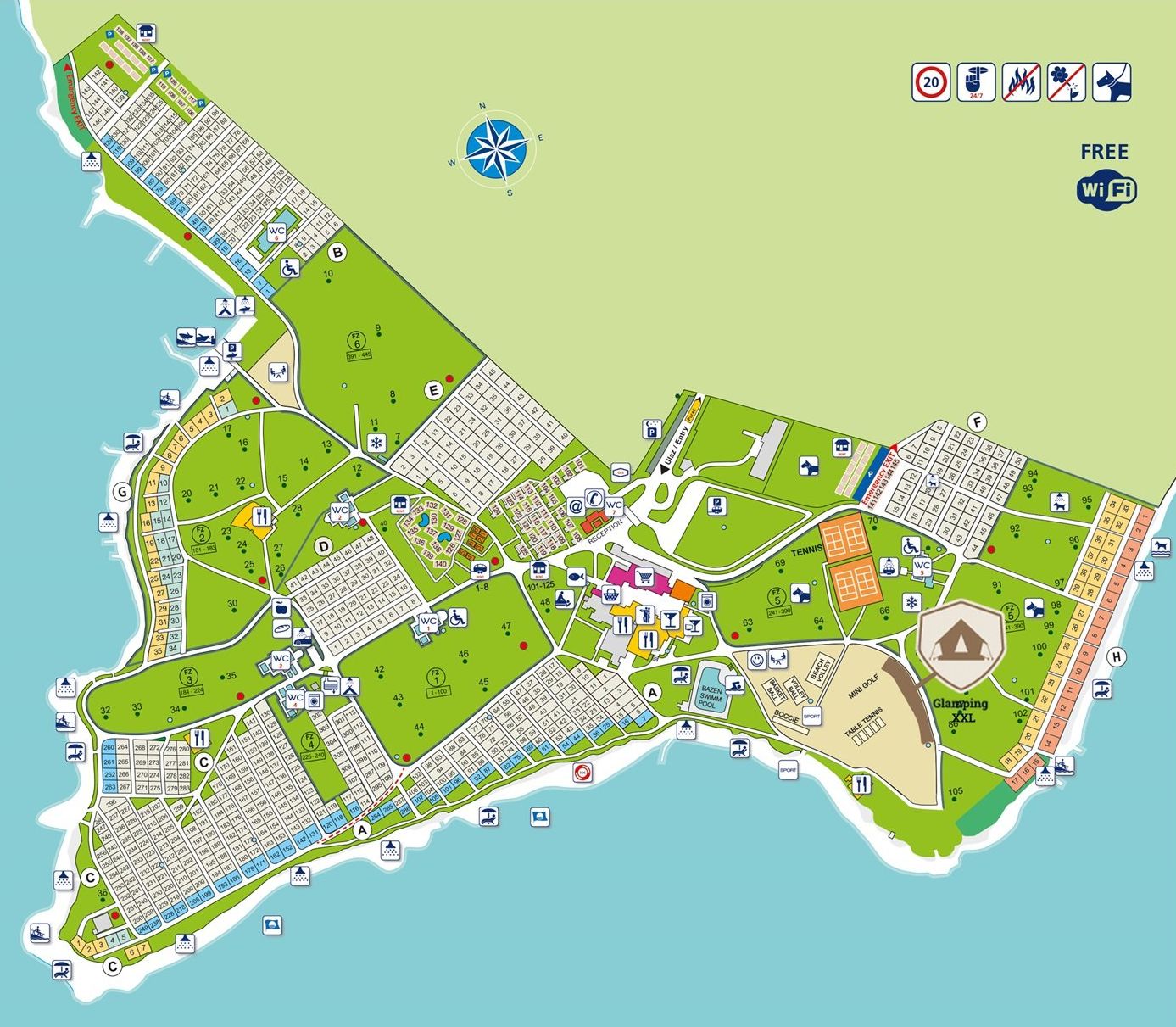

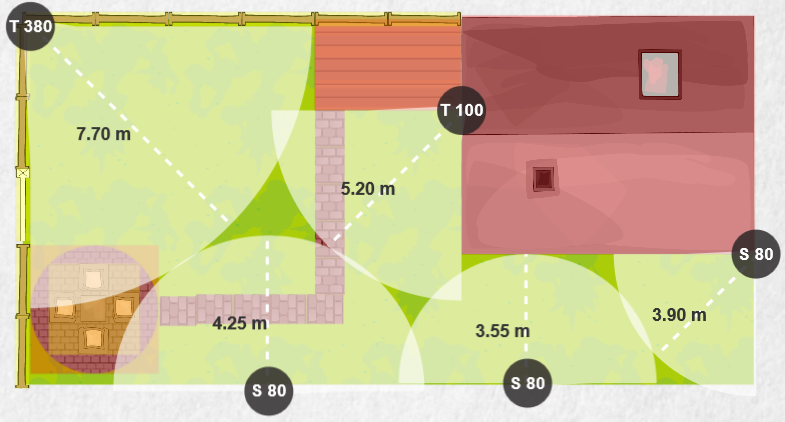


 Aan het einde van dit thema kan ik:
Aan het einde van dit thema kan ik: Het thema 'Afstanden' bestaat uit de volgende onderdelen:
Het thema 'Afstanden' bestaat uit de volgende onderdelen: Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.

 In dit thema leer je te redeneren met afstanden.
In dit thema leer je te redeneren met afstanden.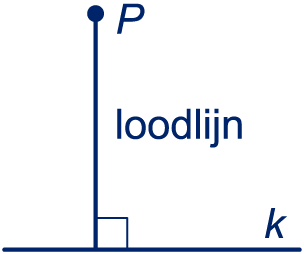 Met afstand bedoelen we de lengte van de kortste verbinding. De afstand van twee punten
Met afstand bedoelen we de lengte van de kortste verbinding. De afstand van twee punten  Lijn
Lijn  Lijnstuk
Lijnstuk  Een halve lijn heeft één grenspunt, loopt dus aan één kant van het grenspunt onbeperkt door.
Een halve lijn heeft één grenspunt, loopt dus aan één kant van het grenspunt onbeperkt door. De middelloodlijn van lijnstuk
De middelloodlijn van lijnstuk  De deellijn van een hoek deelt een hoek in twee even grote hoeken. Alle punten, die op de deellijn liggen, liggen even ver van de benen van een hoek af.
De deellijn van een hoek deelt een hoek in twee even grote hoeken. Alle punten, die op de deellijn liggen, liggen even ver van de benen van een hoek af.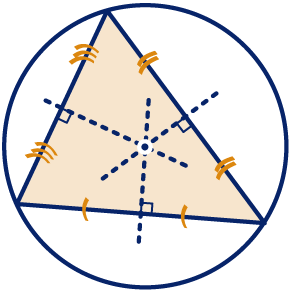 De drie middelloodlijnen van een driehoek gaan door één punt. Dit punt ligt even ver van de hoekpunten van de driehoek en is het middelpunt van de omgeschreven cirkel.
De drie middelloodlijnen van een driehoek gaan door één punt. Dit punt ligt even ver van de hoekpunten van de driehoek en is het middelpunt van de omgeschreven cirkel.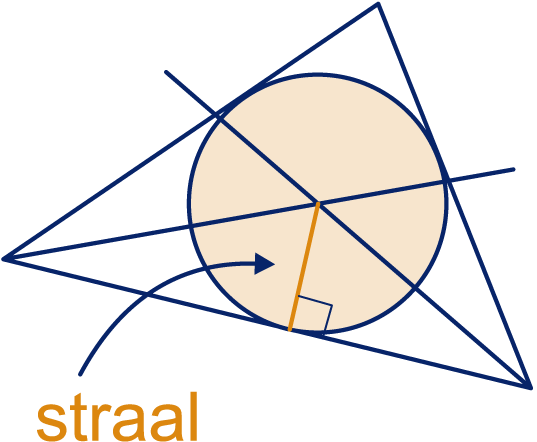 De drie deellijnen van de hoeken van een driehoek gaan door één punt. Dit punt ligt even ver van de drie zijden van de driehoek en is het middelpunt van de ingeschreven cirkel. Als je de cirkel wilt tekenen, moet je eerst de straal vinden. Laat vanuit het middelpunt een loodlijn neer op één van de zijden, dan is dat de straal.
De drie deellijnen van de hoeken van een driehoek gaan door één punt. Dit punt ligt even ver van de drie zijden van de driehoek en is het middelpunt van de ingeschreven cirkel. Als je de cirkel wilt tekenen, moet je eerst de straal vinden. Laat vanuit het middelpunt een loodlijn neer op één van de zijden, dan is dat de straal. In deze opdracht ga je een beveiligingssysteem voor een museum ontwerpen.
In deze opdracht ga je een beveiligingssysteem voor een museum ontwerpen.


