Het arrangement Fysica geschikt voor niveau 3 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 05-09-2019 14:21:33
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Op de arbeidsmarkt is behoefte aan medewerkers met kennis en vaardigheden op het gebied van fysica. Ook voor doorstroom naar niveau 4 hebben deze kennis en vaardigheden toegevoegde waarde. Beginnend beroepsbeoefenaars die dit keuzedeel hebben gevolgd, zijn daarom kansrijker op de arbeidsmarkt. Bovendien verloopt de doorstroom naar niveau 4-kwalificaties soepeler voor studenten die dit keuzedeel hebben gevolgd. Dit keuzedeel is gericht op kennis van de fysica (natuurkunde, mechanica, wiskunde). De inhoud heeft betrekking op de algemene eigenschappen van materie, straling en energie. Het gaat om het onderzoeken en beschrijven van onderwerpen zoals kracht, evenwicht en beweging, arbeid en vermogen voor zover hierbij geen scheikundige veranderingen optreden. Daarnaast zijn wiskundige bewerkingen als het oplossen van vergelijkingen met twee onbekenden, merkwaardige producten en meetkunde onlosmakelijk verbonden aan dit keuzedeel. Het keuzedeel sluit aan op het keuzedeel Fysica niveau 2. De vakkennis en vaardigheden vormen een voorbereiding op doorstroom naar de werktuig(bouw)-kundige richtingen op niveau 4.
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 240 uur 0 minuten
- Trefwoorden
- fysica, mechanica, natuurkunde, wiskunde
Bronnen
| Bron | Type |
|---|---|
|
https://www.youtube.com/watch?v=QP-gY4hYI1Q https://www.youtube.com/watch?v=QP-gY4hYI1Q |
Video |
|
https://www.youtube.com/watch?v=uiyLXJEVmkU https://www.youtube.com/watch?v=uiyLXJEVmkU |
Video |
|
https://www.youtube.com/watch?v=9PoqPto_8TM https://www.youtube.com/watch?v=9PoqPto_8TM |
Video |
|
https://www.youtube.com/watch?v=SSfc3zkb12Q https://www.youtube.com/watch?v=SSfc3zkb12Q |
Video |
|
https://www.youtube.com/watch?v=ua_tozQSMUA https://www.youtube.com/watch?v=ua_tozQSMUA |
Video |
|
https://www.youtube.com/watch?v=QcF25PYwIaM https://www.youtube.com/watch?v=QcF25PYwIaM |
Video |
|
Toetsen Wiskunde https://maken.wikiwijs.nl/p/questionnaire/standalone/3538948 |
Link |
|
https://www.youtube.com/watch?v=vz2cYR7txJY https://www.youtube.com/watch?v=vz2cYR7txJY |
Video |
|
https://vimeo.com/149565072 https://vimeo.com/149565072 |
Video |
|
https://www.youtube.com/watch?v=e2fQmzxVr9s https://www.youtube.com/watch?v=e2fQmzxVr9s |
Video |
|
https://www.youtube.com/watch?v=wZdWVp-WPog https://www.youtube.com/watch?v=wZdWVp-WPog |
Video |
|
Galloping Gertie https://www.youtube.com/watch?time_continue=88&v=CsKKDLKYsVU |
Video |
|
https://www.youtube.com/watch?v=6ycbDCnoO8M https://www.youtube.com/watch?v=6ycbDCnoO8M |
Video |
|
https://www.youtube.com/watch?v=wJ6HnPeIPIM https://www.youtube.com/watch?v=wJ6HnPeIPIM |
Video |
|
Natuurkunde - Spanning (Basiskennis) https://www.youtube.com/watch?v=DMCX1yMTCbg |
Video |
|
Natuurkunde - Vermogen (Basiskennis) https://www.youtube.com/watch?v=kRne-MwItVg |
Video |
|
Natuurkunde - Serieschakeling vs. parallelschakeling (Basiskennis) https://www.youtube.com/watch?v=RJ8RnXwHxqc |
Video |
Gebruikte Wikiwijs Arrangementen
Oosterhuis, Patrick. (z.d.).
Fysica geschikt voor niveau 3
https://maken.wikiwijs.nl/99930/Fysica_geschikt_voor_niveau_3
Oosterhuis, Patrick. (z.d.).
Vaardigheden student
Oosterhuis, Patrick. (z.d.).
Wiskundige bewerkingen


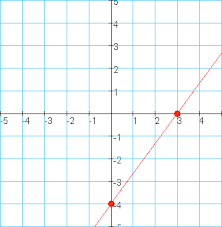
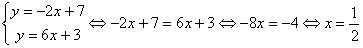
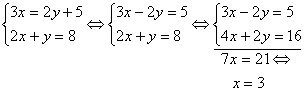
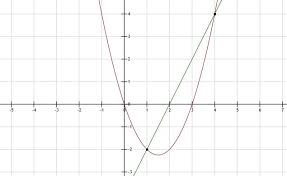
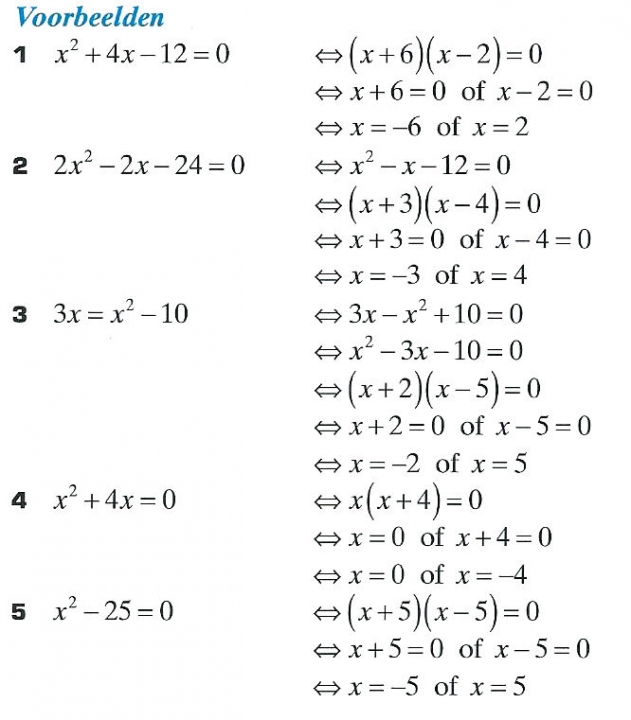

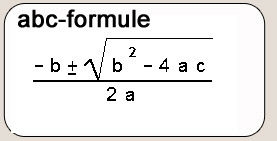



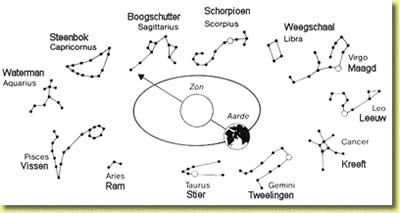 De Babyloniërs hadden ontdekt dat het pad van de zon tussen de vaste sterren een cirkel was met de aarde als middelpunt, dat is de dierenriem. Zij wisten dat de maan en de planeten ook altijd in de buurt van de dierenriem staan. Zij verdeelden de dierenriem in 360 graden. Men vermoedt dat dat getal gekozen is, omdat men graag wilde dat de beweging van de zon in één dag ongeveer één graad is. Dan moet de hele cirkel dus ongeveer 365 graden zijn, en 360 is een veelvoud van 60 dat hier mooi in de buurt ligt. Omdat de Babyloniërs in het zestigtallig stelsel rekenden, werd elke graad in 60 minuten en elke minuut in 60 seconden verdeeld. Niet alleen de dierenriem naar ook elke andere cirkel kan in 360 gelijke delen verdeeld worden, en zo kun je ook een volledige omwenteling in 360 graden verdelen. Dit idee werd gebruikt voor het verdelen van de tijd. Het hemelgewelf draait namelijk in één dag om de aarde, om een denkbeeldige as door de poolster. Men verdeelde zo’n totale omwenteling (de moderne sterredag) in 360 ‘tijdgraden’, en uiteraard 1 tijdgraad in 60 tijdminuten, enzovoort. 1 ‘tijdgraad’ is dus de tijd die de hemel nodig heeft om 1 graad verder te draaien, en dit komt ongeveer overeen met 4 van onze klokminuten.
De Babyloniërs hadden ontdekt dat het pad van de zon tussen de vaste sterren een cirkel was met de aarde als middelpunt, dat is de dierenriem. Zij wisten dat de maan en de planeten ook altijd in de buurt van de dierenriem staan. Zij verdeelden de dierenriem in 360 graden. Men vermoedt dat dat getal gekozen is, omdat men graag wilde dat de beweging van de zon in één dag ongeveer één graad is. Dan moet de hele cirkel dus ongeveer 365 graden zijn, en 360 is een veelvoud van 60 dat hier mooi in de buurt ligt. Omdat de Babyloniërs in het zestigtallig stelsel rekenden, werd elke graad in 60 minuten en elke minuut in 60 seconden verdeeld. Niet alleen de dierenriem naar ook elke andere cirkel kan in 360 gelijke delen verdeeld worden, en zo kun je ook een volledige omwenteling in 360 graden verdelen. Dit idee werd gebruikt voor het verdelen van de tijd. Het hemelgewelf draait namelijk in één dag om de aarde, om een denkbeeldige as door de poolster. Men verdeelde zo’n totale omwenteling (de moderne sterredag) in 360 ‘tijdgraden’, en uiteraard 1 tijdgraad in 60 tijdminuten, enzovoort. 1 ‘tijdgraad’ is dus de tijd die de hemel nodig heeft om 1 graad verder te draaien, en dit komt ongeveer overeen met 4 van onze klokminuten.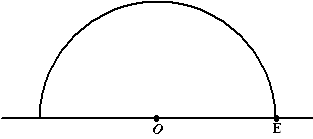 Als we de cirkel door midden snijden dan ontstaat er een rechte lijn. Door midden snijden is dus eigenlijk delen door 2, oftewel
Als we de cirkel door midden snijden dan ontstaat er een rechte lijn. Door midden snijden is dus eigenlijk delen door 2, oftewel 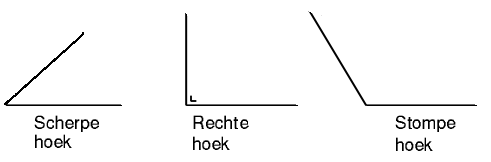
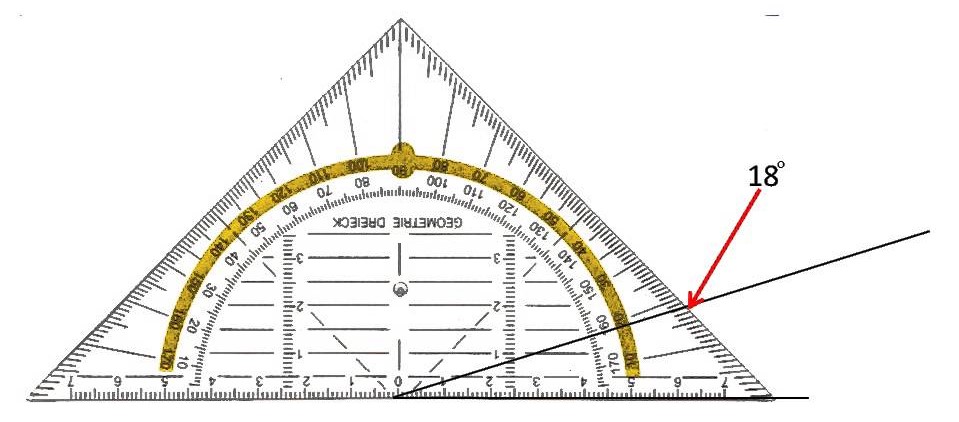
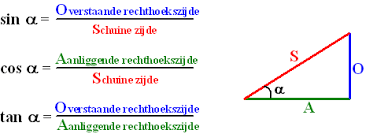
 De tangens van A is dus de lengte van B naar C gedeeld door de lengte van A naar B. In een formule uitgeschreven: tan A = BC / AB
De tangens van A is dus de lengte van B naar C gedeeld door de lengte van A naar B. In een formule uitgeschreven: tan A = BC / AB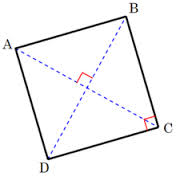 Wanneer we dit in een voorbeeld uitwerken en we nemen hiervoor een driehoek met gelijke rechthoekzijden van 4 cm dan weten we nu al dat we een hoek van 45o gaan krijgen. De driehoek die ontstaat is immers één van de twee driehoeken die ontstaat wanneer we een vierkant over de schuine zijde (diagonaal) doorsnijden. Hiermee snijden we ook de 'haakse' hoek precies doormidden en dus moet de overgebleven hoek 45o zijn.
Wanneer we dit in een voorbeeld uitwerken en we nemen hiervoor een driehoek met gelijke rechthoekzijden van 4 cm dan weten we nu al dat we een hoek van 45o gaan krijgen. De driehoek die ontstaat is immers één van de twee driehoeken die ontstaat wanneer we een vierkant over de schuine zijde (diagonaal) doorsnijden. Hiermee snijden we ook de 'haakse' hoek precies doormidden en dus moet de overgebleven hoek 45o zijn.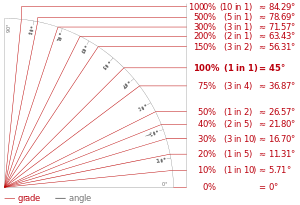 Wanneer we de waarde van tangens D opzoeken in de figuur (links) dan zien we dat de bijbehorende hoek gelijk is aan 45o. Ook zien we dat dit een stijgingspercentage van 100% betekent.
Wanneer we de waarde van tangens D opzoeken in de figuur (links) dan zien we dat de bijbehorende hoek gelijk is aan 45o. Ook zien we dat dit een stijgingspercentage van 100% betekent.





 om vervolgens het antwoord 45 te krijgen. Let op, we hebben nu een omgekeerde bewerking van de tangens uitgevoerd. Met het sommetje 4 / 4 berekenen we de tangens (tan) en om de functie tan-1 op de rekenmachine geeft de bijbehorende hoek.
om vervolgens het antwoord 45 te krijgen. Let op, we hebben nu een omgekeerde bewerking van de tangens uitgevoerd. Met het sommetje 4 / 4 berekenen we de tangens (tan) en om de functie tan-1 op de rekenmachine geeft de bijbehorende hoek.





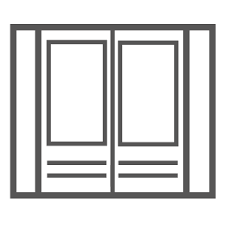 Een timmerman heeft een groot rechthoekig raamkozijn gemaakt. Hoe kan hij door twee maal te meten, met een rolmaat of meetlint, de conclusie trekken dat alle hoeken 'haaks' (90o) zijn?
Een timmerman heeft een groot rechthoekig raamkozijn gemaakt. Hoe kan hij door twee maal te meten, met een rolmaat of meetlint, de conclusie trekken dat alle hoeken 'haaks' (90o) zijn?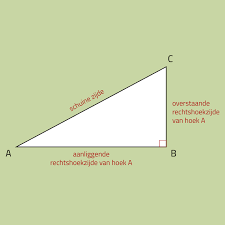




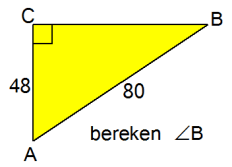
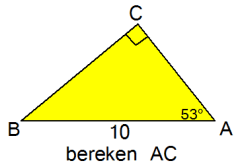
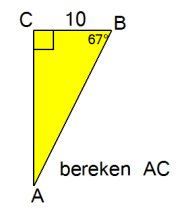
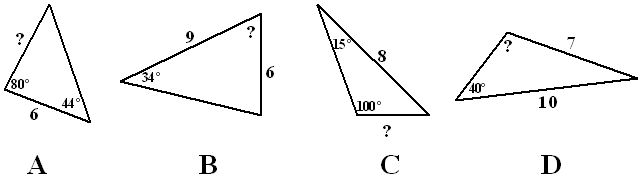
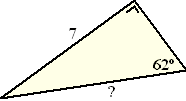 Bereken het vraagteken in de driehoek hiernaast.
Bereken het vraagteken in de driehoek hiernaast. Bereken het vraagteken in de driehoek hiernaast.
Bereken het vraagteken in de driehoek hiernaast.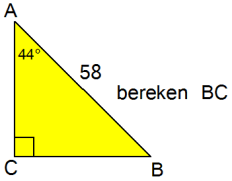
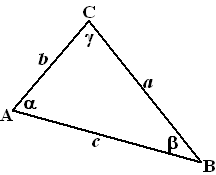 Voordat we met de theorie van deze twee regels aan de slag gaan moeten we eerst enkele afspraken maken.
Voordat we met de theorie van deze twee regels aan de slag gaan moeten we eerst enkele afspraken maken.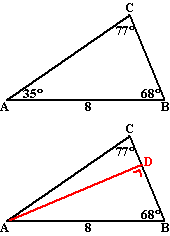
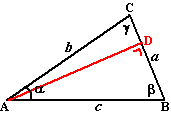 Dit was eigenlijk twee keer "SOS".
Dit was eigenlijk twee keer "SOS".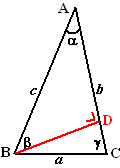 En als je de driehoek draait, dan kun je natuurlijk precies hetzelfde nóg een keer doen!!! Dat zou dan geven C/sinγ = A/sinα
En als je de driehoek draait, dan kun je natuurlijk precies hetzelfde nóg een keer doen!!! Dat zou dan geven C/sinγ = A/sinα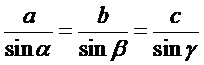
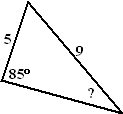 Voorbeeld 1
Voorbeeld 1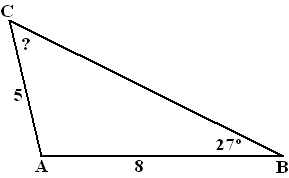 De sinusregel geldt ook voor driehoeken met een stompe hoek, maar er is een kleine complicatie.....
De sinusregel geldt ook voor driehoeken met een stompe hoek, maar er is een kleine complicatie.....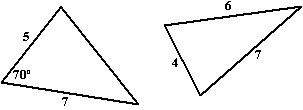 Zie je al dat het niet wil met de sinusregel? Dat komt natuurlijk omdat je in deze twee gevallen nergens een hoek en de bijbehorende zijde ertegenover weet.
Zie je al dat het niet wil met de sinusregel? Dat komt natuurlijk omdat je in deze twee gevallen nergens een hoek en de bijbehorende zijde ertegenover weet.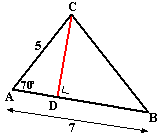 In driehoek ADC geldt dan cos70º = AD/5 dus AD = 5 • cos70º
In driehoek ADC geldt dan cos70º = AD/5 dus AD = 5 • cos70º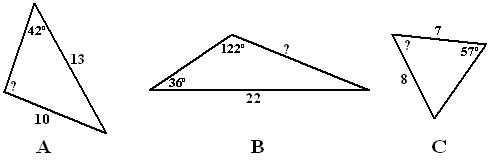
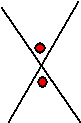 X
X
 Z
Z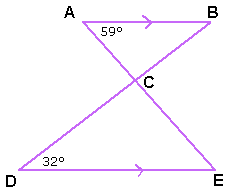 Voorbeeld 1
Voorbeeld 1 E tegenover
E tegenover 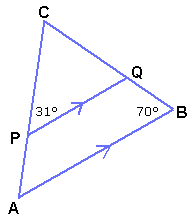 Hier is PQ evenwijdig aan AB. Wat zijn zijn de hoeken in A en Q?
Hier is PQ evenwijdig aan AB. Wat zijn zijn de hoeken in A en Q?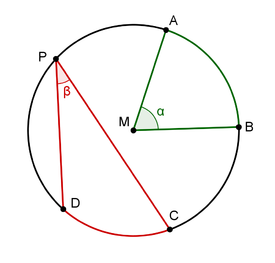 Dit zijn hoeken in en op cirkels. Een middelpuntshoek van een cirkel is een hoek waarvan het hoekpunt samenvalt met het middelpunt van de cirkel. Een omtrekshoek van een cirkel is een hoek waarvan het hoekpunt op de cirkel ligt en de benen gevormd worden door twee koorden. Een koorde is de wiskundige benaming voor het lijntje tussen P en C of P en D. De lijnen tussen M en A en M en B zijn dat eigenlijk ook maar deze noemen we stralen omdat ze beginnen in het middelpunt van de cirkel.
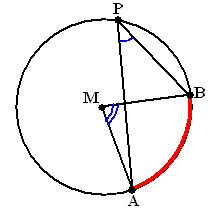
Dit zijn hoeken in en op cirkels. Een middelpuntshoek van een cirkel is een hoek waarvan het hoekpunt samenvalt met het middelpunt van de cirkel. Een omtrekshoek van een cirkel is een hoek waarvan het hoekpunt op de cirkel ligt en de benen gevormd worden door twee koorden. Een koorde is de wiskundige benaming voor het lijntje tussen P en C of P en D. De lijnen tussen M en A en M en B zijn dat eigenlijk ook maar deze noemen we stralen omdat ze beginnen in het middelpunt van de cirkel.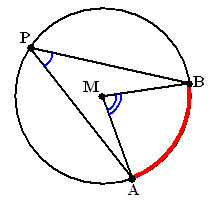 Er bestaan ook een relatie tussen de middelpuntshoek en de omtrekshoek. De middelpuntshoek is namelijk 2x zo groot als omtrekshoek. En dat kunnen we eenvoudig laten zien en meten. Het bewijs hiervoor gaat te ver en zullen we ook niet gaan behandelen.
Er bestaan ook een relatie tussen de middelpuntshoek en de omtrekshoek. De middelpuntshoek is namelijk 2x zo groot als omtrekshoek. En dat kunnen we eenvoudig laten zien en meten. Het bewijs hiervoor gaat te ver en zullen we ook niet gaan behandelen.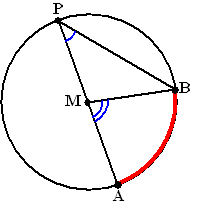
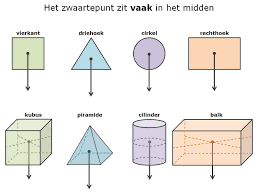
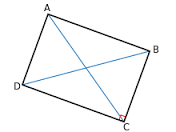 Om het zwaartepunt van een vierkant of een rechthoek te vinden kunnen we eenvoudig de diagonalen van deze rechthoek tekenen en het snijpunt van deze diagonalen is daarmee het zwaartepunt.
Om het zwaartepunt van een vierkant of een rechthoek te vinden kunnen we eenvoudig de diagonalen van deze rechthoek tekenen en het snijpunt van deze diagonalen is daarmee het zwaartepunt.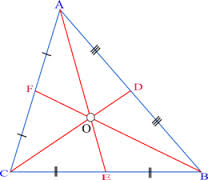 Driehoek
Driehoek Cirkel
Cirkel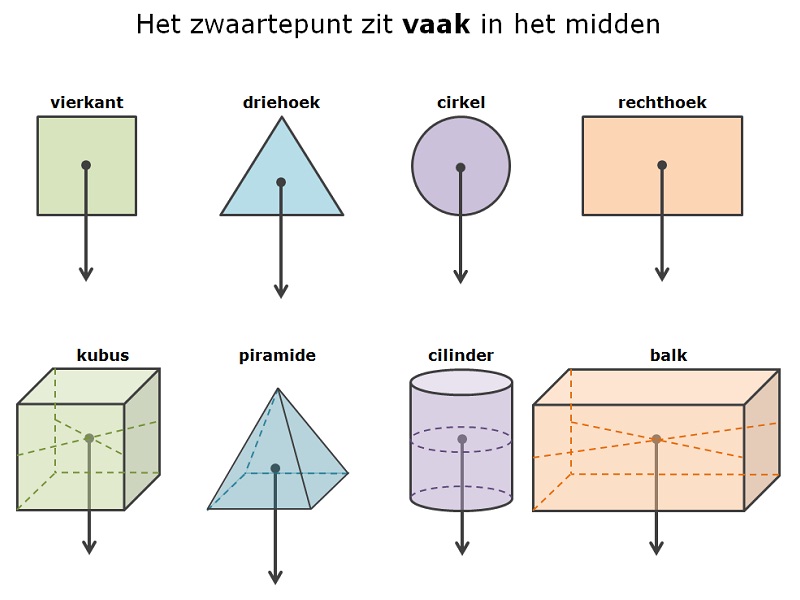






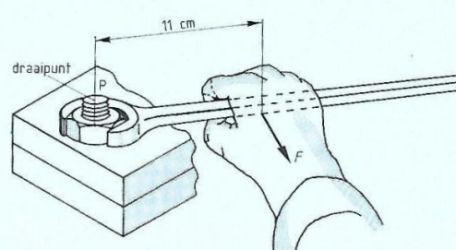
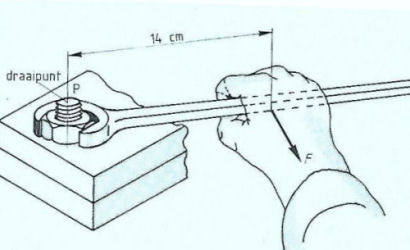
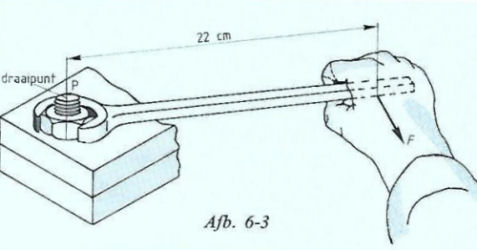
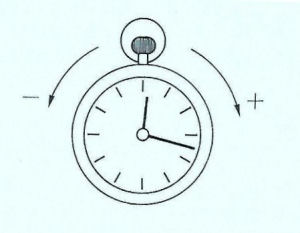 Verder spreken we nog iets af, namelijk: als de eventuele draaiing in de richting van de wijzers van de klok is dan noemen we dit een positief moment. Gaan we tegen de wijzers van de klok in dan is dit een negatief moment.
Verder spreken we nog iets af, namelijk: als de eventuele draaiing in de richting van de wijzers van de klok is dan noemen we dit een positief moment. Gaan we tegen de wijzers van de klok in dan is dit een negatief moment.
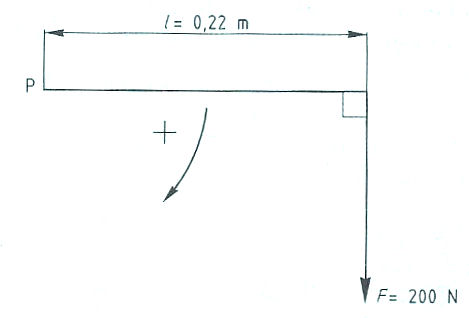
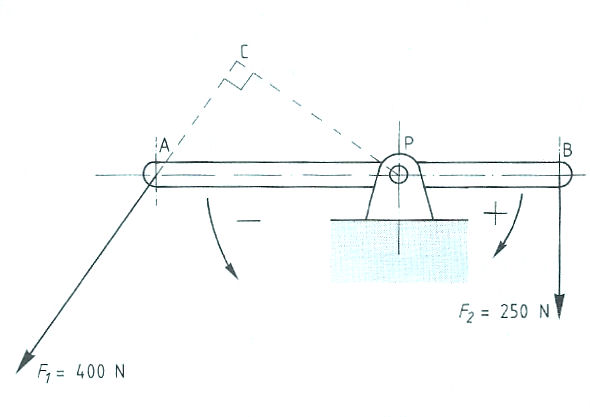
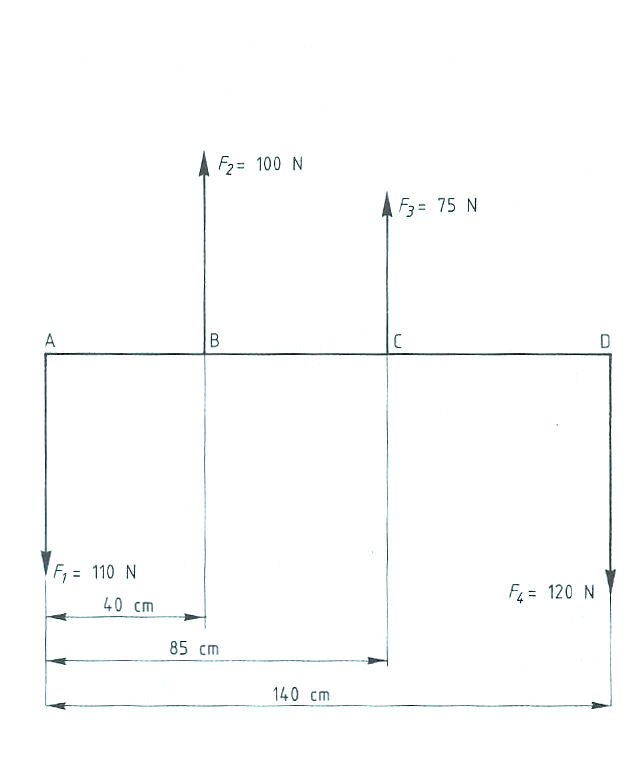
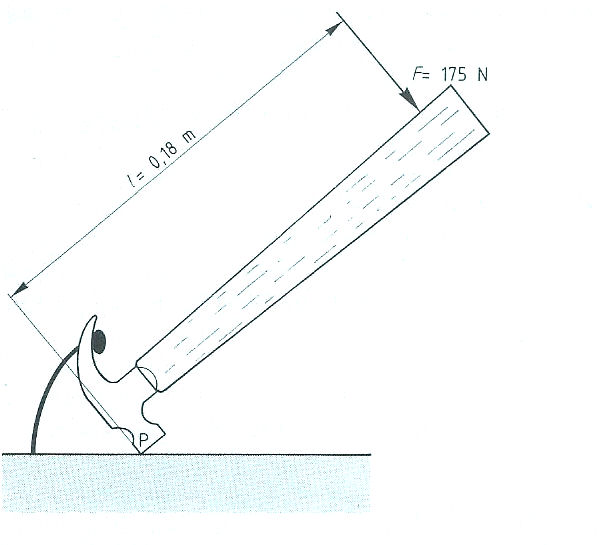
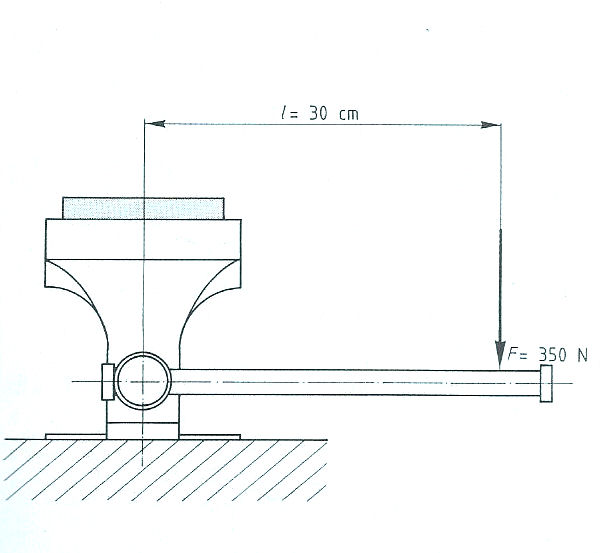
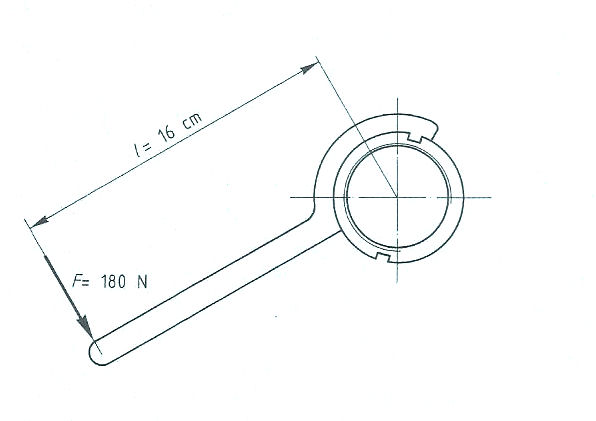
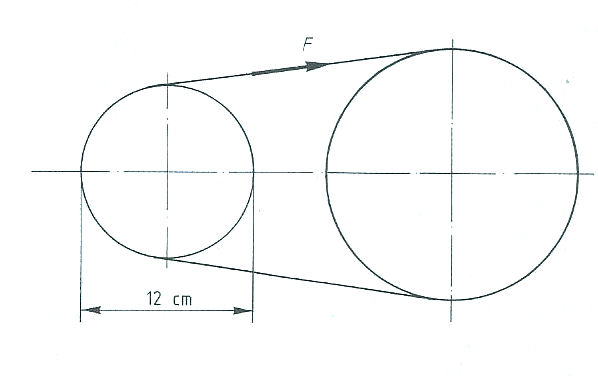
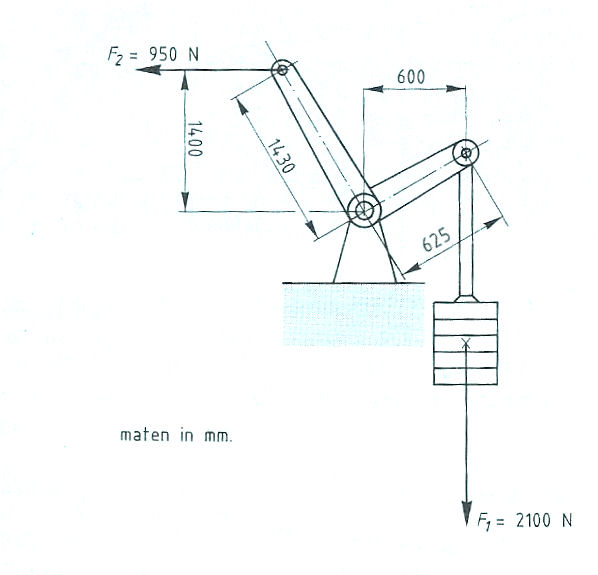
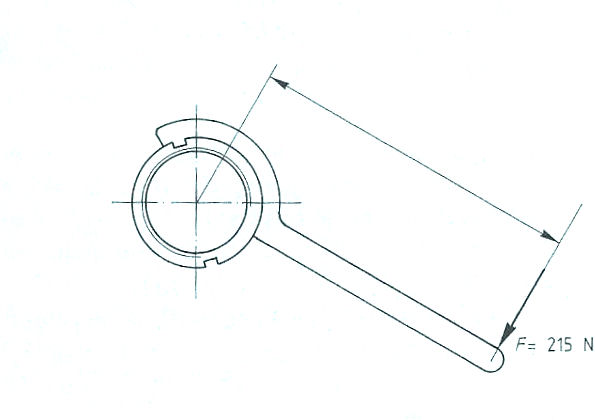
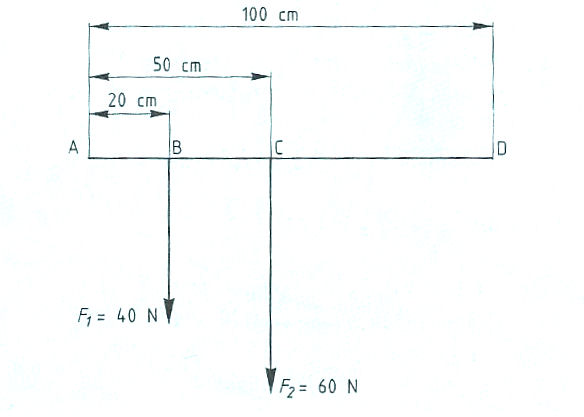
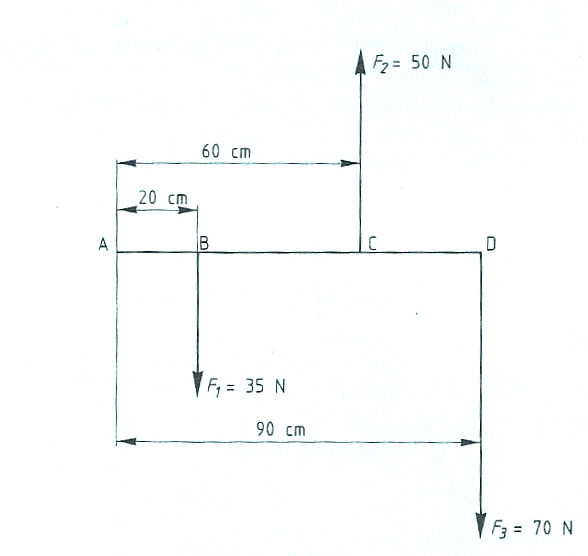
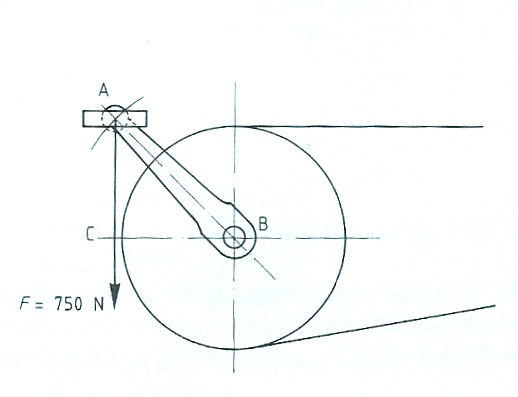
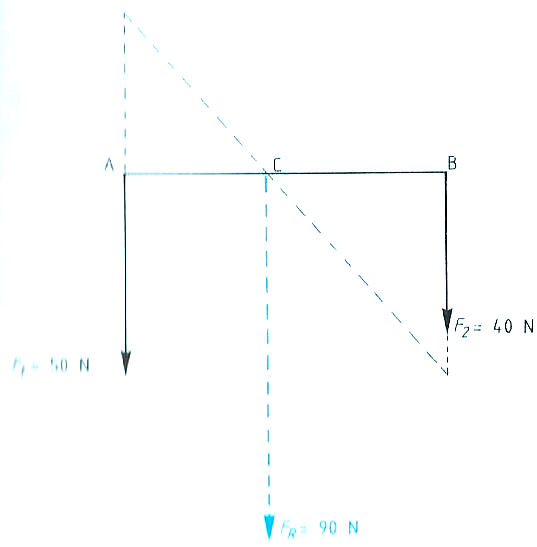
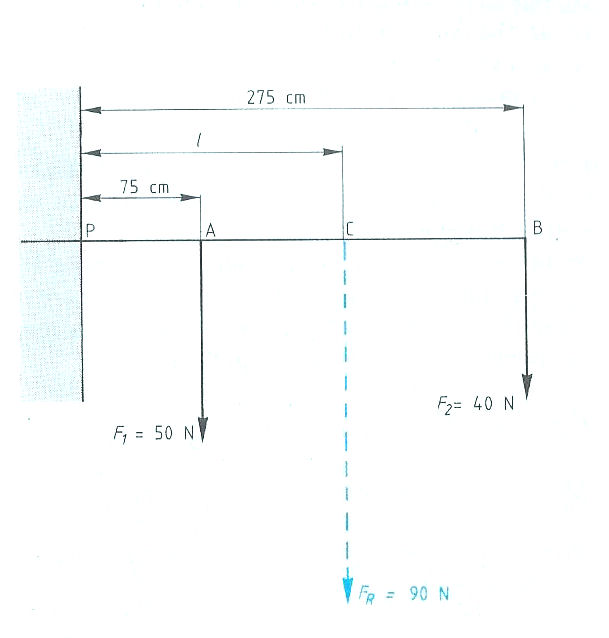

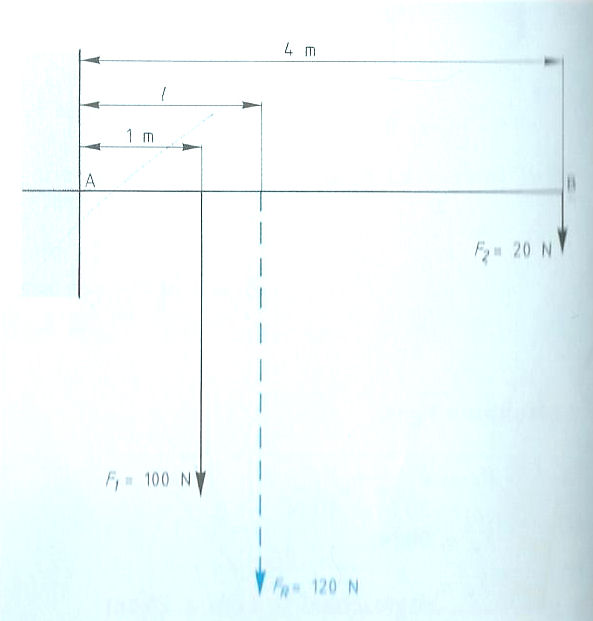
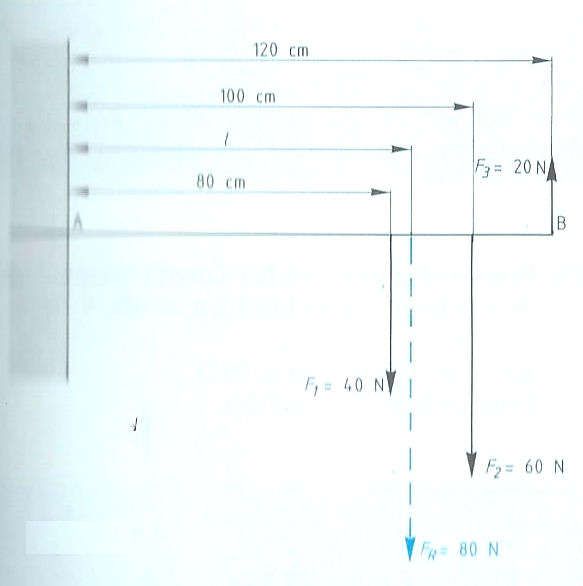
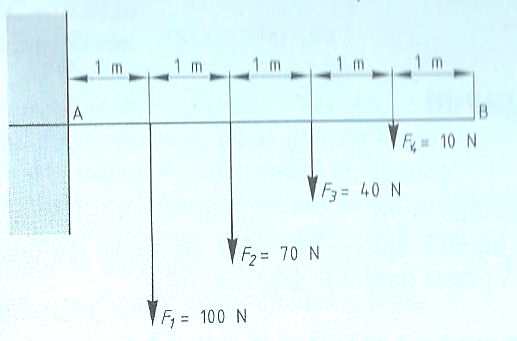
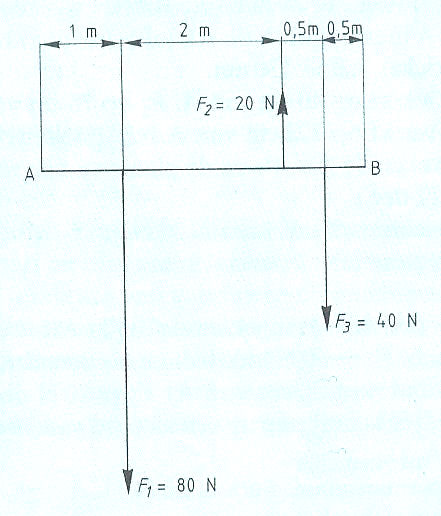
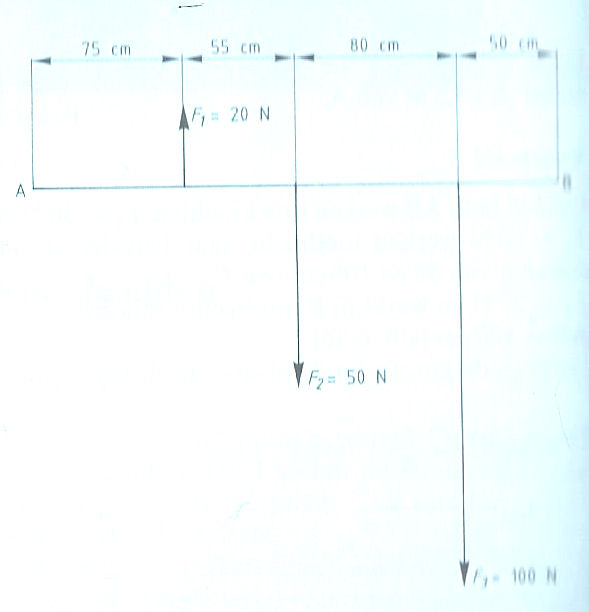
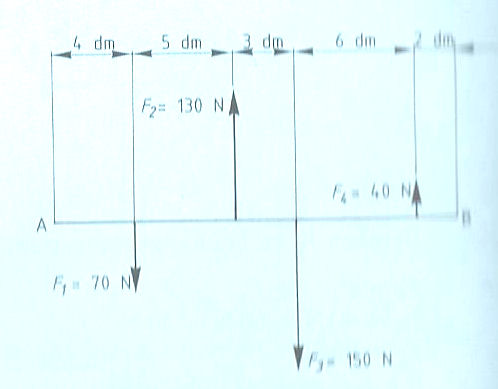
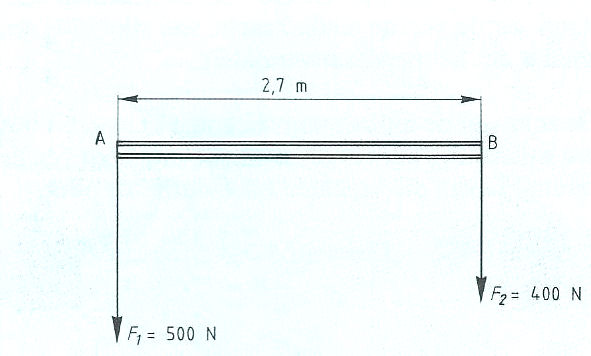
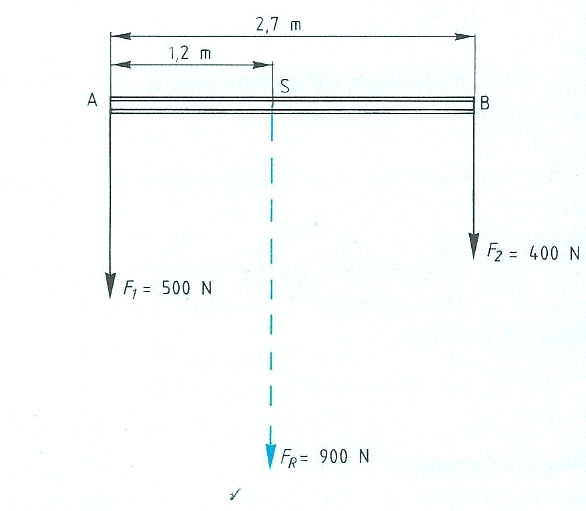
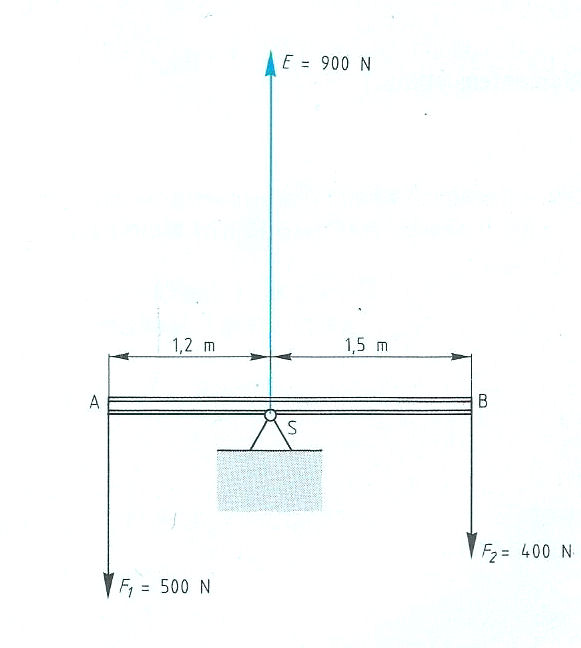
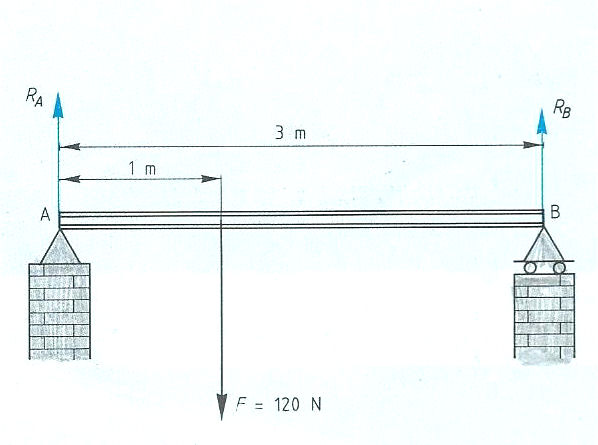
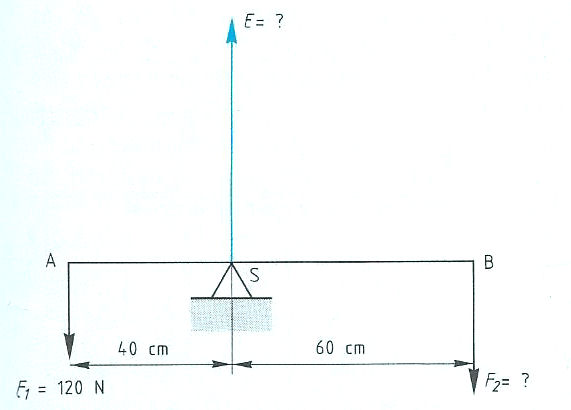
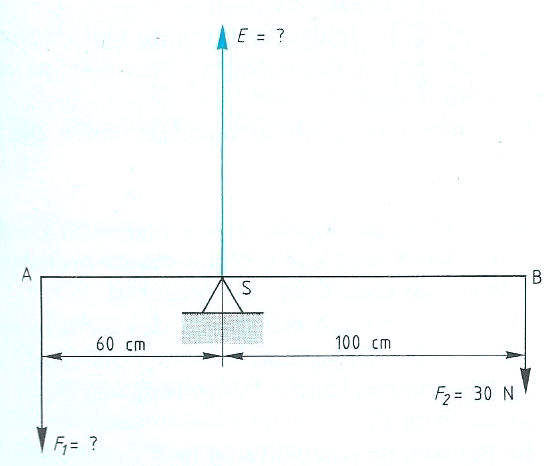
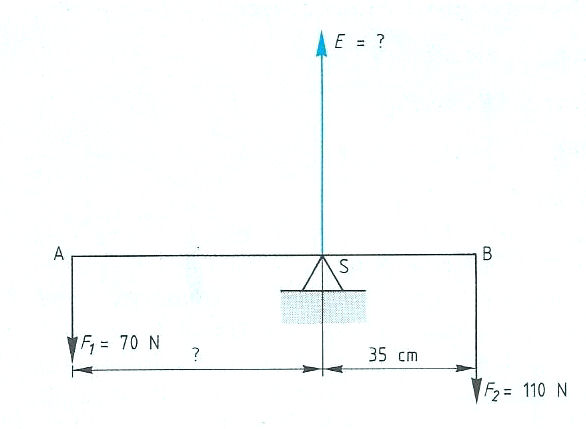
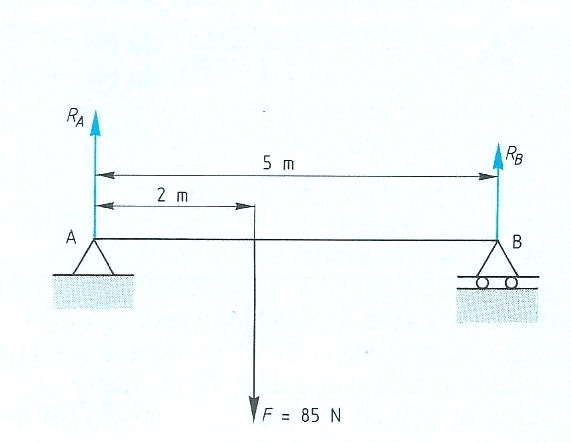
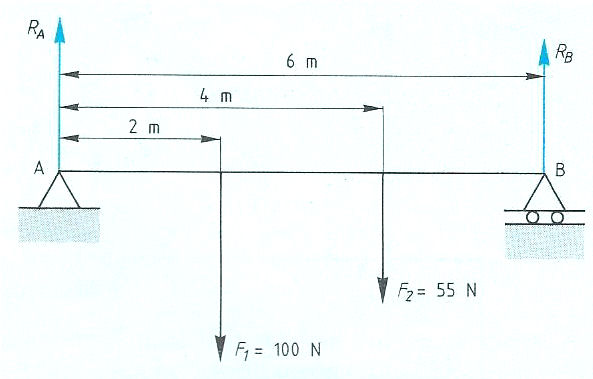
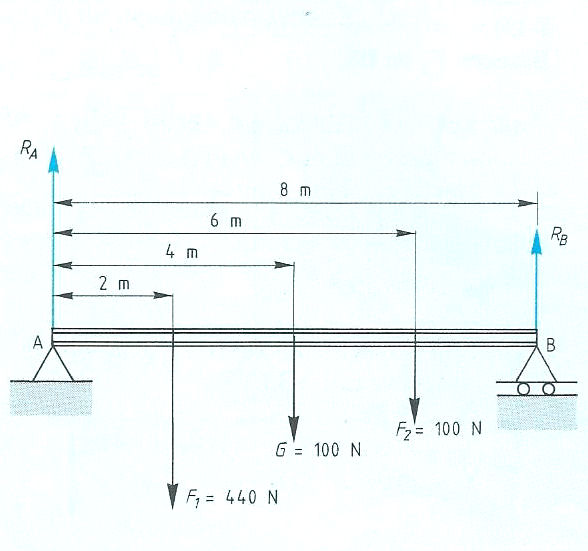
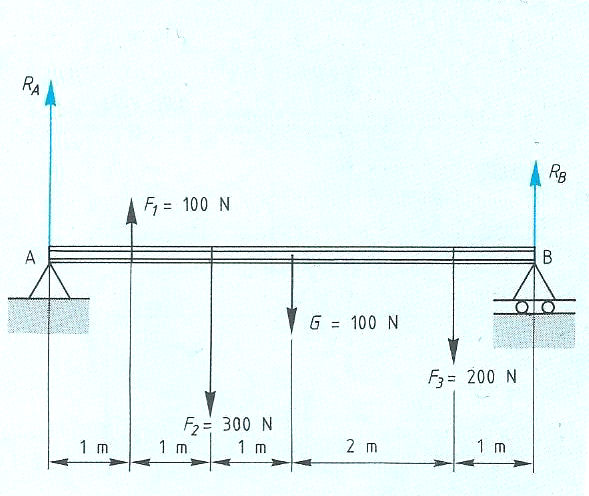
 Evenwichtsvoorwaarden met één steunpunt vinden toepassing bij:
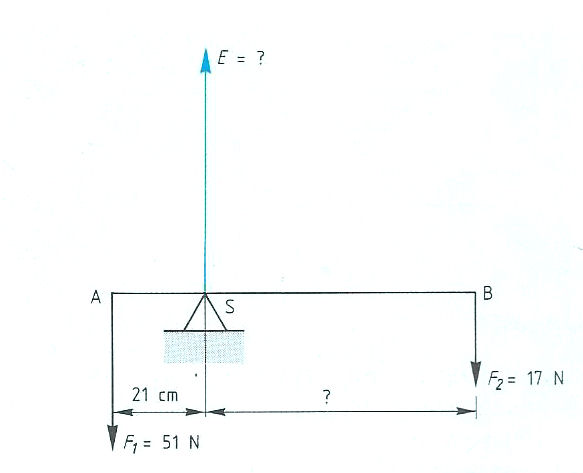
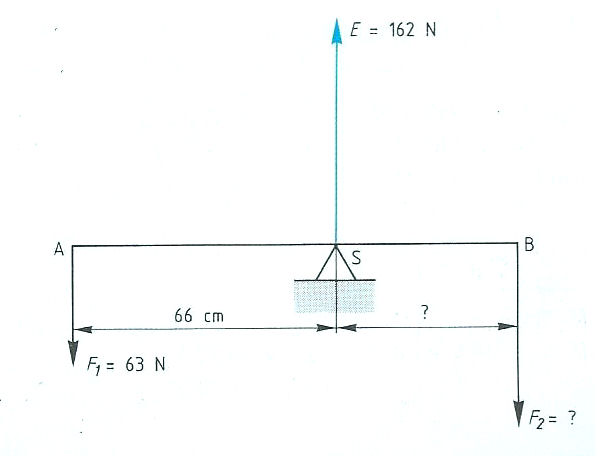
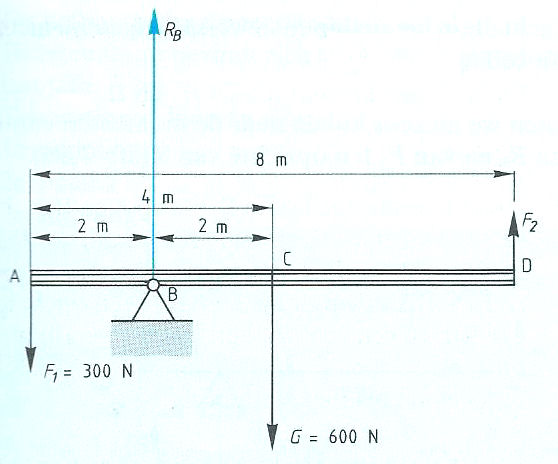
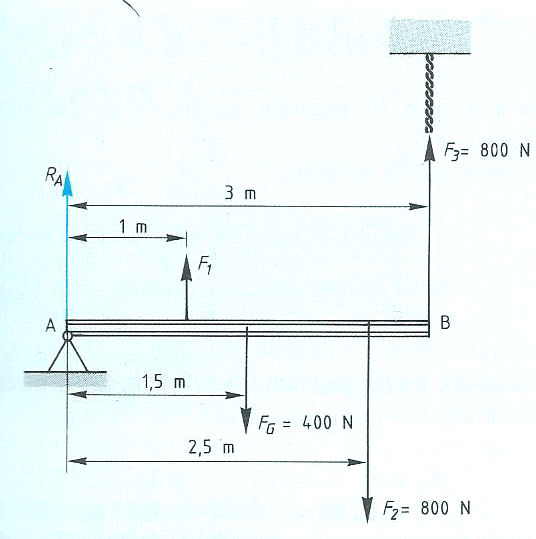
Evenwichtsvoorwaarden met één steunpunt vinden toepassing bij: Het is ook mogelijk dat het steunpunt zich niet in het midden, maar aan één van de uiteinden bevindt zoals:
Het is ook mogelijk dat het steunpunt zich niet in het midden, maar aan één van de uiteinden bevindt zoals:
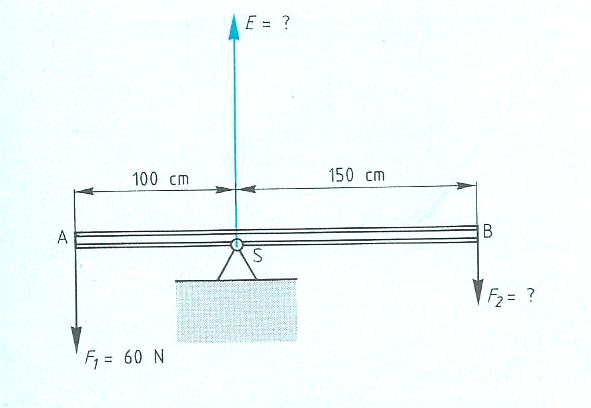
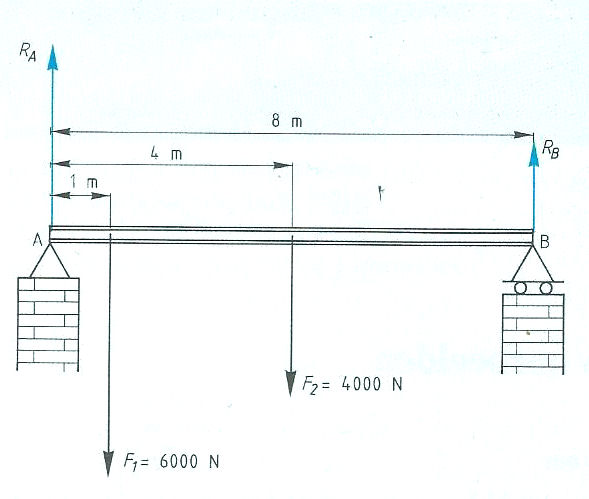
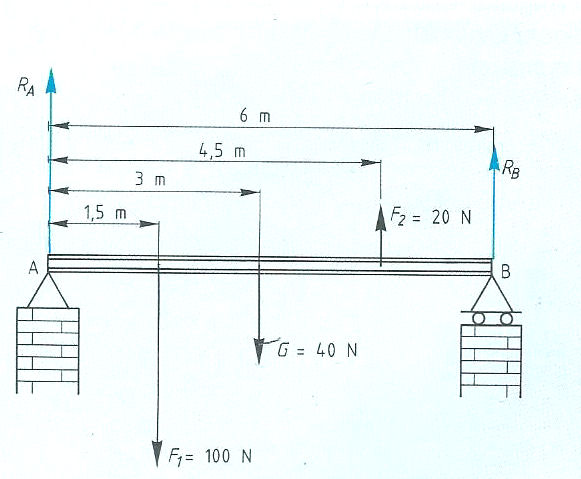
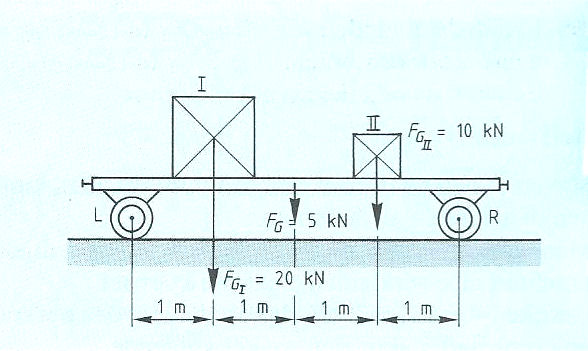

 Kinematica of bewegingsleer is een onderdeel van de klassieke mechanica en houdt zich bezig met beweging. Van bewegende lichamen worden de chemische en fysische eigenschappen, met uitzondering van de afmetingen, buiten beschouwing gelaten, evenals de erop werkende krachten.
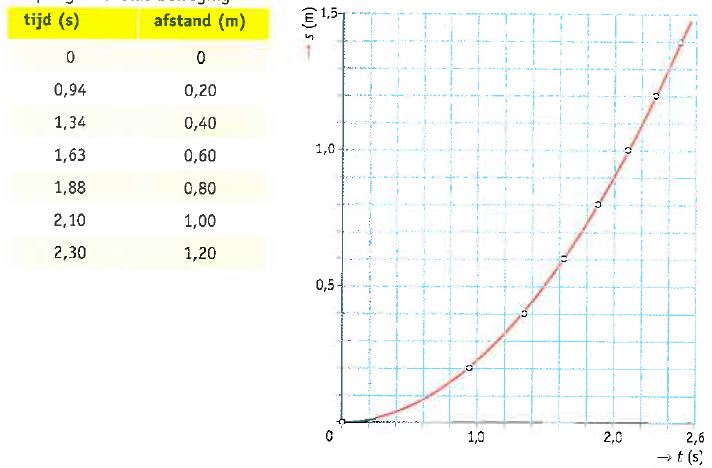
Kinematica of bewegingsleer is een onderdeel van de klassieke mechanica en houdt zich bezig met beweging. Van bewegende lichamen worden de chemische en fysische eigenschappen, met uitzondering van de afmetingen, buiten beschouwing gelaten, evenals de erop werkende krachten.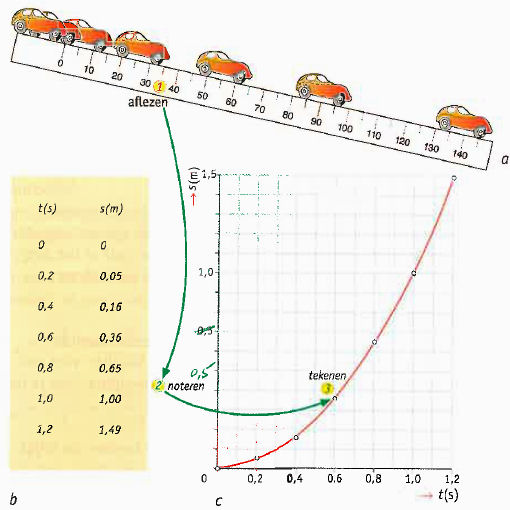 Gegevens verzamelen uit een stroboscopische foto, In de afbeelding hiernaast, zie je een schematische weergave van een stroboscopische foto. Om gegevens uit zo'n stroboscopische foto af te kunnen lezen, moet je twee dingen weten:
Gegevens verzamelen uit een stroboscopische foto, In de afbeelding hiernaast, zie je een schematische weergave van een stroboscopische foto. Om gegevens uit zo'n stroboscopische foto af te kunnen lezen, moet je twee dingen weten: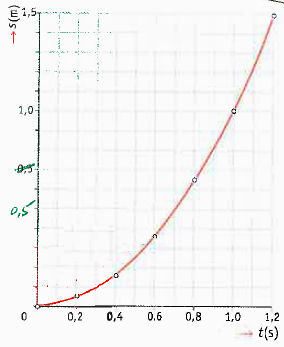 Je kunt de qeqevens uit een stroboscopische foto verwerken tot een (s,t)-diagram. Daarbij ga je als volgt te werk:
Je kunt de qeqevens uit een stroboscopische foto verwerken tot een (s,t)-diagram. Daarbij ga je als volgt te werk: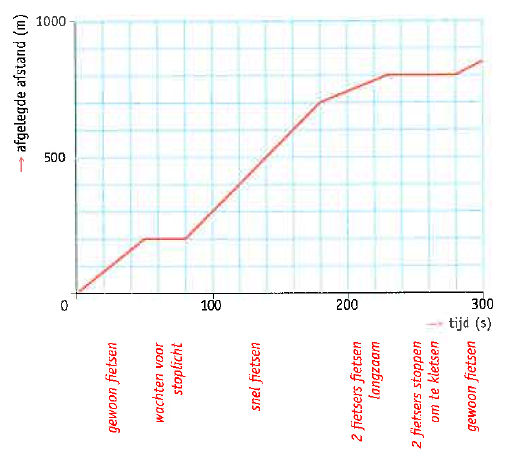 In dit geval kun je s en t aflezen uit het (s,t)-diagram. Als je s invult in meters en t in seconden, vind je de gemiddelde snelheid in m/s.
In dit geval kun je s en t aflezen uit het (s,t)-diagram. Als je s invult in meters en t in seconden, vind je de gemiddelde snelheid in m/s. Jenny Wolf schaatste op 11 december 2009 een wereldrecord op de 500 meter. Haar tussentijd na 100 meter was 10,19s, de eindtijd 37,00s.
Jenny Wolf schaatste op 11 december 2009 een wereldrecord op de 500 meter. Haar tussentijd na 100 meter was 10,19s, de eindtijd 37,00s.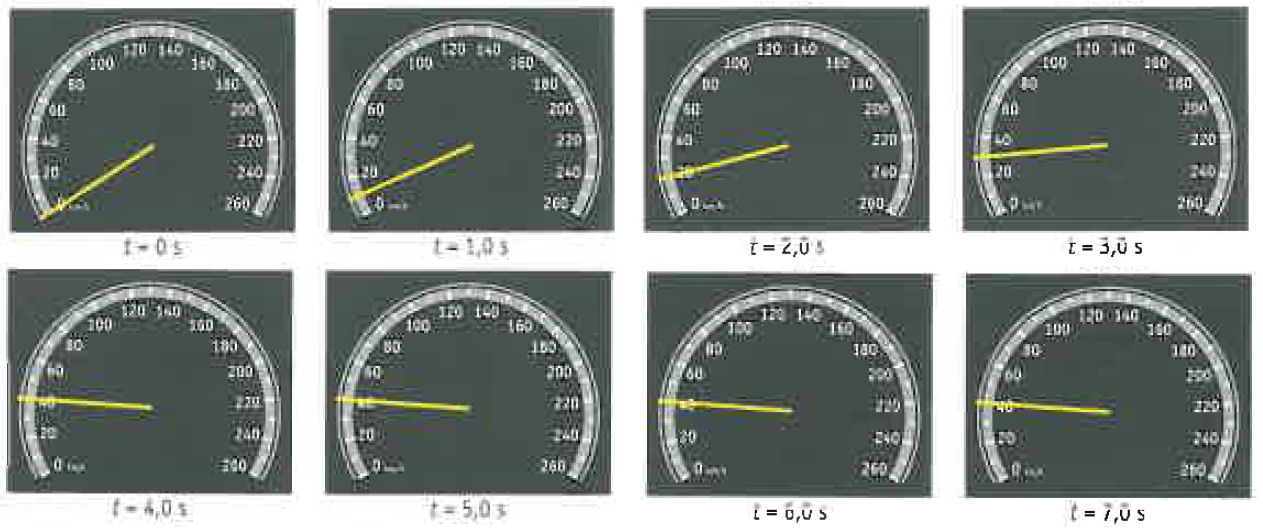
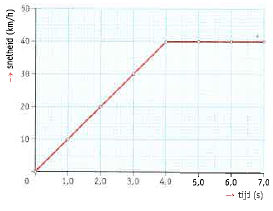 Met de bovenstaande gegevens kun je een (v,t)-diagram tekenen van de beweging. In de figuur hiernaast zie je hoe zo'n (v,t)-diagram eruitziet.
Met de bovenstaande gegevens kun je een (v,t)-diagram tekenen van de beweging. In de figuur hiernaast zie je hoe zo'n (v,t)-diagram eruitziet.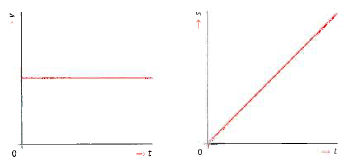

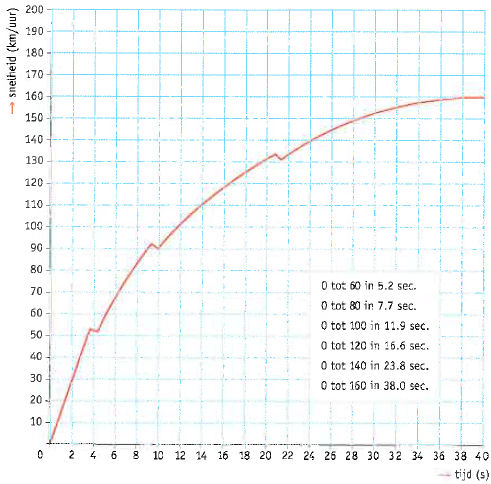 Versnelde bewegingen
Versnelde bewegingen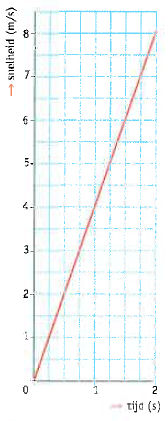 In de linker afbeelding is het begin van de beweging ’vergroot' weergegeven. Je ziet dat de snelheid in de eerste twee seconden gelijkmatig toeneemt. Na één seconde is de snelheid 4 m/s, na twee seconden 8 m/s. Er komt dus elke seconde 4 m/s bij. Zo'n beweging waarvan de snelheid gelijkmatig groter wordt, wordt een eenparige beweging genoemd.
In de linker afbeelding is het begin van de beweging ’vergroot' weergegeven. Je ziet dat de snelheid in de eerste twee seconden gelijkmatig toeneemt. Na één seconde is de snelheid 4 m/s, na twee seconden 8 m/s. Er komt dus elke seconde 4 m/s bij. Zo'n beweging waarvan de snelheid gelijkmatig groter wordt, wordt een eenparige beweging genoemd.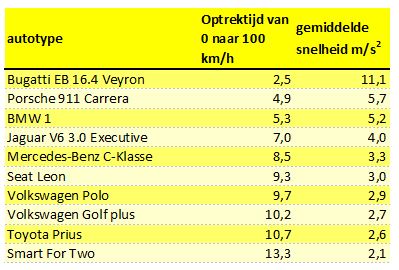 In autoblad en op internet vind je testrapporten van allerlei autotypes. In zo'n autotest kun je onder andere lezen hoe snel de geteste auto optrekt van 0 naar 100 km/h. Met deze gegevens kun je zelf berekenen hoe groot de gemiddelde versnelling tijdens het optrekken is.
In autoblad en op internet vind je testrapporten van allerlei autotypes. In zo'n autotest kun je onder andere lezen hoe snel de geteste auto optrekt van 0 naar 100 km/h. Met deze gegevens kun je zelf berekenen hoe groot de gemiddelde versnelling tijdens het optrekken is.
 Voorbeeld
Voorbeeld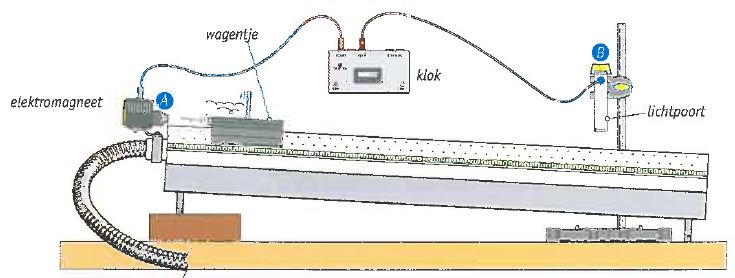
 De valbeweging
De valbeweging De tegenwerkende krachten verminderen
De tegenwerkende krachten verminderen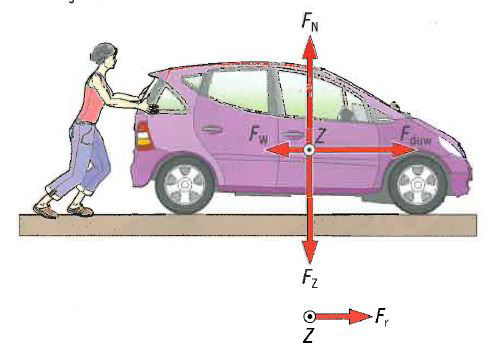 De nettokracht
De nettokracht

 De versnelling berekenen
De versnelling berekenen Voorbeeld
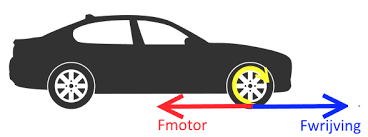
Voorbeeld Een automotor gebruikt de chemische energie in de benzine om de auto voort te stuwen. Als de benzine op is, levert de motor geen voortstuwende kracht meer. Door tanken, voorzie je de auto van nieuwe chemische energie.
Een automotor gebruikt de chemische energie in de benzine om de auto voort te stuwen. Als de benzine op is, levert de motor geen voortstuwende kracht meer. Door tanken, voorzie je de auto van nieuwe chemische energie. Newtonmeter en joule
Newtonmeter en joule Voorbeeld
Voorbeeld Voorbeeld
Voorbeeld De achtbaan
De achtbaan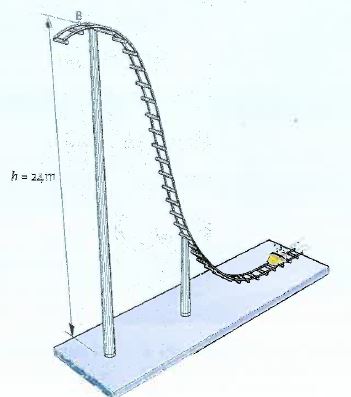 Voorbeeld
Voorbeeld 1 - Bewegingen in actiefilms
1 - Bewegingen in actiefilms 2 - Reisplanner
2 - Reisplanner 3 - Welke rem is het beste
3 - Welke rem is het beste 4 - Remmen in de regen
4 - Remmen in de regen De sterkteleer is de tak van de mechanica die de effecten bestudeert van spanning en vervorming in een vervormbaar lichaam dat wordt blootgesteld aan een uitwendige belasting.
De sterkteleer is de tak van de mechanica die de effecten bestudeert van spanning en vervorming in een vervormbaar lichaam dat wordt blootgesteld aan een uitwendige belasting. Galloping Gertie
Galloping Gertie
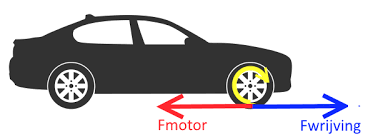 Dit zijn tegenovergestelde krachten op een materiaal die langs dezelfde werklijn op het materiaal werken.
Dit zijn tegenovergestelde krachten op een materiaal die langs dezelfde werklijn op het materiaal werken.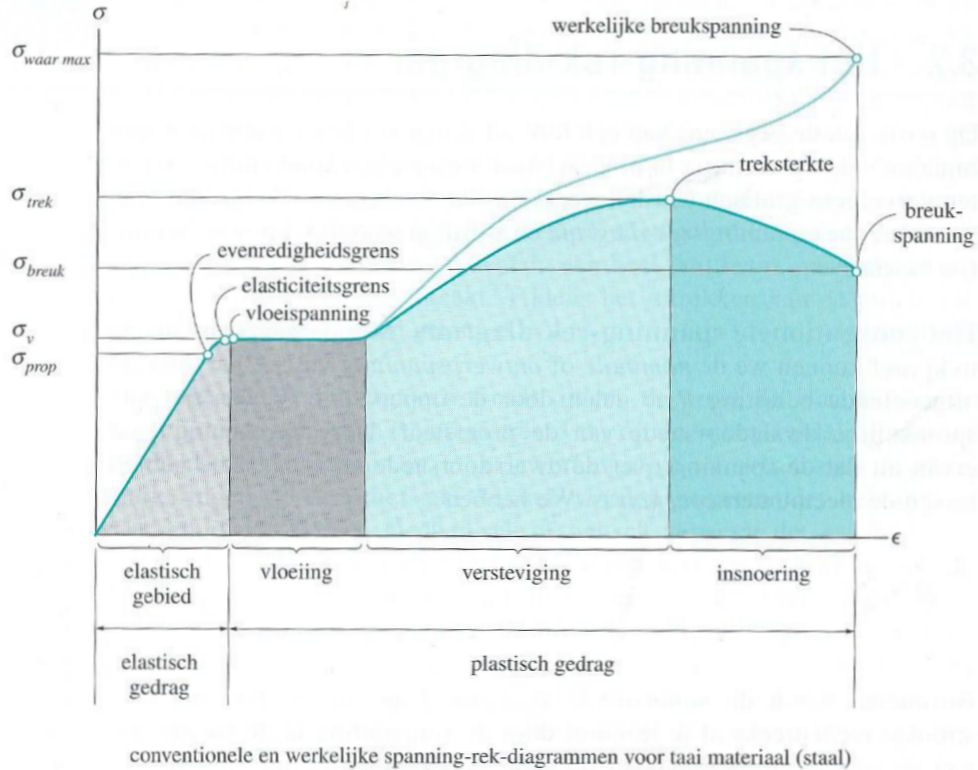 Meerdere soorten σ en
Meerdere soorten σ en 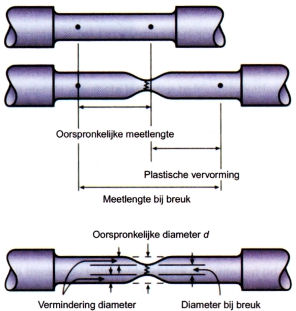 Komen we boven deze spanningdan gaat het materiaal eerst plastisch worden, het gaat van vorm veranderen. Dit veranderen gaat in verschillende fasen en de eerste is vloeien. Tijdens deze fase zal het materiaal minder vormvast worden, oftewel het gaat rekken.
Komen we boven deze spanningdan gaat het materiaal eerst plastisch worden, het gaat van vorm veranderen. Dit veranderen gaat in verschillende fasen en de eerste is vloeien. Tijdens deze fase zal het materiaal minder vormvast worden, oftewel het gaat rekken. Loodrecht op de trek- en druk krachten staat een afschuivingskracht. Ook deze kracht is net als de trek en druk afhankelijk van het oppervlak van het materiaal. En in het verlengde hiervan kunnen we ook vrijwel dezelfde formules gebruiken, alleen noemen we deze nu de schuifspanning en de glijdingshoek.
Loodrecht op de trek- en druk krachten staat een afschuivingskracht. Ook deze kracht is net als de trek en druk afhankelijk van het oppervlak van het materiaal. En in het verlengde hiervan kunnen we ook vrijwel dezelfde formules gebruiken, alleen noemen we deze nu de schuifspanning en de glijdingshoek.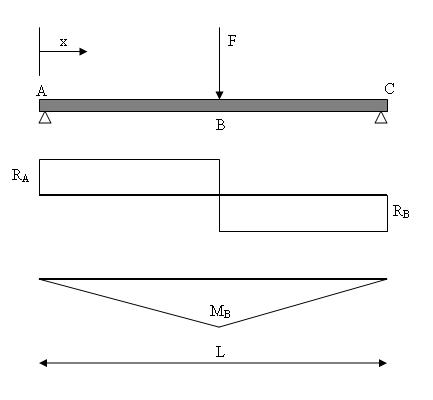 Buigbelasting
Buigbelasting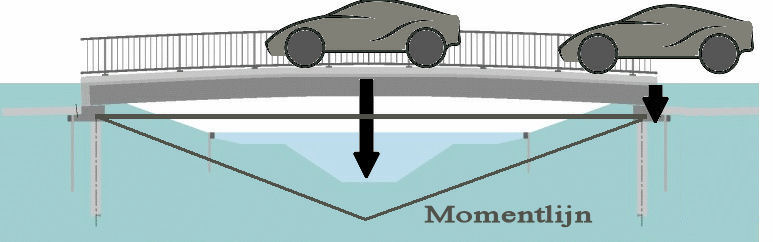
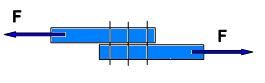 In deze situatie worden zowel de platen en de bouten belast. Voor de bouten:
In deze situatie worden zowel de platen en de bouten belast. Voor de bouten: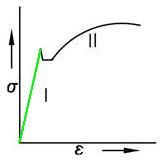 Hier vertegenwoordigt E de evenredigheidsconstante, die wordt aangeduid met de term elasticiteitsmodulus, ook wel Young's modulus genoemd - naar Thomas Young, die er in 1807 een uiteenzetting over publiceerde.
Hier vertegenwoordigt E de evenredigheidsconstante, die wordt aangeduid met de term elasticiteitsmodulus, ook wel Young's modulus genoemd - naar Thomas Young, die er in 1807 een uiteenzetting over publiceerde. Voorbeeld
Voorbeeld Een knik is een ongecontroleerde, plaatselijke scherpe verbuiging (een plastische vervorming) in een rechte of licht gekromde staaf of balk, onder verlies van stabiliteit, veroorzaakt door een uitwendige kracht. Bij een knik blijft, in tegenstelling tot bij een breuk, het verband (gedeeltelijk) intact.
Een knik is een ongecontroleerde, plaatselijke scherpe verbuiging (een plastische vervorming) in een rechte of licht gekromde staaf of balk, onder verlies van stabiliteit, veroorzaakt door een uitwendige kracht. Bij een knik blijft, in tegenstelling tot bij een breuk, het verband (gedeeltelijk) intact.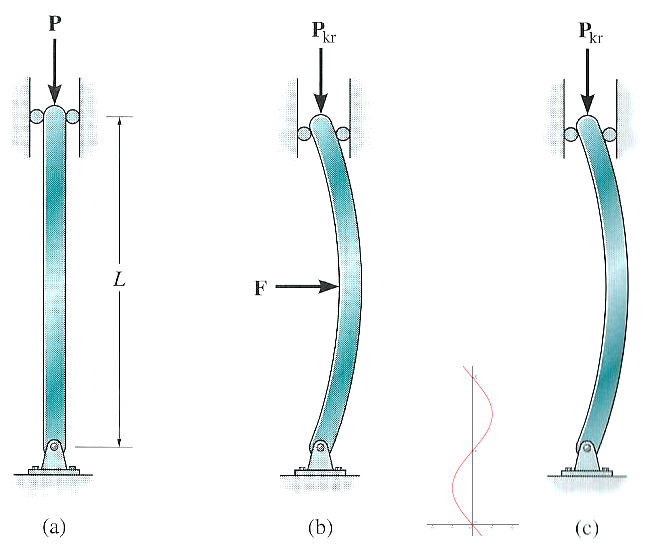

 Een mogelijkheid is dus ook om tussen kolommen die tot knik kunnen neigen, één of meer stalen trek/drukstaven aan te brengen om zo de "kniklengte" te verkorten. Hiermee vang je de denkbeeldige kracht 'F' uit afbeelding 'b' op en heeft deze geen invloed meer op de uitbuiging van de kolom. Nu de lengte dus korter is zal de sinus-vorm ook korter zijn en daarmee ook de uitwijking van deze sinus vorm. Een prettig voordeel hierbij is dat de Fkr dan ook weer omhoog gaat en de kolom dus meer gewicht kan hebben.
Een mogelijkheid is dus ook om tussen kolommen die tot knik kunnen neigen, één of meer stalen trek/drukstaven aan te brengen om zo de "kniklengte" te verkorten. Hiermee vang je de denkbeeldige kracht 'F' uit afbeelding 'b' op en heeft deze geen invloed meer op de uitbuiging van de kolom. Nu de lengte dus korter is zal de sinus-vorm ook korter zijn en daarmee ook de uitwijking van deze sinus vorm. Een prettig voordeel hierbij is dat de Fkr dan ook weer omhoog gaat en de kolom dus meer gewicht kan hebben.

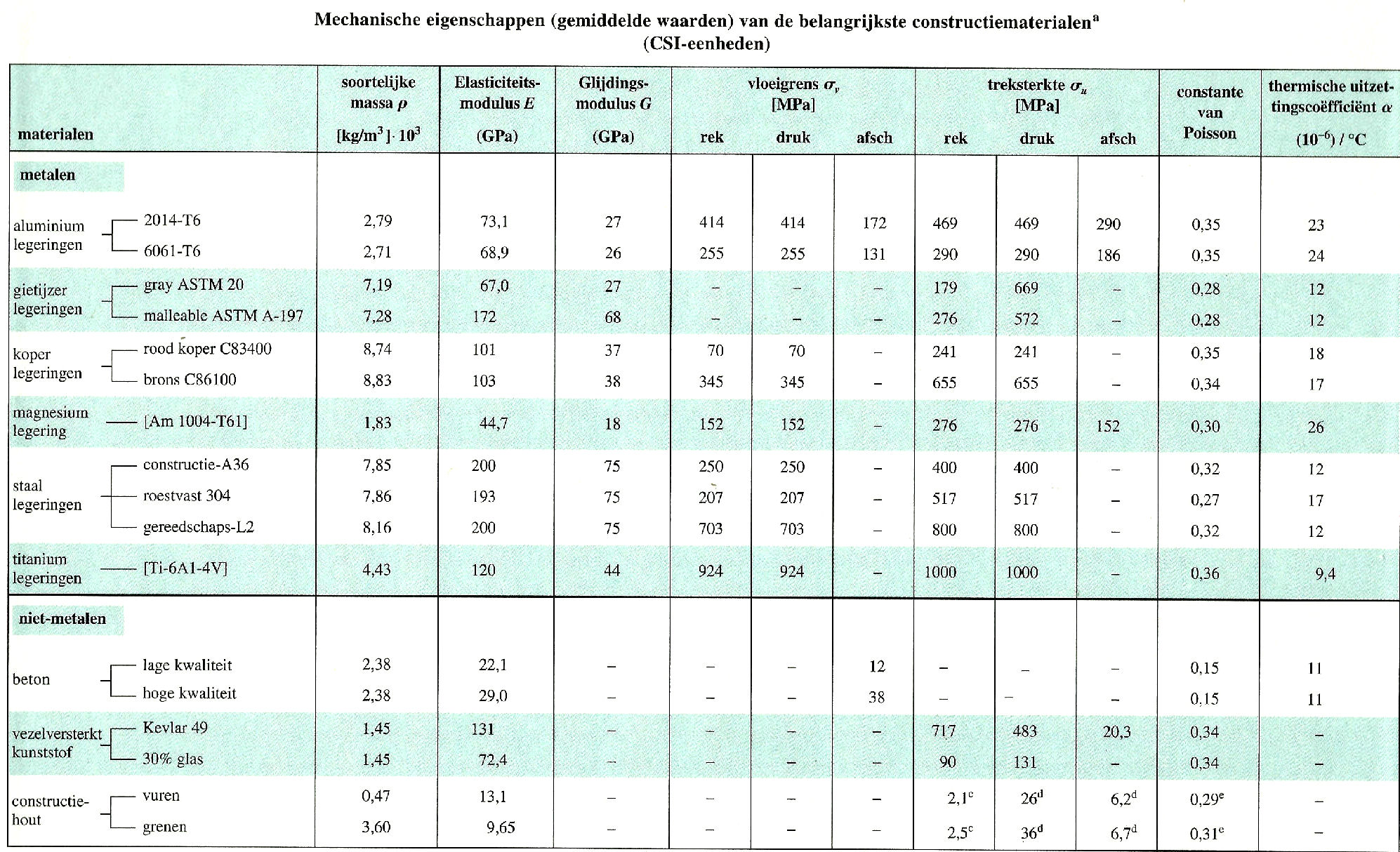
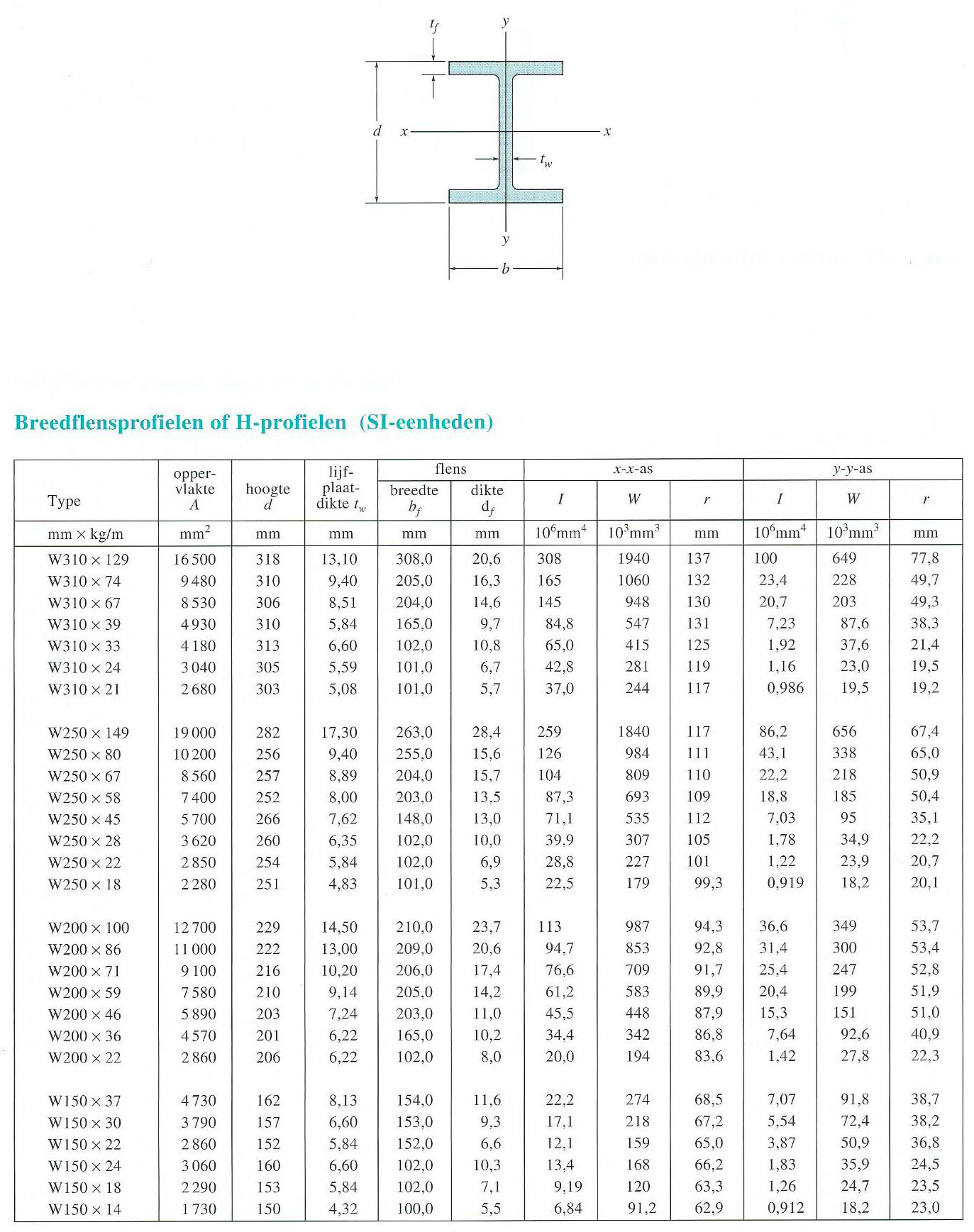
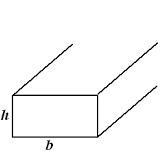
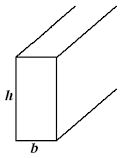
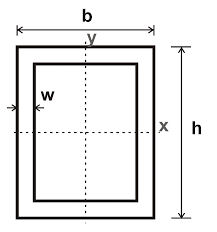 Stel je hebt een koker profiel met een hoogte van 500 mm en een breedte van 250 mm en een bijbehorende wanddiskte van 25 mm. Wat is nu het traagheidsmoment in mm4.
Stel je hebt een koker profiel met een hoogte van 500 mm en een breedte van 250 mm en een bijbehorende wanddiskte van 25 mm. Wat is nu het traagheidsmoment in mm4.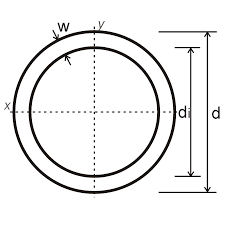

 Tegenwoordig staat het woord 'Energie' op allerlei manieren in de belangstelling. We moeten onze maatschappij 'groen maken' met als doel dat we onze huidige wereld door kunnen geven aan de volgende generatie. Hoe we dit doen? Door allerlei technieken te gebruiken die de ruime hoeveelheid 'groene energie' te ontginnen. Eigenlijk wil dit zeggen weer terug naar de een soort van mijnbouw maar nu op energie vormen die al jaren opgeslagen liggen in onze aarde of die dagelijks op ons afkomen via straling. We moeten dan denken aan waterkracht, zonne-energie of warmte vanuit de aarde.
Tegenwoordig staat het woord 'Energie' op allerlei manieren in de belangstelling. We moeten onze maatschappij 'groen maken' met als doel dat we onze huidige wereld door kunnen geven aan de volgende generatie. Hoe we dit doen? Door allerlei technieken te gebruiken die de ruime hoeveelheid 'groene energie' te ontginnen. Eigenlijk wil dit zeggen weer terug naar de een soort van mijnbouw maar nu op energie vormen die al jaren opgeslagen liggen in onze aarde of die dagelijks op ons afkomen via straling. We moeten dan denken aan waterkracht, zonne-energie of warmte vanuit de aarde.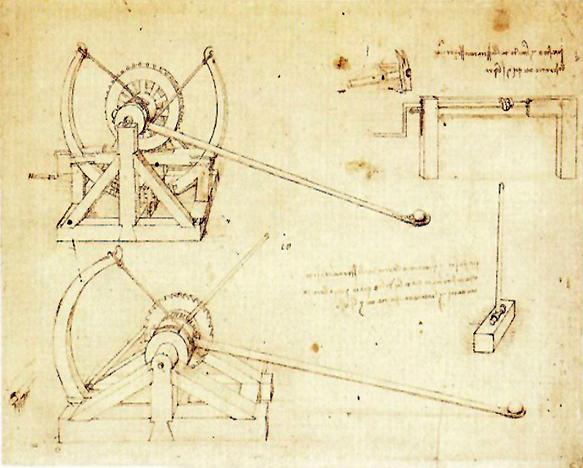 Het bovenstaande geeft aan waar de meeste mensen aan denken bij het woord Energieleer. Maar achter deze gedachten gaat een theorie schuil die al veel ouder is dan het gebruik van bijvoorbeeld olie. De oude Grieken, Leonarda da Vincil en later onder andere Newton onderzochten met hun kennis al naar systemen om energie om te zetten naar beweging. De meest oudste is wel het omzetten van windenergie naar een beweging. Deze beweging kan dan ingezet worden voor ellerlei toepassingen. Bij voorbeeld da Vinci heeft hier hele gedetaileerde tekeningen van gemaakt.
Het bovenstaande geeft aan waar de meeste mensen aan denken bij het woord Energieleer. Maar achter deze gedachten gaat een theorie schuil die al veel ouder is dan het gebruik van bijvoorbeeld olie. De oude Grieken, Leonarda da Vincil en later onder andere Newton onderzochten met hun kennis al naar systemen om energie om te zetten naar beweging. De meest oudste is wel het omzetten van windenergie naar een beweging. Deze beweging kan dan ingezet worden voor ellerlei toepassingen. Bij voorbeeld da Vinci heeft hier hele gedetaileerde tekeningen van gemaakt. Onder vermogen verstaan we de verrichte arbeid per tijdseenheid.
Onder vermogen verstaan we de verrichte arbeid per tijdseenheid. Een heimachine is ook een toepassing van potentiële energie. Is het heiblok eenmaal naar boven gebracht
Een heimachine is ook een toepassing van potentiële energie. Is het heiblok eenmaal naar boven gebracht Voorbeeld 4
Voorbeeld 4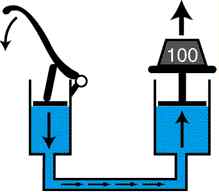 Hydrostatica beschrijft de toestand van vloeistoffen in een evenwichts toestand, aldus Wikipedia. Maar wat wordt hiermee dan bedoeld? Wanneer we de zin uit elkaar trekken dan vallen 3 woorden op: toestand, vloeistoffen en evenwicht. In de volgende paragrafen zullen deze drie woorden steeds weer terug komen. Even als 3 belangrijke wetten van 3 verschillende natuurkundigen.
Hydrostatica beschrijft de toestand van vloeistoffen in een evenwichts toestand, aldus Wikipedia. Maar wat wordt hiermee dan bedoeld? Wanneer we de zin uit elkaar trekken dan vallen 3 woorden op: toestand, vloeistoffen en evenwicht. In de volgende paragrafen zullen deze drie woorden steeds weer terug komen. Even als 3 belangrijke wetten van 3 verschillende natuurkundigen.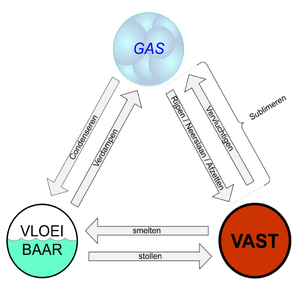 Maar zo kunnen we nog wel een paar voorbeelden verzinnen. Het eindresultaat is dat alle materialen dus 3 verschillende vormen kennen: Aggregatietoestanden.
Maar zo kunnen we nog wel een paar voorbeelden verzinnen. Het eindresultaat is dat alle materialen dus 3 verschillende vormen kennen: Aggregatietoestanden. Archimedes was een van de vele belangrijke Griekse wetenschappers die onze Aarde heeft grootgebracht. Veel van onze hedendaagse natuurkundige wetten berusten op deze oude beschaving. Onze schepen zouden niet kunnen varen zonder zijn ontdekking. Hierover is een leuk verhaal bekend.
Archimedes was een van de vele belangrijke Griekse wetenschappers die onze Aarde heeft grootgebracht. Veel van onze hedendaagse natuurkundige wetten berusten op deze oude beschaving. Onze schepen zouden niet kunnen varen zonder zijn ontdekking. Hierover is een leuk verhaal bekend.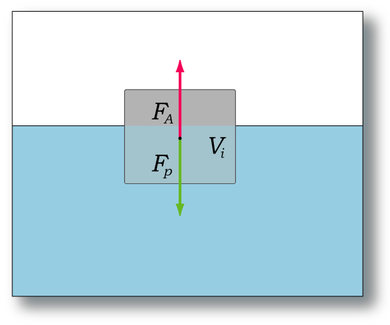 De wet van Archimedes zegt ons dat:
De wet van Archimedes zegt ons dat: Van de Franse wis- en natuurkundige Pascal is de volgende wet:
Van de Franse wis- en natuurkundige Pascal is de volgende wet: Druk
Druk PSI
PSI Alleen gebruiken ze andere eenheden dan wij binnen het SI stelsel. En daardoor krijg je dus ook andere getallen en dat kan best wel verwarrend zijn. Voor de fabrikanten omdat ze nu twee verschillende apparaten moeten maken en voor de gebruiker om het juiste apparaat te gaan gebruiken. De fabrikanten hebben het opgelost door de schalen voor de drkken te combineren tot één meter zodat zegeen 2 apparaten hoeven te maken. En de gebruiker is hier ook goed mee bediend want hij of zij leest gewoon de schaal af die bij het land hoort.
Alleen gebruiken ze andere eenheden dan wij binnen het SI stelsel. En daardoor krijg je dus ook andere getallen en dat kan best wel verwarrend zijn. Voor de fabrikanten omdat ze nu twee verschillende apparaten moeten maken en voor de gebruiker om het juiste apparaat te gaan gebruiken. De fabrikanten hebben het opgelost door de schalen voor de drkken te combineren tot één meter zodat zegeen 2 apparaten hoeven te maken. En de gebruiker is hier ook goed mee bediend want hij of zij leest gewoon de schaal af die bij het land hoort.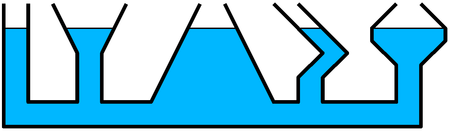 Wet van de communicerende vaten
Wet van de communicerende vaten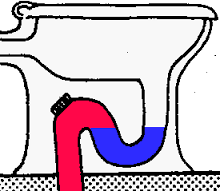 In de inleiding werd een toepassing van deze wet al genoemd in de vorm van een zwanehals. Deze zijn bedoeld als een stankafsluiter voor het riool. Wanneer je de WC doorspoeld dan ontstaat er een overdruk in het eerste vat en deze gaat zich verdelen over het andere vat totdat het weer stabiel is. Ondertussen heb je wel weer een schoon toilet.
In de inleiding werd een toepassing van deze wet al genoemd in de vorm van een zwanehals. Deze zijn bedoeld als een stankafsluiter voor het riool. Wanneer je de WC doorspoeld dan ontstaat er een overdruk in het eerste vat en deze gaat zich verdelen over het andere vat totdat het weer stabiel is. Ondertussen heb je wel weer een schoon toilet. Een andere mooie toepassing zijn de diverse watertorens die we in de stad vinden. Ook dit is een regelrechte toepassing van de wet van Pascal. Deze watertorens vinden we steeds minder in onze steden en worden veelal vervangen door pompen die op electriciteit werken. Maar deze 'oude' oplossingen zijn wel de 'groenste' voorziening in onze steden en ze worden nog steeds gebruikt.
Een andere mooie toepassing zijn de diverse watertorens die we in de stad vinden. Ook dit is een regelrechte toepassing van de wet van Pascal. Deze watertorens vinden we steeds minder in onze steden en worden veelal vervangen door pompen die op electriciteit werken. Maar deze 'oude' oplossingen zijn wel de 'groenste' voorziening in onze steden en ze worden nog steeds gebruikt. De algemene gaswet bij constante temperatuur wordt de wet van Boyle genoemd, en vernoemd naar de Ierse filosoof en scheikundige Robert Boyle (1627-1691). Deze wet beschrijft het gedrag van ideale gassen bij constante temperatuur:
De algemene gaswet bij constante temperatuur wordt de wet van Boyle genoemd, en vernoemd naar de Ierse filosoof en scheikundige Robert Boyle (1627-1691). Deze wet beschrijft het gedrag van ideale gassen bij constante temperatuur:

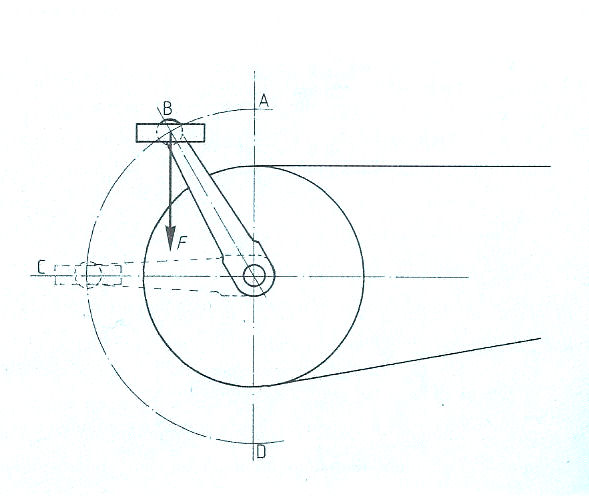
 Een hydromotor of hydraulische motor is een omzetter van hydraulische energie naar mechanische energie. De hydromotor wordt gebruikt in hydraulische en hydrostatische aandrijvingen, zoals het zwenksysteem van een kraan, maar ook de aandrijving van een zwaarlastvoertuig middels wielmotoren. Omzetters in hydrodynamische systemen noemt men turbines. Men onderscheidt onder andere:
Een hydromotor of hydraulische motor is een omzetter van hydraulische energie naar mechanische energie. De hydromotor wordt gebruikt in hydraulische en hydrostatische aandrijvingen, zoals het zwenksysteem van een kraan, maar ook de aandrijving van een zwaarlastvoertuig middels wielmotoren. Omzetters in hydrodynamische systemen noemt men turbines. Men onderscheidt onder andere: Er zijn veel toepassingen voor hydromotoren. Je kunt denken aan het verplaatsen van zware lasten, immers de hydrauliek vermenigvuldigd de uitgeoefend krachten veelvuldig en daardoor uitstekend geschikt voor zwaarwerk. Ook geven deze motoren de ontwerpers veel vrijheden bij het ontwerpen van machines. Er hoeven immers geen tandwielen of assen gebruikt te worden. Men kan eenvodig waar nodig een motor plaatsen.
Er zijn veel toepassingen voor hydromotoren. Je kunt denken aan het verplaatsen van zware lasten, immers de hydrauliek vermenigvuldigd de uitgeoefend krachten veelvuldig en daardoor uitstekend geschikt voor zwaarwerk. Ook geven deze motoren de ontwerpers veel vrijheden bij het ontwerpen van machines. Er hoeven immers geen tandwielen of assen gebruikt te worden. Men kan eenvodig waar nodig een motor plaatsen.
 Tot nu toe hebben we het over 'Electriciteit' gehad. Er zijn enkele basisbegrippen en wetten en toepassingen voorbij gekomen. Eigenlijk is 'Electriciteit' een verzamelbegrip voor allerlei situaties waarbij energie wordt omgezet danwel overgedragen. En dan ook nog eens hele specifieke ebergie, namelijk elektrische energie. Wanneer we een handboor gebruiken om een gaatje te boren dan gebruiken we lichamelijke energie die we omzetten in mechanische energie. En die valt niet onder de verzamelnaam electriciteit. De elektrische variant echter weer wel, want hier wordt elektrische energie omgezet in mechanische energie.
Tot nu toe hebben we het over 'Electriciteit' gehad. Er zijn enkele basisbegrippen en wetten en toepassingen voorbij gekomen. Eigenlijk is 'Electriciteit' een verzamelbegrip voor allerlei situaties waarbij energie wordt omgezet danwel overgedragen. En dan ook nog eens hele specifieke ebergie, namelijk elektrische energie. Wanneer we een handboor gebruiken om een gaatje te boren dan gebruiken we lichamelijke energie die we omzetten in mechanische energie. En die valt niet onder de verzamelnaam electriciteit. De elektrische variant echter weer wel, want hier wordt elektrische energie omgezet in mechanische energie. Door meerdere transistoren samen te brengen in één behuizing krijg je meer komplexe schakelingen. De Integrated Circuits (IC) kunnen tesamen een tijdklokje vormen of een micro-processor in je computer of zelfs een komplete mobiele telefoon gaan worden. De onderdelen hierin zijn dan zo kleing geworden dat grote stroomsterktes hier absoluut taboe zijn. Wat dan ook wel weer heel prettig is want dan kan de batterij ook lekker lang meegaan.
Door meerdere transistoren samen te brengen in één behuizing krijg je meer komplexe schakelingen. De Integrated Circuits (IC) kunnen tesamen een tijdklokje vormen of een micro-processor in je computer of zelfs een komplete mobiele telefoon gaan worden. De onderdelen hierin zijn dan zo kleing geworden dat grote stroomsterktes hier absoluut taboe zijn. Wat dan ook wel weer heel prettig is want dan kan de batterij ook lekker lang meegaan.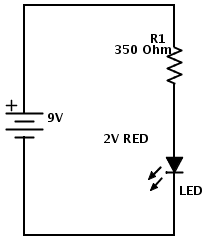 Serie schakeling
Serie schakeling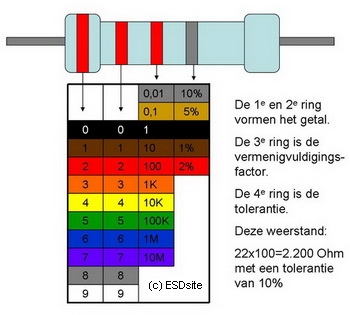 Je zult bij het bouwen of repareren van een project soms tegen het probleem aanlopen datj e een weerstand nodig hebt die je niet in huis hebt. Je kunt dan natuurlijk weer op de fiets naar de elektronicawinkel, of online de gewenste spullen bestellen en vervolgens twee dagen niets doen totdat de bestelling arriveert, maar dat kost veel tijd.
Je zult bij het bouwen of repareren van een project soms tegen het probleem aanlopen datj e een weerstand nodig hebt die je niet in huis hebt. Je kunt dan natuurlijk weer op de fiets naar de elektronicawinkel, of online de gewenste spullen bestellen en vervolgens twee dagen niets doen totdat de bestelling arriveert, maar dat kost veel tijd.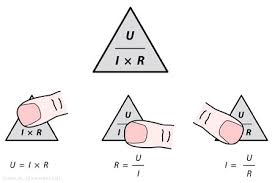 Even terughalen 'de wet van Ohm'
Even terughalen 'de wet van Ohm'
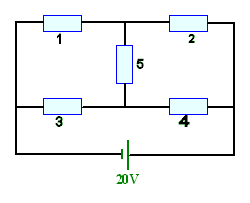 R1 = 10 ohm
R1 = 10 ohm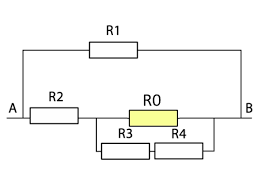 R0,3,4 = 10 ohm
R0,3,4 = 10 ohm

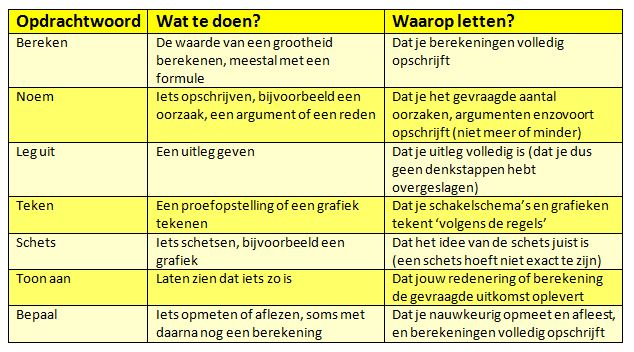



 Bij natuur- en scheikunde moet je af en toe berekeningen maken. Dit is een goede aanpak:
Bij natuur- en scheikunde moet je af en toe berekeningen maken. Dit is een goede aanpak:


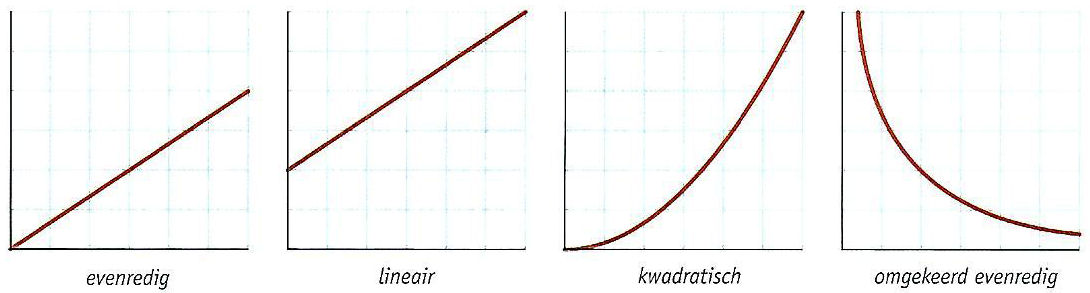
 Bij een
Bij een  Een aantal aanwijzingen:
Een aantal aanwijzingen: