De informatie hoort bij de Stercollecties wiskunde voor voor leerjaar 3 en 4 vmbo-b
van Stichting VO-content.
Een Stercollectie is leermateriaal dat voldoet aan de volgende kenmerken:
- kerndoelen of eindtermen dekkend.
- gebaseerd op de door de SLO ontwikkelde leerdoelspecificaties voor het vak wiskunde.
- onderdeel van een leerlijn.
- voor een vak, een afdeling, een leerjaar.
- leerboek en werkboekvervangend.
- digitaal met onderdelen op papier.
- beschikbaar via VO-cotent.nl en Wikiwijs.
- wordt onderhouden en geactualiseerd op basis van gebruikerservaringen.
Voor wiskunde vmbo zijn de volgende acht Stercollecties ontwikkeld:
- wiskunde vmbo b: leerjaar 1, 2, 3 en 4
- wiskunde vmbo kgt: leerjaar 1, 2, 3 en 4
De Stercollecties wiskunde draaien in een browser (IE8, Chrome, FireFox, Safari).
Docentenmateriaal
Exclusief voor leden van VO-content is er bij de Stercolelcties docentenmateriaal ontwikkeld.
Dat materiaal bestaaat uit:
- een docentenhandleiding
- extra opgaven (op papier)
- toetsen
Is uw school lid van VO-content, maar kunt u het docentenmateriaal niet vinden,
neem dan contact op met de helpdesk: http://www.vo-content.nl/contact/helpdesk/
Ontwikkelproces en kwaliteitszorgsysteem
Voor de ontwikkeling van de Stercollecties wiskunde maakt StudioVO gebruik van ervaren docenten en redacteurs. Samen met de SLO is er voor de Stercollecties een kwaliteitszorgsysteem ontwikkeld. Dit systeem bestaat uit drie onderdelen: de oorsprong van het leermateriaal, het gebruik van het leermateriaal en de correctheid van het materiaal.
Feedback, vragen of opmerkingen:
We willen u graag nadrukkelijk wijzen op de mogelijkheid om uw bevindingen, wensen of verbetersuggesties aan ons door te geven. Wij zullen waar mogelijk gebruik maken van deze reacties om het materiaal verder te verbeteren en waar nodig te corrigeren.
Ga naar http://www.vo-content.nl/contact/helpdesk/ met opmerkingen, feedback en/of vragen over de Stercollecties wiskunde.
Thema's leerjaar 4
Voor leerjaar 4 zijn in het totaal 7 thema's beschikbaar.
Een kubus, balk, bol, piramide, prisma, allemaal voorbeelden van ruimtelijke figuren. In dit thema staan deze ruimtelijke figuren centraal.
Je bekijkt van een aantal bekende figuren hoe ze er uitzien. Je gaat aan de slag met uitslagen en aanzichten. En je leert hoe je de inhoud van een balk kunt uitrekenen en hoe je inhoudsmaten kunt omrekenen.
Het thema ruitmtelijke figuren bestaat uit de volgende drie pragrafen:
Ruitmelijke figuren
Uitslag en aanzicht
Inhoud
1 Ruimtelijke figuren
Vlakke en ruimtelijke figuren
Bekijk eerst dit filmpje hieronder.
Opgave 1:
Opgave 2:
Maak de tabel hieronder af
Figuur
Vlak
Ruimtelijk
Naam Figuur
A
B
C
D
E
F
G
H
I
J
K
L
M
Hoekpunten, grensvlakken en ribben.
Bekijk deze filmpjes hieronder
Bestudeer de kennisbank hieronder.
Opgave 3:
In de kennisbankjes staat een piramide die bestaat uit driehoeken en een vierkant.
Er kan ook een piramide gemaakt worden met alleen maar driehoeken. Hiernaast zie je zo een piramide.
Beantwoord de volgende vragen over deze piramide
a) Hoeveel platte grensvlakken heeft deze piramide?
b) Hoeveel ribben heeft deze piramide?
c) Hoeveel hoekpunten heeft deze piramide?
Opgave 4:
Hieronder staat een ruimtefiguur dat is opgebouwd uit twee ruimtefiguren die we kennen.
Beantwoord onderstaande vragen over dit ruimtefiguur
a) Uit welke twee bekende ruimte figuren herken je?
b) Hoeveel grensvlakken heeft dit figuur?
c)Hoeveel ribben heeft dit figuur?
d) Hoeveel hoekpunten heeft dit figuur?
Opgave 5:
Teken de tabel over in je schrift en vul hem in.
Aantal platte grensvlakken
Aantal gebogen grensvlakken
Aantal hoekpunten
Aantal ribben
Kubus
Piramide (met vierkant)
5
Cilinder
Kegel
Bol
Balk
Opgave 6:
Opgvae 7:
Je ziet balk ABCD.EFGH.
a) In de bovenste figuur zijn 4 ribben aangegeven die evenwijdig lopen. Hoe herken je deze?
b) Schrijf de namen van deze ribben op.
c) Het voorvlak en het achtervlak zijn even groot. Welke twee vlakken zijn dat?
d) Welke ribben zijn even lang? Schrijf al je antwoorden op.
Opgave 8:
Hieronder zie je een lucifersdoosje
Het heeft de vorm van een balk ABCD.EFGH.
AB = 3 cm, BC = 4 en AE = 1
.
a) Welke ribben zijn gelijk aan ribbe AB?
b) Welke ribben zijn allemaal 3 cm lang?
c) Welk grensvlak is gelijk aan grensvlak ABFE?
d) Welke vorm hebben alle grensvlakken?
Opgave 9:
Opgave 10:
Bekijk de balk ABCD·EFGH hieronder.
In de balk zie je diagonaalvlak ABGH getekend.
Je ziet ook een lichaamsdiagonaal BH getekend.
a) Hoeveel verschillende diagonaalvlakken heeft balk ABCD·EFGH?
Schrijf ze allemaal op.
b) Volgens Yvonne hebben alle diagonaalvlakken dezelfde vorm en zijn ze even groot. Heeft Yvonne gelijk?
c) Hoeveel verschillende lichaamsdiagonalen heeft balk ABCD·EFGH?
Schrijf ze allemaal op.
d) Volgens Yvonne zijn alle lichaamsdiagonalen even lang. Heeft Yvonne gelijk?
Opgave 11:
2 Uitslag en aanzicht
kennisbank uitslagen ruimtefiguren
Uitslagen - Voorbeeld 1
Je ziet hieronder een uitslag van een dobbelsteen.
In de uitslag zijn de ogen getekend.
Ga na:
Als de 2 boven ligt, ligt de 5 onder.
Als de 1 boven ligt, ligt de 6 onder.
Als de 3 boven ligt, ligt de 4 onder.
Het aantal ogen van de bovenkant en de onderkant is opgeteld altijd 7.
Hier zie je een bouwplaat van een raceauto.
Een bouwplaat is een soort uitslag.
Toch zijn er wel verschillen.
Een bouwplaat heeft vaak plakrandjes.
Een bouwplaat kan uit losse stukken bestaan.
Bekijk dit filmpje
Opgave 1:
Hieronder zie je een dobbelsteen.
.
Voor een dobbelsteen geldt dat de som van de ogen van de onderkant en bovenkant altijd 7 is. Dus als de 6 boven ligt, ligt de 1 onder.
a) Teken minimaal drie echt verschillende uitslagen van de dobbelsteen.
Klaar?
b) Vergelijk jouw uitslagen met die van een klasgenoot.
Hebben jullie dezelfde uitslagen of juist verschillende?
Opgave 2:
Hieronder zie je twee uitslagen van kubussen.
a) Zet bij elke uitslag of je er een kubus van kunt maken.
Opgave 3:
Hieronder zie je een lucifersdoosje.
Het is een balk ABCD.EFGH met AB = 4 cm, BC = 3 cm en AE = 1 cm.
a) Teken eerst het luciferdoosje ( balk) met de juiste maten.
b) Maak de uitslag van balk ABCD.EFGH in je schrift.
Opgave 4:
Hier zie je een kubus die voor de helft is geverfd.
a) Teken er een uitslag van op het werkblad. De ribben zijn 3 cm.
Opgave 5:
Wat is het verschil tussen een uitslag en een bouwplaat?
Opgave 6:
Hier zie je drie bouwplaten voor een frisdrankverpakking.
a) Welke is fout.
b) Zo'n frisdrankverpakking is eigenlijk een balk.
De hoogte is 8 cm, de lengte 4 cm en de breedte 3 cm.
Teken een uitslag van zo'n balk op het werkblad.
Opgave 7:
Hieronder zie je een halve kubus. Naast de halve kubus zie je het begin van de een uitslag van de halve kubus.
Neem het begin van de uitslag over en maak de uitslag af.
a) Zet de letters op de juiste plaats in de uitslag.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
In een eerder thema heb je al veel met procenten gerekend. In dit thema staat opnieuw het rekenen met procenten centraal.
Dit rekenthema bestaat uit de volgende drie paragrafen:
Procenten: herhaling
Procenten: erbij en eraf
Nog meer procenten
1 Procenten - herhaling
kennisbank procenten
Opgave 1:
Reken uit ( gebruik manier 1)
a) 6% van 250=….......
b) 12% van 250=…......
c) 25% van 250=….....
d) 45% van 250=…......
Opgave 2:
Een klas van 30 leerlingen heeft een proefwerk wiskunde gemaakt.
20% van de leerlingen heeft een onvoldoende gehaald.
a) Hoeveel leerlingen zijn dat?
Opgave 3:
Bekijk het cirkeldiagram.
Je ziet hoe de leerlingen van het Hoge Zand college naar school komen. ( gebruik manier 1)
Op 'Het Hoge Zand' zitten in totaal 750 leerlingen. ( gebruik manier 1)
.
a) Hoeveel leerlingen komen er op de fiets naar school?
b) Hoeveel leerlingen komen er met de bus naar school?
Opgave 4:
Lieke spaart voor een auto. Ze besluit goed te gaan sparen.
Er staat nu al €7.000 op haar spaarrekening. Ze krijgt hier 0,8% rente over.
a) Hoeveel staat er na één jaar op haar spaarrekening?
b) Hoeveel staat er na twee jaar op haar spaarrekening?
Kennisbank hoeveel procent is het ?
Opgave 5:
Je krijgt €25,−zakgeld per maand.
Daarvan geef je €15,− uit aan beltegoed.
a) Hoeveel procent is dat?
Opgave 6:
In klas 3B zitten 28 leerlingen.
Voor een proefwerk wiskunde hadden 11 leerlingen een onvoldoende.
a) Hoeveel procent van de leerlingen had een onvoldoende?
Rond je antwoord af op twee cijfers achter de komma.
Opgave 7:
Isabel heeft € 150,− voor haar verjaardag gekregen. Van dat geld koopt ze een nieuwe broek van € 97,50.
De rest van het geld zet ze op haar spaarrekening.
a) Hoeveel procent van het geld zet ze op de spaarrekening?
Opgave 8:
In de tabel en in het cirkeldiagram zie je het bestedingspatroon van de familie Satir.
Neem de tabel over en vul de ontbrekende getallen in.
Opgave 9:
Op een opleiding zijn 724 van de 1 364 studenten meisjes.
a) Hoeveel procent van de studenten ongeveer zijn jongens?
Opgave 10:
Op basisschool De Kameleon bestaat 45% van de kinderen uit meisjes. Dit komt overeen met 180 kinderen.
a) Hoeveel kinderen zitten er in totaal op basisschool De Kameleon?
Opgave 11:
2 Erbij - eraf
Kennisbank procenten erbij
Opgave 1:
Een televisietoestel van € 650 wordt 8% duurder.
a) Bereken de nieuwe prijs.
Opgave 2:
Alicia heeft € 375 op een spaarrekening. De bank geeft 5% rente per jaar.
a) Hoeveel heeft Alicia op haar spaarrekening staan als er na één jaar rente wordt bijgeschreven?
Opgave 3:
Op 1 januari 2011 heeft Peter € 1500,- op een spaarrekening gestort. De bank geeft 6% rente op de spaarrekening.
De bank betaalt op 1 januari 2012 voor het eerst rente uit. Peter stort geen extra geld en heeft ook geen geld van de rekening opgenomen.
a) Hoeveel euro staat er op 1 januari 2012 op de rekening?
Kennisbank procenten eraf
Opgave 4:
In 2010 was de winst van een rijwielhandelaar € 65.000,-
In 2011 was zijn winst 2% lager.
a) Hoeveel was de winst in 2011 ?
Opgave 5:
In 2012 zijn er 2 miljoen Nederlanders naar Duitsland op vakantie geweest. In 2011 waren dat er 10% minder.
a) Hoeveel Nederlanders zijn er in 2011 naar Duitsland op vakantie geweest?
Opgave 6:
Met een kortingskaart reis je met 33 % korting op een entreekaartje voor de dierentuin.
Een kaartje kost normaal € 24,00.
a) Hoeveel moet je nu betalen aan entree?
Kennisbank procentuele toename:
Opgave 7:
Door een slechte oogst is de prijs van een kilo appels gestegen van € 1,99 naar € 2,29.
a) Met welk bedrag is de prijs gestegen?
b) Met hoeveel procent is de prijs gestegen?
Opgave 8:
Gerard zet een jaar lang € 400 op een spaarrekening.
Na dat jaar keert de bank rente uit. Op de rekening staat dan € 410.
a) Welk bedrag heeft Gerard aan rente gekregen?
b) Hoeveel procent is de rente?
Opgave 9:
De winst van een bakker was vorig jaar € 80.000.
Dit jaar is de winst € 84.000.
a) Met hoeveel euro is de winst toegenomen?
b) Met hoeveel procent is de winst toegenomen?
Kennisbank procentuele afname.
Opgave 10:
Een televisietoestel van €1359, kost in de uitverkoop nog €1149 .
a) Hoeveel euro is de korting?
b) Hoeveel procent is de korting?
Opgave 11:
Een broek van € 19, 99 kost in de uitverkoop nog € 14,99.
a) Hoeveel procent is de korting?
Opgave 12:
Tom van Dijk heeft een timmerbedrijf. De specialiteit van het bedrijf is kasten.
Om één kast te maken maakt Tom de volgende kosten:
- Arbeidskosten € 200,-
- Materiaalkosten € 80,-
De verkoopprijs berekent Tom door de kostprijs met 25% te verhogen.
a) Hoe hoog is de kostprijs van één kast? € …………
b) Wat is de verkoopprijs van één kast? € …………
Opgave 13:
3 Nog meer procenten
Kennisbank Prijzen met of zonder BTW
BTW staat voor Belasting Toegevoegde Waarde. Als je een product koopt, betaal je btw.
Voor de meeste producten is de btw 21%.
Met behulp van het schema kun je prijzen zonder btw omrekenen naar prijzen met 21% btw en omgekeerd.
Bij het omrekenen van een prijs zonder BTW naar een prijs met BTW of omgekeerd kan je een rekenschema ( Formule vorm) gebruiken:
Prijs zonder BTW → x 1,21 → Prijs met BTW
Prijs met BTW → : 1,21 → Prijs zonder BTW
Schilders mogen van de overheid 9% in plaats van 21% btw rekenen.
Op veel boeken zit ook geen 21%, maar 9% btw.
Om extra te oefenen kan je de volgende link gebruiken.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Voor geschiedenis heb je de volgende vier cijfers gehaald:
6,5 7,5 8,5 8 en 4,5
Alle cijfers tellen even zwaar mee.
a) Bereken het gemiddelde. Laat zien hoe je het doet.
Opgave 2:
Piet gaat een paar dagen vissen. Dit is wat hij vangt:
Vrijdag : 2 vissen
Zaterdag : 0 vissen
Zondag : 4 vissen
a) Hoeveel vissen ving hij gemiddeld per dag?
Opgave 3:
Voor wiskunde heb je de volgende vier cijfers gehaald:
5,2 7,3 7,5 en 6,0
Alle cijfers tellen even zwaar mee.
a) Bereken het gemiddelde. Laat zien hoe je het doet.
b) Voor op het rapport wordt het gemiddelde afgerond op een geheel getal.
Welk cijfer krijg je op je rapport voor geschiedenis?
Opgave 4:
In de tabel zie je hoeveel boeken een winkelier de afgelopen week heeft verkocht.
dag
maandag
dinsdag
woensdag
donderdag
vrijdag
zaterdag
aantal boekenaantal boeken
280
250
350
275
525
1020
a) Bereken het gemiddeld aantal verkochte boeken per dag.
Opgave 5:
Simone heeft voor Engels de volgende cijfers gehaald:
9 8 7 6,5 7 5,5 10 7 7 5 10
Alle cijfers tellen even zwaar mee.
a) Bereken het gemiddelde in twee decimalen nauwkeurig.
Laat zien hoe je het doet.
b) Voor op het rapport wordt het gemiddelde afgerond op een geheel getal.
Welk cijfer krijgt Simone op haar rapport?
Opgave 6:
In een wielerwedstrijd rijdt het peleton het eerste uur gemiddeld 39 km/uur,
het tweede uur 41 km/uur en het derde uur 42 km/uur.
a) Bereken de gemiddelde snelheid over deze drie uren.
Rond je antwoord af op één cijfer achter de komma.
Opgave 7:
Een taxichauffeur reed 5 ritten.
Dit waren de afstanden:
Rit 1: 49 km
Rit 2: 15,5 km
Rit 3: 107,5 km
Rit 4: 44 km
Rit 5: 198,3 km
a) Bereken de gemiddelde ritlengte (rond naar boven af op hele kilometers).
Opgave 8:
De spelers van een voetbalploeg organiseerden een wafelverkoop.
De vijf ploegen (duiveltjes, miniemen, kadetten, tweede ploeg en de eerste ploeg)
verkochten samen 450 pakken wafels. De ploeg van de duiveltjes telt 14 spelers,
die van de miniemen 22, die van de kadetten 18, die van de tweede ploeg 16 en
de eerste ploeg 20.
a) Hoeveel pakken wafels werden er
gemiddeld verkocht per ploeg?
b) Hoeveel pakken wafels werden er
gemiddeld verkocht per speler?
2 gewogen gemiddelde
Bekijk eerst dit filmpje
Kennisbank Gewogen gemiddelde.
Opgave 1:
Bekijk de volgende twee situaties:
Situatie I Je hebt voor vier wiskunde proefwerken de volgende cijfers gehaald: 4, 7, 7 en 6.
Ieder cijfer telt even zwaar.
Situatie II Je hebt voor Nederlands drie cijfers gehaald. Voor de overhoringen een 7 en een 8. Voor een proefwerk een 5.
Het proefwerk telt drie keer zo zwaar als een overhoring.
In welke situatie(s) heb je te maken met een gewogen gemiddelde?
a) II en IIII beide geen gewogen gemiddelde
b) II wel gewogen gemiddelde en IIII geen gewogen gemiddelde
c) II geen gewogen gemiddelde en IIII wel gewogen gemiddelde
d) II en IIII beide gewogen gemiddelde
Opgave 2:
Het gezin Molenmaker bestaat uit de drieling Ilse, Lotte en Mara van 3 jaar,
Jelle van 6, Aron van 9, vader Anton van 35 en moeder Mieke van 33.
a) Bereken de gemiddelde leeftijd.
Opgave 3:
Minke heeft de volgende cijfers gehaald voor Wiskunde .
vak
cijfers
gem.
verzorging
7,5 (1x) 6,4 (2x) 8,0 (4x) 4,7 (3 x) 9,1 (2x)
a) Bereken het gemiddelde cijfer.
Opgave 4:
Anne heeft de volgende cijfers voor Engels gehaald.
a) Bereken haar gemiddelde cijfer voor Engels
Bekijk eerst dit filmpje
Kennisbank gemiddelde uit tabel
Opgave 5:
In de tabel staan de leeftijden van de leerlingen uit klas 4 basis.
a) Bereken hoeveel leerlingen in klas 4 basis zitten.
b) Berkene het totaal aantal jaren van de leerlingen.
c) Berkenen de gemiddelde leeftijd van de leerlingen.
Opgave 6:
Hieronder zie je een tabel met leeftijden van leerlingen.
Links staan de leeftijd in jaren en rechts de frequentie.
a) Bereken de gemiddelde leeftijd van deze leerlingen ?
b) Hoeveel procent van deze leerlingen is 16 jaar of ouder?
Opgave 7:
Hieronder zie je een tabel met de gemiddelde cijfers voor wiskunde van een tweede klas.
a) Bereken het gemiddelde van de cijfers .
b) Bepaal hoeveel procent van de leerlingen een cijfer heeft tussen de 6 en 8.
3 Frequentietabel
Bekijk eerst dit filmpje
Kennisbank Frequentietabel
Opgave 1:
In de frequentietabellen zie je de rapportcijfers van klas 3A (links) en klas 3B (rechts).
cijfer
frequentie
rel. frequentie
5
5
17,2%
6
9
31%
7
11
37,9%
8
3
10,3%
9
1
4%
29
100%
cijfer
frequentie
rel. frequentie
5
4
20,0%
6
7
35,0%
7
4
20,0%
8
3
15%
9
2
10%
20
100%
a) Hoeveel leerlingen van klas 3A hebben er een onvoldoende op hun rapport?
En hoeveel leerlingen van klas 3B?
b) In welke klas is het percentage onvoldoendes het grootst?
c) In welke klas is het percentage met een hoog rapport cijfer (8 of hoger) het grootst?
d) Bereken van beide klassen het gemiddelde rapportcijfer.
Opgave 2:
Hieronder zie je de proefwerkcijfers van klas 3A voor Engels.
4
5
7
5
10
9
8
4
6
6
7
7
8
3
7
6
6
7
7
9
7
6
7
6
6
8
7
7
8
a) Neem de onderstaande frequentietabel over en vul hem verder in.
Rond de relatieve frequenties af op één cijfer achter de komma.
cijfer
turven
frequentie
rel. frequentie
3
|
1
3,4%
4
||
5
6
7
8
9
10
29
100%
b) Welke frequentie hoort bij het cijfer 8?
c) Welk cijfer heeft de hoogste frequentie?
Opgave 3:
Hieronder zie je de proefwerkcijfers van klas 3A voor Engels.
5
7
5
10
9
8
4
6
6
7
7
8
3
7
6
6
7
7
9
7
6
7
6
6
8
7
7
8
a) Neem de onderstaande frequentietabel over en vul hem verder in.
Rond de relatieve frequenties af op één cijfer achter de komma.
cijfer
turven
frequentie
rel. frequentie
3
4
5
6
7
8
9
10
...
……
b) Wat is het voordeel van een frequentietabel?
c) Welke frequentie hoort bij het cijfer 88?
d) Welk cijfer heeft de hoogste frequentie?
Opgave 4:
Hieronder zie je de proefwerkcijfers van klas 3B voor Engels.
5 6 5 7 7 8 5 4 6 6 8 7 9 4 6 9 8 7 6 5
a) Maak met de cijfers een frequentietabel.
Bekijk eerst dit filmpje
Kennisbank indeling in klassen
Opgave 5:
Hieronder zie je de proefwerkcijfers van klas 3A voor Engels.
4,
3,8
5,9
6,1
6,5
8,5
4,9
9,1
7,2
7,3
6,5
7,9
6,7
5,5
6,4
5,7
7,6
6,5
7,1
8,1
8,5
6,8
5,1
8,2
7,5
6,9
6,2
7,1
7,3
5,7
a) Neem de onderstaande frequentietabel over en vul hem verder in.
Rond de relatieve frequenties af op één cijfer achter de komma.
klasse
turven
frequentie
rel. frequentie
3,5 tot 4,5
4,5 tot 5,5
5,5 tot 6,55
6,5 tot 7,5
7,5 tot 8,5
8,5 tot 9,5
...
……
b) Wat is het klassenmidden van de klasse '8,5 tot 9,5?
c) Wat is de klassenbreedte van iedere klasse?
d) Welk klasse heeft de hoogste frequentie?
e) Hoeveel procent van de leerlingen heeft lager een cijfer dan 6,5?
Opgave 6:
In de frequentietabel zie je verdeling van de lengtes in cm van 90 meisjes.
klasseklasse (cm)
frequentiefrequentie
150 tot 160
6
160 tot 170
26
170 tot 180
37
180 tot 190
17
190 tot 200
4
90
a) Wat is het klassenmidden van de klasse '150 tot 160'?
b) Wat is de klassenbreedte van iedere klasse?
c) Welk klasse heeft de hoogste frequentie?
d) Hoeveel procent van de meisjes is korter dan 160 cm?
e) Bij de frequentietabel is een staafdiagram getekend. Welke waarden staan bij de horizontale as?
En hoe breed zijn de staven?
Opgave 7:
In de frequentietabel zie je verdeling van de gewichten (in kg) van een groep personen.
klasse (kg)
frequentie
45 tot 50
1
50 tot 55
5
55 tot 60
8
60 tot 65
15
65 tot 70
19
70 tot 75
9
75 tot 80
3
a) Wat is het klassenmidden van de klasse '50 tot 55'?
b) Wat is de klassenbreedte van iedere klasse?
c) Welk klasse heeft de hoogste frequentie?
d) Hoeveel procent van deze groep personen weegt minder dan 70 kg?
e) Bij de frequentietabel is het begin van een staafdiagram getekend.
f) Neem het staafdiagram over en maak het verder af.
12 Andere verbanden
Bekijk eerst dit filmpje
Kennisbank andere verbanden
Voorbeeld Een vierkant heeft zijden van a cm.
De oppervlakte van het vierkant is a⋅a
Met de formule opp=a⋅a kun je de volgende tabel invullen:
a (cm)
0
1
2
3
4
opp (cm2)
0
1
4
9
16
De grafiek van dit verband is geen rechte lijn.
De grafiek is een vloeiende gebogen lijn.
Een rechthoek heeft een zijde van a cm en een zijde van 2⋅a cm.
De oppervlakteoppervlakte van de rechthoek is 2⋅a⋅a
Bekijk de tabel:
a
0
1
2
3
4
oppervlakte
0
2
8
18
....
a) Welke oppervlakteoppervlakte hoort bij a=4?
Opgave 2:
Je ziet een rij stippenfiguren.
a) Neem de tabel over en vul hem in.
figuurnummer
1
2
3
4
aantal stippen
1
b) Bekijk de formules hieronder. Welke formule past bij het verband tussen het figuurnummeren het aantal stippen?
A. aantal stippen=2×figuurnummer +aantal stippen.
B aantal stippen=figuurnummer×figuurnummer.
c) Bereken het aantal stippen voor het vijfde figuur in de rij.
d) Bereken ook het aantal stippen voor het tiende figuur in de rij.
Opgave 3:
Kijk naar de formule: uitkomst= getal × getal + 3.
a) Neem de tabel hieronder over en vul hem verder in.
getal
0
1
2
3
4
5
uitkomst
3
4
``
``
``
``
b) teken in een assenstelsel de grafiek bij de tabel.
Opgave 4:
Kijk naar de formule: uitkomst= getal × getal + 2 × getal
a) Neem de tabel hieronder over en vul hem verder in.
getal
0
1
2
3
4
5
uitkomst
0
``
``
``
``
``
b) Teken in een assenstelsel de grafiek bij de tabel.
Opgave 5:
Een rechthoek heeft een oppervlakte van 40.
Voor de rechthoek geldt de formule:
lengte × breedte = 40
a) Neem de tabel over en vul hem verder in.
breedte
1
2
5
10
20
lengte
``
``
``
``
``
b) Neem het assenstelsel over en teken de grafiek bij de tabel.
Opgave 6:
Een bedrijfseconoom heeft een model opgesteld waarmee hij de dagelijkse verkoop van asperges kan voorspellen:
verkoop= 1000 : prijs
De dagelijkse verkoop in kg hangt af van de prijs in euro.
De formule is geldig voor prijzen tussen de 2 en 16 euro.
a) Neem de tabel over en vul hem verder in.
prijs
2
4
8
10
16
verkoop
``
``
``
``
``
b) Neem het assenstelsel over en teken de grafiek bij de tabel.
c) Het winkelbedrijf heeft voor de zaterdag 400 kg asperges ingekocht.
Welke prijs moet het winkelbedrijf vaststellen om alle asperges te verkopen?
Opgave 7:
Bekijk de volgende formule:
uitkomst= 24 : getal +6
Het verband tussen getal en uitkomst is een hyperbolisch verband.
a) Neem de tabel over en vul hem verder in.
getal
1
2
4
6
12
uitkomst
``
``
``
``
``
b) Neem het assenstelsel over en teken de grafiek bij de tabel.
Opgave 8:
Een rechthoek heeft een omtrek van 18 cm.
Als je de lengte van de rechthoek weet, kun je de breedte uitrekenen.
a) Hoe groot is de breedte van de rechthoek als de lengte 5 cm is.
b) Bereken ook de breedtebreedte van de rechthoek als de lengte 7 cm is.
c) Het verband tussen lengte en de breedte kun je weergeven in en formule.
Welke van onderstaande formules geeft het verband goed weer.
breedte = 9 + lengte.
breedte=9−lengte.
breedte=18+lengte
breedte=18−lengte
e) De oppervlakte van de rechthoek kun je berekenen met de formule: oppervlakte = 9× lengte − lengte × lengte
Neem onderstaande tabel over en vul hem verder in.
lengte
5
6
8
9
oppervlakte
20
``
``
``
f) Waarom mag je voor de lengte geen getallen groter dan 9 invullen?
Opgave 9:
De afstand die een auto auto tijdens het remmen aflegt, heet de remweg. De lengte van de remweg hangt onder andere af van de snelheid van de auto.
Met onderstaande formule kun je de remweg op een droog wegdek berekenen als je de snelheid weet. remweg = 0,006 × snelheid × snelheid
In de formule is de remwegremweg in meter en de snelheidsnelheid in km per uur.
a) Laat met een berekening zien dat bij een snelheid van 30 km per uur de remweg 5,4 meter is.
b) Monica beweert: 'Als de snelheid van de auto 2 keer zo groot wordt, wordt de remweg 2 keer zo lang'.
Heeft Monica gelijk? Leg je antwoord uit.
c) Als het wegdek nat is, wordt de remweg langer. Bekijk de twee grafieken.
Eén grafiek hoort bij de remweg op een droog wegdek. De andere grafiek hoort bij de remweg op een nat wegdek.
Welke grafiek, A of B, hooft bij een remweg op een nat wegdek?
d) De remweg op een nat wegdek kun je met de volgende formule berekenen:
remweg= 0,009 × snelheid × snelheid
Ook in deze formule is de remweg in meter en de snelheid in km per uur.
Op een nat wegdek is de remweg langer dan op een droog wegdek.
e) Hoeveel meter is het verschil bij een snelheid van 50 km/uur.
Opgave 10:
Als je van Maastricht naar Groningen reist, leg je 320 kilometer af.
Je kunt de reis op verschillende manieren maken: lopend, per fiets, scooter, auto, trein enzovoort.
De tijd die je voor deze reis nodig hebt, hangt af van je gemiddelde snelheid.
Je kunt die tijd uitrekenen met de woordformule:
Tijd = 320 : gemiddelde snelheid
Hierin is tijd in uren en gemiddelde snelheid in kilometer per uur.
Patrick en Mirjam fietsen van Maastricht naar Groningen.
Hun gemiddelde snelheid is 16 kilometer per uur.
a) Bereken hoeveel uur de reis duurt. Schrijf je berekening op.
1 Allerlei verbanden
Bestudeer uit de Kennisbank wiskunde de volgende onderdelen:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Voorbeeld Je ziet een schematisch reuzenrad. Het rad draait heel langzaam rond. Tijdens het instappen draait het rad gewoon door.
Tom draait rond in het reuzenrad.
In de tabel zie je steeds op welke hoogte (hh in m) hij zich bevindt.
tijdtijd (sec)
0
20
40
60
80
100
120
140
160
180
200
220
hoogtehoogte (m)
5
8
13
18
21
18
13
8
5
8
13
18
Uit de tabel kun je afleiden dat:
het instapplatform zich 5 m boven de grond bevindt.
In de grafiek hieronder is een periodiek verband weergegeven.
a) Op welke hoogte ligt de evenwichtslijn. Teken de evenwichtslijn in de figuur.
b) Hoelang is de periode? Geef de periode aan in de figuur.
c) Hoe groot is de amplitude? Geef de amplitude aan in de figuur.
Opgave 3:
Hieronder zie je de grafiek van Mieke die touwtjespringt. De grafiek begint op het moment dat het springtouw boven Mieke's hoofd zit.
a) Wat is het maximum van de grafiek ?
b) Wat is het minimum van de grafiek ?
c) Wat is de evenwichtsstand van de grafiek ?
d) Wat is de amplitude van de grafiek ?
e) Wat is de periode van de grafiek ?
Opgave 4:
in de grafiek hieronder is een periodiek verband weergegeven.
a) Op welke hoogte ligt de evenwichtslijn. Teken de evenwichtslijn in de figuur.
b) Hoelang is de periode? Geef de periode aan in de figuur.
c) Hoe groot is de amplitude? Geef de amplitude aan in de figuur.
Opgave 5:
Hieronder zie je een grafiek die hoort bij het reuzenrad van Rotterdam. De grafiek laat zien op welke hoogte het reuzenradkarretje na zoveel seconden is.
a) Wat is het maximum en het minimum van de grafiek?
b) Hoe lang is een periode?
c) Bepaal de evenwichtstand en de amplitude?
Opgave 6:
Deze grafiek hieronder gaat over een skicabine, die mensen van het dal naar het bergstation brengt.
a) Bij welke hoogte kan je instappen?
b) welek hoogte kan de sticabine bereiken?
c) Hoeveel minuten doet de cabine erover om mensen van het dal naar het bergstation te brengen en vervolgens weer terug te keren?)
Opgave 7 :
De grafiek hieronder laat het temperatuurverloop in een aquarium zien.
a) Hoeveel graden schommelt de temperatuur?
b) Wat is de gemiddelde temperatuur in het aquarium?
c) Hoelang is de periode?
d) Om 12.40 uur en 15.20 uur is de temperatuur 20°C.
e) Op welke tijdstippen vóór 24.00 uur is de temperatuur weer 20°C?
Opgave 8:
Op een kerktoren zit een torenklok. De grote wijzer van de torenklok is van het midden van de klok tot het topje 0,50 meter lang. Het midden van de klok bevindt zich precies 50 meter boven de grond.
a) Op welke hoogte is het topje van de grote wijzer om 12 uur?
En om 12.15 uur en om 12.30 uur?
b) Er is een periodiek verbandt tussen de hoogte en het aantal minuten.
c) Geef van dit periodiek verband de periode, de evenwichtsstand en de amplitude.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
In een bioscoop zijn 200 goedkope en 400 dure plaatsen.
De goedkope plaatsen kosten € 8,-€ de dure plaatsen kosten € 12,-€
De opbrengst is afhankelijk van het aantal verkochte goedkope
plaatsen (goedkoop) en het aantal verkochte dure plaatsen (duur).
In formulevorm: opbrengs t= 8 × goedkoop +12 × duuropbrengst.
a) Bereken de opbrengst als er 80 goedkope en 100 dure plaatsen worden verkocht.
b) Neem de tabel over en vul deze verder in.
goedkoop=80
goedkoop =120
goedkoop=160
goedkoop =200
duur=100
….….
….….
….….
….….
duur=200
3040
3360
….….
….….
duur=300
….….
….….
….….
5200
duur=400
….….
….….
….….
6400
Opgave 2:
De hoeveelheid energie E in kcal die iemand per dag nodig heeft, is afhankelijk van zijn gewicht G in kg en de die dag geleverde inspanning.
De geleverde inspanning wordt weergegeven met de inspanningsindex I. De index kan variëren van 10 (weinig inspaning) tot 15 veel inspanning.
De formule van het verband tussen E, G en I luidt:
E= 6 × G +12 × I x l
a) Bereken het aantal benodigde kilocalorieën als G=75 en I=10.
b) Voor een automonteur geldt een inspanningsindex I=14. Bereken het aantal benodigde kilocalorieën als je weet dat de automonteur 90 kg weegt.
c) Voor een scholier geldt een inspanningsindex I=12. Zoek uit hoe zwaar de scholier is als je weet dat het aantal benodigde kilocalorieën 2148 kcal is.
Opgave 4:
De remweg van een auto r in meters van een auto hangt af van de snelheid v van de auto in m/s, de remvertraging a van de auto in m/s² en de reactietijd t van de bestuurder in sec.
In formulevorm:
r= v2 : 2 ⋅ a + v ⋅ t
De remvertraging van een auto is 4 m/s².
De reactietijd van de bestuurder is 0,5 sec.
a) Bereken de remweg als de auto met een snelheid van 10 m/s rijdt.
b) Bereken ook de remweg als de auto twee keer zo hard rijdt.
c) Zoek uit, door te proberen, bij welke snelheid in m/s de auto een remweg van ongeveer 100 meter heeft.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Hier vind je de examentraining Tabel-Grafiek-Formule. In deze examentraining staat de examenstof nogmaals kort uitgelegd, kun je oefenopgaven maken en ga je aan de slag met opdrachten uit eerdere examens.
Overleg met de docent wanneer je de examentraining gaat doen.
Met welke formule kun je de omtrekomtrek van een cirkel uitrekenen?
a) omtrek cirkel = π × diameter
b) omtrek cirkel = π × straal
c) omtrek cirkel = π × straal
Opgave 2:
Opgave 3:
Voor de omtrek van een cirkel geldt: omtrek cirkel= π x diameter
π is een Griekse letter. Spreek uit: 'pie'. π is ongeveer 3,14.
Vul in:
a) Van de cirkel hierboven is de straal ……
b) Van de cirkel hiernaast is de diameter…… c) De omtrek van de cirkel bereken je als volgt:
omtrek cirkel =π x ........................
Opgave 4:
Van een 2-euromunt is de diameter ongeveer 25 mm.
a) Hoe groot is de omtrek van 2-euromunt?
Opgave 5:
Van een 1-euromunt is de straal ongeveer 12 mm.
a) Bereken de omtrek van een 1-euromunt.
Rond je antwoord af op één decimaal achter de komma.
Opgave 6:
Van een munt van 10 eurocent is de omtrek ongeveer 58 mm.
a) Bereken de diameter van een munt van 10 eurocent.
Rond af op één cijfer achter de komma.
Opgave 7:
a) Bereken de omtrek van de tafel hierboven ?
Opgave 8:
Gegeven een zwembad met een straal van 4 meter
a) Bereken de omtrek van het zwembad. Rond af op 2 decimalen.
Opgave 9:
Bekijk de figuur hieronder.
a) Hoe groot is de omtrek van deze figuur ?
Opgave 10:
Bekijk de figuur hieronder
De figuur bestaat uit twee rechte lijnstukken (AB en AC) en een kwart cirkel (cirkelboog BC).
Bereken de omtrek van de figuur.
Opgave 11:
Bekijk de tekening Hieronder. Je ziet zeven cirkeltjes die precies passen binnen een grote cirkel.
De kleine cirkeltjes hebben ieder een omtrek van 6,28 cm.
Gebruik π=3,14 om de volgende vragen te beantwoorden.
a) Hoe groot is de diameter van een klein cirkeltje?
b) Hoe groot is de omtrek van de grote cirkel?
Opgave 12:
Bekijk het figuur hiernaast.
Het figuur bestaat uit twee rechte lijnstukken (MA en MB) en
een deel van een cirkel (cirkelboog AB).
a) Bereken de omtrek van het figuur.
Rond af op één cijfer achter de komma.
Opgave 13:
Vier cirkeltjes passen precies binnen een vierkant.
De omtrek van één cirkeltje is 12,56 cm.
a) Bereken de omtrek van het vierkant.
1 Omtrek cirkel
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
a) Bereken de oppervlakte van de tafel hierboven ?
Opgave 2 :
Je ziet hieronder twee vijvers in het blauw.
a) Bereken de oppervlakte van iedere cirkel.
Opgave 3 :
De middencirkel van een voetbalveld heeft officieel een straal van 9,15 m vanaf het middelpunt van het veld.
a) Hoe groot is de oppervlakte van de middencirkel?
Opgave 4 :
Een cd-rom heeft een straal van 6 cm.
Het gaatje in het midden heeft een straal van 1 cm.
a) Hoe groot is de oppervlakte van de cd-rom ongeveer?
Gebruik π=3,14.
Opgave 5 :
Bekijk de figuur hieronder. Je ziet het Chinese yin-en-yang-teken.
Je wilt een yin-en-yang-teken met een straal van 10 cm tekenen.
Hoe groot is de oppervlakteoppervlakte van het zwarte deel van je yin-en-yang-teken?
Neem π≈3,14
Opgave 6 :
Bekijk de figuur hieronder.
De figuur bestaat uit twee rechte lijnstukken (AB en AC) en een kwart cirkel ((cirkelboog BC).
a) Bereken de oppervlakte van de figuur.
Opgave 7:
Vier cirkeltjes passen precies binnen een vierkant.
De oppervlakte van één cirkeltje is 314 cm2.
a) Bereken de oppervlakte van het vierkant.
Opgave 8:
Bekijk het figuur hiernaast.
Het figuur bestaat uit twee rechte lijnstukken (MA en MB) en
een deel van een cirkel (cirkelboog AB).
a) Bereken de oppervlakte van het figuur.
Rond af op één cijfer achter de komma.
Opgave 9:
Op ruitjespapier van 1 cm bij 1 cm zijn twee cirkels getekend. Zie figuur hieronder.
De grootste cirkel heeft een diameter van 7 cm.
De kleinste cirkel heeft een diameter van 6 cm.
a) Bereken de oppervlakte van het blauwe gedeelte.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Om snel medische hulp te kunnen bieden staan in een aantal plaatsen in Nederland speciale helikopters klaar.
Op het kaartje is voor drie van die plaatsen met cirkels aangegeven in welk gebied de helikopters ingezet kunnen worden.
Er geldt dat:
de gele gebieden door één van de helikopters bereikt kunnen worden.
het blauwe gebied door twee helikopters bereikt kan worden.
de delen die buiten de cirkels vallen kunnen niet door één van deze drie helikopters bereikt kunnen worden.
a) Teken een punt P en teken alle punten die precies 3 cm van punt P af liggen.
b) Teken ook alle punten die precies 5 cm van punt P af liggen.
c) kleur het gebied tussen de twee cirkels.
Wat kun je zeggen over de punten die in dat gebied liggen?
d) ereken de oppervlakte van het gekleurde gebied.
Opgave 6
Je ziet een cirkel met middelpunt M en een cirkel met middelpunt N.
Van beide cirkels is de straal 3 cm.
Je ziet ook de punten A, B en C.
a) Waar of niet waar?
Punt A ligt minder dan 3 cm van N en meer dan 3 cm van M.
b) Waar of niet waar?
Punt B ligt minder dan 3 cm van N en minder dan 3 cm van M.
c) Waar of niet waar?
Punt C ligt meer dan 3 cm van N en meer dan 3 cm van M.
Opgave 7
In 2011 is een deel van de televisie- en radiozendmast in het Drentse Hoogersmilde ingestort.
Op dezelfde dag was er ook al brand in de zendmast Lopik in IJsselstein.
Als gevolg van deze gebeurtenissen zat een groot deel van Nederland zonder FM-ontvangst.
Op het kaartje hieronder zie je waar de beide zendmasten staan.
De zendmast in Hoogersmilde heeft een bereik van ruim 50 km. De zendmast van Lopik heeft een bereik van 70 kilometer.
a) Download het kaartje en geef op het kaartje aan in welke delen er geen FM-ontvangst was door de gebeurtenissen.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Hier vind je de examentraining Meetkunde. In deze examentraining staat de examenstof nogmaals kort uitgelegd, kun je oefenopgaven maken en ga je aan de slag met opdrachten uit eerdere examens.
Overleg met de docent wanneer je de examentraining gaat doen.
Dit thema bestaat uit de volgende drie paragrafen:
Boomdiagram
Tabel
Wegendiagram
1 Boomdiagram
Bekijk eerst dit filmpje
Kennisbank boomdiagram
Opgave 1:
Een gezin heeft drie kinderen. Je kijkt naar het geslacht van de kinderen. In het boomdiagram hieronder zie je alle mogelijkheden.
a) Hoeveel verschillende mogelijkheden zijn er?
b) Hoeveel verschillende mogelijkheden met twee meisjes zijn er? Schrijf die mogelijkheden op.
c) Hoeveel verschillende mogelijkheden met één jongen?
Schrijf ook die mogelijkheden op.
Opgave 2:
Je gooit een munt drie keer op. Je kijkt of je 'kop' of 'munt' gooit. Je ziet het begin van een boomdiagram hieronder.
a) Neem het boomdiagram over en maak het verder af.
b) Hoeveel verschillende mogelijkheden zijn er?
c) Hoeveel verschillende mogelijkheden met één keer munt?
Schrijf die mogelijkheden op.
d) Vergelijk het boomdiagram van vraag 1 met het boomdiagram van vraag 2. Wat valt je op?
Opgave 3:
Je gooit een munt drie keer op. Je kijkt of je 'kop' of 'munt' gooit. Je ziet het begin van een boomdiagram.
a) Neem het boomdiagram over en maak het verder af.
b) Hoeveel verschillende mogelijkheden zijn er?
c) Hoeveel verschillende mogelijkheden met één keer munt?
Schrijf die mogelijkheden op.
d) Vergelijk het boomdiagram van vraag 1 met het boomdiagram van vraag 2. Wat valt je op?
Opgave 4:
Je gooit 4 keer met een 2euro munt (kop of munt).
a) teken het boomdiagram van deze situatie.
b) Hoeveel verschillende uitkomsten zij er ?
c) Hoeveel verschillende mogelijkheden met twee kop zijn er? Schrijf die mogelijkheden op.
Opgave 5:
Op een sportdag heb je 's morgens de keuze uit volleybal, voetbal en hockey.
's Middags heb je de keuze uit korfbal, voetbal en tennis.
Je mag 's morgens en 's middags niet dezelfde sport kiezen.
a) Maak een boomdiagram bij de situatie.
b) Hoeveel verschillende mogelijkheden zijn er?
In hoeveel van deze mogelijkheden zit er voetbal bij?
c) Waarom kun je nu het aantal verschillende routes niet zomaar met een vermenigvuldiging uitrekenen?
Opgave 6:
De code van een kluis bestaan uit 4 cijfers, het cijfer 0, twee keer het cijfer 4 eb het cijfer 8.
a) Hoeveel codes zij er mogelijk
Opgave 7:
Bij een vereniging worden 3 mensen (A,B en C) in het bestuur gekozen die de functie van voorzitter, penningmeester en secretaris moeten vervullen.
a) Op hoeveel manieren kan men deze 3 functies over deze 3 mensen verdelen?
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
gegevens uit een boomdiagram aflezen en een boomdiagram (af)maken.
gegevens uit een wegendiagram aflezen en een tabel wegendiagram (af)maken.
een tabel als hulpmiddel gebruiken om de mogelijkheden van een telprobleem weer te geven.
Kennisbank tabel
Opgave 1:
Tijdens een toets moet je twee vierkeuzevragen beantwoorden. Je kunt bij iedere vraag kiezen uit A, B, C of D.
In de tabel hieronder zie je alle mogelijke combinaties.
a) Hoeveel mogelijkheden zijn er.
b) Je kunt de combinaties ook in een boomdiagram weergeven. Teken het boomdiagram.
c) Welke weergave vind je overzichtelijker, het boomdiagram of de tabel?
Opgave 2:
Je gooit met twee rode dobbelstenen. In de tabel zie je de mogelijke combinaties. Je ziet dat er 36 combinaties zijn.
a) In hoeveel combinaties komt er een 66 voor?
b) Je had de combinaties ook in een boomdiagram kunnen weergeven.
Wat is het voordeel van de weergave in een tabel boven de weergave in een boomdiagram?
c) Inge vindt dat er minder dan 3636 combinaties zijn.
Volgens haar is de combinatie 1,3 gelijk aan de combinatie 3,1.
Ben je het met Inge eens?
d) Hoeveel verschillende combinaties zijn er volgens Inge.
Opgave 3:
Je gooit met twee rode dobbelstenen.
Je kijkt naar de som van het aantal ogen.
a) Neem dat tabel over en vul hem verder in.
b) Hoeveel combinaties hebben als som 55?
Schrijf die combinaties op.
c) Welke uitkomst komt het vaakst voor?
Opgave 4:
Aan een voetbalpoule doen vier teams mee. Ieder team speelt twee keer tegen ieder ander team: één thuiswedstrijd en één uitwedrstrijd.
In de tabel zie je de uitslagen van de wedstrijden.
Je ziet dat de uitslag van Ajax - PSG 1−1 was en dat de uitslag van PSG - Ajax 2−0 was.
a) Waarom staan er mintekens op de diagonaal in de tabel?
b) Hoeveel wedstrijden zijn er in het totaal gespeeld.
c) Voor een overwinning krijg je 3 punten, voor een gelijkspel 1 punt en als je verliest, krijg je 0 punten.
Hoeveel punten heeft Ajax gehaald?
d) Reken ook uit hoeveel punten de andere teams hebben gehaald.
Wie heeft de poule gewonnen?
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Je gaat uit eten. Als voorgerecht kun je kiezen tussen een cocktail of soep. Bij het hoofdgerecht heb je de keuze uit vlees, vis of vegetarisch. Het nagerecht is ijs of gebak.
In het wegendiagram zie je de mogelijke combinaties.
a) Hoeveel combinaties zijn er mogelijk?
b) Je kiest als hoofdgerecht voor vis. Hoeveel combinaties zijn er dan nog mogelijk?
Opgave 2:
Tijdens een toets moet je drie meerkeuzevragen beantwoorden.
Je kunt bij iedere vraag kiezen uit A, B of C.
a) Maak een wegendiagram voor de antwoorden op de vragen.
b) Hoeveel mogelijke combinaties zijn er mogelijk?
c) Je weet dat het antwoord op eerste meerkeuzevraag A is.
Hoeveel combinaties zijn er dan nog over?
Opgave 3:
Bij een worp met een dobbelsteen heb je zes mogelijkheden.
a) Je gooit twee keer met een dobbelsteen.
Maak een wegendiagram voor twee keer werpen.
b) Hoeveel mogelijke combinaties zijn er mogelijk bij twee keer werpen met een dobbelsteen?
c) Hoeveel combinaties zijn er mogelijk bij drie keer werpen met een dobbelsteen?
Opgave 4:
Jorrick heeft de keuze uit 33 broeken: een blauwe, een groene en een bruine.
Hij wil de broek combineren met een rood, wit of blauw shirt.
Voor zijn sokken heeft hij de keuze uit vier kleuren: zwarte, bruine, groene en blauwe.
a) Maak een wegendiagram bij de situatie.
b) Hoeveel combinaties zijn er mogelijk?
c) Jorrick wil vandaag geen blauw dragen.
Hoeveel combinaties blijven er dan nog over?
Opgave 5:
Een code bestaat uit eerst een letter en dan twee cijfers, bijvoorbeeld B24 of C11. Voor de letter gebruik je A, B, C, D of E. Voor beide cijfers 1 t/m 4.
a) Denk aan een wegendiagram. Hoeveel verschillende codes zijn er mogelijk?
b) Stel dat de twee cijfers in de code verschillend moeten zijn.
Dus B24 is een goede code, maar C11 mag niet.
Probeer uit te zoeken hoeveel verschillende codes er dan mogelijk zijn?
Opgave 6:
Bekijk de menukaart van pizzeria Bella Italia.
Je gaat bij dit restaurant eten en bestelt een voorgerecht, een hoofdgerecht en een nagerecht.
a) Denk aan een wegendiagram.
Hoeveel verschillende combinaties zijn er mogelijk?
b) Welke combinaties kosten precies € 12,20?
Schrijf ze allemaal op.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
In deze examentraining ga je aan de slag met een heel examen. Een wiskunde-examen bestaat gemiddeld uit zo'n 24 vragen verdeeld over een aantal opgaven. Je krijgt in onderdeel B per pagina de vragen van één opgave aangeboden. Voor je de vragen gaat maken, kun je de bijbehorende theorie uit de Kennisbank bestuderen.
Kennisbank
In de thema´s/opdrachten van de Stercollecties wiskunde wordt regelmatig verwezen naar de Kennisbank wiskunde. In de Kennisbank vind je de theorie die je nodig hebt voor het beantwoorden van de vragen en het maken van de opdrachten.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 3.0 Nederland licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
Rearrangeerbare stercollectie wiskunde voor voor leerjaar 3 en 4 VMBO B van Stichting VO-content. De stercollectie is ontwikkeld op basis van de eindtermen voor het vak wiskunde.
Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO
Rearrangeerbare stercollectie wiskunde voor voor leerjaar 3 en 4 VMBO B van Stichting VO-content. De stercollectie is ontwikkeld op basis van de eindtermen voor het vak wiskunde.
Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO
/f.jwwb.nl%2Fpublic%2Fu%2Fu%2Fv%2Ftemp-mhahpydpjsbzlprrcyjm%2Fan3j1m%2FKnipsel-8.jpg)
/f.jwwb.nl%2Fpublic%2Fu%2Fu%2Fv%2Ftemp-mhahpydpjsbzlprrcyjm%2Fh69tzc%2Faaa-6.jpg)
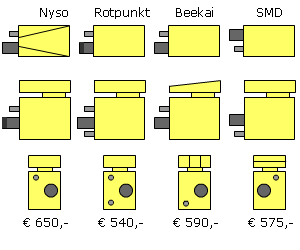
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. 
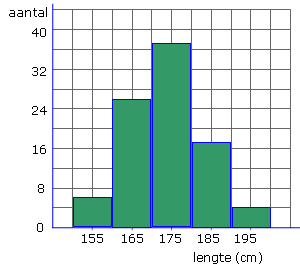
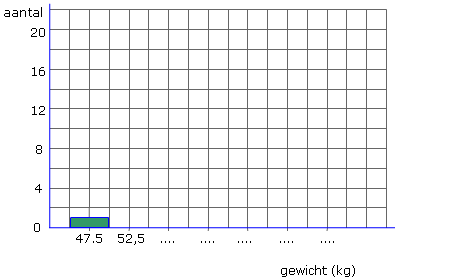
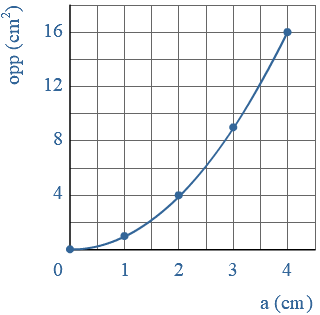
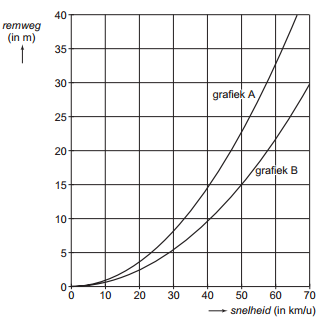
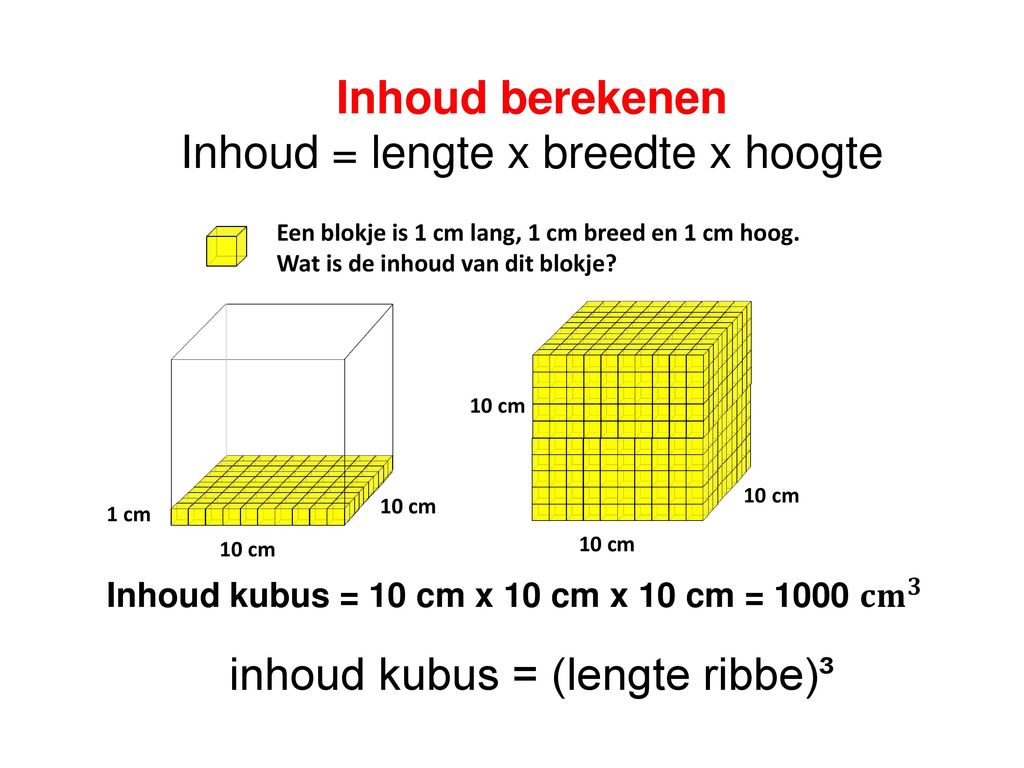
Bestudeer uit de Kennisbank wiskunde de volgende onderdelen:
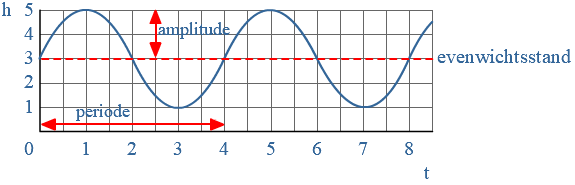
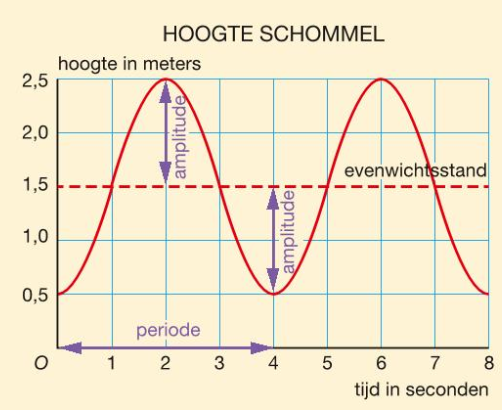
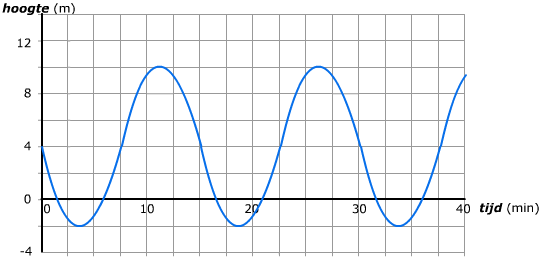
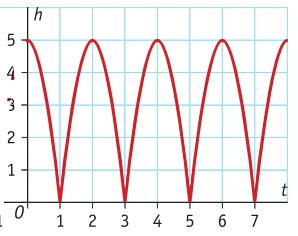
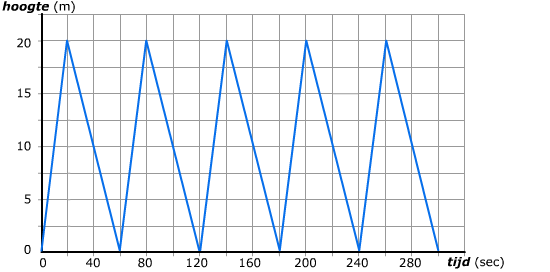
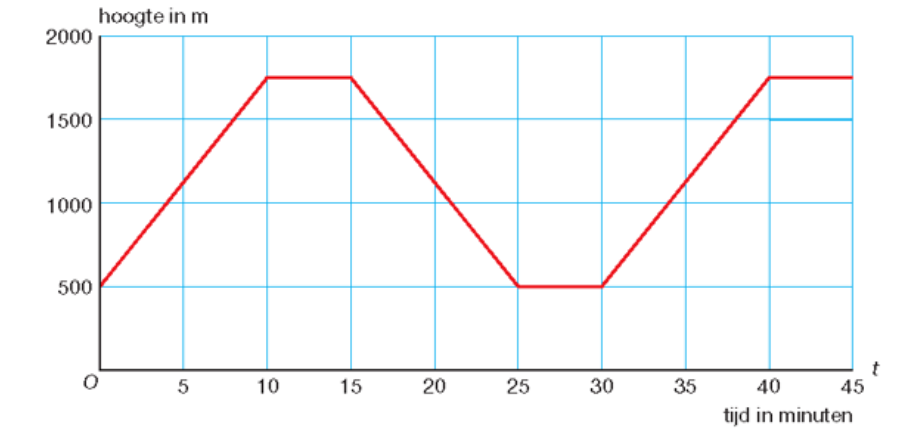
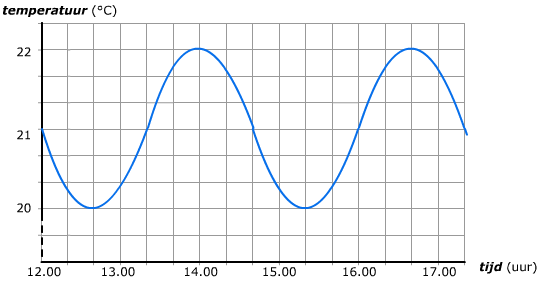
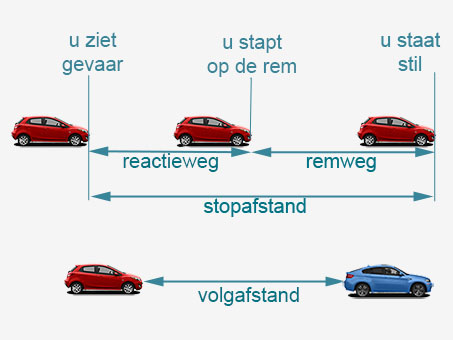
Je hebt de thema's Verbanden afgerond.
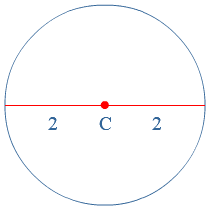
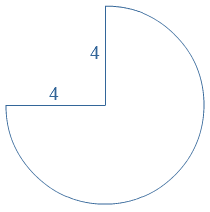
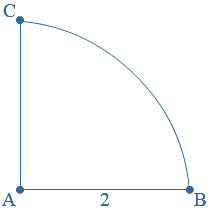
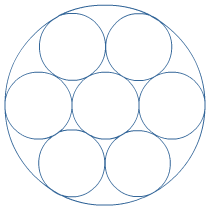
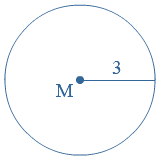
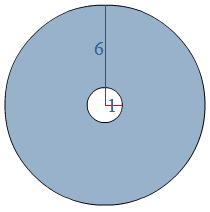
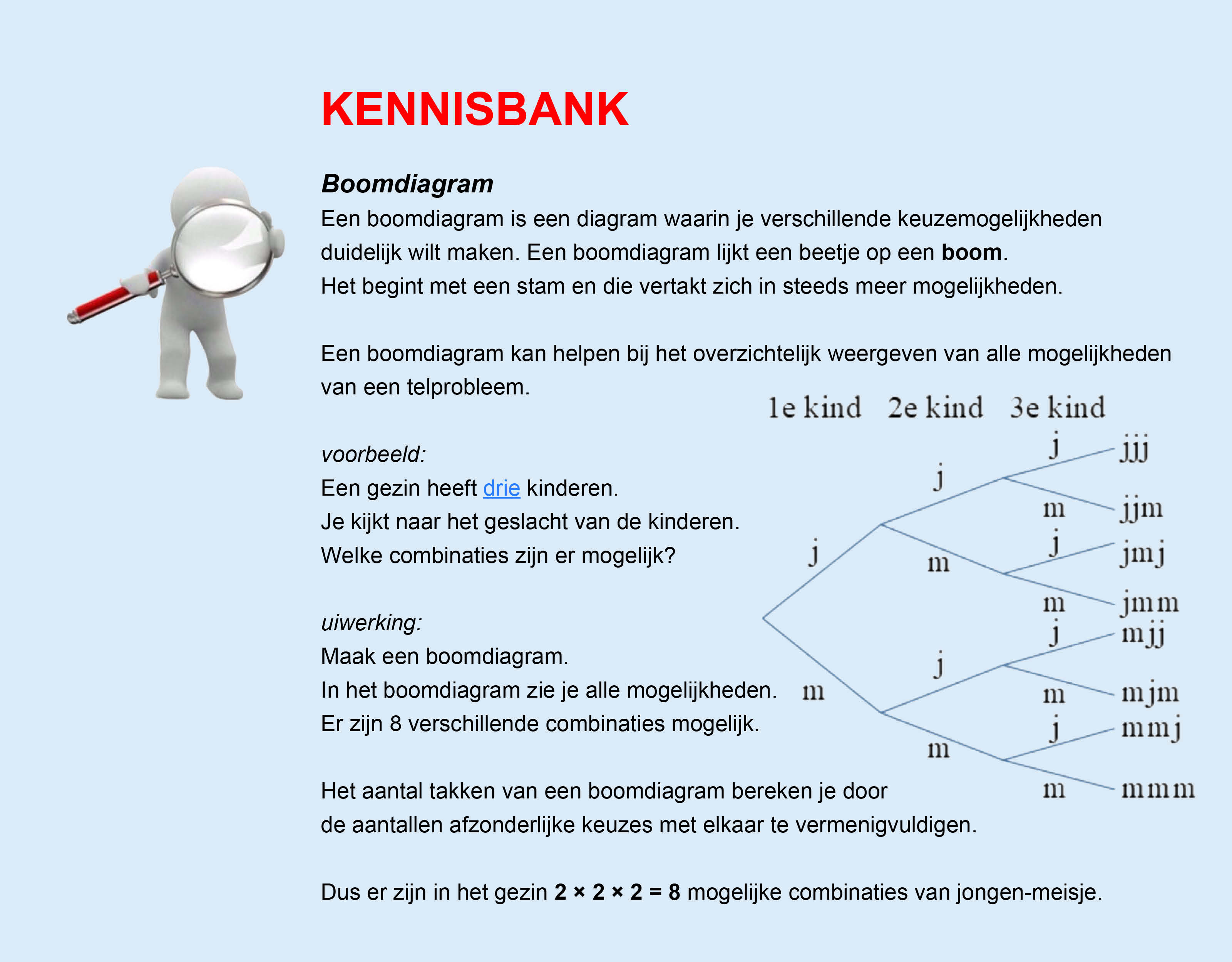
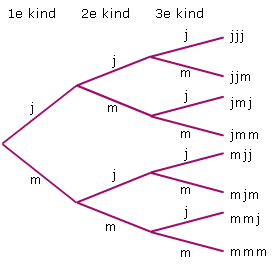
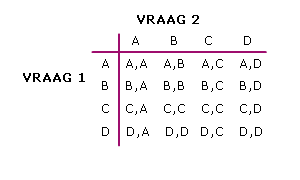
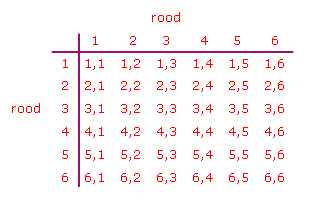
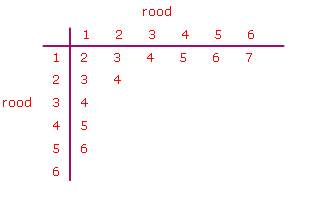
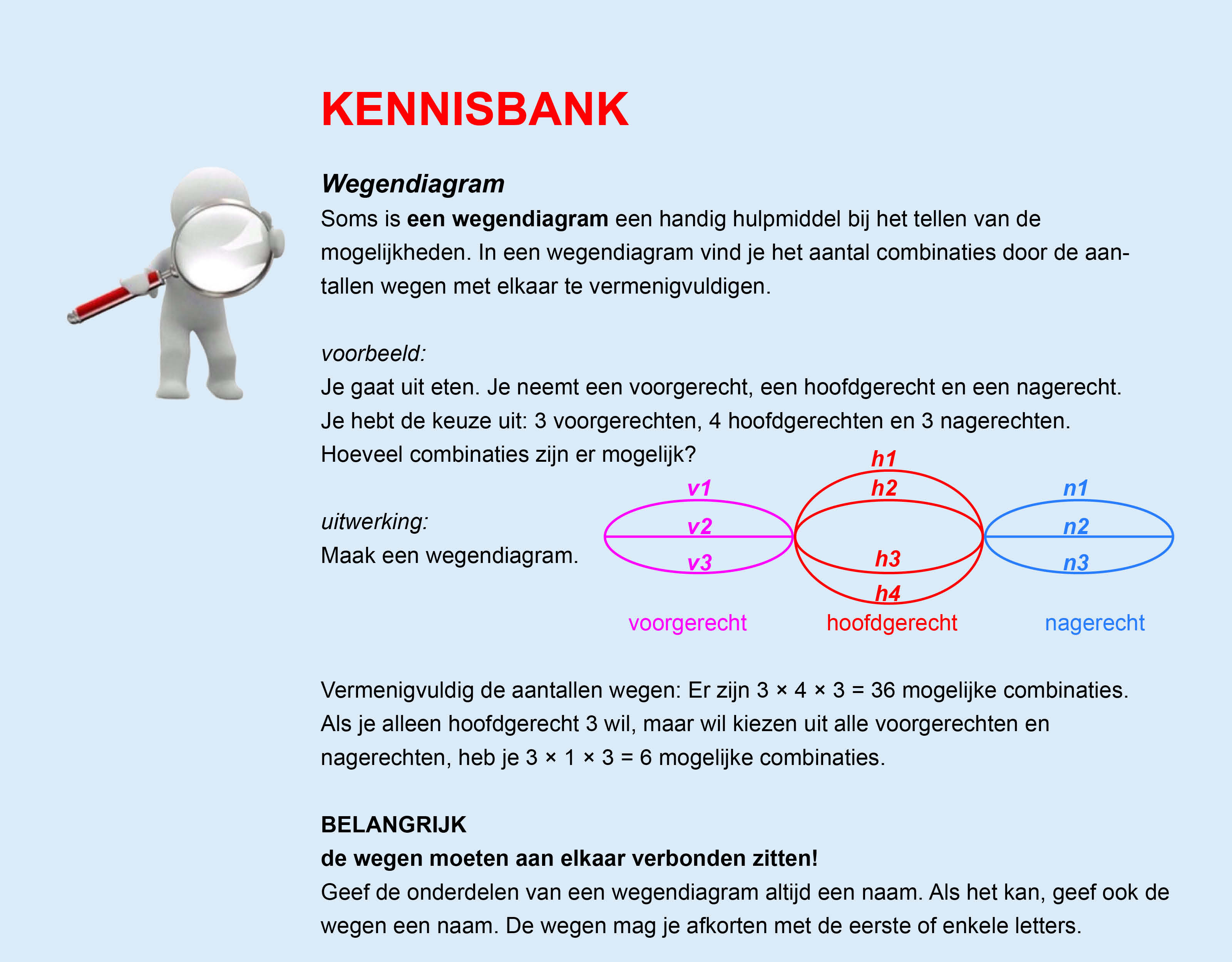
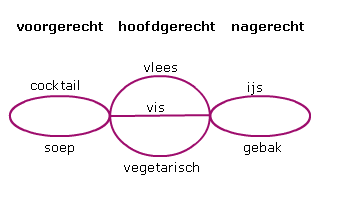
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
