HIERVAN OPDRACHTEN IN OVERLEG...MAKEN IN APART SCHRIFT
1 Rekenen-1
Thema: Rekenen -1
Rekenen en wiskunde zijn niet hetzelfde, maar hebben wel veel met elkaar te maken. In dit eerste thema leer je in de pragrafen de volgende vaardigheden:
1.1 Afronden
1.2 Schatten
1.3 Rekenregels
1.4 Verhoudingen
1.5 Verhoudingstabel
1.6 Vergelijken
1.7 Op schaal
1.8 Rekenen
1.9 Erbij/eraf
1.10 Groeifactor
Extra - 24 spel
Procenten in Excel
1.1 - Afronden
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje .
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje .
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Ken je het 24-spel? Dit spel is geschikt om goed te leren hoofdrekenen.
Je krijgt een speelkaart met 4 getallen. Met deze 4 getallen moet het getal 24 gemaakt worden door optellen, aftrekken, delen en vermenigvuldigen.
Alle 4 getallen moeten precies één keer gebruikt worden.
Hiernaast zie je een speelkaart.
Lukt het je om de oplossing te vinden?
Probeer vervolgens een aantal series op te lossen.
Het spel is soms lastiger dan je misschien denkt.
Procenten in Excel
Je hebt vast al wel eens eerder met het programma Excel gewerkt.
In dit rekenprogramma kun je ook rekenen met procenten.
Download het practicum Procenten in Excel.
Download ook het bijbehorende Excelbestand Procenten.xlsx.
Sla de bestanden op op een plaats waar je ze gemakkelijk terug kunt vinden.
Open het pdf-bestand.
Werk de opdrachten in het bestand stap voor stap door.
Klaar?
Je hoort van je docent hoe het ingevulde werkblad wordt nagekeken.
Vergelijk jouw antwoorden met die van het antwoordmodel.
Zijn er verschillen dan overleg je met een ander wat de aanpak moet zijn.
Neem de tijd om dat ook echt te vertellen...
Maak een aantekening ( achter in je schrift)
Bekijk deze aantekeningen nog eens voordat je het grote PTA krijgt.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Tabellen, grafieken en formules in Excel
Je hebt vast al wel eens eerder met het programma Excel gewerkt.
In dit rekenprogramma kun je ook werken met tabellen, grafieken en formules.
Download het practicum Tabellen, grafieken en formules in Excel.
Download ook het bijbehorende Excelbestand TGF.xlsx.
Sla de bestanden op op een plaats waar je ze gemakkelijk terug kunt vinden.
Open het pdf-bestand.
Werk de opdrachten in het bestand stap voor stap door.
Klaar?
Je hoort van je docent hoe het ingevulde werkblad wordt nagekeken.
3 Rekenen-2
Thema: Rekenen-2
In dit derde thema ga je opnieuw veel rekenen.
Het thema herhaalt een aantal zaken die je in de eerste twee jaar ook wel bent tegengekomen, maar je leert ook nieuwe dingen.
Het thema bestaat uit de volgende paragrafen:
3.1 Lengtematen
3.2 Oppervlaktematen
3.3 Inhoudsmaten
3.4 Tijd / snelheid
3.5 Massa / dichtheid
3.6 Machten
3.7 Grote getallen
3.8 Kleine getallen
3.9 Wortels
3.1 - Lengtematen
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Hier vind je de examentraining Rekenen. In deze examentraining staat de examenstof nogmaals kort uitgelegd, kun je oefenopgaven maken en ga je aan de slag met opdrachten uit eerdere examens.
Overleg met de docent wanneer je de examentraining gaat doen.
Driehoeken, vierhoeken en cirkels zijn voorbeelden van vlakke figuren die je in dit thema regelmatig zult tegenkomen. Je kijkt naar de eigenschappen van deze figuren, je rekent met hoeken en je kijkt wat er gebeurt als je de figuren vergroot of verkleind.
Een aantal onderwerpen die in dit thema behandeld worden, ben je ook in de onderbouw al tegengekomen. Maar er komen ook enkele zaken aan de orde die waarschijnlijk nieuw voor je zijn.
Het thema bestaat uit de volgende paragrafen:
4.1 Driehoeken
4.2 Pythagoras
4.3 Oppervlakte driehoek
4.4 Vergroten
4.5 Vierhoeken
4.6 Oppervlakte vierhoeken
4.7 F- en Z-hoeken
4.8 Omtrek cirkel
4.9 Oppervlakte Cirkel
4.10 Gebieden
4.1 - Driehoeken
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
In het thema 'Situatie en verbanden' ben je al heel wat verbanden tegengekomen. In dit thema ga je aan de slag met één soort verbanden, namelijk lineaire verbanden.
Het thema bestaat uit de pragrafen:
5.1 Grafiek, Tabel, Formule
5.2 Formule maken
5.3 In Excel
5.4 Vergelijking
5.5 Oplossen
5.6 Rekenschema's
5.7 Balansmethode
5.1 - G-T-F
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Rechte lijnen in Excel
Je hebt vast al wel eens eerder met het programma Excel gewerkt.
In dit rekenprogramma kun je ook grafieken maken, onder andere bij een lineair verband.
In het bestand zie je in rij 3 de algemene vorm van een lineair verband.
Hoe de grafiek bij dit verband loopt, hangt af van de getallen die je voor a (= hellingsgetal) en b (= startgetal) invult.
In dit bestand kun je de waarde van het hellingsgetal a en het startgetal b veranderen met behulp van de twee schuifbalkjes.
- Gebruik de schuifbalkjes en kijk steeds hoe de formule verandert.
- Kijk ook hoe de grafiek verandert.
- Gebruik voor a en b zowel positieve als negatieve getallen.
- Wanneer loopt de grafiek horizontaal?
5.4 - Vergelijking
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Je hebt vast al wel eens eerder met het programma Excel gewerkt.
In dit rekenprogramma kun je ook diagrammen maken.
Download het practicum Diagrammen in Excel.
Download ook het bijbehorende Excelbestand Diagrammen.xlsx.
Sla de bestanden op op een plaats waar je ze gemakkelijk terug kunt vinden.
Open het pdf-bestand.
Werk de opdrachten in het bestand stap voor stap door.
Klaar?
Je hoort van je docent hoe het ingevulde werkblad wordt nagekeken.
Je weet nu hoe je een cirkeldiagram in Excel maakt.
Je gaat nu ook een bevolkings'piramide' in Excel maken.
Download de opdracht Bevolkings'piramide' in Excel.
Download ook het bijbehorende Excelbestand Bevolking.xlsx.
Sla de bestanden op op een plaats waar je ze gemakkelijk terug kunt vinden.
Open het pdf-bestand.
Werk de opdrachten in het bestand stap voor stap door.
Klaar?
Je hoort van je docent hoe het ingevulde werkblad wordt nagekeken.
6.4 - Grafen
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Een kubus, balk, bol, piramide, prisma, allemaal voorbeelden van ruimtelijke figuren. In dit thema staan deze ruimtelijke figuren centraal.
Je bekijkt onder andere hoe ze er uit zien, hoe je ze kunt tekenen, welke doorsneden je van deze figuren kunt maken en hoe je de inhoud van deze ruimtelijke figuren kunt berekenen. Je leert ook ook werken met ruimtecoördinaten en je leert de Stelling van Pythagoras in de ruimte toe te passen.
Het thema ruimtelijke figuren bestaat uit de volgende paragrafen:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
In het thema 'Situaties en verbanden' ben je al heel wat verbanden tegengekomen. In dit thema ga je aan de slag met één soort verbanden, namelijk kwadratische verbanden.
Het thema kwadratisch verband bestaat uit de volgende pragrafen:
8.1 Formule-grafiek
8.2 Parabool
8.3 Oplossing
8.4 Twee oplossingen
8.1 - Formule-grafiek
Bestudeer uit de Kennisbank wiskunde de vier pagina's van het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Kwadratische verbanden in Excel
Je hebt vast al wel eens eerder met het programma Excel gewerkt.
In dit rekenprogramma kun je ook parabolen tekenen. Hoe dat gaat? Probeer maar eens.
Download het practicum Parabool in Excel.
Download ook het bijbehorende Excelbestand Parbool.xlsx.
Sla de bestanden op op een plaats waar je ze gemakkelijk terug kunt vinden.
Open het pdf-bestand.
Werk de opdrachten in het bestand stap voor stap door.
Klaar?
Je hoort van je docent hoe het ingevulde werkblad wordt nagekeken.
Examenvragen
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren.
De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook
wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
Je hebt de knopjes 'cos', 'sin' en 'tan' vast al eens op je rekenmachine zien staan. Deze knopjes heb je soms nodig als je de hoek van een driehoek of de lengte van een zijde van een driehoek wilt berekenen.
Het berekenen van hoeken of zijden met behulp van cos(inus), sin(us) en tan(gens) wordt ook wel goniometrie genoemd; de naam van dit thema.
In de filmpjes hieronder wordt uitgelegd hoe je een en ander kunt berekenen voor de tangens
het zijn filmpjes van de wiskunde academie
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
11.1 Boomdiagram
11.2 Tabel maken en lezen
11.3 Wegendiagram lezen en maken
11.4 Kansberekening
11.5 Verwachting
Leerdoelen
Aan het eind van dit hoofdstuk weet je
wat een boomdiagram is en hoe je mogelijkheden overzichtelijk kunt weergeven in een boomdiagram.
dat in sommige gevallen een tabel een handig hulpmiddel is om de mogelijkheden van een telprobleem weer te geven.
wat een wegendiagram is en weet je hoe je het aantal combinaties die in een wegendiagram
zijn weergegeven kunt berekenen.
wat iemand bedoelt als hij zegt dat de kans op een gebeurtenis 70% is.
dat het maken van een boom- of wegendiagram kan helpen bij het berekenen van de kans
op een bepaalde gebeurtenis.
dat je met de verwachting kunt aangeven hoe vaak een bepaalde gebeurtenis waarschijnlijk voorkomt.
11.1 Boomdiagram
Wat je in deze paragraaf gaat leren:
- Hoe kun je gegevens in een boomdiagram tekenen
- Hoe kun je de verschillende mogelijkheden berekenen met een
boomdiagram
opgave 1
kennisbank
opgave 2
opgave 3
opgave 4
bekijk het filmpje
opgave 5
opgave 6
\
Antwoorden en uitwerkingen worden beschikbaar via meneer Emmerzaal of meneer Vriends.
Bekijk de leertaak om te zien waar je antwoorden aan moeten voldoen.
11.2 Tabel
Wat je in deze paragraaf gaat leren:
- Hoe kun je gegevens makkelijk rangschikken in een tabel
- Hoe kun je het aantal mogelijkheden snel berekenen met behulp van een tabel
opgave 1
kennisbank
opgave 2
opgave 3
opgave 4
bekijk het fimpje
opgave 5
opgave 6
EXTRA opgave 7
Antwoorden en uitwerkingen kun je krijgen via meneer Emmerzaal of meneer Vriends.
Kijk in je leertaak waar je antwoorden en uitwerkingen aan moeten voldoen.
11.3 Wegendiagram
Wat je in deze paragraaf gaat leren:
- Hoe kun je gegevens in een wegendiagram tekenen
- Hoe kun je de verschillende mogelijkheden berekenen met een
wegendiagram
opgave 1
kennisbank
opgave 2
opgave 3
bekijk het fimpje
opgave 4
opgave 5
opgave 6
bekijk het filmpje
opgave 7
opgave 8
Antwoorden en uitwerkingen kun je krijgen van meneer Emmerzaal of meneer Vriends.
Via de leertaak kun je zien waar je antwoorden aan moeten voldoen.
11.4 Kans
Wat je in deze paragraaf gaat leren:
- Hoe kun een kans berekenen bij een situatie
- Hoe kun je de verschillende kansen berekenen
opgave 1
kennisbank
opgave 2
opgave 3
opgave 4
opgave 5
bekijk het filmpje
opgave 6
opgave 7
opgave 8
bekijk het filmpje
opgave 9
Antwoorden en uitweringen zijn te verkrijgen via meneer Emmerzaal of meneer Vriends
In de leertaak kun je zien waar de antwoorden aan moeten voldoen.
11.5 Verwachting
Wat je in deze paragraaf gaat leren:
- Hoe kun je een verwachting berekenen bij een bepaalde situatie
- Hoe kun je de verschillende verwachtingen berekenen bij een tabel of diagram
opgave 1
kennisbank
opgave 2
kennisbank
opgave 3
opgave 4
opgave 5
opgave 6
Antwoorden en uitwerkingen kun je krijgen via mevrouw Emmerzaal of meneer Vriends.
In de leertaak staat waar de opdrachten aan moeten voldoen.
Samenvatting
Diagnostische toets
Als je deze toets gaat maken, zorg ervoor dat je alle overige opdrachten gemaakt hebt.
Deze toets is een goede voorbereiding op de vragen over hoofdstuk 11 in het PTA.
Succes!
Lees de vragen goed.
Schrijf je berekening erbij of geef een uitleg hoe je aan je antwoord komt.
Teken met potlood en geodriehoek.
opgave 1
opgave 2
opgave 3
opgave 4
opgave 5
opgave 6
opgave 7
opgave 8
opgave 9
opgave 10
opgave 11
opgave 12
Als je deze vragen gemaakt hebt, kun je aan de docent een antwoordmodel vragen.
Hieronder vind je nog een aantal invulvragen en meerkeuzevragen.
Aan de eind van de toets zie je je score.
Zorg dat je ongeveer 80% van het te behalen aantal punten haalt.
Aan het eind van je toets kun je van de vragen die je fout had, zien wat het goede antwoord was.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
Kijk de oefenPTA, nadat je hem gemaakt hebt, goed na!
oefenPTA opgave 1
oefenPTA opgave 2
oefenPTA opgave 3
oefenPTA opgave 4
oefenPTA opgave 5
oefenPTA opgave 6
oefenPTA opgave 6
oefenPTA opgave 7
oefenPTA opgave 8
oefenPTA opgave 9
oefenPTA opgave 10
oefenPTA opgave 11
oefenPTA opgave 12
oefenPTA opgave 13
oefenPTA opgave 14
Antwoorden komen in de leertaak.
PTA H11+12
Als je de volgende opgaven maakt, heb je een goede voorbereiding op je PTA.
opgave 1
opgave 2
opgave 3
opgave 4
opgave 5
opgave 6
opgave 7
opgave 8
opgave 9
opgave 10
opgave 11
opgave 12
opgave 13
PTA 1: H1, 2, 3 en 5
Om jullie goed voor te bereiden voor het eindexamen gaan we verschillende hoofdstukken herhalen.
We gaan nu H1, 2, 3 en 5 herhalen en daar krijgen jullie een PTA over.
Er zijn niet zo heel veel weken meer voor jullie gaan starten met de examens.
Het is niet slim als je de vragen die je nu hebt op het examen nog hebt dus zorg dat je dit tijdens de lessen te weten komt.
Het is heel erg belangrijk dat je in de lessen vragen stelt!!
Hoe gaan we deze hoofdstukken herhalen?
- maak de oefenopdrachten per onderwerp. Hiertussen staan ook de belangrijkste kennisbanken die je moet weten.
- maak examenopdrachten
Stel regelmatig (veel) vragen.
Samenvattingspowerpoints
Van hoofdstuk 3 en 5 zijn powerpoints beschikbaar.
Je kan ook in deze powerpoint kijken, deze gaat over hoofdstuk 3. POWERPOINT
Je kan ook in deze powerpoint kijken, deze gaat over hoofdstuk 5. POWERPOINT (bekijk tot en met paragraaf 5.5)
Hoofdstuk 1 - oefenopdrachten
kennisbank
PTA 1.1: opgave 1
kennisbank
PTA 1.1: opgave 2
PTA 1.1: opgave 3
kennisbank
PTA 1.1: opgave 4
PTA 1.1: opgave 5
kennisbank
PTA 1.1: opgave 6
PTA 1.1: opgave 7
PTA 1.1: opgave 8
kennisbank
PTA 1.1: opgave 9
kennisbank
PTA 1.1: opgave 10
PTA 1.1: opgave 11
Mocht je van bovenstaande opdachten over procenten nog veel fouten gemaakt hebben, oefen dan extra met de opgaven 4 MAVO ONDERDEEL PROCENTENAntwoorden
kennisbank
PTA 1.1: opgave 12
PTA 1.1: opgave 13
kennisbank
PTA 1.1: opgave 14
PTA 1.1: opgave 15
Mocht je van bovenstaande opdachten over verhoudingen nog veel fouten gemaakt hebben, oefen dan extra met de opgaven 4 MAVO ONDERDEEL VERHOUDINGENAntwoorden
Een fabrikant wil sandwiches op een mooie manier verpakken. Hiernaast zie je drie sandwichverpakkingen die hij als voorbeeld heeft gebruikt. De zijvlakken van de verpakkingen zijn rechthoeken en driehoeken.
Hieronder staat een tekening van zo’n verpakking.
De afmetingen van de verpakking zijn: AE = 20 cm, AB = 18 cm, EF = 7 cm, hoek A = 40° en hoek B = 78°.
Op de uitwerkbijlage is een begin gemaakt met de uitslag van de verpakking op schaal 1 : 4.
Maak de uitslag verder af. Zet de letters erbij.
Meten en meetkunde opdracht 6
Verfblikken zijn er in allerlei maten. Zie de foto hieronder. In deze opgave gaan we steeds uit van een wiskundig model van een verfblik: een cilinder met een cirkel als bodem en een cirkel als deksel. We houden geen rekening met de dikte van het blik.
Een verfblik heeft een hoogte van 14 cm en een straal van 8 cm.
Teken op schaal 1:4 de uitslag van dit verfblik. Schrijf op hoe je de maten van je tekening gevonden hebt.
Hieronder een schets van een bouwkavel met een huis. De familie zoekt nog een plek voor de afvalcontainers. Deze willen ze zó op het terras plaatsen dat ze niet zichtbaar zijn vanuit de woonkamer.
Kleur op de uitwerkbijlage het hele gebied van het terras dat niet zichtbaar is vanuit de woonkamer. Laat zien hoe je aan je antwoord komt.
Op de uitwerkbijlage staat een kaart van de Grote Oceaan. Op deze kaart ligt Paaseiland op een afstand van 3,2 cm van de Galapagoseilanden, op 1,5 cm van het eiland Pitcairn en op 4,8 cm van het eiland Kiribati.
Geef op de uitwerkbijlage met punt P aan waar Paaseiland ligt. Laat duidelijk zien hoe je aan je antwoord gekomen bent.
Meten en meetkunde opdracht 9
In een pretpark staat een zweefmolen die Vertical Swing wordt genoemd. In de tekening zie je een gedeelte van de zweefmolen met twee armen en aan één arm een kabel en een stoeltje. De kabel KS heeft een lengte van 8 meter. Als de zweefmolen op een bepaalde snelheid is, maakt de kabel met de arm een hoek van 132°.
Als de zweefmolen op topsnelheid is , is de afstand van het midden van de zweefmolen (M) tot het stoeltje (S) 12,6 meter. Als de zweefmolen één keer ronddraait, legt het stoeltje een bepaalde afstand af.
Bereken hoeveel meter deze afgelegde afstand is. Schrijf je berekening op.
Meten en meetkunde opdracht 10
In kubus ABCD EFGH met zijden van 5 cm is driehoek ACF getekend. Punt S is het snijpunt van de diagonalen AC en BD.
Muriël snijdt van deze kubus de piramide met grondvlak ABC en top Faf.
Bereken hoeveel cm3 de inhoud van de figuur is, die overblijft. Schrijf je berekening op.
.
Meten en meetkunde opdracht 11
Bekijk het uitlegfilmpje over inhoud van een prisma
In het assenstelsel is een prisma getekend. De maten in cm staan erbij.
Er geldt dat AB = CD en AE = DE.
Bereken hoeveel liter de inhoud van het prisma is. Schrijf je berekening op.
.
Meten en meetkunde opdracht 12
Laurens wil een poort metselen voor in zijn tuin.
Er komen stenen langs de boog EF, zie de schets links.
Boog EF is een deel van een cirkel met middelpunt M en een straal van 1,13 meter. Hoek M in driehoek EMF is 154°.
De stenen zijn 7 cm breed. Zie de schets rechts.
Bereken hoeveel hele stenen langs cirkelboog EF komen. Schrijf je berekening op.
.
Meten en meetkunde opdracht 13
In een pretpark staat een zweefmolen die Vertical Swing wordt genoemd.
De zweefmolen heeft 12 armen op gelijke afstand van elkaar, waaraan kabels met stoeltjes hangen.
In het bovenaanzicht zie je de armen A en B aangegeven.
Bereken hoeveel graden de hoek tussen arm A en arm B is. Schrijf je berekening op.
.
Meten en meetkunde opdracht 14
Op de foto zie je een kunstwerk, dat IJslandse kinderen samen met de Engelse wiskundige en kunstenaar Edmund Harriss hebben gebouwd.
Hiervoor werden 20 dezelfde puzzelstukken gebruikt.
In de afbeeldingen hieronder zie je hoe zo’n puzzelstuk gemaakt wordt.
Op elke zijde van een gelijkzijdige driehoek worden vier cirkels getekend.
Het puzzelstuk wordt uitgezaagd volgens cirkelvormige lijnen.
De puzzelstukken passen in elkaar zoals afgebeeld.
Teken de cirkelvormige lijn waarlangs gezaagd moet worden, zodat een puzzelstuk ontstaat.
.
Meten en meetkunde opdracht 15
De puzzelstukken passen in elkaar zoals afgebeeld.
Het zwarte puzzelstuk uit afbeelding c staat ook op de uitwerkbijlage. Onder de afbeelding staat een tabel, waarin je gegevens over de symmetrie van het puzzelstuk kunt invullen.
In het assenstelsel is een prisma getekend. De maten in cm staan erbij.
Er geldt dat AB = CD en AE = DE.
Bereken hoeveel cm EH is. Schrijf je berekening op. Rond je antwoord af op een geheel getal.
Meten en meetkunde opdracht 17
Gegeven is de gelijkzijdige driehoek ABC met zijden van 35 cm. In de driehoek zijn de hoogtelijnen getekend. Deze hoogtelijnen snijden elkaar in punt S.
Bereken hoeveel cm2 de oppervlakte van driehoek ABC is.
Schrijf je berekening op.
Op de foto zie je een leerling in Kenia in zijn schoolbank zitten.
Het tafelblad is voor deze leerling te hoog. De school wil daarom banken in verschillende maten gaan maken die goed passen bij de leerlingen. In de tabel hieronder zie je welke maat schoolbank bij welke leerling past.
Deze tabel kan zo voortgezet worden.
Welke maat schoolbank heeft een leerling met een lengte van 1,90 m nodig? Leg je antwoord uit.
Omgaan met verbanden opdracht 2
Kijk nog eens naar de foto bij vraag 1.
Bij elke maat schoolbank hoort een bepaalde zithoogte. Hieronder zie je een tabel, waarin de maat van de schoolbank en de bijbehorende zithoogte in cm staat.
Leg met een berekening uit waarom er geen schoolbanken met maat 30 gemaakt zullen worden.
Omgaan met verbanden opdracht 3
We bekijken de groei van een maisplant.
Op 1 mei wordt een zaadje in de grond gestopt. Na 12 dagen komt er een blad boven de grond. Neem aan dat er daarna om de 6 dagen een nieuw blad bijkomt.
Onderstaande foto’s zijn om de 6 dagen genomen.
Op de derde foto kun je zien dat het vijfde blad erbij is gekomen.
Bepaal met de gegevens op welke datum deze foto gemaakt is.
Leg uit hoe je aan je antwoord komt.
Omgaan met verbanden opdracht 4
In figuur 1 zie je een vierkant. Dit vierkant wordt in tweeën gedeeld, dan ontstaat figuur 2. Daarna wordt een helft weer in tweeën gedeeld (figuur 3) enzovoort. Dit kan eindeloos zo doorgaan. Eén driehoek wordt steeds grijsgekleurd.
Het vierkant heeft een zijde van 32 cm.
Er is een verband tussen de oppervlakte van de grijze driehoek O en het figuurnummer f.
Bij elke maat schoolbank hoort een bepaalde zithoogte. Hieronder zie je een tabel, waarin de maat van de schoolbank en de bijbehorende zithoogte in cm staat.
Er is een lineair verband tussen de zithoogte en de maat van de schoolbank.
Geef een woordformule die bij dit verband hoort.
Omgaan met verbanden opdracht 6
In Duitsland kostte een huis op 1 januari 1996 gemiddeld 190 000 euro.
Op 1 januari 2008 was deze prijs gedaald tot 160 000 euro.
Ga ervan uit dat de daling van de huizenprijs in Duitsland lineair was en in de jaren na 2008 op dezelfde manier doorgaat.
Hoeveel euro zou een huis in Duitsland dan gemiddeld kosten op 1 januari 2020?
Laat zien hoe je aan je antwoord komt.
Omgaan met verbanden opdracht 7 Uitlegfilmpje Formule bij een grafiek maken
De landen waarin olie geproduceerd wordt, gebruiken een deel van de olie zelf. In de grafiek zie je het eigen gebruik van olie van één van deze landen in de afgelopen jaren. Bij deze grafiek hoort een lineair verband.
Geef een formule die hoort bij de grafiek.
Neem voor het aantal jaren na 2000 de letter t en voor het eigen gebruik in duizend tonnen de letter G.
De prijs van een taxirit wordt bepaald door een instaptarief en een kilometertarief. Een rit tot twee kilometer kost alleen het instaptarief. Is de rit langer dan twee kilometer, dan komt er nog een bedrag bij voor elke extra kilometer.
Het taxibedrijf heeft een dagtarief en een nachttarief.
In de tabel hieronder staan deze tarieven voor personentaxi’s.
Hieronder is de grafiek voor het nachttarief getekend.
Bepaal vanaf hoeveel hele kilometers een taxirit volgens het nachttarief bij Pentax meer dan € 25,00 kost.
Laat zien hoe je aan je antwoord komt. Je mag de grafiek gebruiken.
Omgaan met verbanden opdracht 9
Bekijk eerst de twee uitlegfilmpjes over werken met exponentiële verbanden
In 2014 waren er in Nederland 8 miljoen auto's. De verwachting is dat dit aantal auto's de komende jaren blijft groeien.
Jens denkt dat er per jaar 200 000 auto's per jaar bij zullen komen.
Manou denkt dat het aantal auto's met 2,5% per jaar zal groeien.
Volgens wie zal het aantal auto's dan het eerst de grens van 12 miljoen bereiken? Laat met een berekening zien hoe je aan je antwoord komt.
Omgaan met verbanden opdracht 10
Onderzoekers voorspelden dat de gemiddelde huizenprijs met 5% per jaar zou dalen.Op 1 januari 2008 was de gemiddelde huizenprijs in Nederland afgerond 250 000 euro. Vanaf dat moment begonnen de huizenprijzen te dalen.
Bereken in welk jaar de gemiddelde huizenprijs op 1 januari voor het eerst lager is dan 200 000 euro. Laat zien hoe je aan je antwoord komt.
De snelheid van het geluid is lager als de temperatuur van de lucht lager is.
Voor de snelheid van het geluid in lucht kan de volgende formule gebruikt worden
\(v= 20 \cdot \sqrt{273 +T}\)
Hierin is v de snelheid van het geluid in m/s en t de luchttemperatuur in °C.
Hieronder is de grafiek die hoort bij bovenstaande formule getekend.
De grafiek lijkt op een rechte lijn.
Leg aan de hand van de formule uit waarom de grafiek geen rechte lijn kan zijn.
Omgaan met verbanden opdracht 12
Nynke staat op een uitkijktoren.
Het kijkbereik is de afstand die je bij helder weer kunt kijken. Het kijkbereik hangt af van de hoogte waarop je staat. De formule die bij benadering het verband aangeeft tussen de hoogte waarop je staat en het kijkbereik is.
\(K= 2 \times \sqrt{\pi \times H}\)
Hierin is k het kijkbereik in kilometer en H de hoogte waarop je staat in meter.
Nynke denkt dat als de hoogte waarop je staat tweemaal zo groot is, het kijkbereik dan ook tweemaal zo groot is.
Heeft Nynke gelijk? Laat zien hoe je aan je antwoord komt. (noteer berekeningen)
.
Omgaan met verbanden opdracht 13
Voordat je aan opdracht 13 t/m 15 gaat werken kijk je eerst het uitlegfilmpje over kwadratische verbanden
Om te oefenen met gewichtloosheid maken astronauten paraboolvluchten.
Het vliegtuig vliegt op een hoogte van 6100 meter. Op een zeker moment zet de piloot de motoren op vol vermogen en gaat het vliegtuig steil omhoog. Op een bepaalde hoogte zet de piloot de motoren uit (in de tekening bij t = 0). Het vliegtuig volgt vanaf dat moment een baan in de vorm van een bergparabool. We noemen dat de parabolische baan. In die parabolische baan heerst er in het vliegtuig gewichtloosheid.
Na 22 seconden verlaat het vliegtuig die parabolische baan en daalt dan weer naar 6100 meter.
De hoogte van het vliegtuig tijdens de parabolische baan kan worden berekend met de volgende formule:
\(Hoogte = - 4,91 \times (t - 11)^2 +8500\)
Hierin is de hoogte in meters en t de tijd in seconden.
Bij t = 0 begint de parabool en bij t = 22 eindigt de parabool.
Bereken hoeveel meter de maximale hoogte van het vliegtuig is tijdens het vliegen van de parabolische baan. Schrijf je berekening op.
.
Omgaan met verbanden opdracht 14
Na de 68 seconden van de eerste paraboolvlucht vliegt het vliegtuig 15 seconden verder op een hoogte van 6100 meter en dan begint de tweede paraboolvlucht. In de uitwerkbijlage is de grafiek getekend van de hoogte van het vliegtuig in meters tijdens de eerste paraboolvlucht en de 15 seconden erna.
Teken in deze figuur op de uitwerkbijlage de grafiek van de tweede paraboolvlucht erbij. Geef duidelijk het beginpunt, toppunt en eindpunt van de paraboolvlucht aan.
Omgaan met verbanden opdracht 15
.James wil een kippenren aanleggen in de vorm van een rechthoek. Hij gebruikt 15 meter gaas om de kippenren rondom af te zetten. De oppervlakte van de kippenren kan James berekenen met de formule:
\(Oppervlakte = 7,5 \times lengte - lengte^2\)
Hierin is lengte in meter en oppervlakte in m2.
De grafiek die bij de formule hoort is een parabool. James denkt dat bij de top van de parabool de lengte precies gelijk is aan 4.
Laat met een berekening of James gelijk heeft.
.
Omgaan met verbanden opdracht 16
Voordat je deze opdracht gaat maken, kijk je eerst de twee uitlegfilmpje over:
In de grafiek hier onder is bij benadering af te lezen hoe groot de zonnehoek gedurende het jaar in Nederland is.
Op 21 juni staat de zon het hoogst en is de zonnehoek 61,5°.
Op 21 december staat de zon het laagst en is de zonnehoek 14,5°.
Bereken van de grafiek de amplitude. Schrijf je berekening op.
Omgaan met verbanden opdracht 17
Geluiden zijn trillingen in de lucht. Een geluid verplaatst zich door de lucht. We spreken dan over geluidsgolven.
Geluid kan zichtbaar worden gemaakt met een apparaat dat een geluidstrilling omzet in een elektrische trilling.
Hierboven zie je wat het apparaat weergeeft bij twee verschillende geluiden. Elk van deze plaatjes geeft een aantal trillingen weer in een bepaalde tijd (bijvoorbeeld 1 milliseconde).
Het aantal trillingen per seconde noemen we de frequentie van het geluid.
Bij welke figuur hoort een hogere frequentie? Leg uit hoe je aan je antwoord komt
Omgaan met verbanden opdracht 18 Van een geluid duurt één trilling 0,8 milliseconde.Geluiden zijn trillingen in de lucht. Een geluid verplaatst zich door de lucht. We spreken dan over geluidsgolven.
1 seconde = 1000 milliseconden.
Hoeveel trillingen zijn dat in 1 minuut? Schrijf je berekening op.
Omgaan met verbanden opdracht 19
Geluiden zijn trillingen in de lucht. Een geluid verplaatst zich door de lucht. We spreken dan over geluidsgolven.
Hieronder staat de grafiek van een geluidsgolf, f.
Geluidsgolf h heeft dezelfde amplitude als geluidsgolf f. De periode van geluidsgolf h is de helft van de periode van geluidsgolf f.
Teken in de figuur op je uitwerkbijlage één periode van geluidsgolf h.
Omgaan met verbanden opdracht 20
In de periode 1995 - 2002 is het aantal telecomwinkels in Nederland bij benadering exponentieel gestegen volgens de formule:
\(A=115\times1,27^t\)
Hierin is A het aantal telecomwinkels in Nederland en t het aantal jaren na 1995. In 1995 waren er 115 telecomwinkels.
Vanaf 2001 groeide het aantal telecomwinkels minder snel. Economen denken dat de groei ongeveer zou plaatsvinden zoals op onderstaande grafiek staat.
In welk jaar zou volgens de grafiek het aantal telecomwinkels in Nederland voor het eerst meer dan tien keer zo groot zijn als in 1995?
Laat in de grafiek zien hoe je aan je antwoord komt.
Omgaan met verbanden opdracht 21
Er is een verband tussen het benodigde vermogen van een houtkachel en de inhoud van de te verwarmen ruimte. Ook hangt het benodigde vermogen af van de isolatie van de ruimte.Het vermogen van een houtkachel is de hoeveelheid warmte die de kachel kan produceren. Dit vermogen wordt aangegeven in kilowatt (kW).
Hieronder zijn in een assenstelsel drie grafieken getekend die dit verband weegeven.
De familie Van Dam heeft een redelijk geïsoleerd huis. Hun woonkamer heeft een inhoud van 60 m3. Zij hebben een houtkachel waarvan het vermogen goed bij de inhoud van de kamer past.
Lees uit de grafiek af hoeveel kW vermogen deze houtkachel heeft. Laat in de grafiek zien hoe je aan je antwoord komt.
Omgaan met verbanden opdracht 22
In een niet geïsoleerde kamer met een inhoud van 80 m3 staat een houtkachel die, wat betreft vermogen, goed bij deze kamer past. Deze kamer wil men groter maken en daarna goed isoleren. Men wil dezelfde houtkachel behouden.
Met hoeveel m3 kan de inhoud van de kamer maximaal worden vergroot zonder dat het vermogen van de houtkachel hoeft te veranderen? Gebruik de grafieken en laat zien hoe je aan je antwoord komt.
Een ijsberg die naar het zuiden drijft, wordt kleiner doordat hij langzaam smelt. Onderzoekers hebben het gewicht van zo’n ijsberg geschat, zie de tabel.IJsbergen ontstaan doordat grote stukken ijs afbreken van een gletsjer en dan de zee in drijven.
T (maanden)
0
2
4
6
8
10
G (tonnen)
80 000
70 000
62 000
55 000
48 000
41000
In de tabel is t de tijd in maanden na het afbreken van de ijsberg en G het geschatte gewicht van de ijsberg in ton.
De onderzoekers hebben een formule gemaakt die goed bij de tabel past:
Op de uitwerkbijlage staat een assenstelsel getekend.
Teken in het assenstelsel de grafiek die bij de formule hoort. Gebruik hierbij de tabel. Maak zelf een juiste verdeling bij de verticale as.
Omgaan met verbanden opdracht 24
Windkracht wordt uitgedrukt in Beaufort (Bft).
Een windkracht van 6 Bft wordt een krachtige wind genoemd.
De windkracht is afhankelijk van de gemiddelde windsnelheid. Bij benadering kun je de gemiddelde windsnelheid berekenen met de formule
\(S=k\times(1+0,14\times k)\)
Hierin is s de gemiddelde windsnelheid in m/s en k de windkracht in Bft.
Teken in het assenstelsel op de uitwerkbijlage de grafiek die bij de formule hoort. Vul eerst de tabel op de uitwerkbijlage in.
Omgaan met verbanden opdracht 25
Hieronder zie je een grafiek van het verloop van de gemiddelde huizenprijs in Duitsland tussen 1996 en 2008.
In Duitsland kostte een huis op 1 januari 1996 gemiddeld 190 000 euro.
Op 1 januari 2008 was deze prijs gedaald tot 160 000 euro.
De huizenprijzen in Nederland zijn in de periode van 1996 tot 2008 juist gestegen.
Op 1 januari 1996 was de gemiddelde huizenprijs afgerond 100 000 euro. Bij benadering steeg de gemiddelde huizenprijs in Nederland in deze periode elk jaar met 12 500 euro.
In welk jaar was de gemiddelde huizenprijs in Nederland op 1 januari voor het eerst hoger dan in Duitsland?
Gebruik de grafiek op de uitwerkbijlage om je antwoord uit te leggen.
Omgaan met verbanden opdracht 26
Het kijkbereik is de afstand die je bij helder weer kunt kijken. Het kijkbereik hangt af van de hoogte waarop je staat. De formule die bij benadering het verband aangeeft tussen de hoogte waarop je staat en het kijkbereik is:Nynke staat op een uitkijktoren.
\(k = 2\times \sqrt{\pi \times H}\)
Hierin is k het kijkbereik in kilometer en h de hoogte waarop je staat in meter.
Op de uitwerkbijlage staat een assenstelsel. Teken de grafiek die bij de formule hoort. Vul hiervoor eerst de tabel in.
Omgaan met verbanden opdracht 27
De landen waarin die geproduceerd wordt gebruiken een deel van de olie zelf. In de grafiek zie je de hoeveelheid olie die het land geproduceerd heeft en het eigen verbruik. Bij beide grafieken hoort een lineair verband.
De geproduceerde olie die overbleef na eigen gebruik werd door dit land verkocht aan het buitenland.
Teken op de uitwerkbijlage de grafiek van de hoeveelheid olie die tussen 2000 en 2008 aan het buitenland verkocht werd.
Omgaan met verbanden opdracht 28
In 1900 waren er in Nederland 200 auto’s. In 1938 waren er al 80 000 auto’s. De groei was in deze jaren exponentieel volgens de formule
\(A=200 \times 1,17^t\)
Hierbij is A het aantal auto’s in Nederland en t het aantal jaren na 1900.
Klopte deze formule voor het aantal auto’s in 2014? Laat zien hoe je aan je antwoord komt. (berekening)
Omgaan met verbanden opdracht 29
Jsbergen ontstaan doordat grote stukken ijs afbreken van een gletsjer en dan de zee in drijven.
Een ijsberg die naar het zuiden drijft, wordt kleiner doordat hij langzaam smelt. Onderzoekers hebben het gewicht van zo’n ijsberg geschat, zie de tabel.
In de tabel is t de tijd in maanden na het afbreken van de ijsberg en G het geschatte gewicht van de ijsberg in ton.
De onderzoekers hebben een formule gemaakt die goed bij de tabel past:
Laat met een berekening zien dat in de twintigste maand volgens de formule ongeveer 1600 ton ijs gesmolten is.
Omgaan met verbanden opdracht 30
Het KNMI in De Bilt laat elke dag een weerballon op. Zo’n ballon is gevuld met heliumgas. Er hangt een zender aan de ballon, die gegevens over het weer doorgeeft.
De hoogte van de stijgende ballon wordt gegeven door de formule
Hierin is de hoogte in km en de tijd het aantal minuten nadat de ballon is losgelaten.
Bereken hoeveel km de ballon tijdens het tweede half uur is gestegen. Schrijf je berekening op.
Omgaan met verbanden opdracht 31
Windkracht wordt uitgedrukt in Beaufort (Bft).
Een windkracht van 6 Bft wordt een krachtige wind genoemd.
De windkracht is afhankelijk van de gemiddelde windsnelheid. Bij benadering kun je de gemiddelde windsnelheid berekenen met de formule
s = k × (1 + 0,14 × k)
Hierin is s de gemiddelde windsnelheid in m/s en k de windkracht in Bft.
De gevoelstemperatuur is afhankelijk van de windsnelheid en de luchttemperatuur. De gevoelstemperatuur kun je berekenen met de formule
g = 1,41 – 1,162 × s + 0,98 × l + 0,0124 × s2 + 0,0185 × s × l
Hierin is g de gevoelstemperatuur in graden Celsius, s de windsnelheid in m/s en l de luchttemperatuur in graden Celsius.
Op een bepaald moment is de luchttemperatuur 3 graden Celsius en is er een windkracht van 5 Bft.
Bereken hoeveel graden Celsius de gevoelstemperatuur op dat moment is. Schrijf je berekening op.
Omgaan met verbanden opdracht 32
IJsbergen ontstaan doordat grote stukken ijs afbreken van een gletsjer en dan de zee in drijven.
Een ijsberg die naar het zuiden drijft, wordt kleiner doordat hij langzaam smelt. Onderzoekers hebben het gewicht van zo’n ijsberg geschat, zie de tabel.
In de tabel is t de tijd in maanden na het afbreken van de ijsberg en G het geschatte gewicht van de ijsberg in ton.
De onderzoekers hebben een formule gemaakt die goed bij de tabel past:
G = 80 000 – 4900 x t + 113 x t2 - t3
Bereken in de hoeveelste maand na het afbreken van de ijsberg het laatste stukje van de ijsberg volgens de formule gesmolten moet zijn. Schrijf je berekening op.
In deze examentraining ga je aan de slag met een heel examen. Een wiskunde-examen bestaat gemiddeld uit zo'n 24 vragen verdeeld over een aantal opgaven. Je krijgt in onderdeel B per pagina de vragen van één opgave aangeboden. Voor je de vragen gaat maken, kun je de bijbehorende theorie uit de Kennisbank bestuderen.
Kennisbank
In de thema´s/opdrachten van de Stercollecties wiskunde wordt regelmatig verwezen naar de Kennisbank wiskunde. In de Kennisbank vind je de theorie die je nodig hebt voor het beantwoorden van de vragen en het maken van de opdrachten.
Exponentiële verbanden in Excel
Je hebt vast al wel eens eerder met het programma Excel gewerkt.
In dit rekenprogramma kun je ook de grafiek bij een exponentieel verband tekenen. Probeer maar eens.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
In het document met de link OEFENSTOF INKLEMMENmaak je steeds een uitgebreide inklemtabel.
Bereken de waarde zo nauwkeurig mogelijk soms wel 2 decimalen....
Schrijf het antwoord apart op met de juiste eenheid. bv Graden of cm
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
We noemen dit verband ook wel Omgekeerd evenrdig... (leg dat maar eens uit) Bestudeer eerst even de uitleg en maak daarna opgave V1 V2 en opgave 1-2-3 van de uitleg
2 In de link hieronder staan extra opgaven over Periodieke verbanden Periodieke verbanden
Lees de uitleg in het begin en maak de opgaven VI en opgave 3 en 4 en 5
3 In de link hieronder staan extra opgaven over Machtsverbanden Machtsverbanden
Lees de uitleg en maak met de formule uit d euitleg opgave 5
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Het arrangement Totaal 3&4M leerjaar 4 Mavo is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 3.0 Nederland licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Deze methode is samengesteld door Dhr. J. Vriends. Voor vragen of opmerkingen kunt u contact opnemen met Dhr. Vriends (docent/ontwikkelaar wiskunde).
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
Rearrangeerbare stercollectie wiskunde voor voor leerjaar 3 en 4 VMBO KGT van Stichting VO-content. De stercollectie is ontwikkeld op basis van de eindtermen voor het vak wiskunde.
Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO
Rearrangeerbare stercollectie wiskunde voor voor leerjaar 3 en 4 VMBO KGT van Stichting VO-content. De stercollectie is ontwikkeld op basis van de eindtermen voor het vak wiskunde.
Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Afronden
Schatten
Rekenregels
Verhoudingen
Verhoudingstabel
Vergelijken
Op schaal
Procenten
Erbij/eraf
Groeifactor
Rekenen 1 - A
Rekenen 1 - B
Tabel
Grafiek
Formule
Lettervariabelen
Rekenen met lettervariabelen
Rekenschema
Rekenschema en lettervariabelen
Situaties en verbanden
Lengtematen
Oppervlaktematen
Inhoudsmaten
Tijd en snelheid
Massa en dichtheid
Machten
Grote getallen
Kleine getallen
Wortels
Rekenen 2
Driehoeken
Pythagoras
Oppervlakte driehoek
Vergroten/verkleinen
Vierhoeken
Oppervlakte vierhoek
F- en Z-hoeken
Omtrek cirkel
Oppervlakte cirkel
Afstanden en gebieden
Vlakke figuren
Lineair verband
Formule maken
Vergelijking en oplossing
Oplossen met grafieken
Oplossen met rekenschema's
Balansmethode
Lineaire verbanden
Gegevens in beeld
Cirkeldiagrammen
Steel-bladdiagram
'Afstand'tabel
Infofiguren
Gemiddelde
Frequentietabel
Modus/mediaan
Informatie verwerking
Ruimtelijke figuren
Uitslagen en aanzichten
Grafen
Doorsnede
Inhoud
Inhoud2
Vergroten/verkleinen
Ruimtecoördinaten
Pythagoras in de ruimte
Ruimtelijke figuren
Formule/grafiek
Parabool
Oplossing zoeken
Twee oplossingen
Kwadratische verbanden
Exponentiele verbanden
Goniometrie
Statistiek
Andere verbanden
Exponentieel verband
Groeifactor
Formule
Oplossing zoeken
Tangens
Rekenen met de tangens
Sinus/cosinus
Hoeken en zijden sin/cos
In de ruimte
Boomdiagram
Tabel
Wegendiagram
Kans
Verwachting
Wortelverband
Machtsverband
Hyperbool
Periodiek verband
Meer dan 2 variabelen
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Ken je het 24-spel? Dit spel is geschikt om goed te leren hoofdrekenen.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. 
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
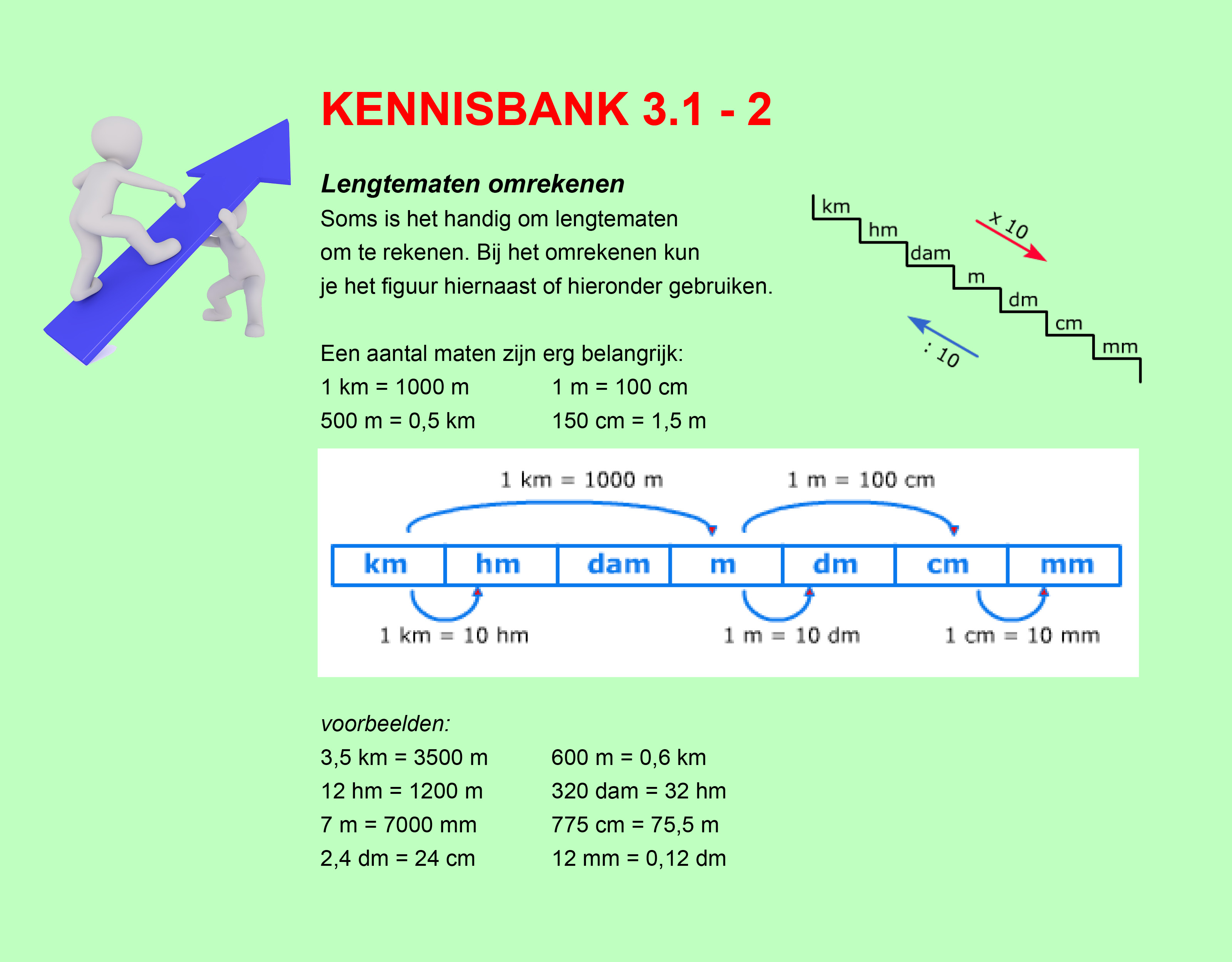
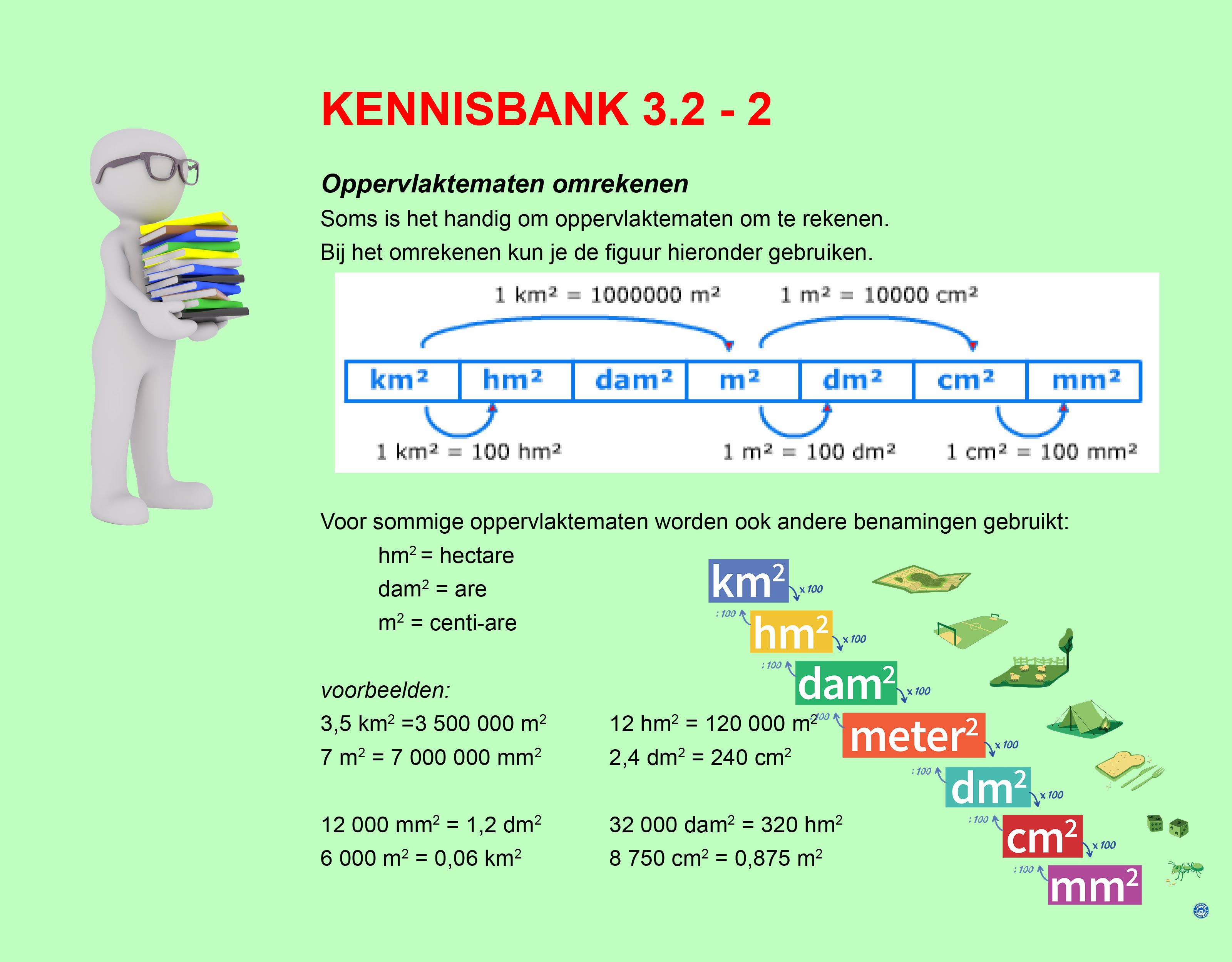
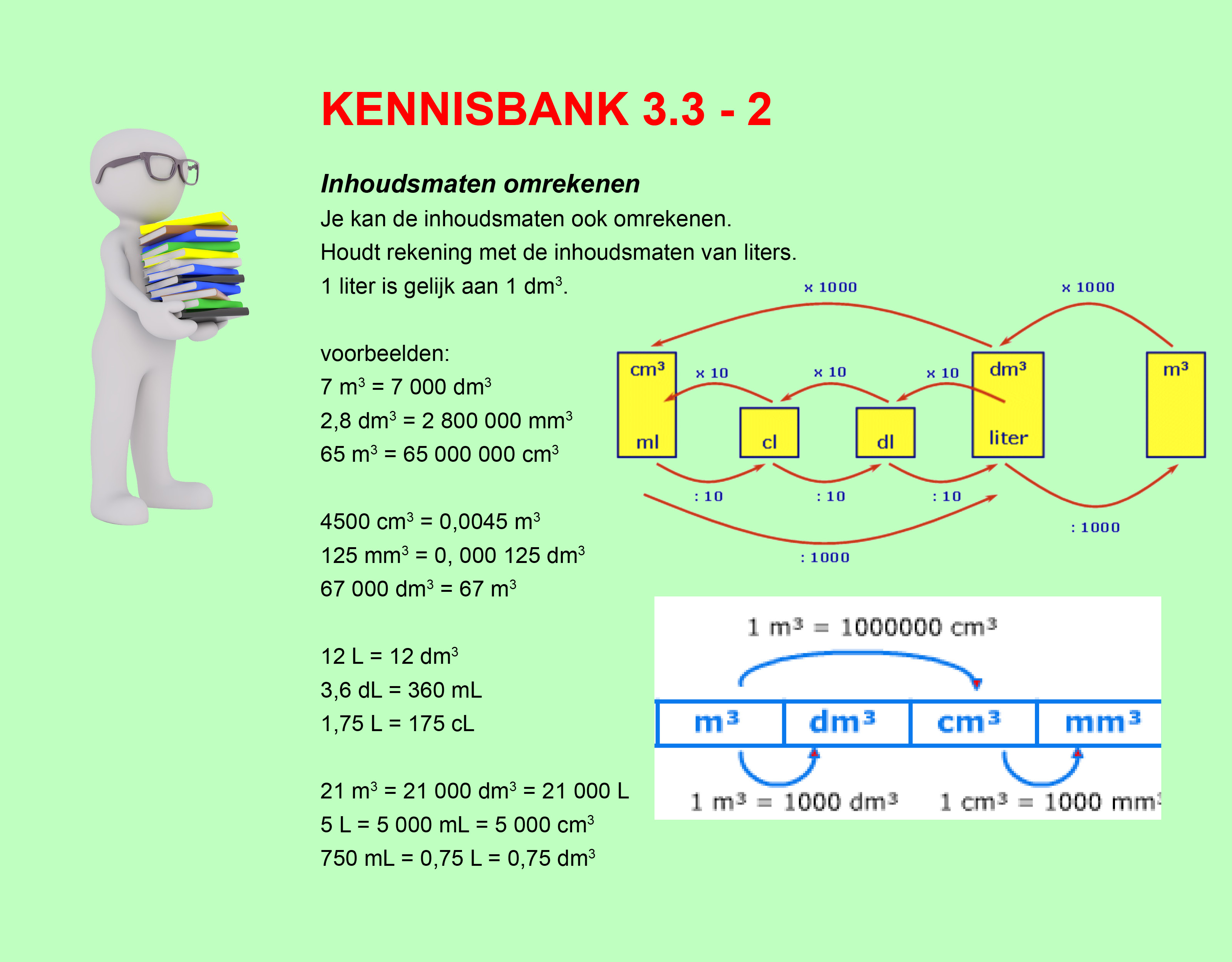
Bestudeer uit de Kennisbank wiskunde de twee pagina's van het onderdeel:
Rekenschema's en lettervariabelen
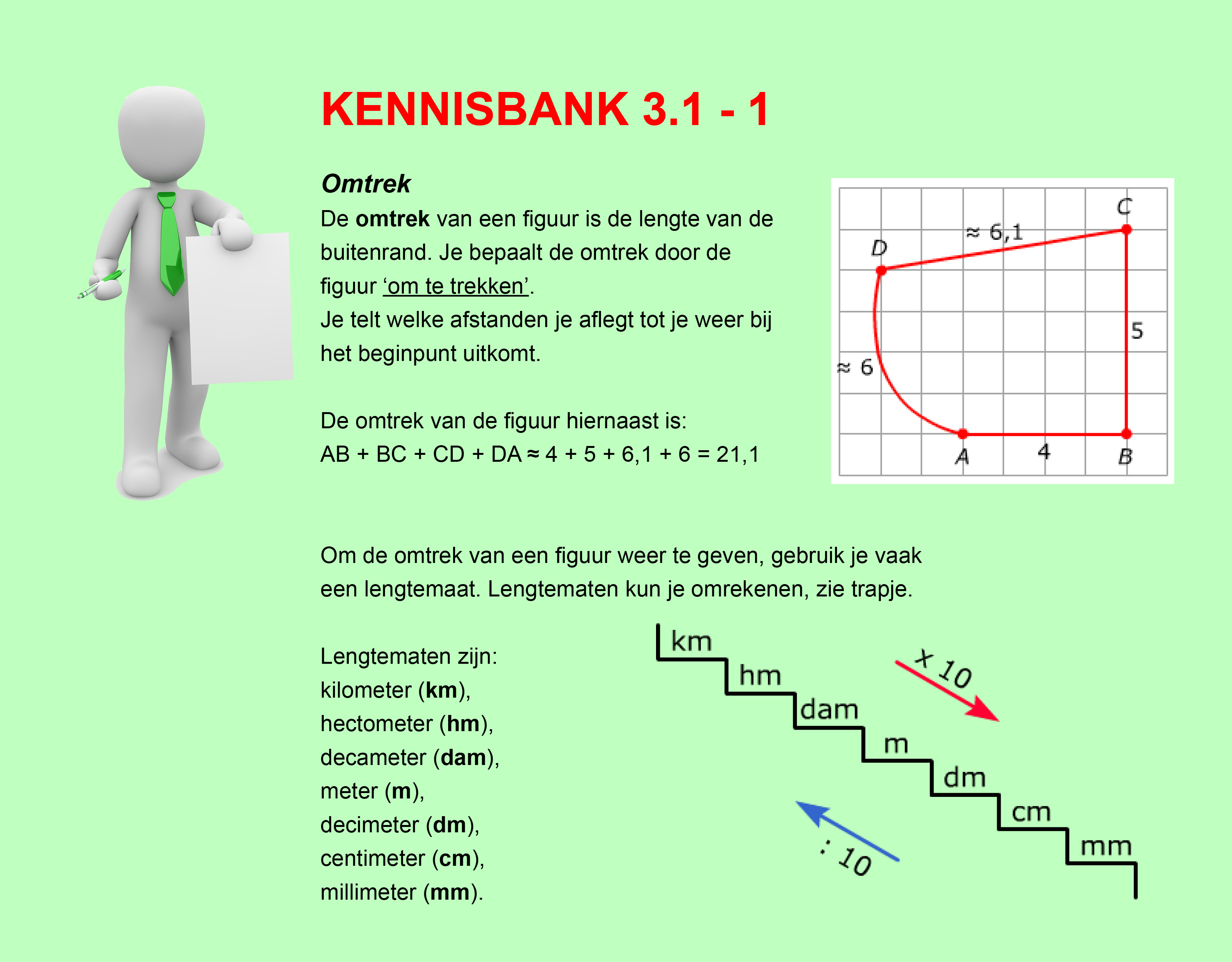
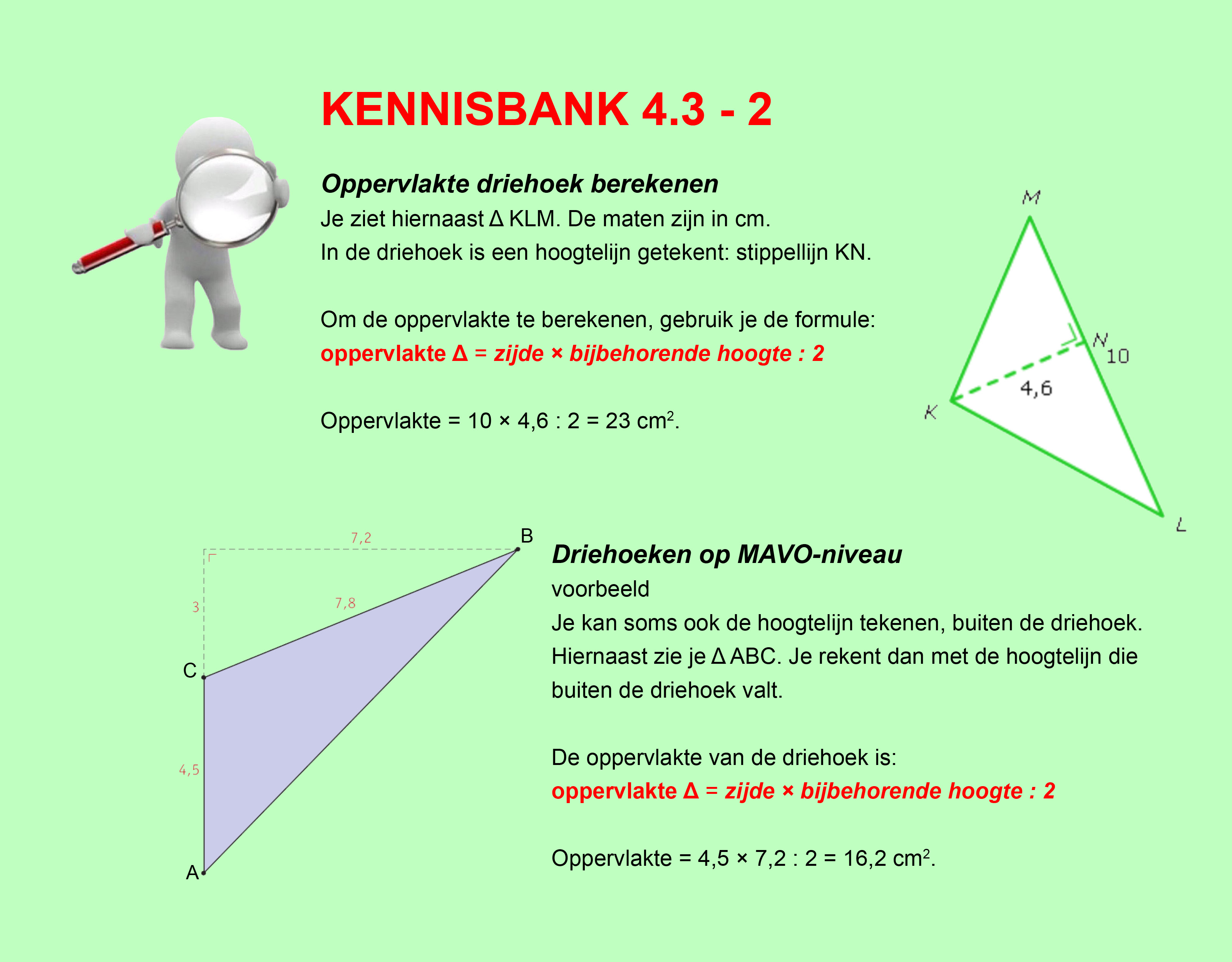
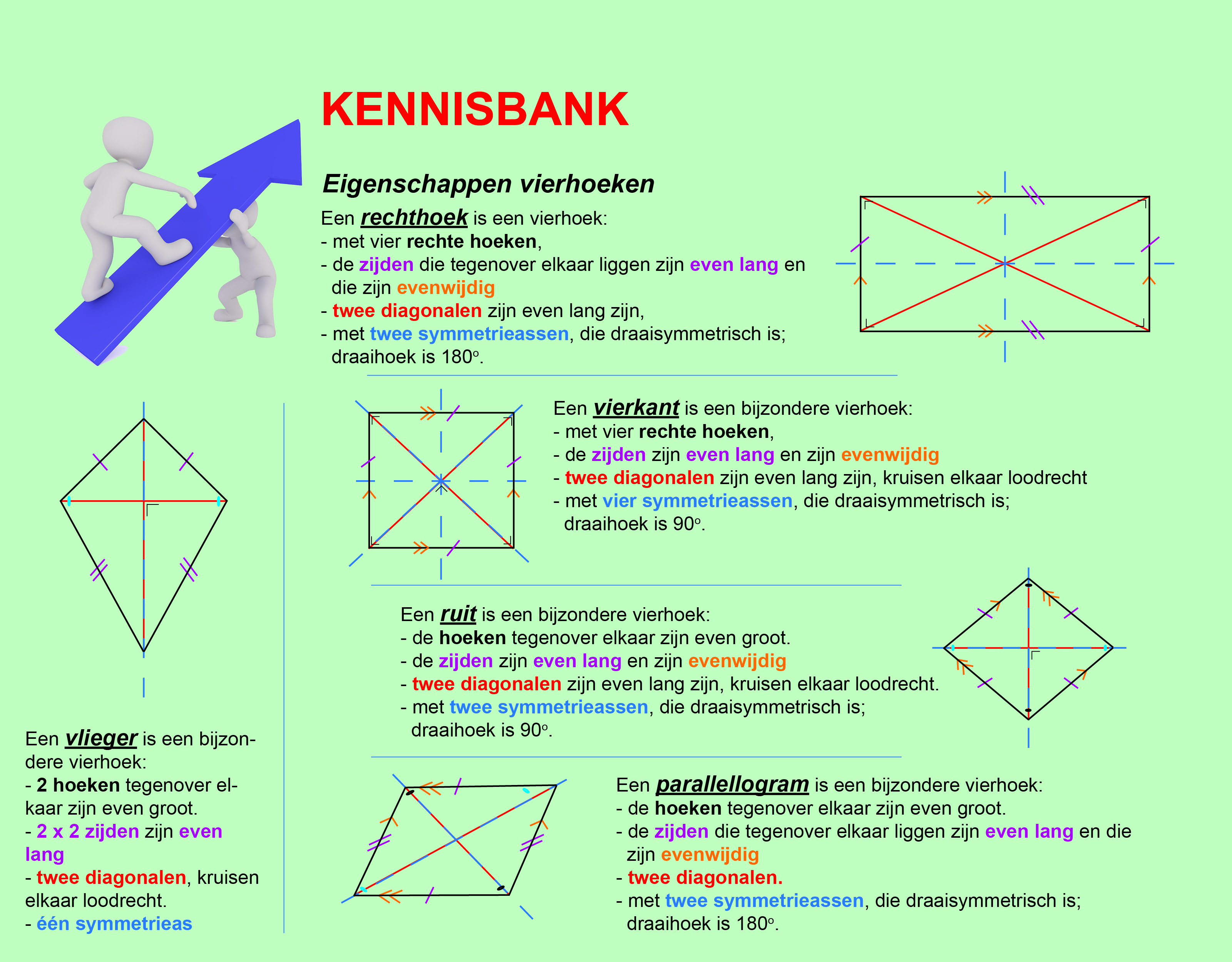
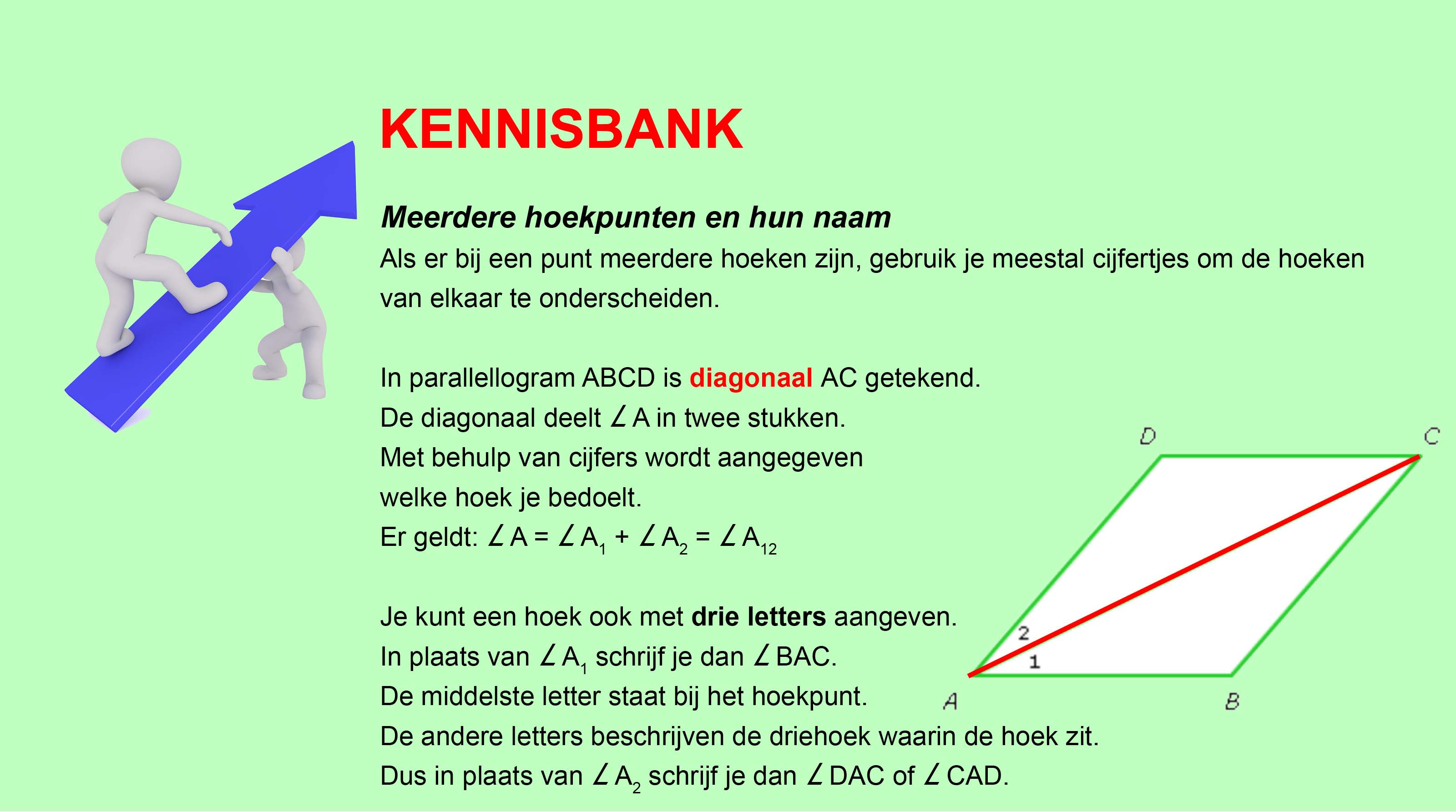
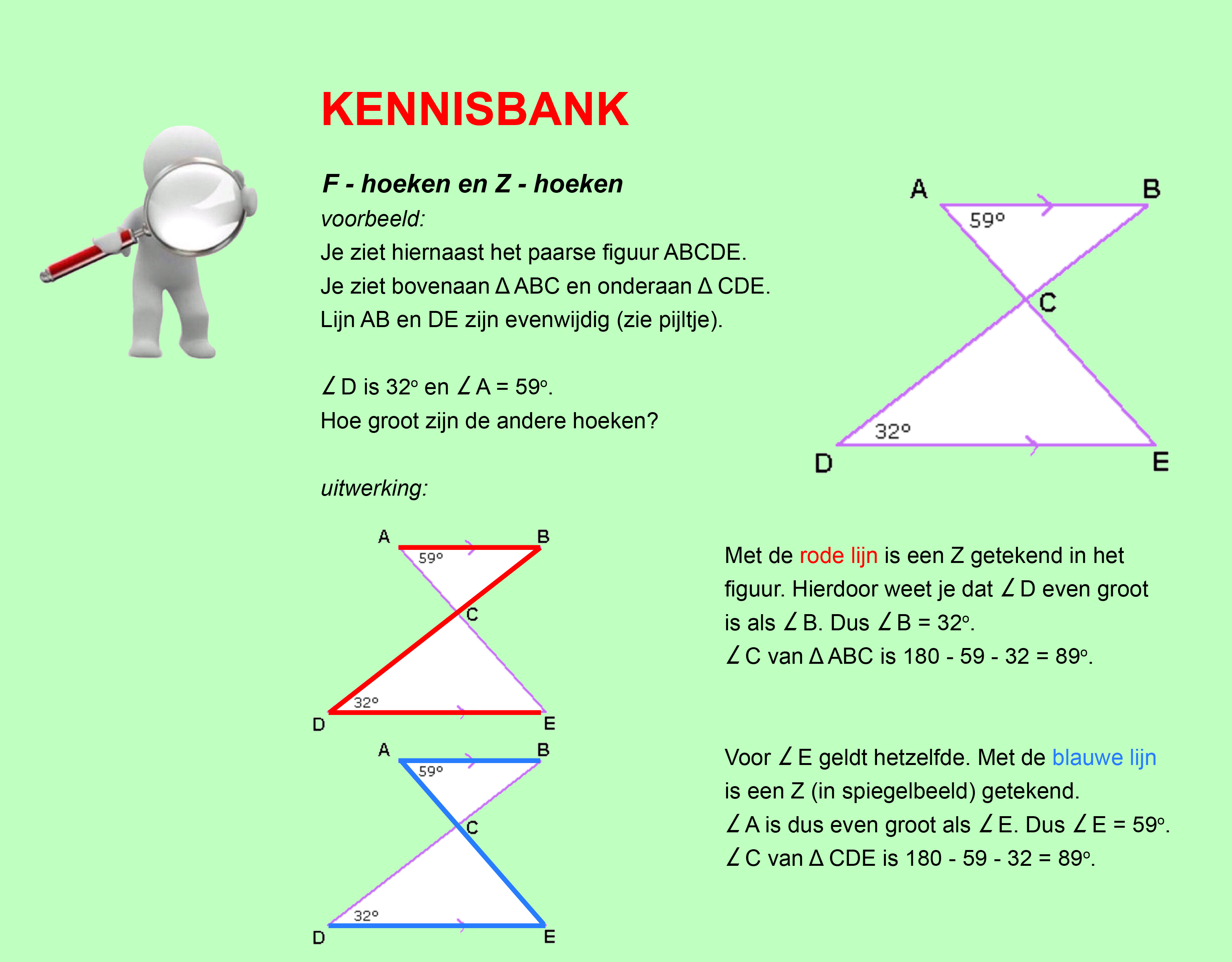
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. 
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. 
Tabel, beelddiagram en staafdiagram
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde de twee pagina's van het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde de pagina's van het onderdeel:
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. 
Bestudeer uit de Kennisbank wiskunde de vier pagina's van het onderdeel:
Bestudeer uit de Kennisbank wiskunde de vijf pagina's van het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. 
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren.
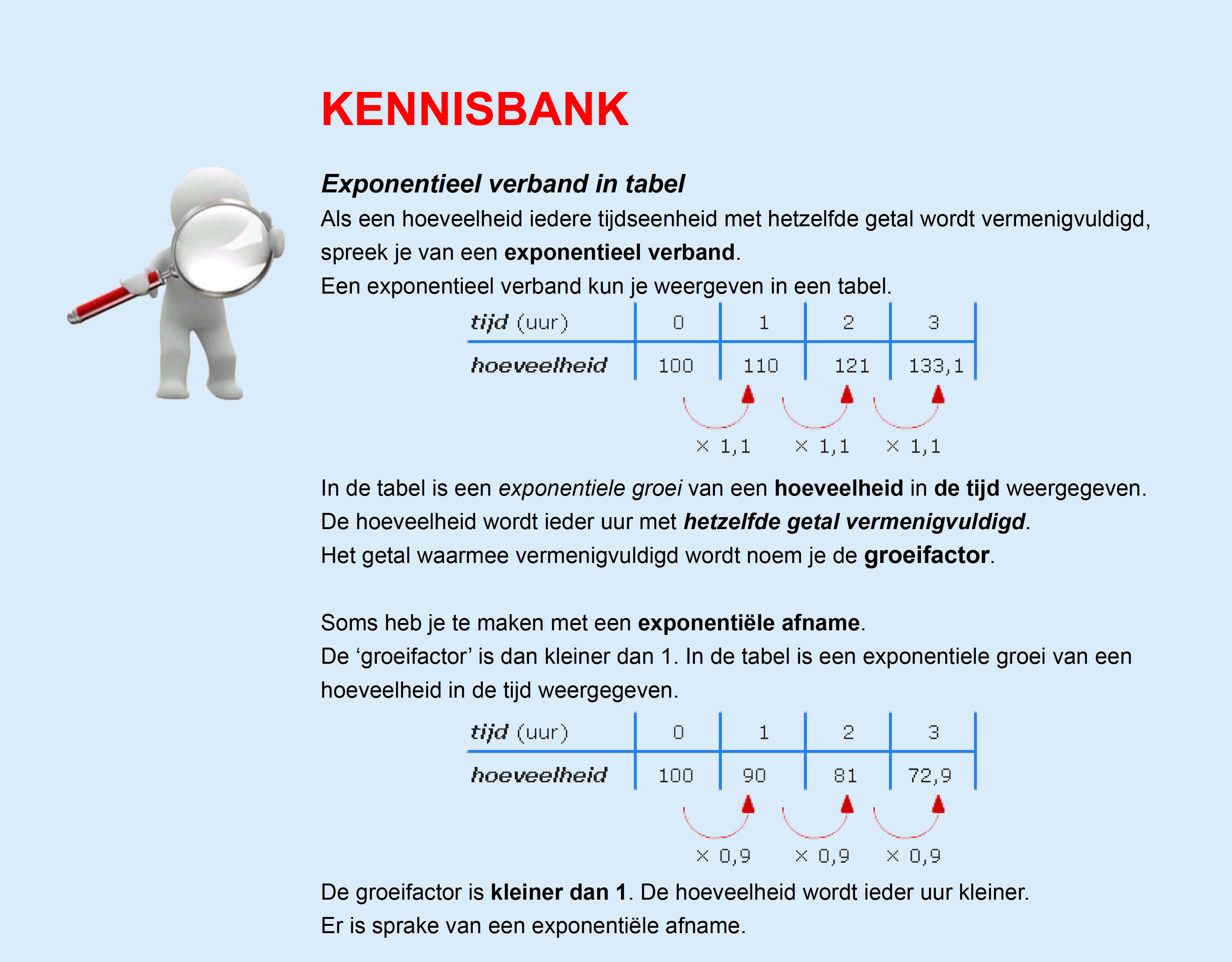
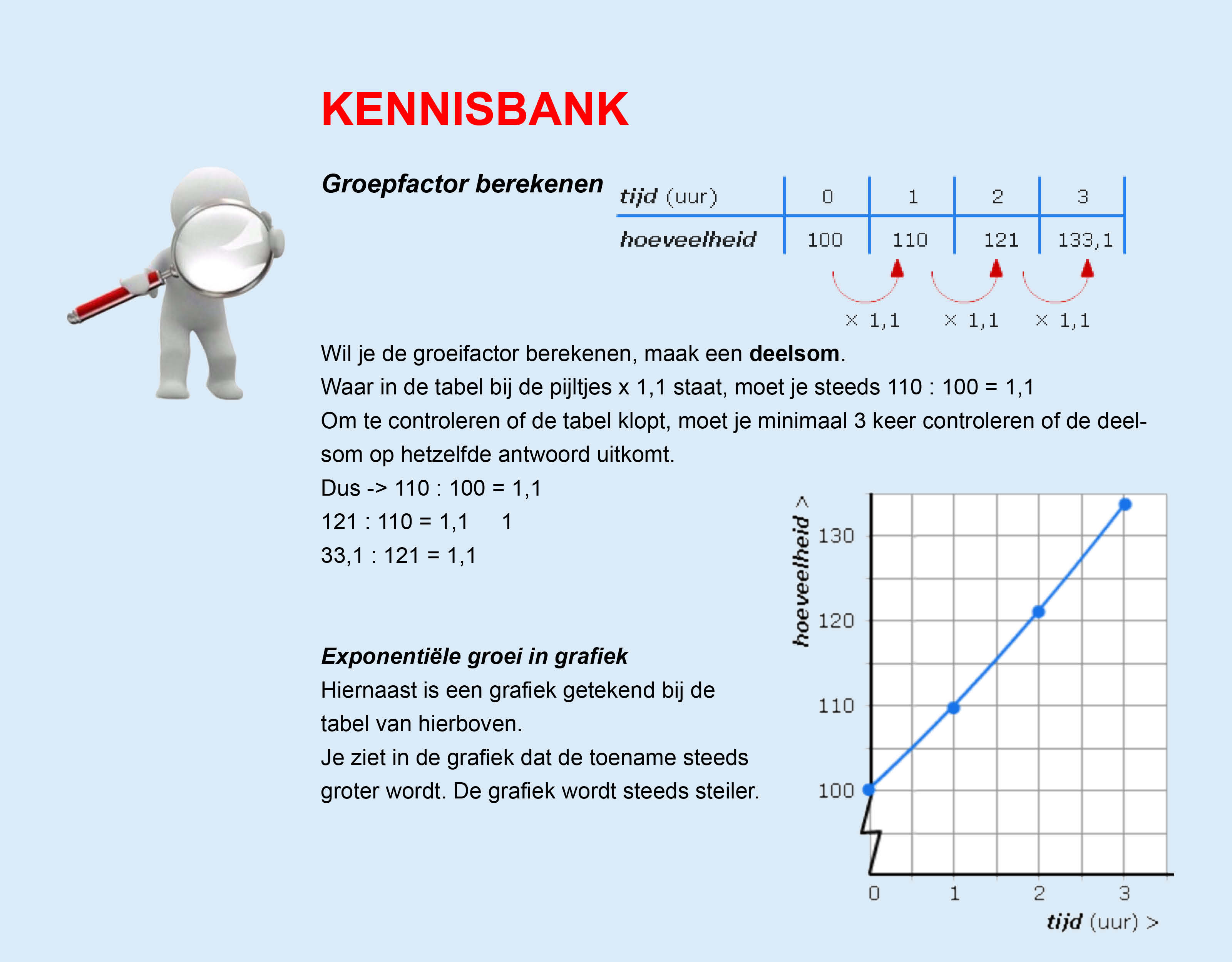
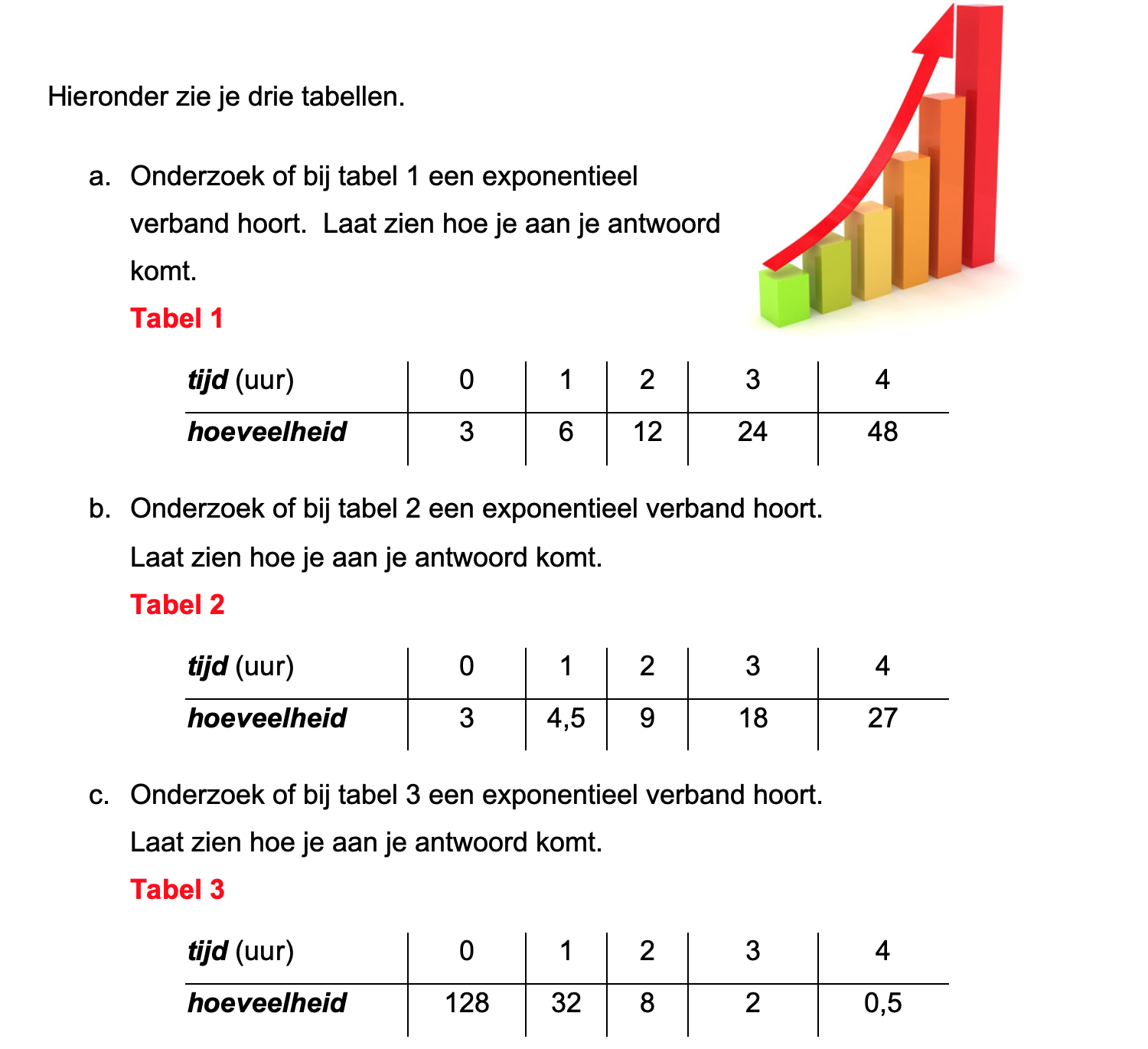
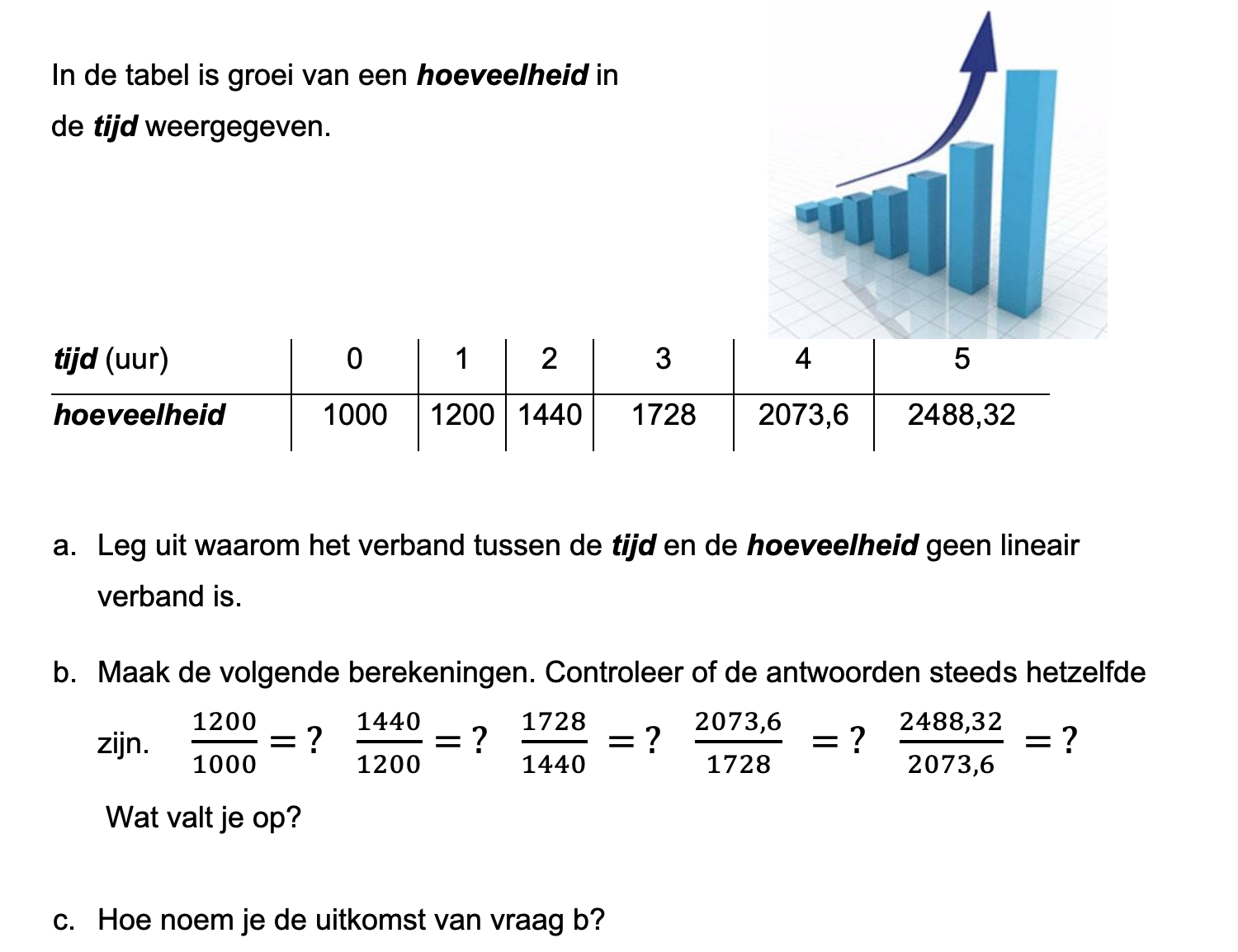
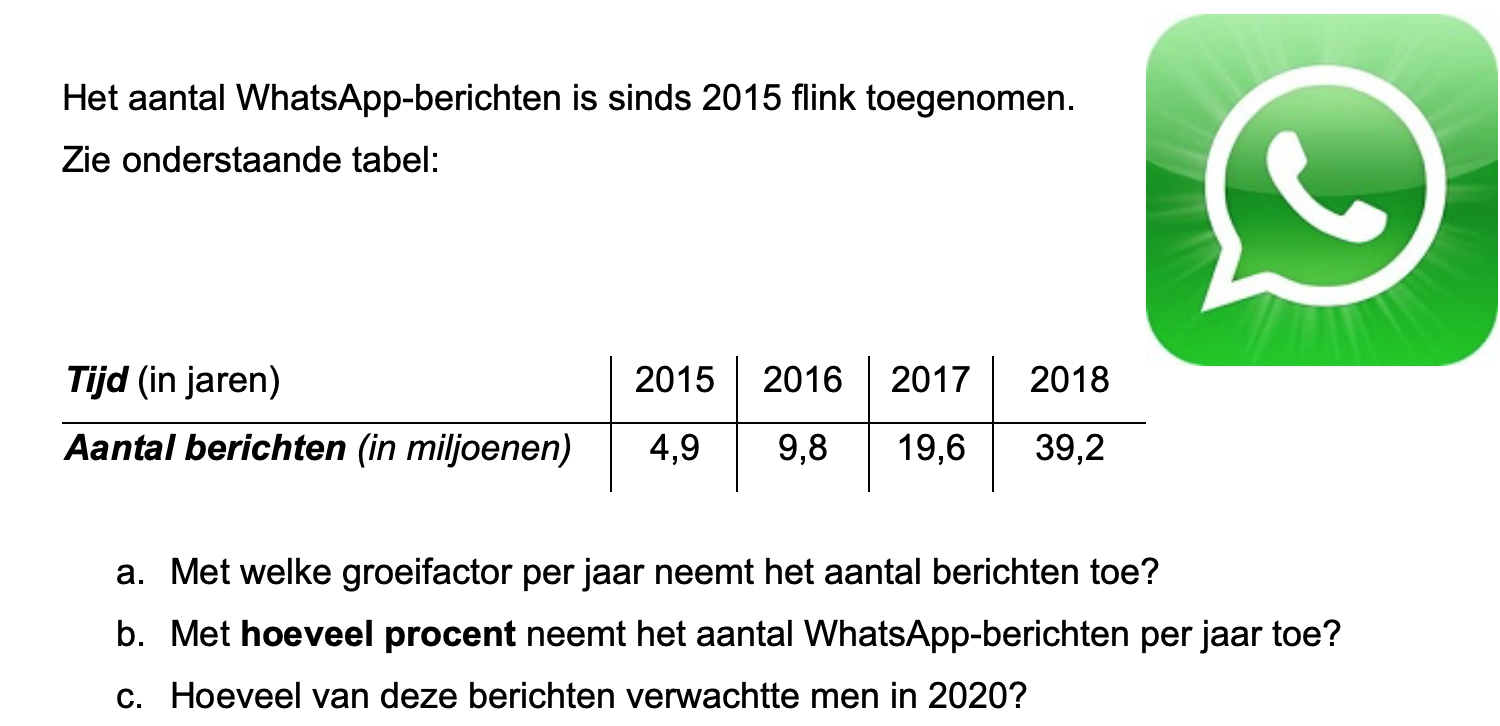
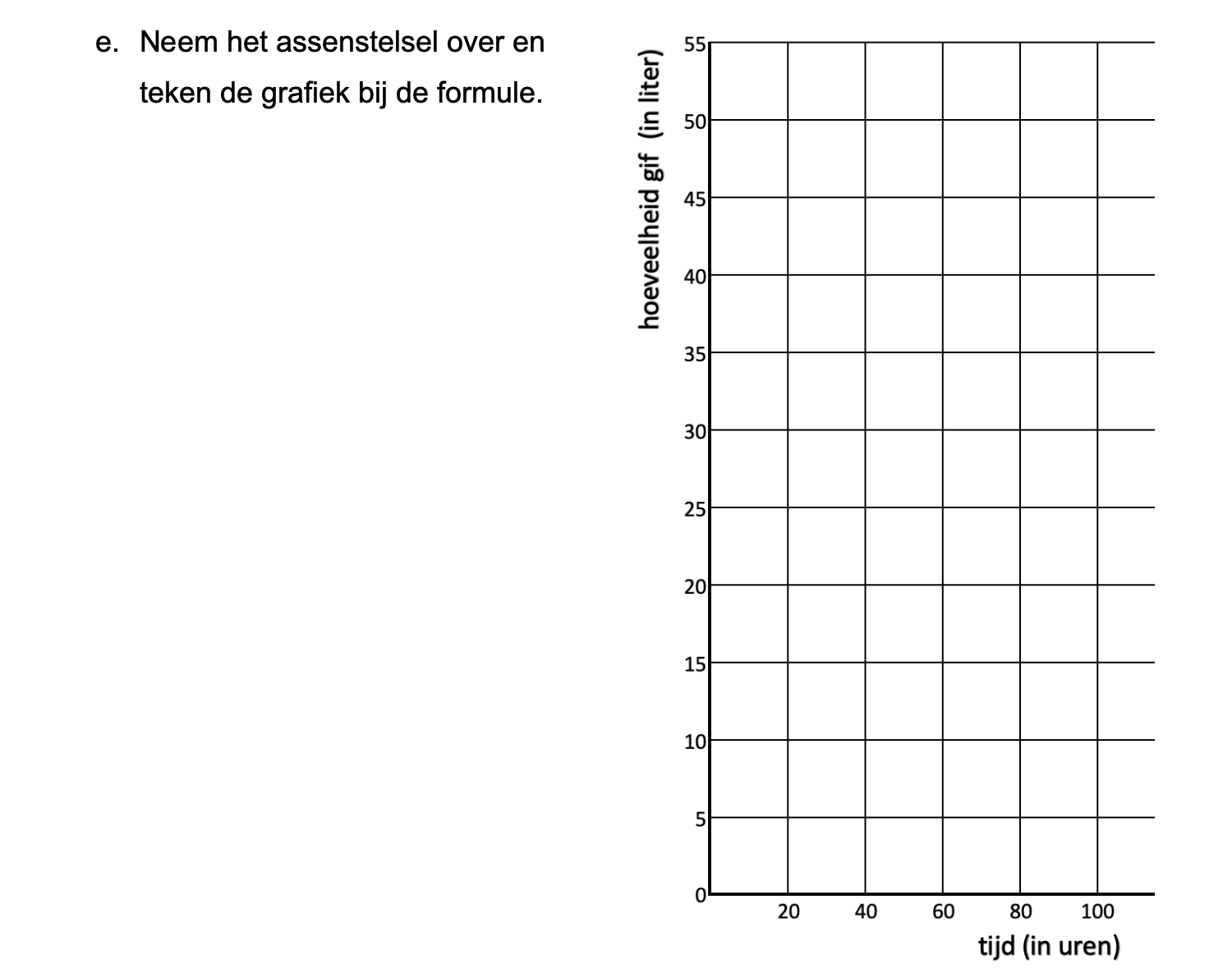
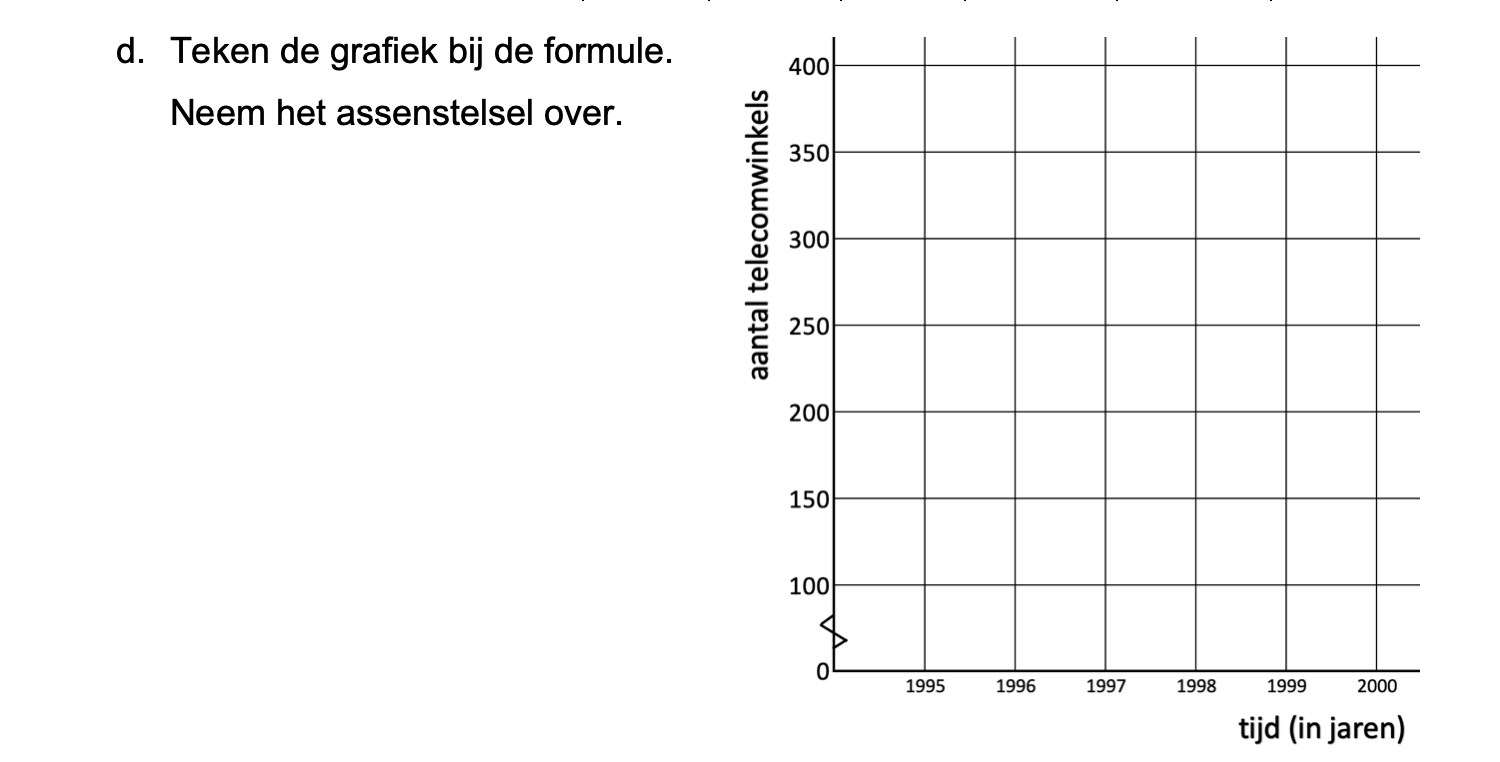
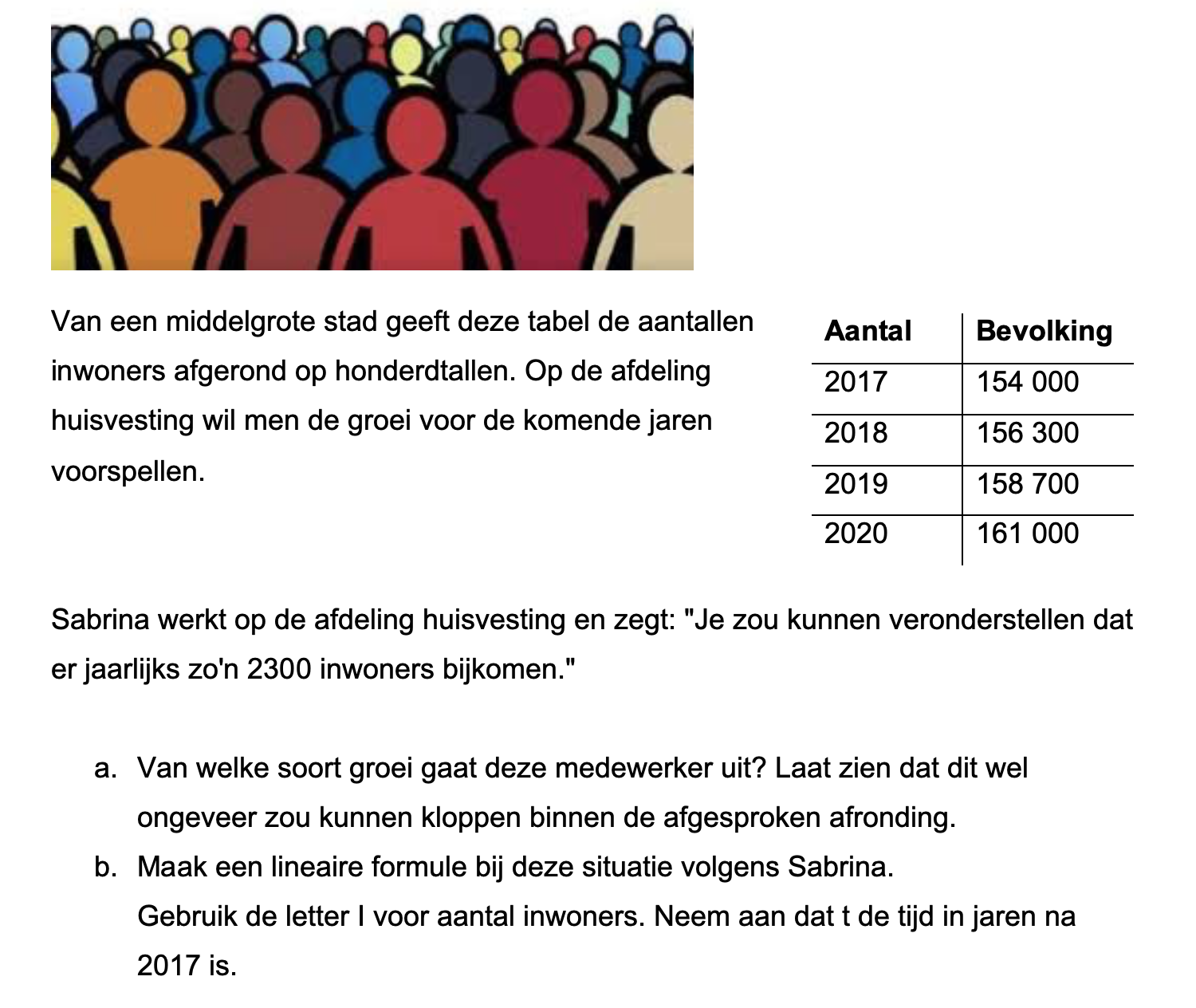
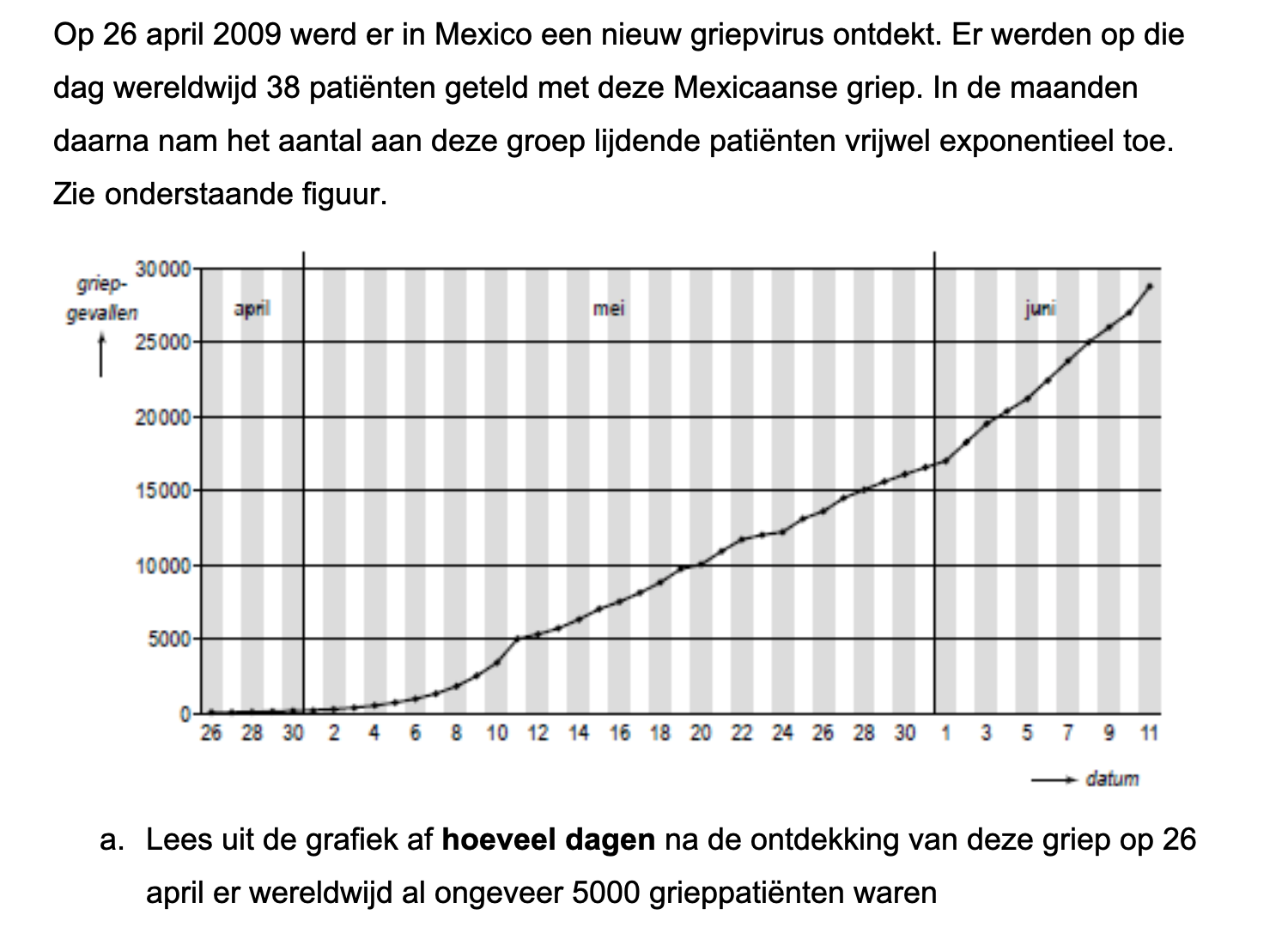
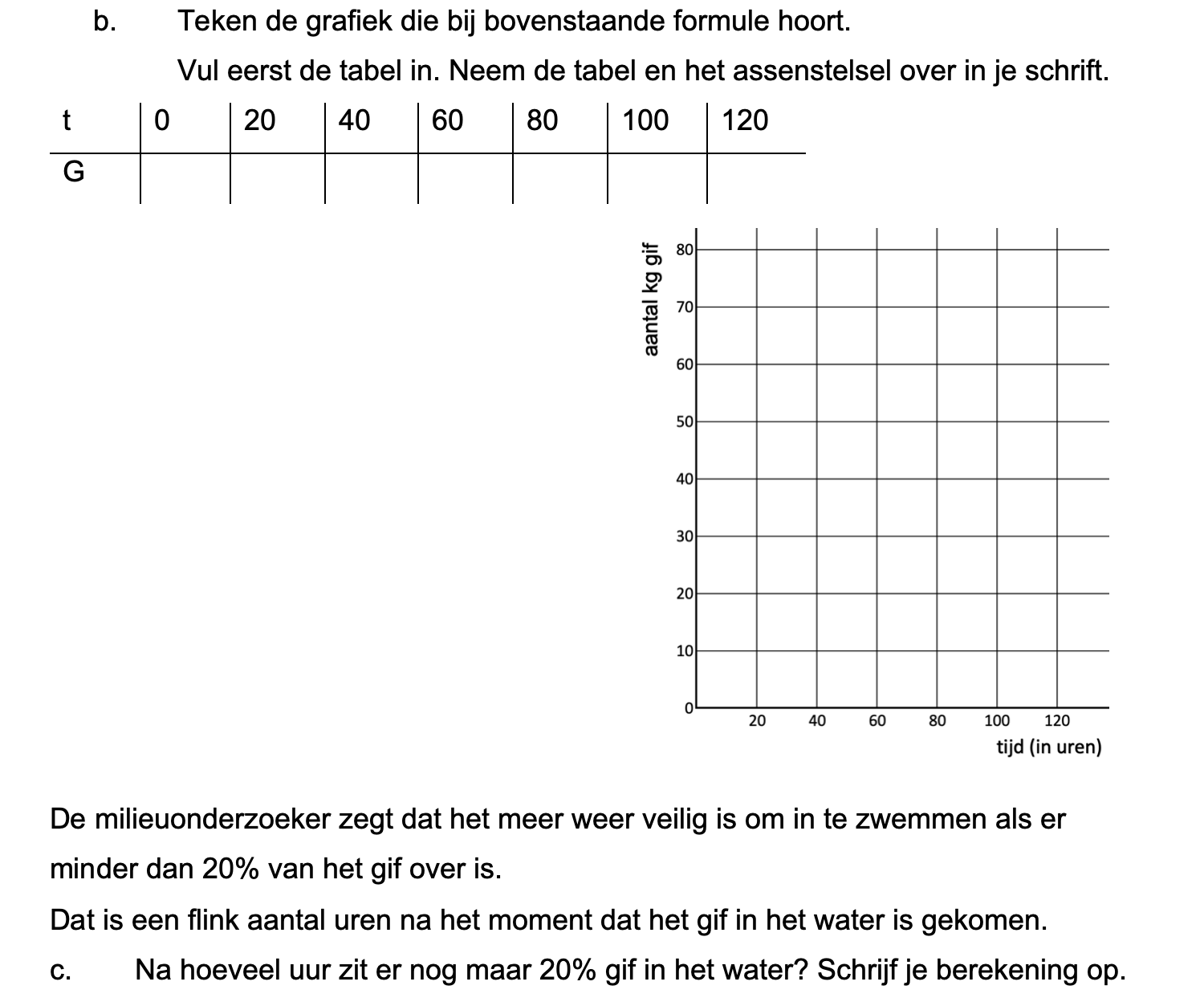
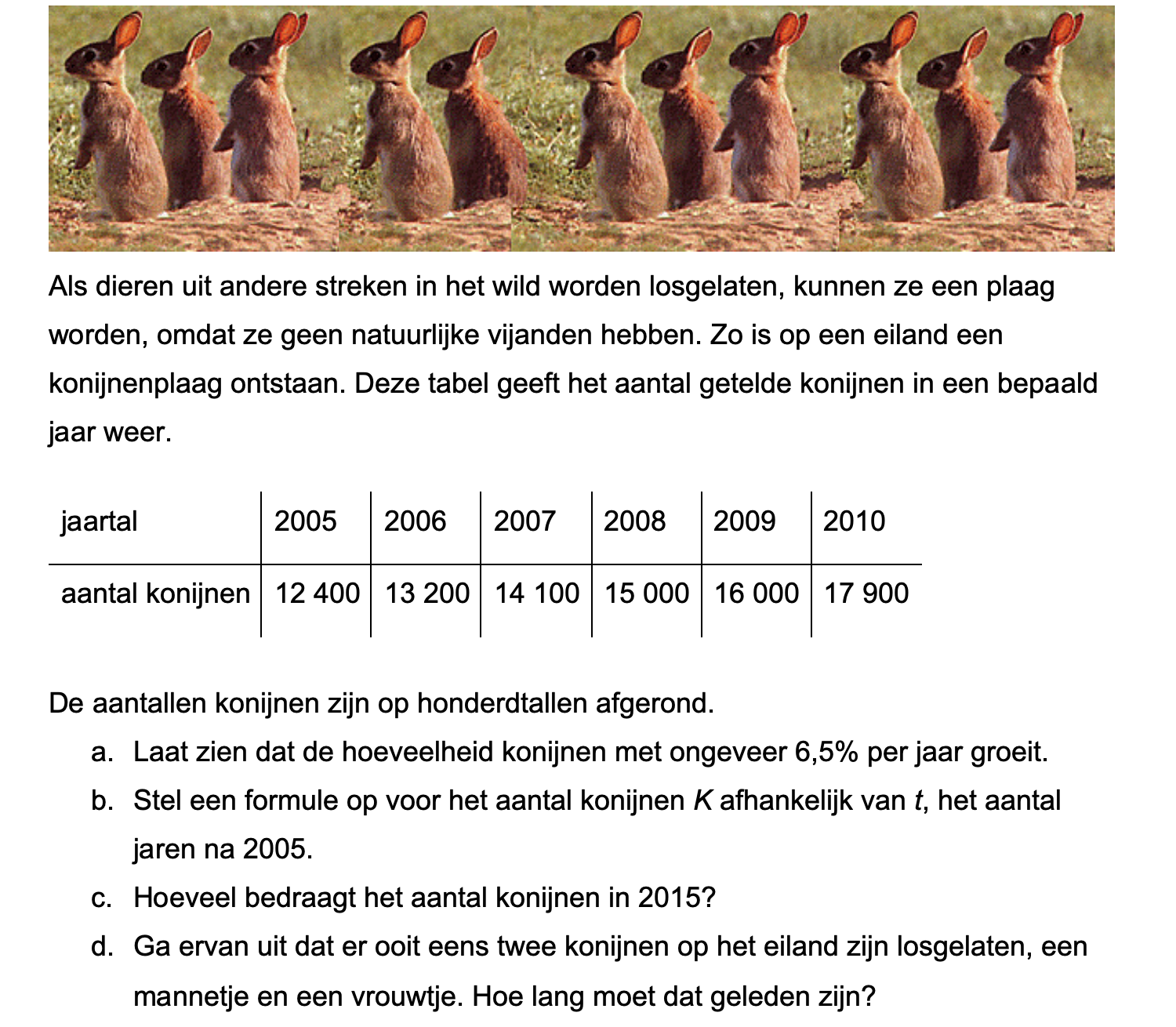
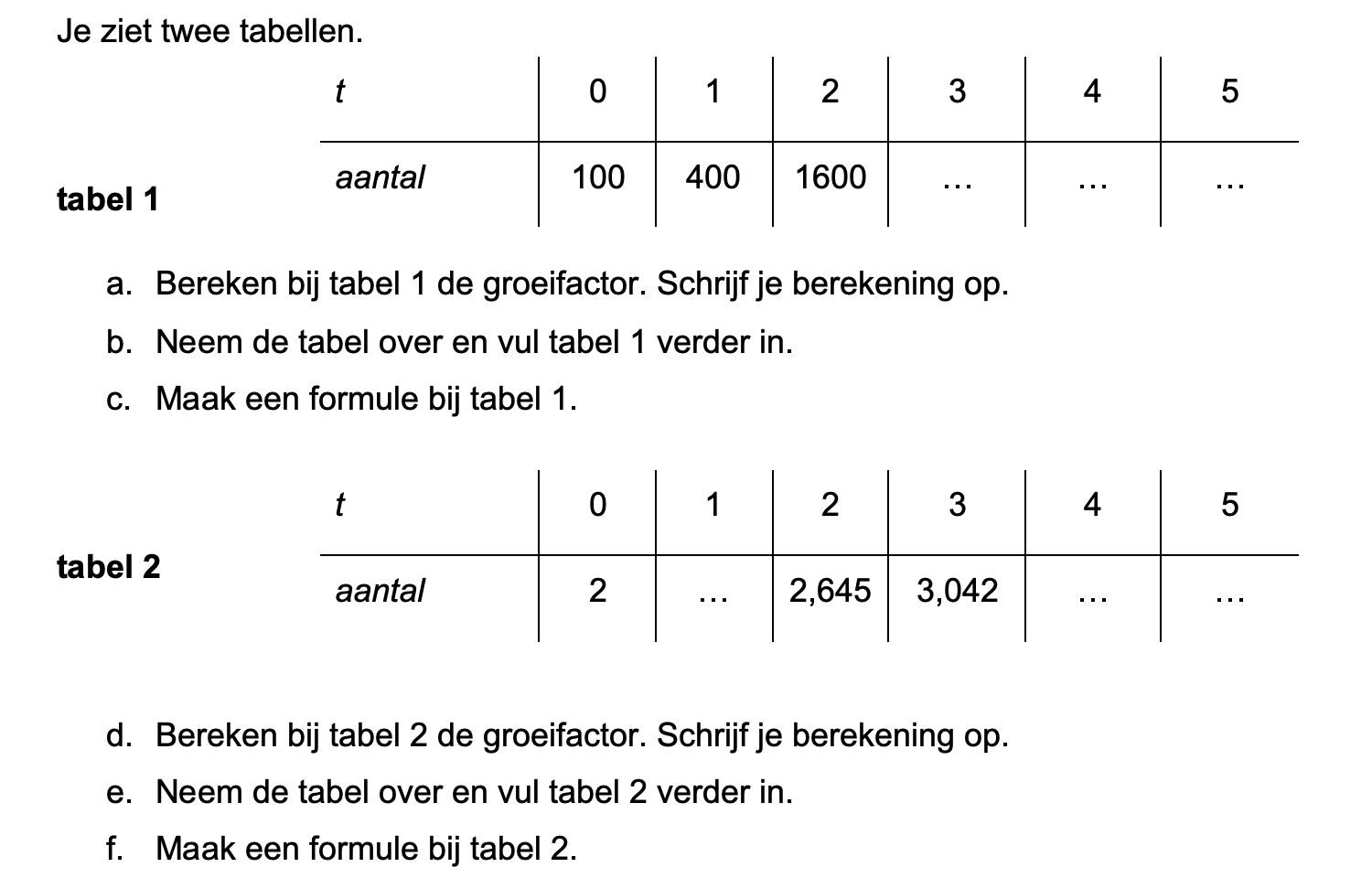
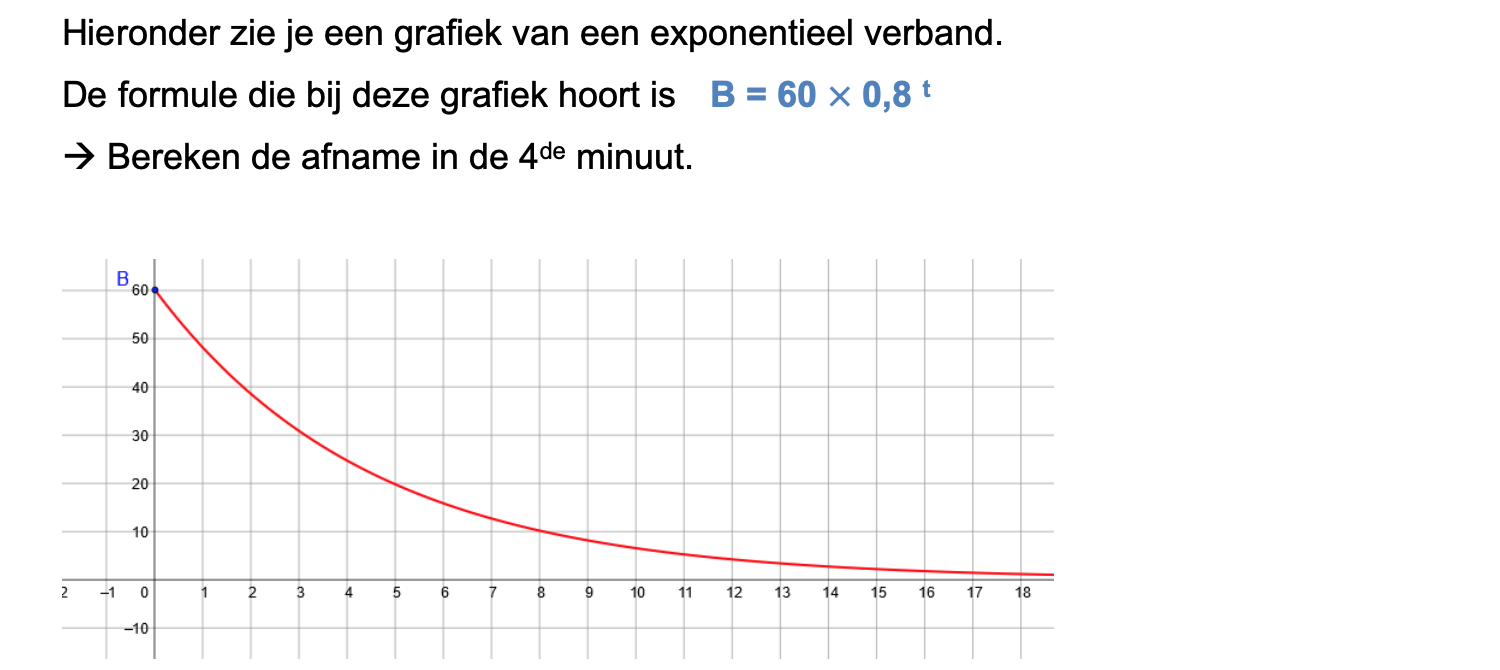
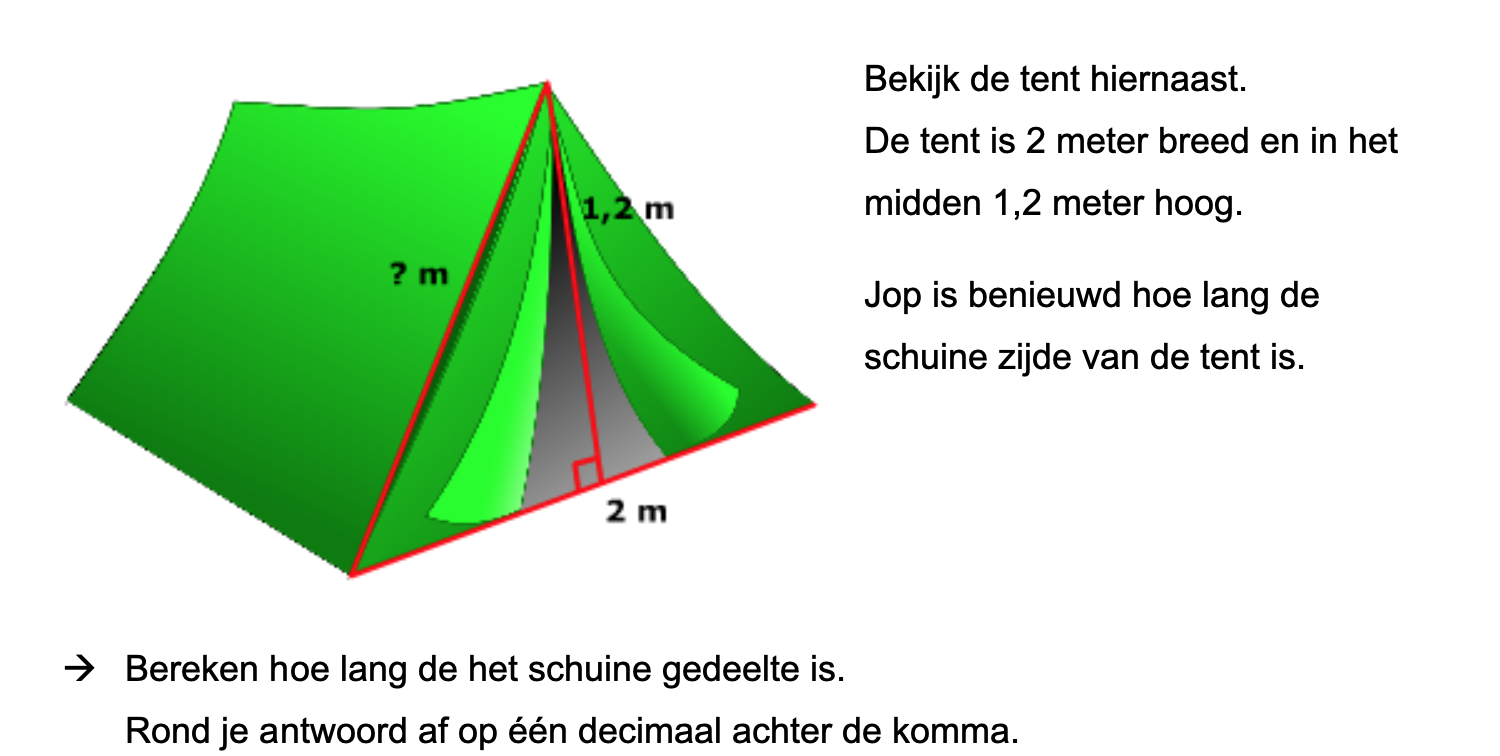
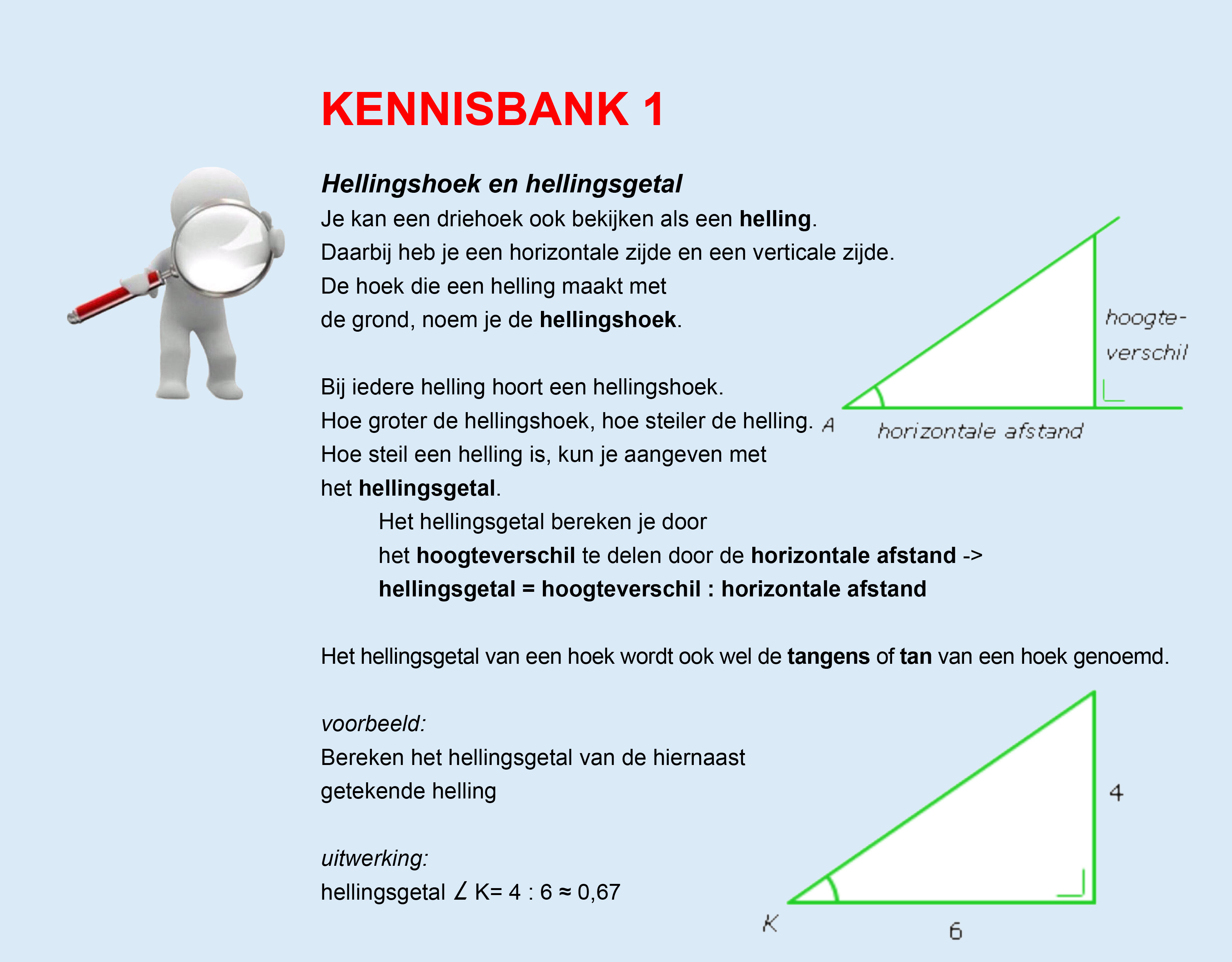
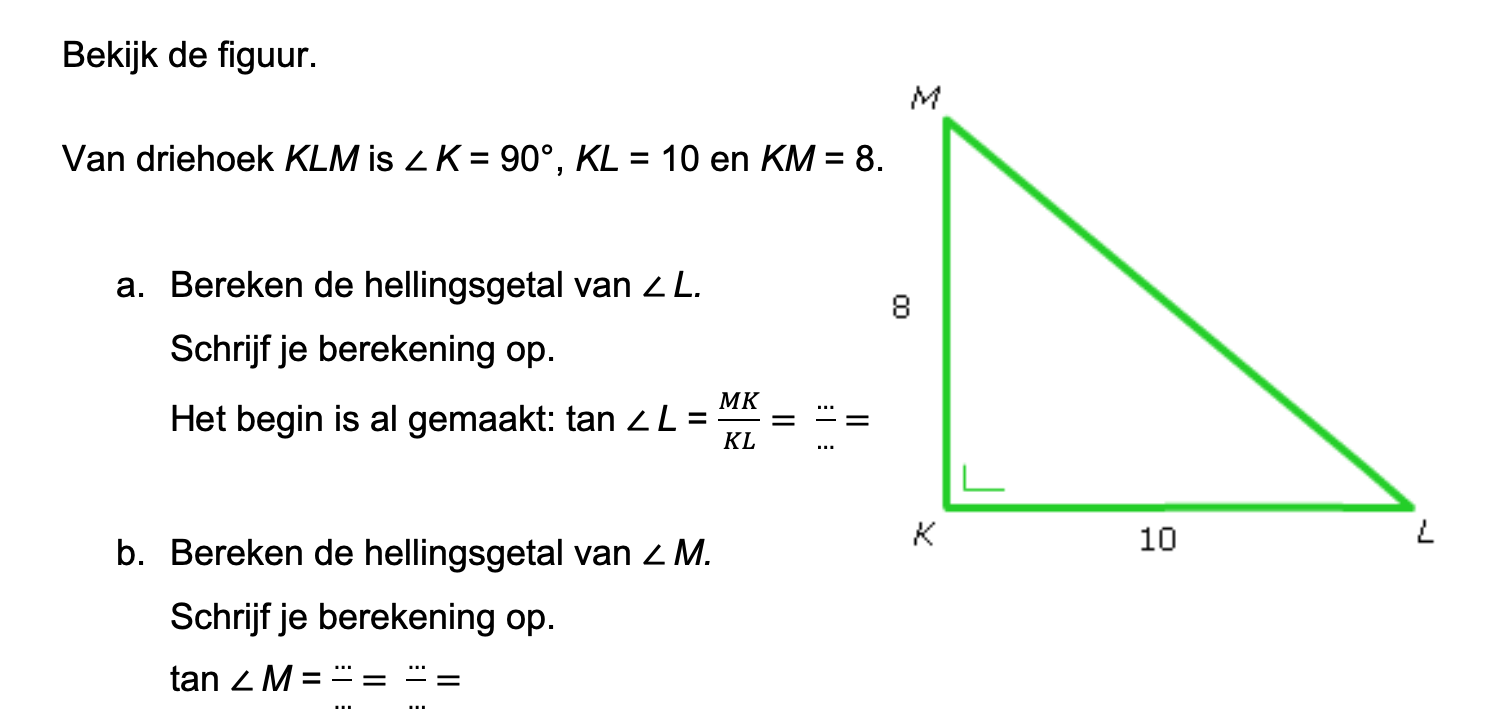
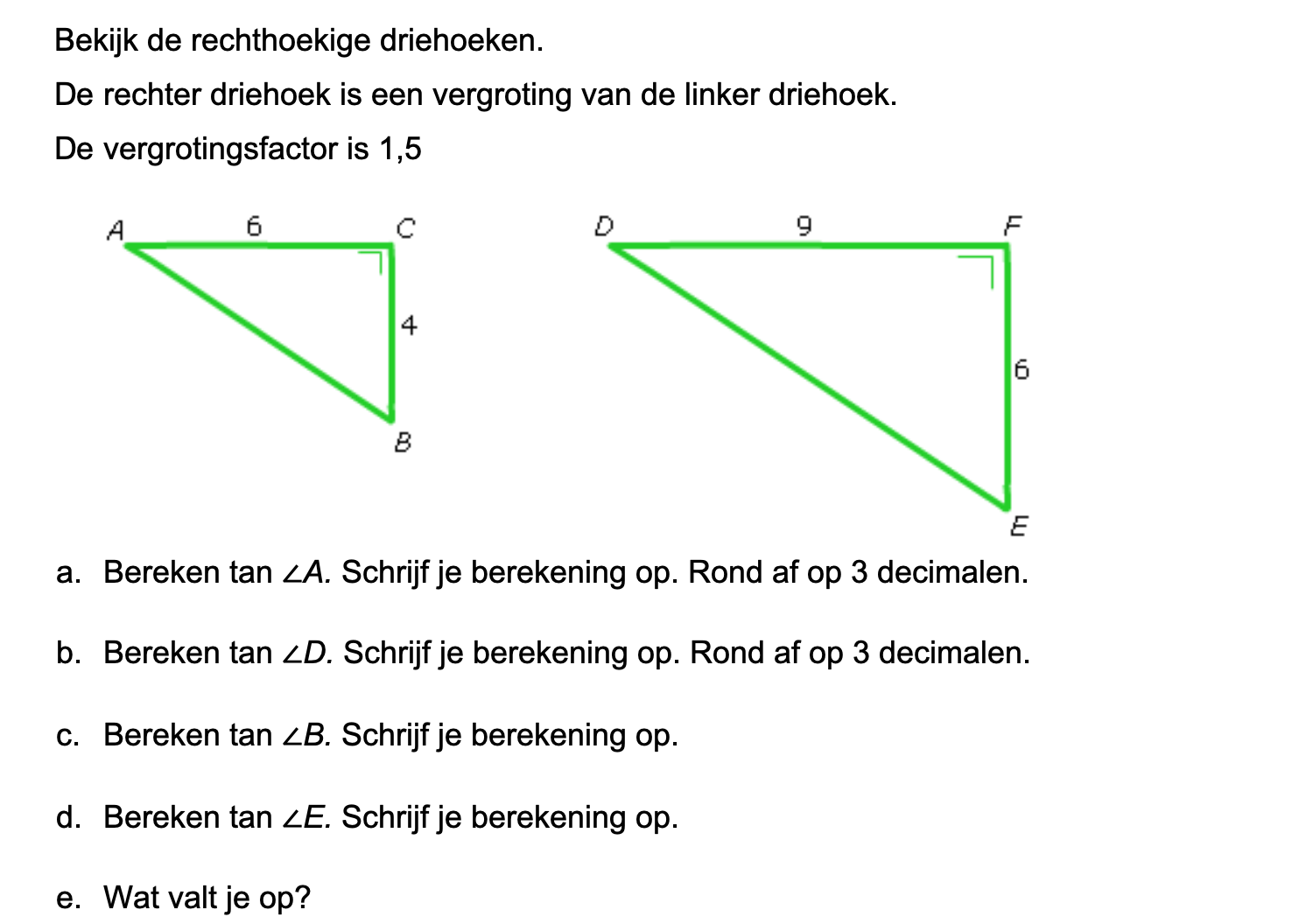
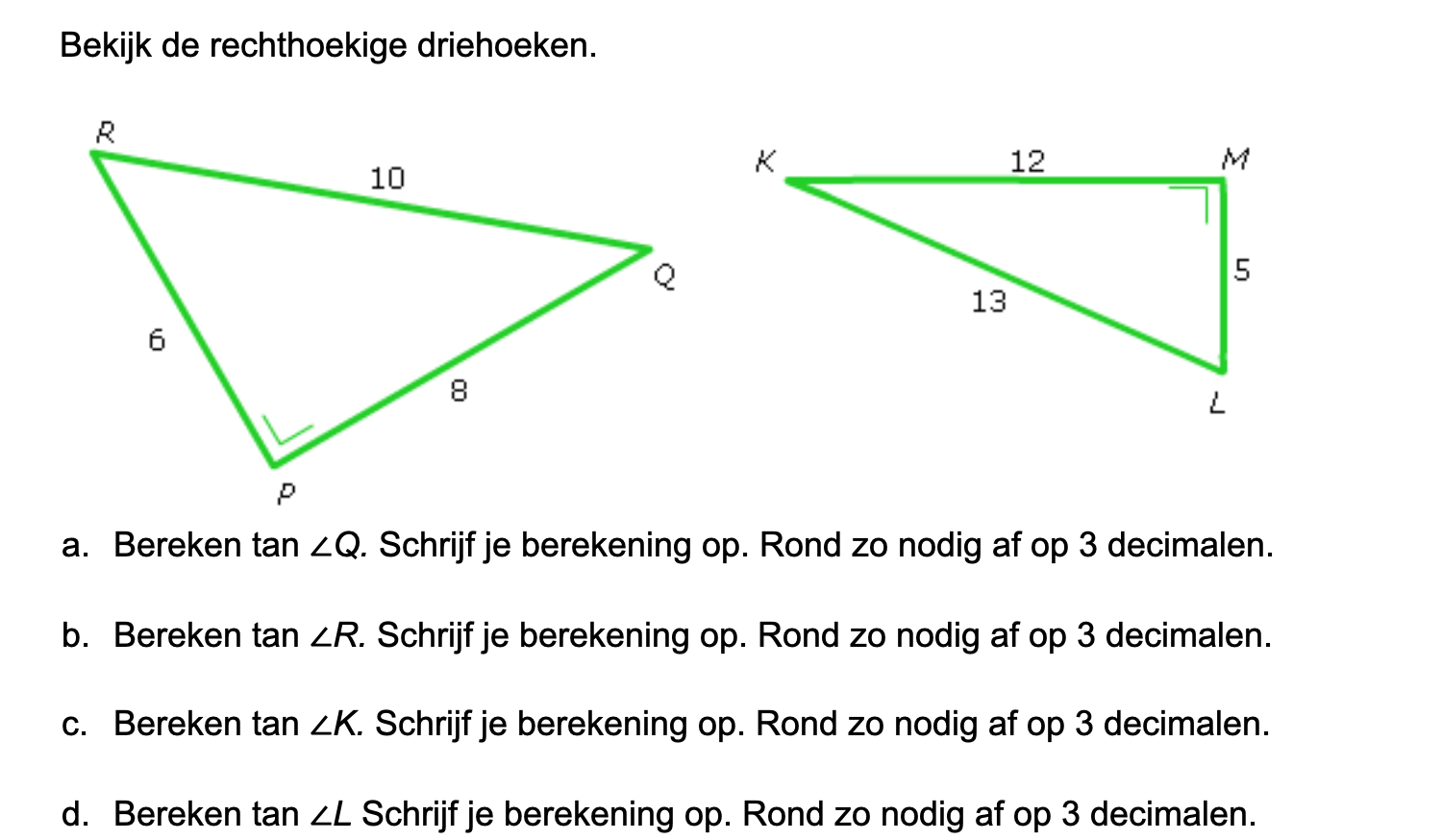
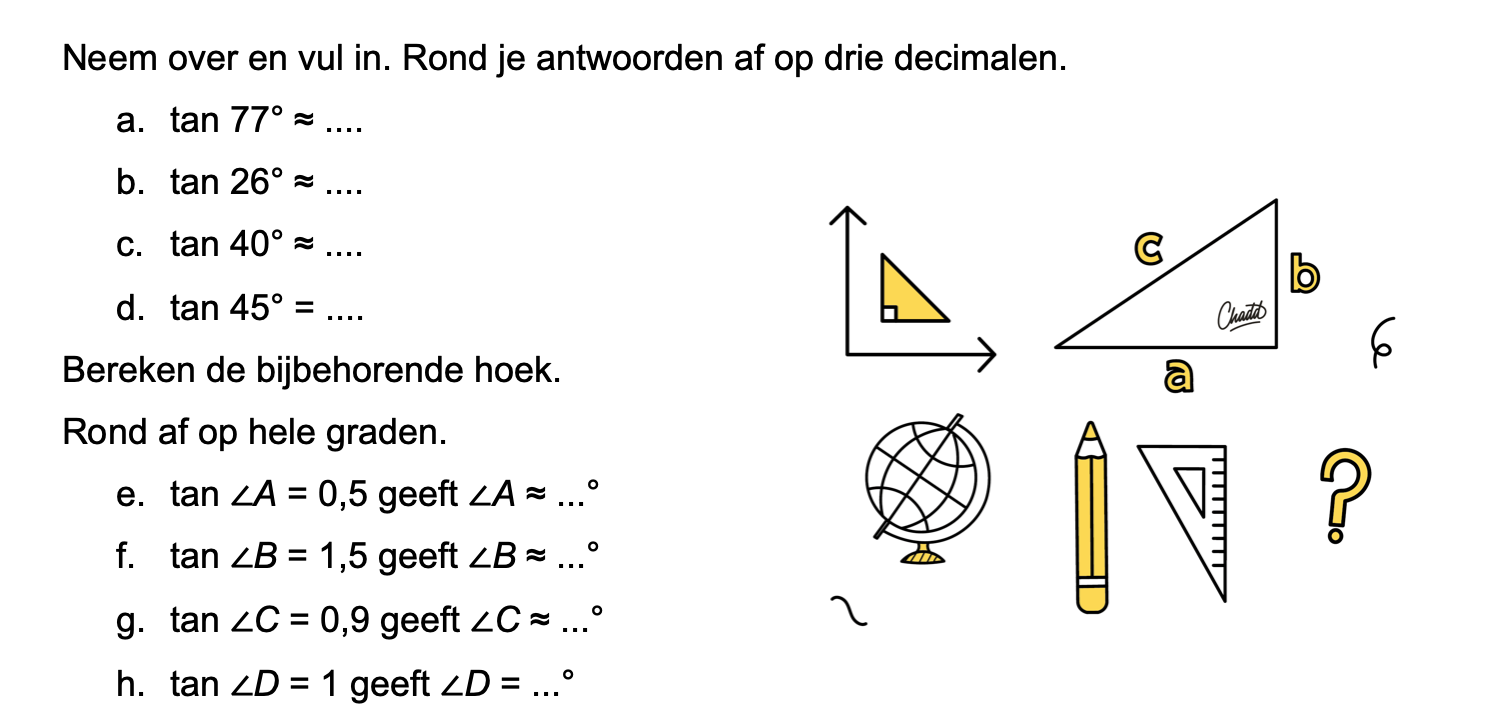
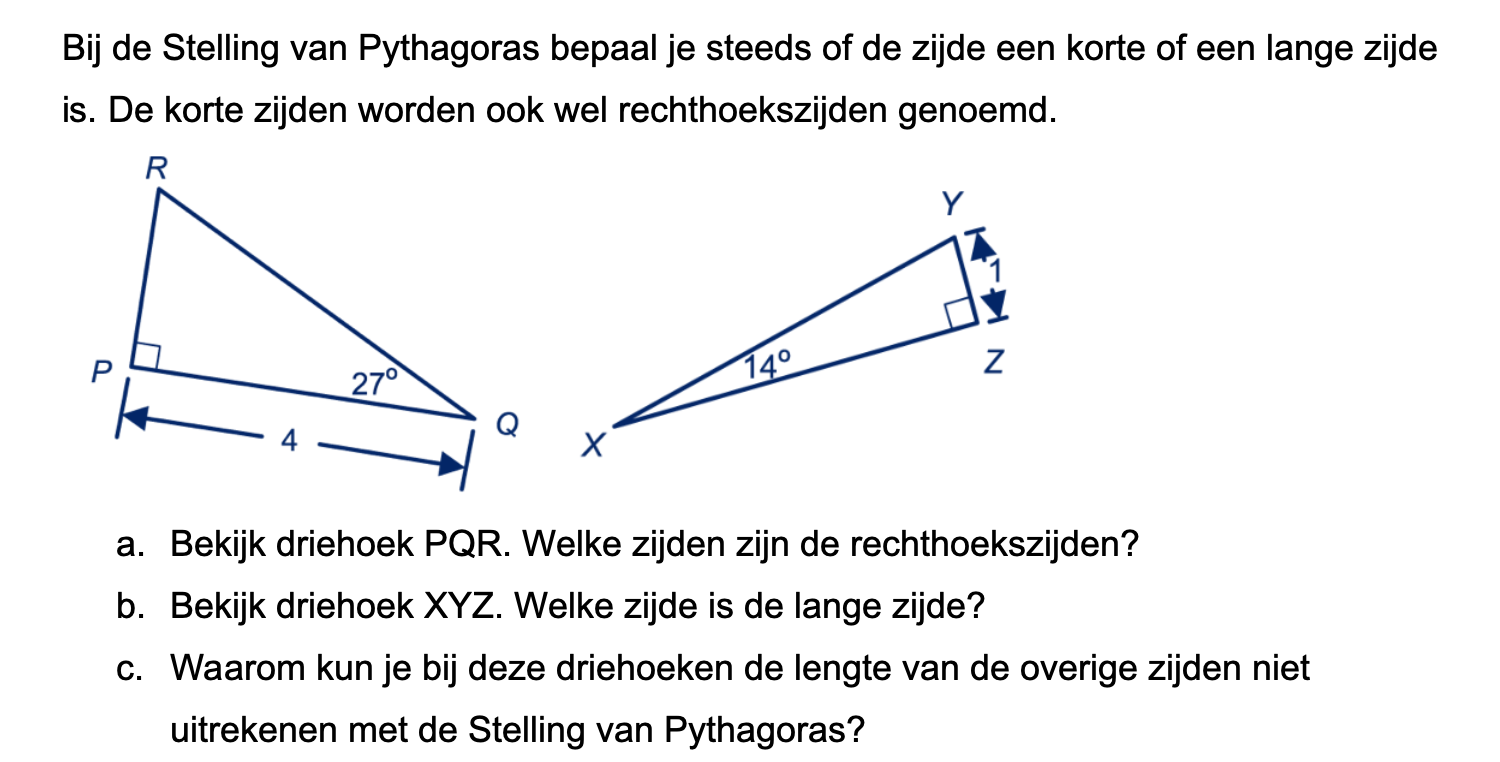
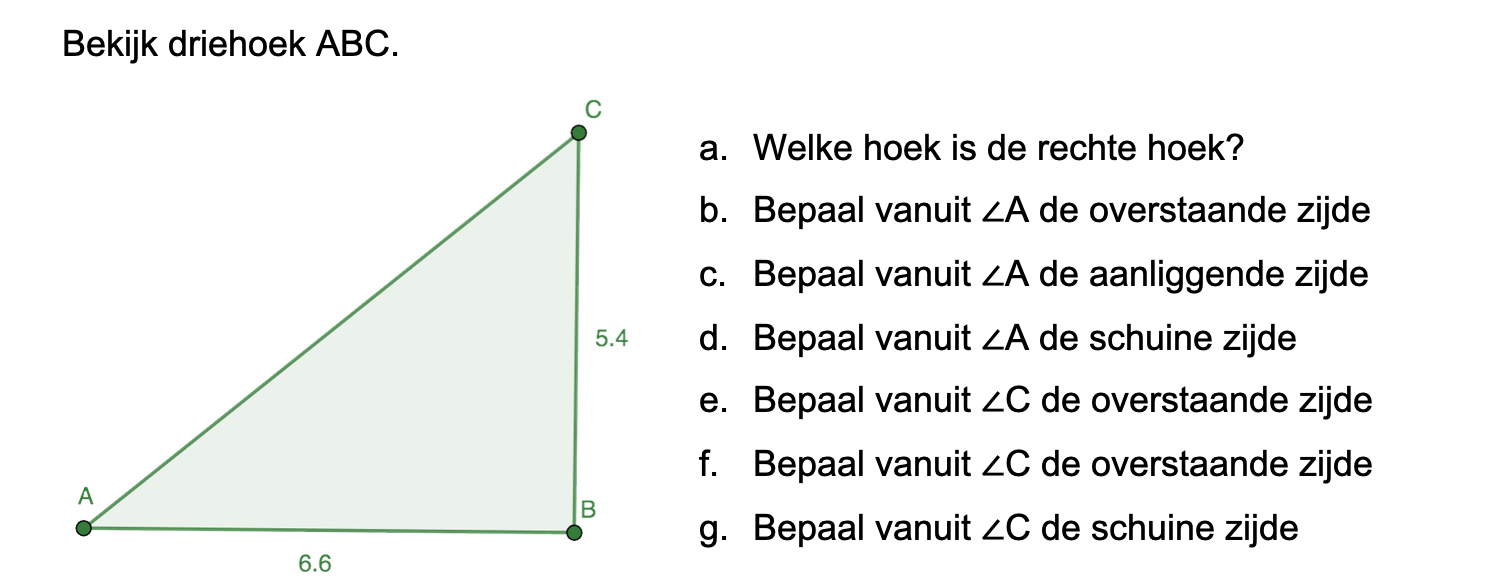
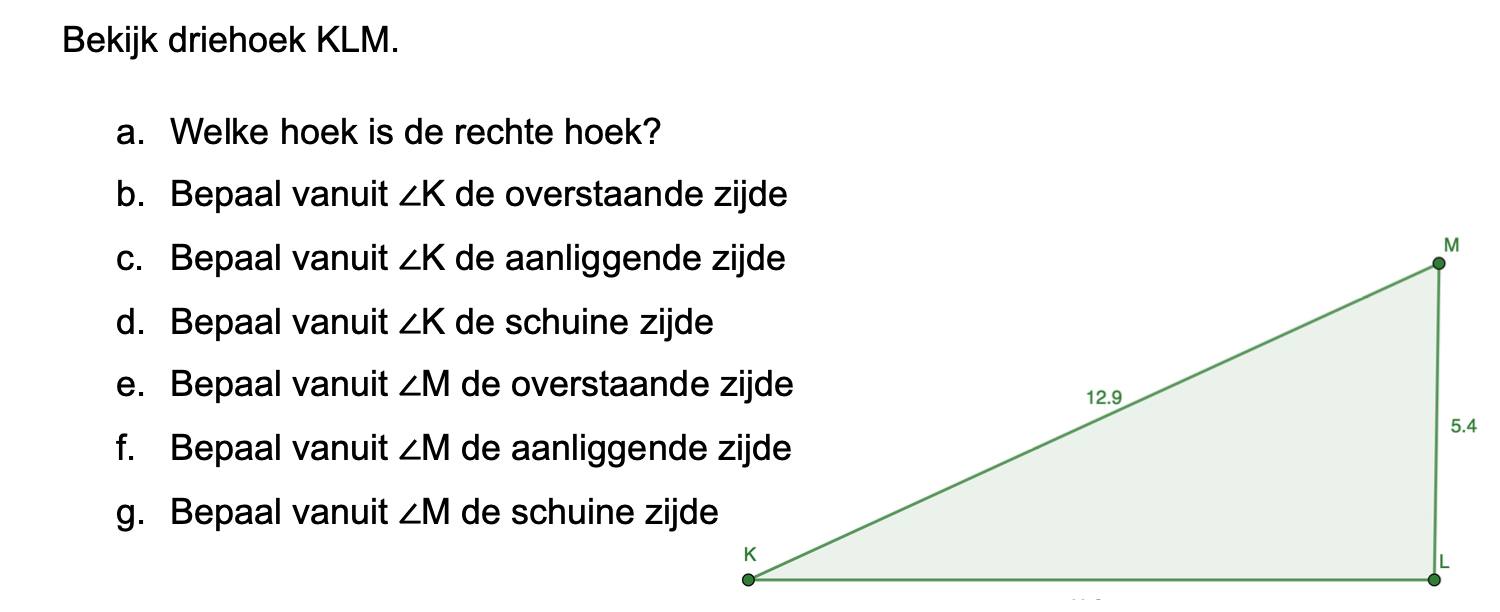
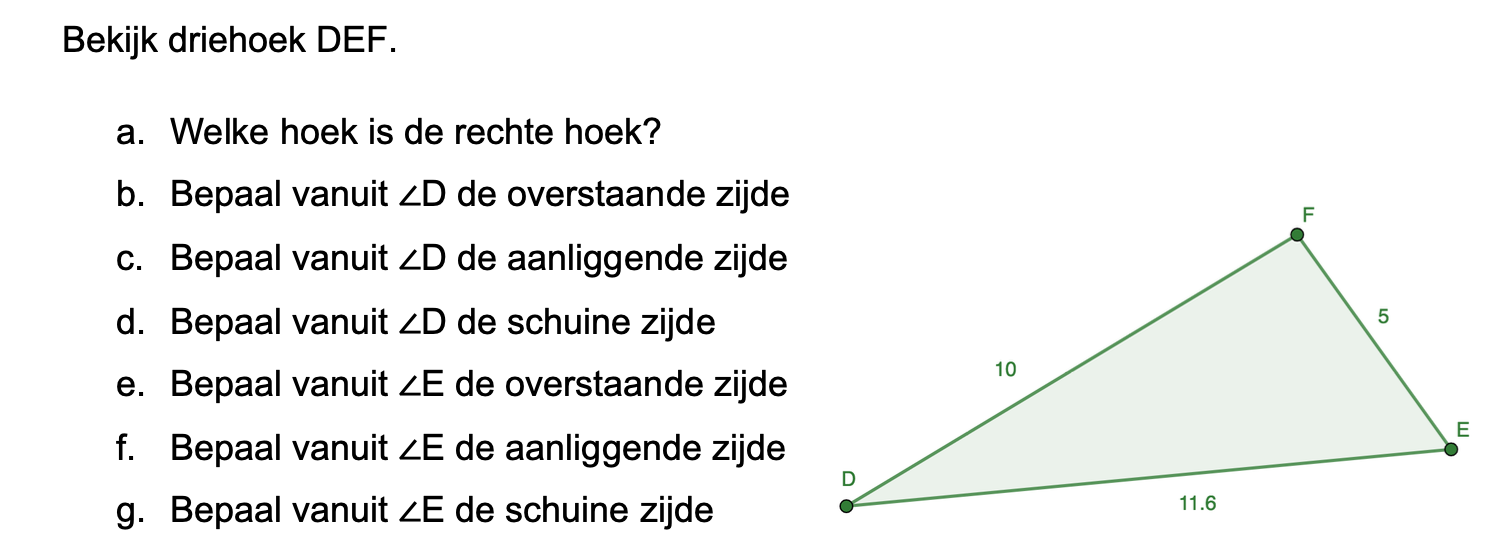
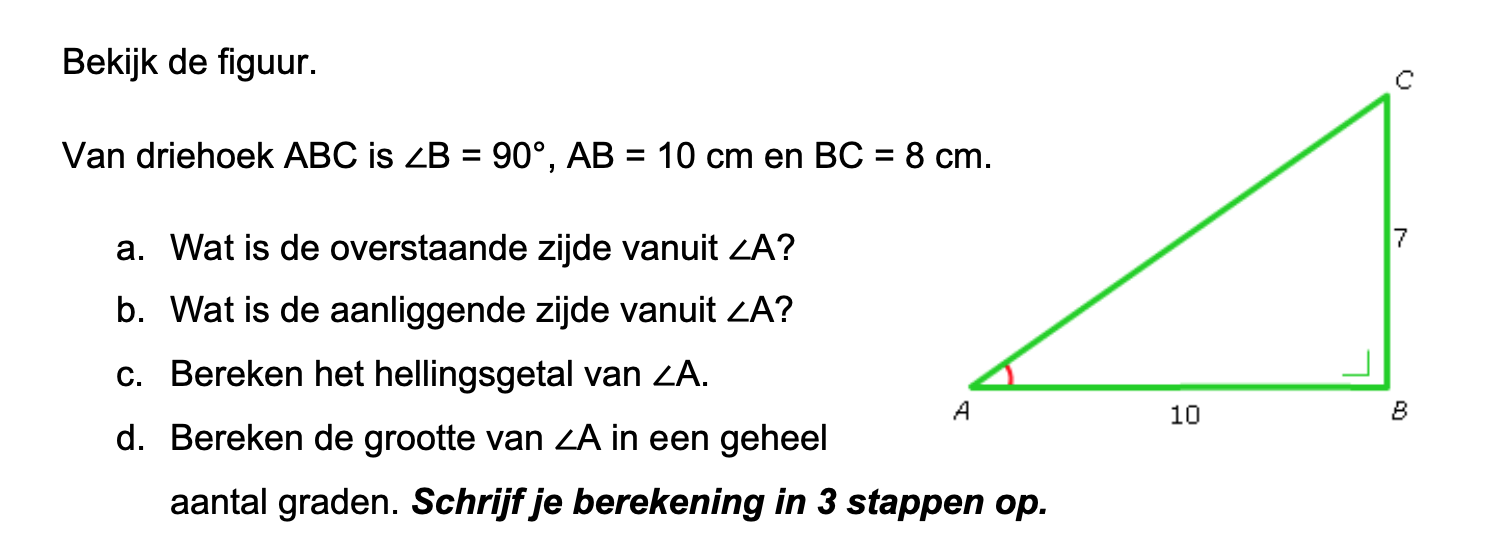
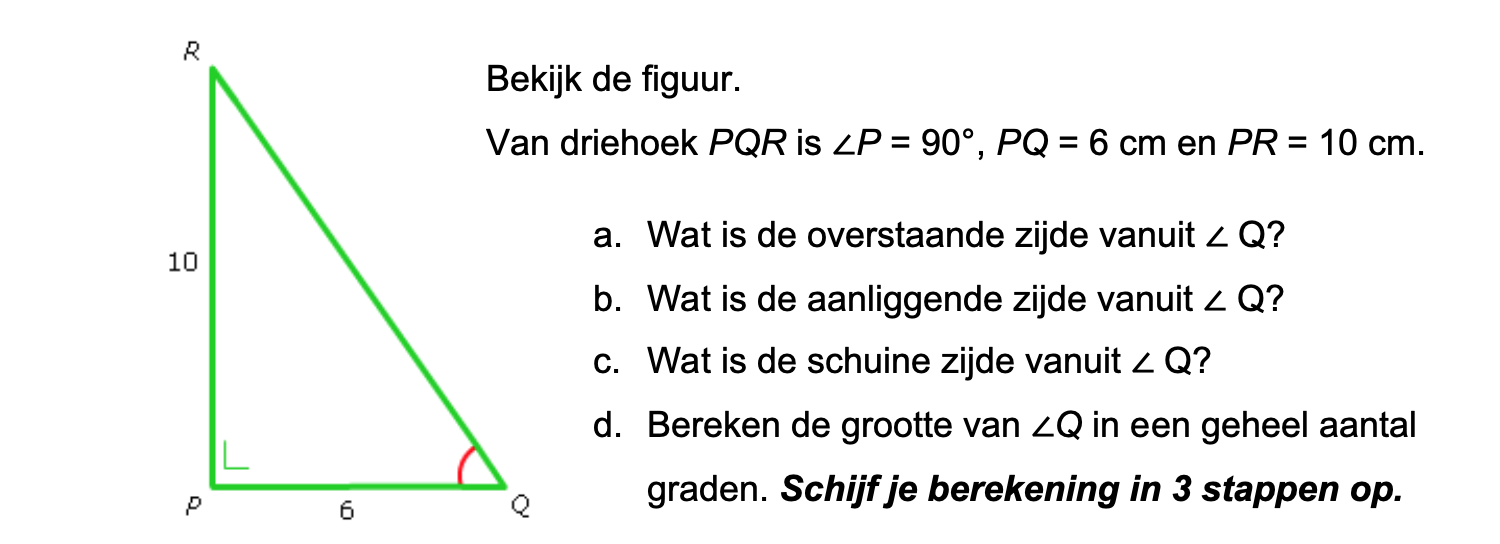
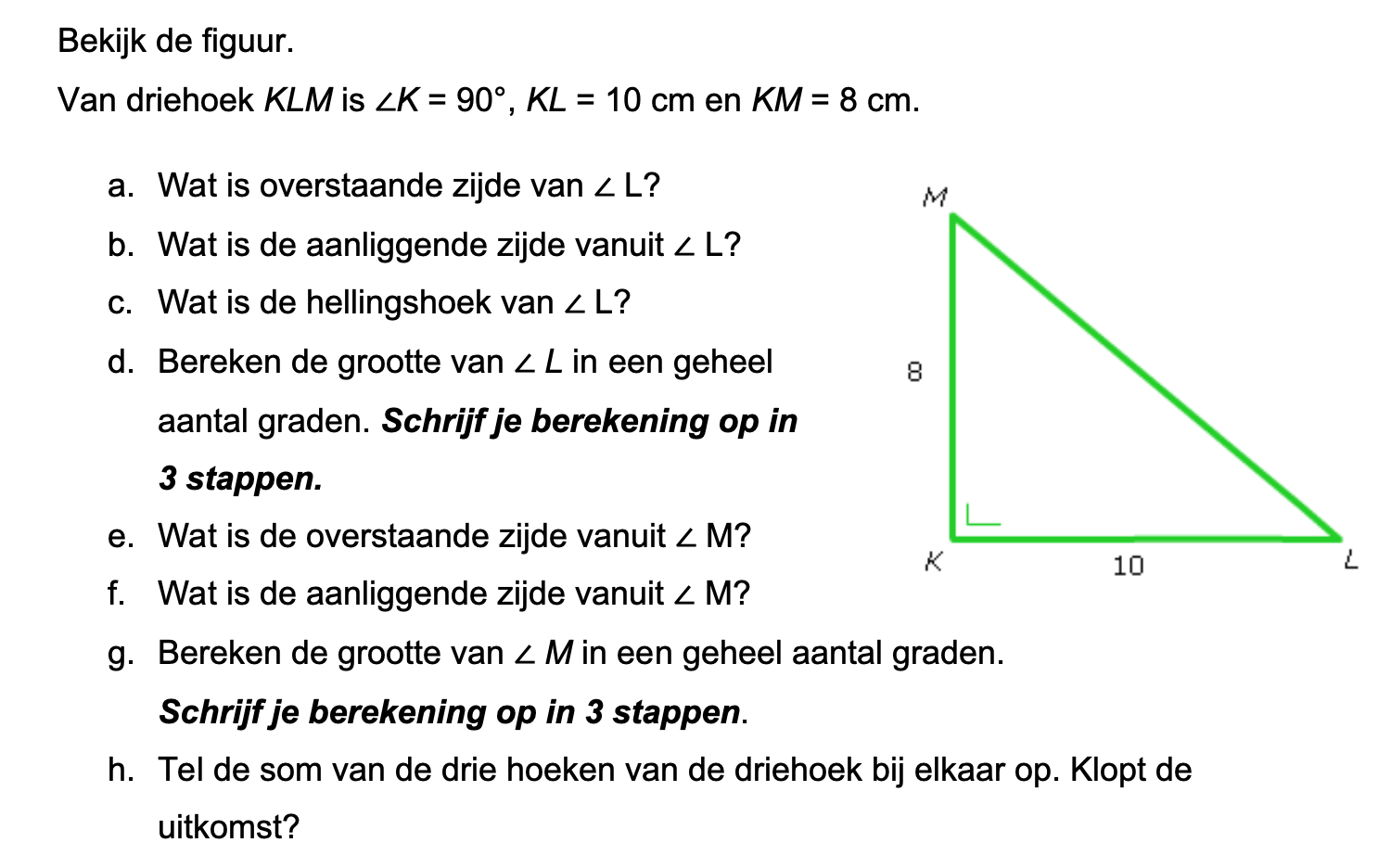
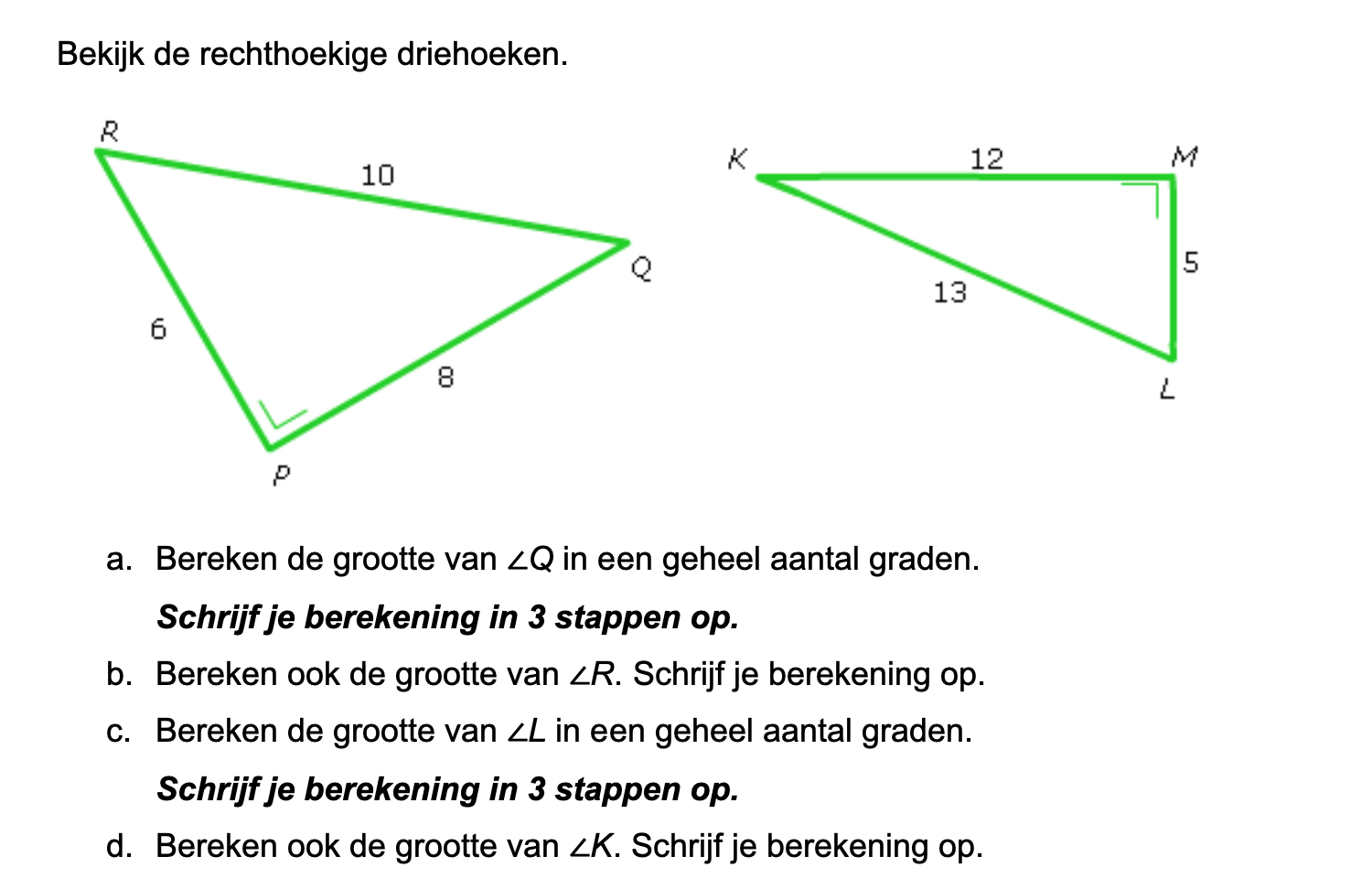
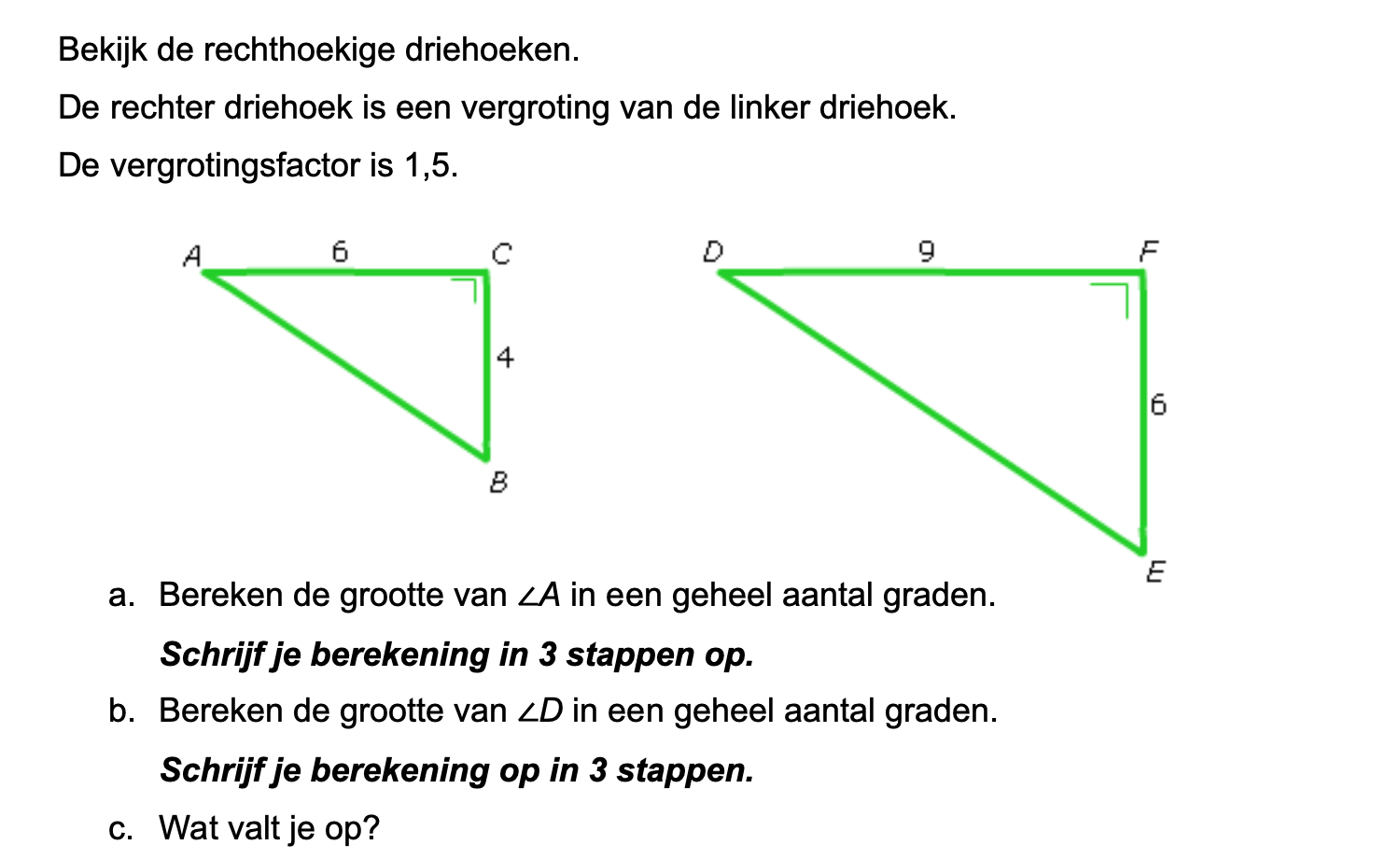
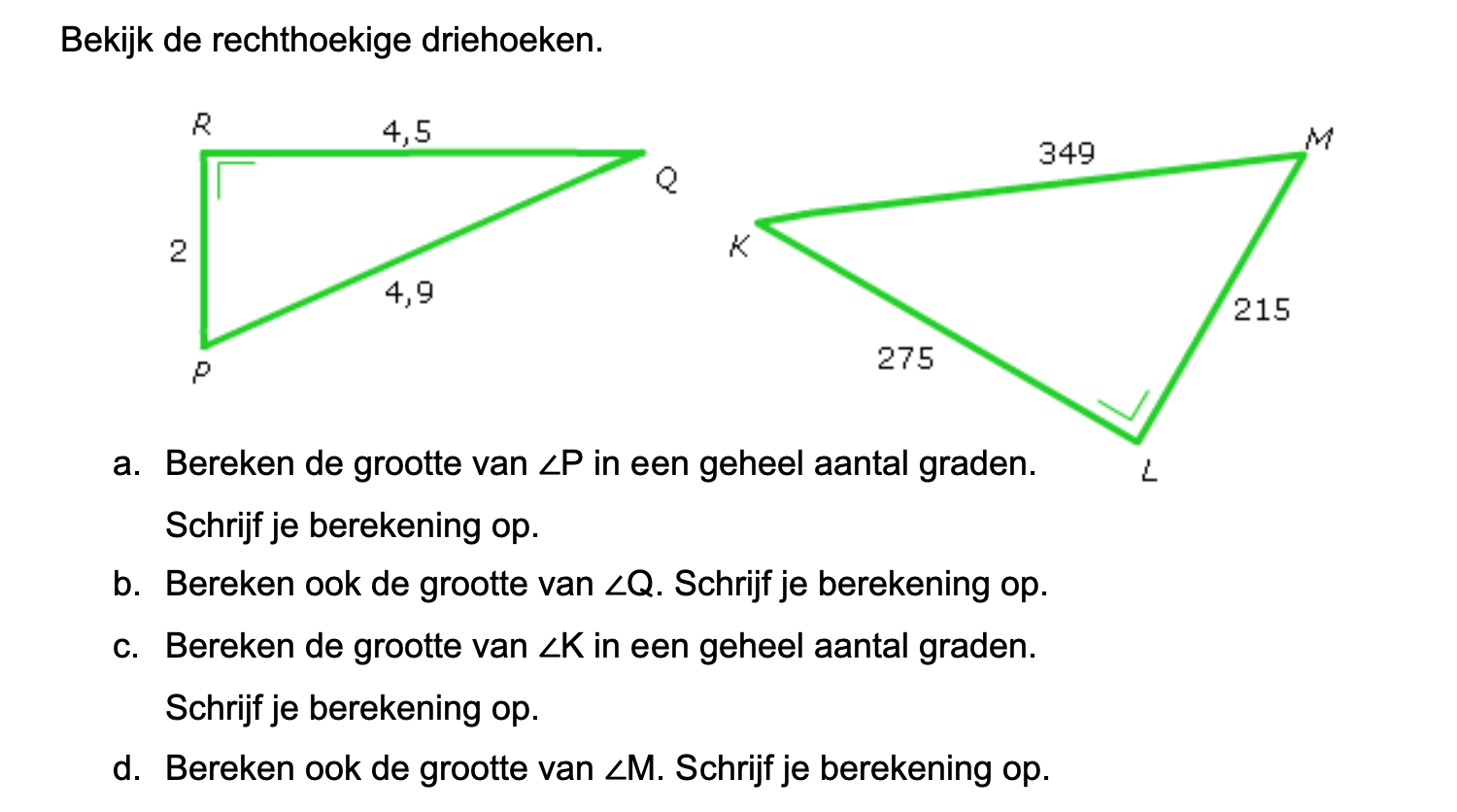
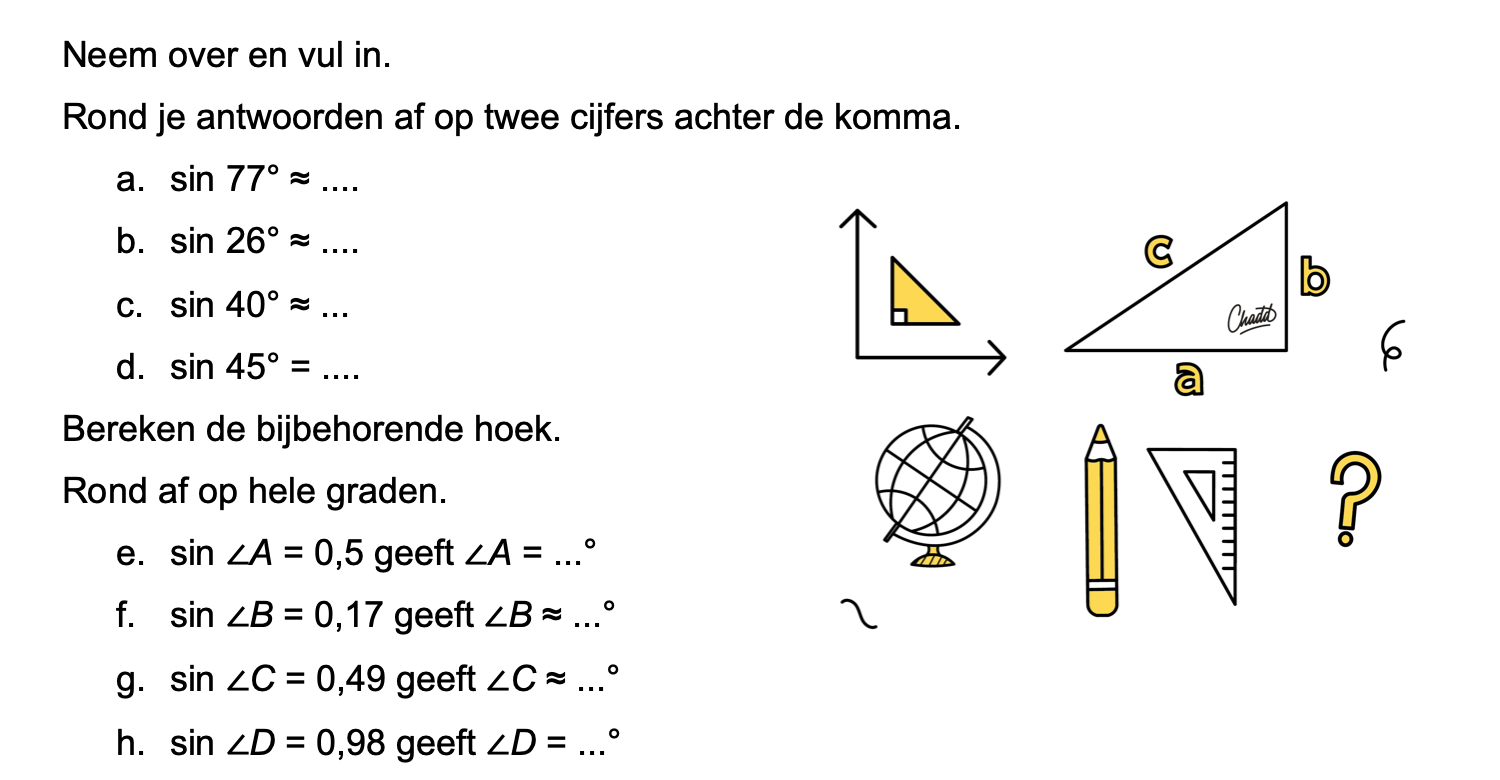
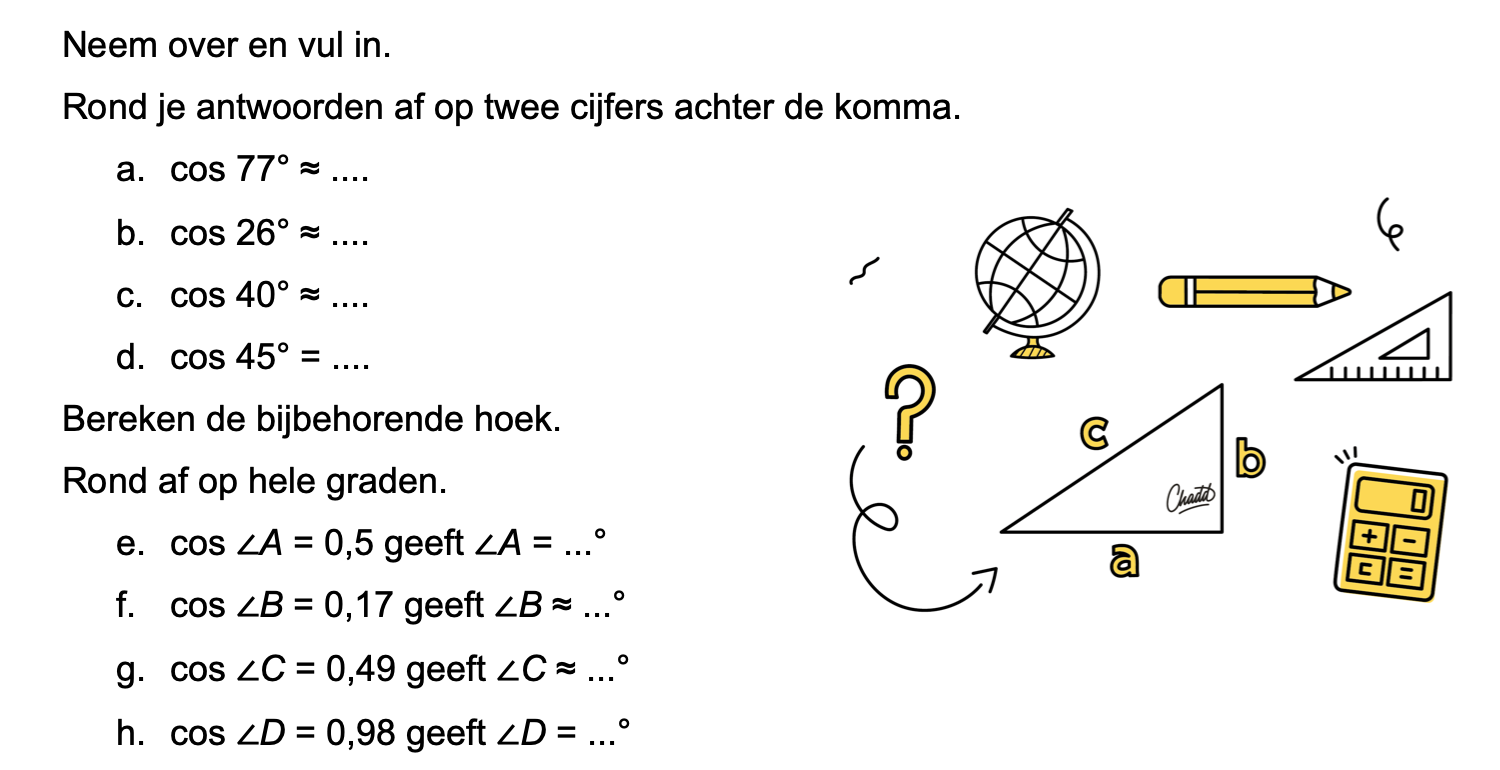
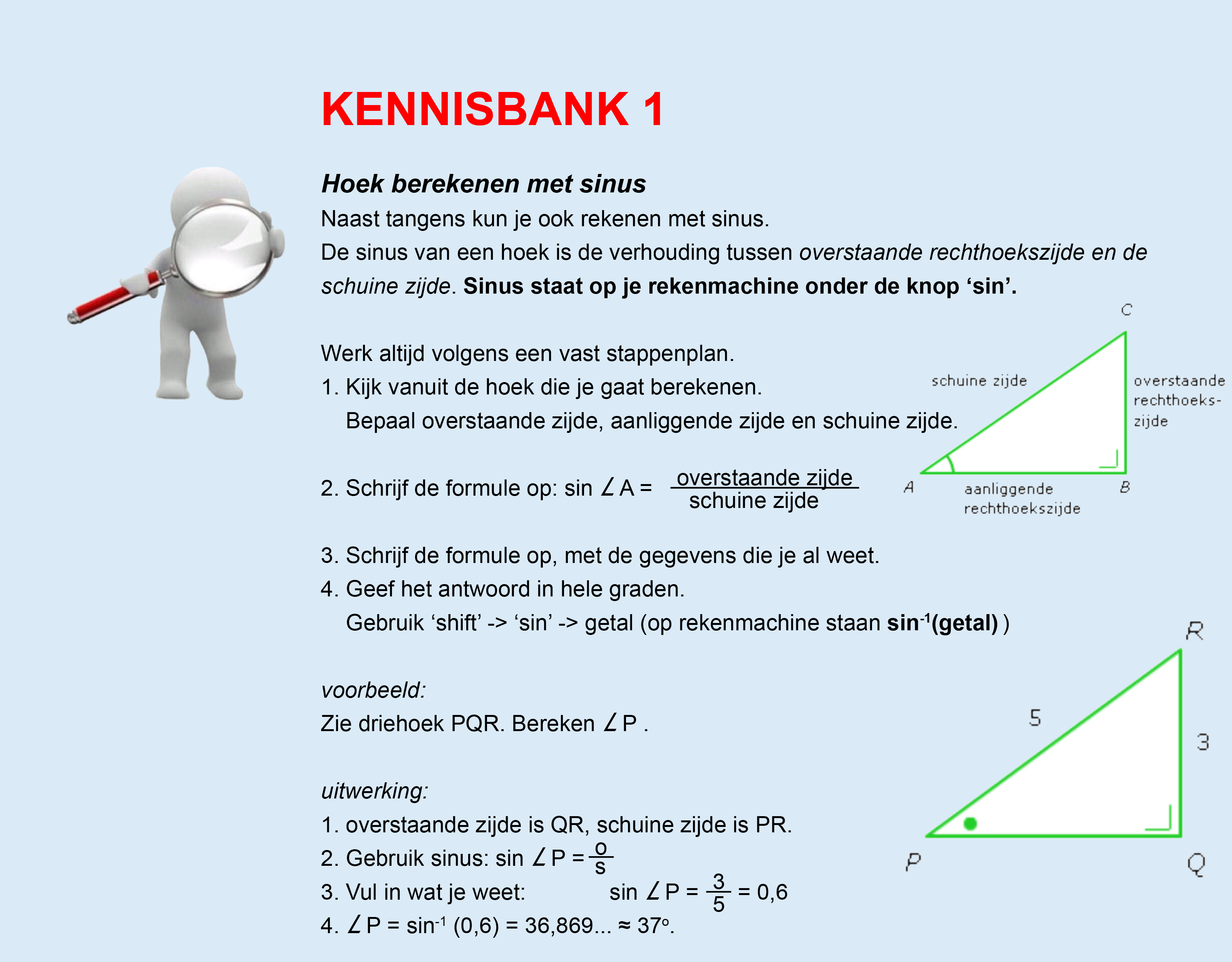
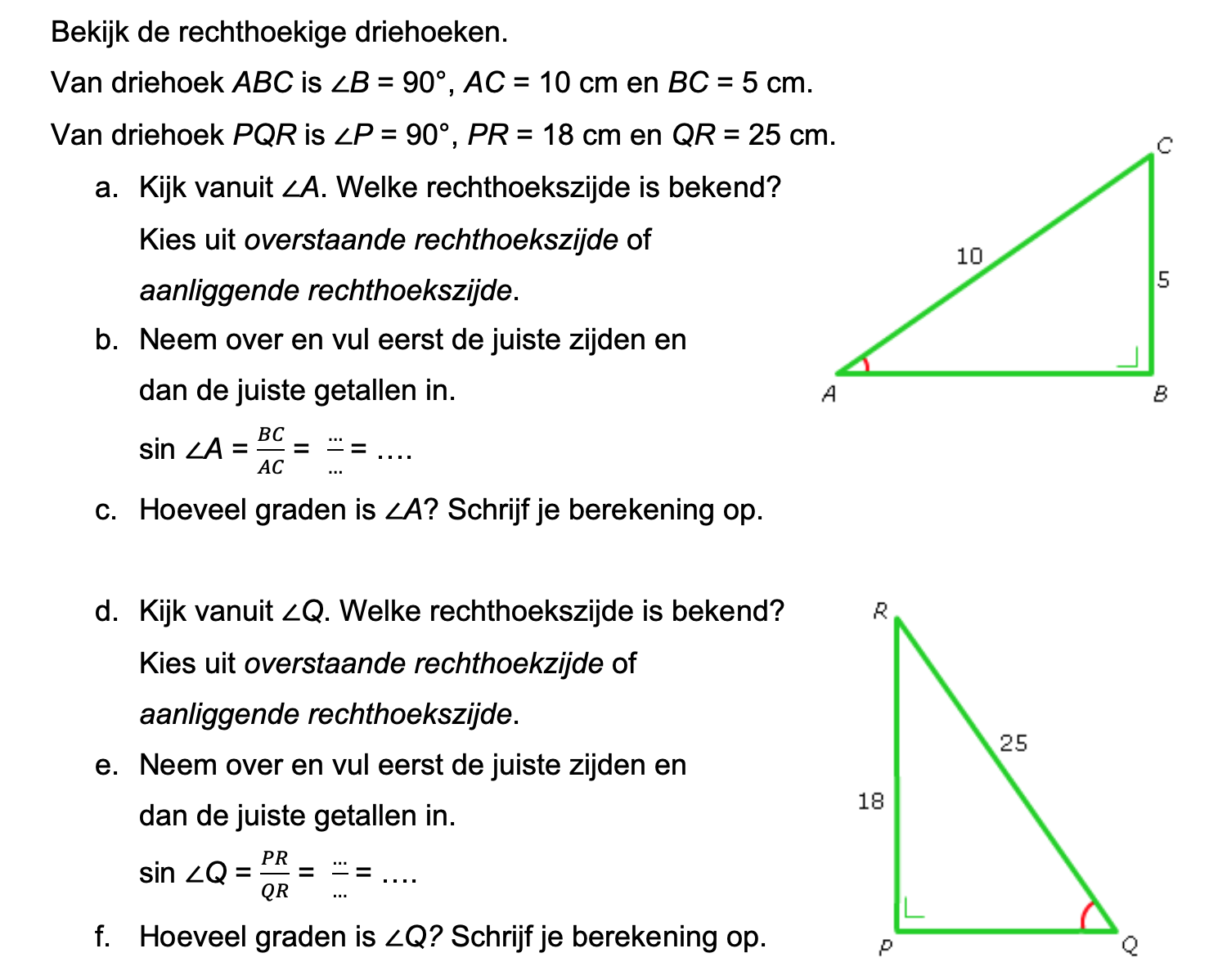
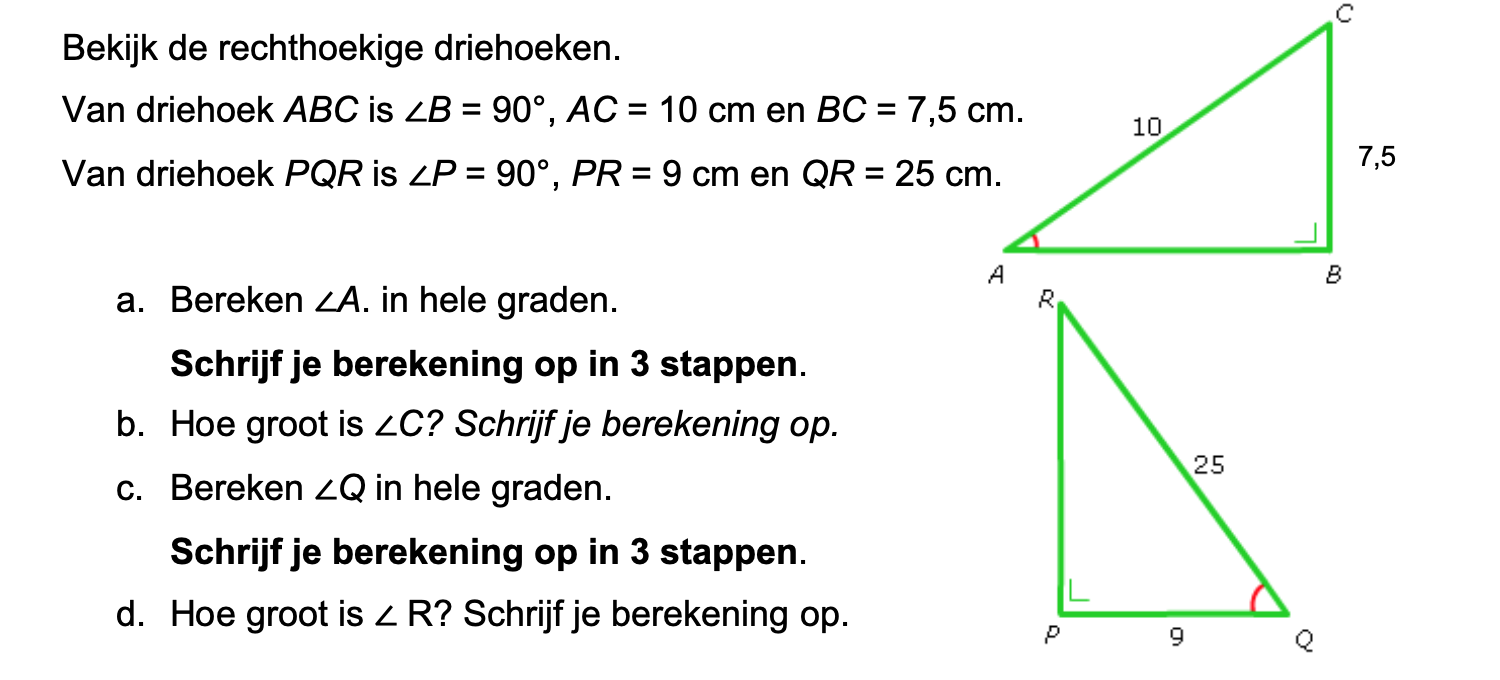
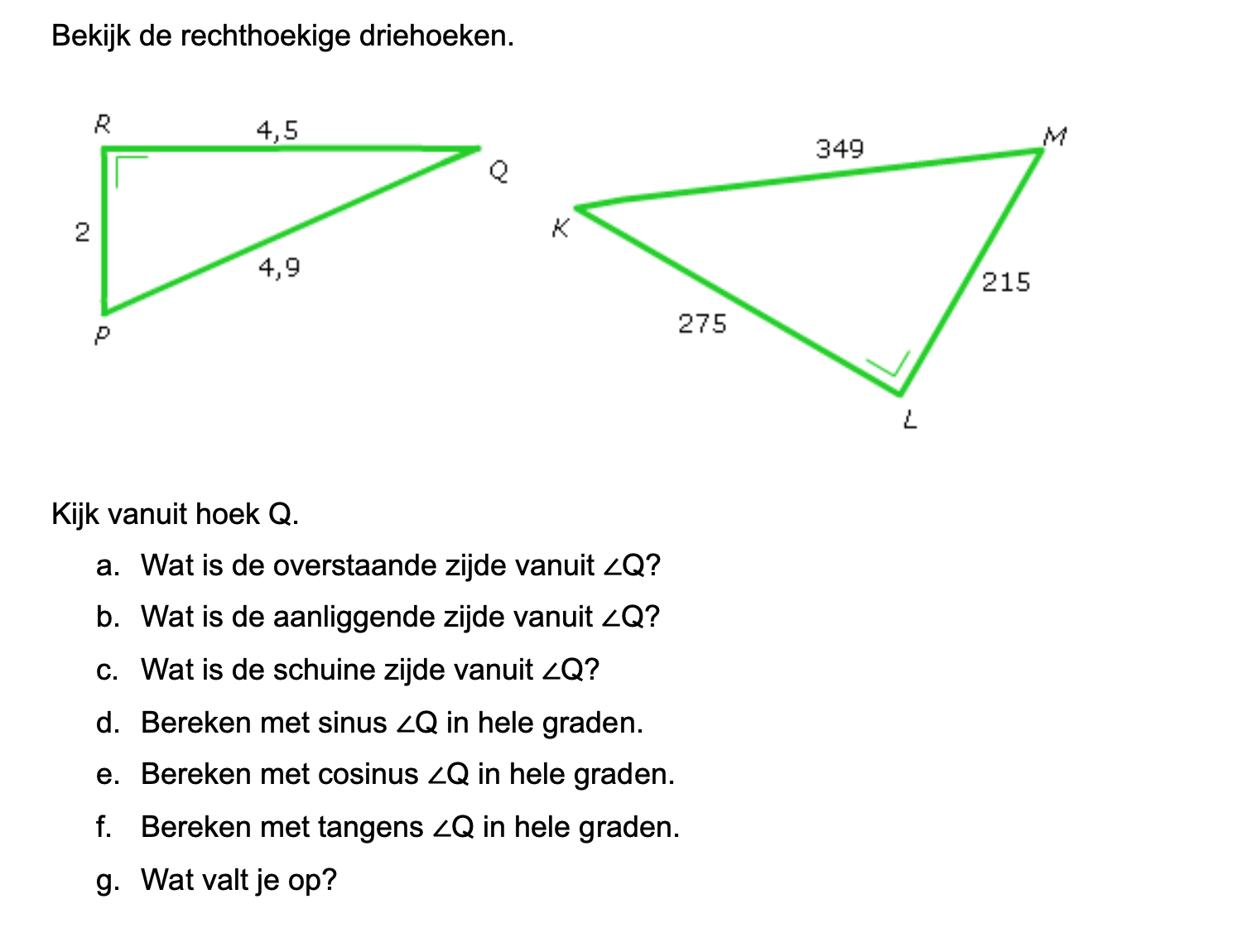
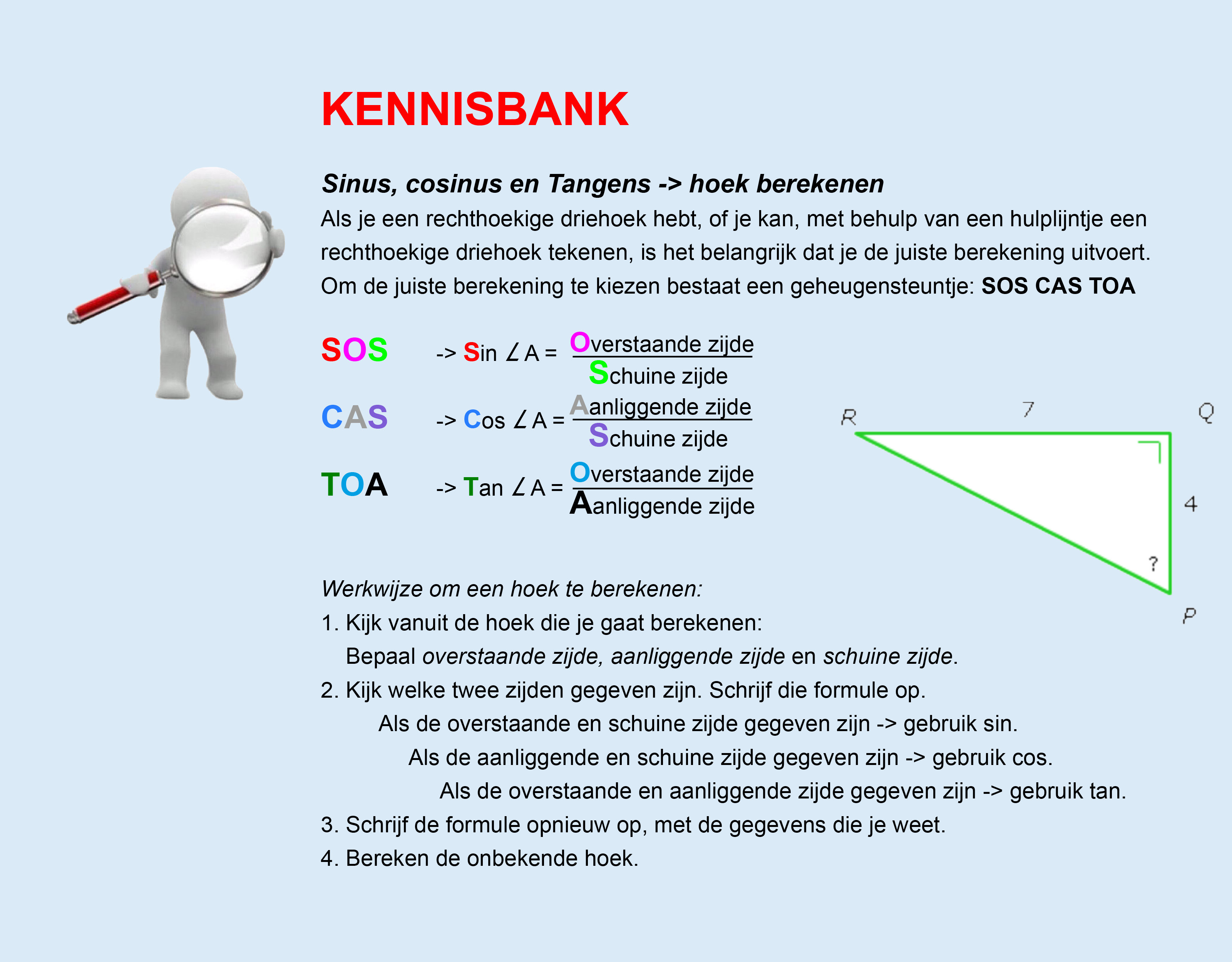
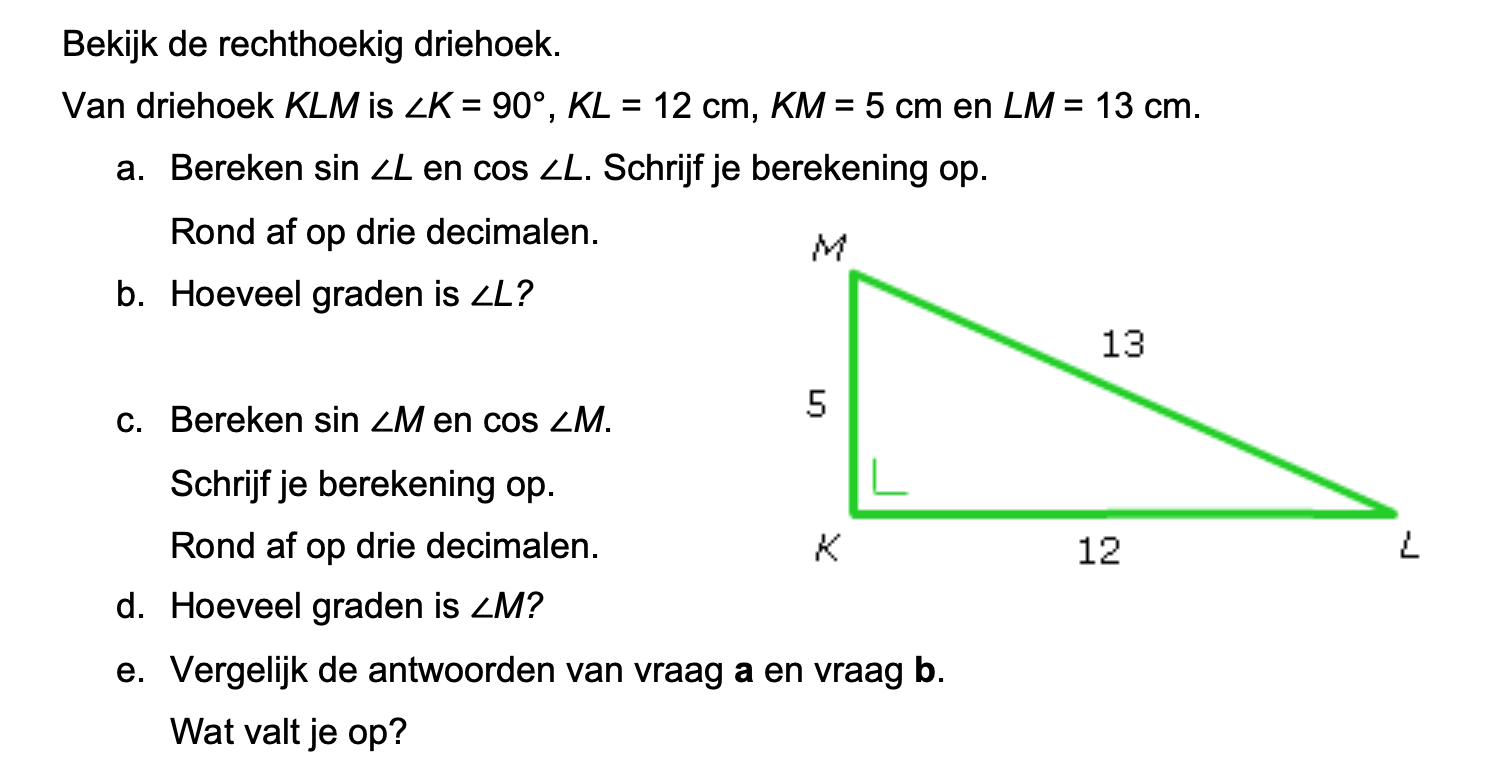
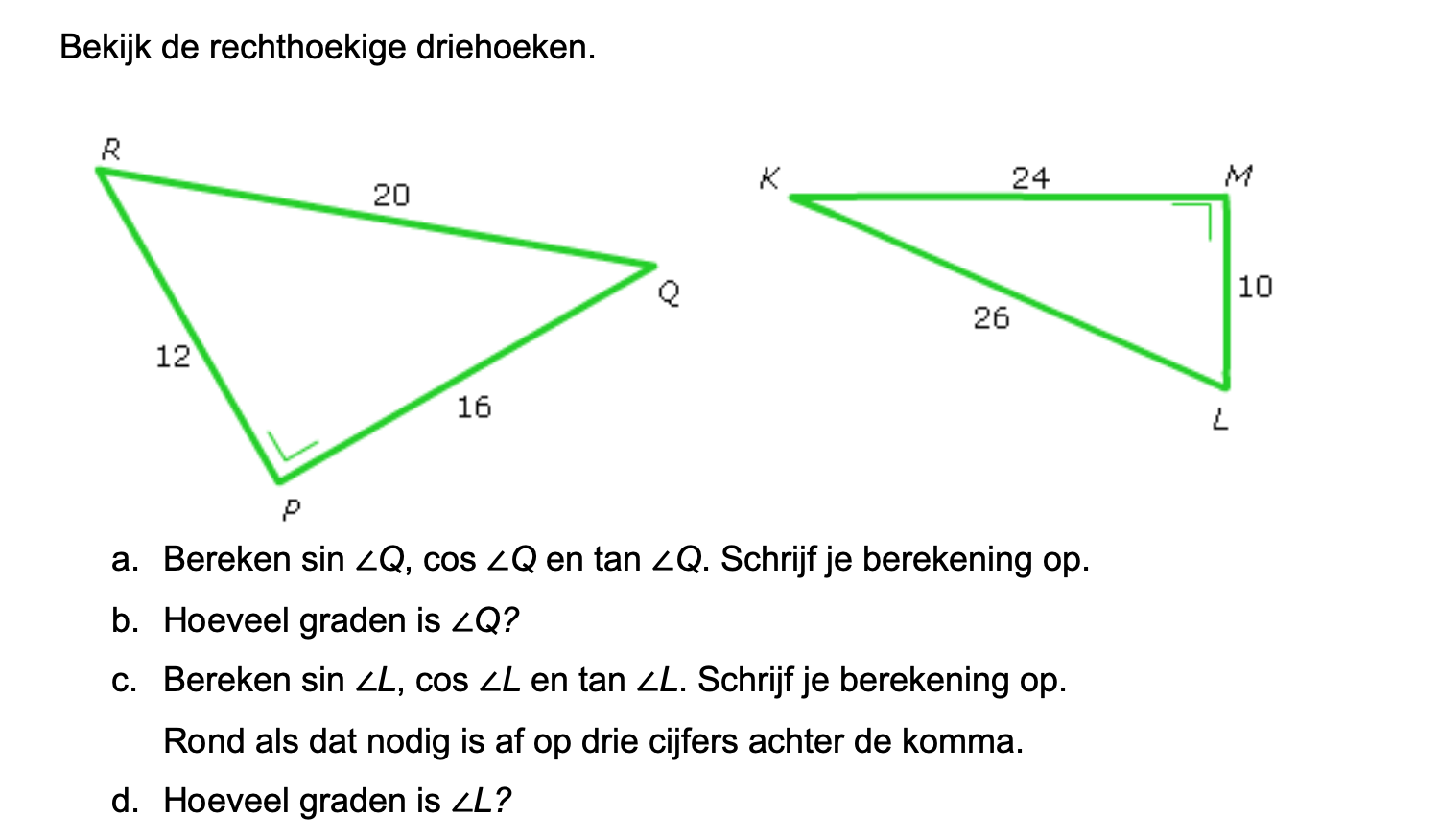
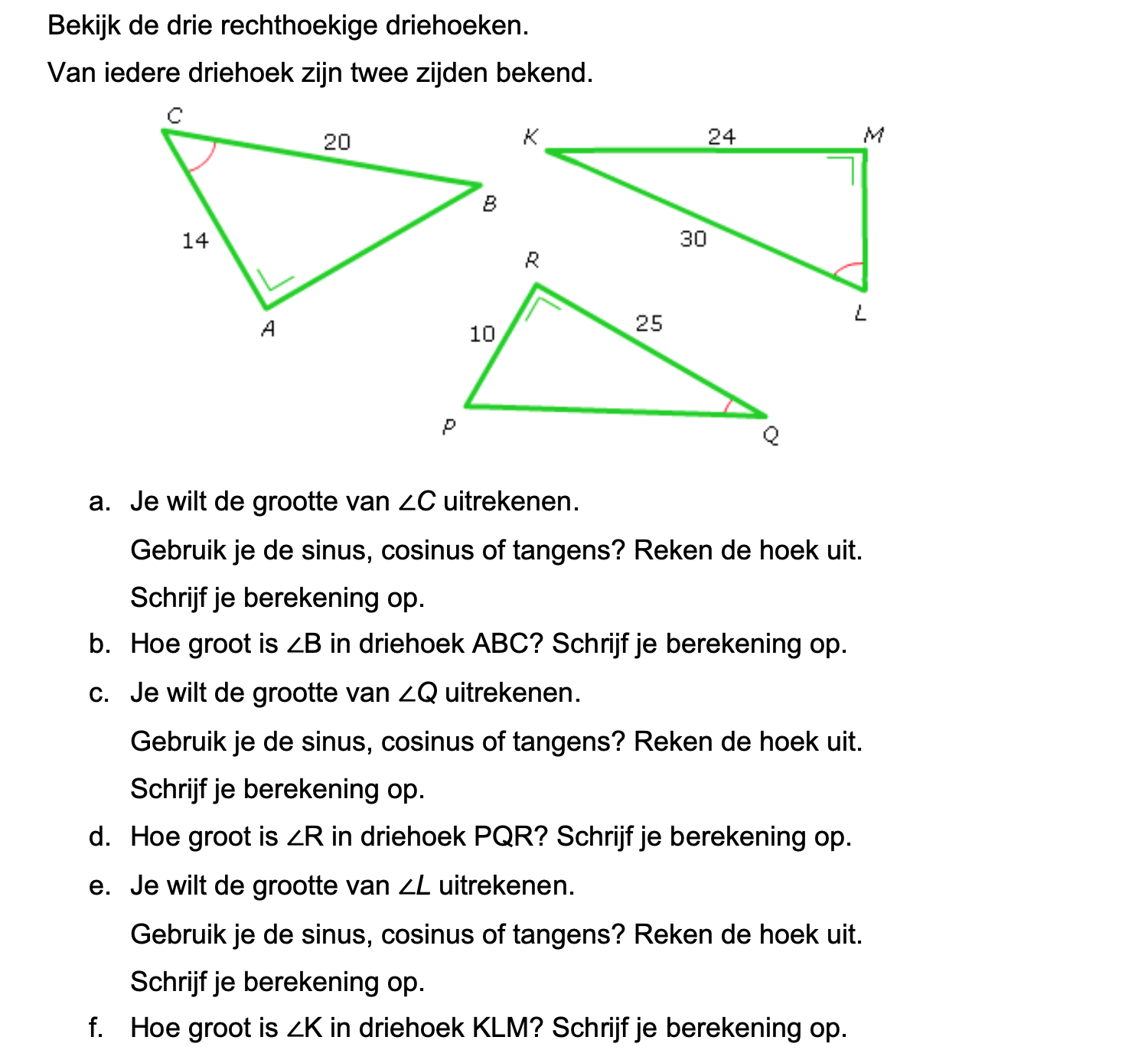
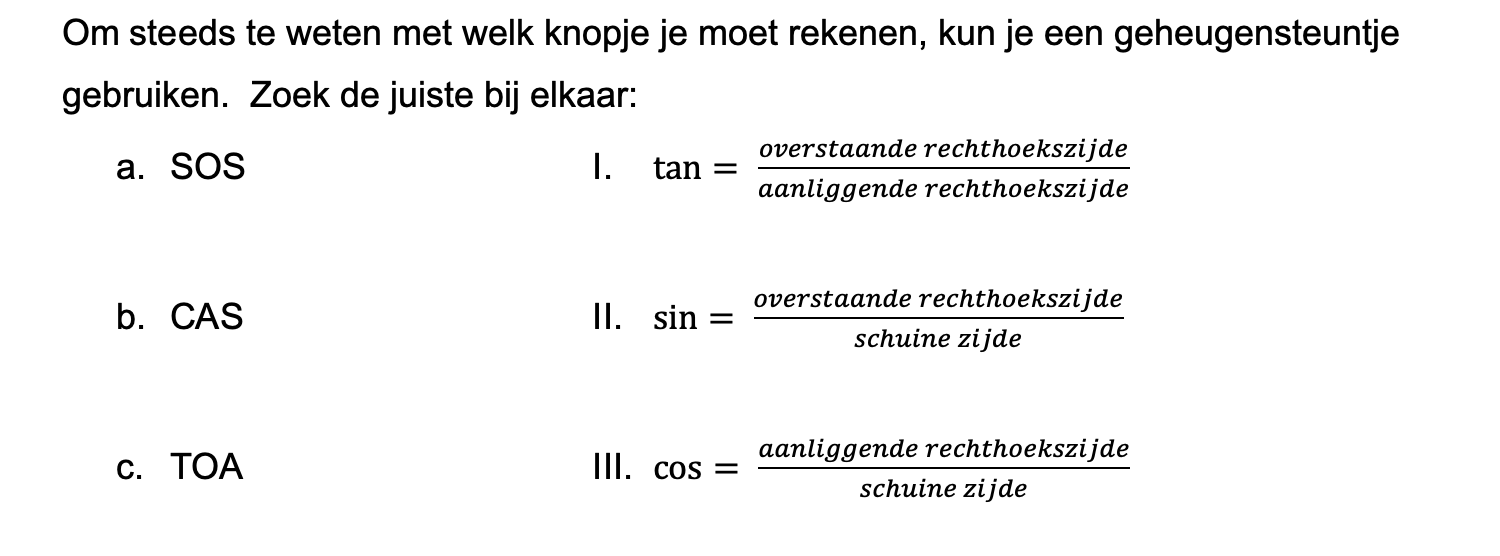
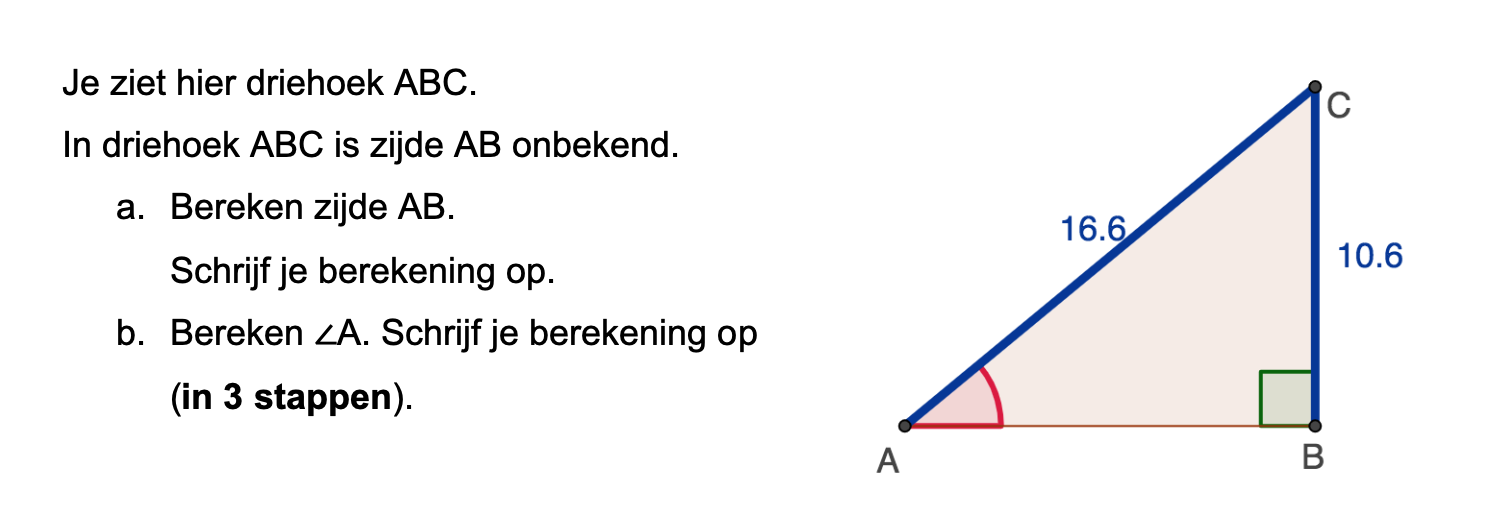
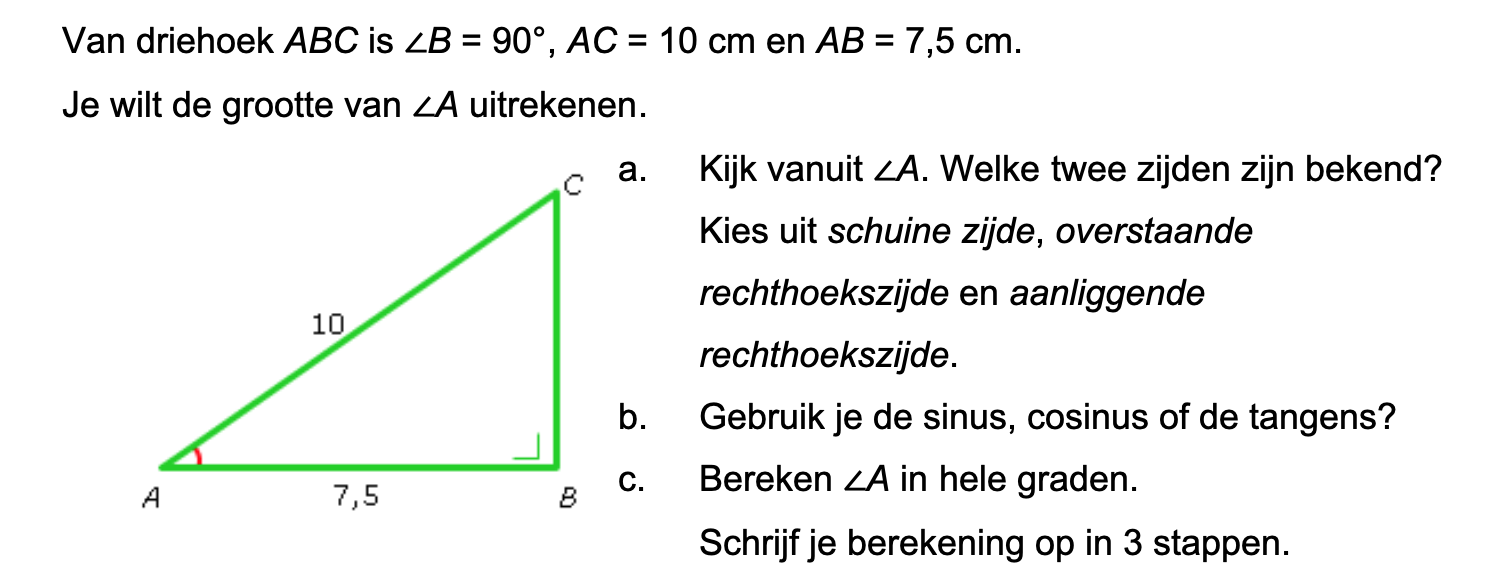
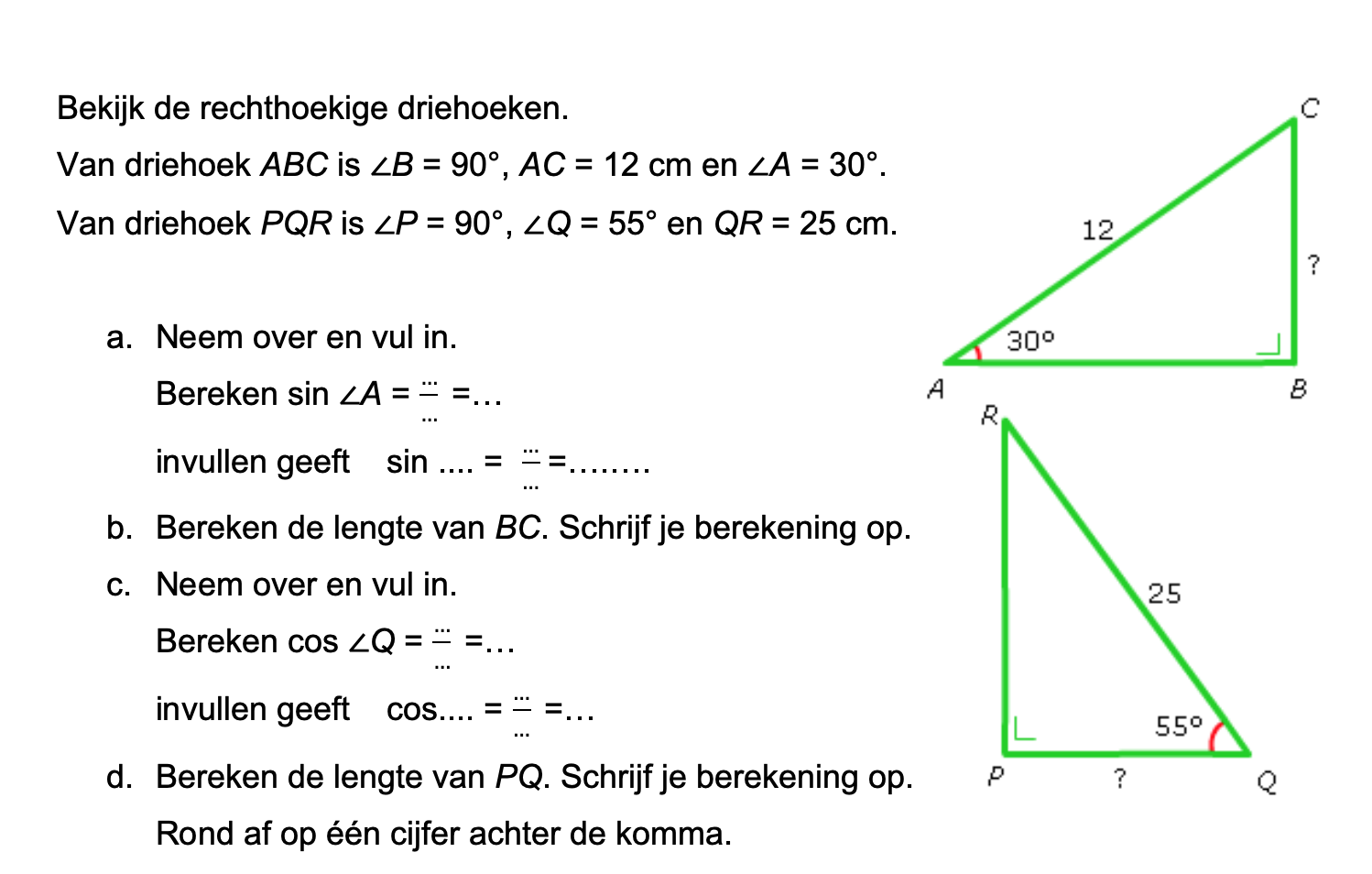
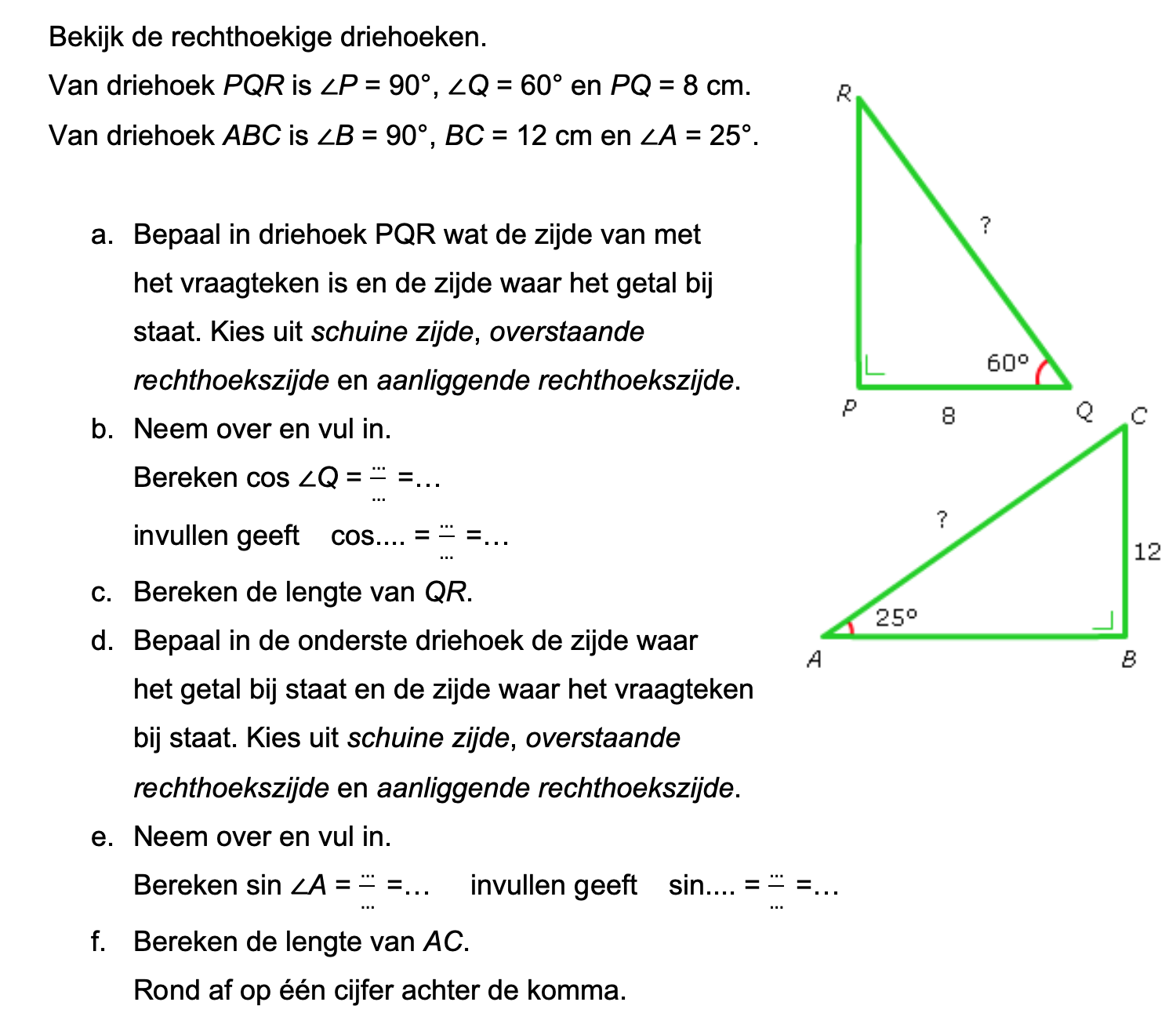
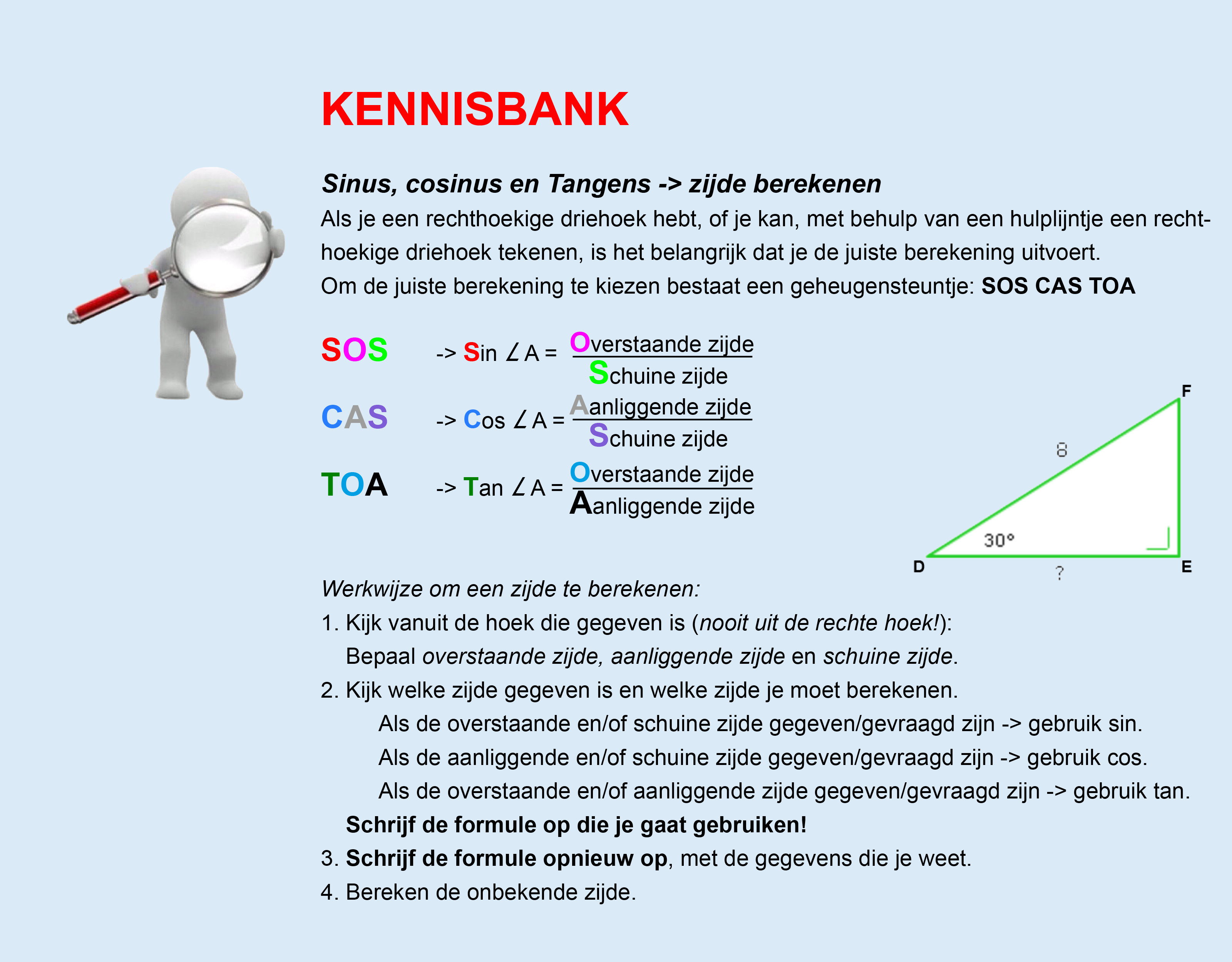
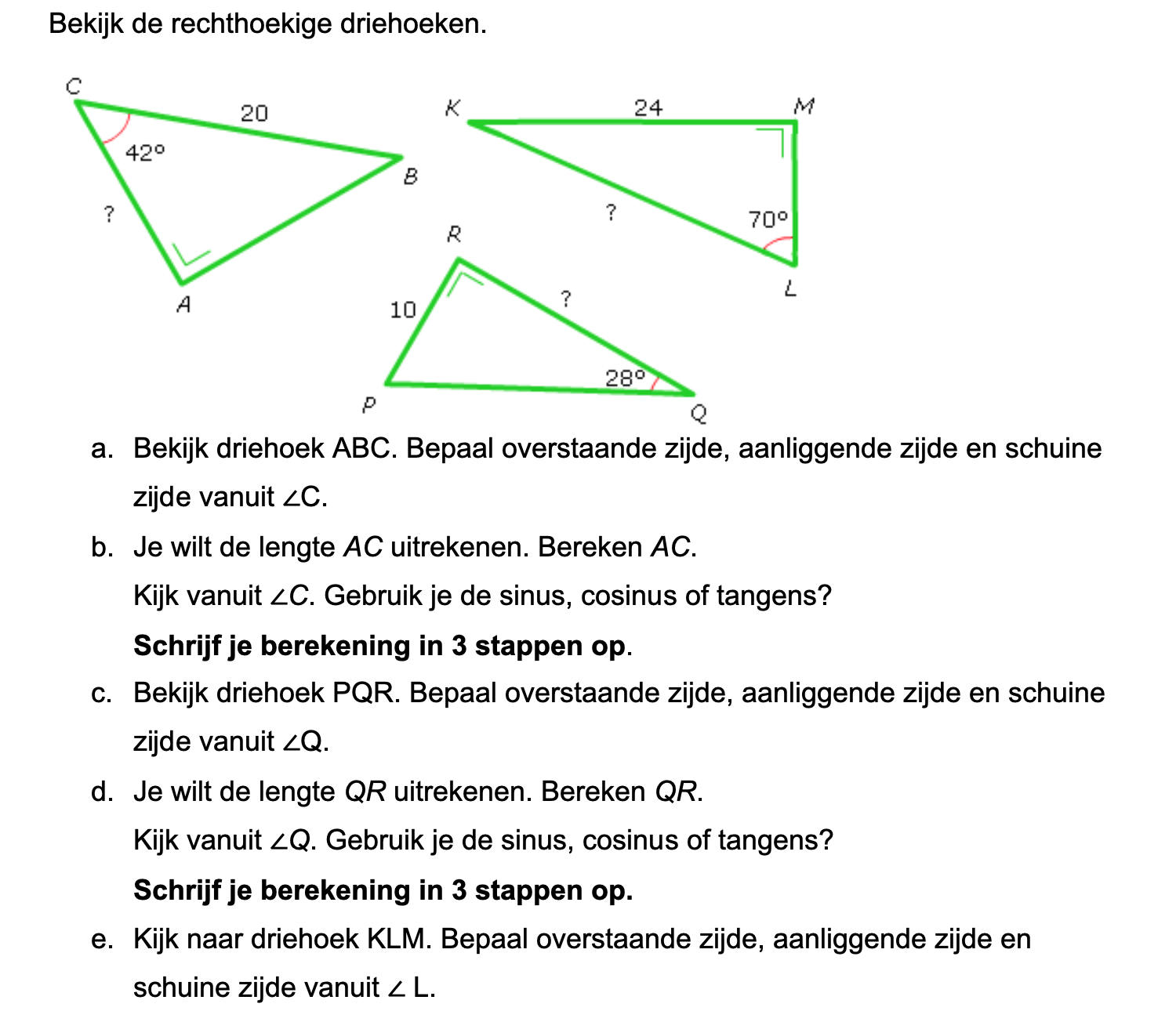
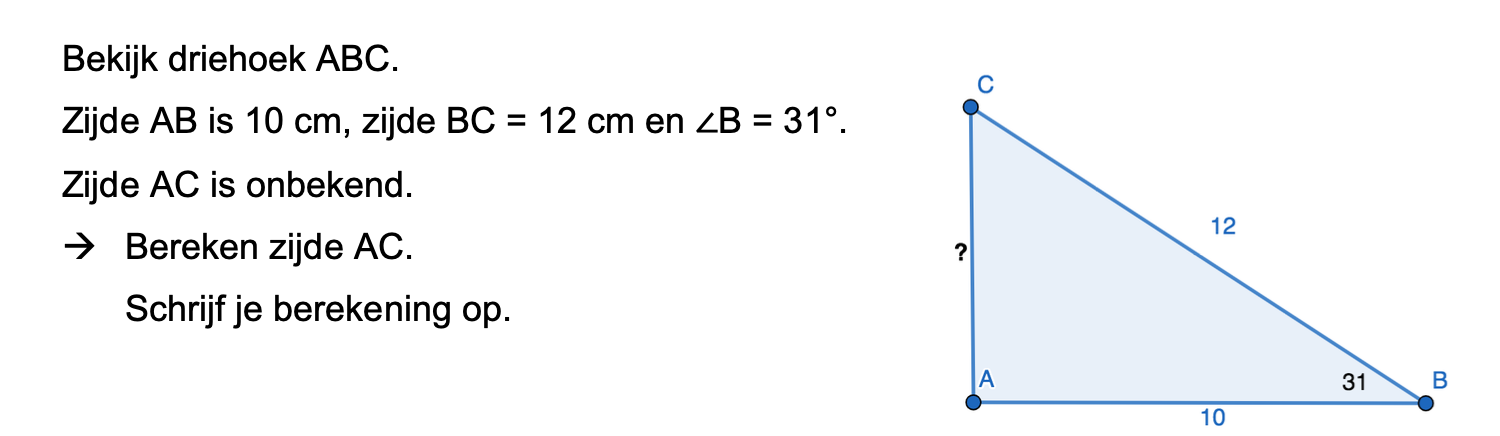
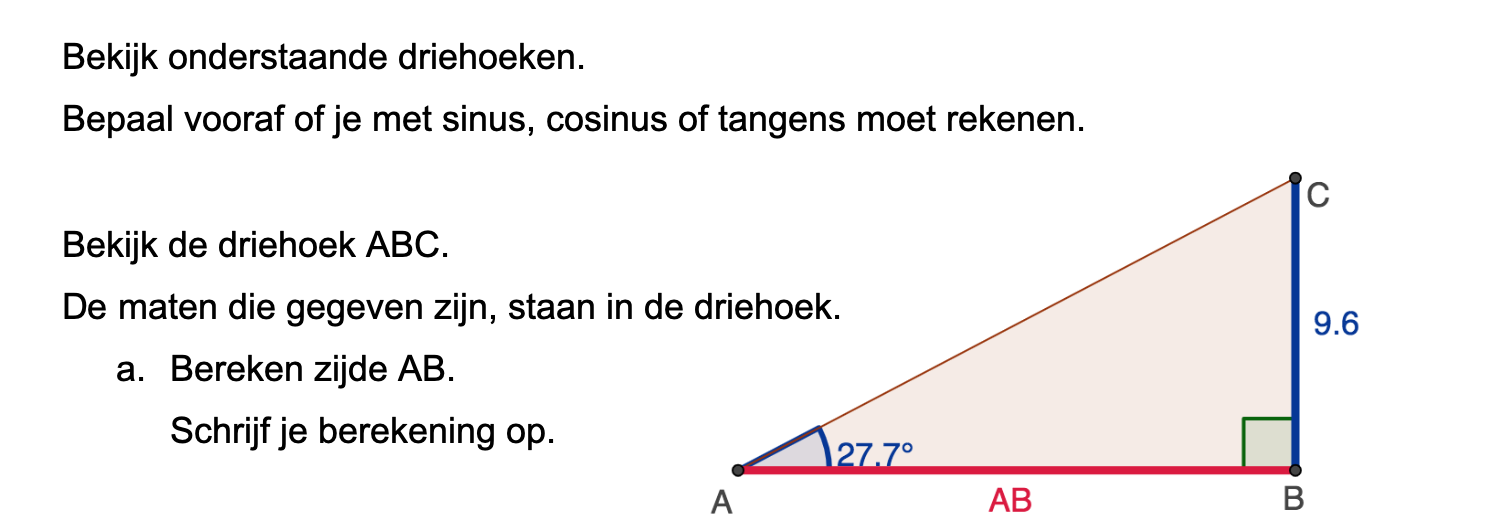
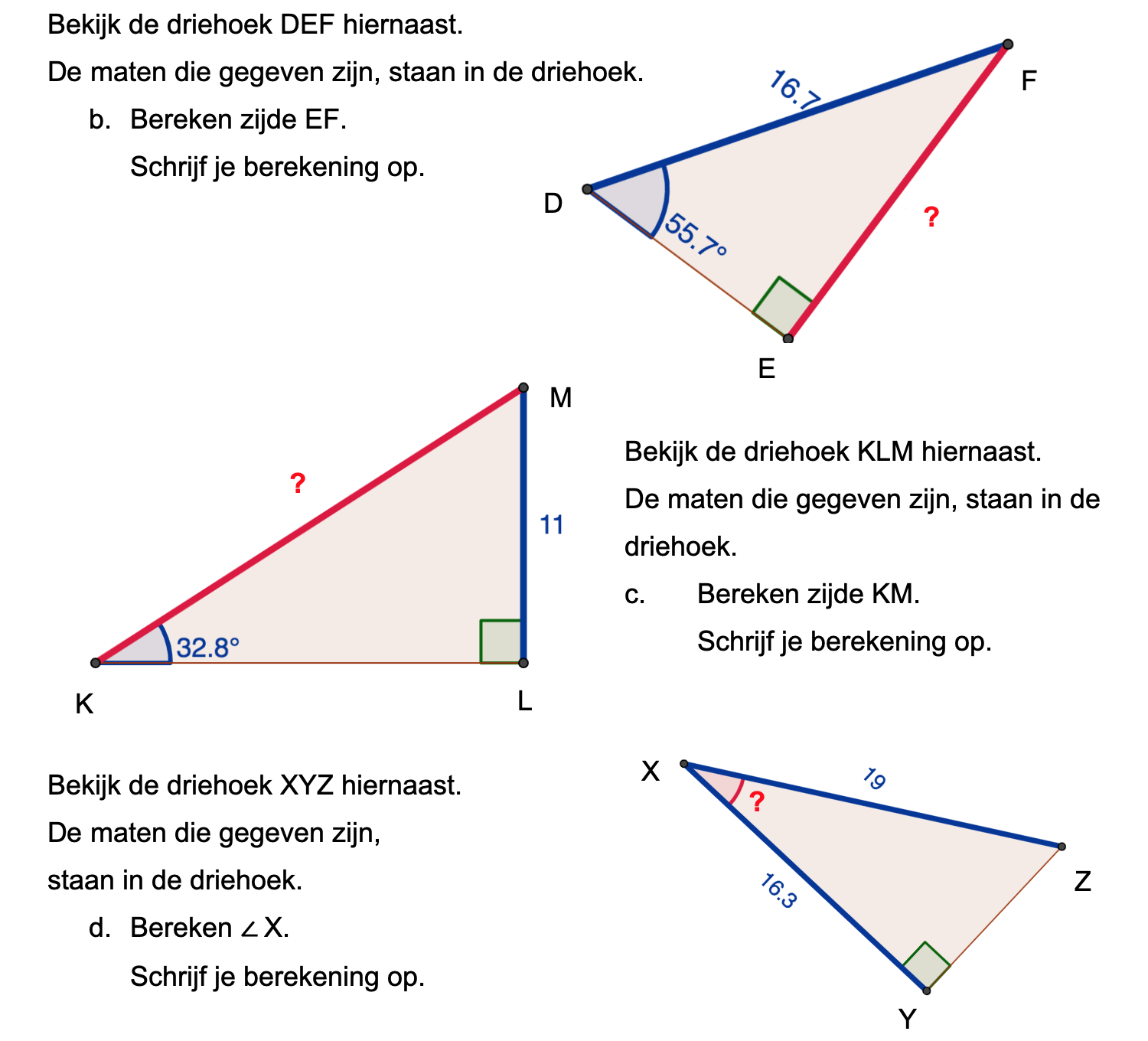
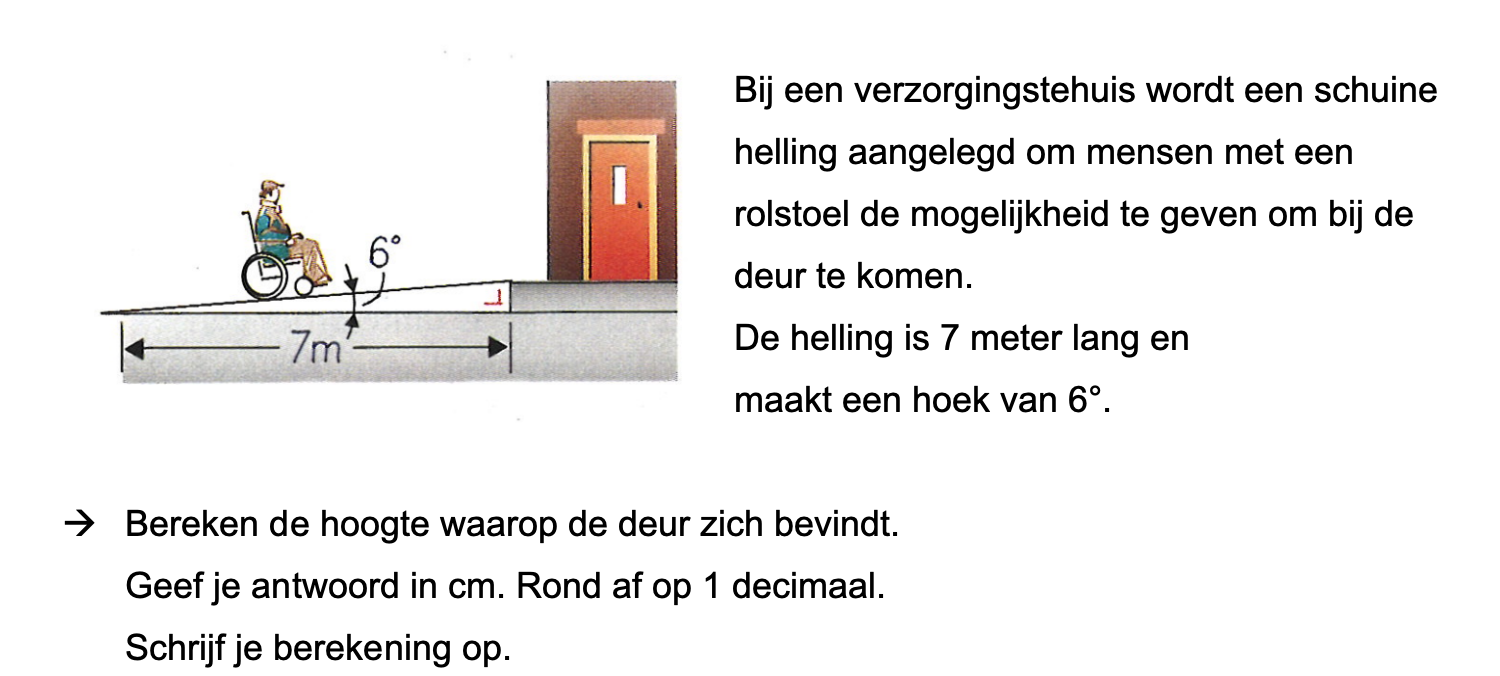
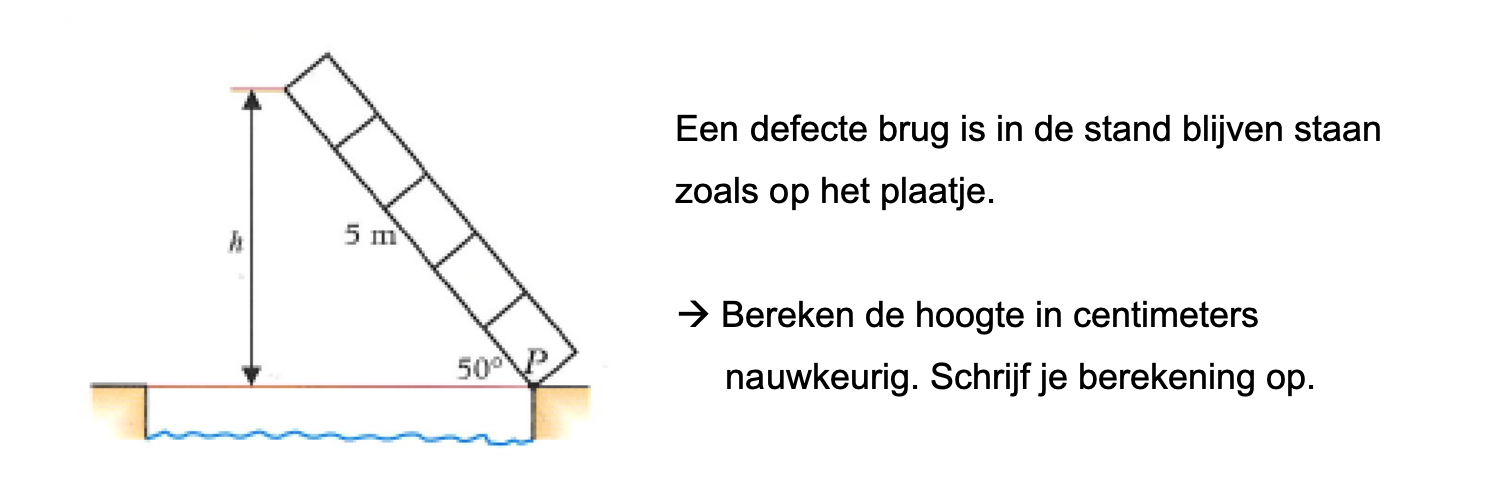
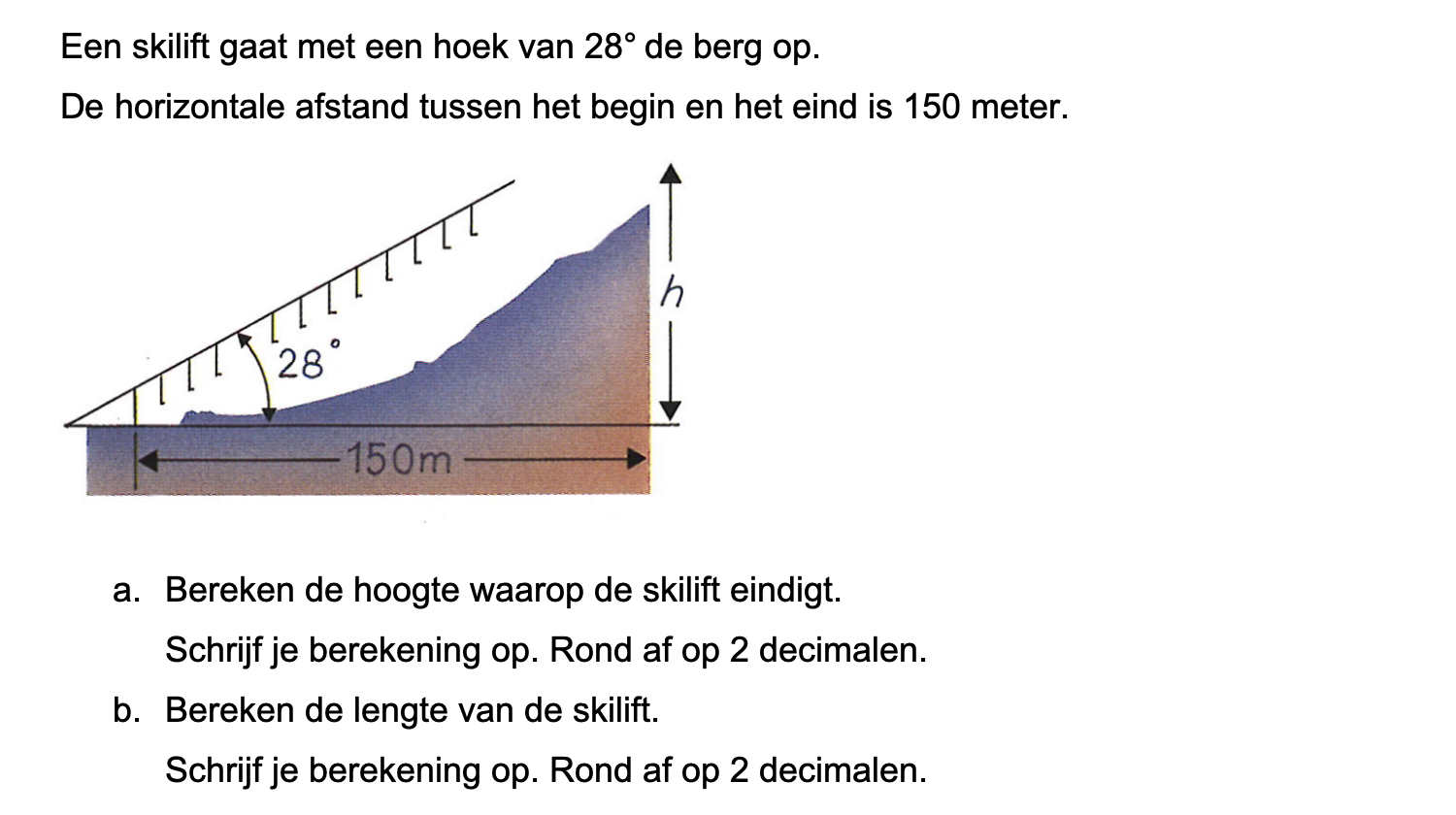
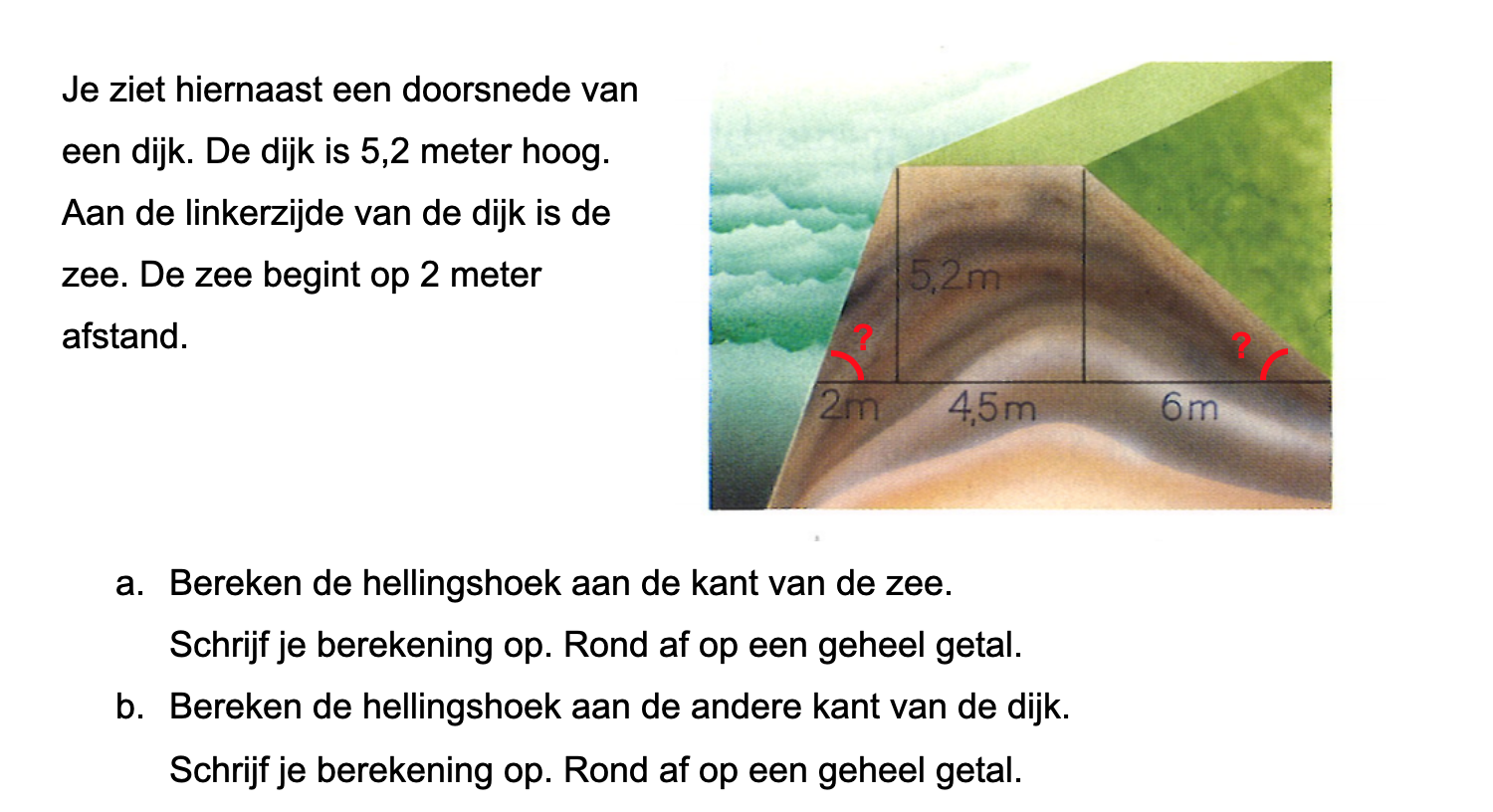
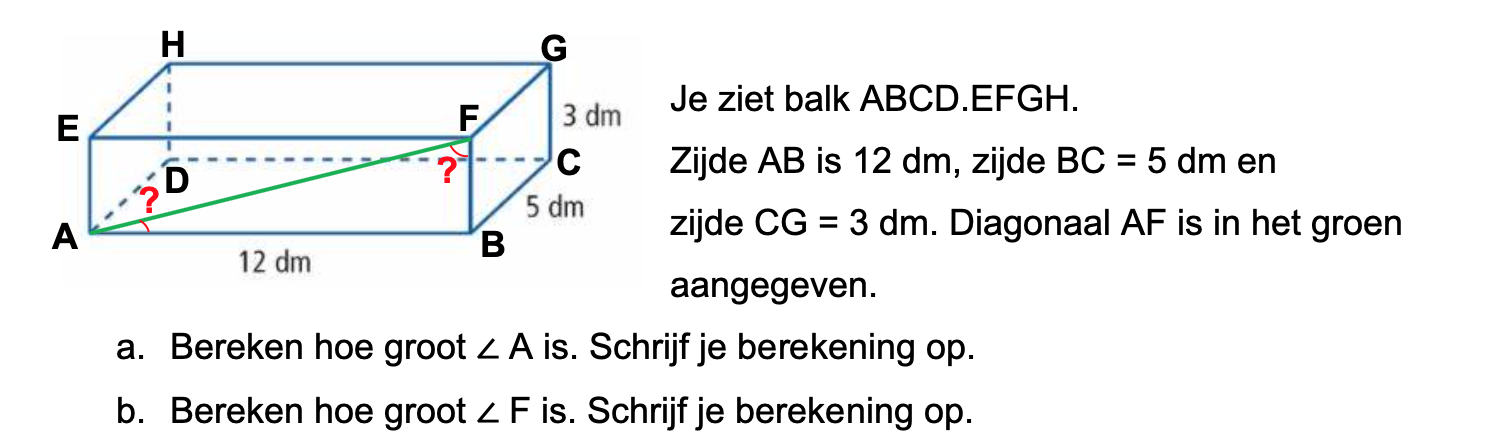
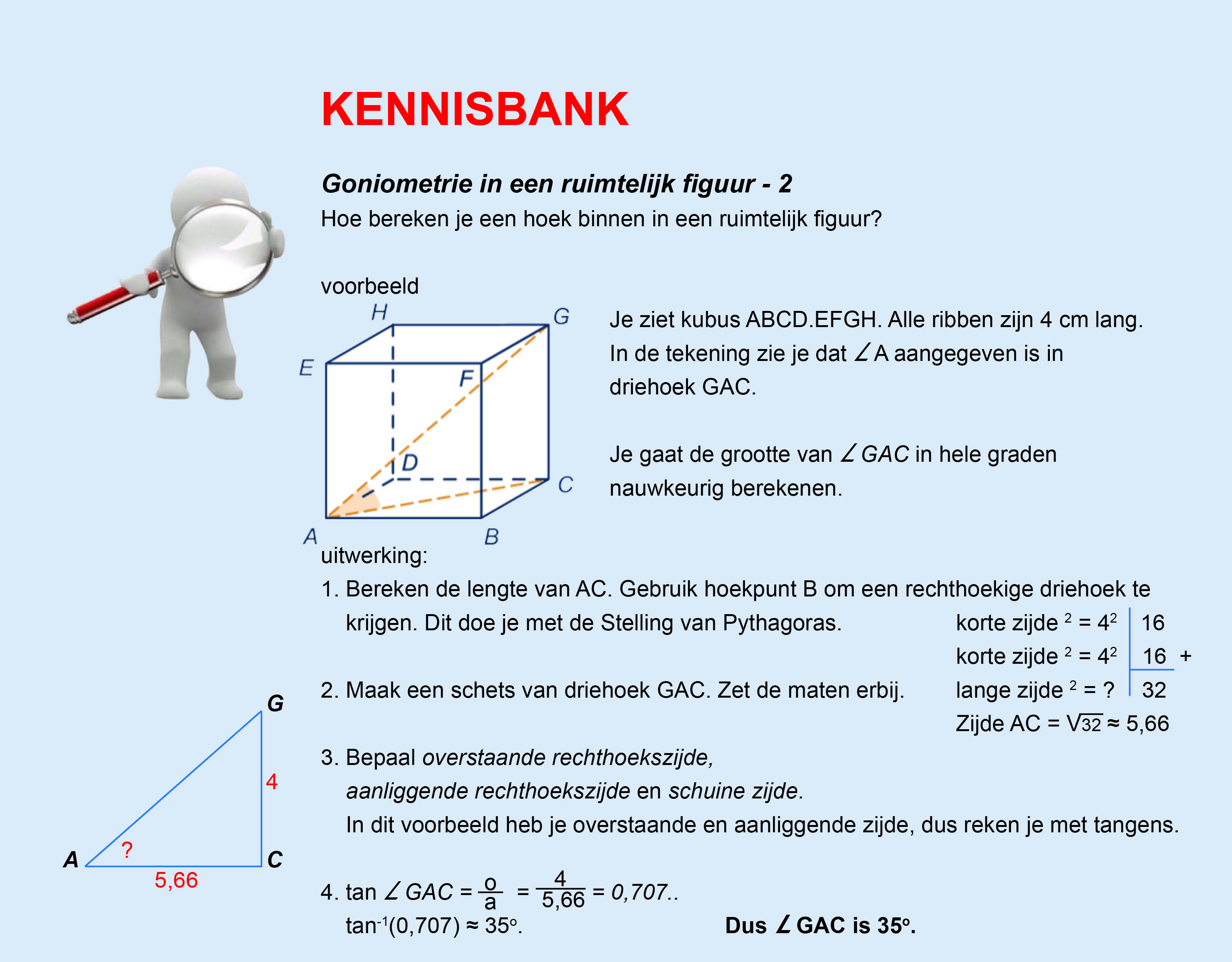
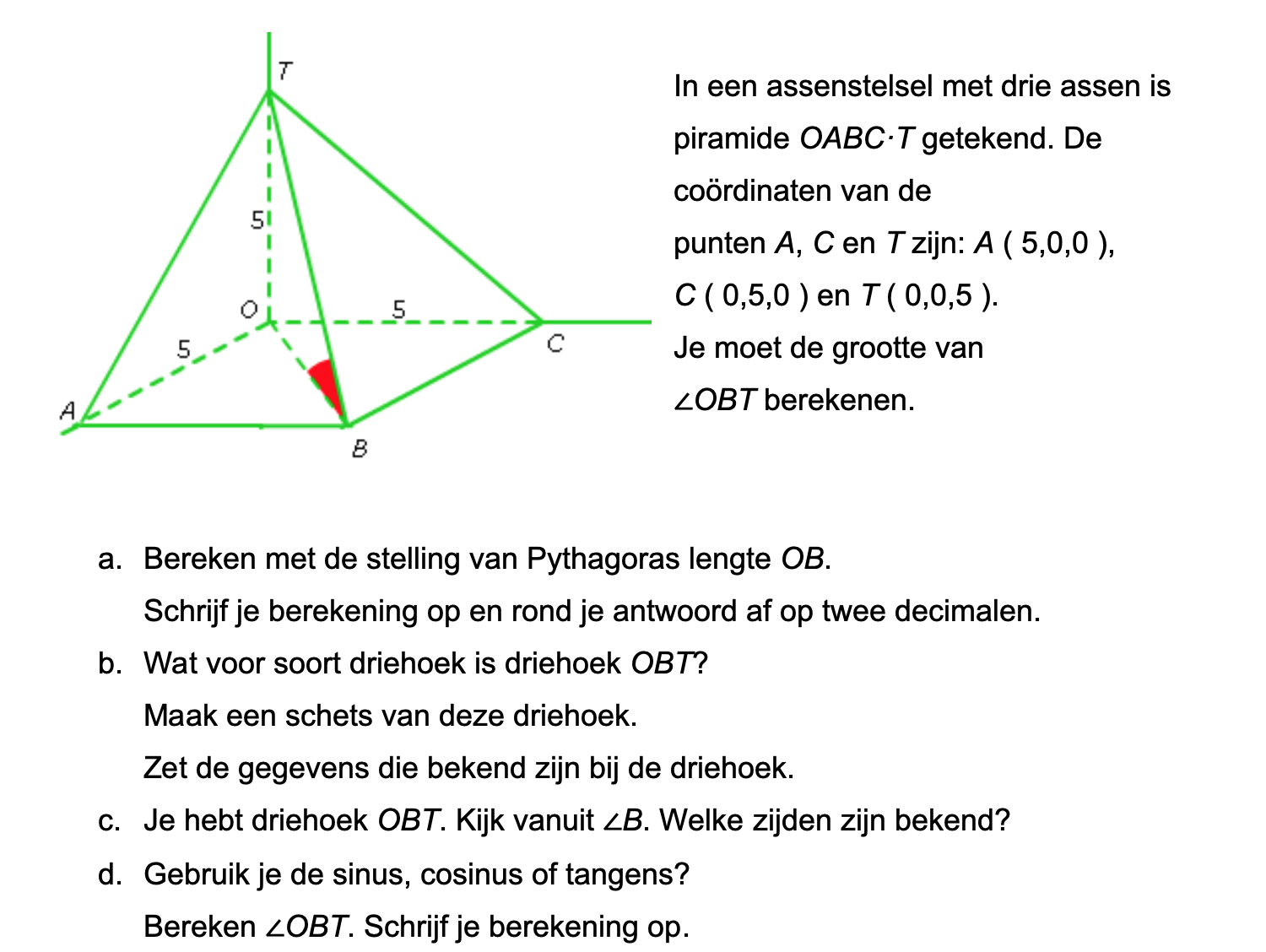
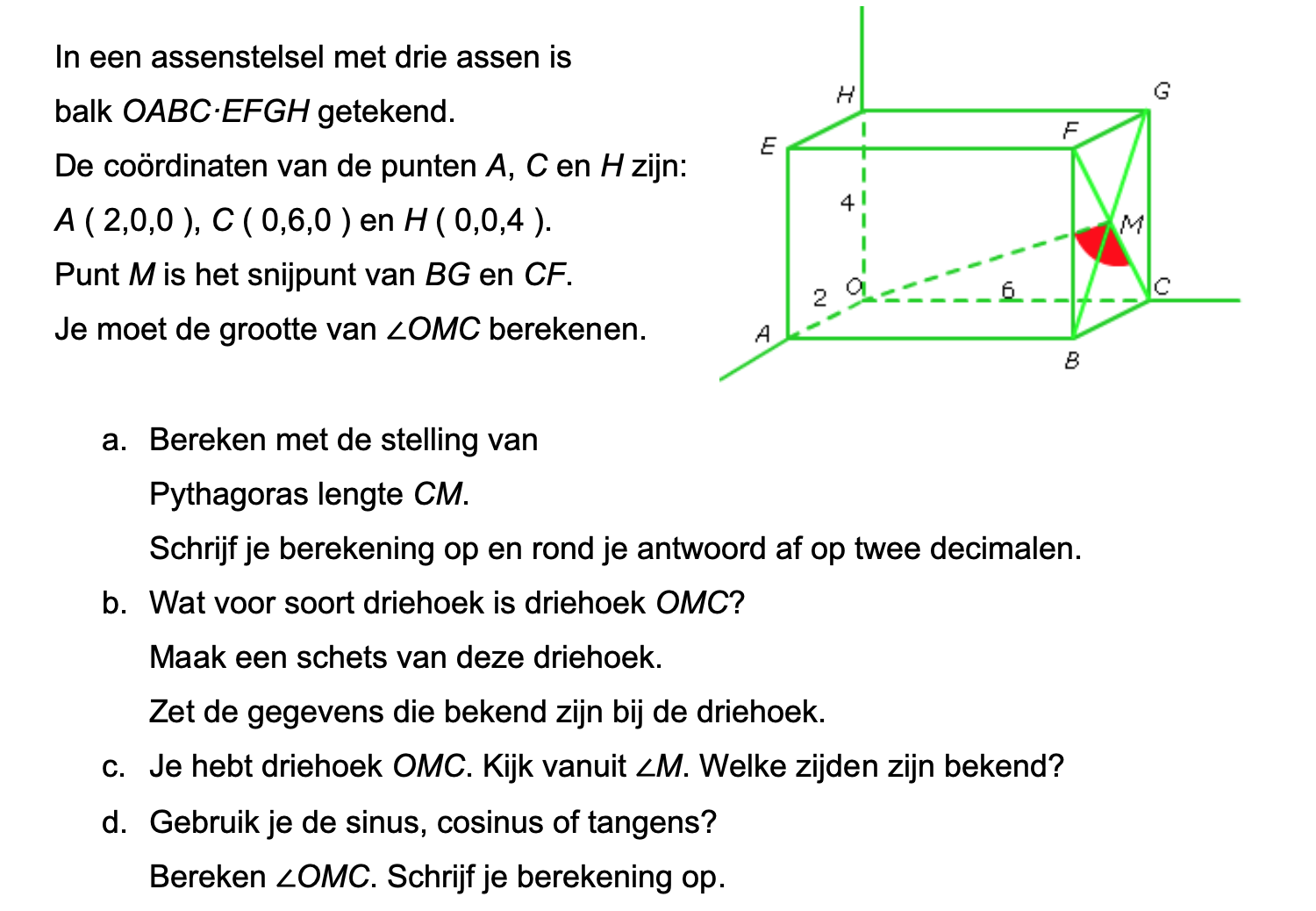
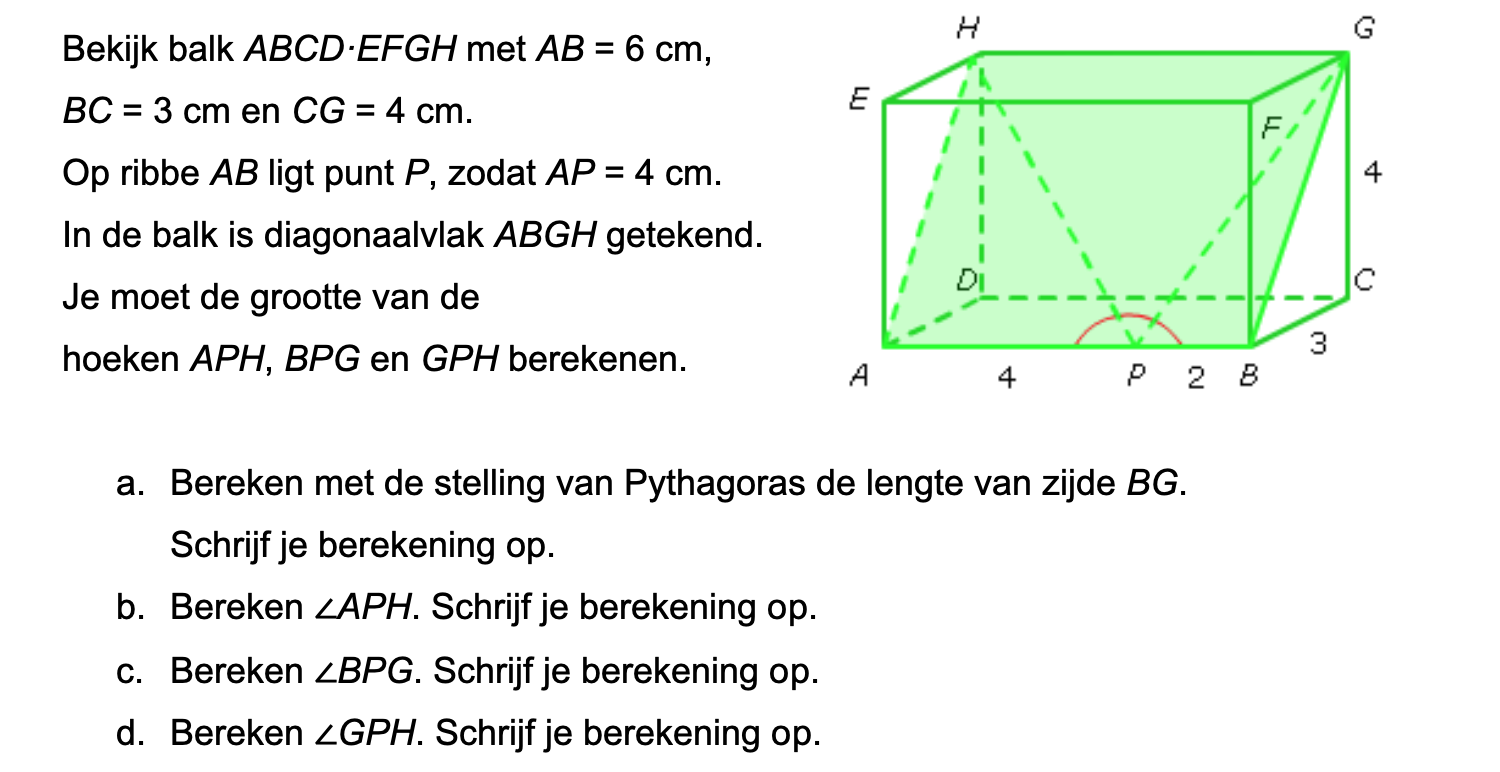
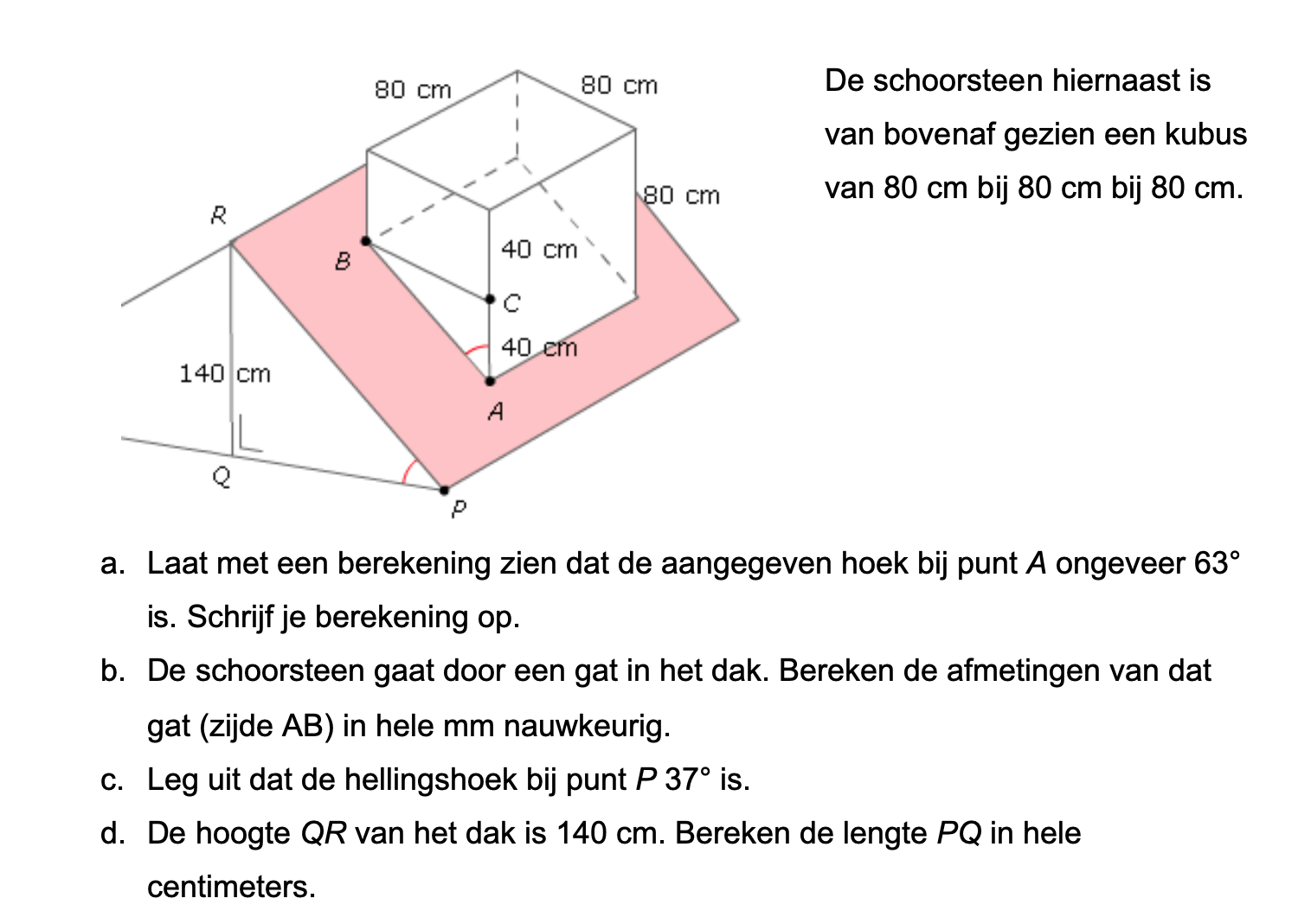
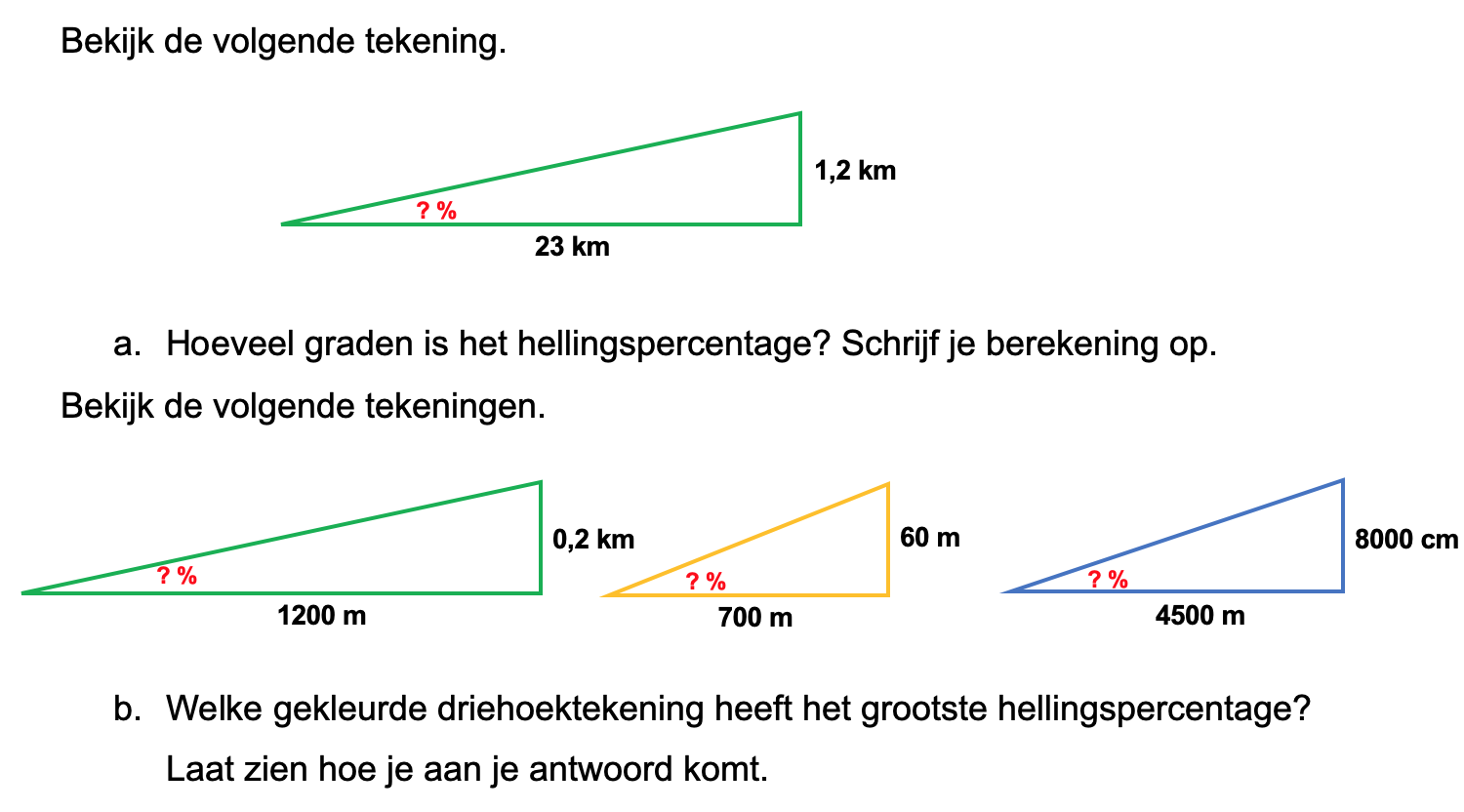
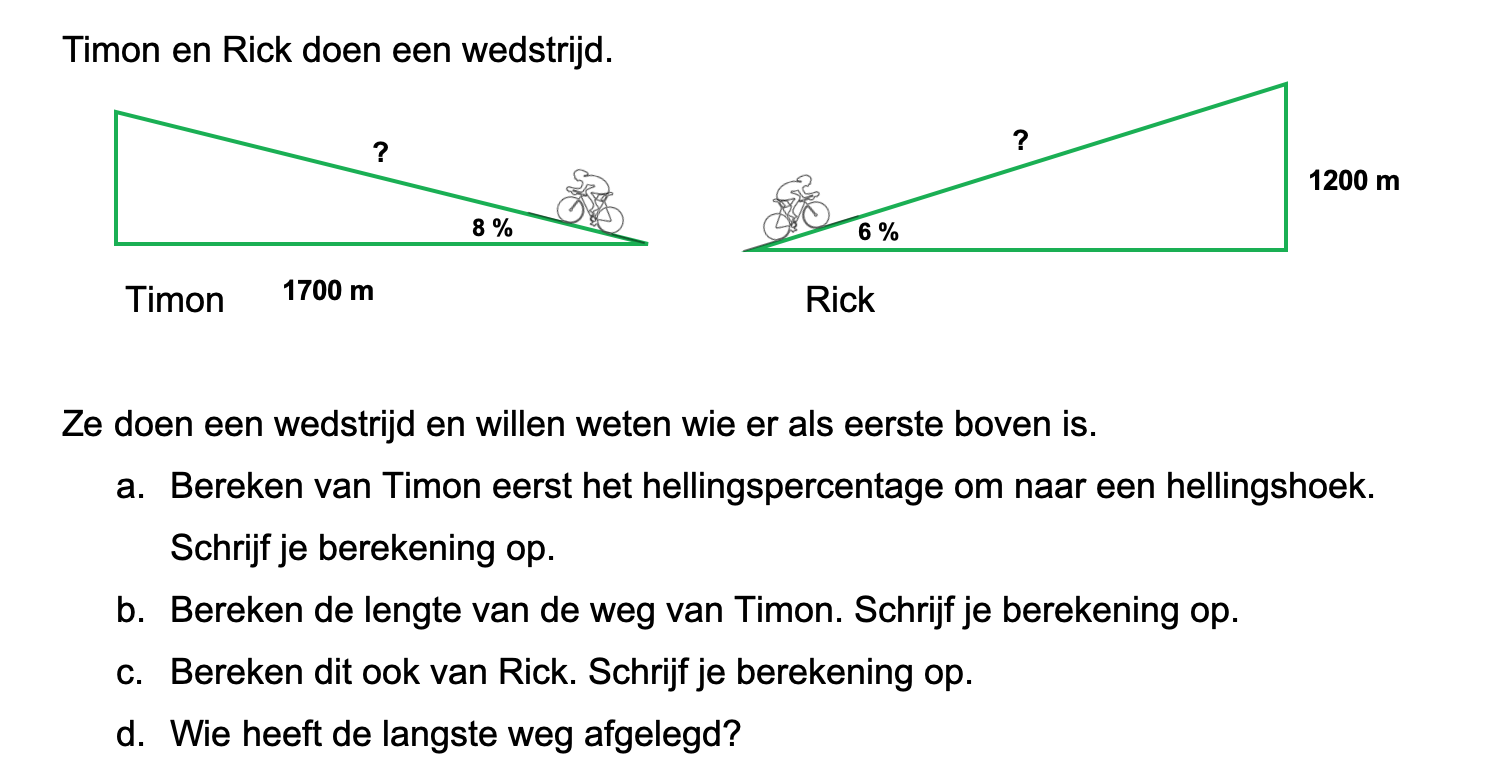
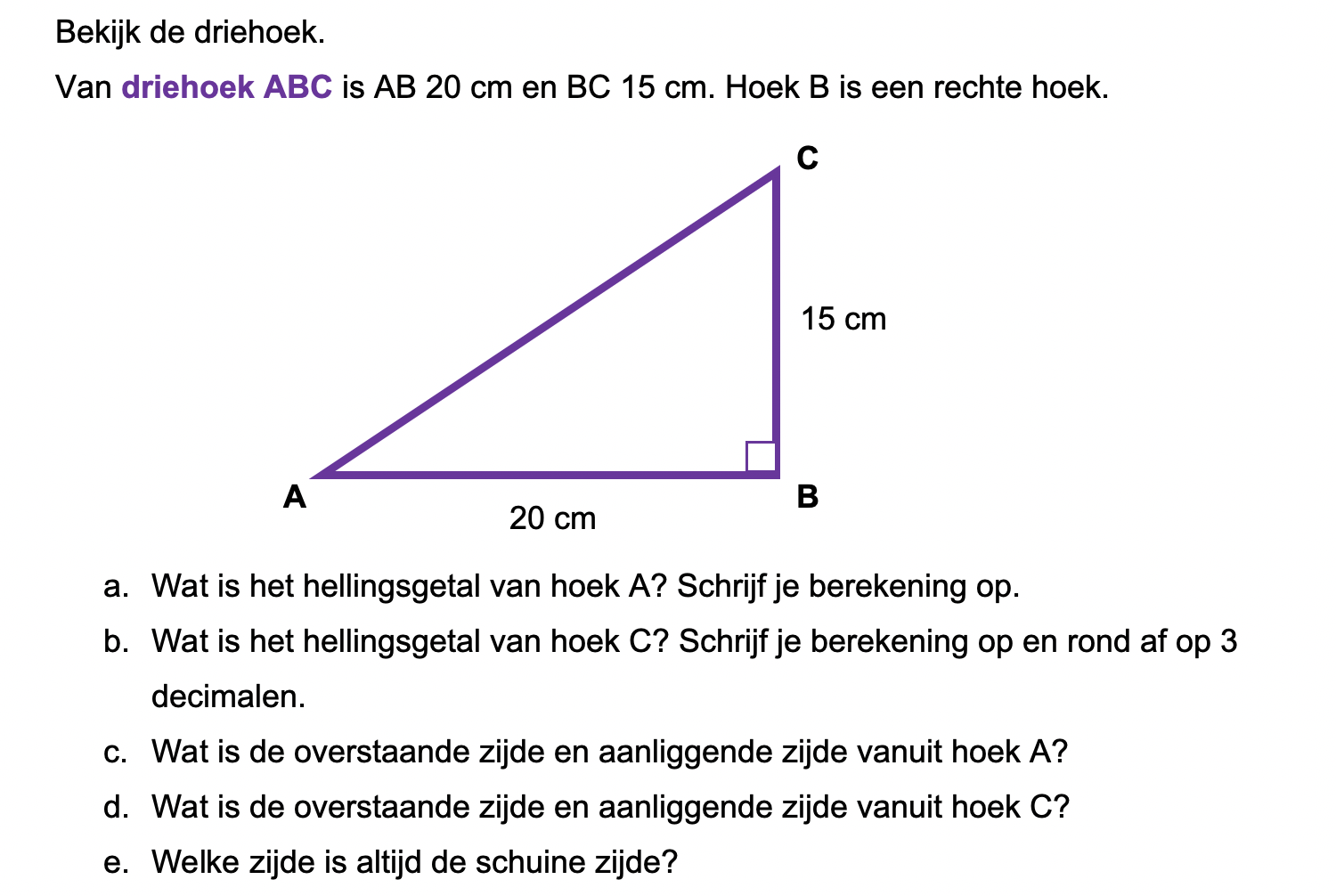
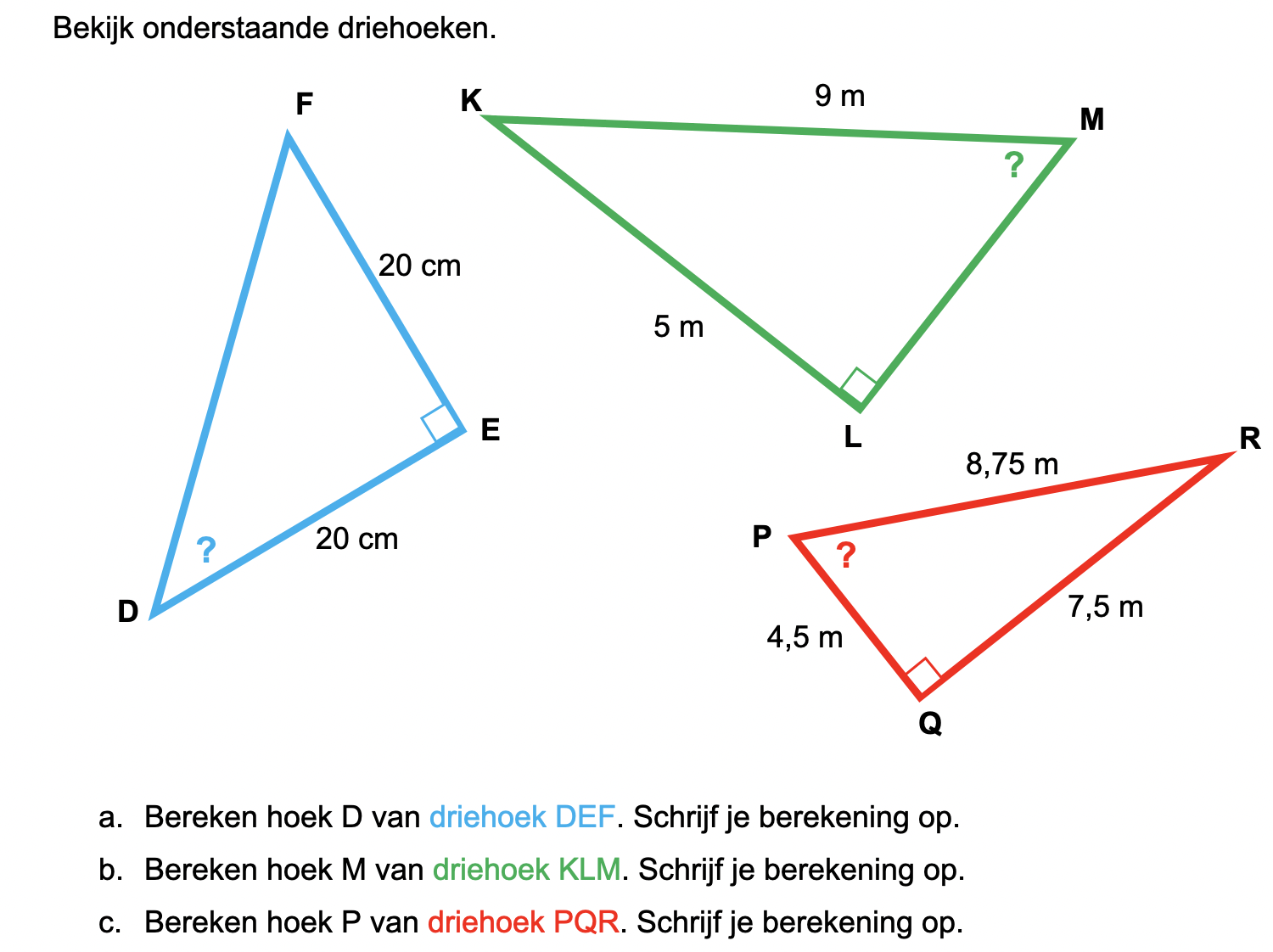
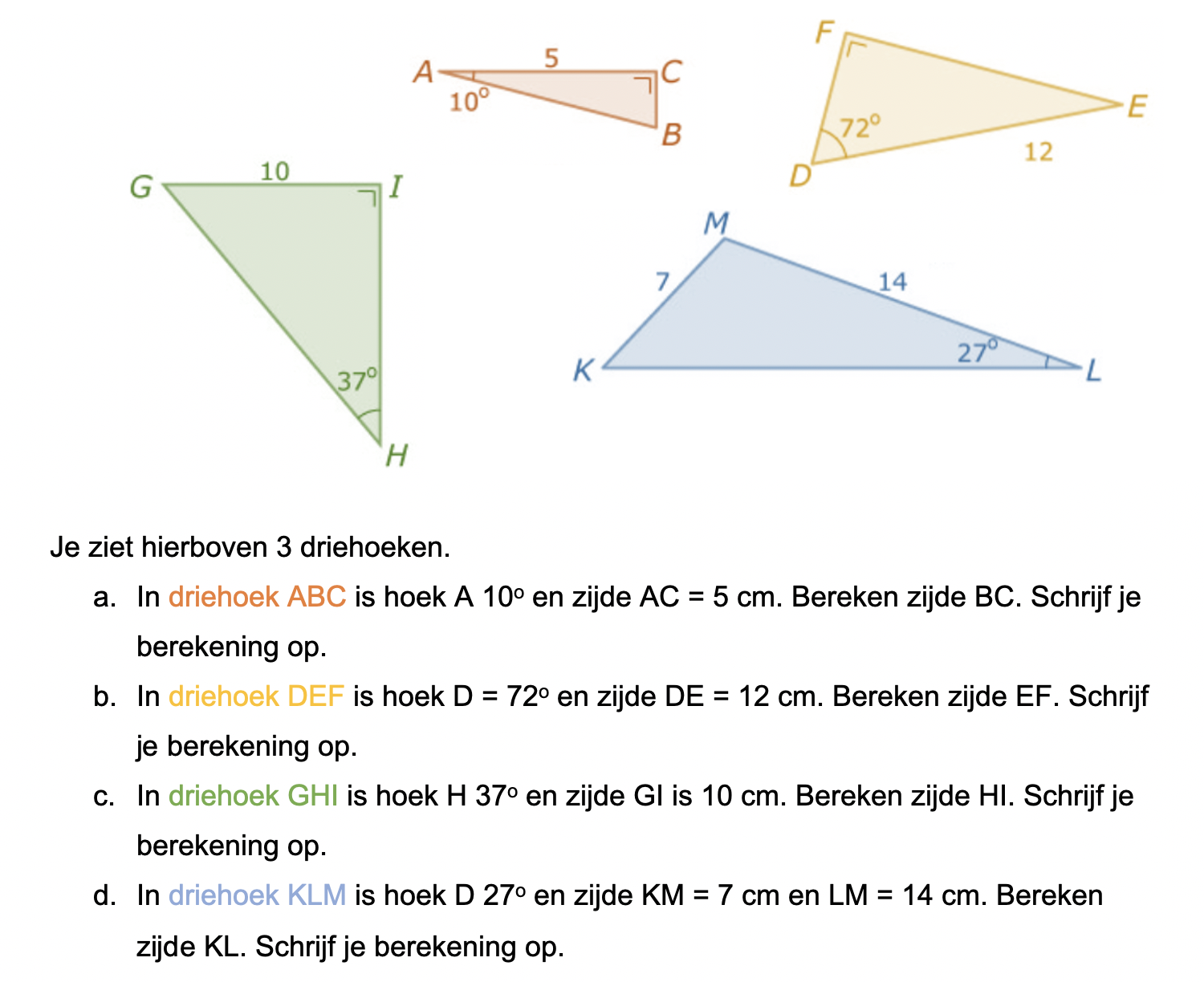
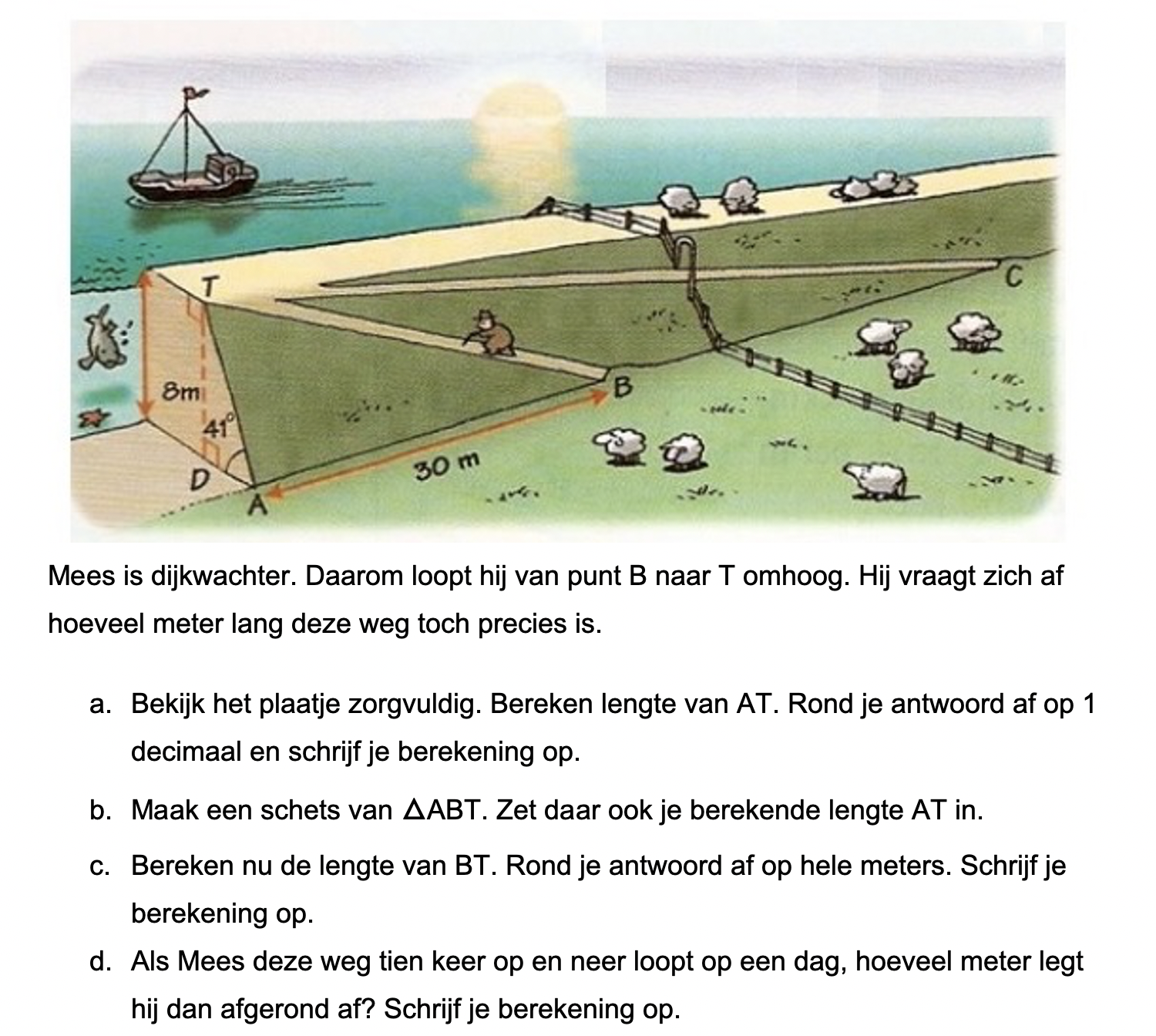
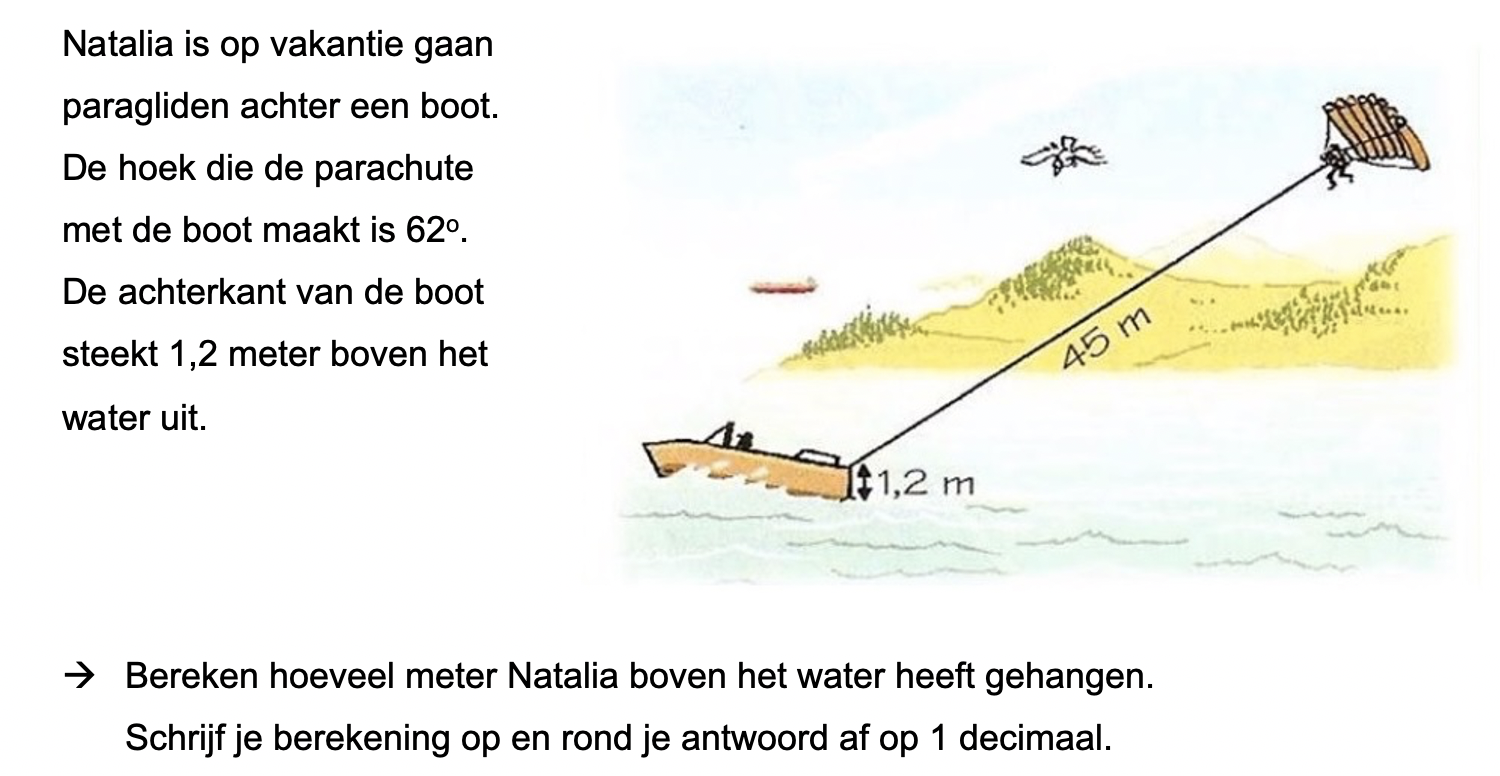
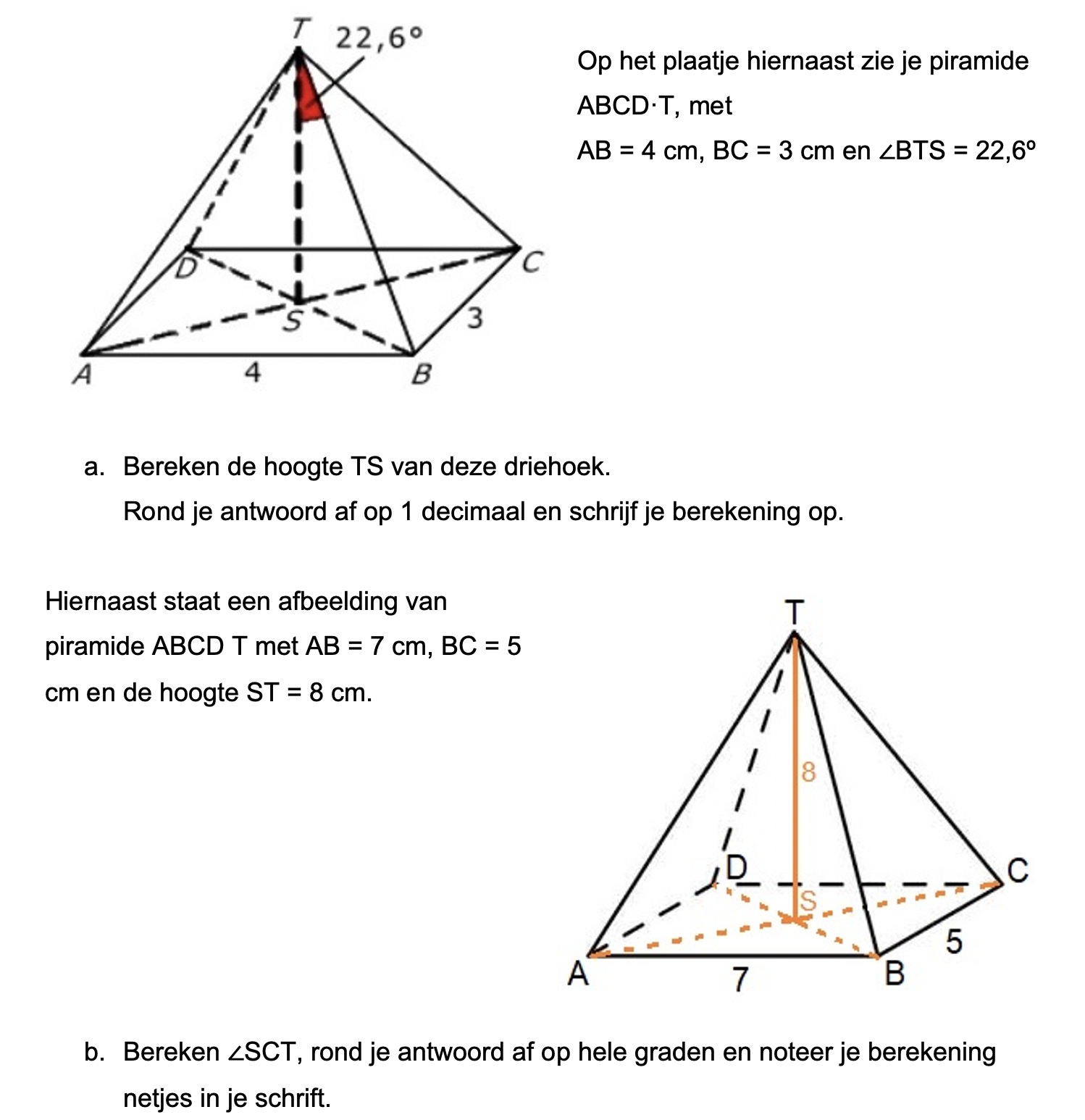
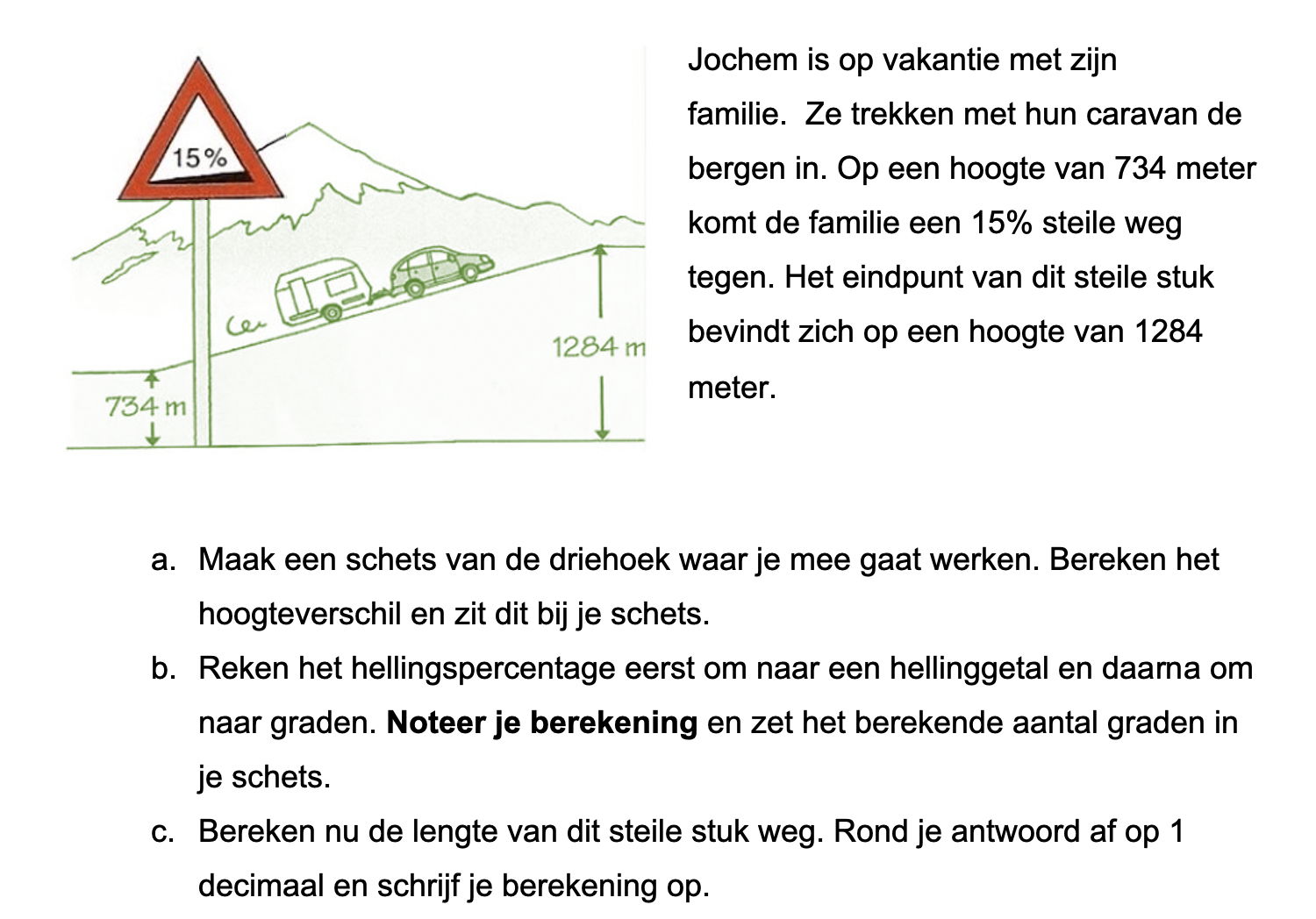
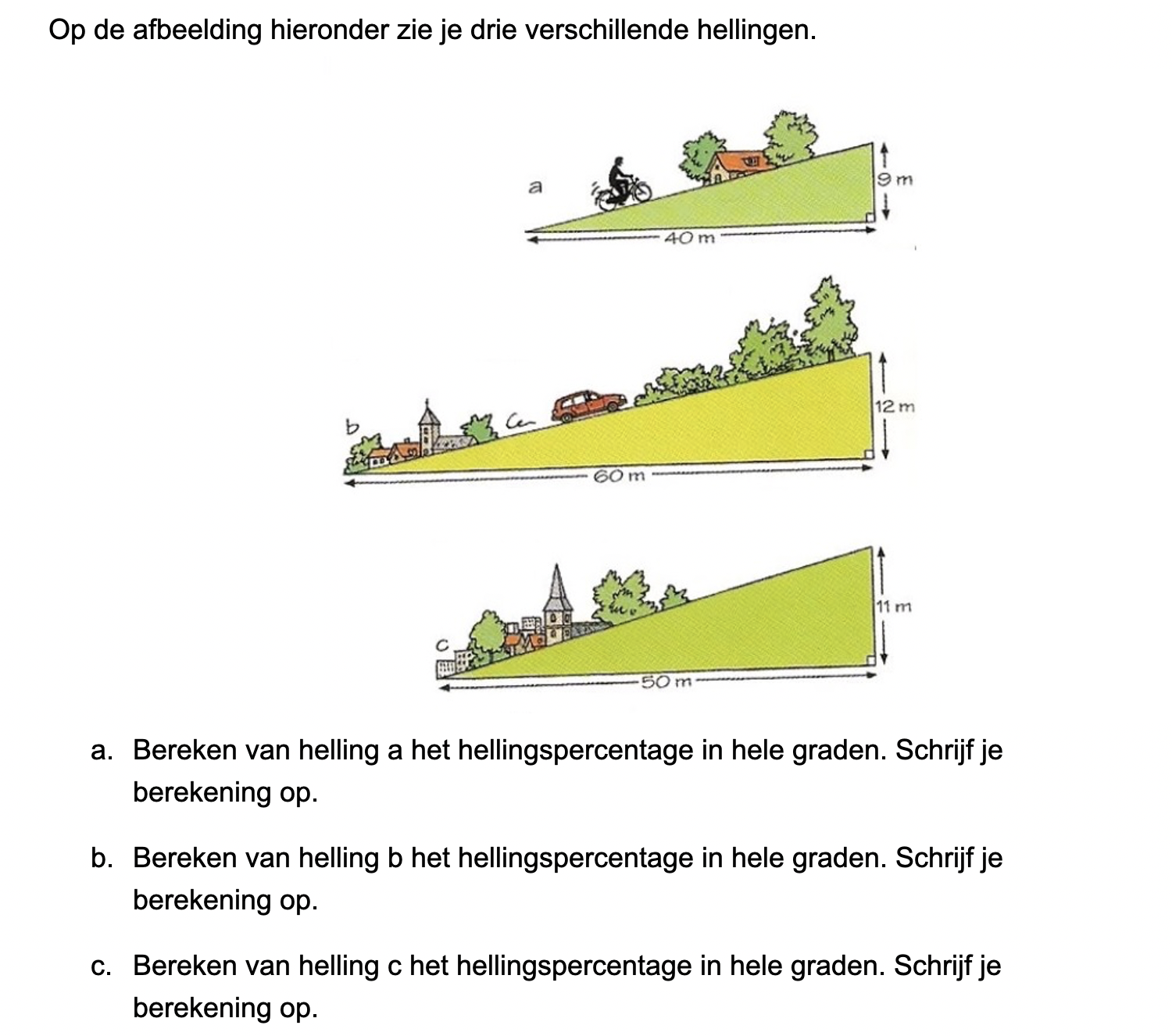
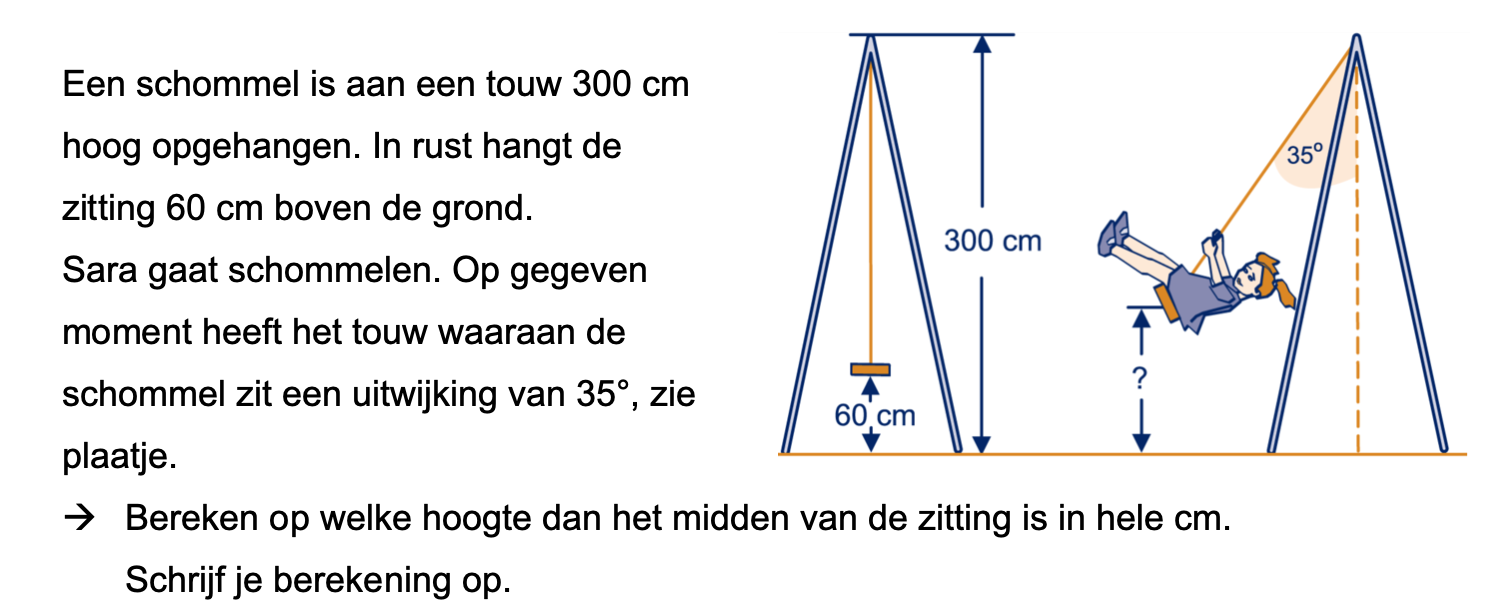
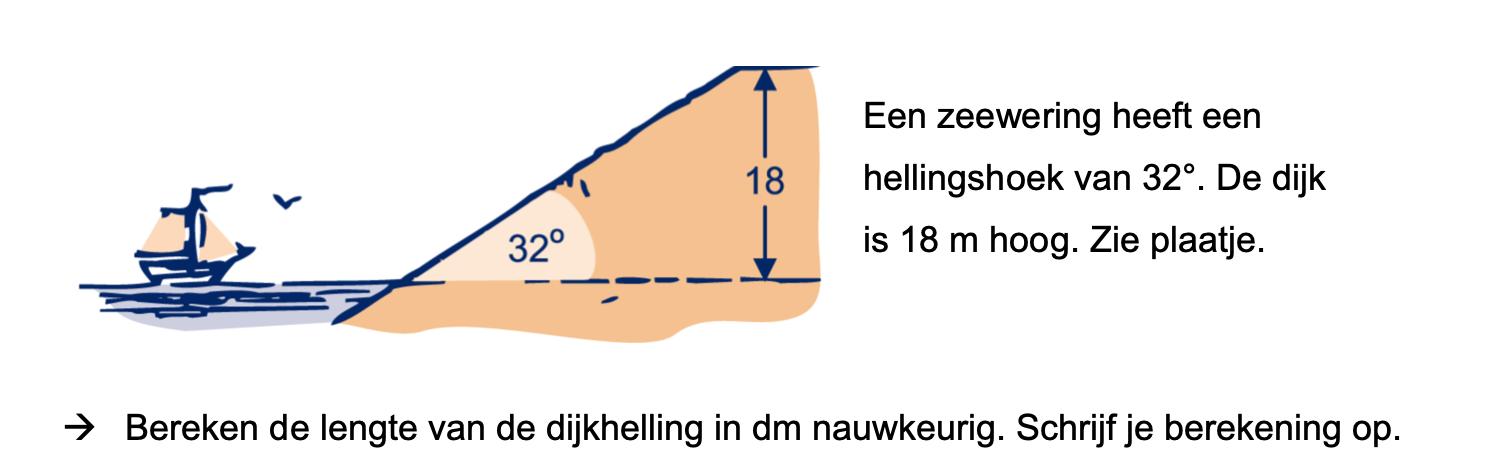
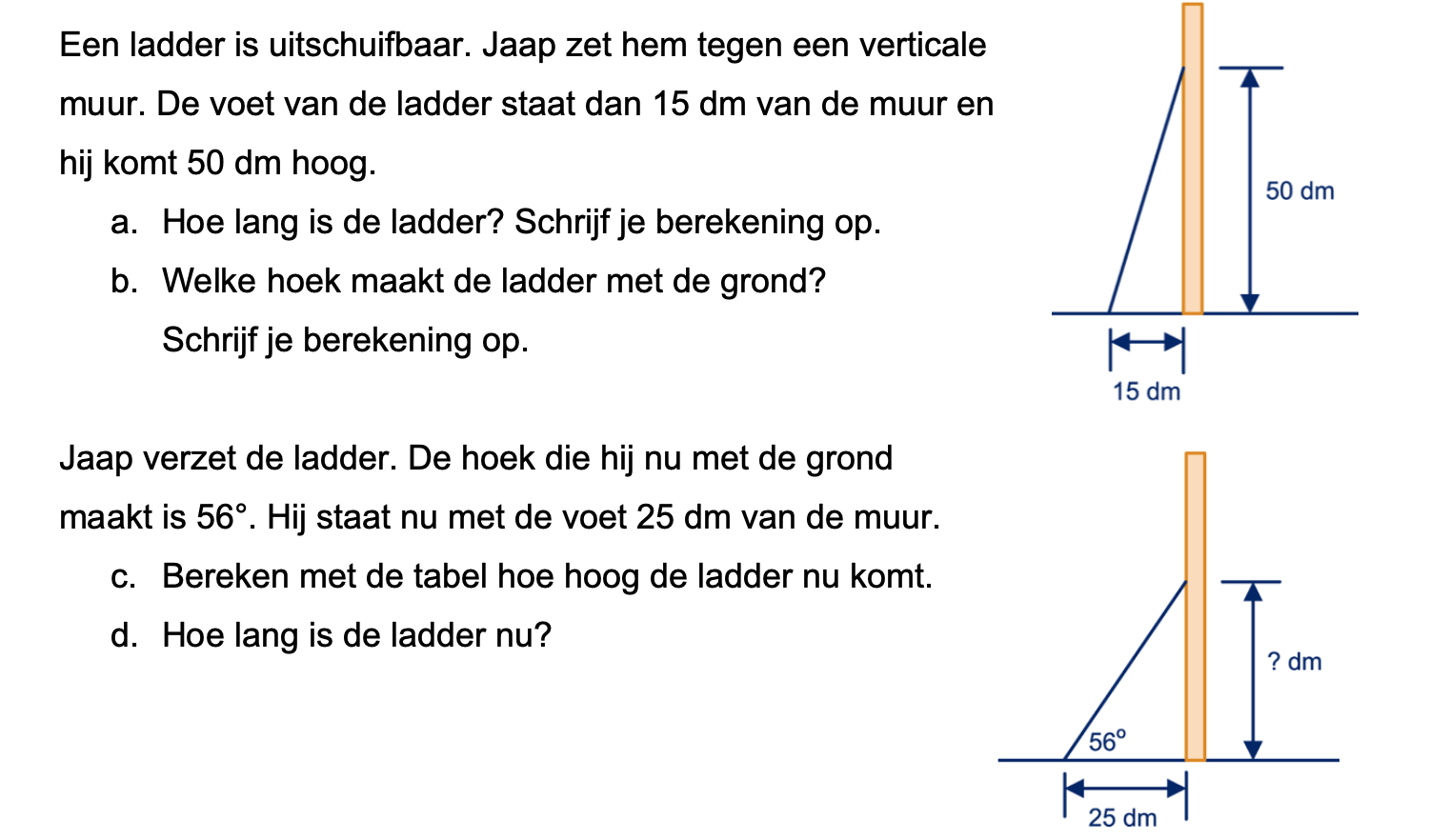
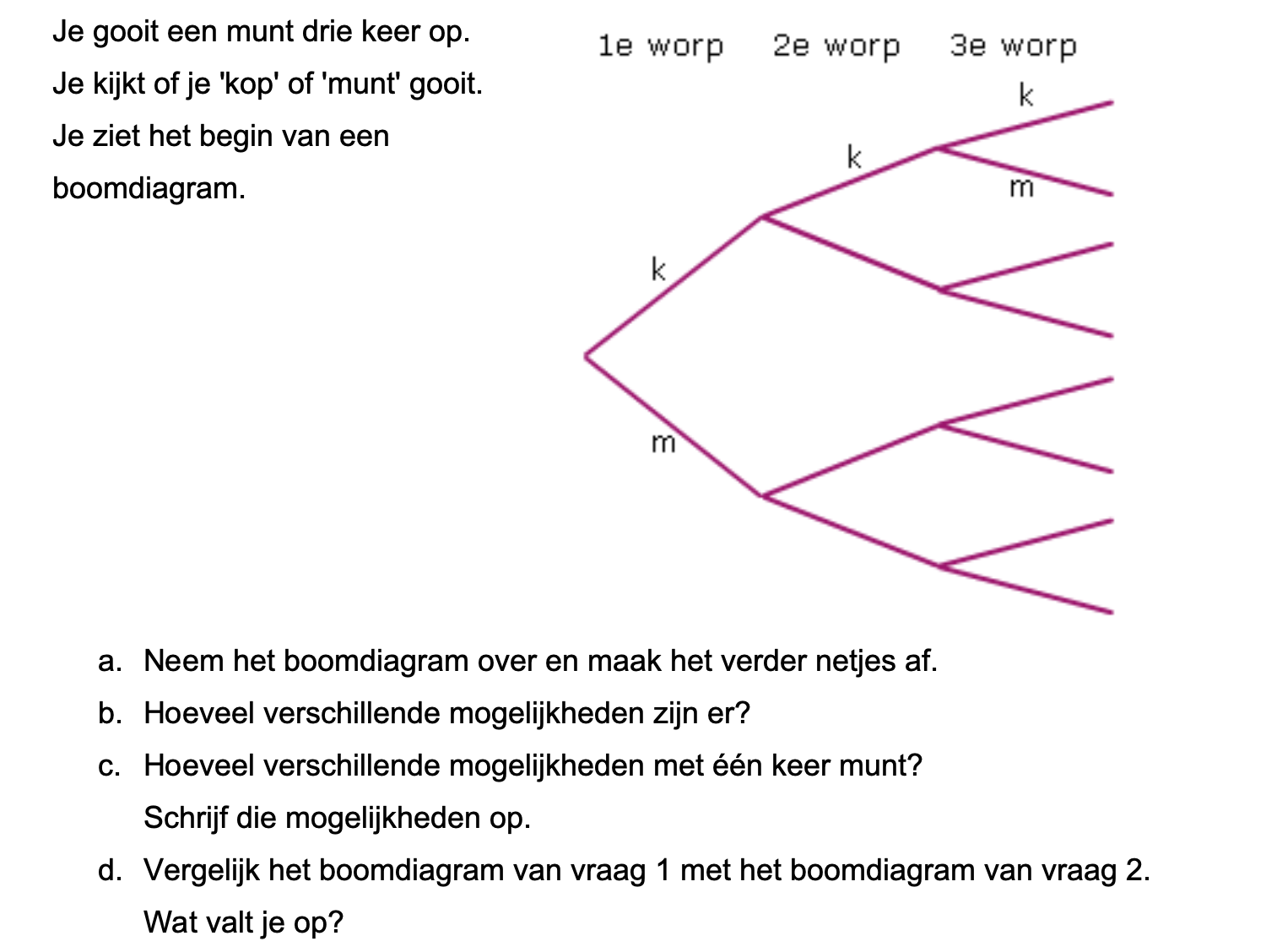
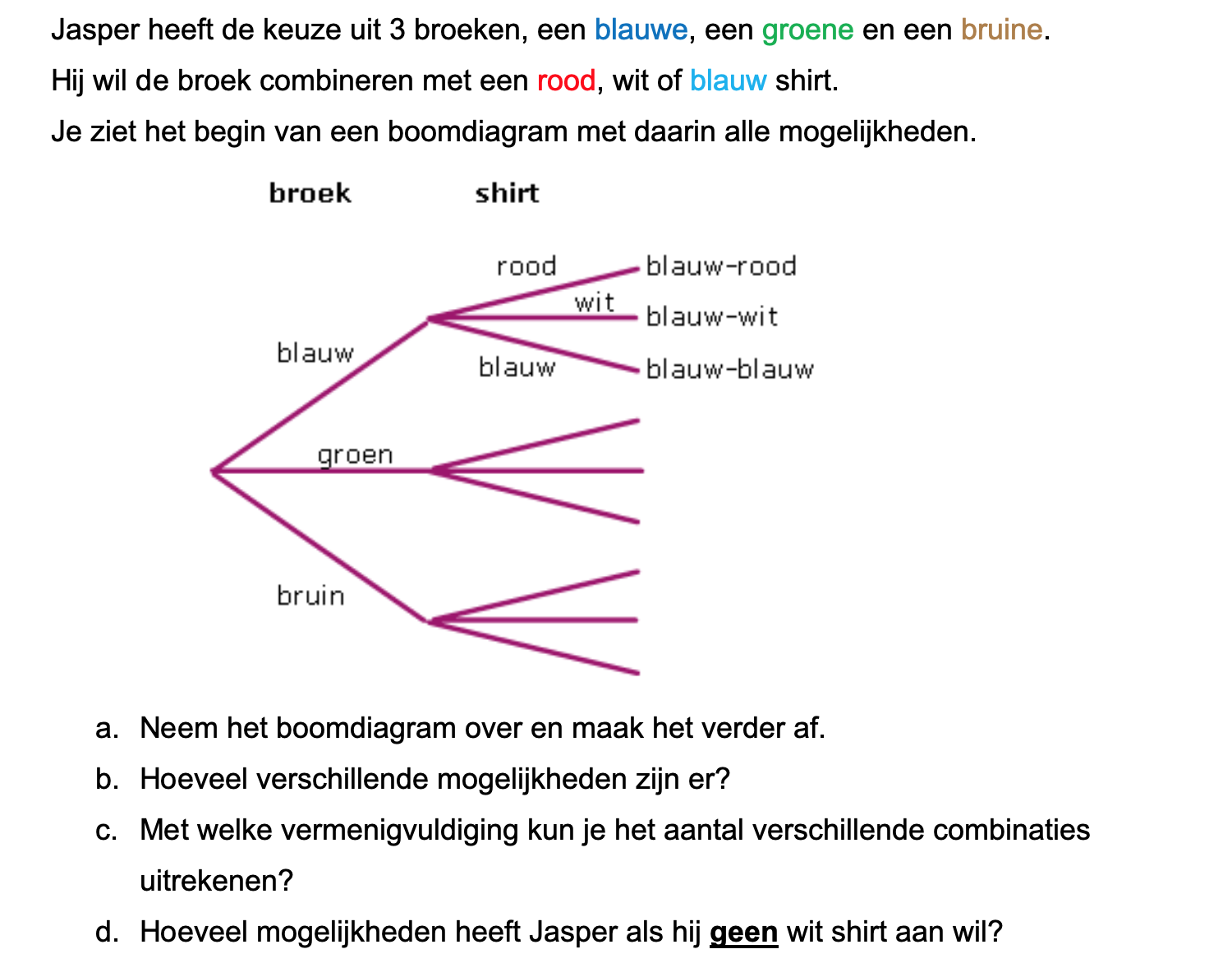
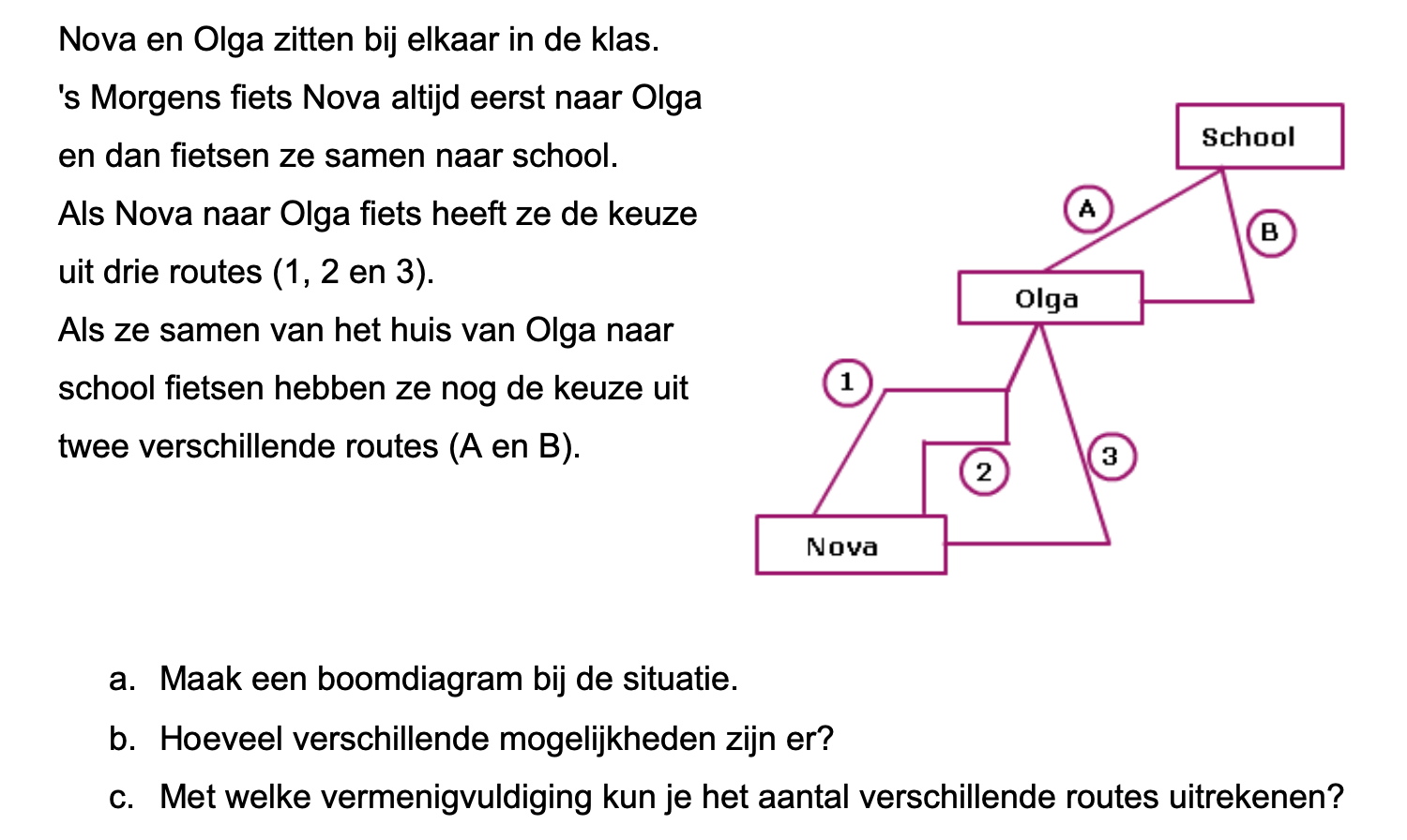
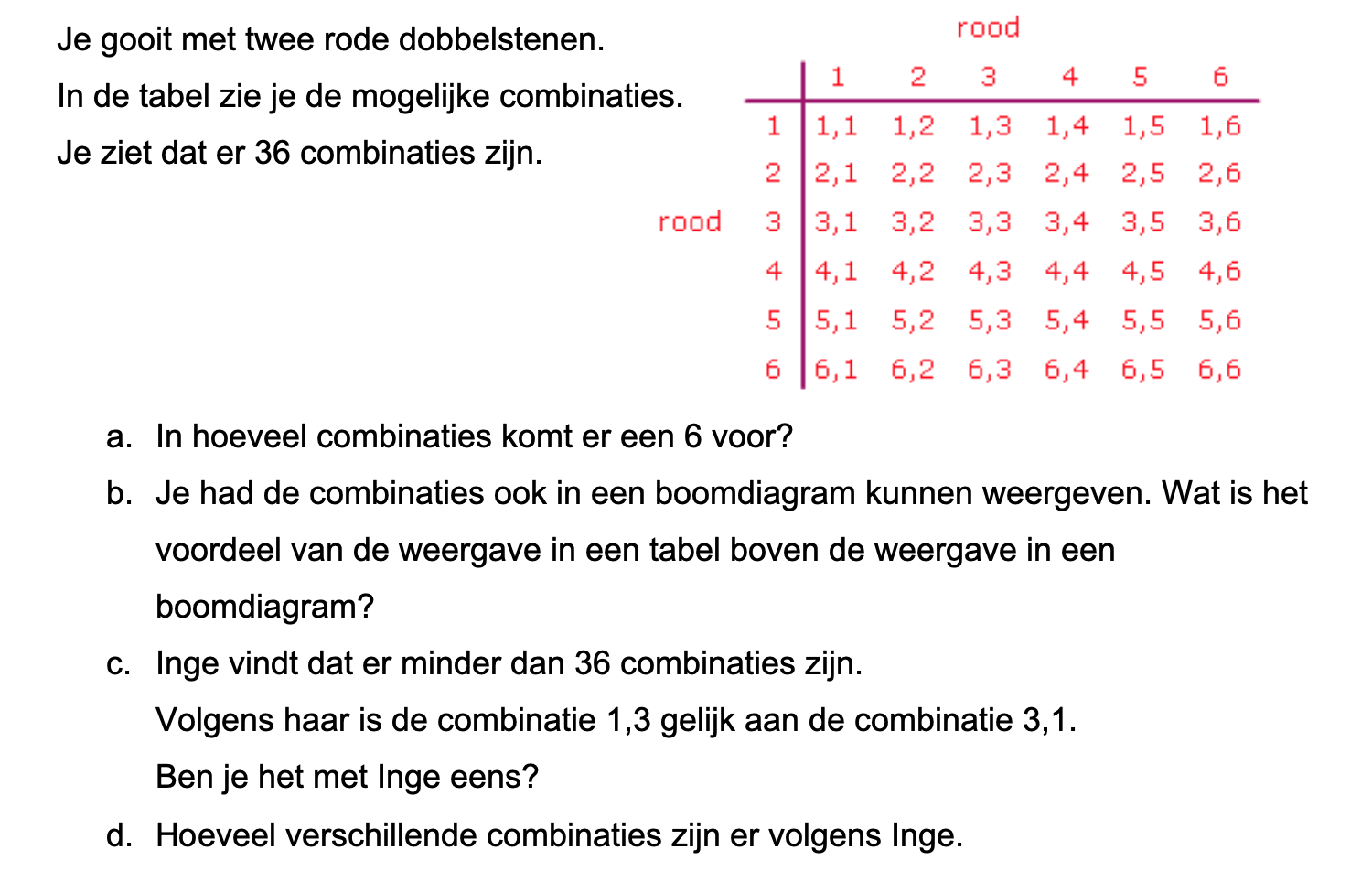
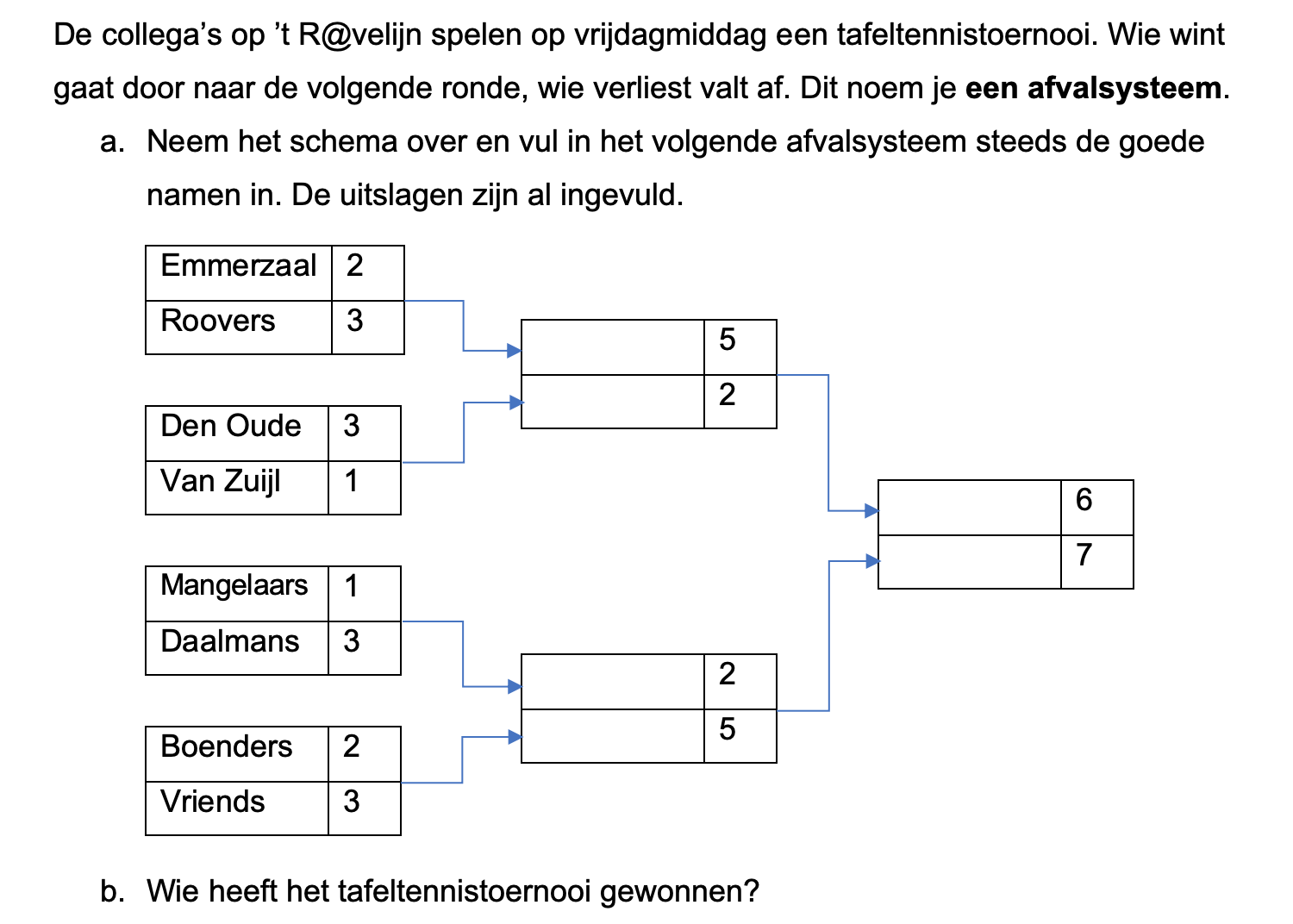
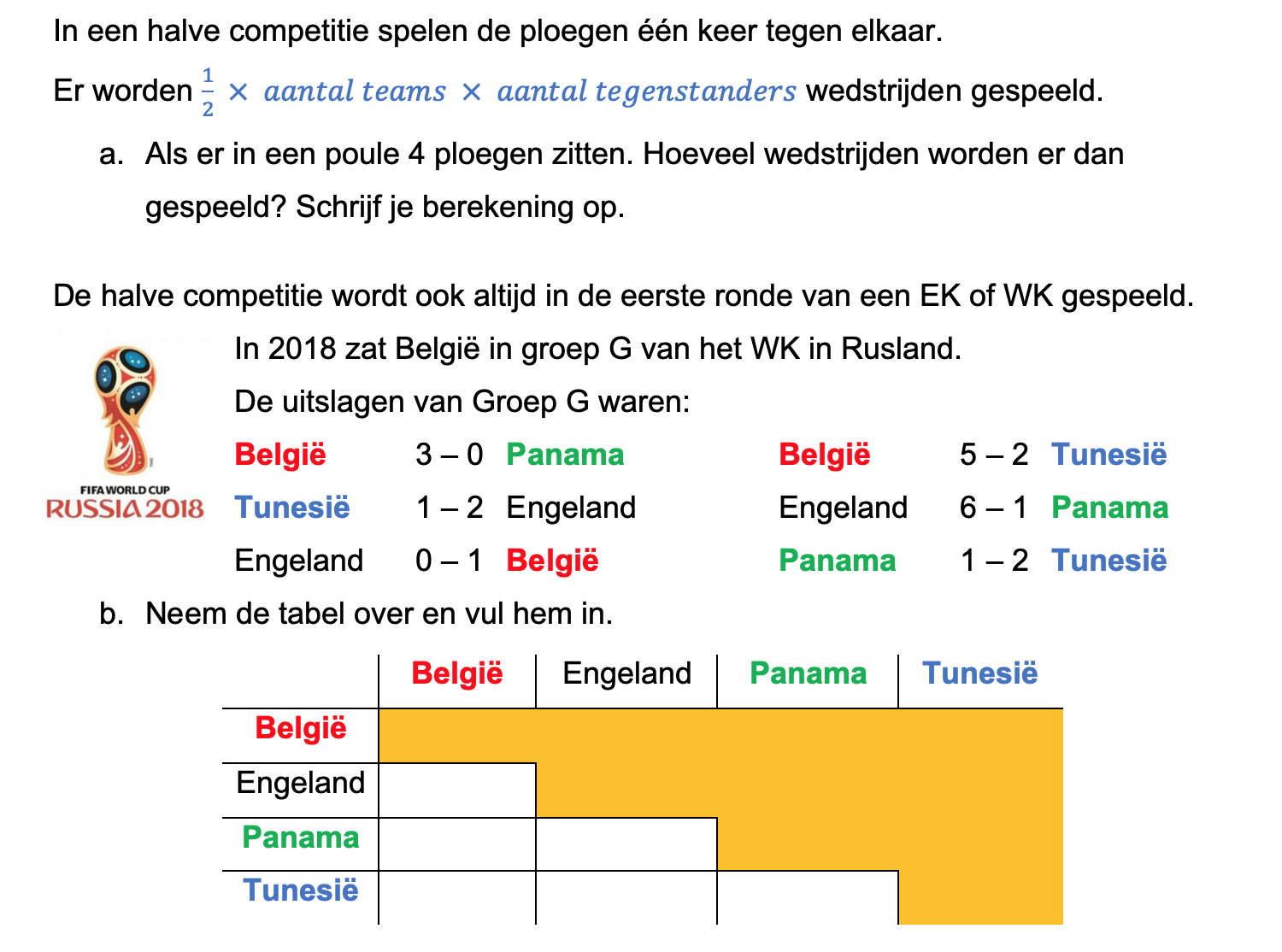
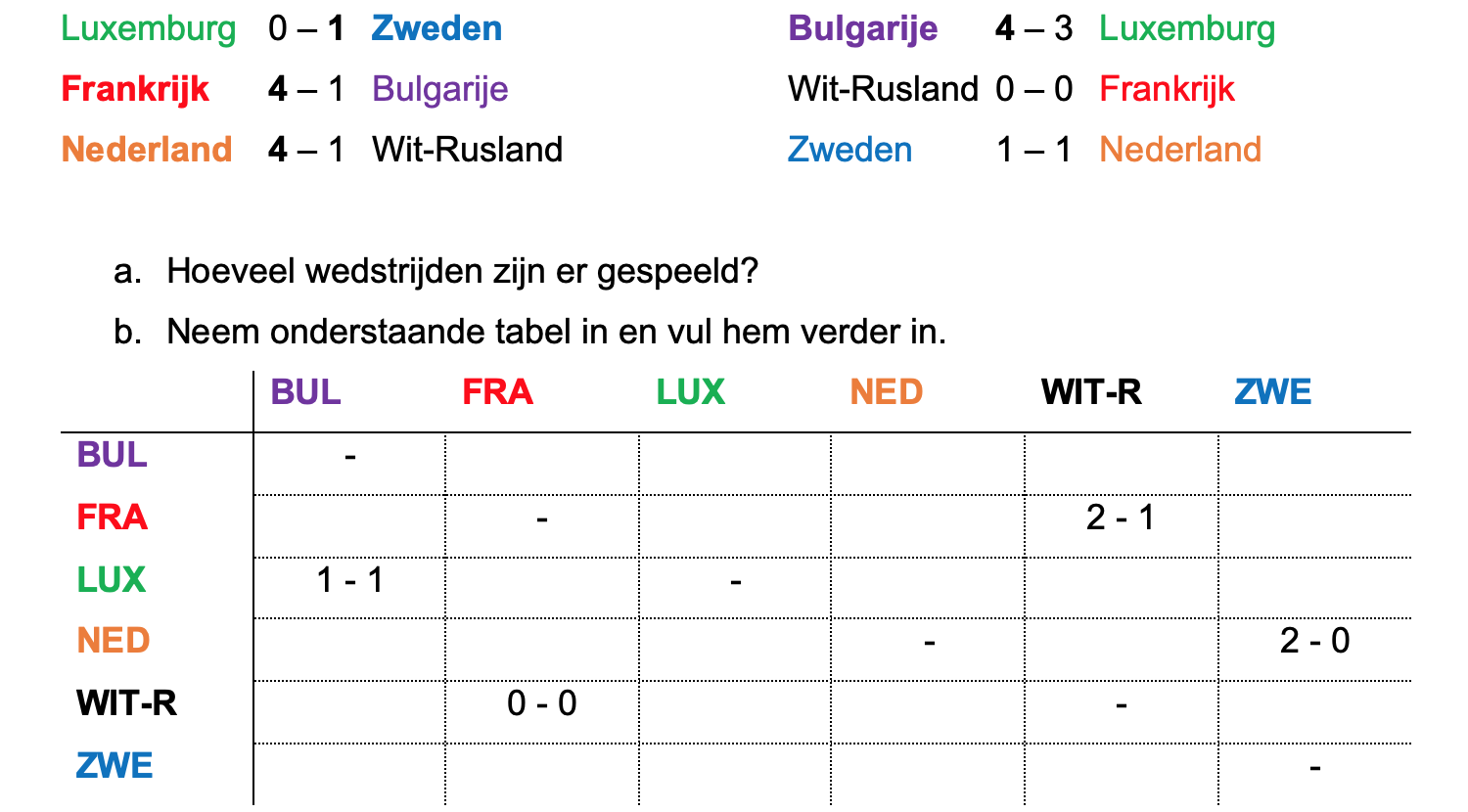
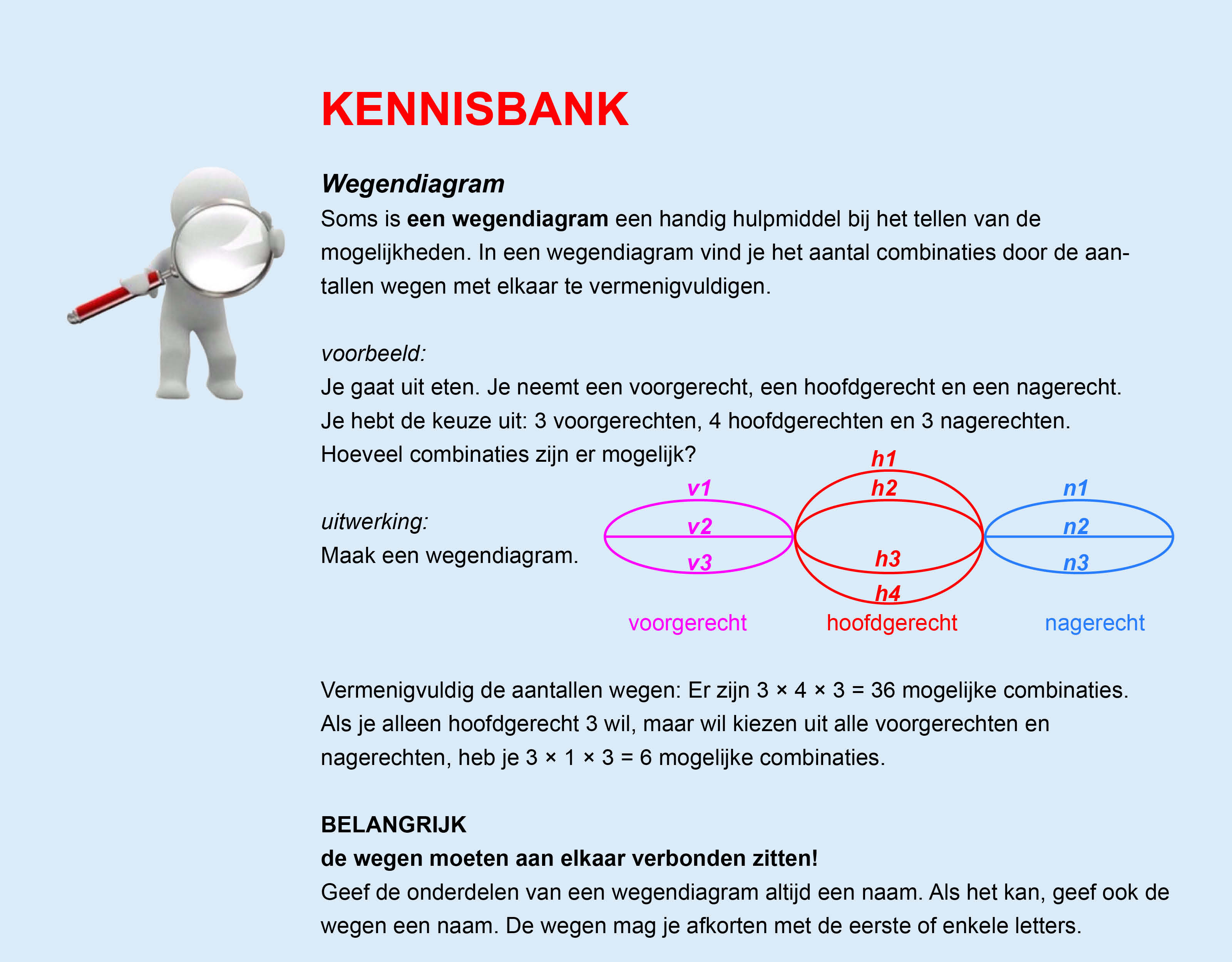
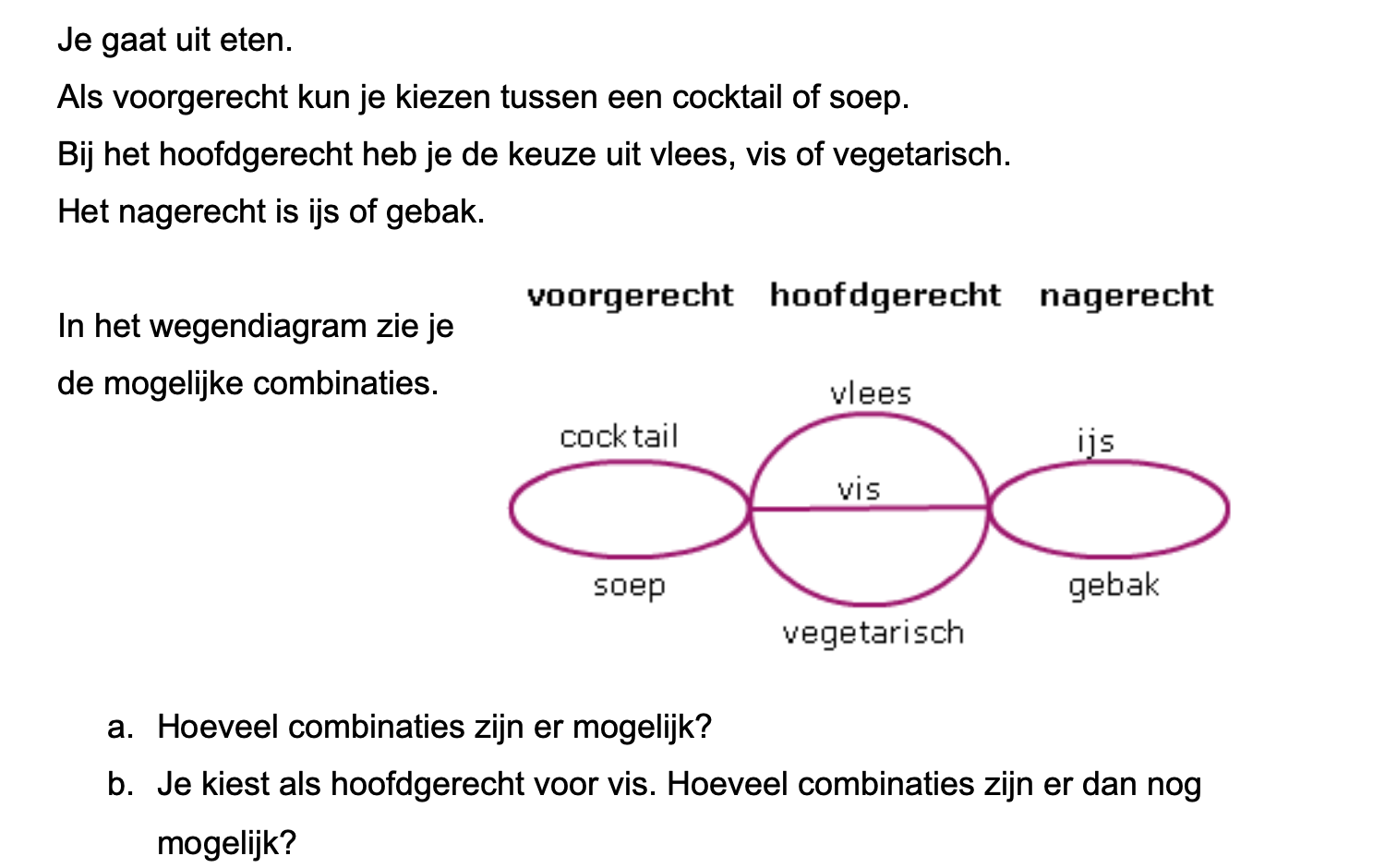
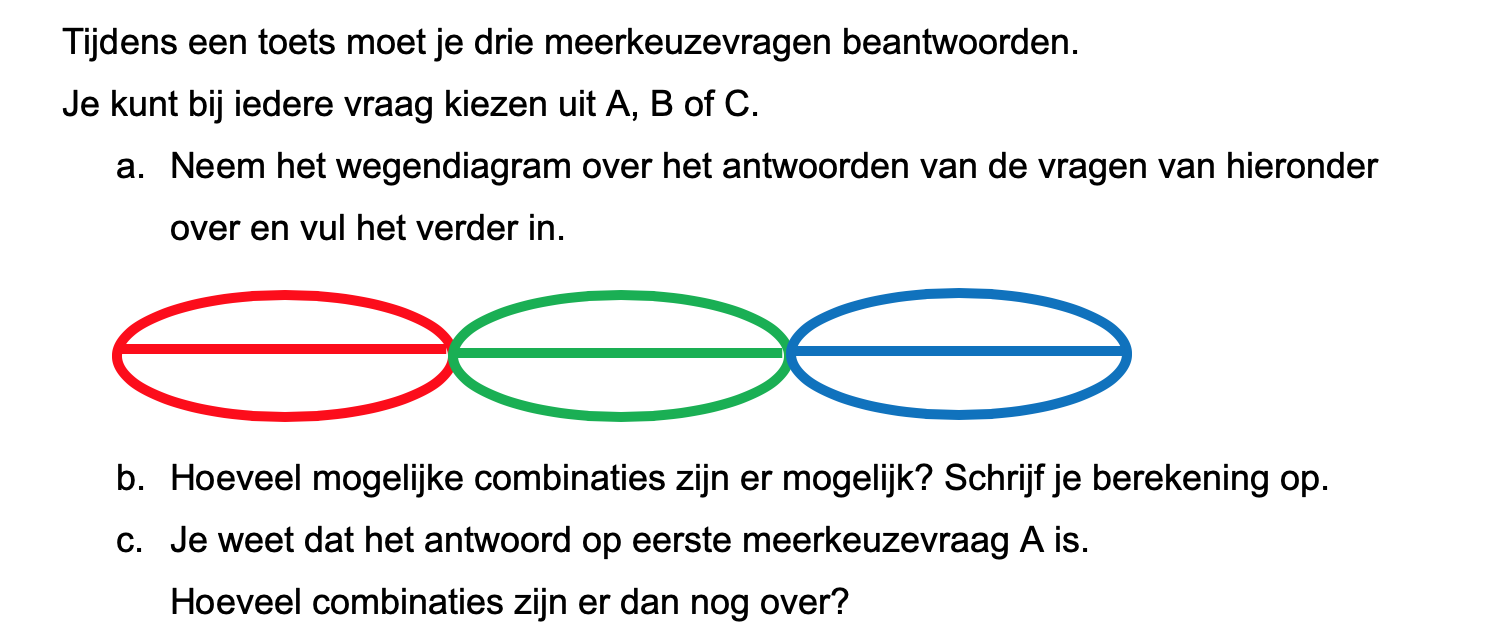
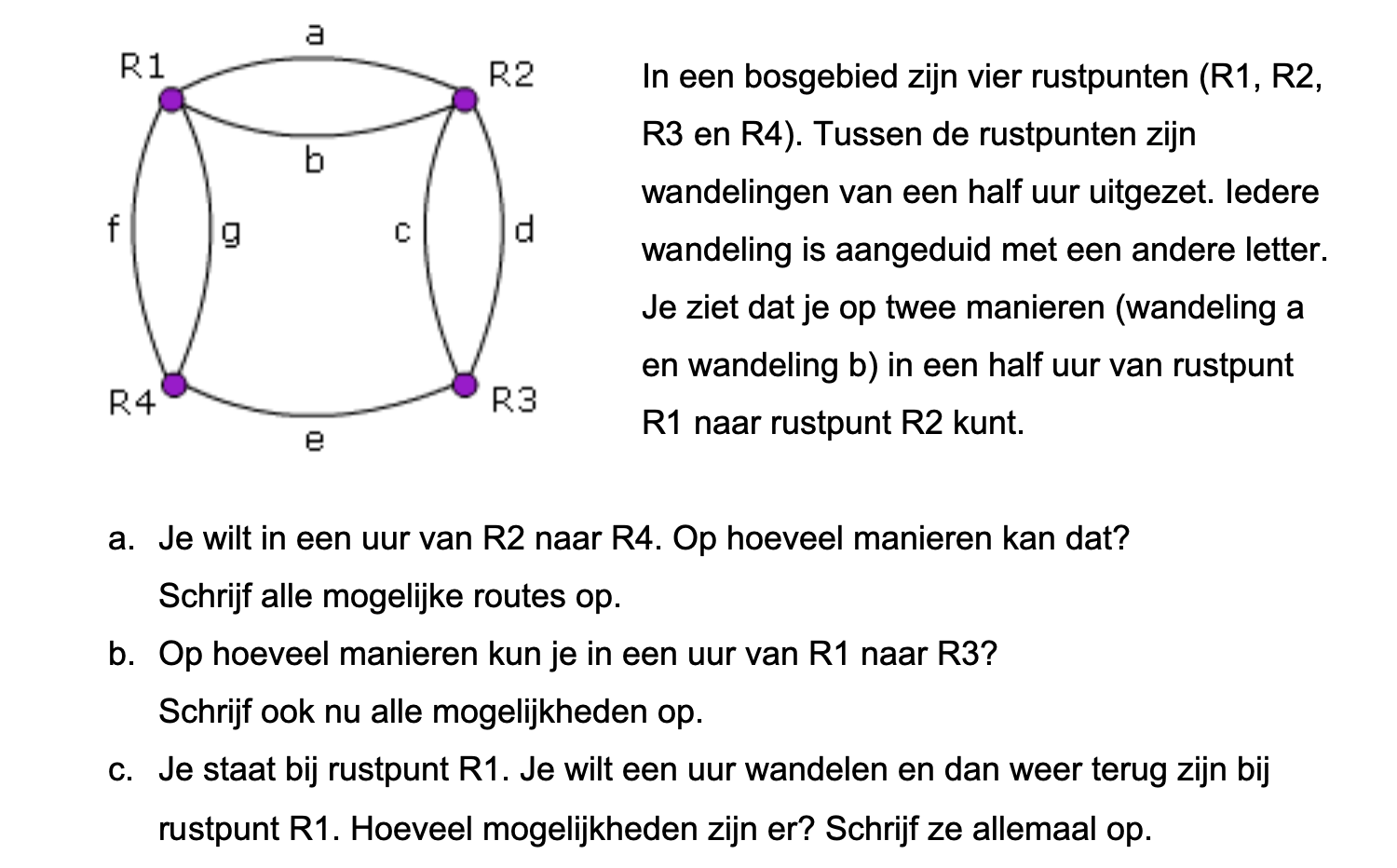
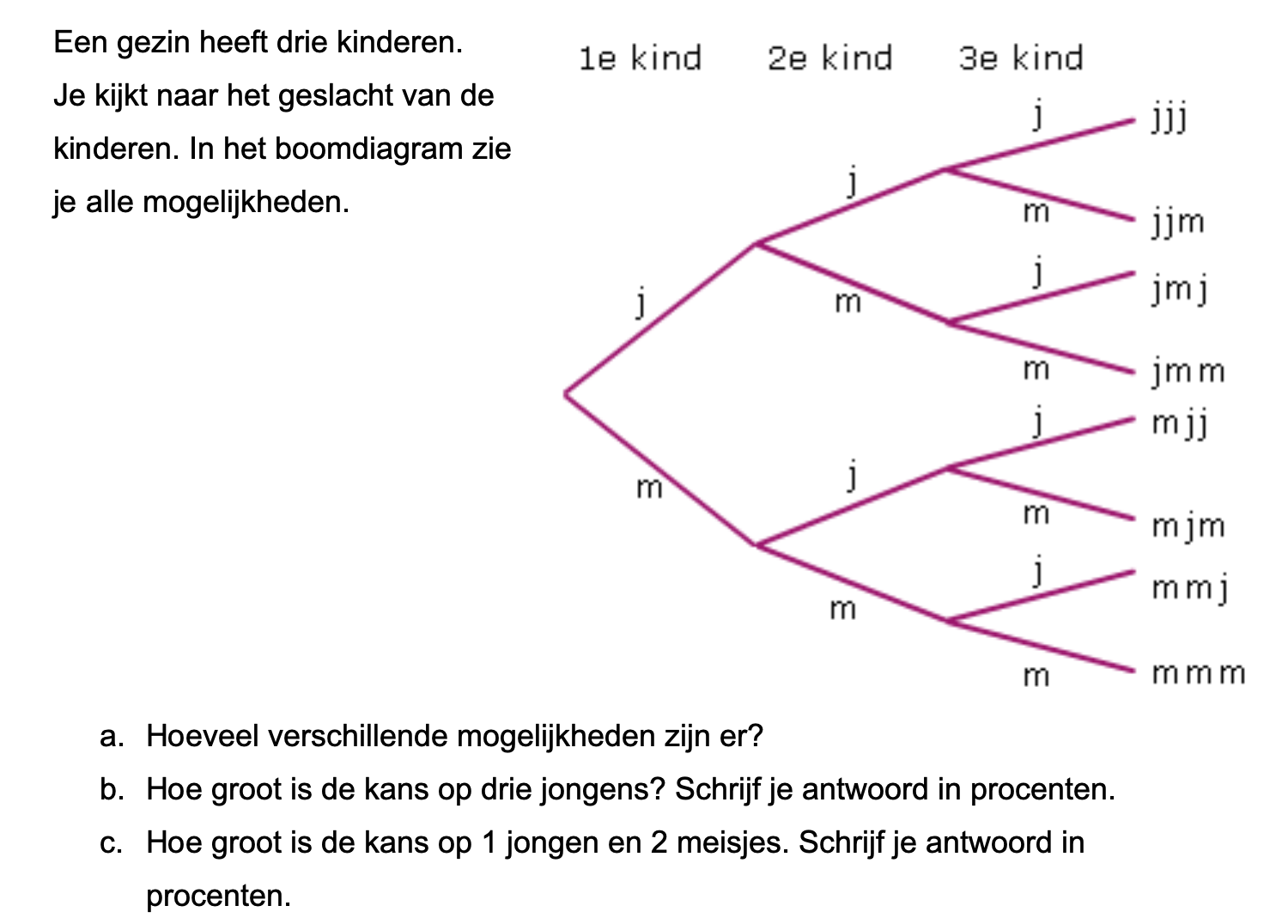
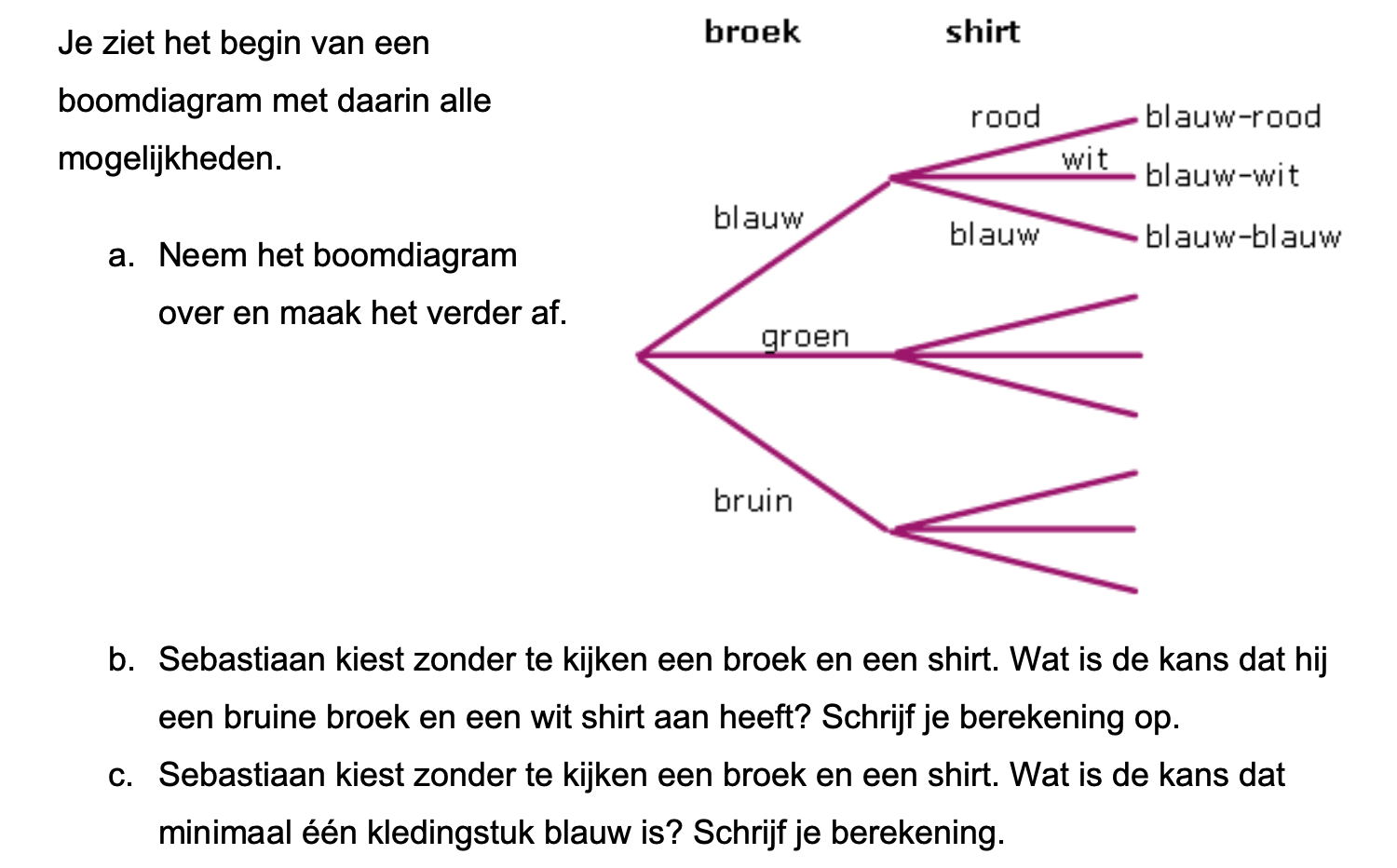
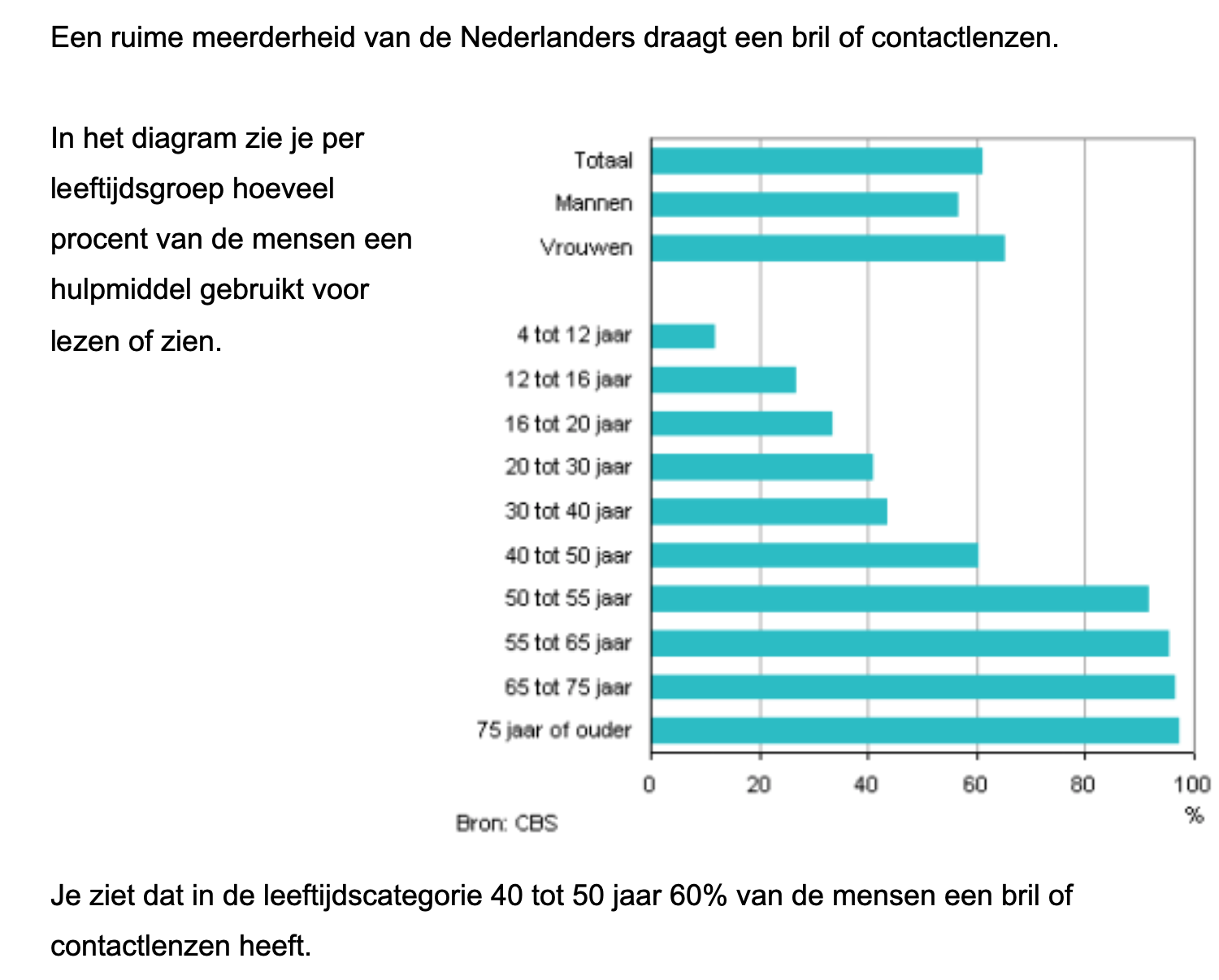
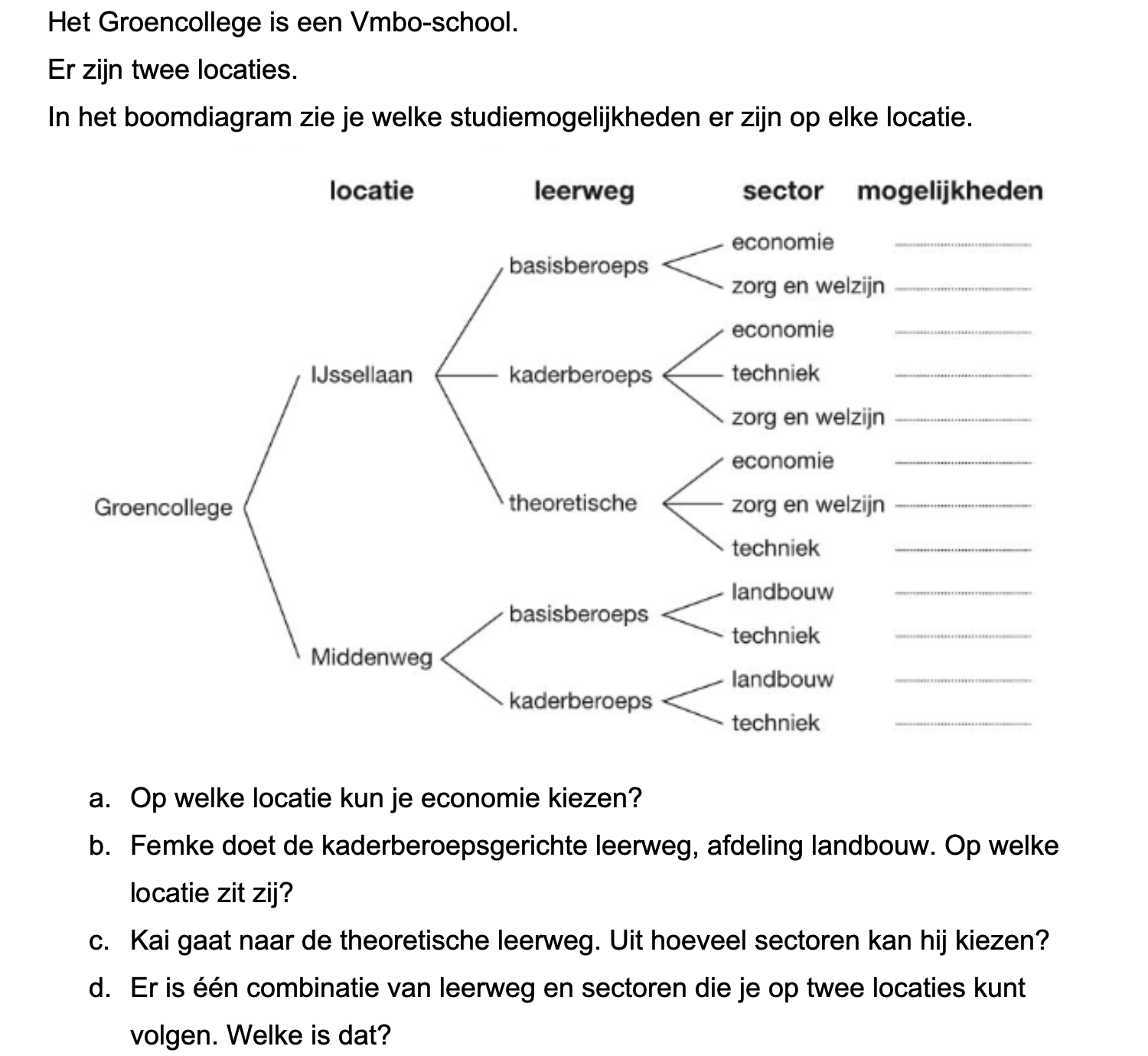
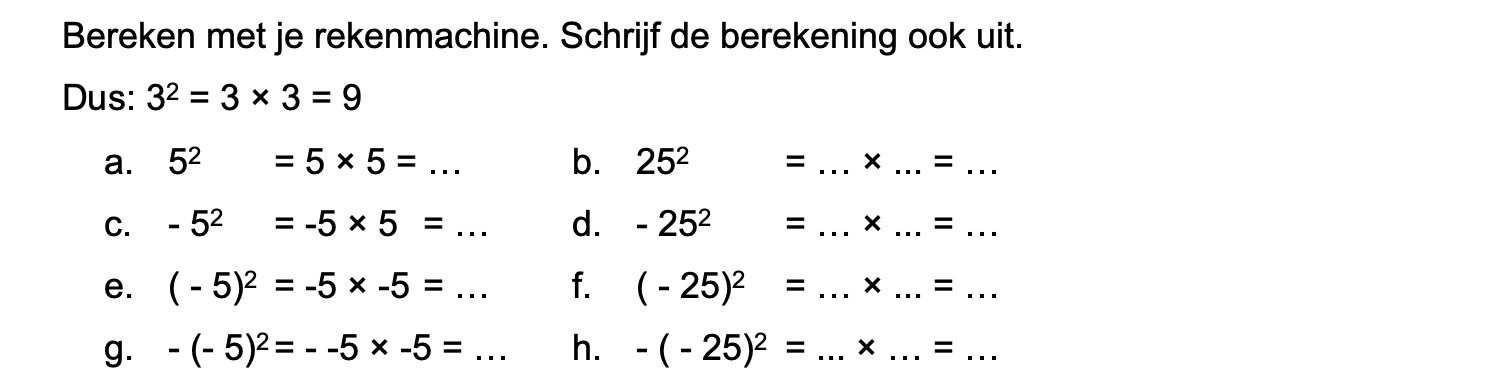
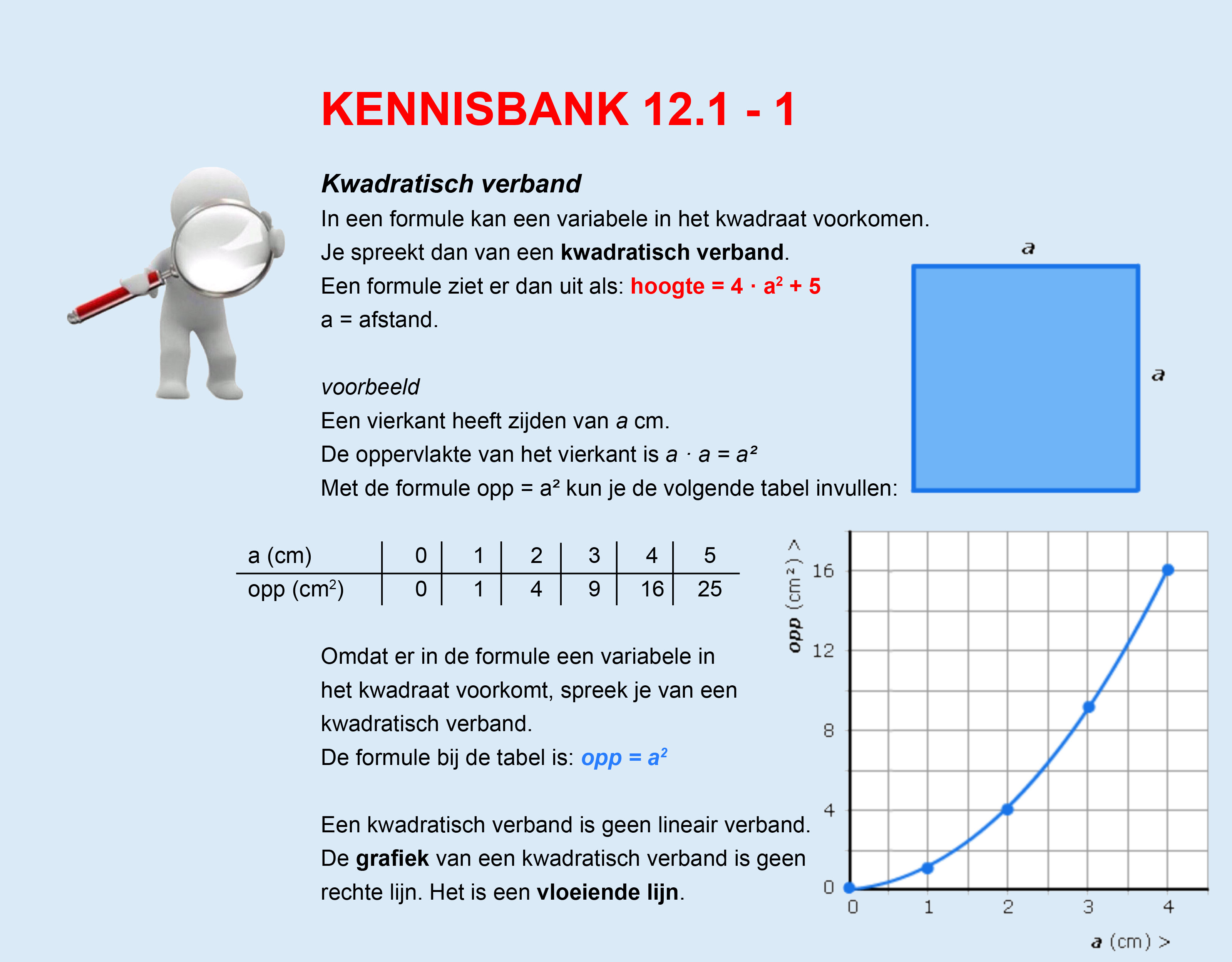
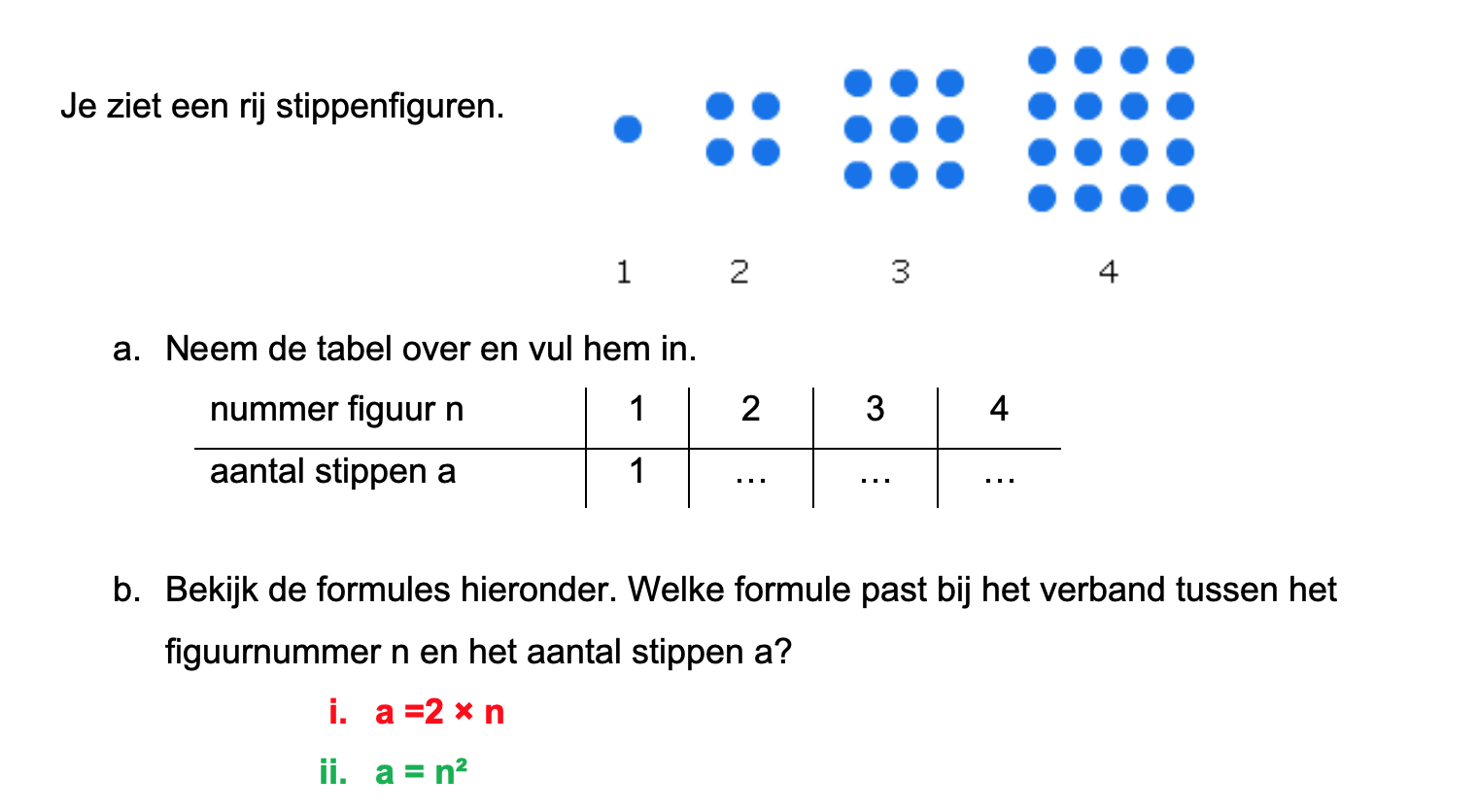
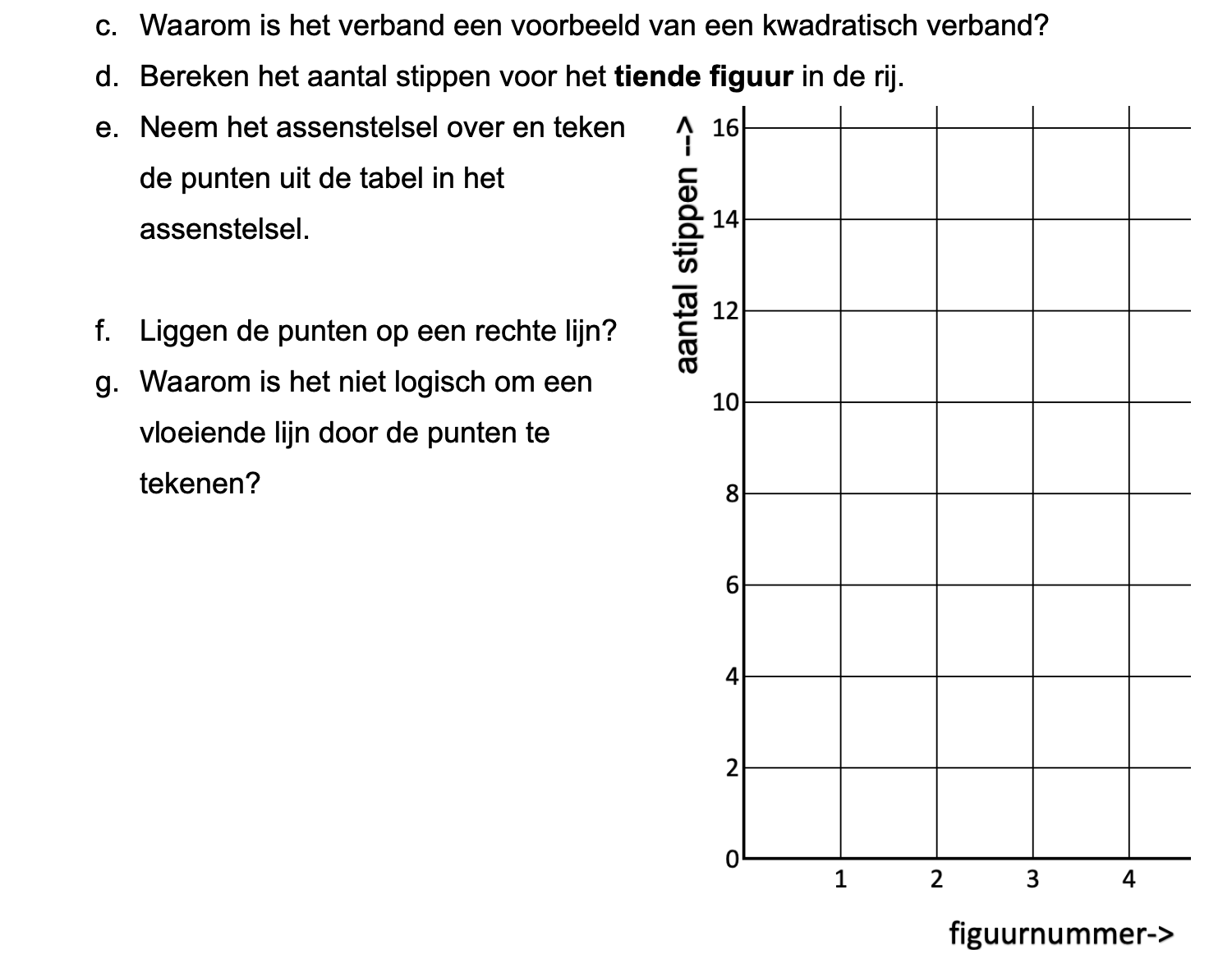
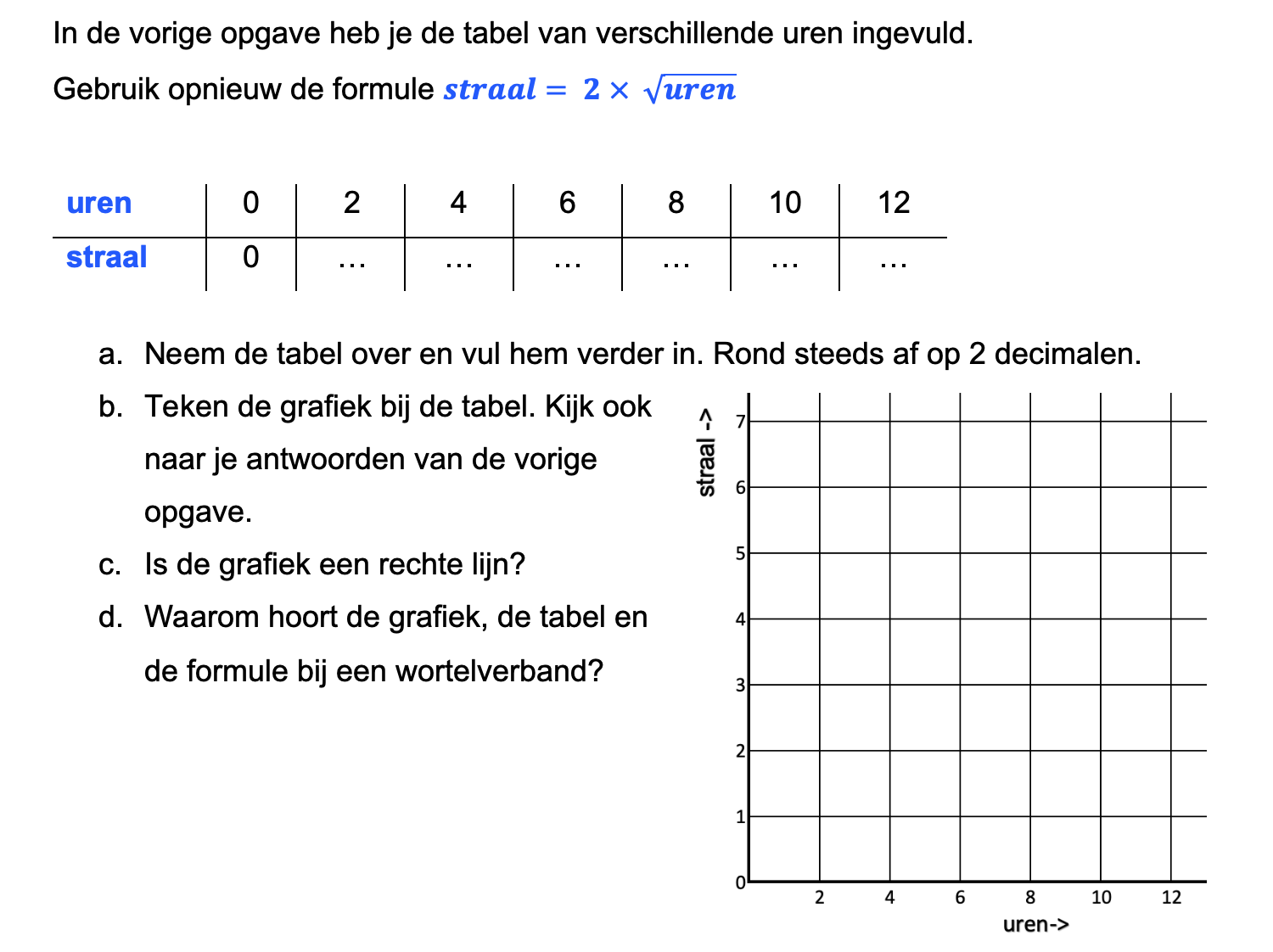
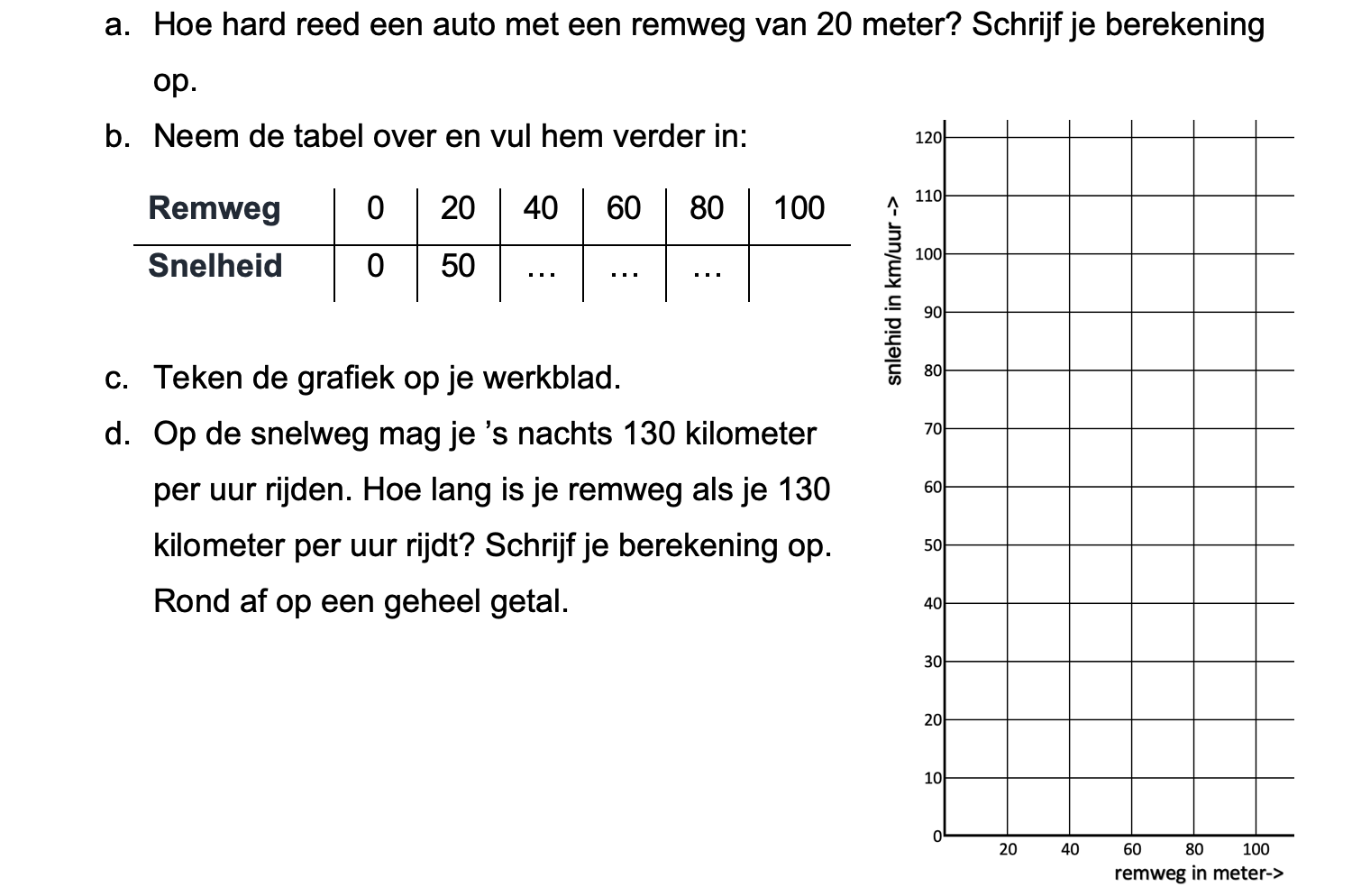
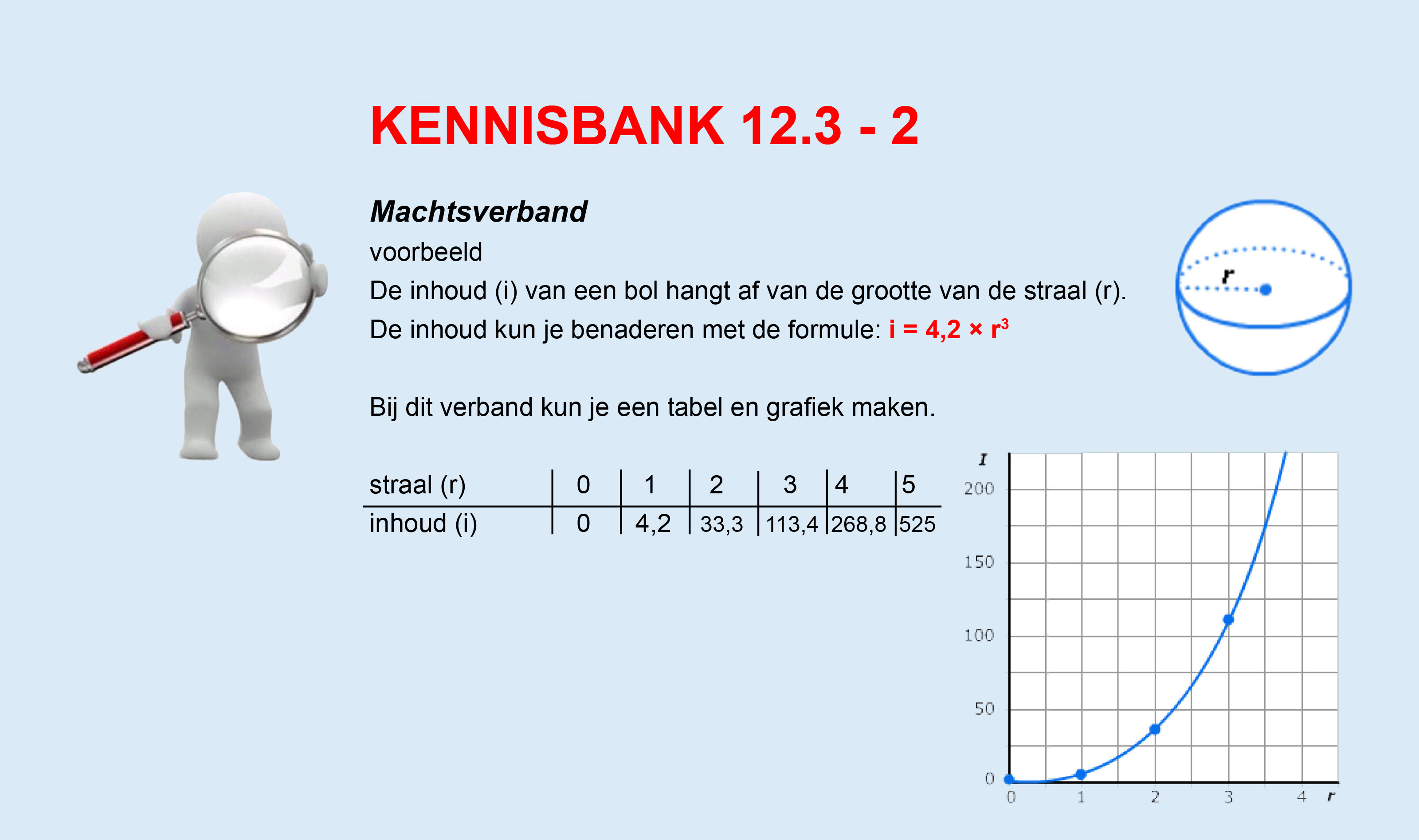
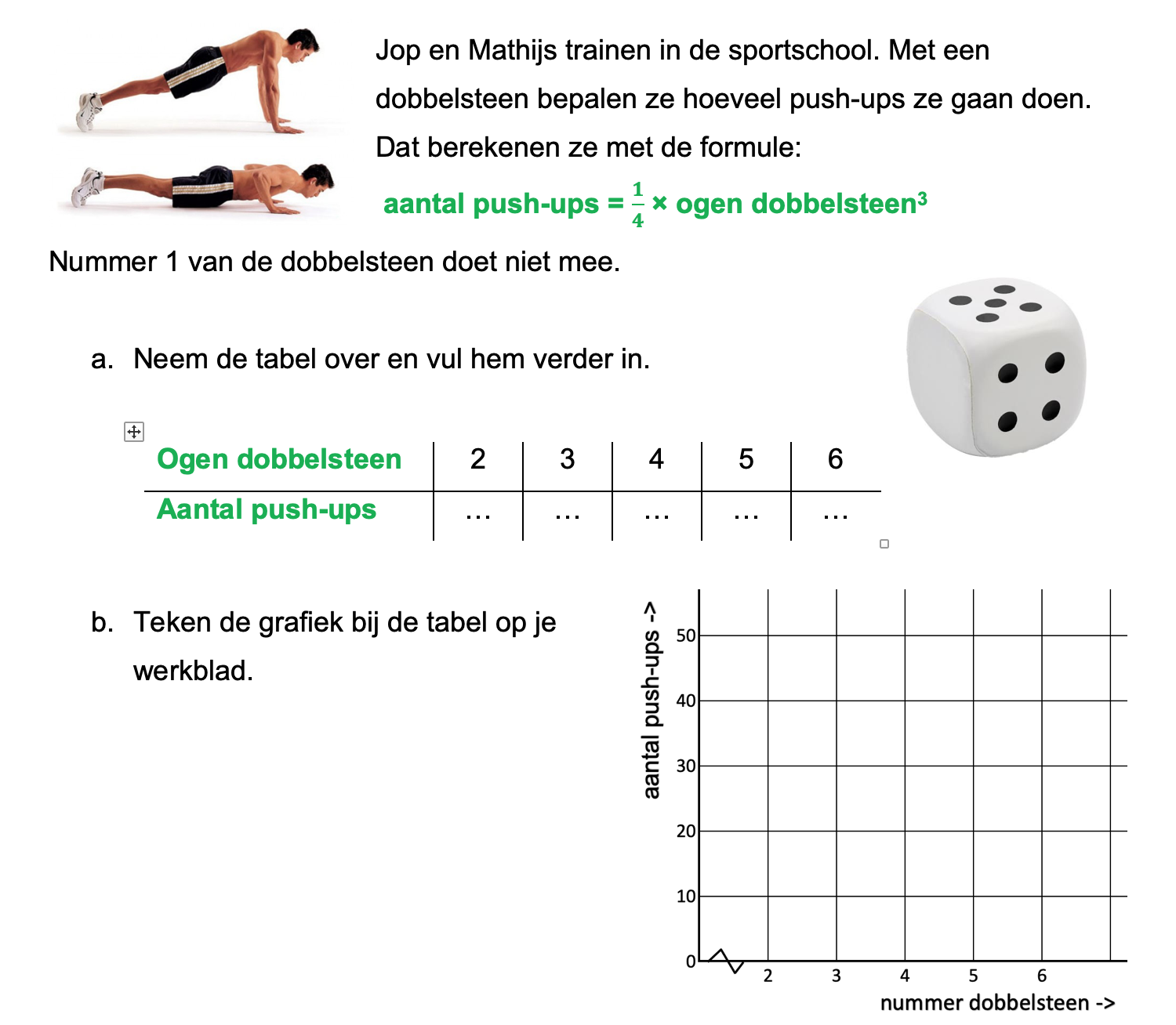
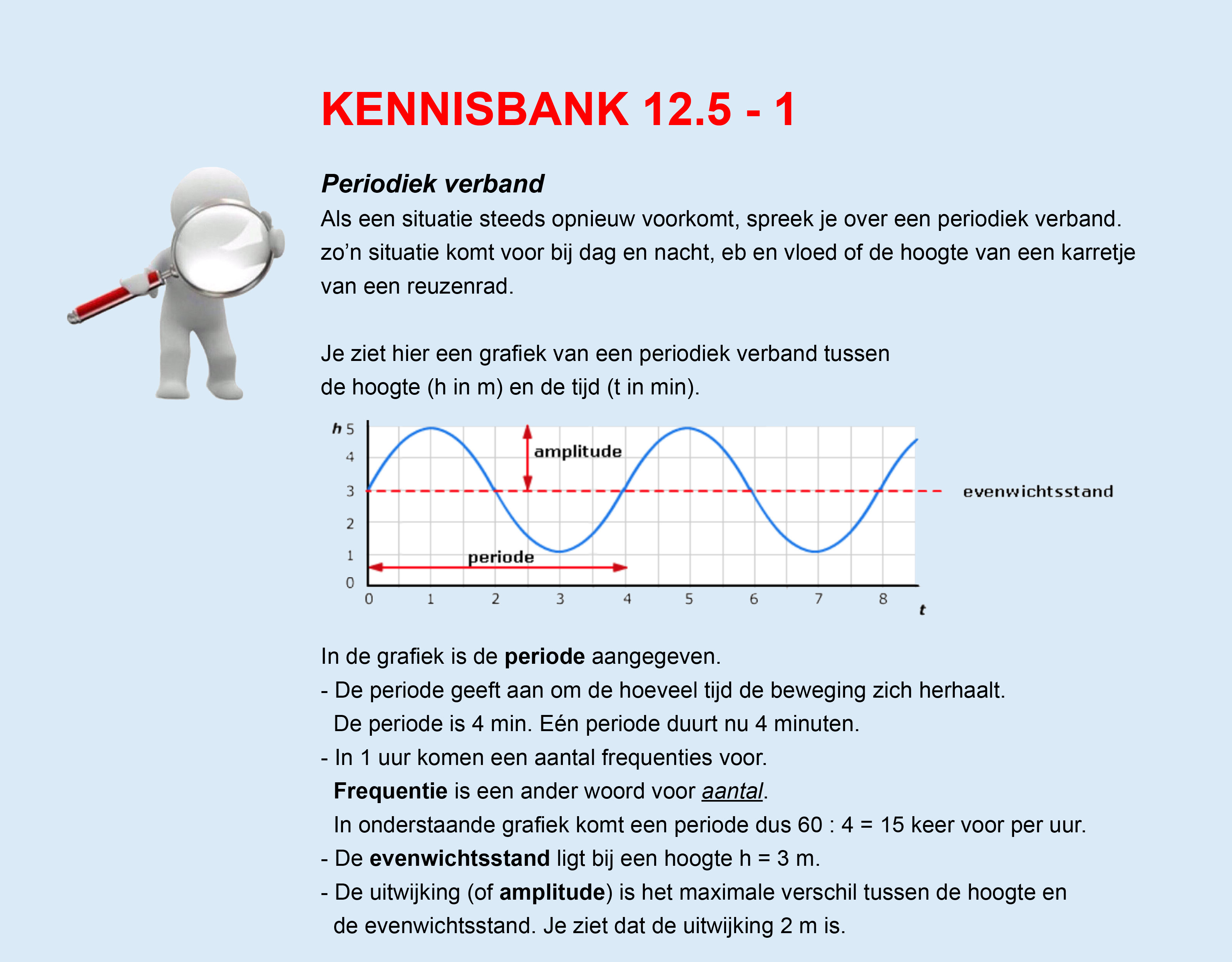
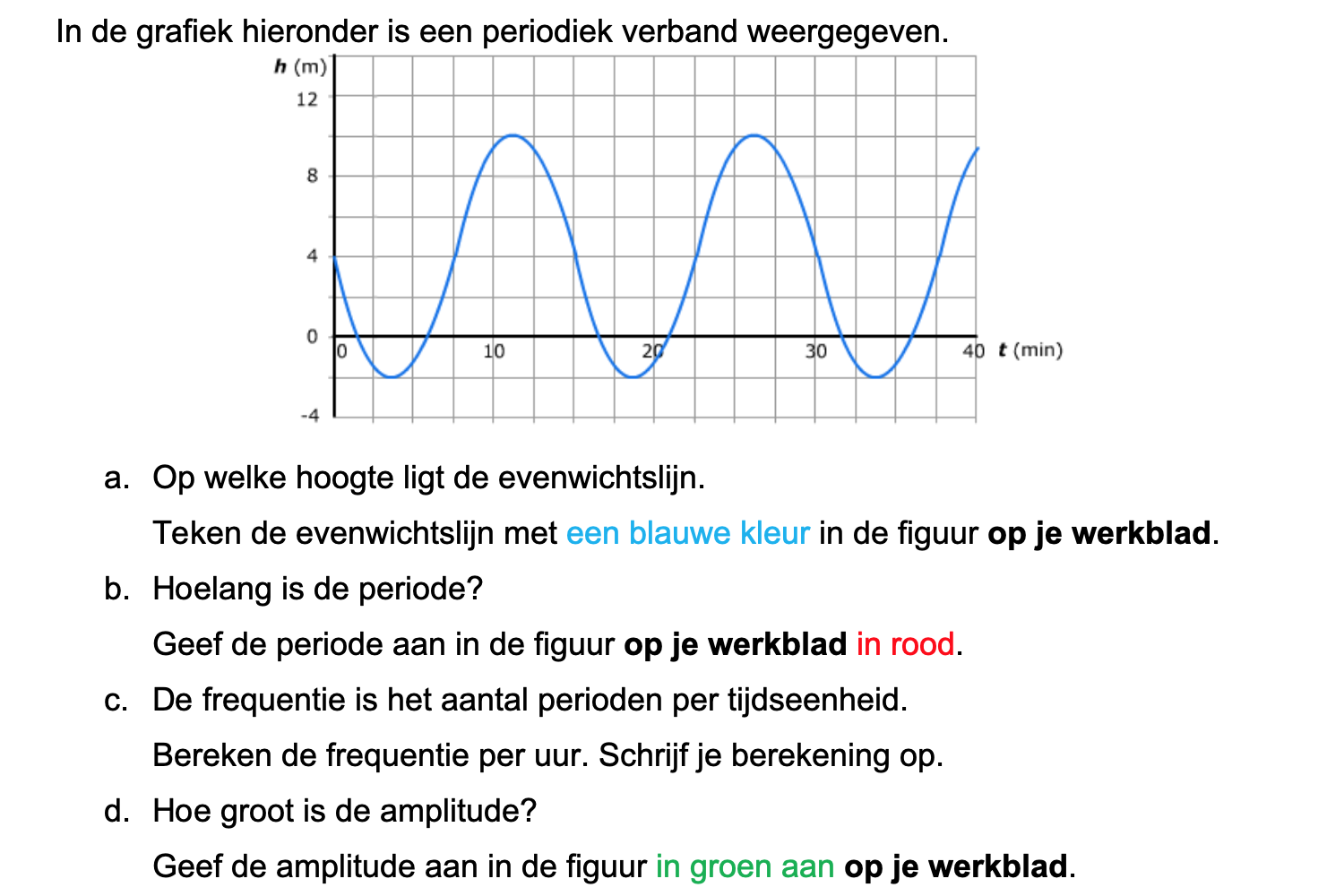
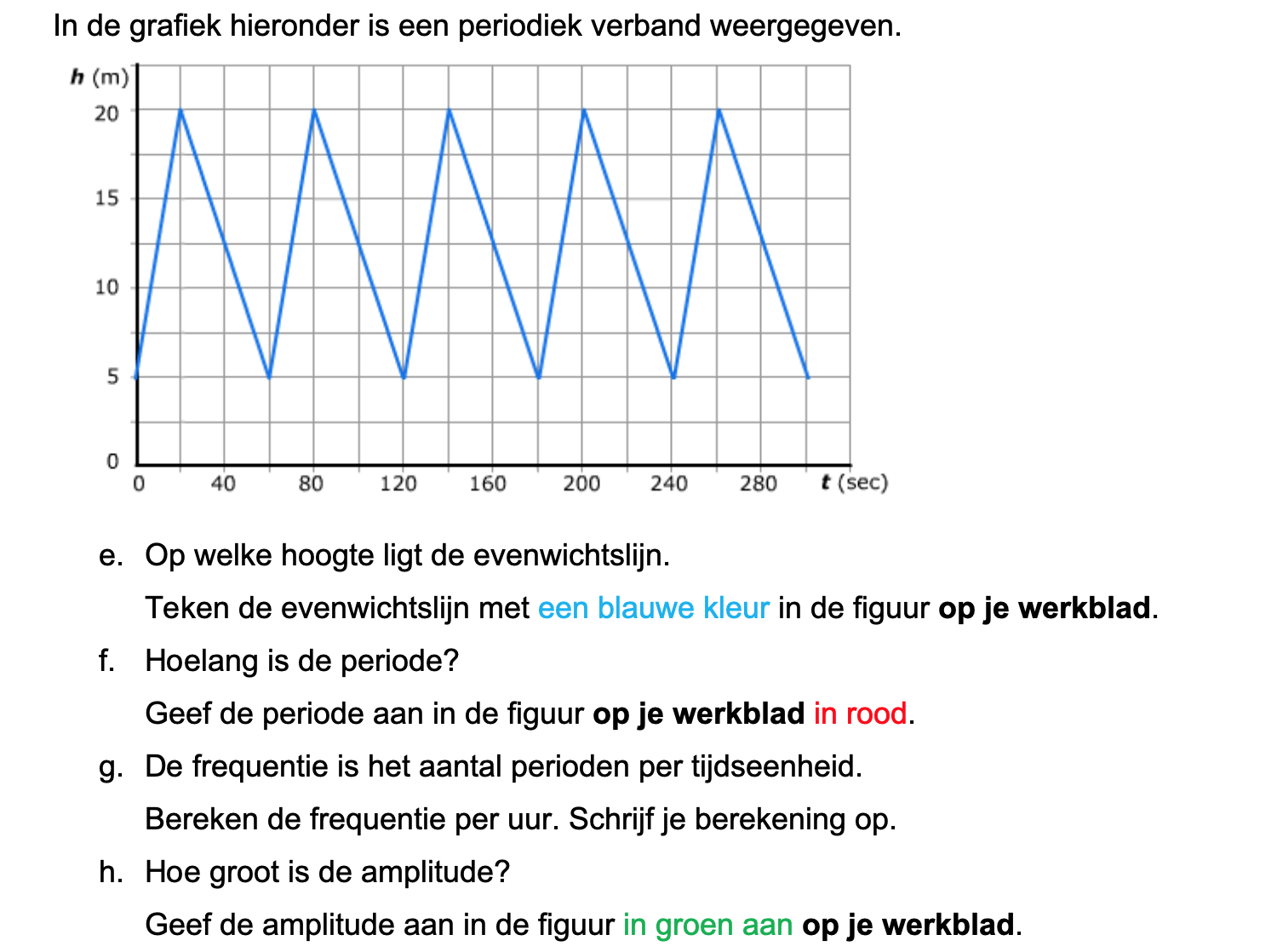
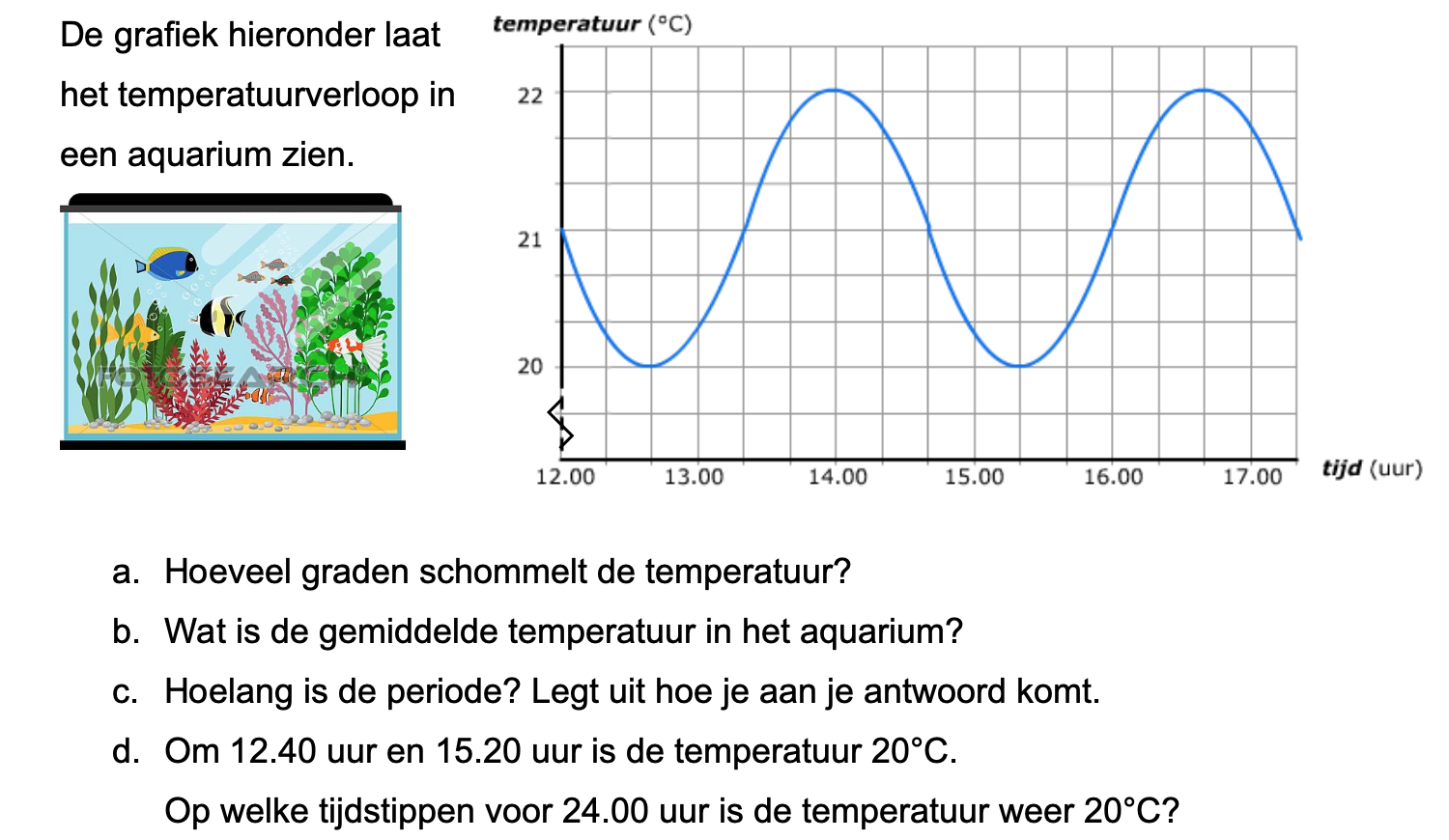
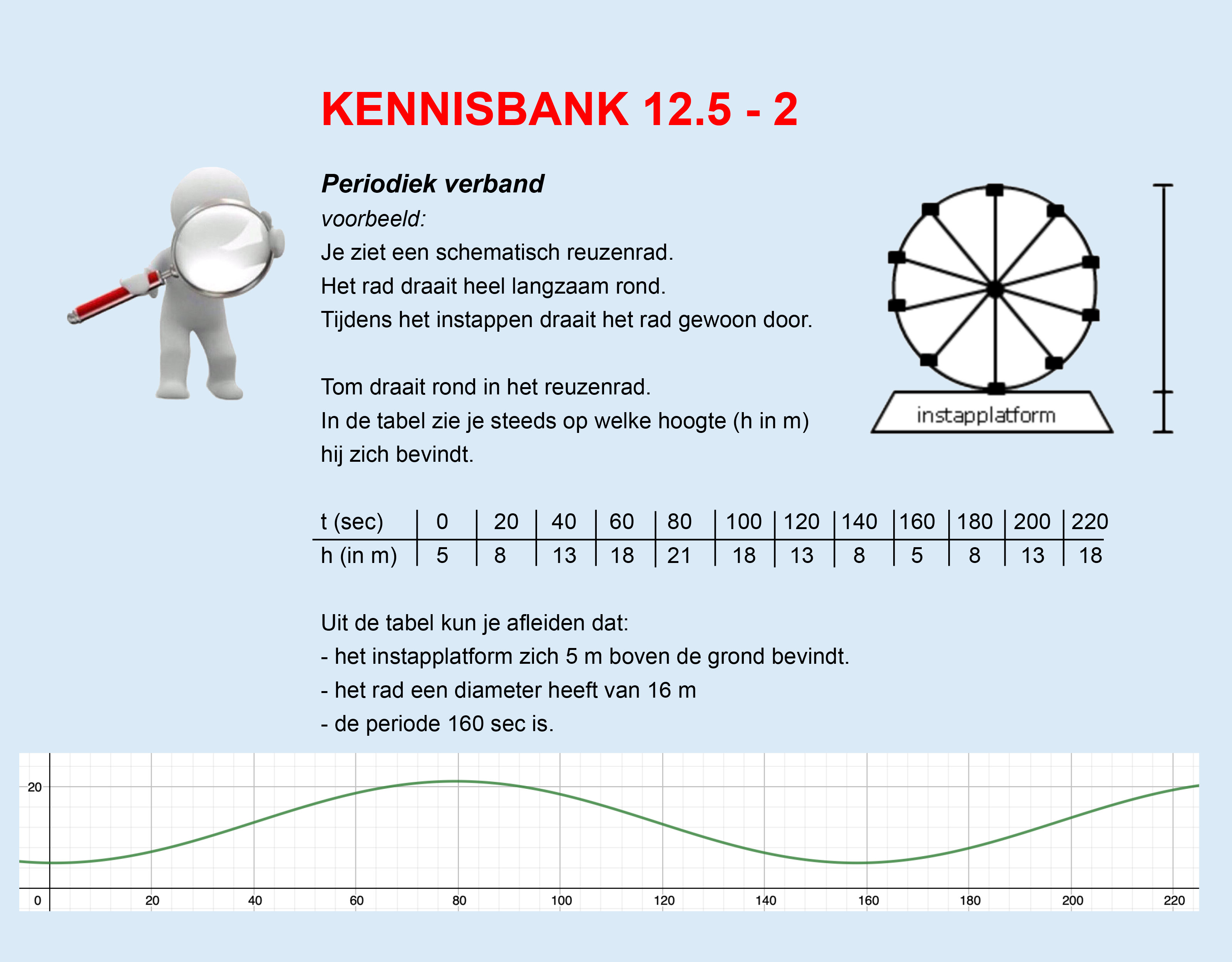
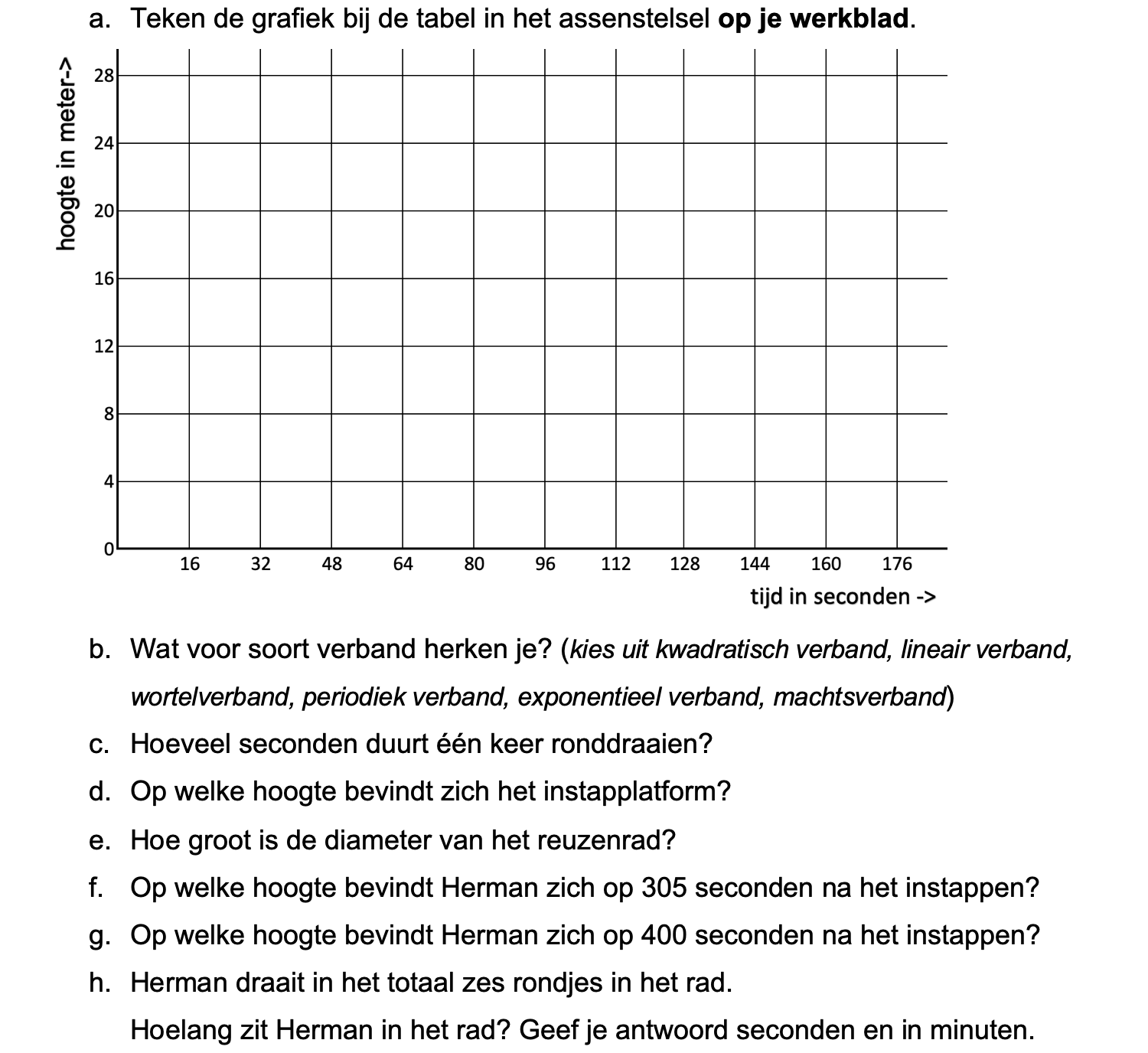
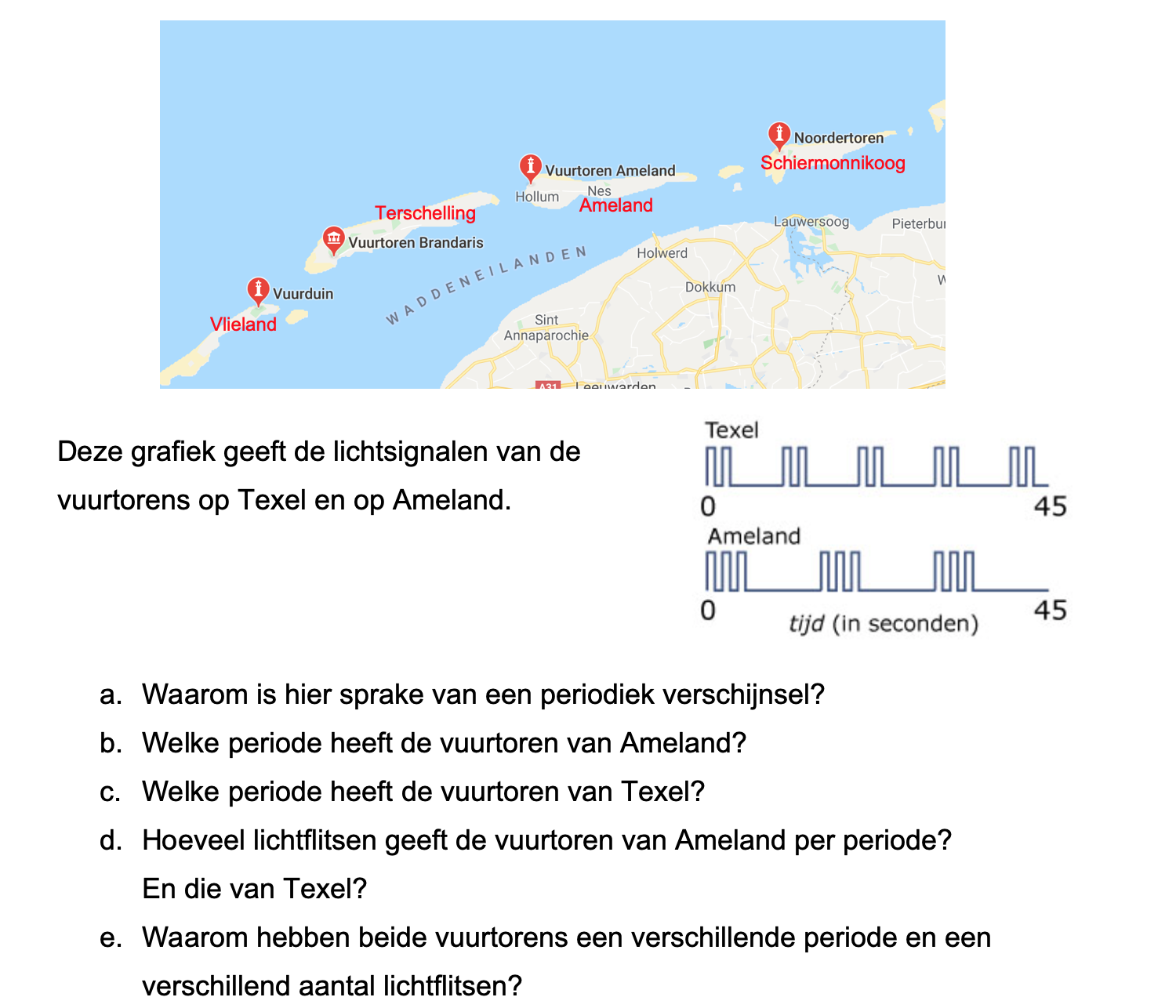
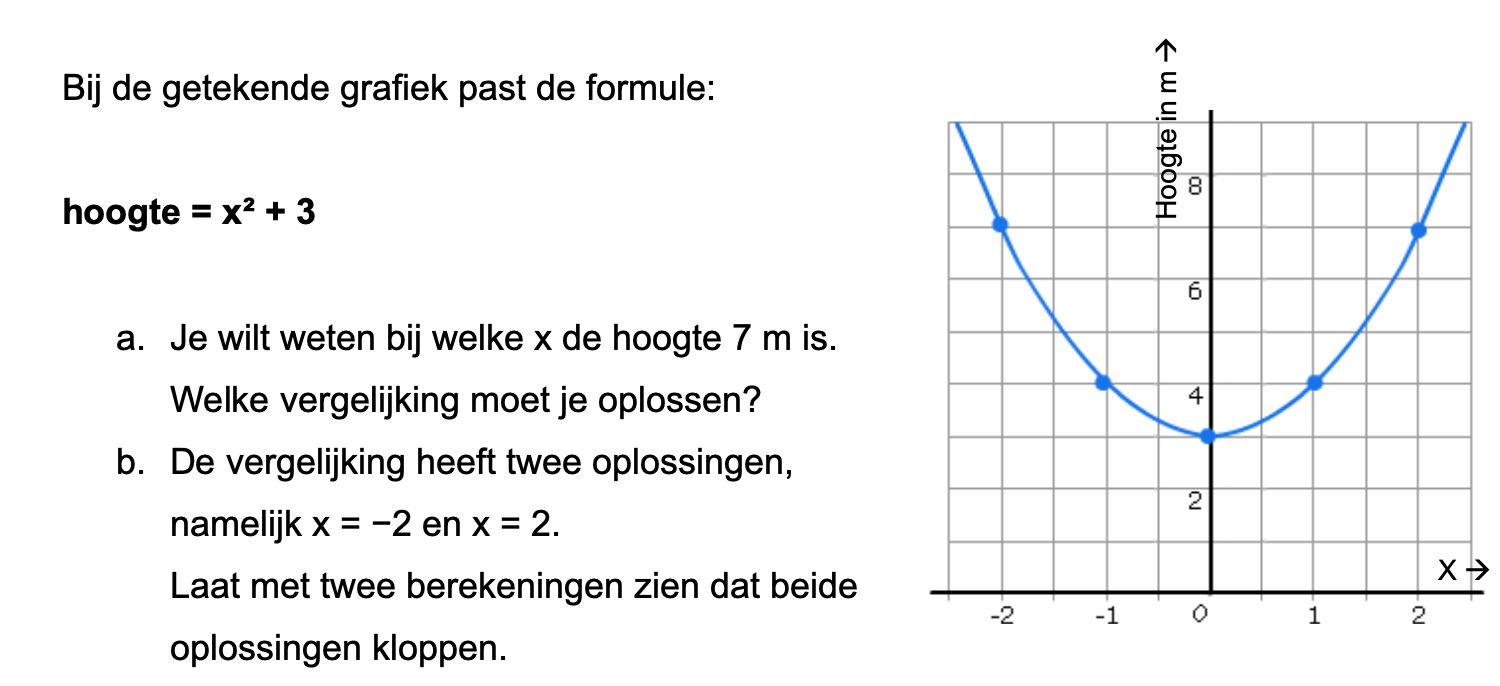
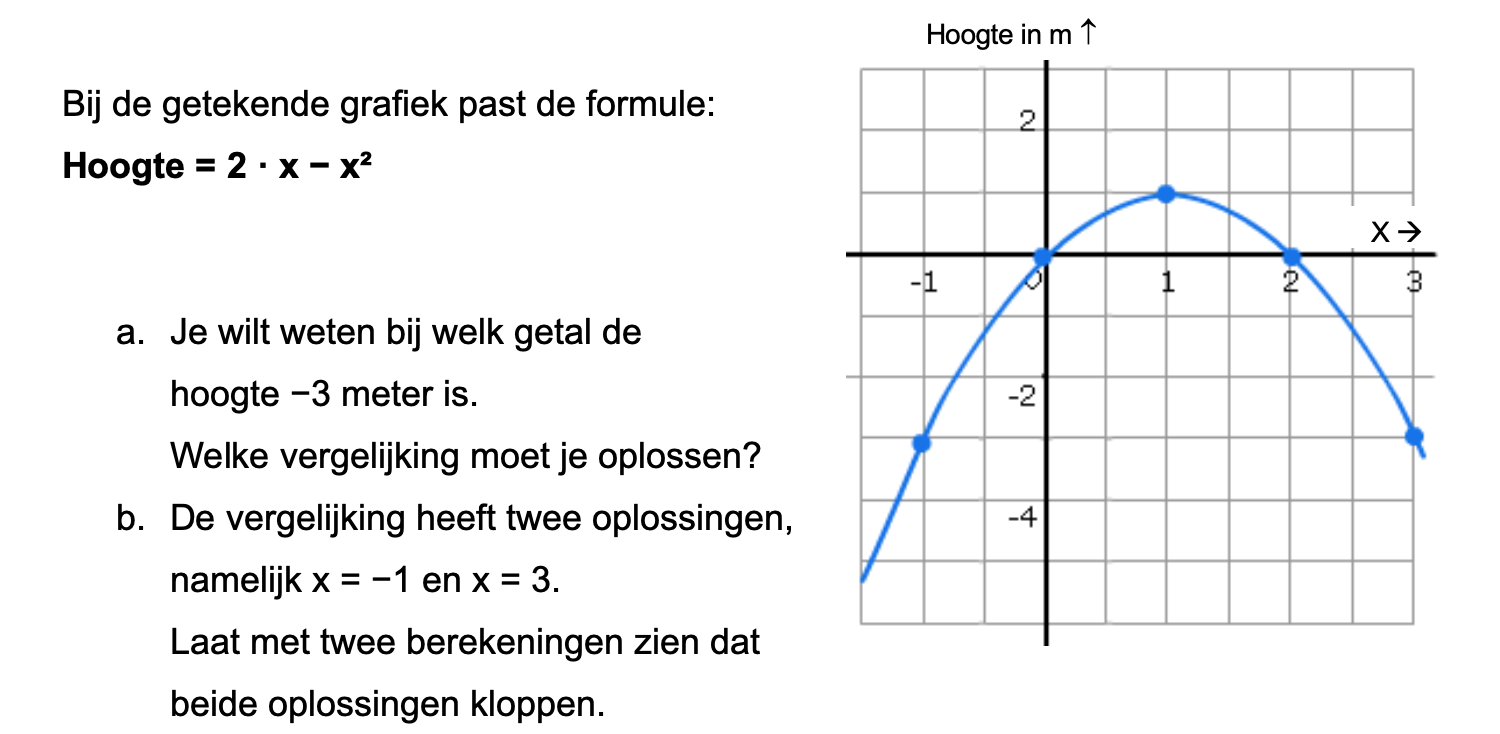
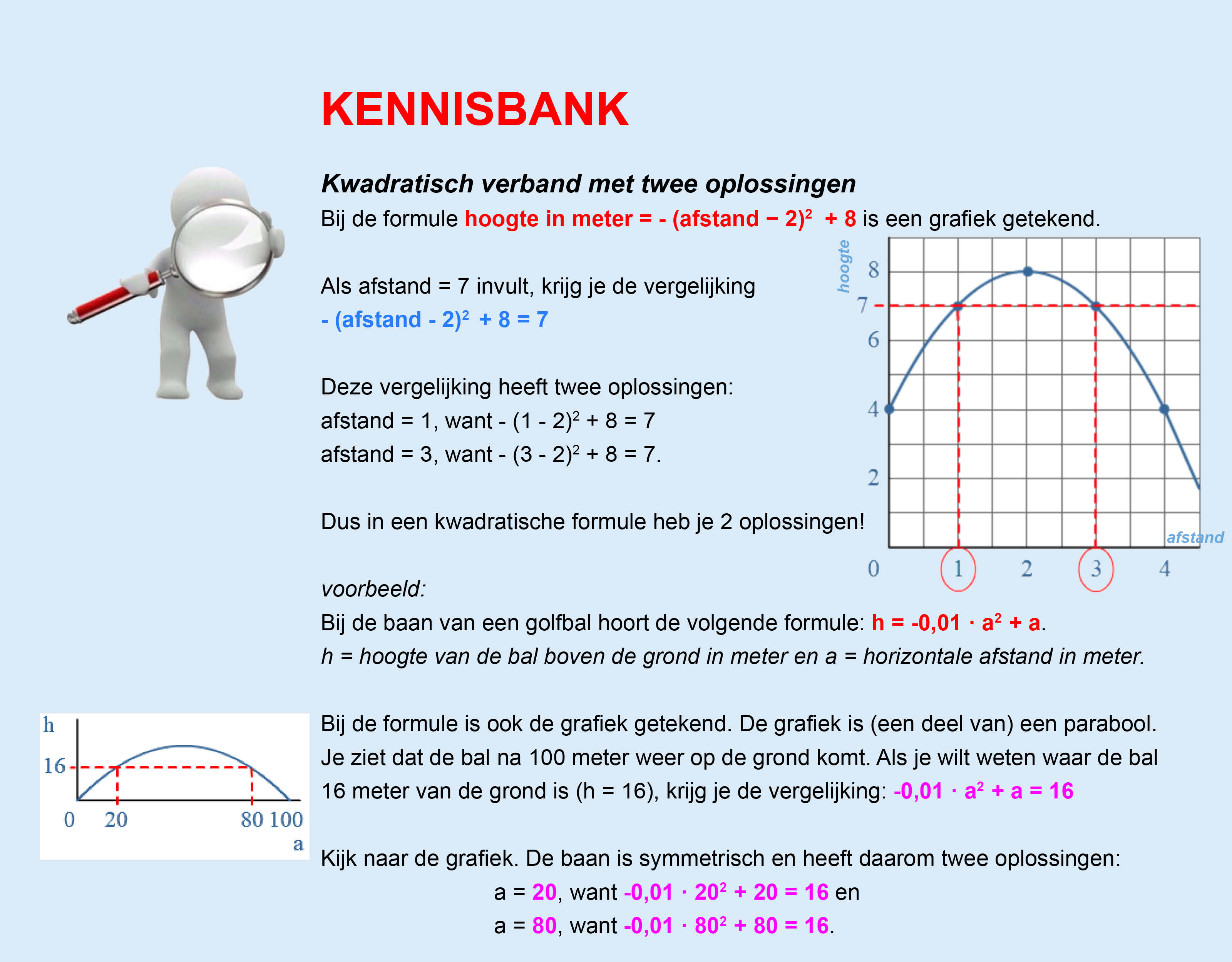
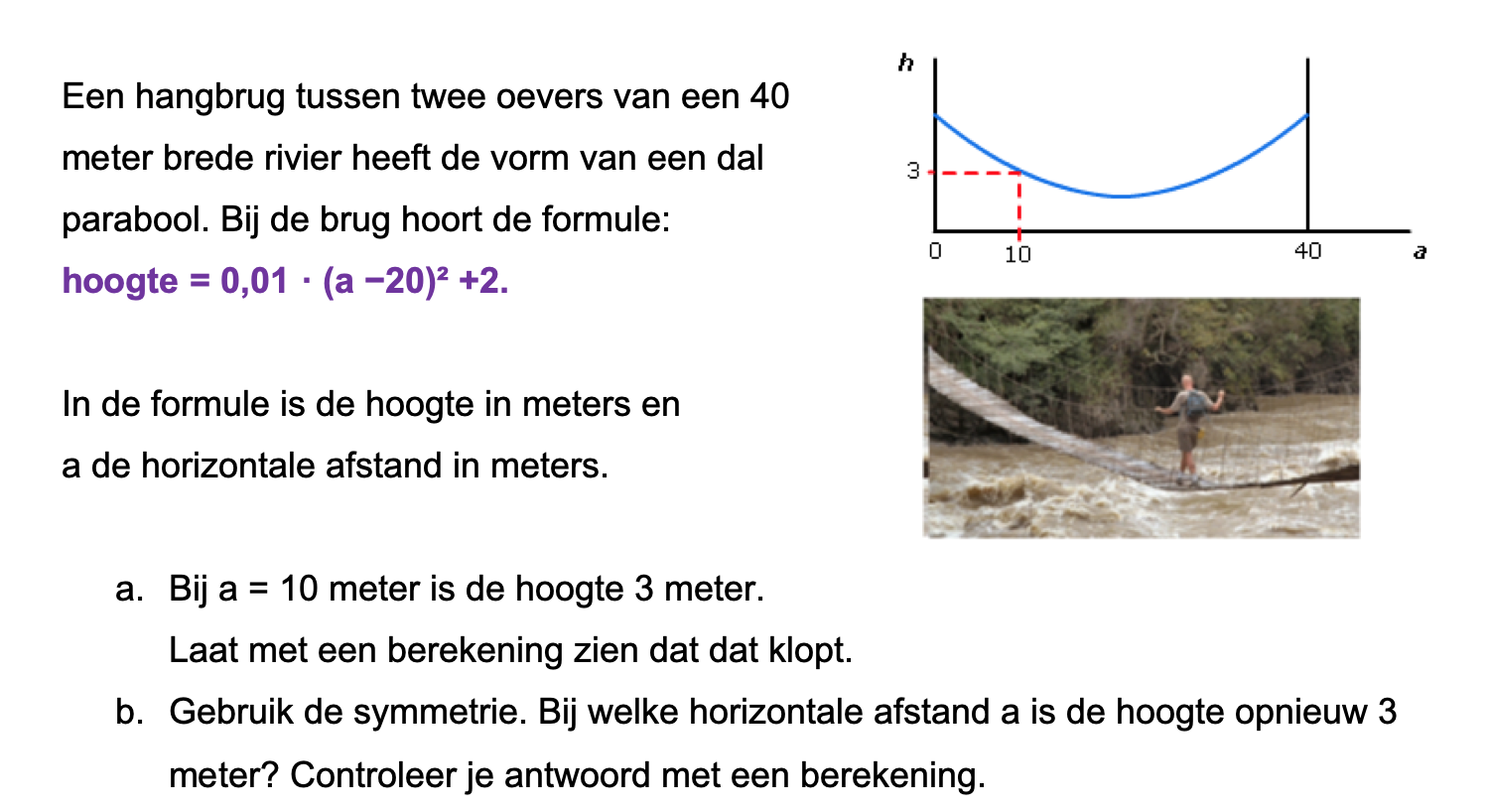
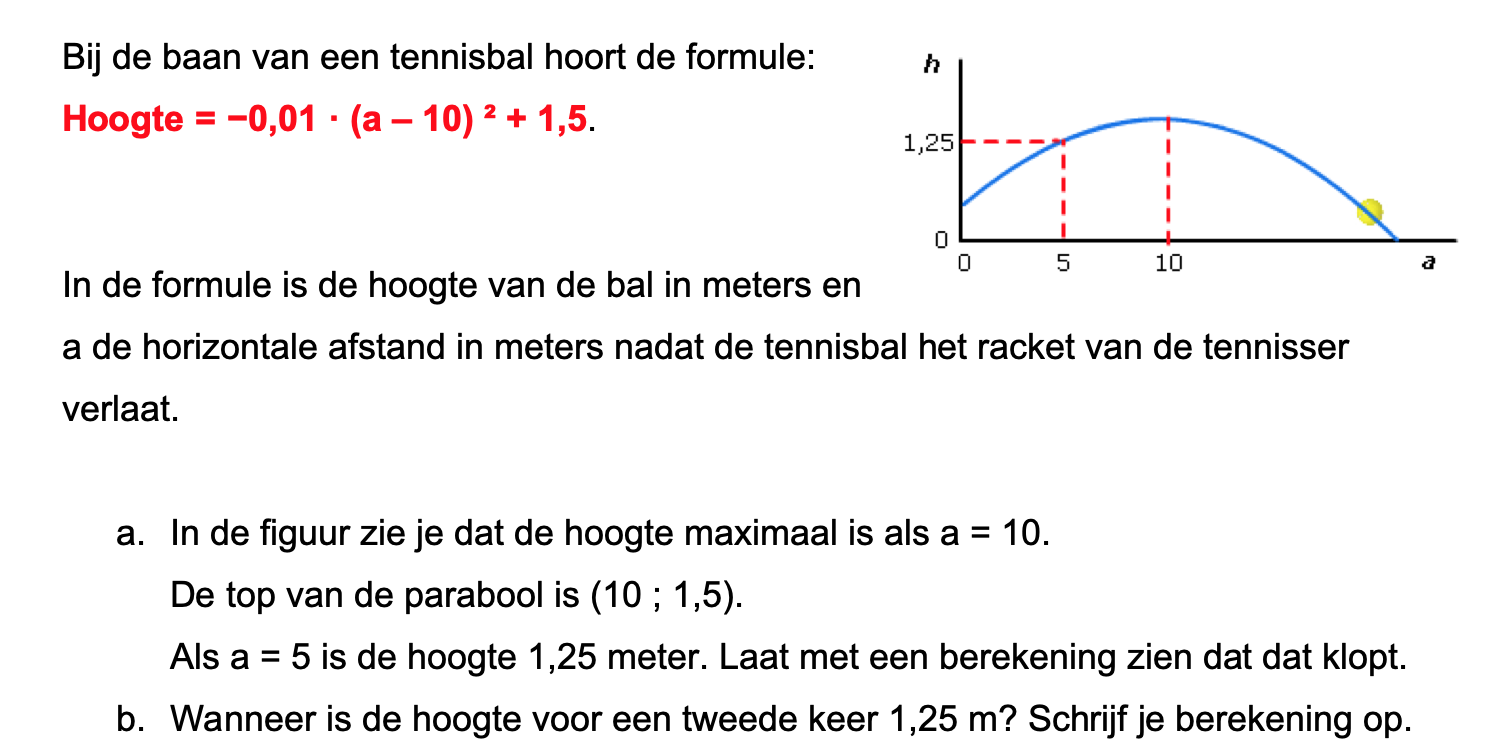
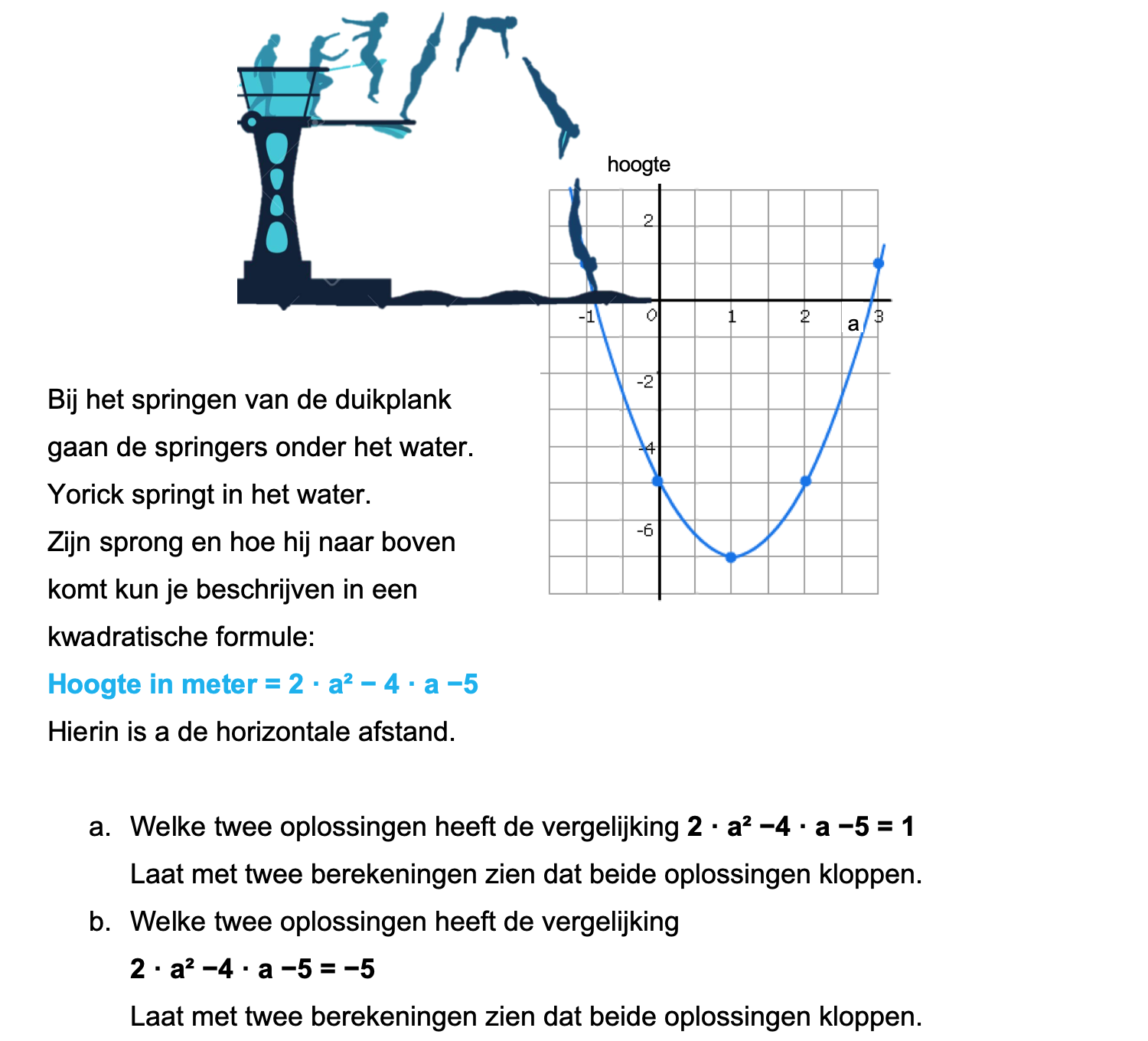
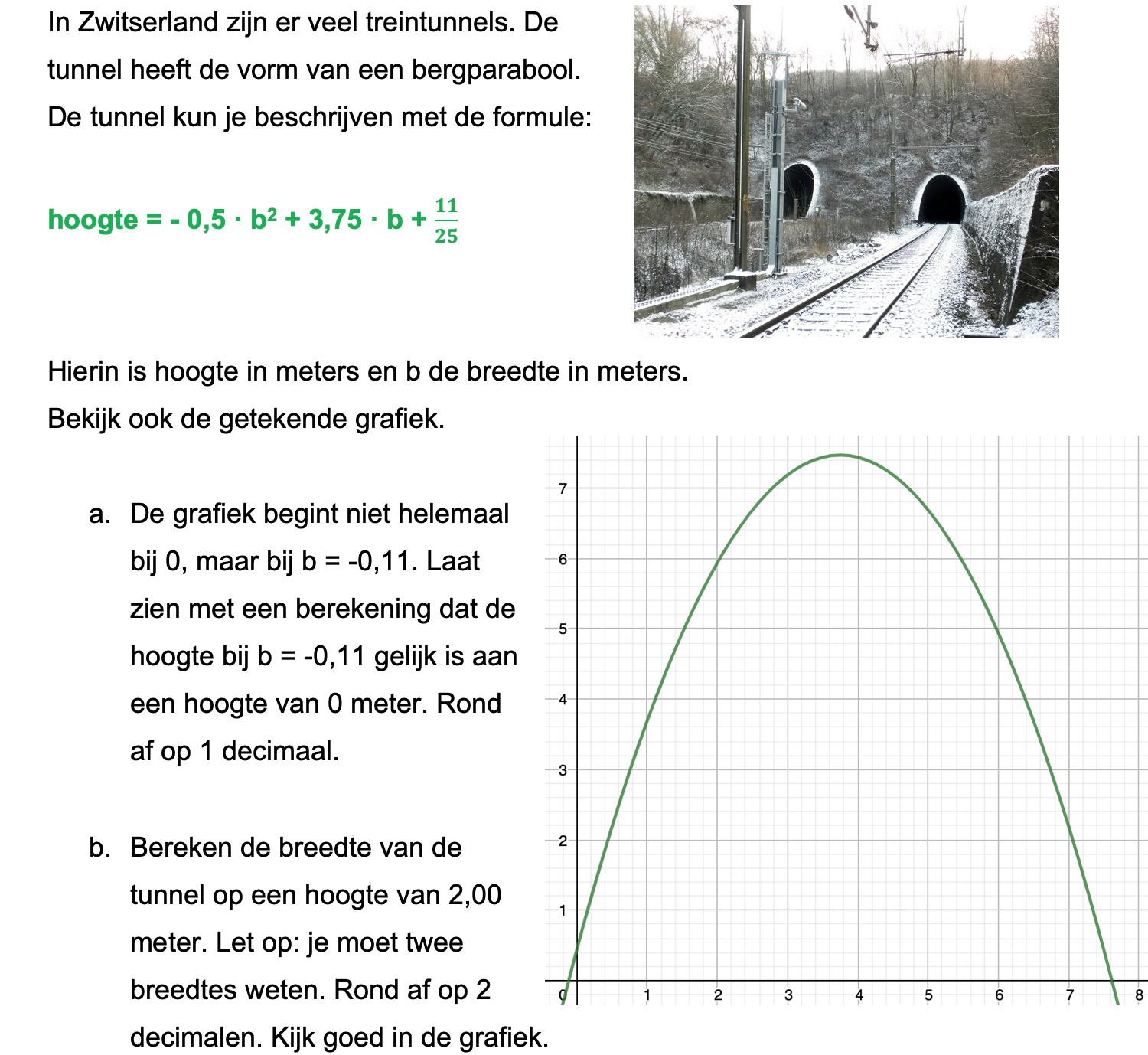
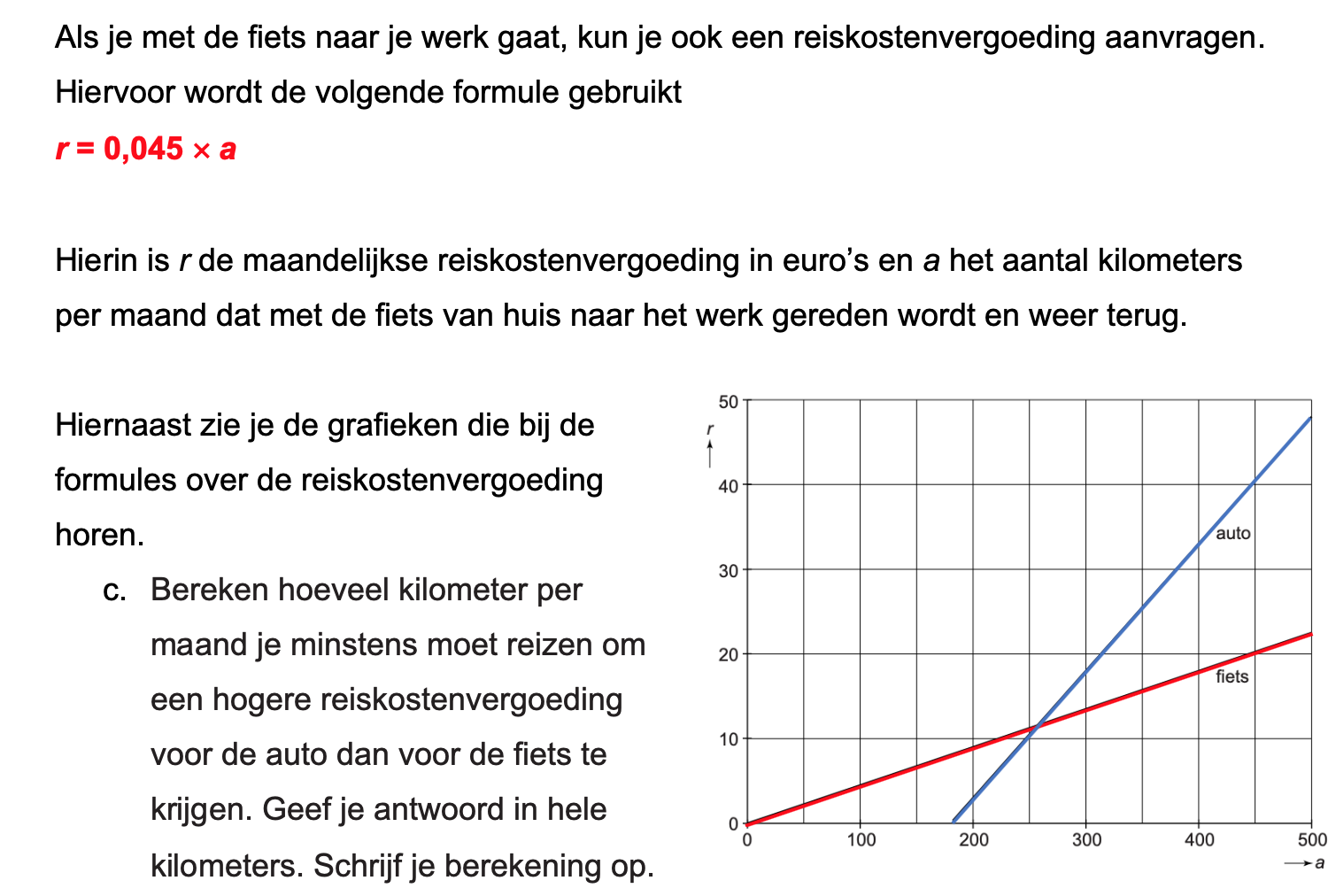
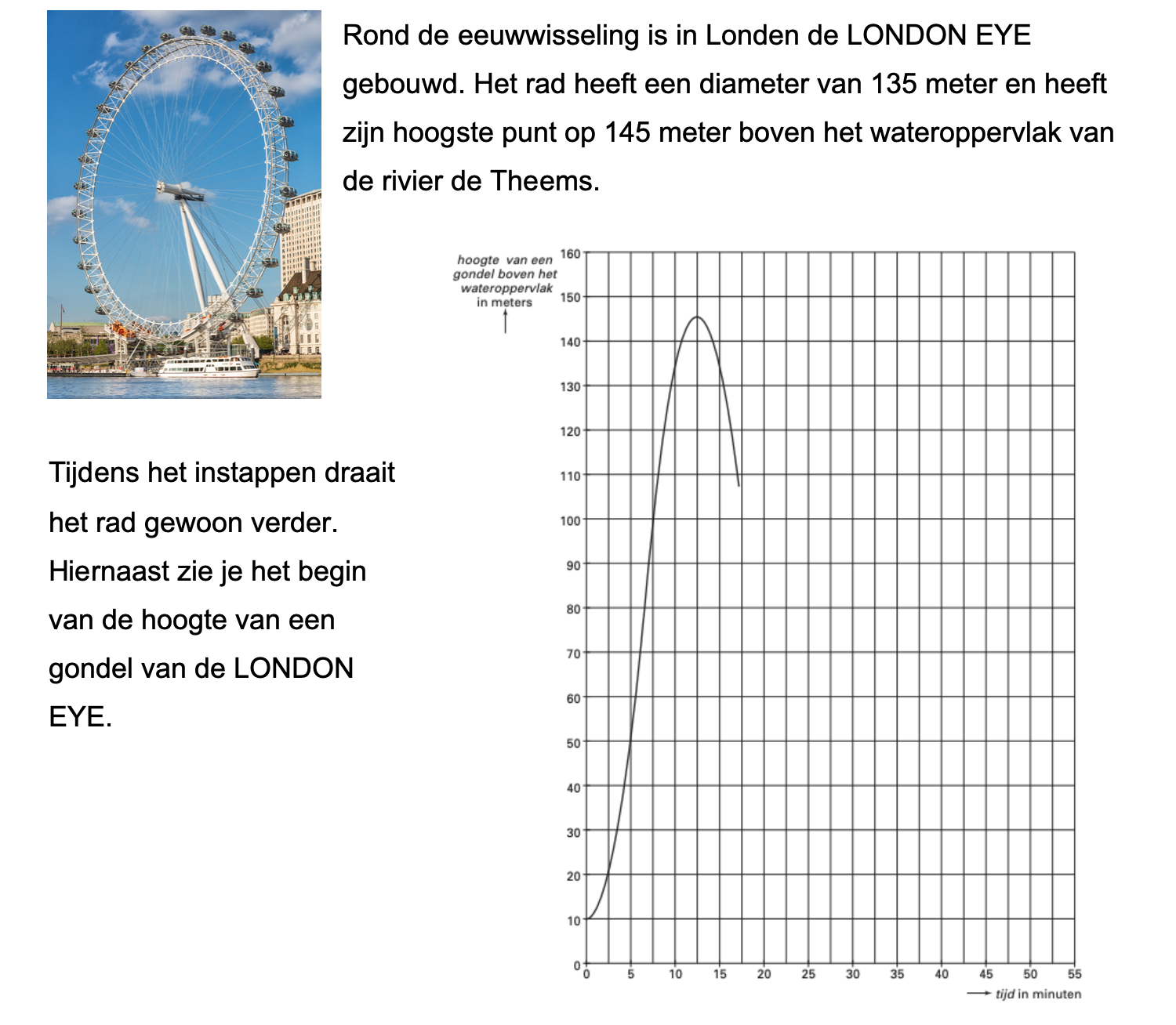
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
\
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
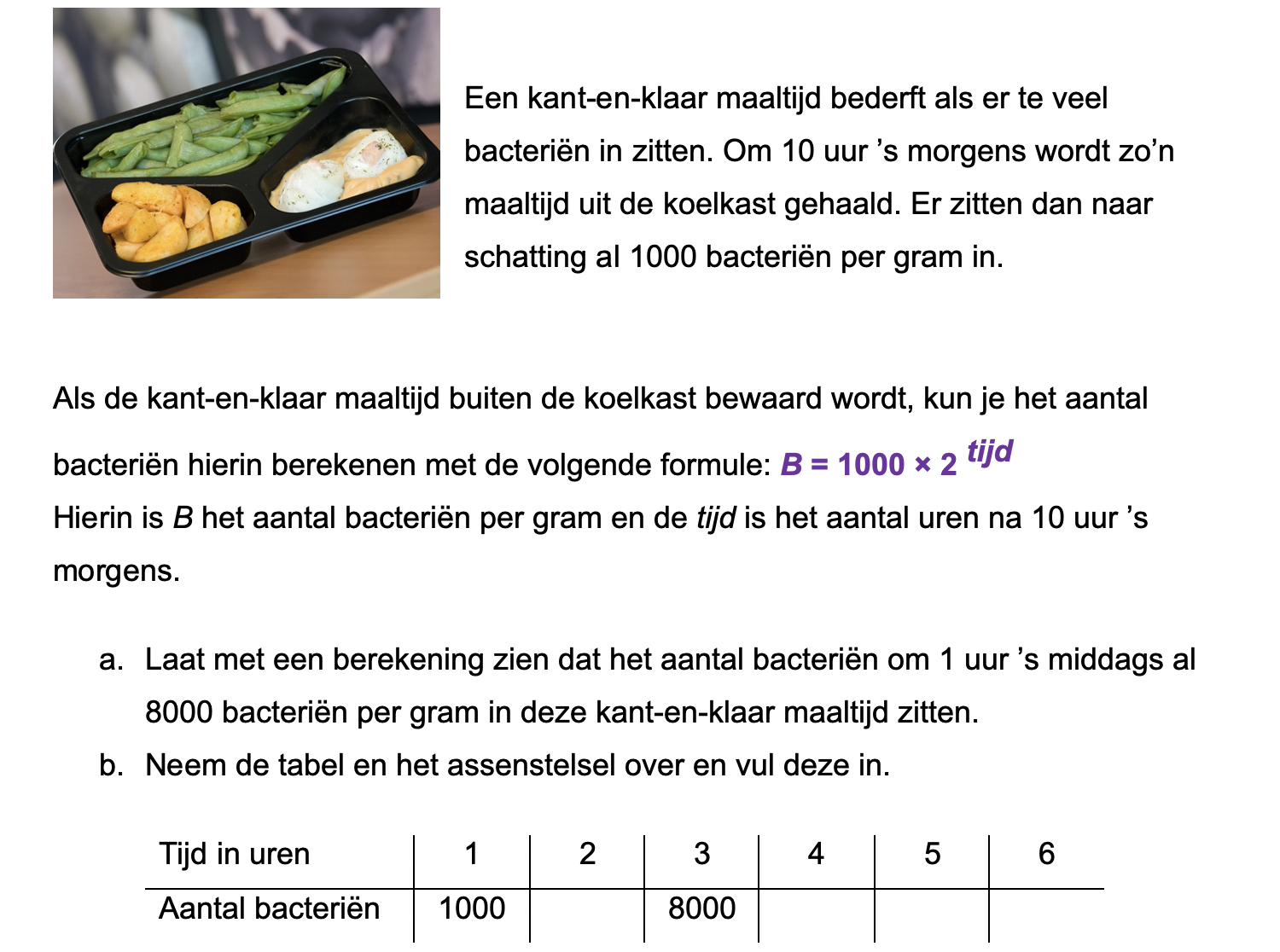
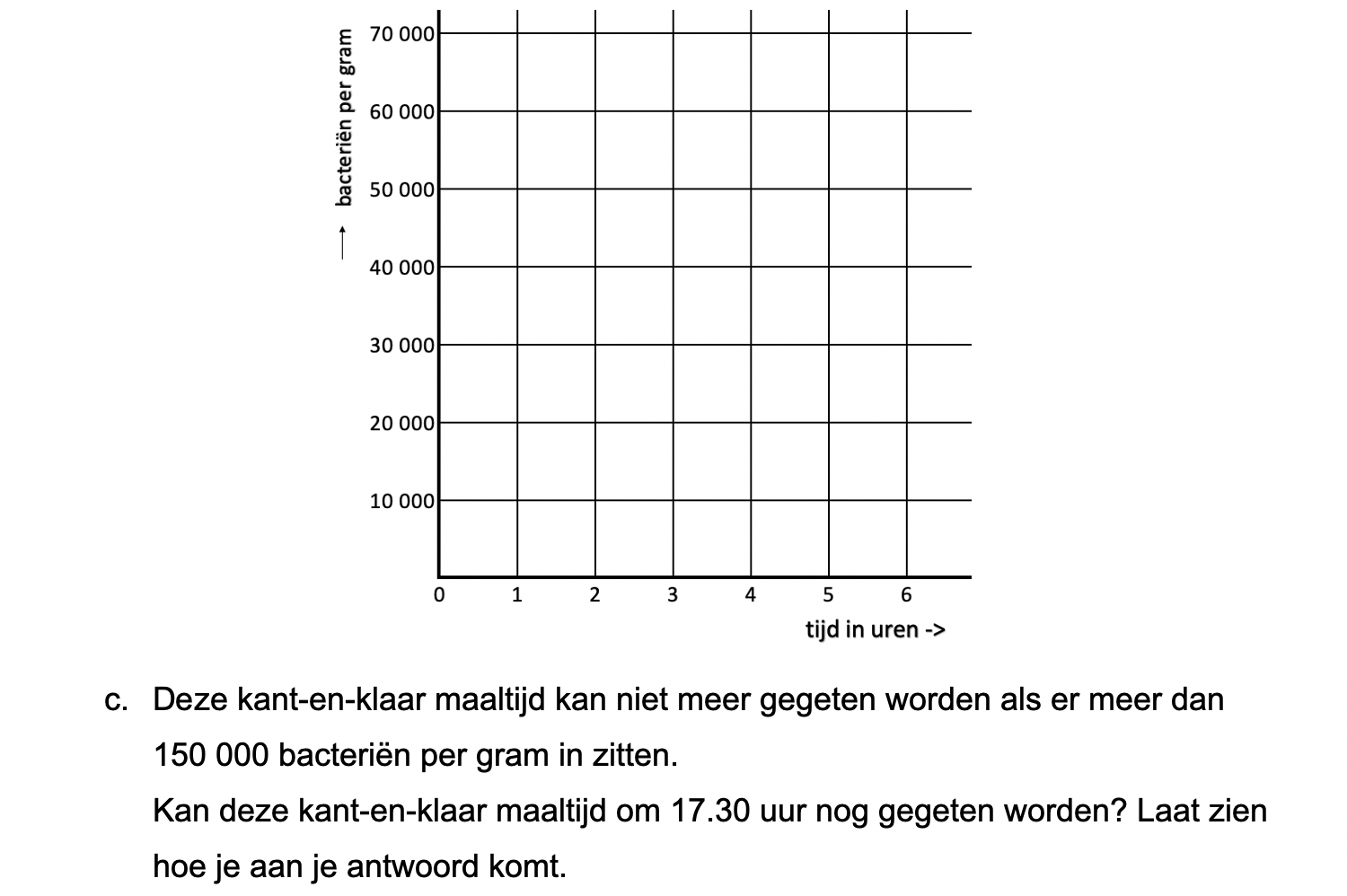
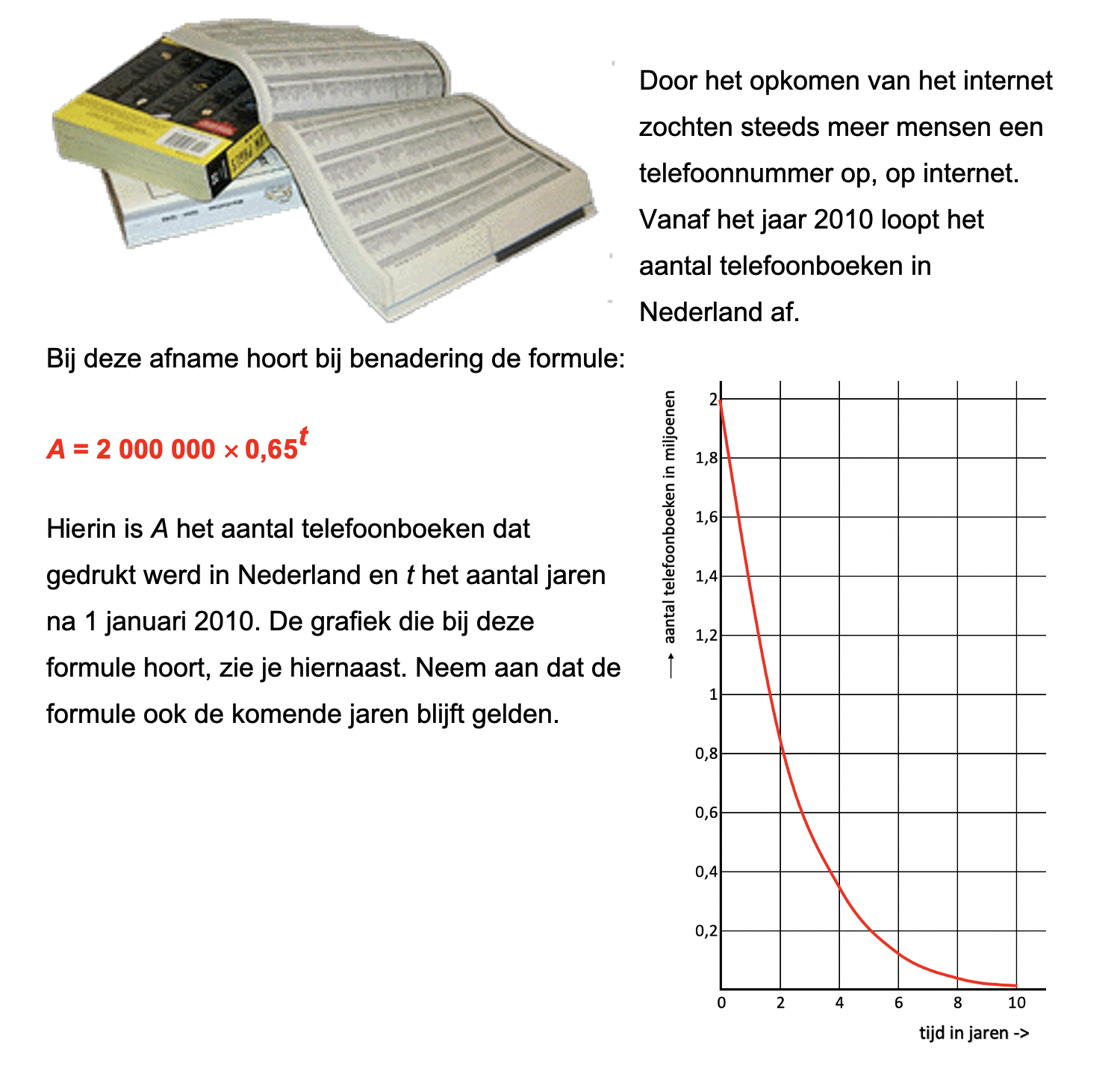
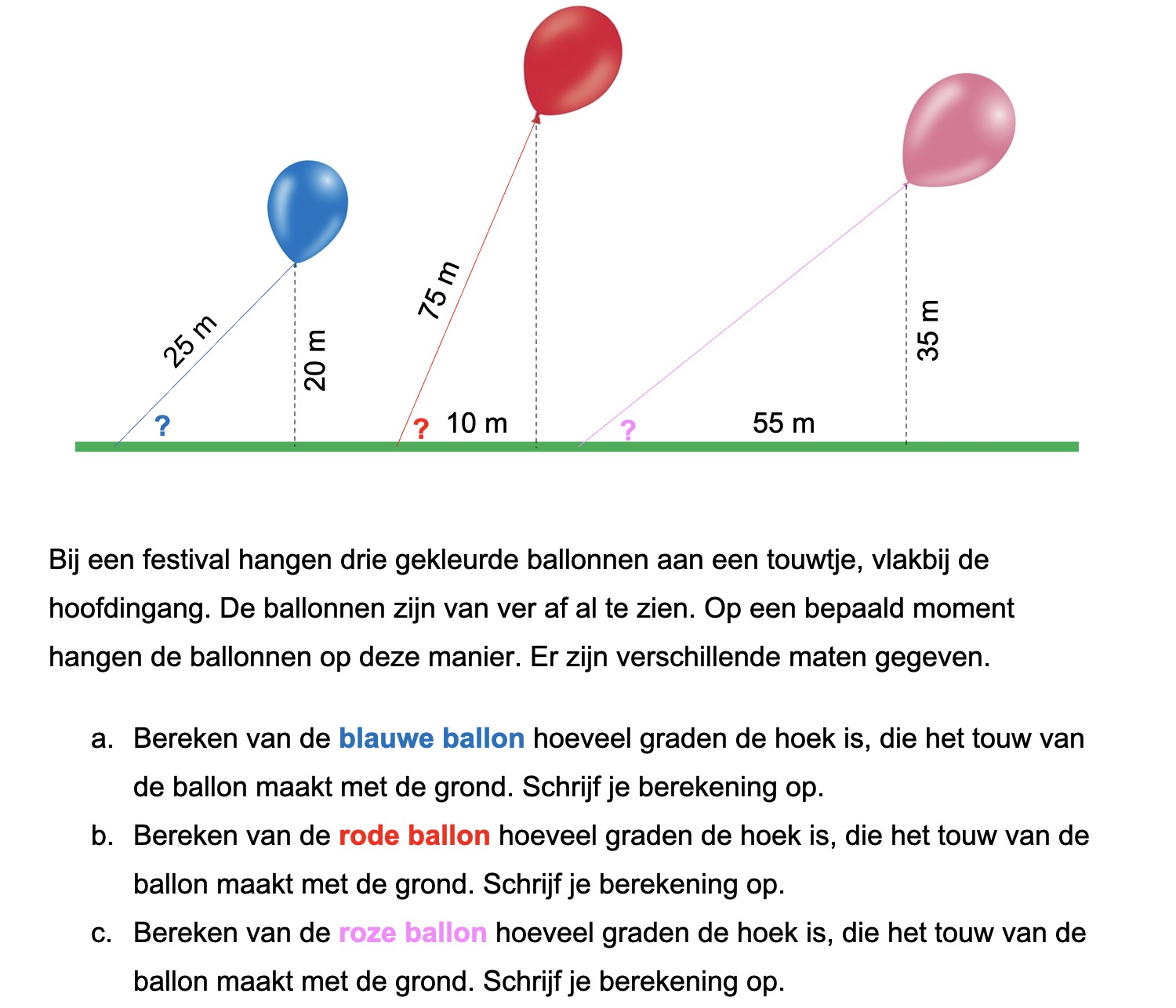
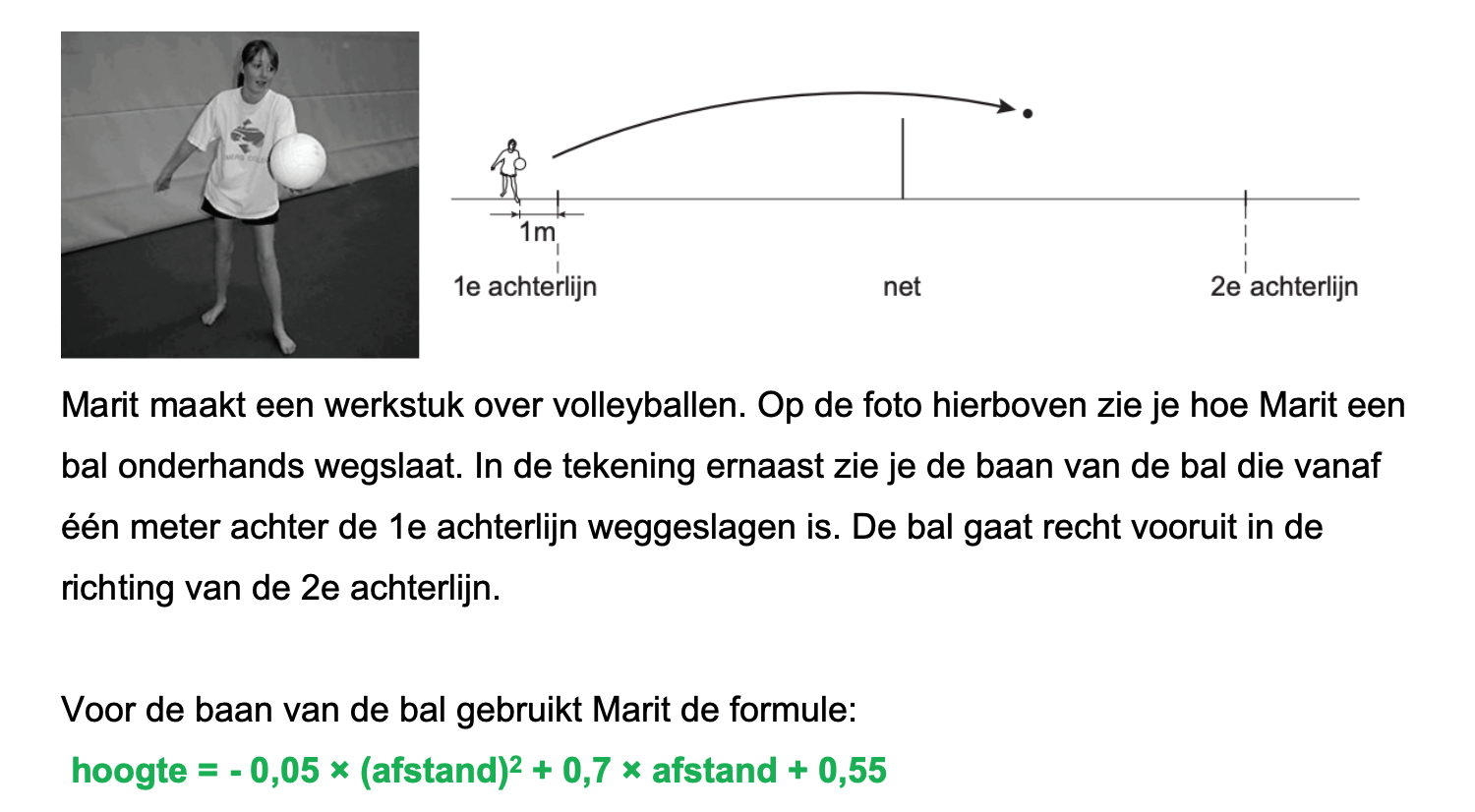
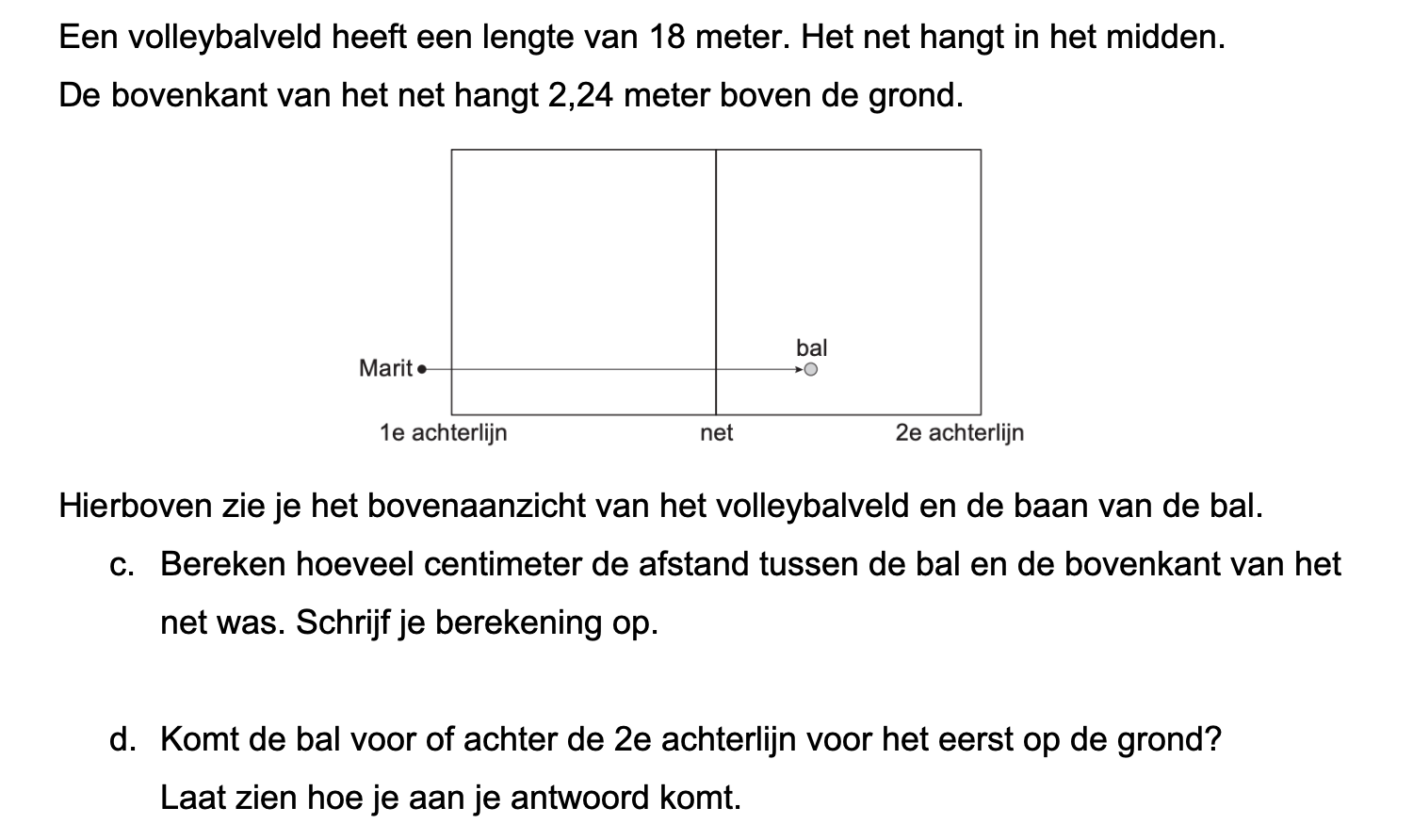
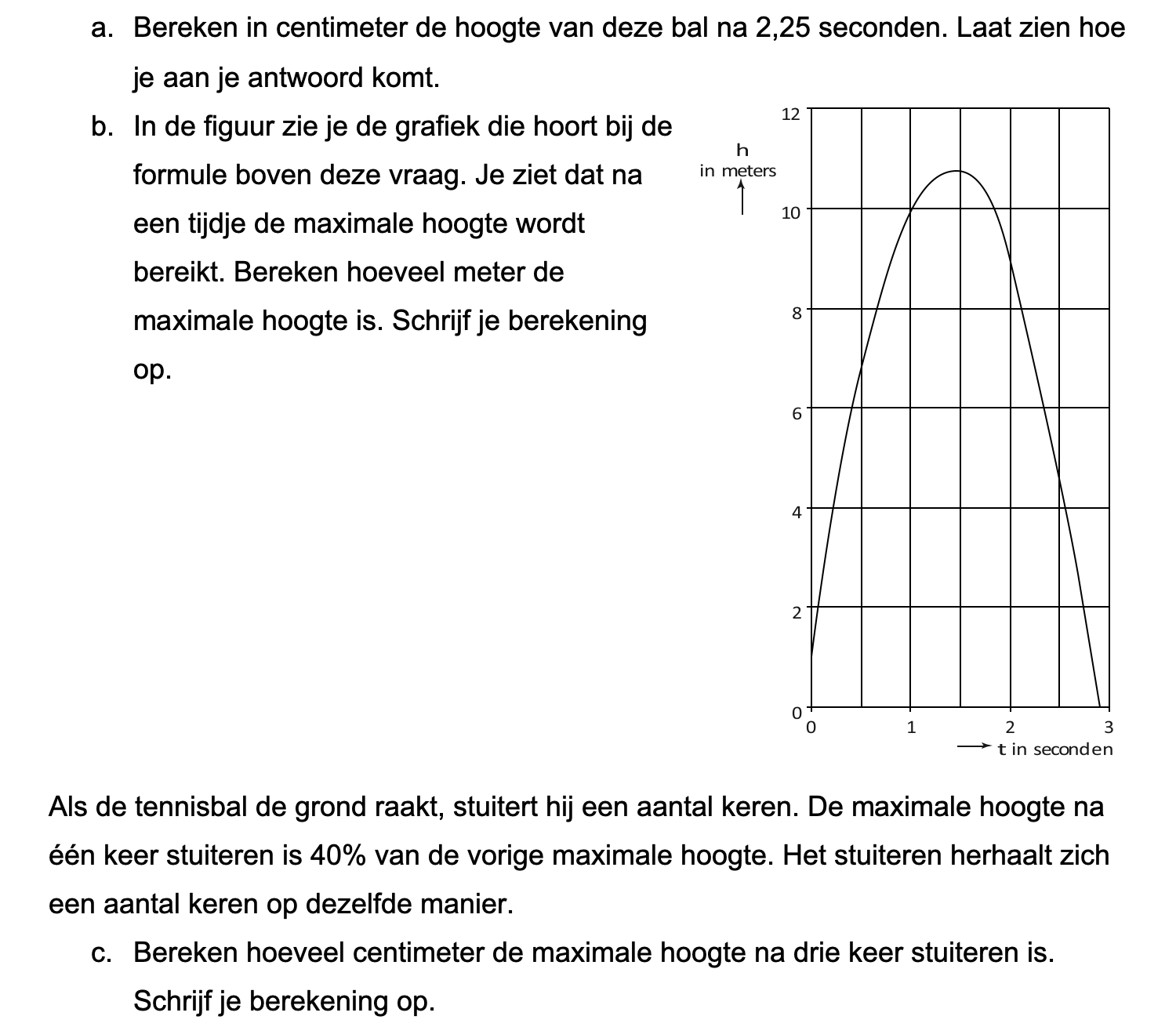
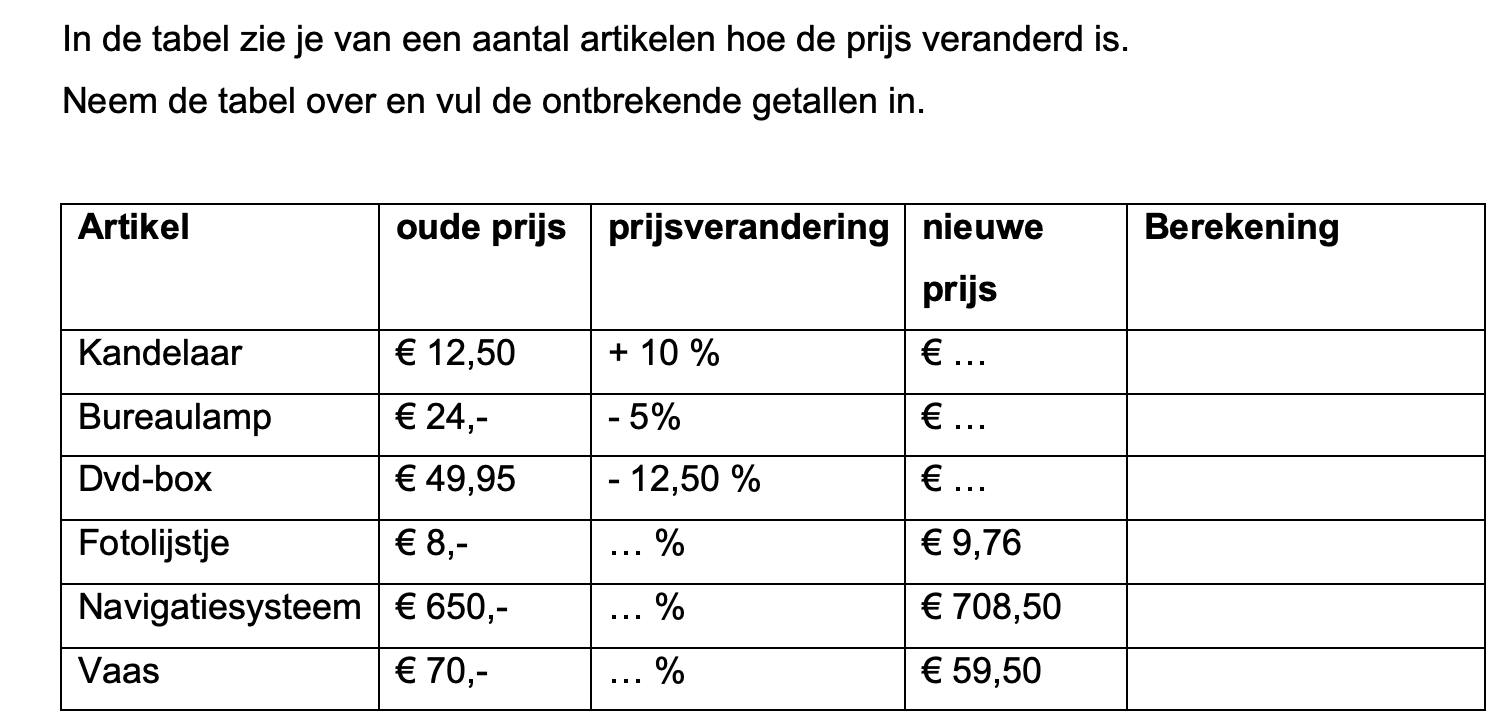
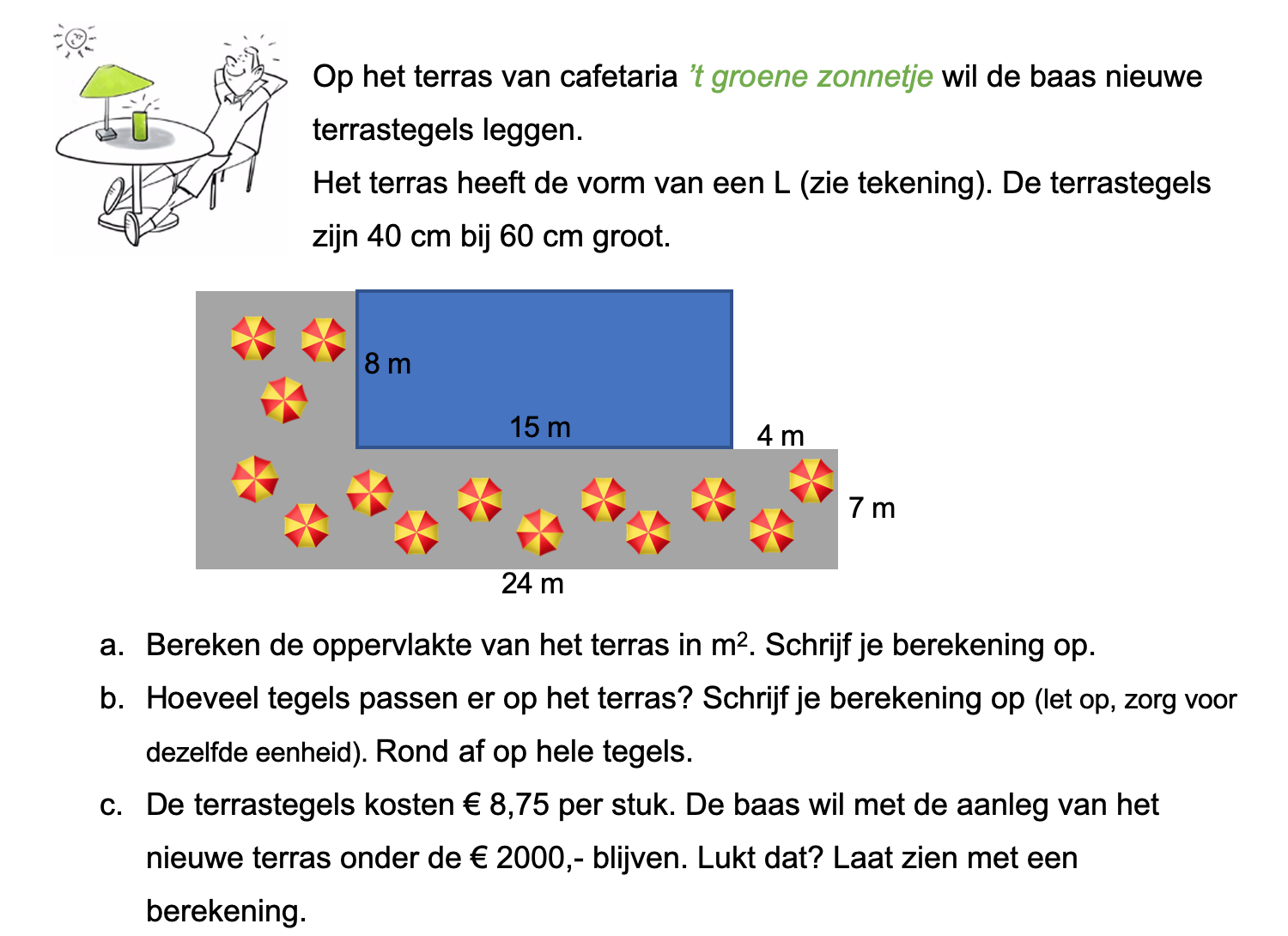
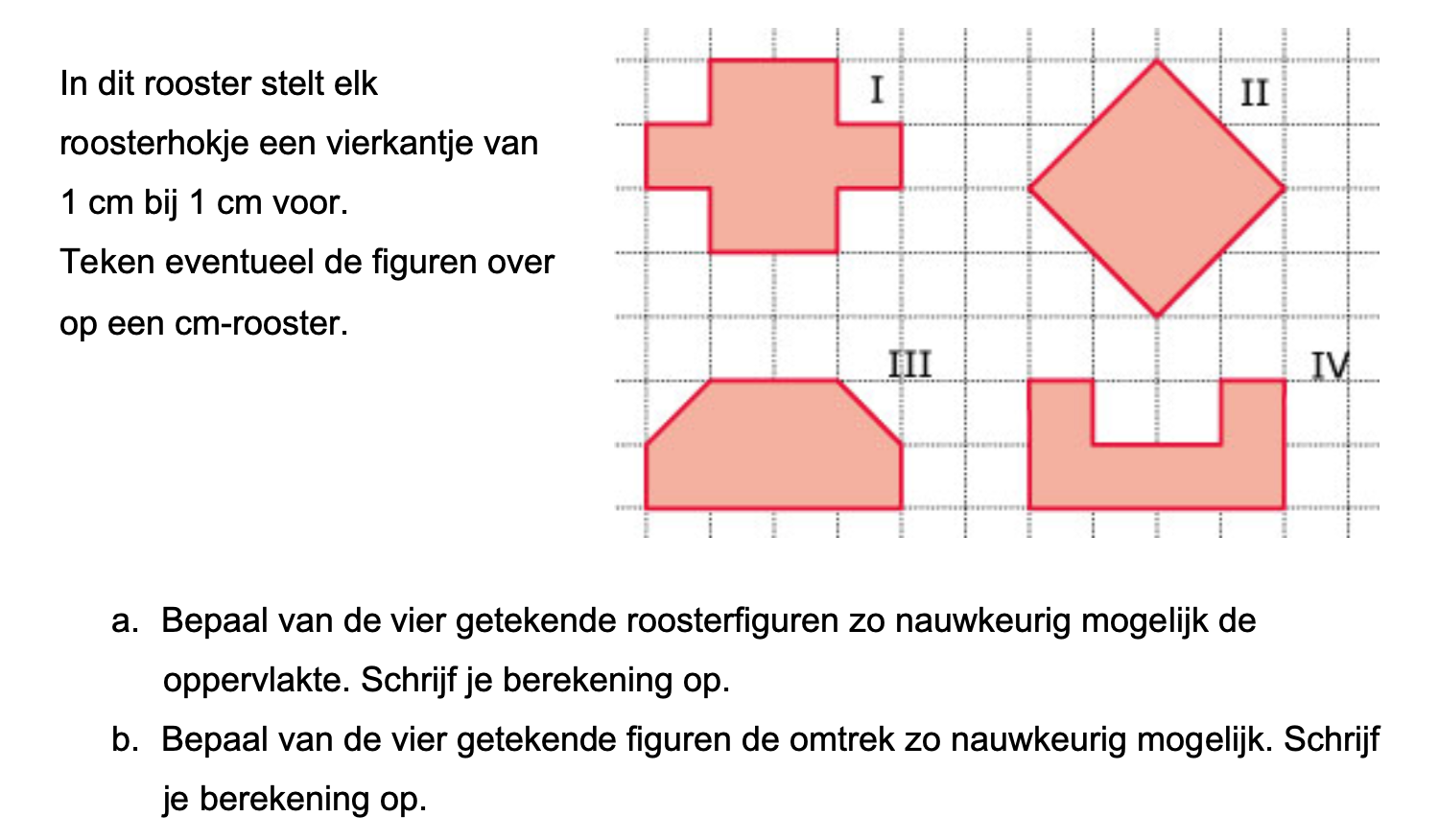
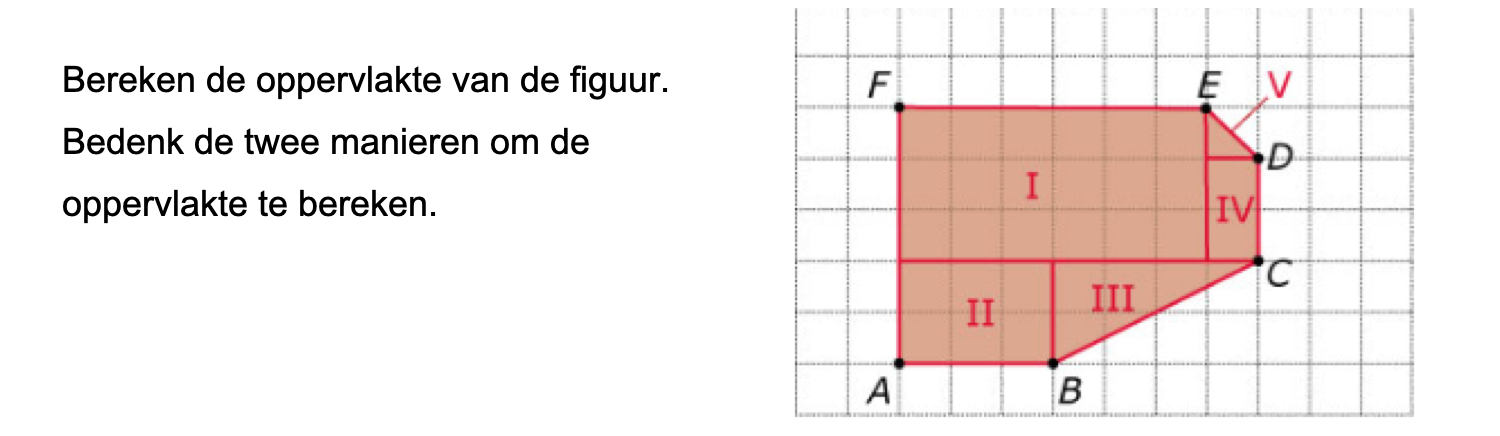
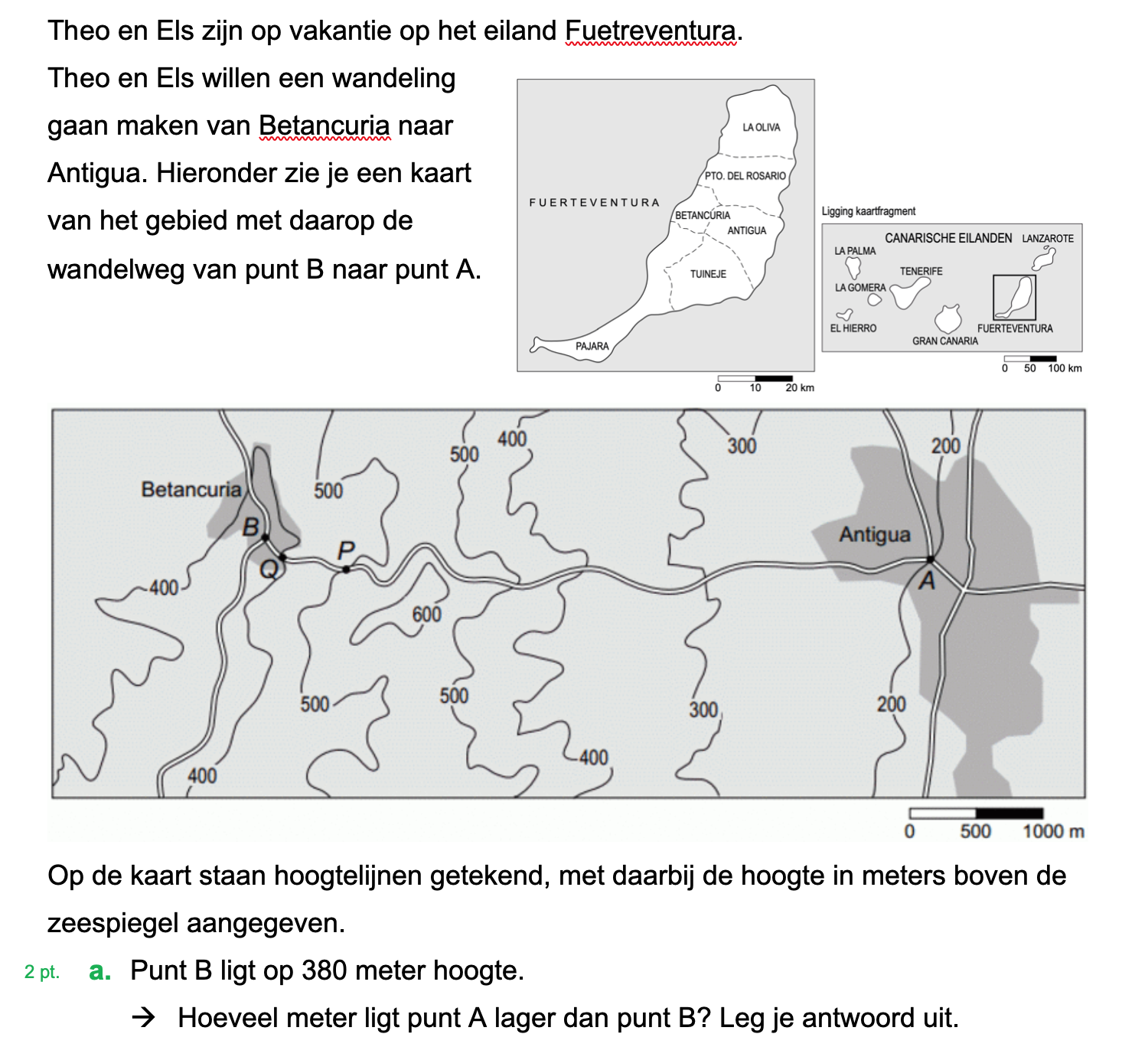
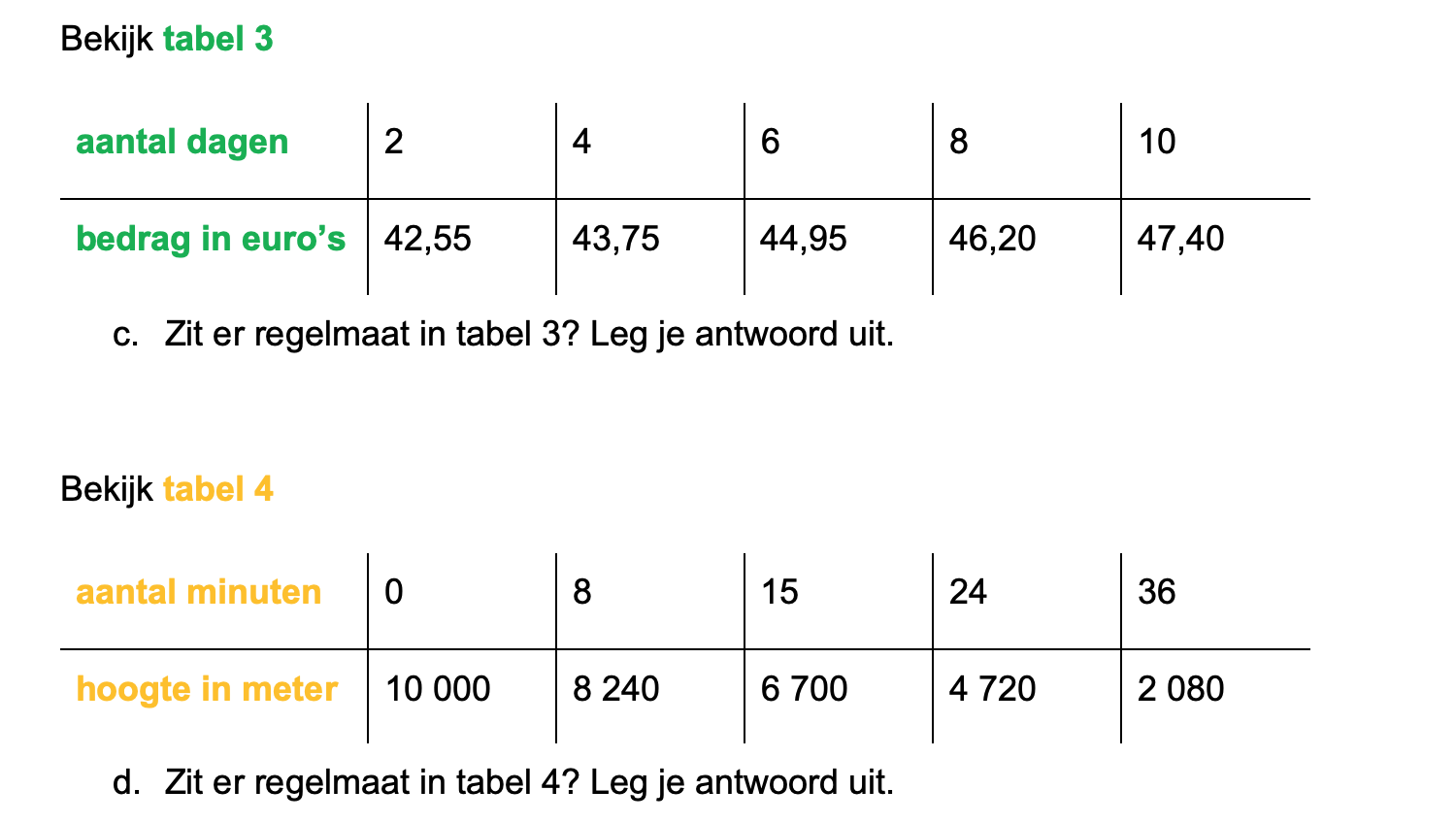
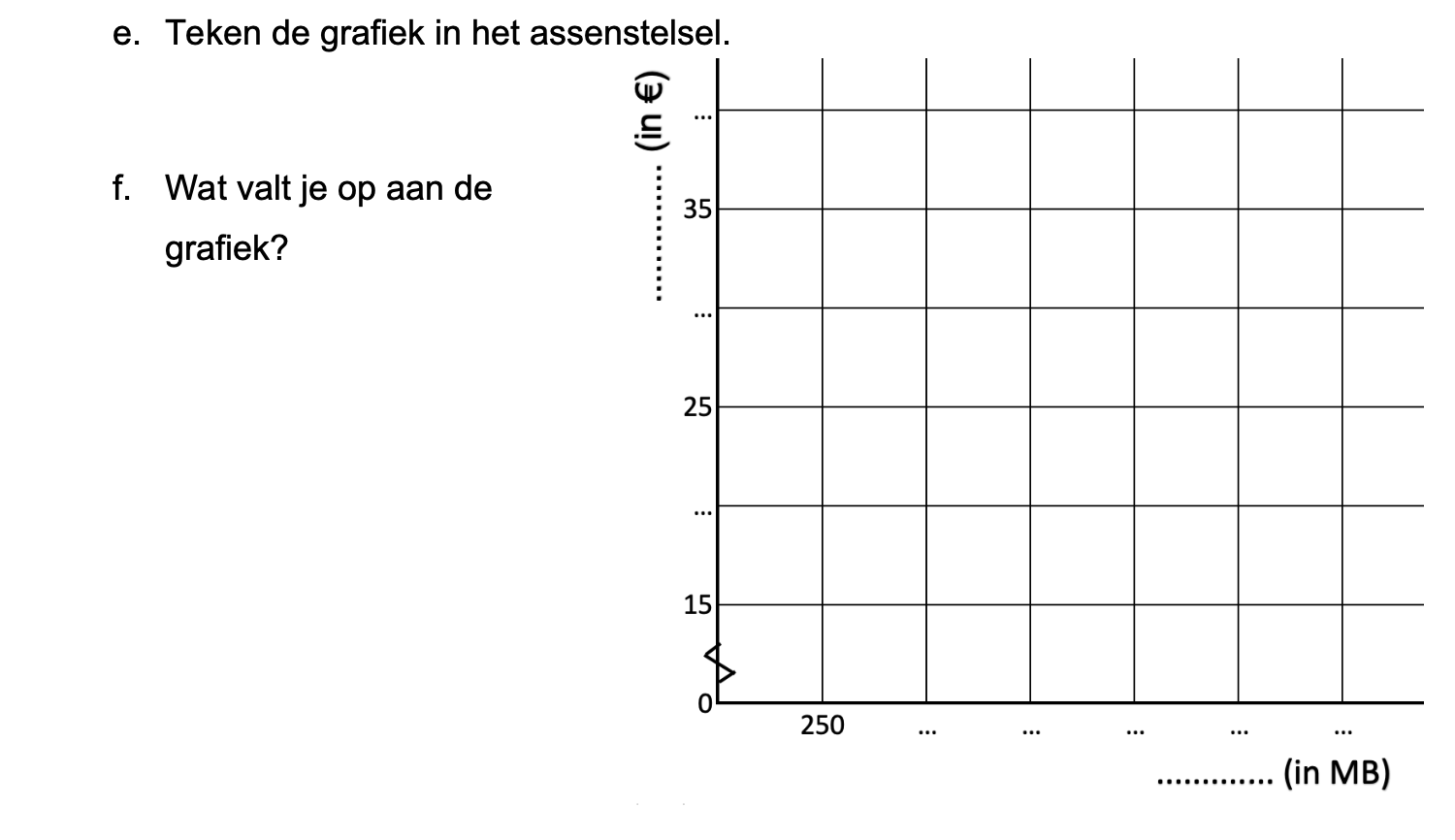
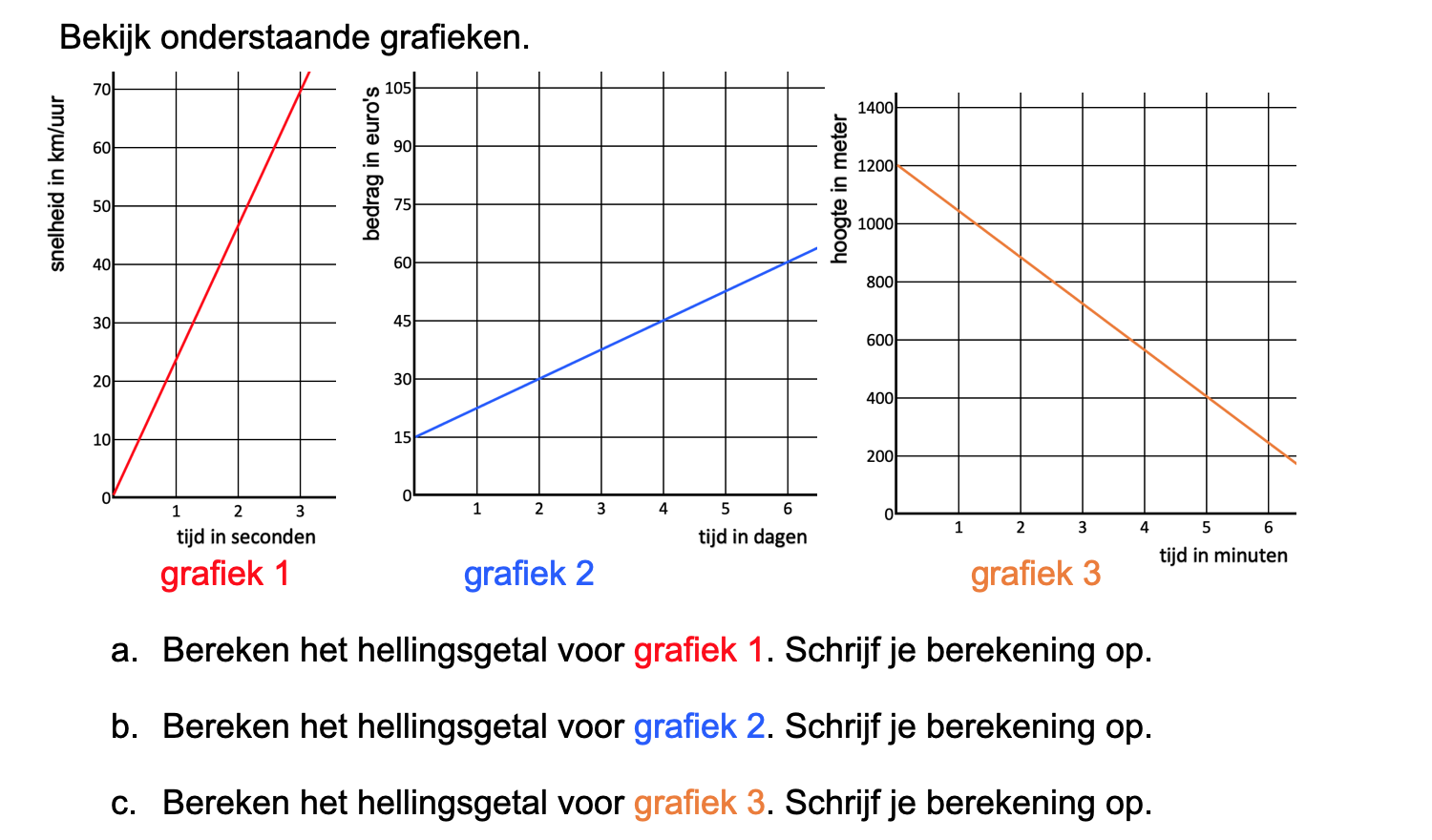
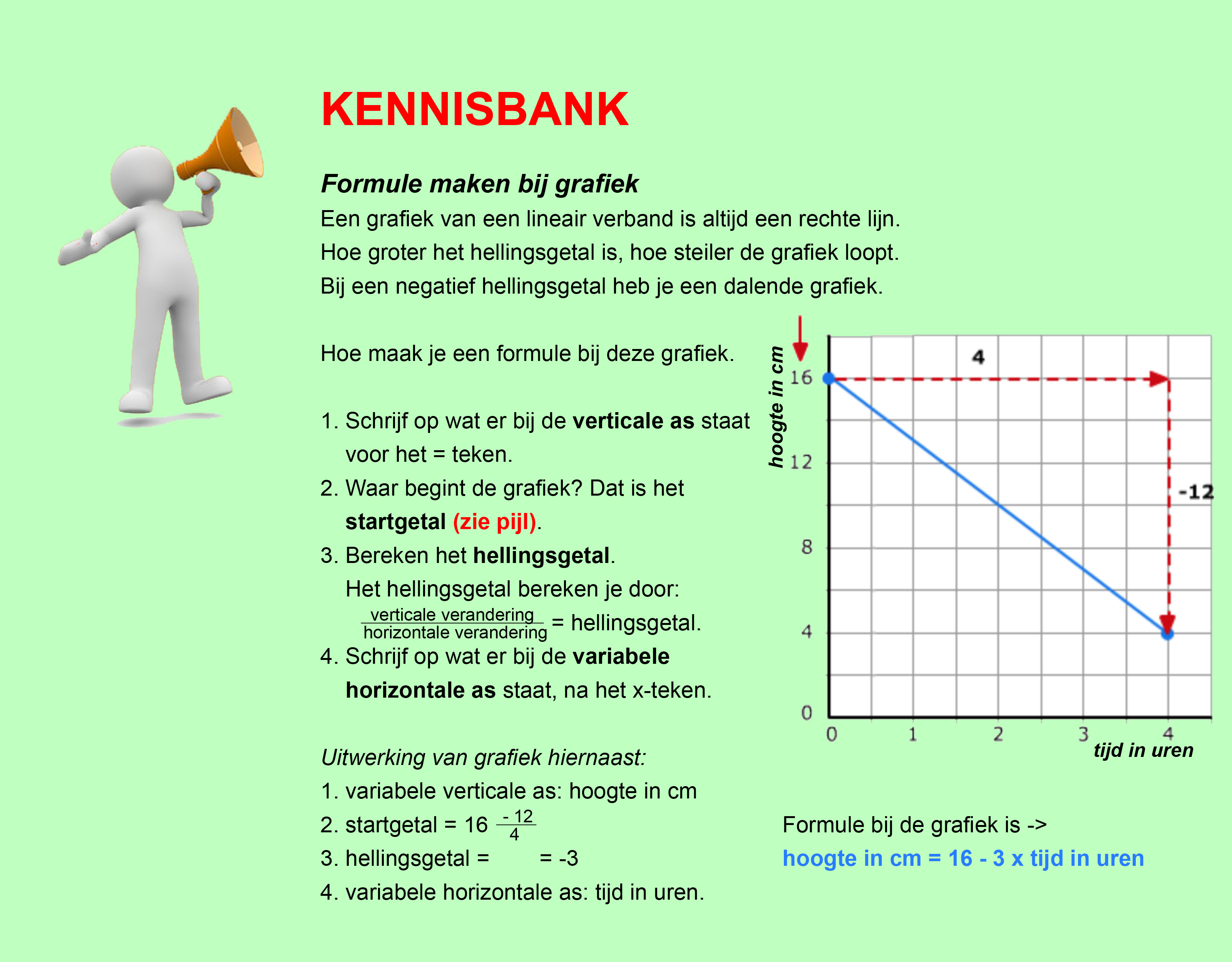
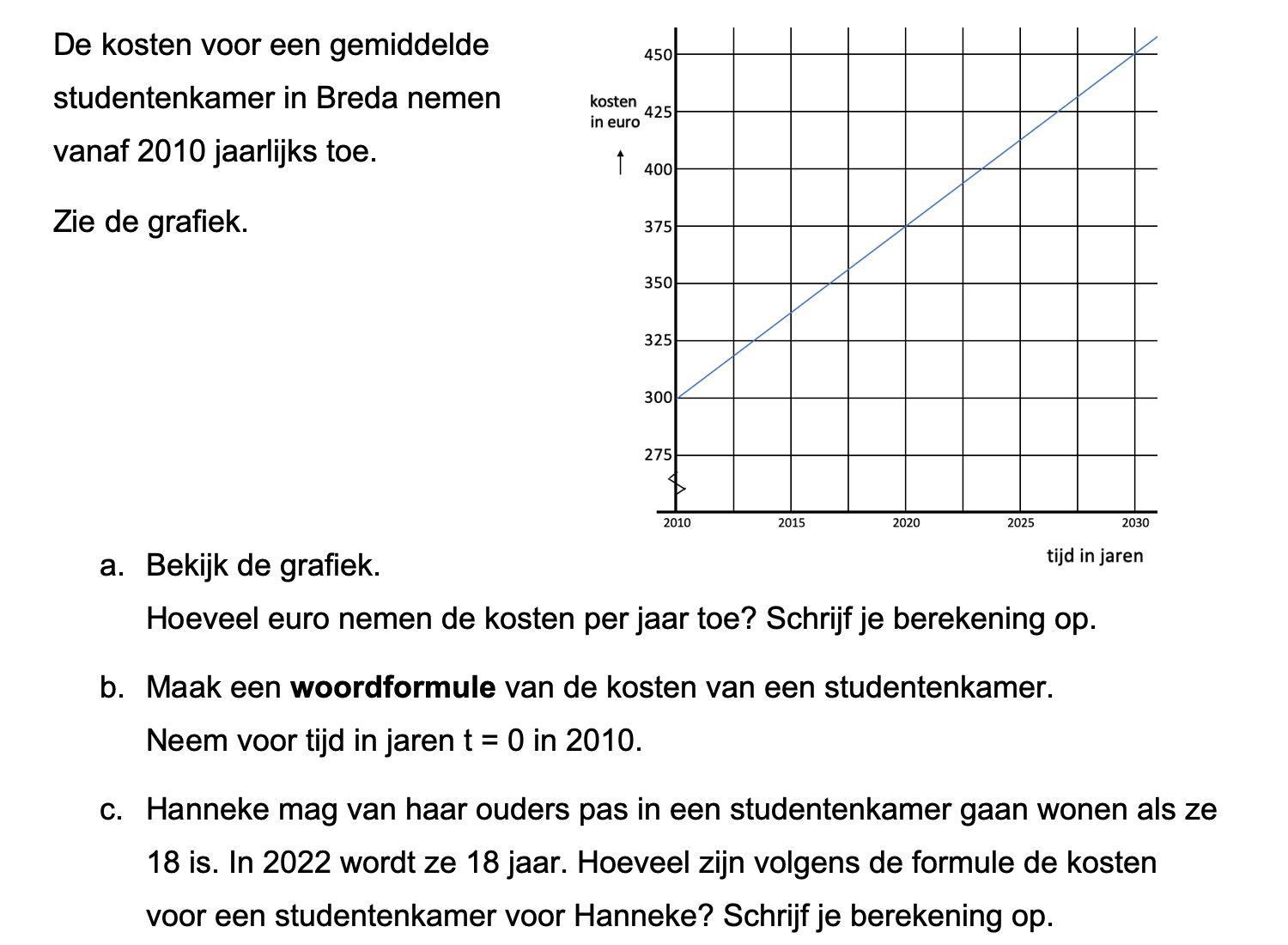
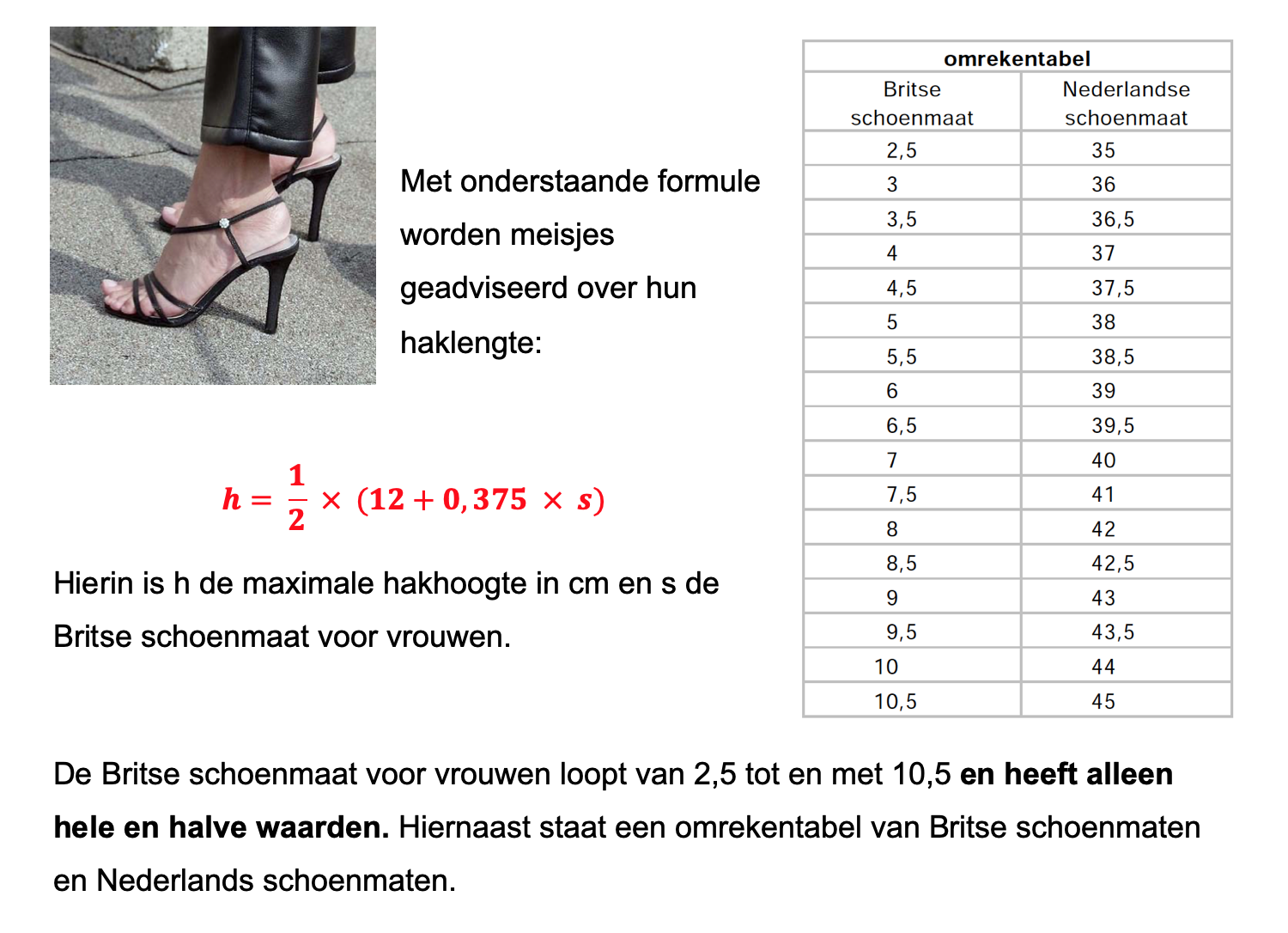
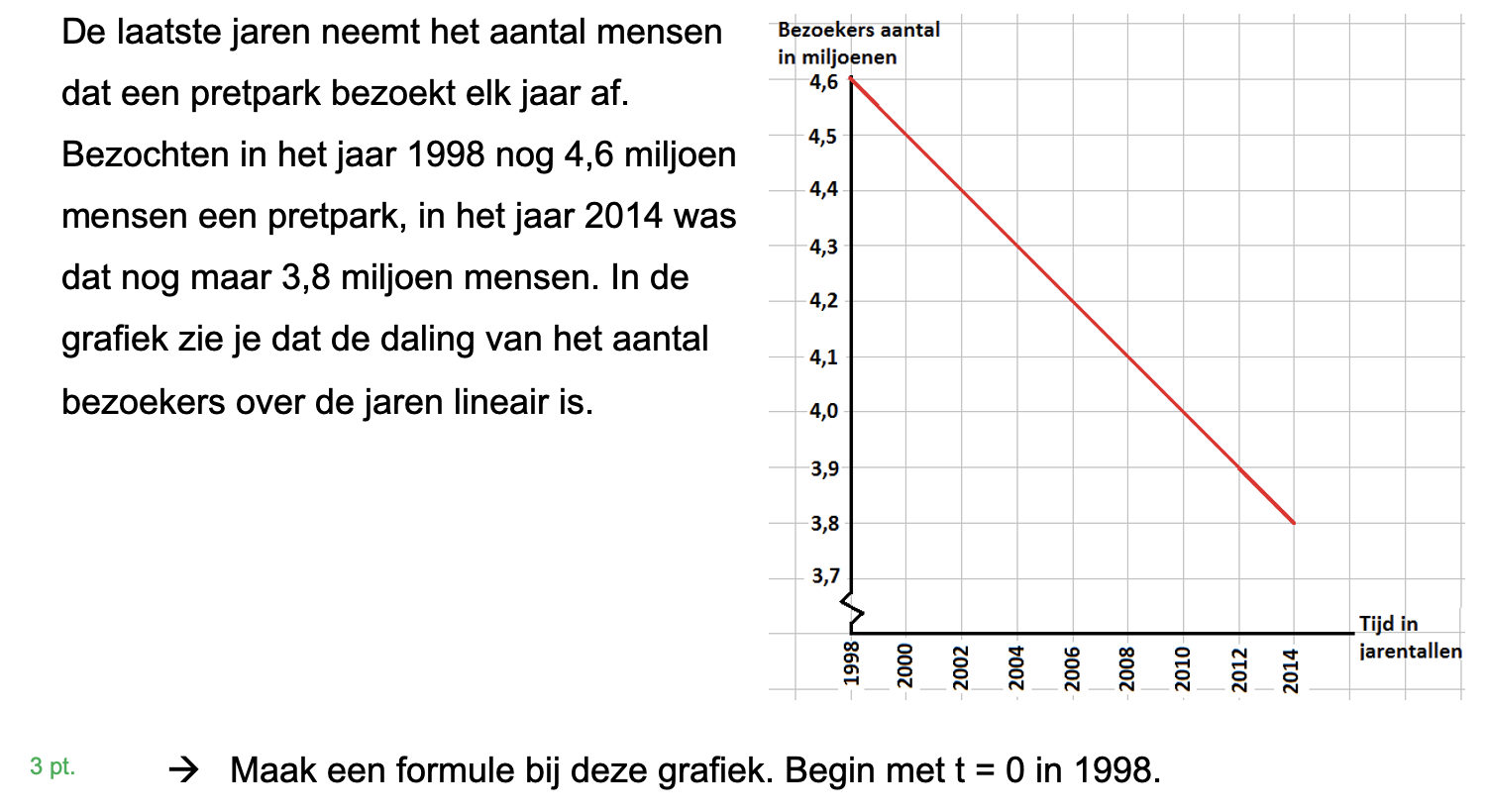
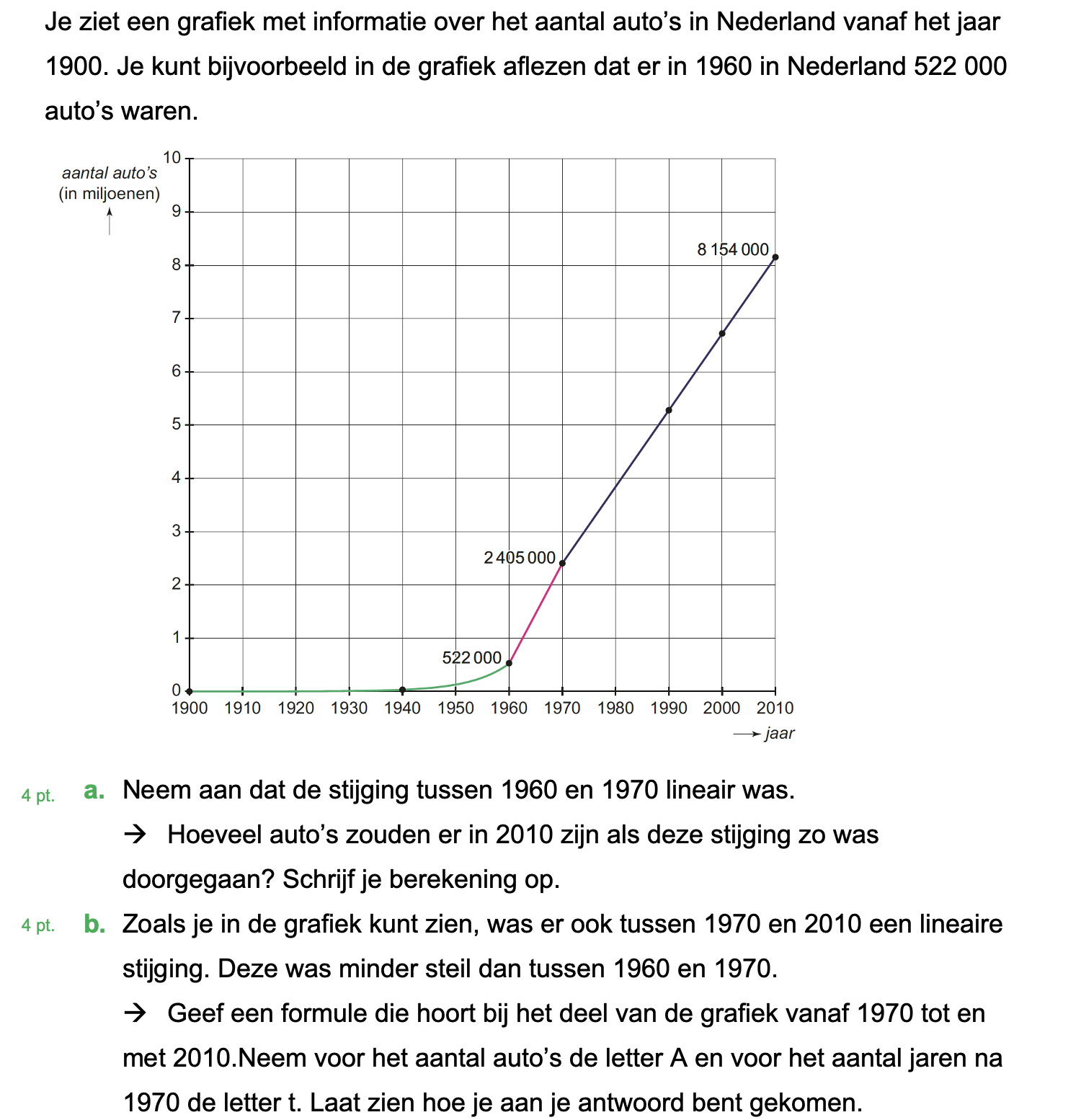
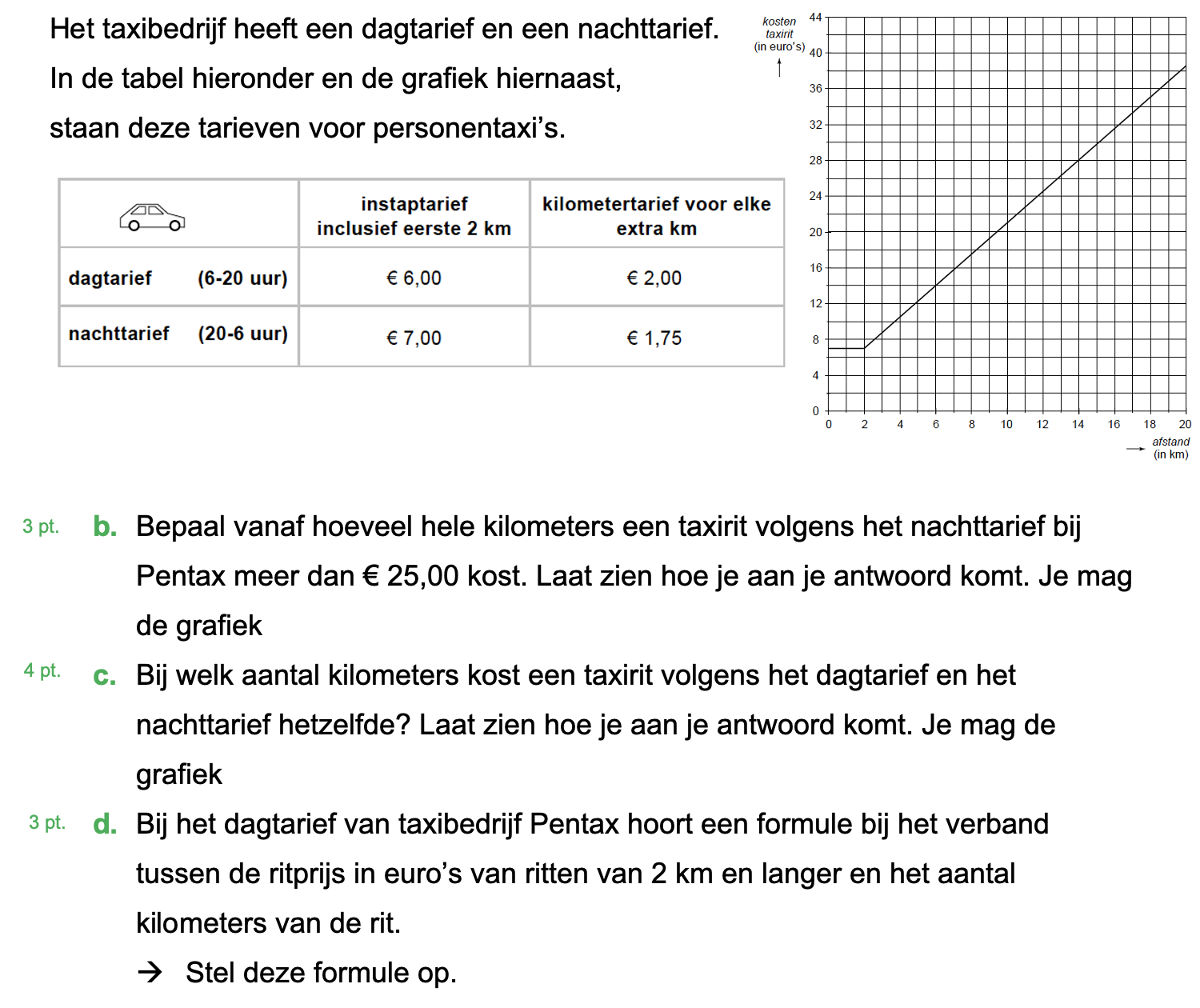
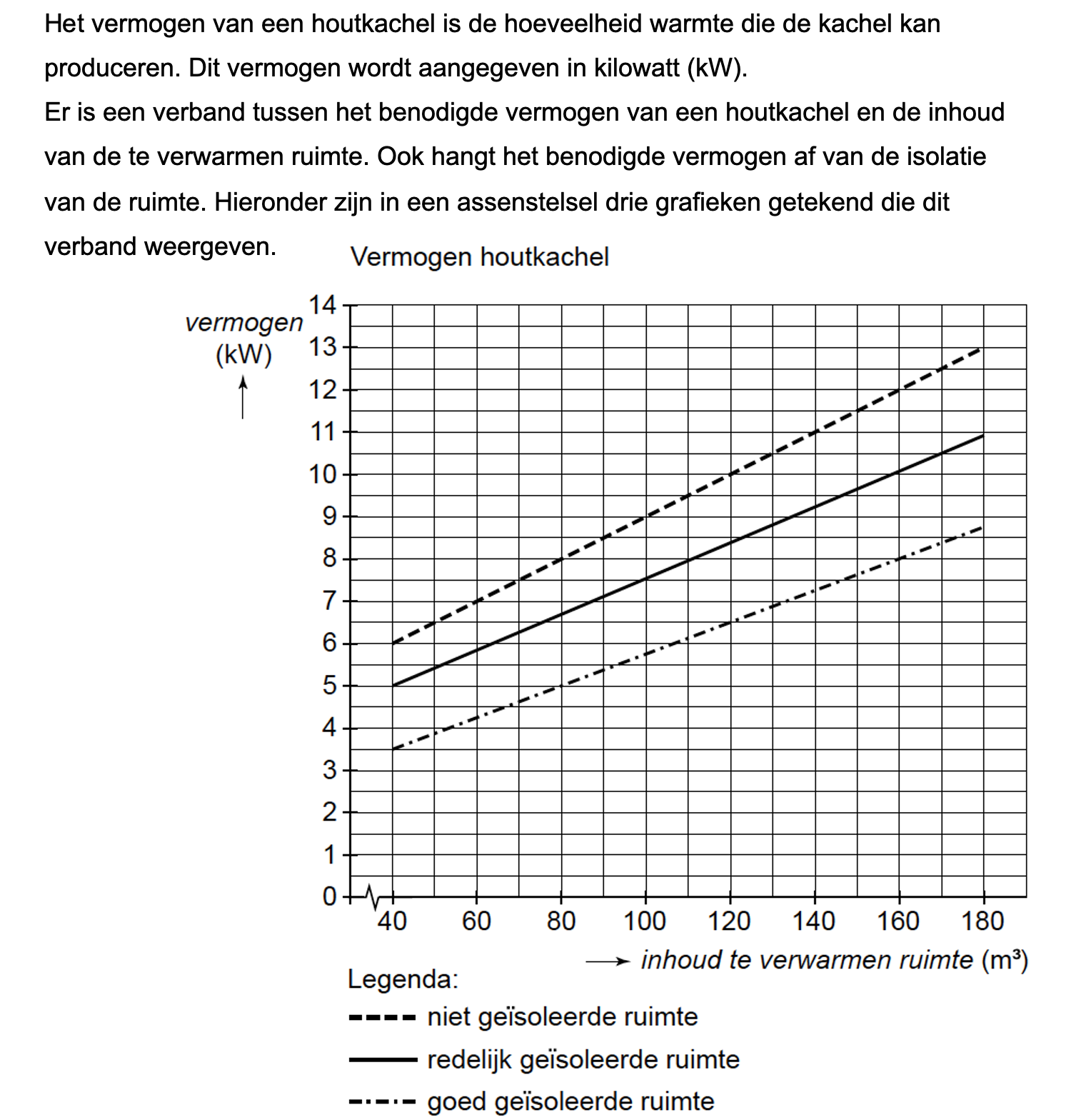
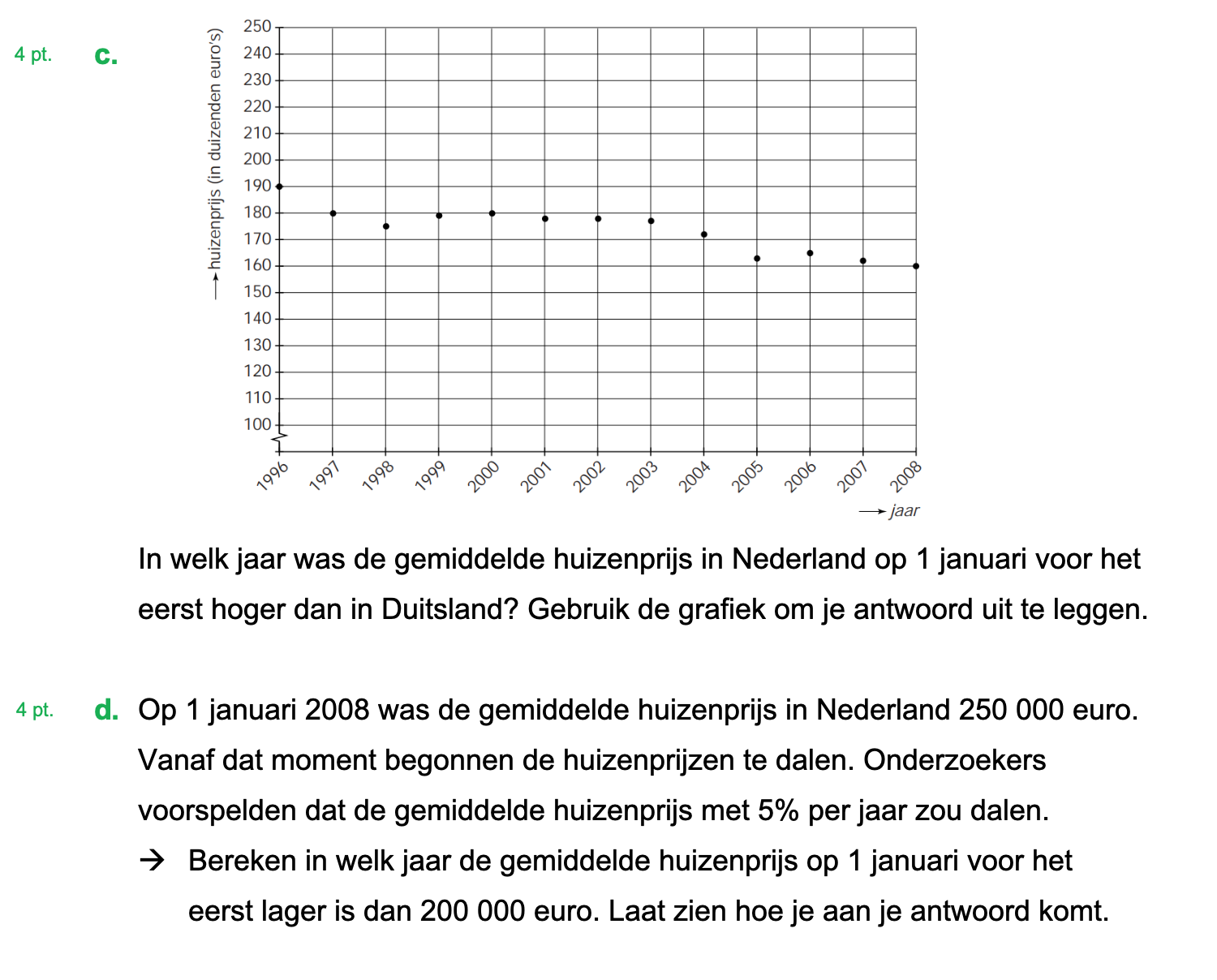
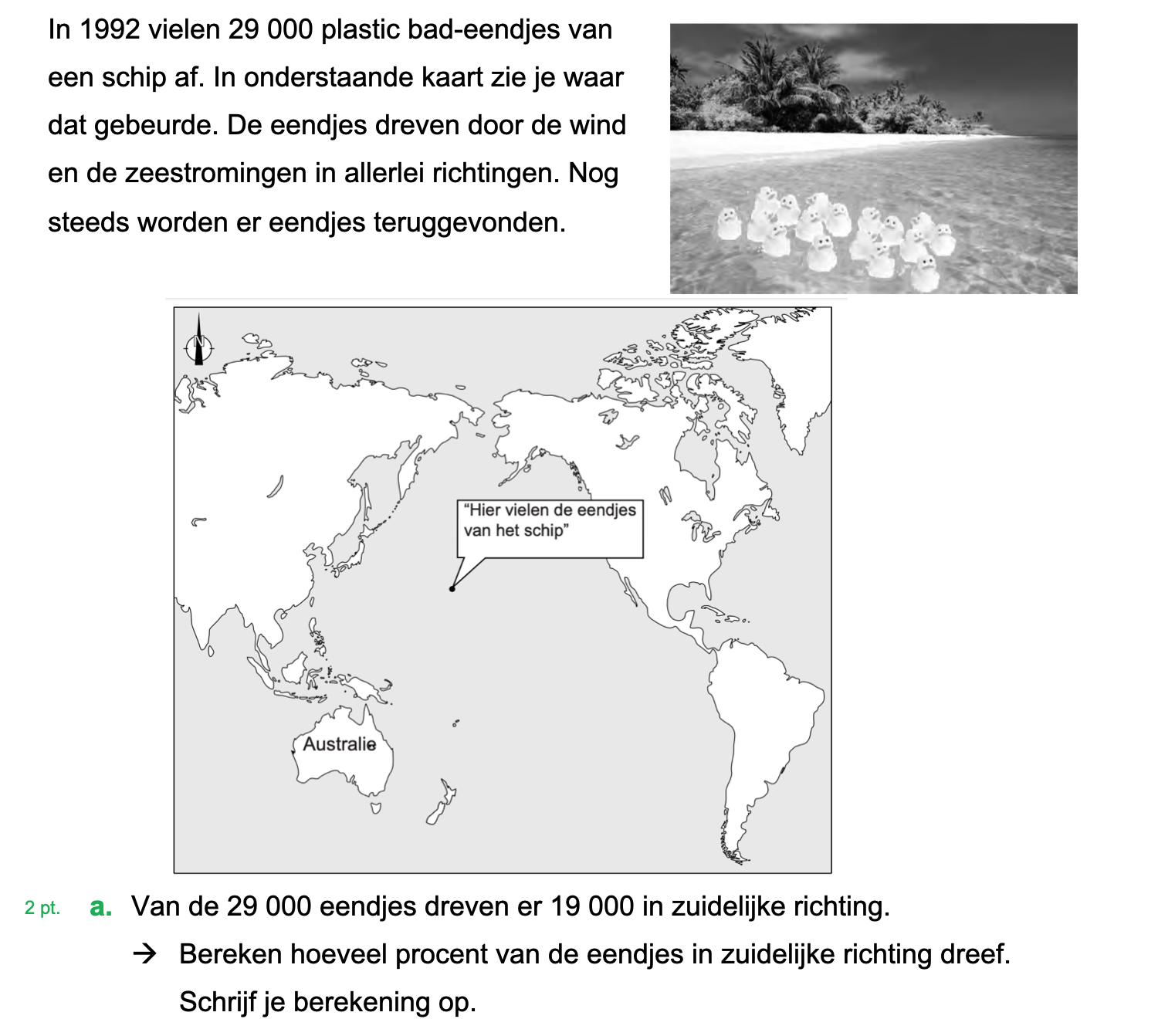
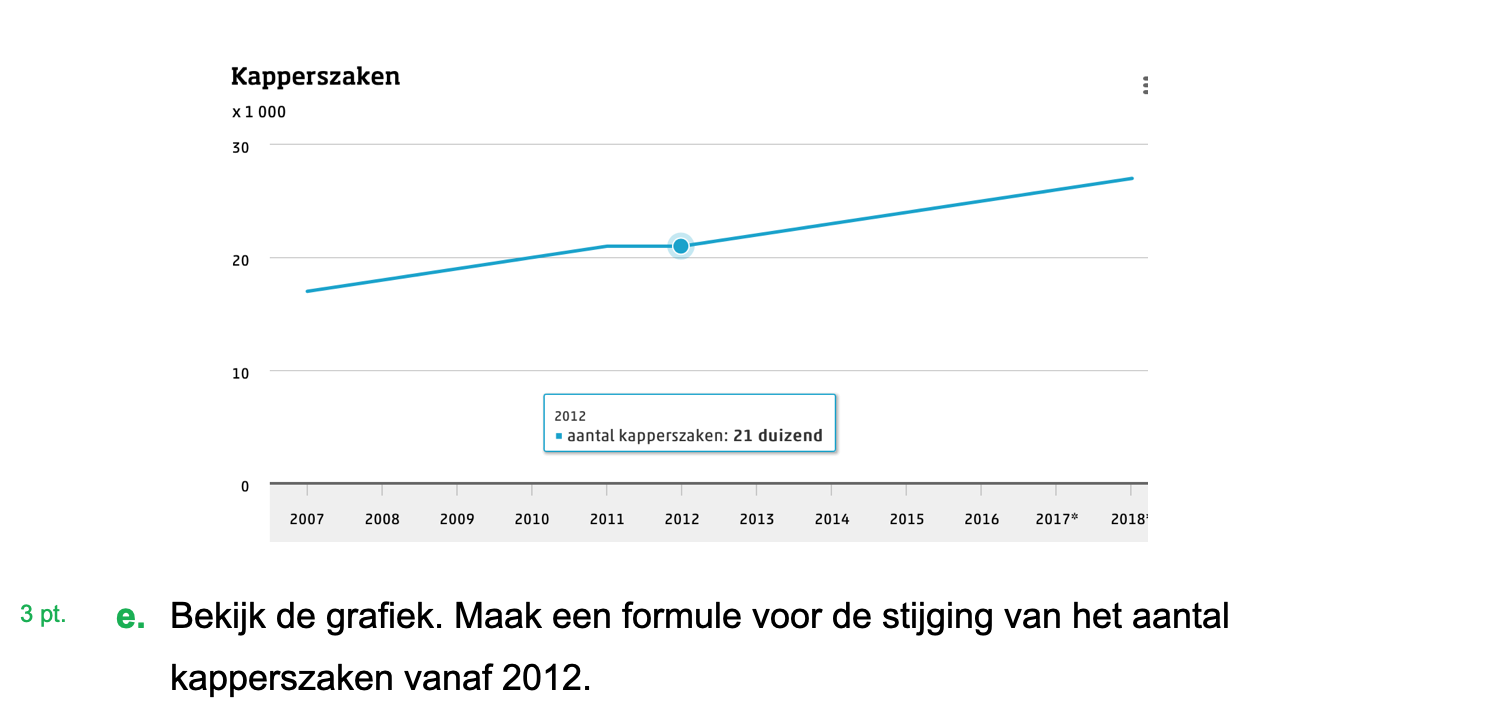
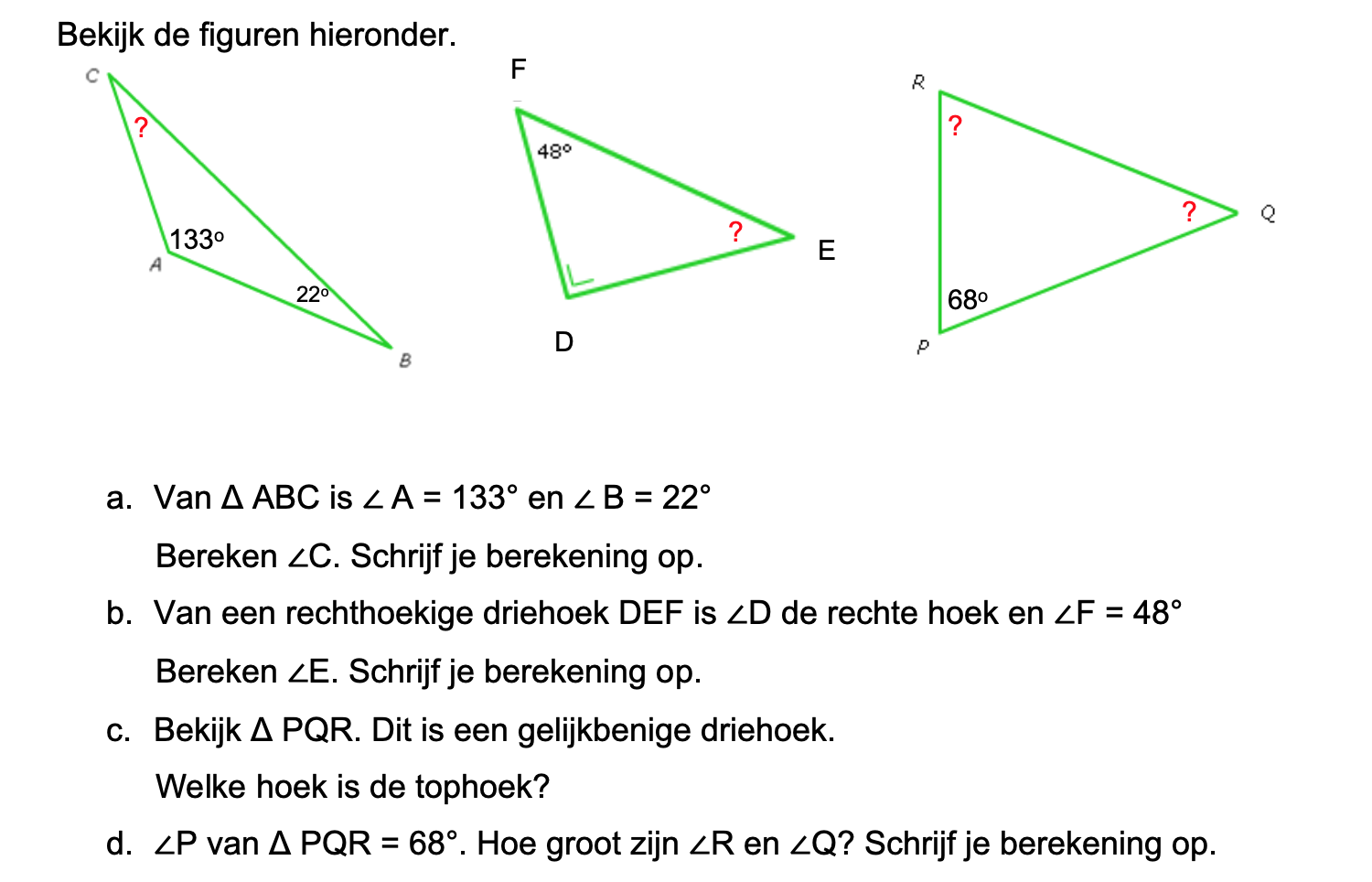
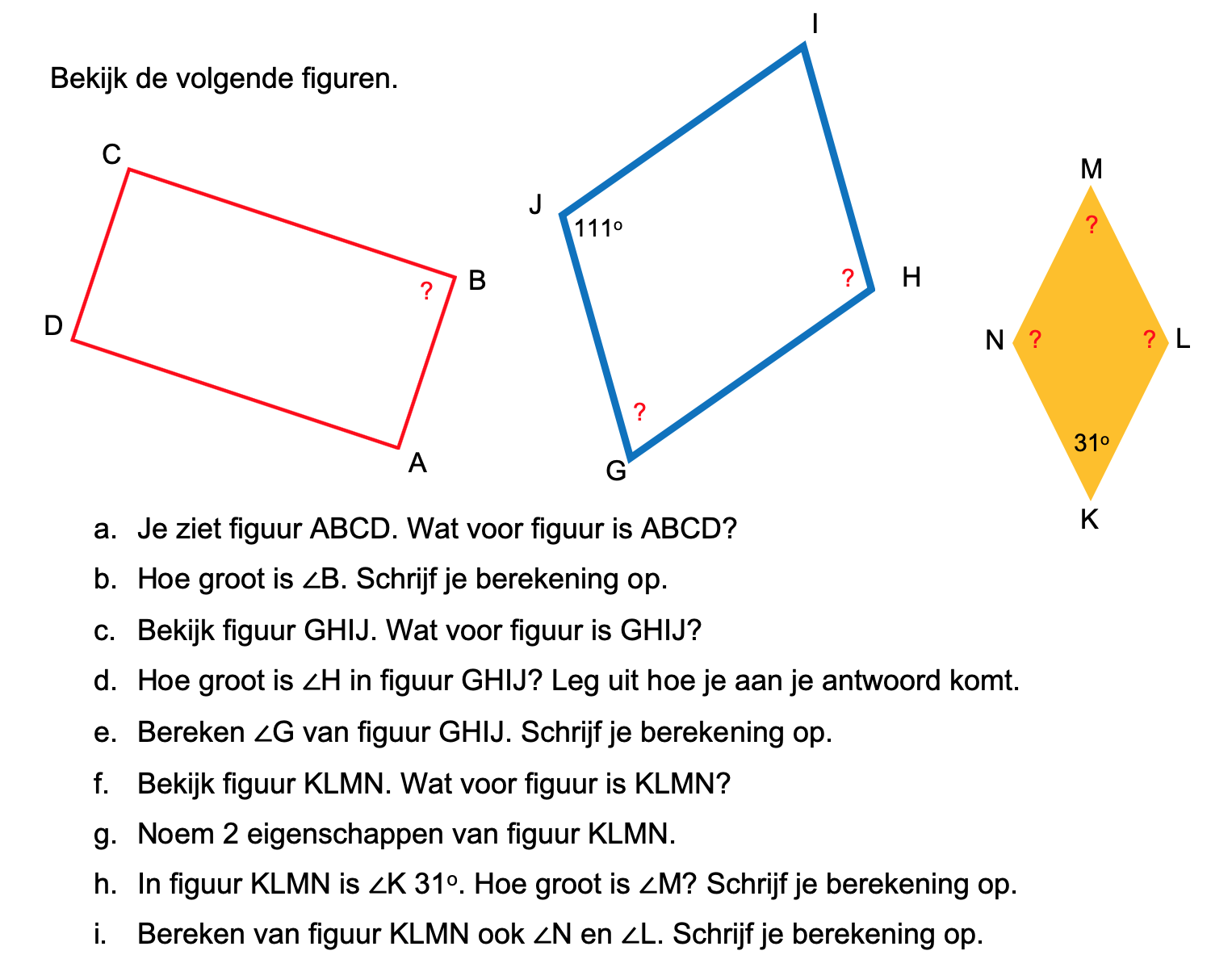
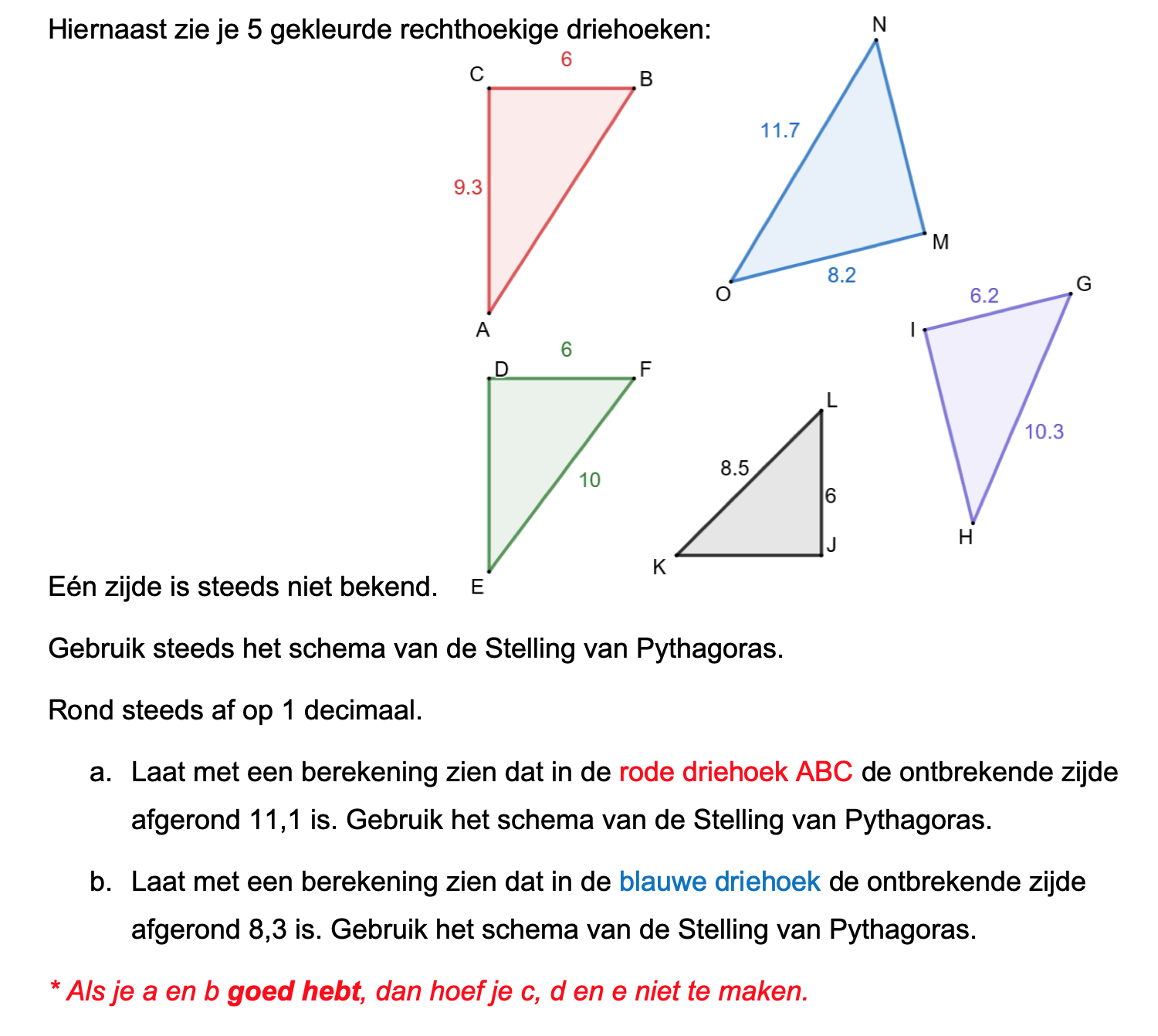
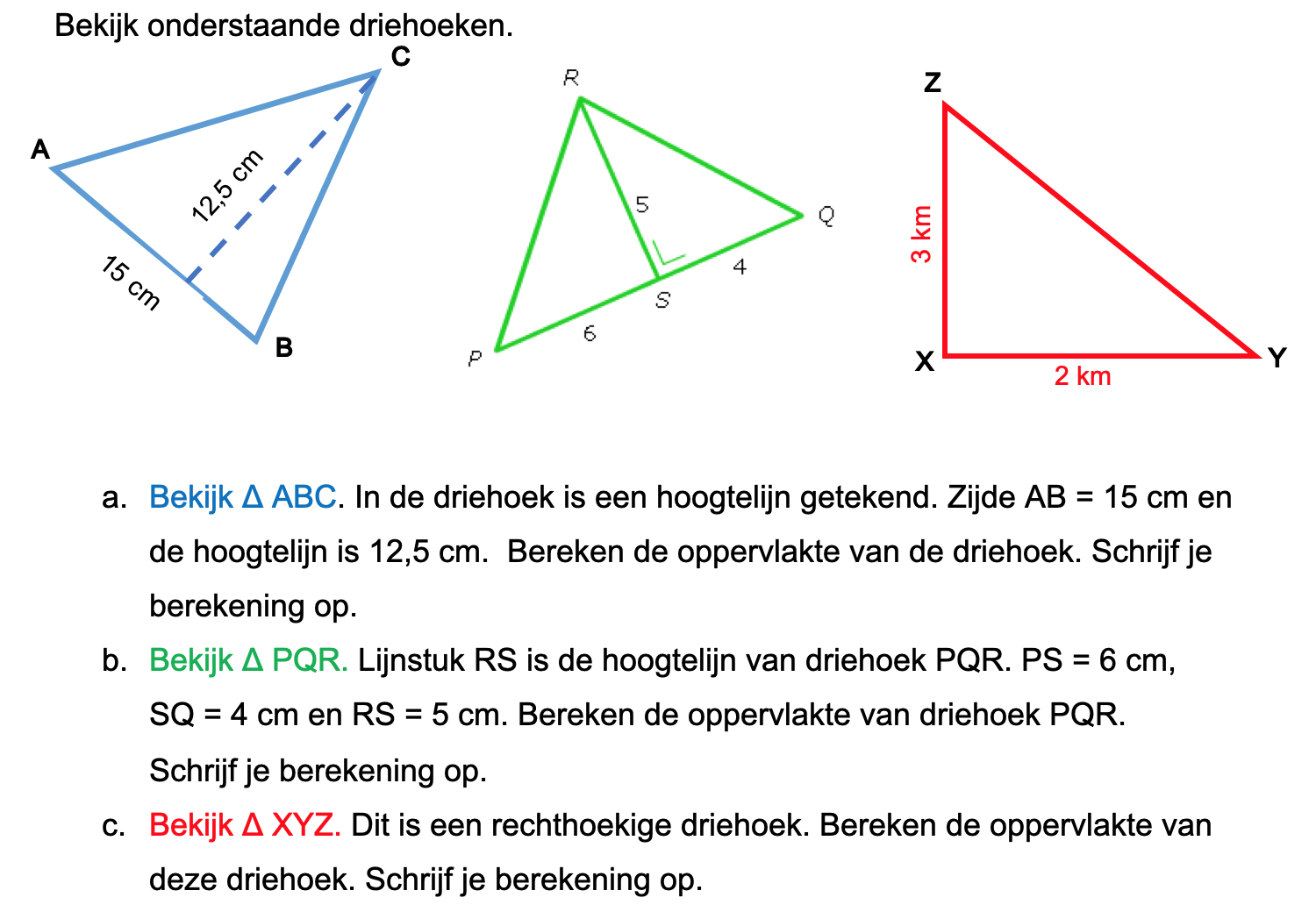
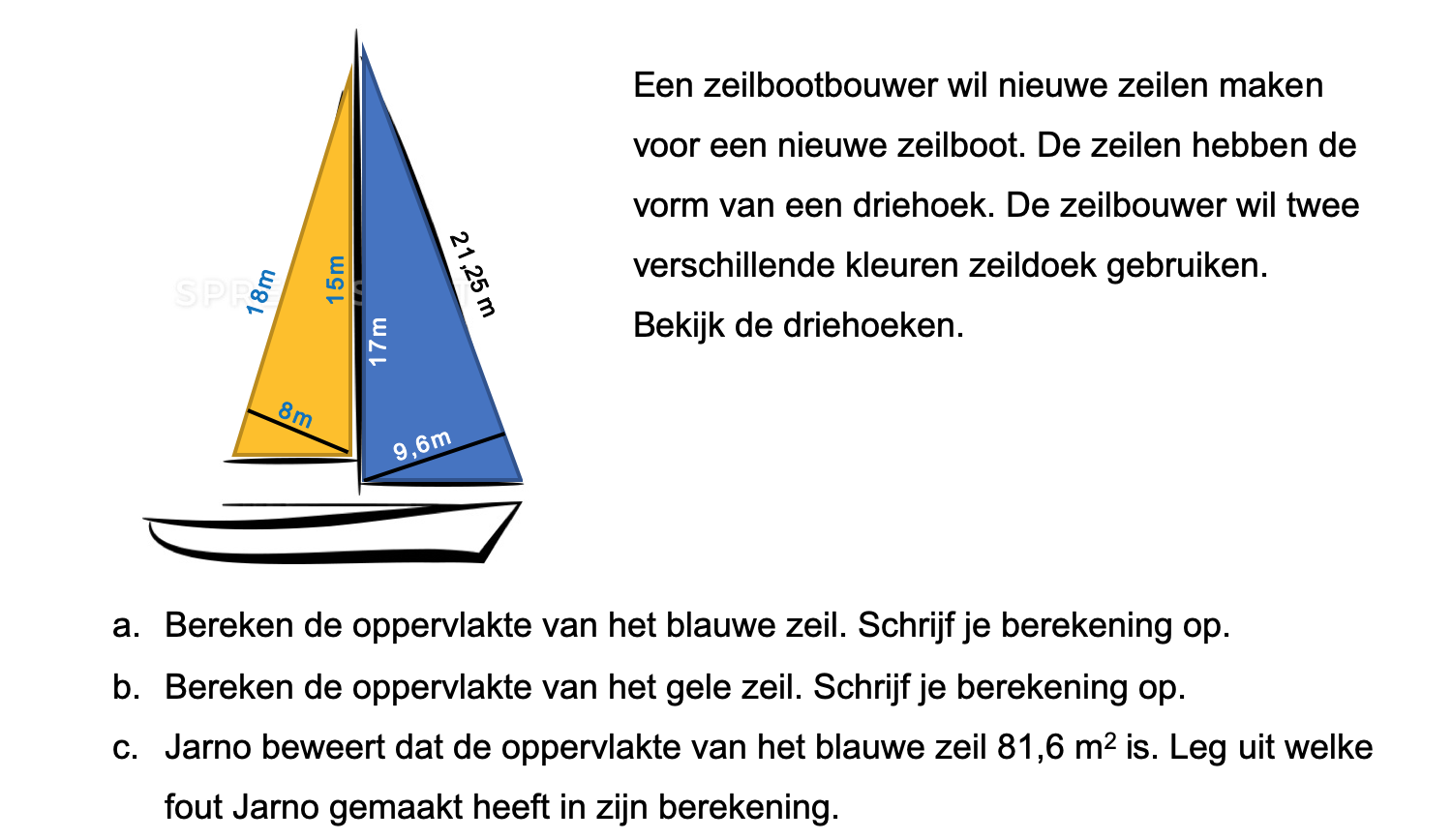
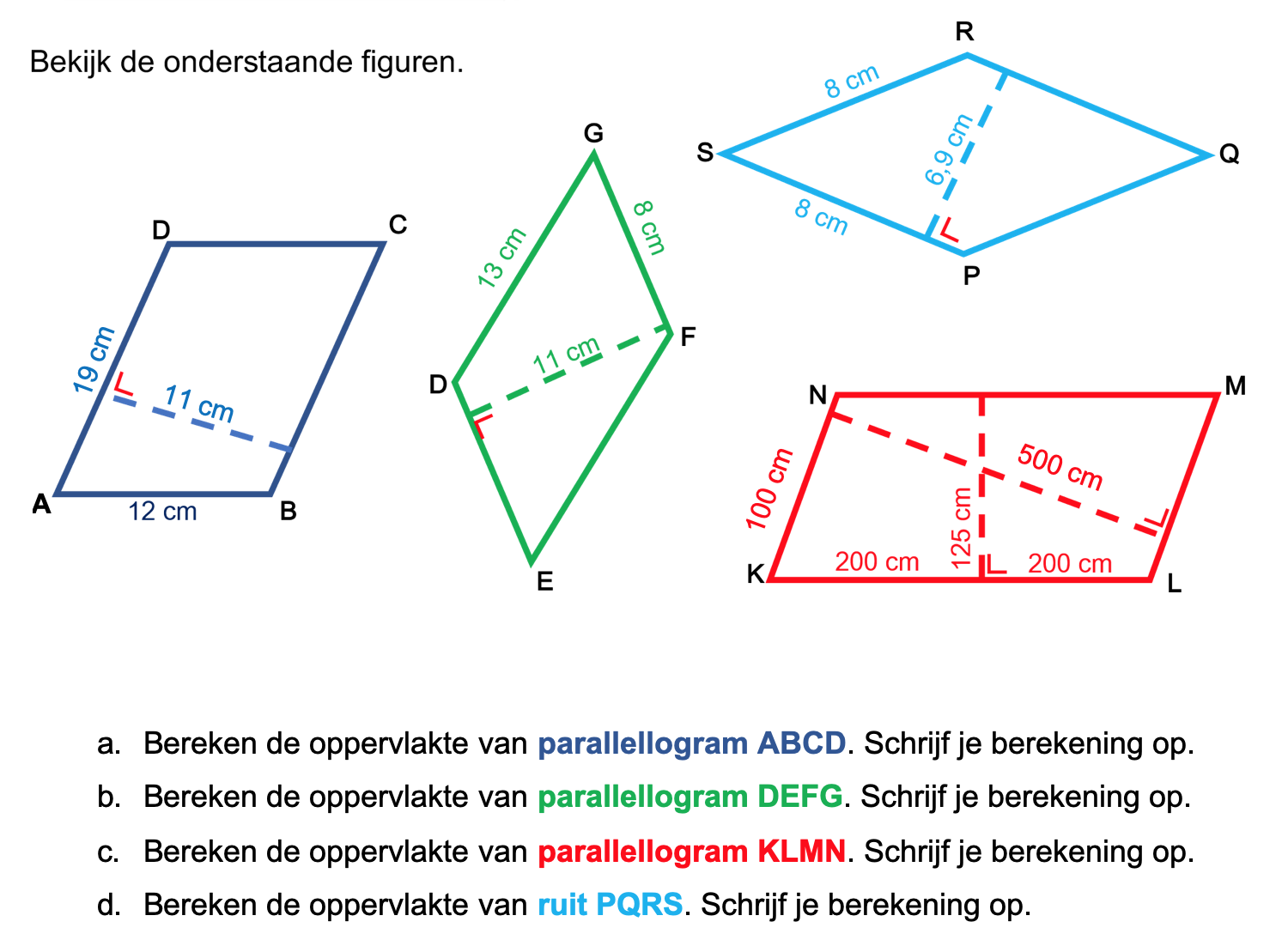
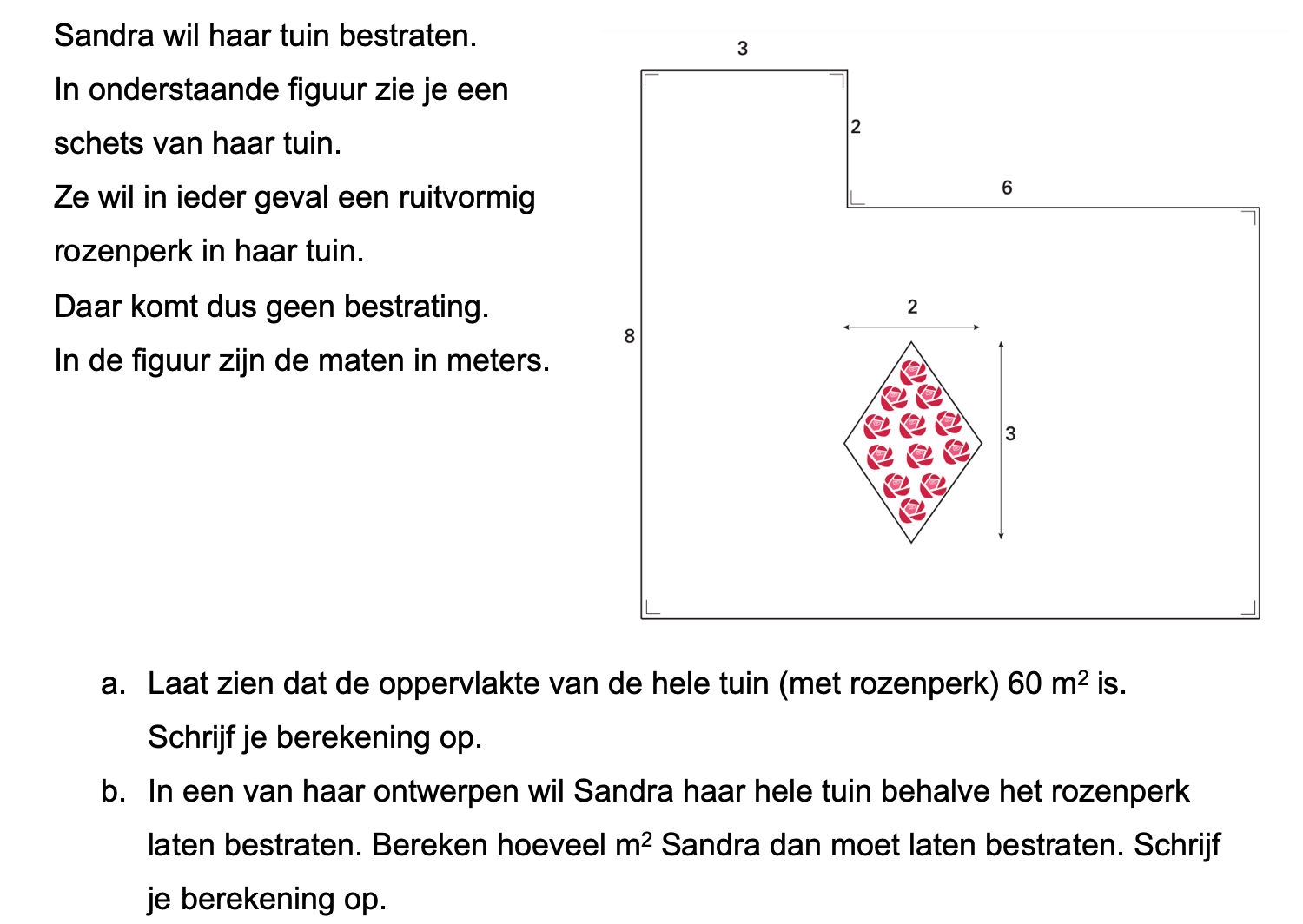
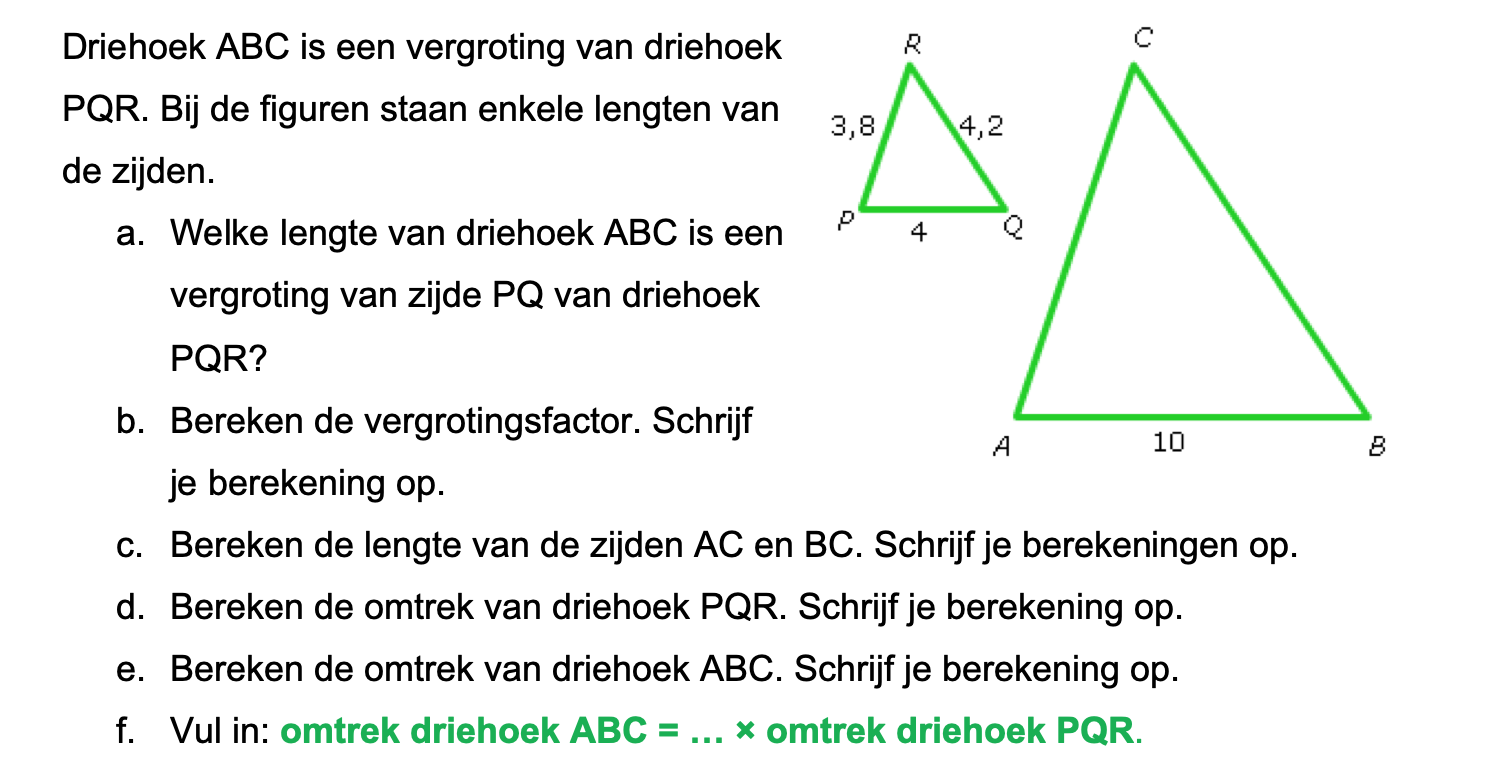
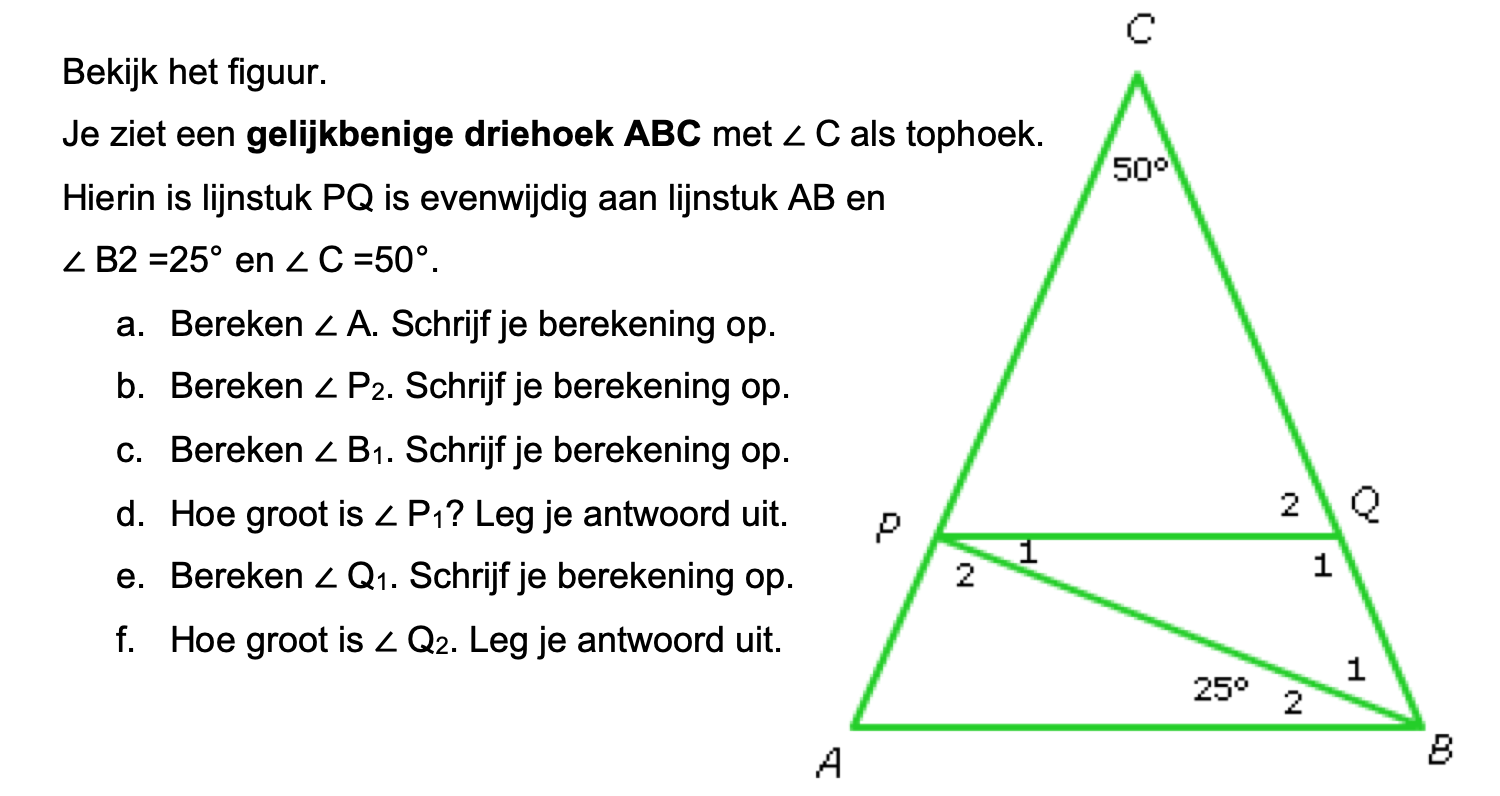
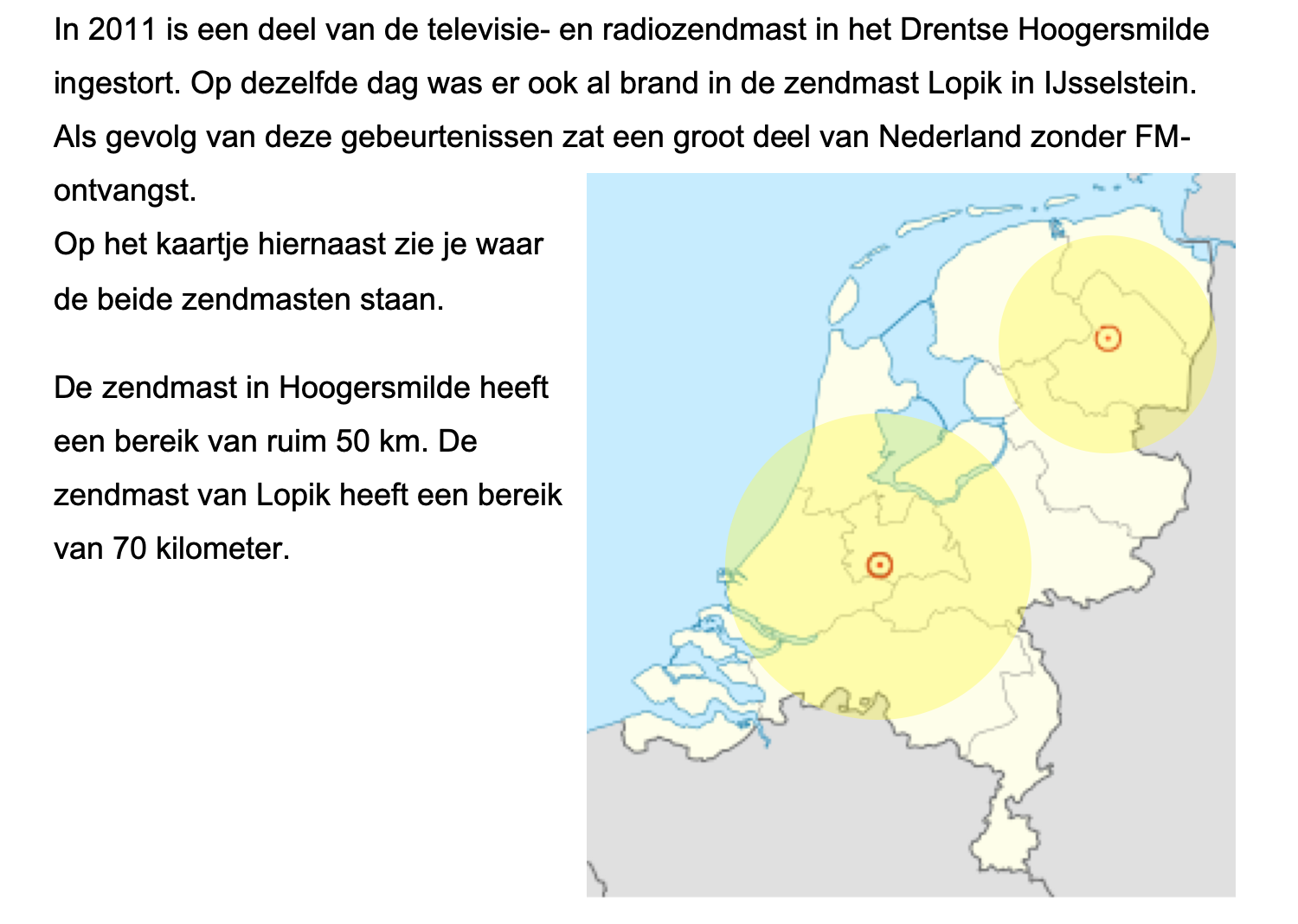
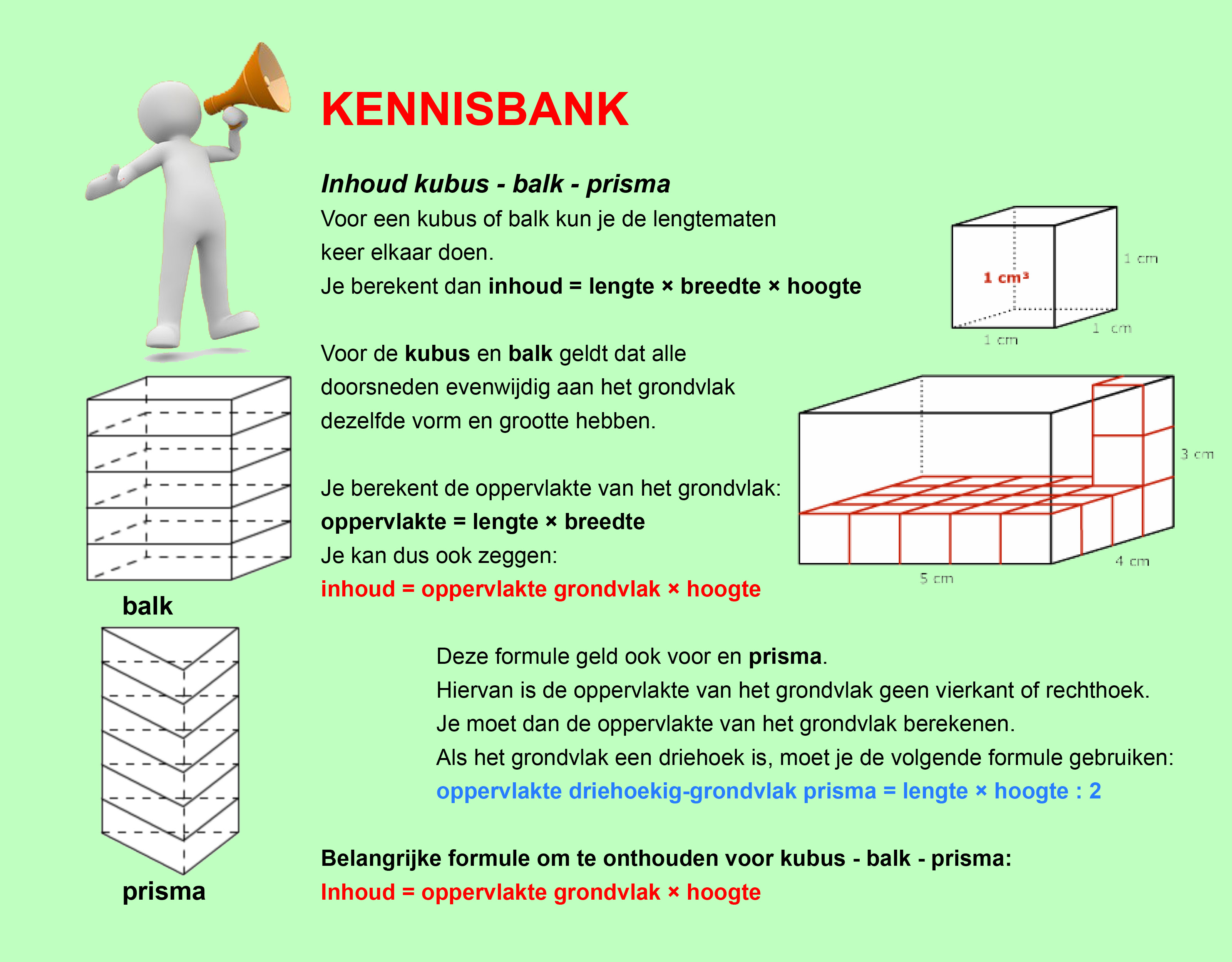
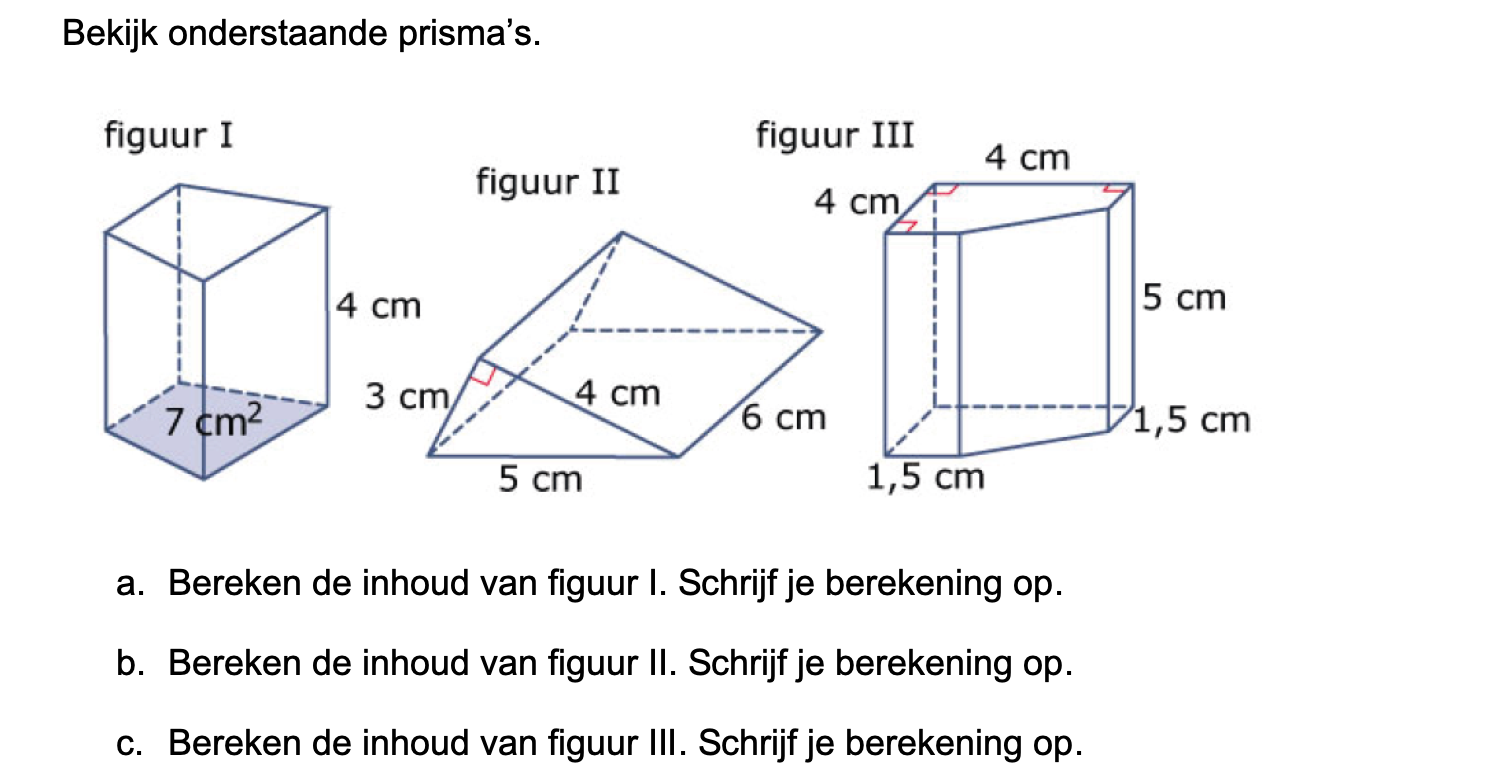
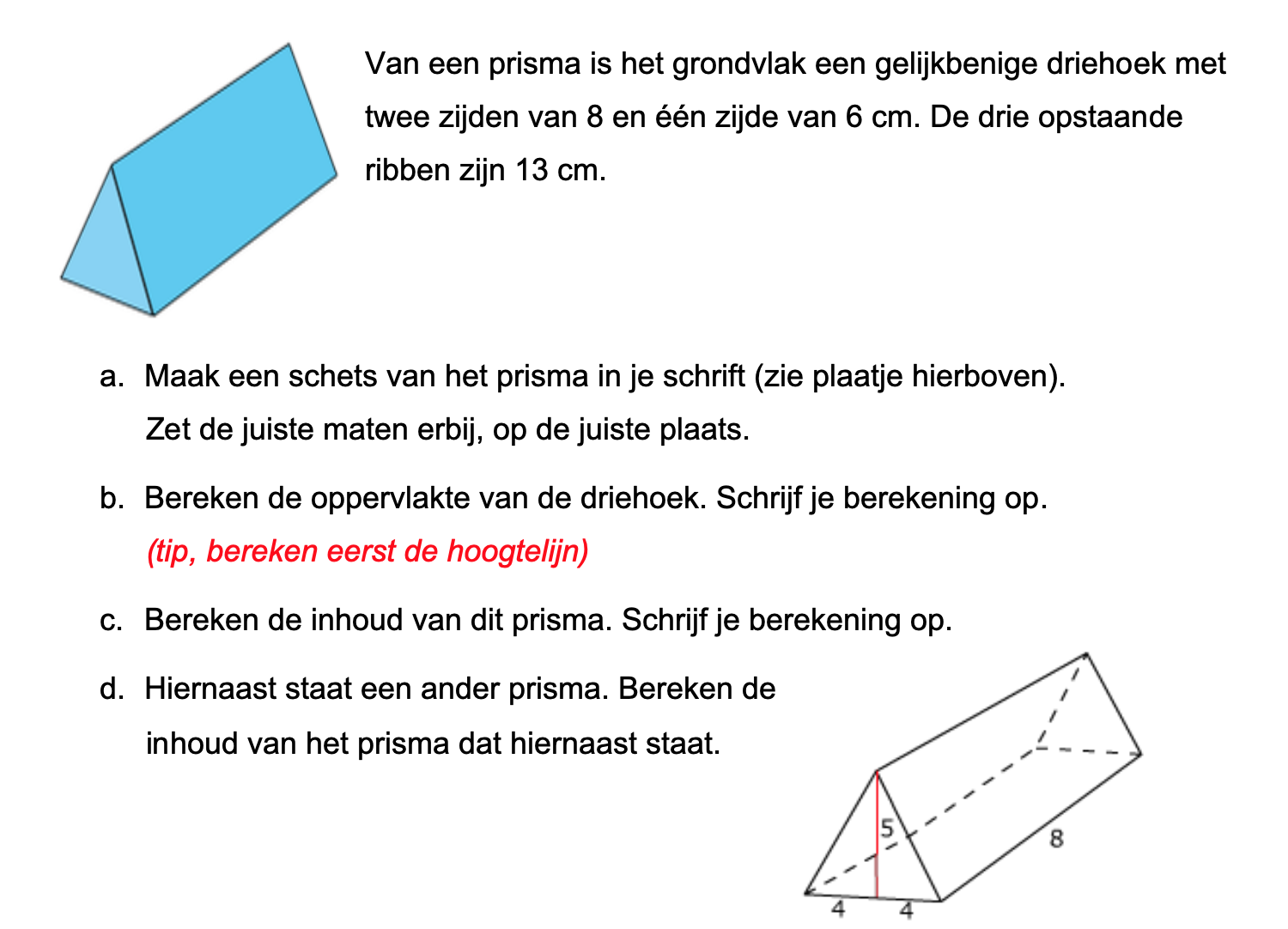
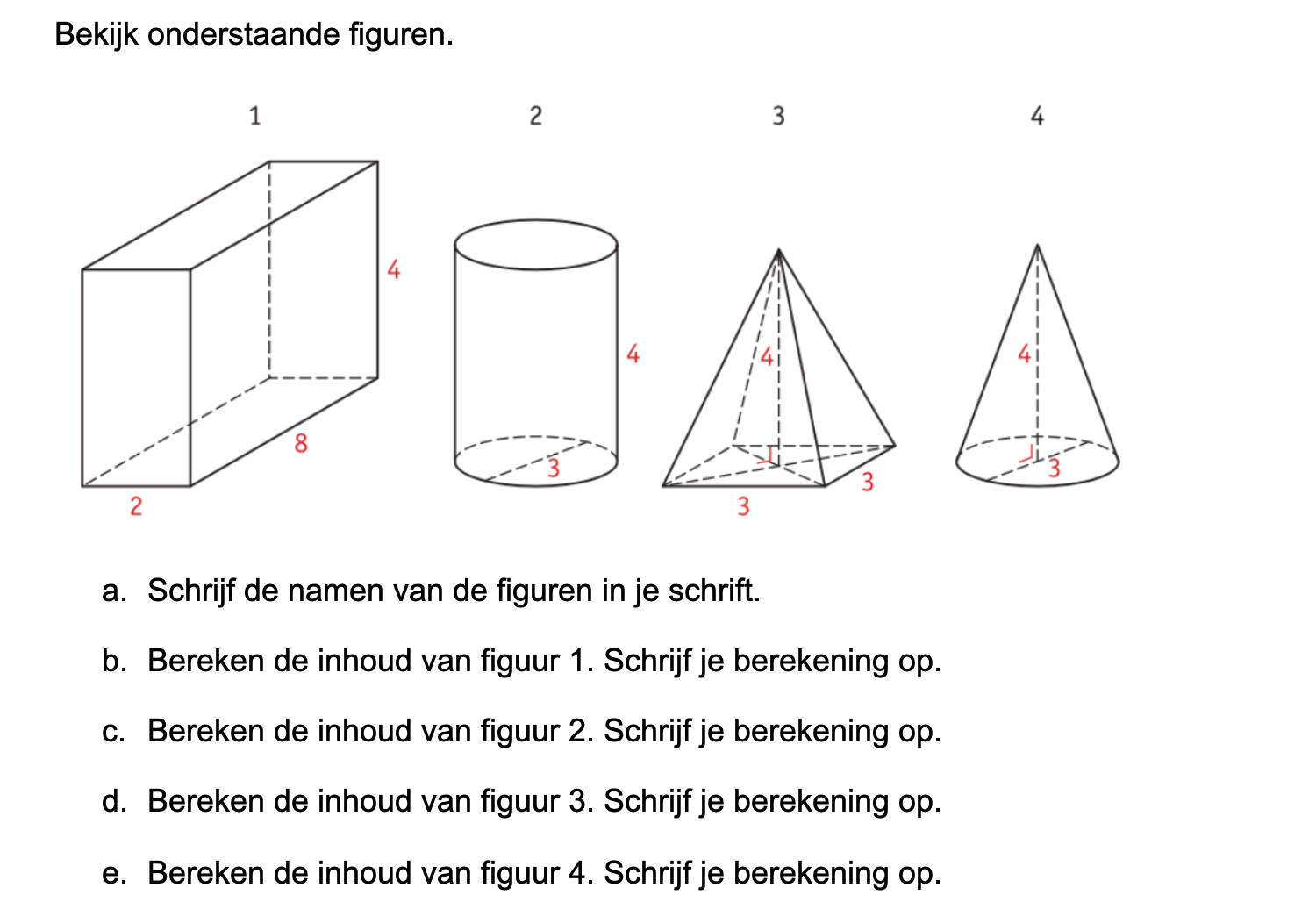
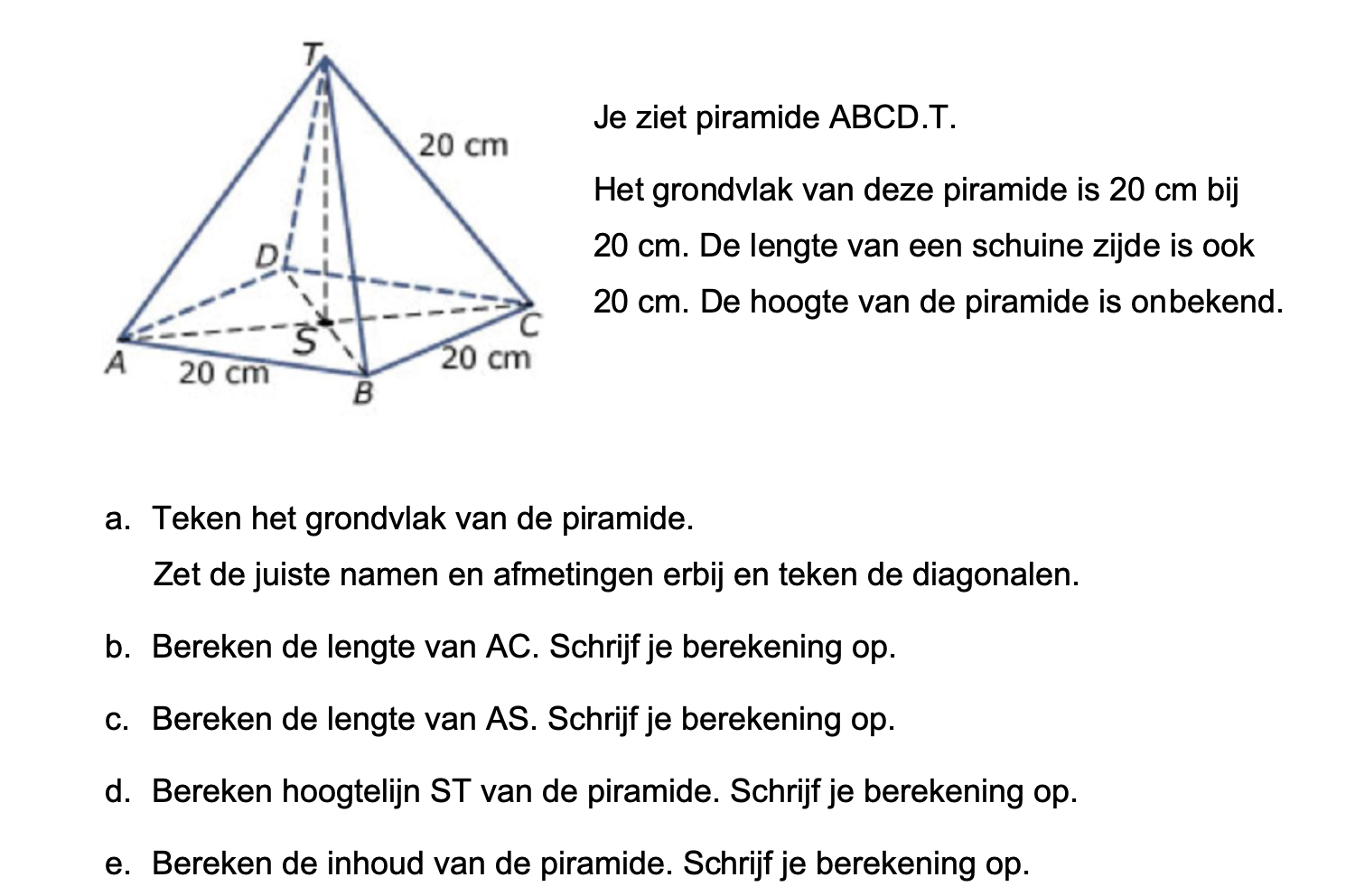
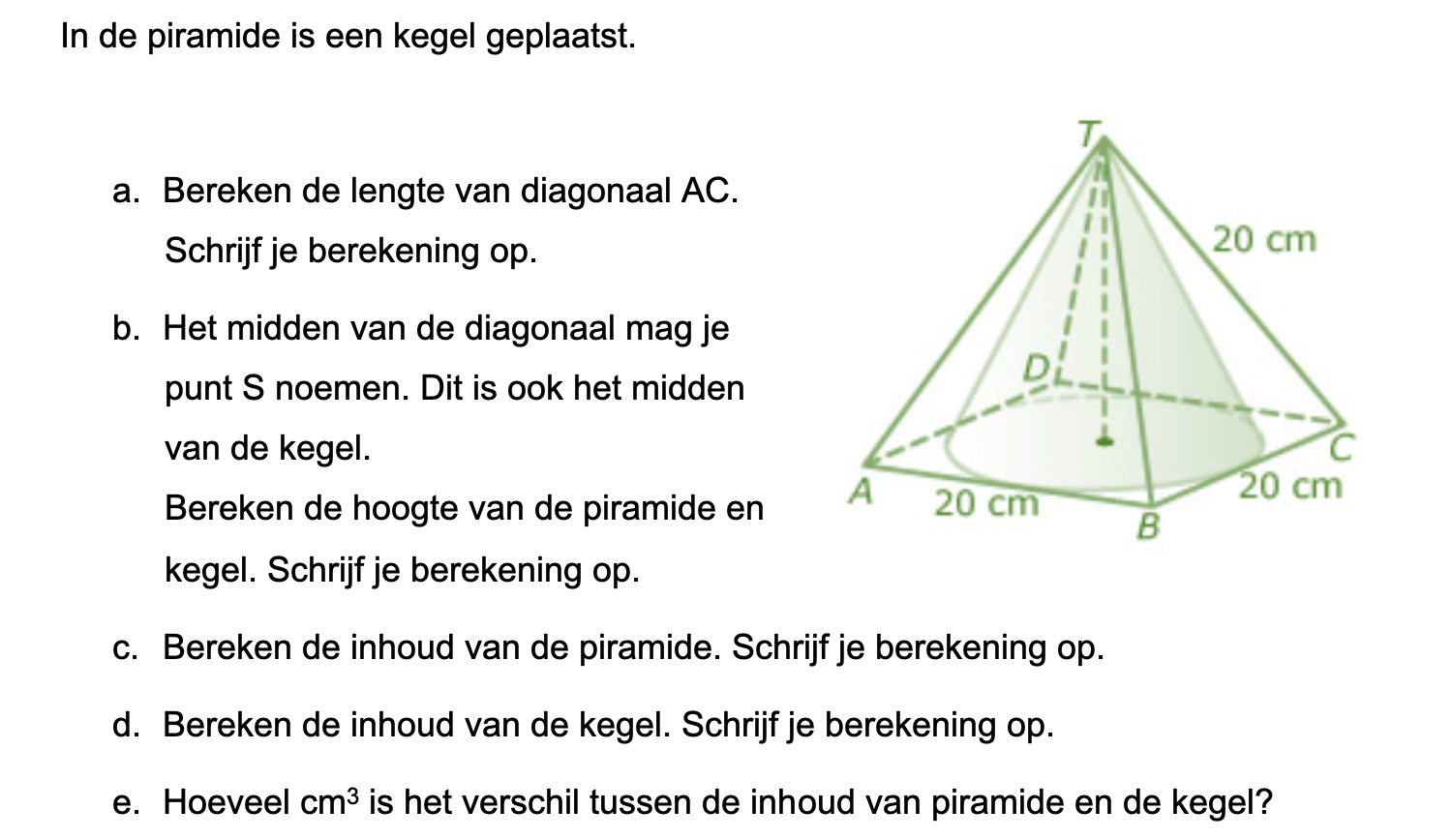
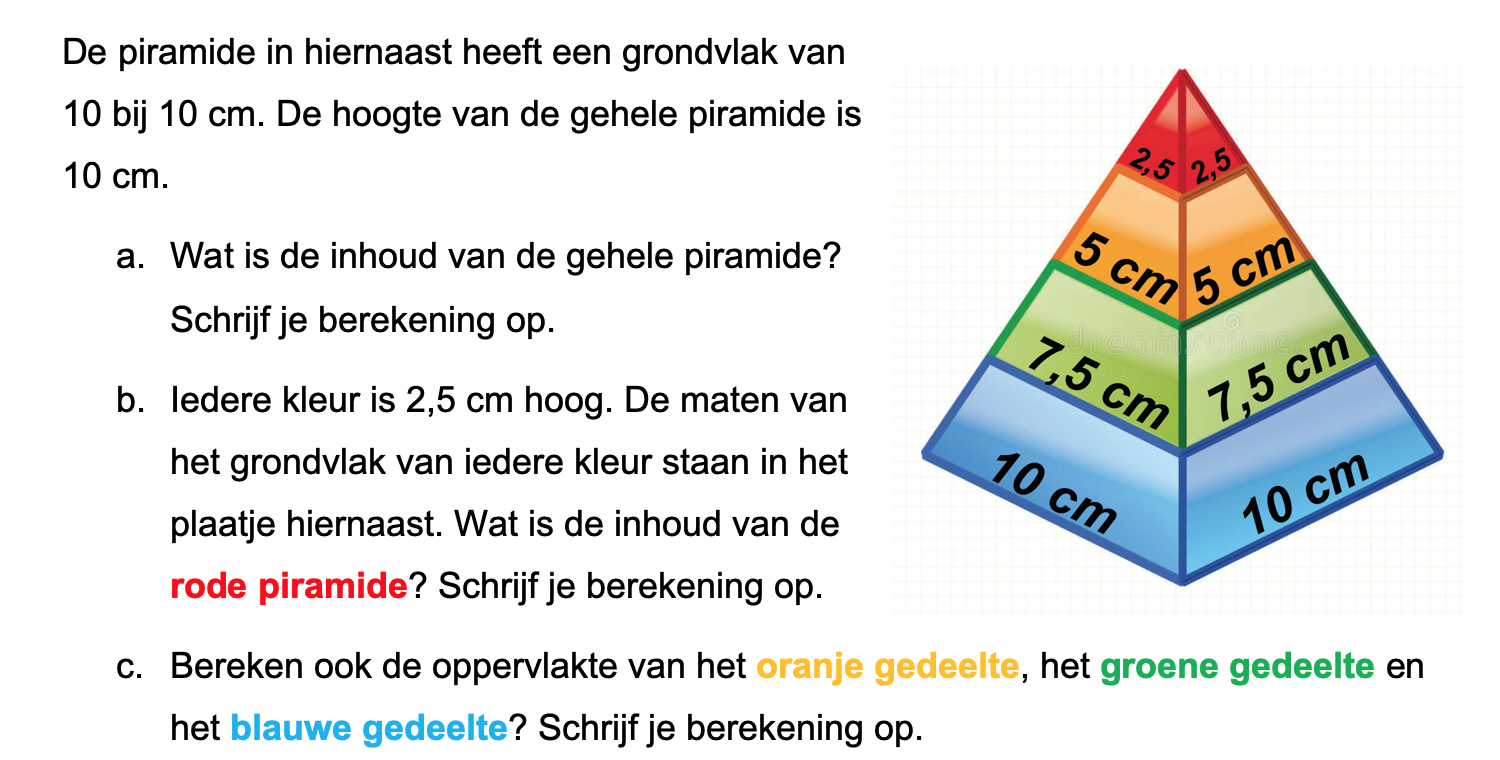
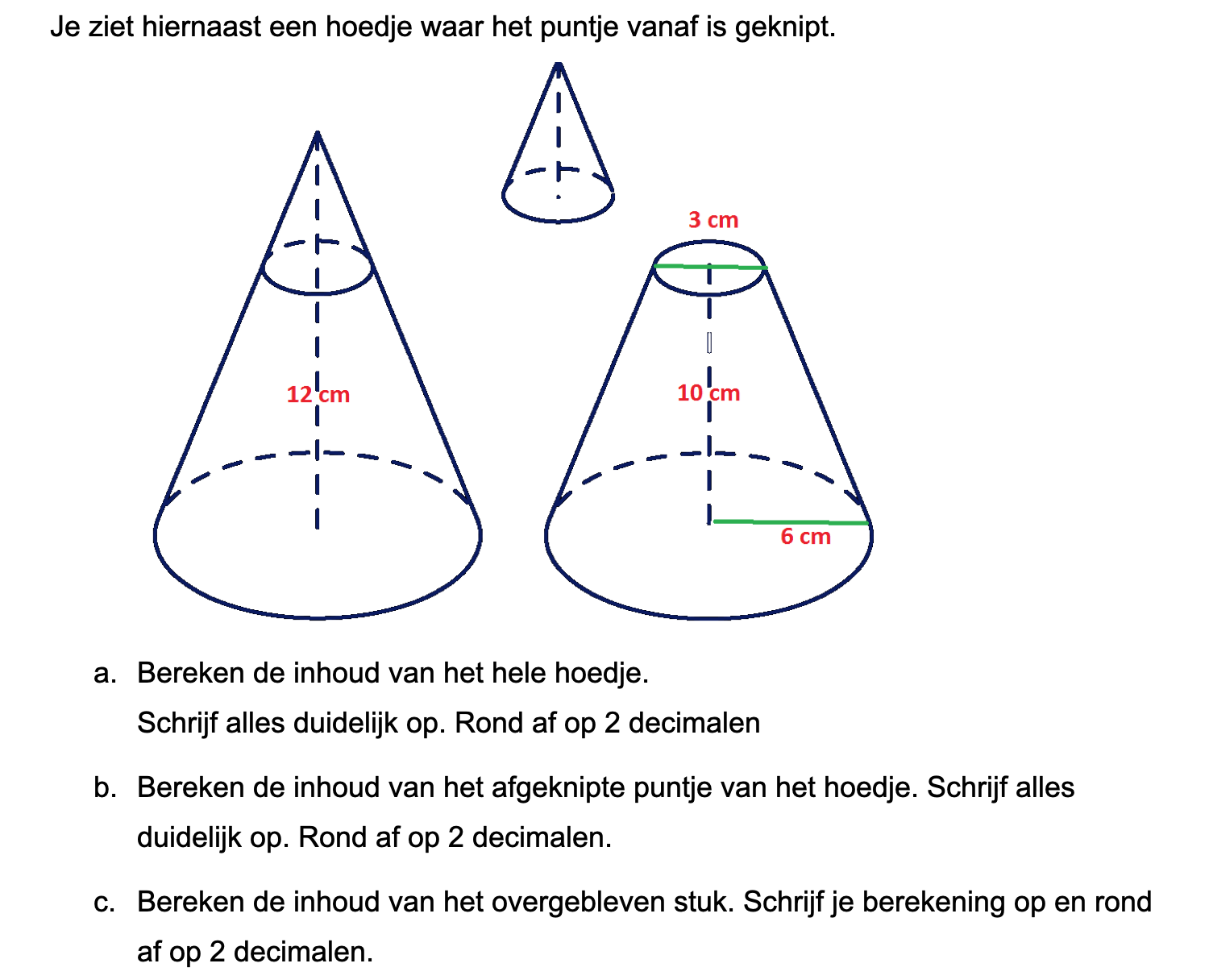
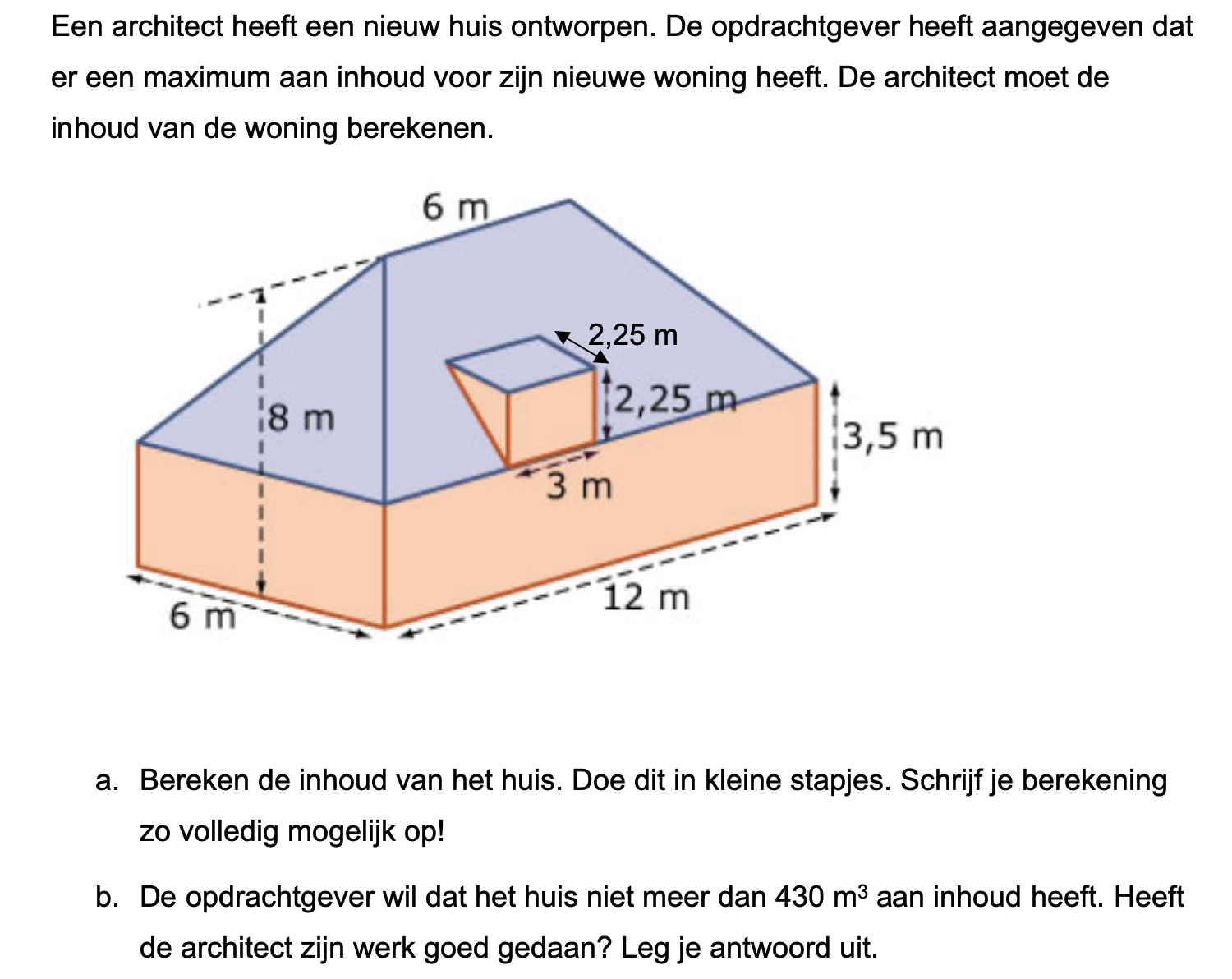
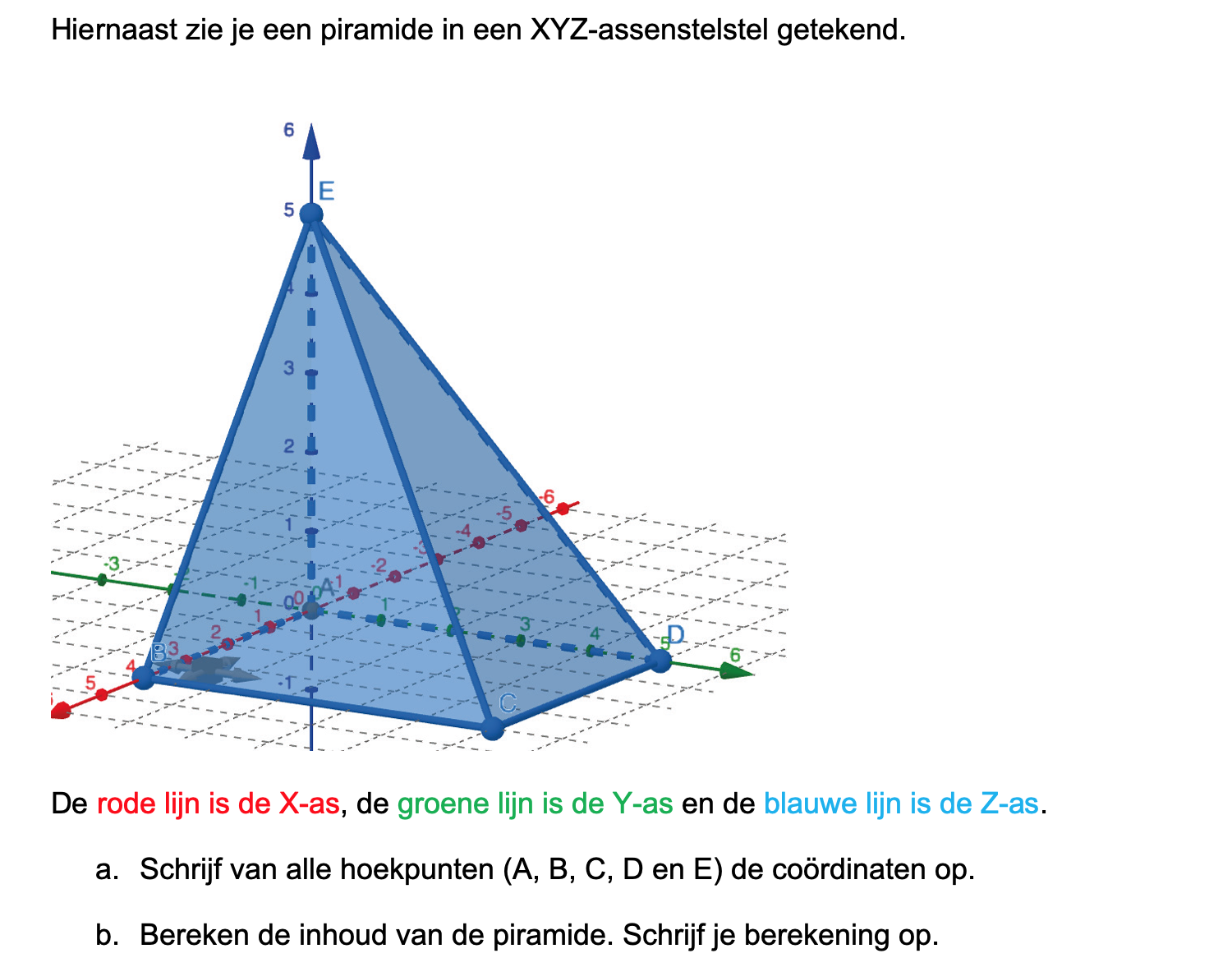
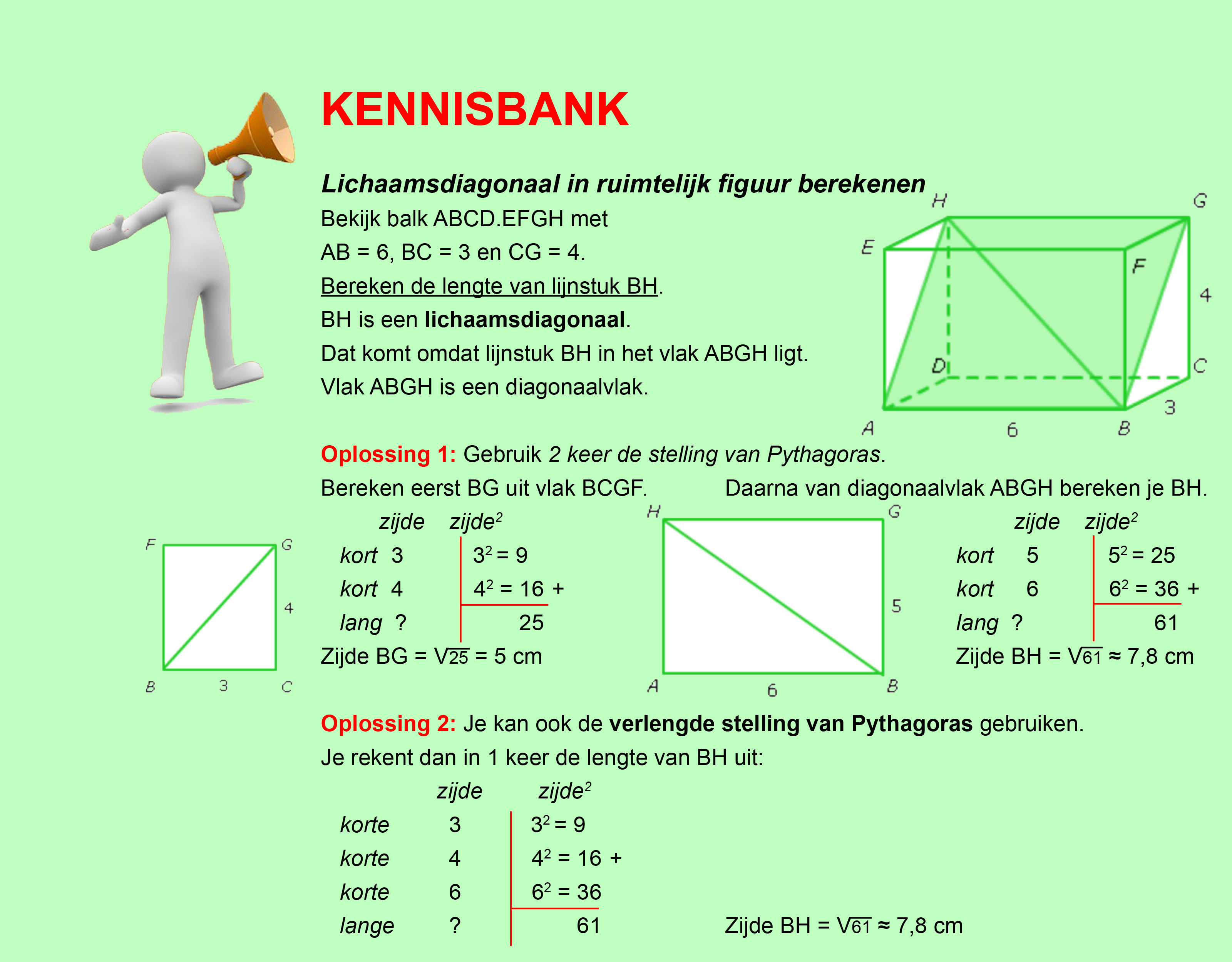
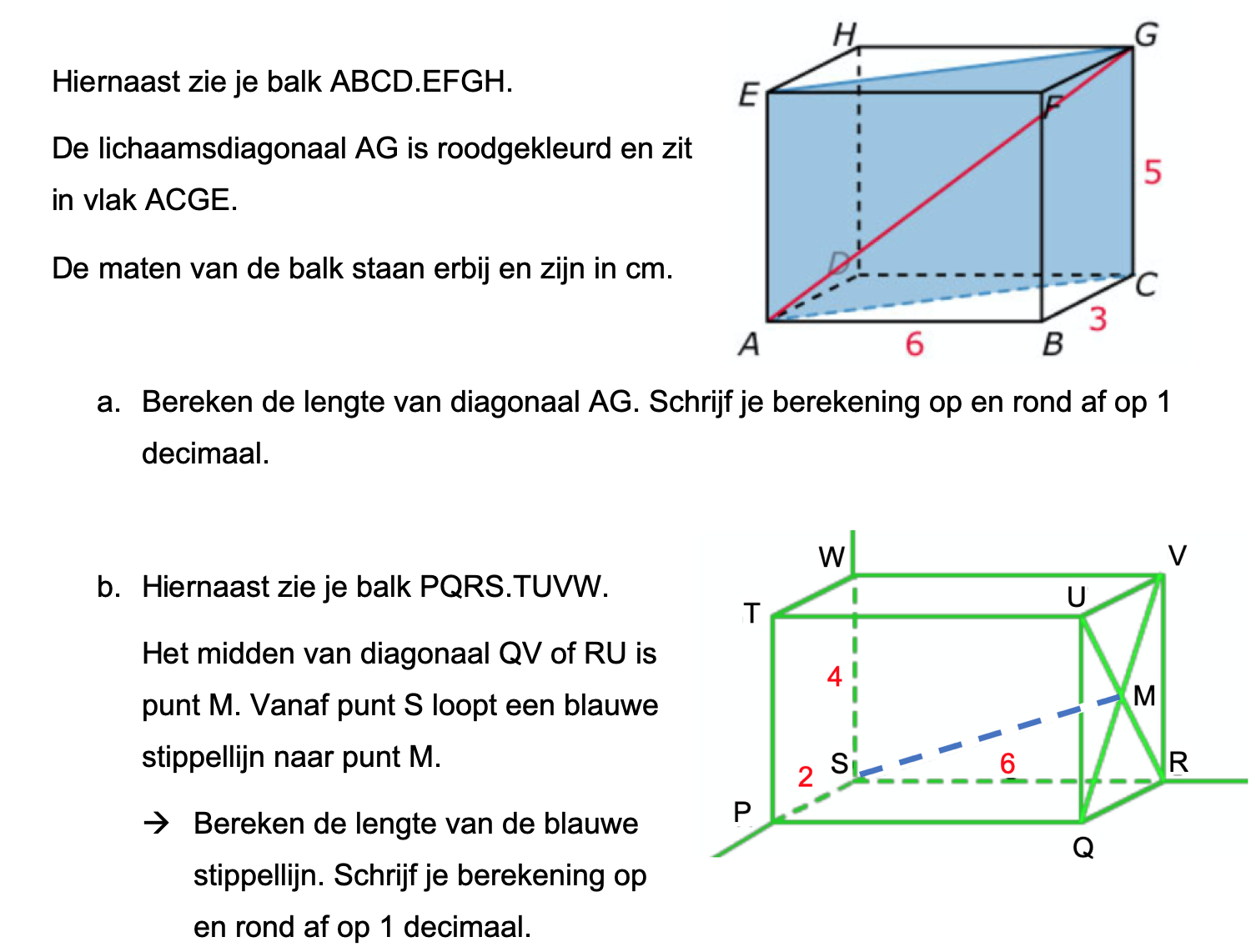
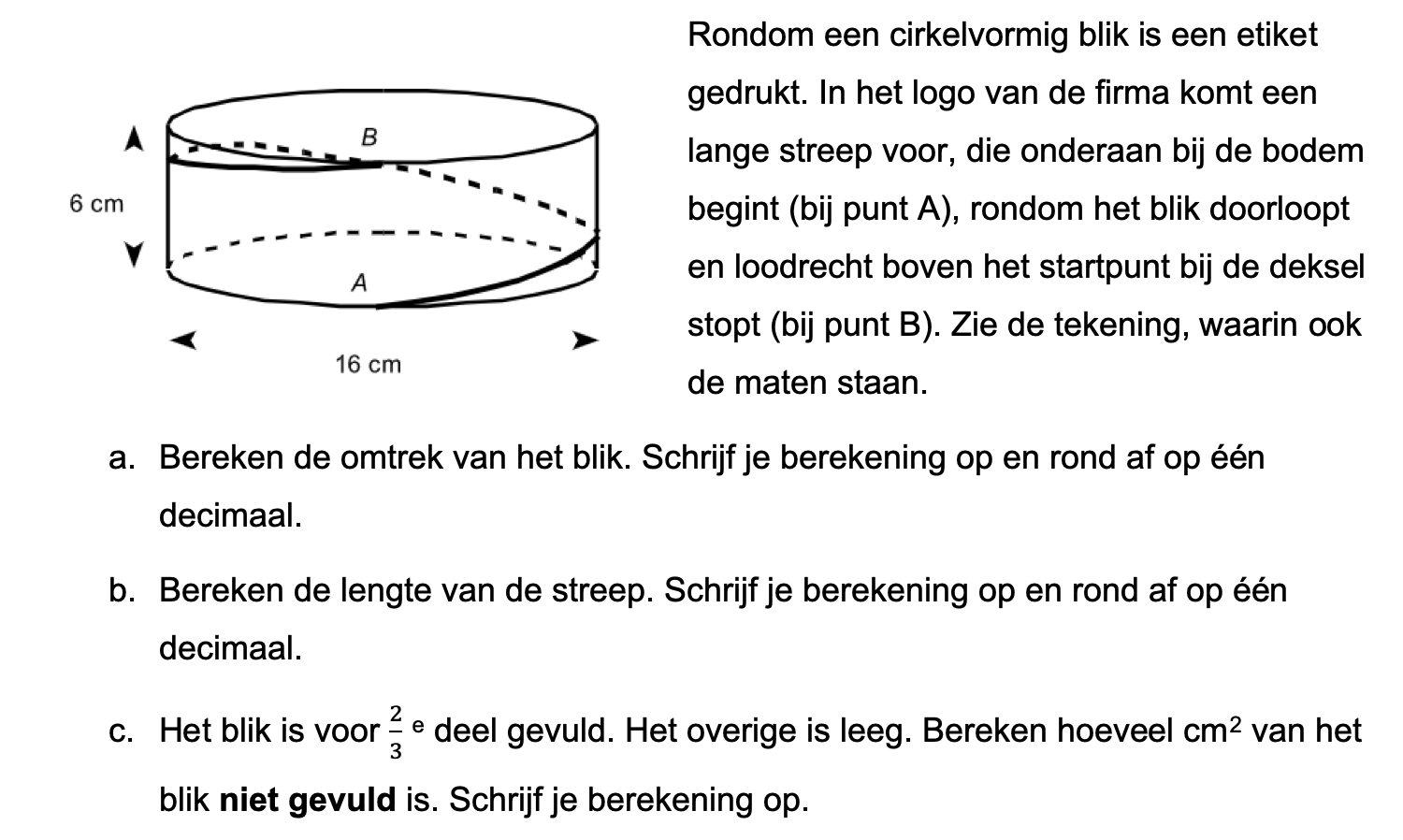
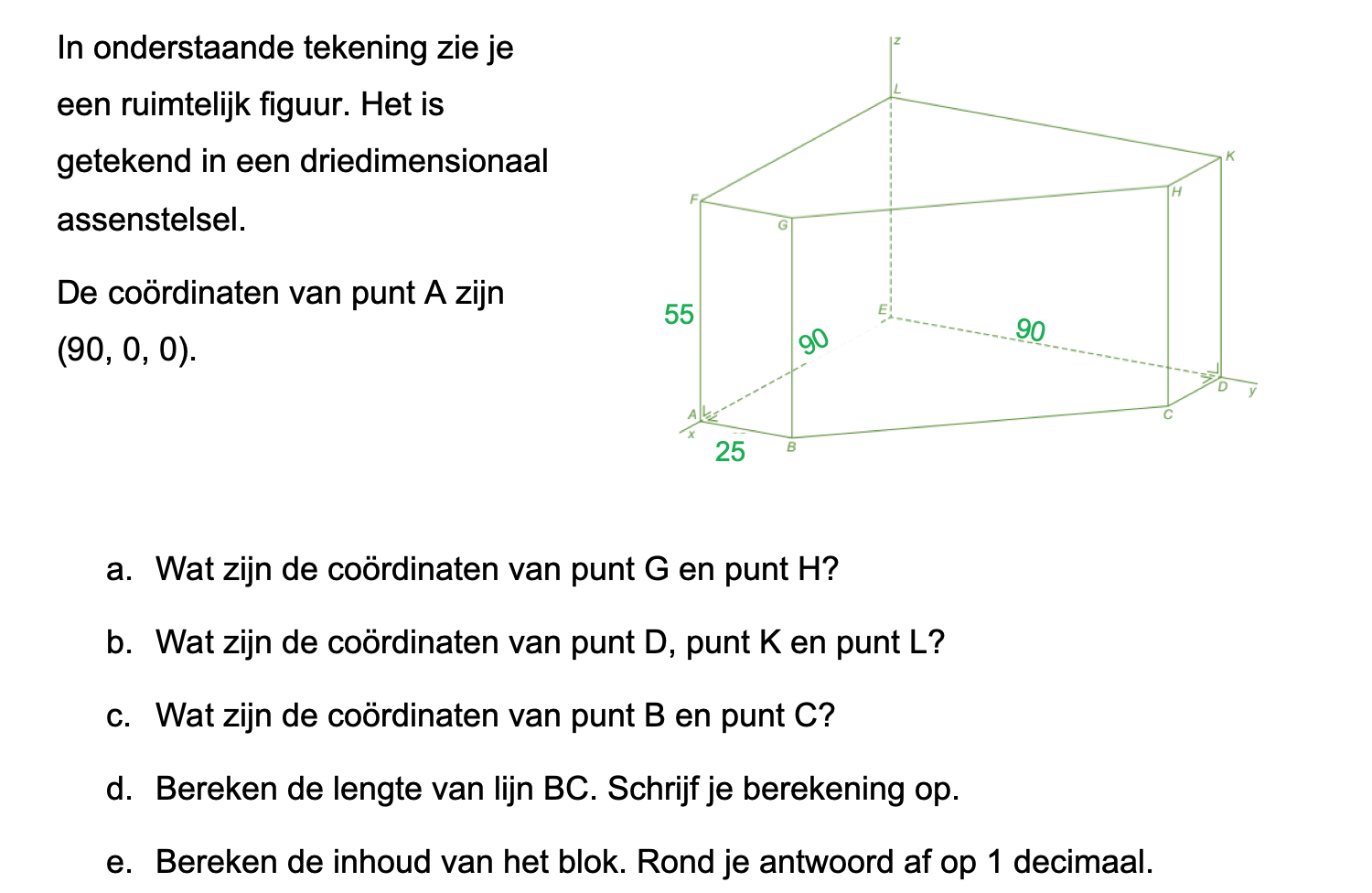
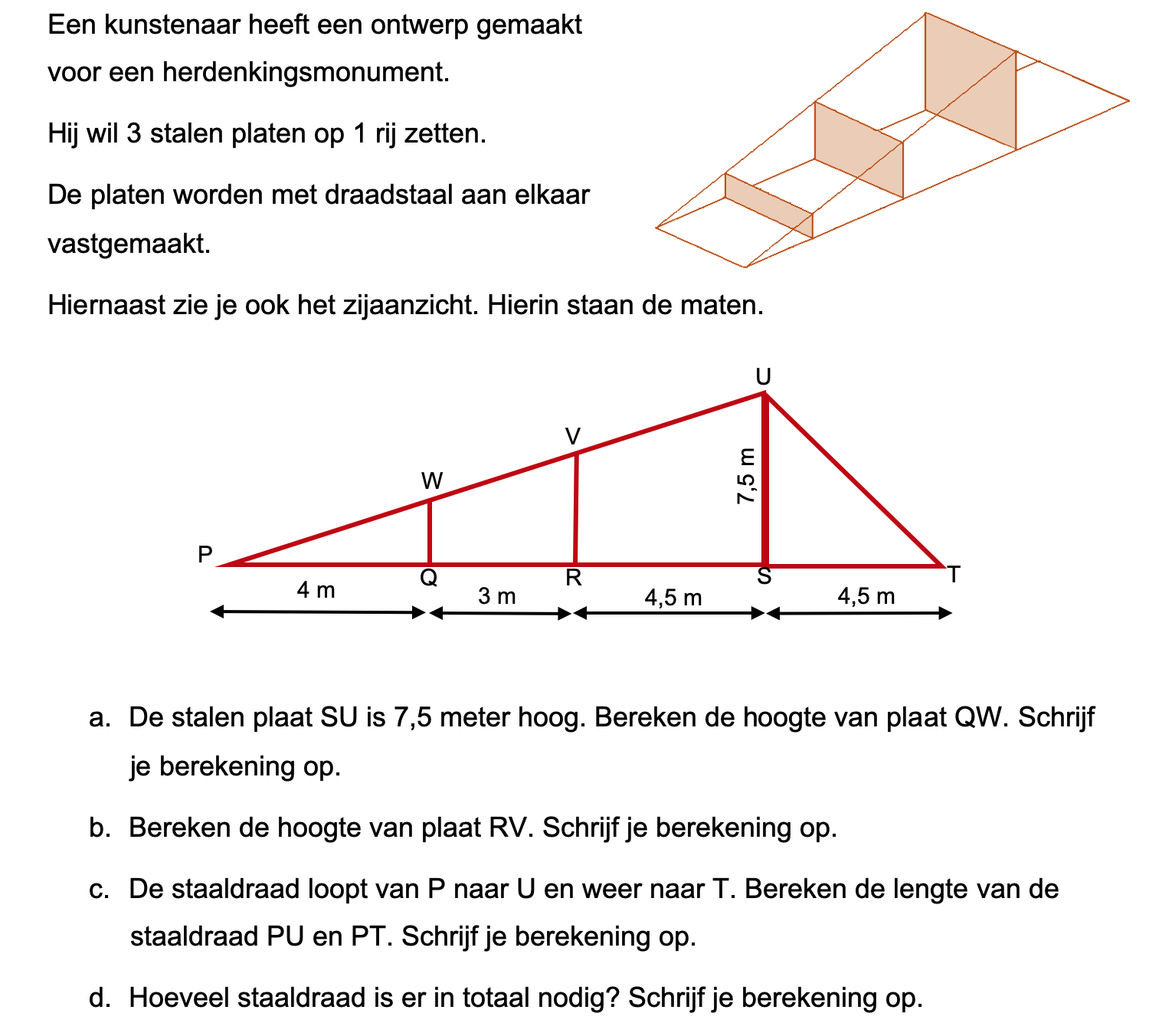
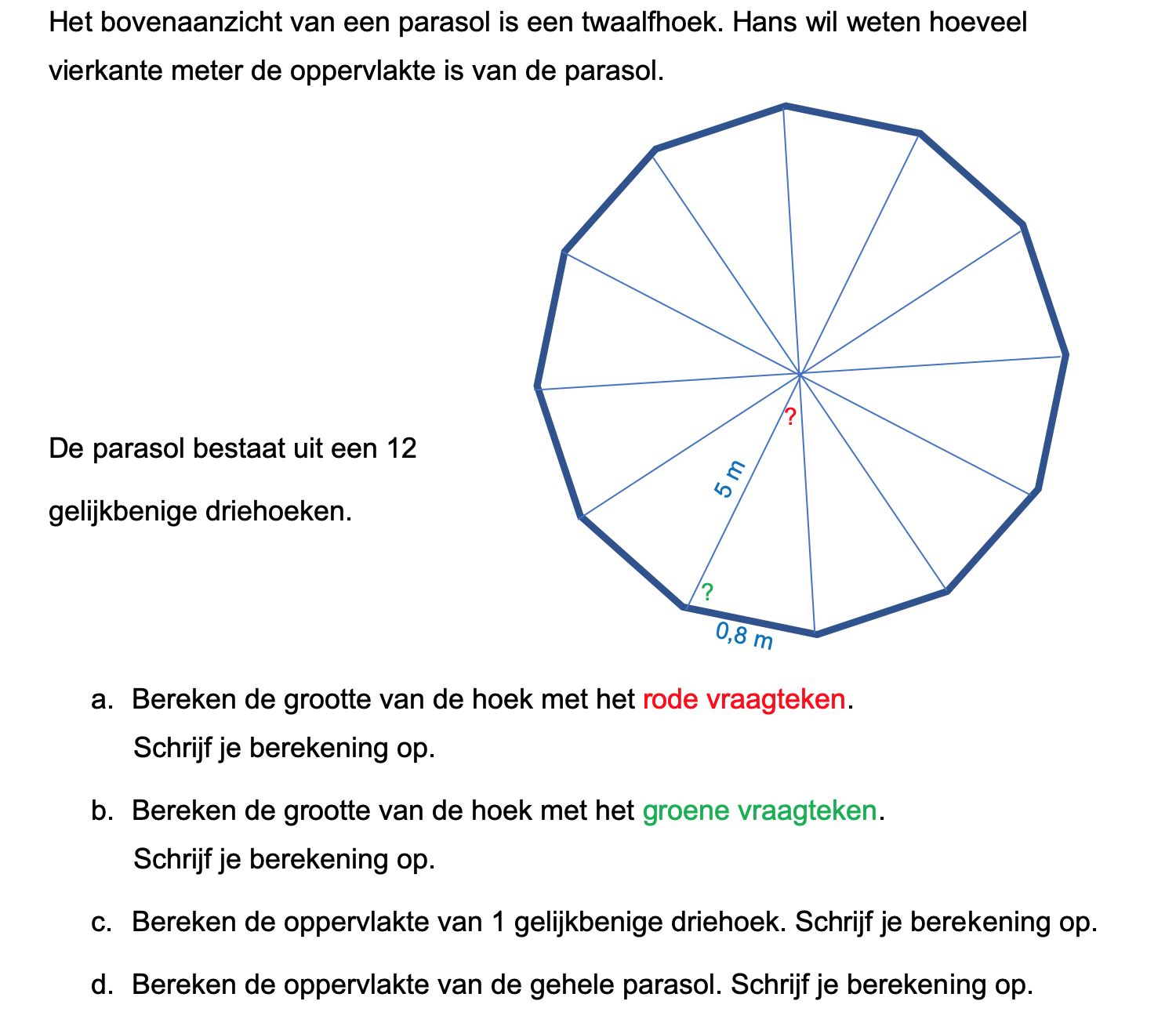
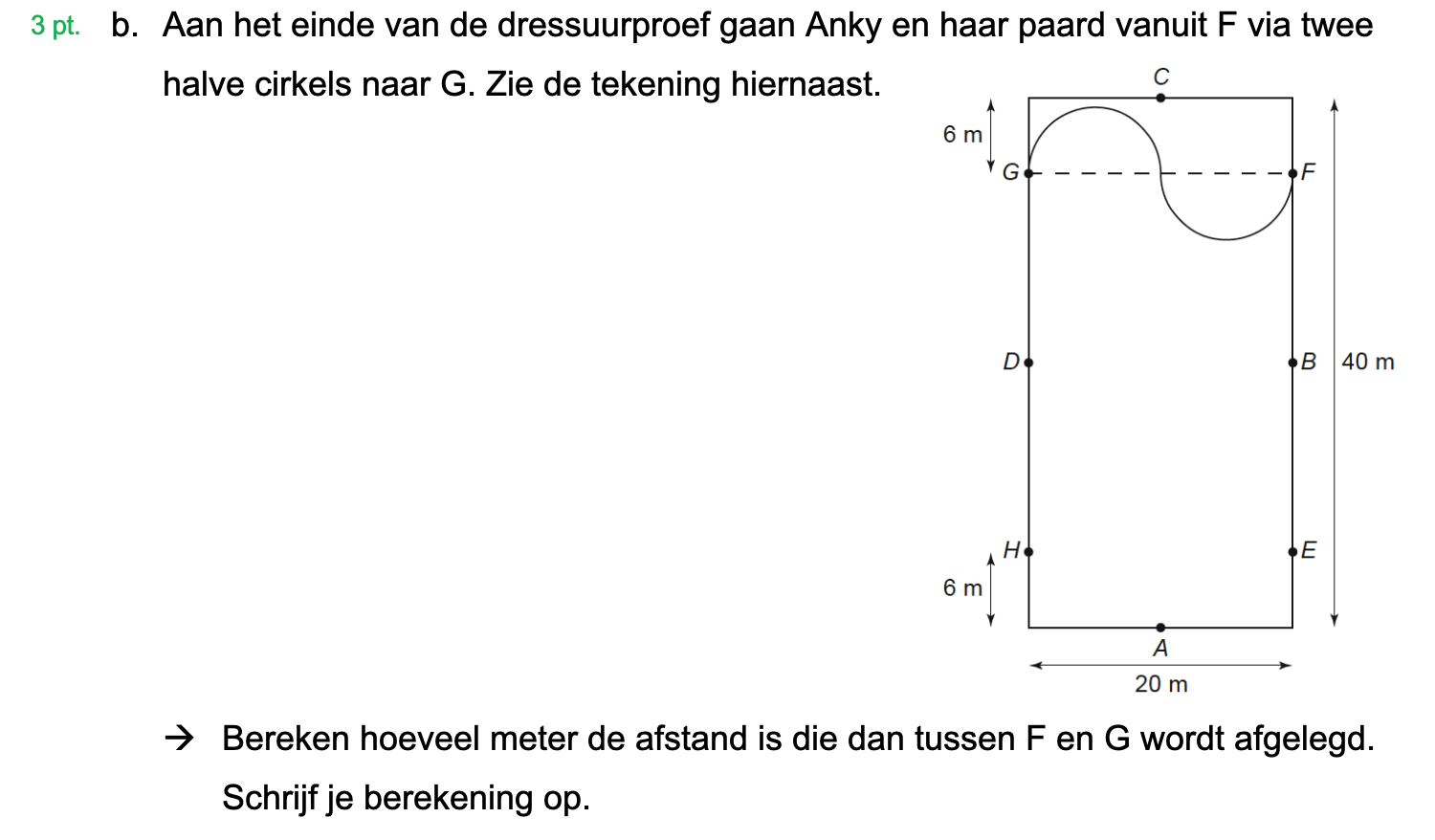
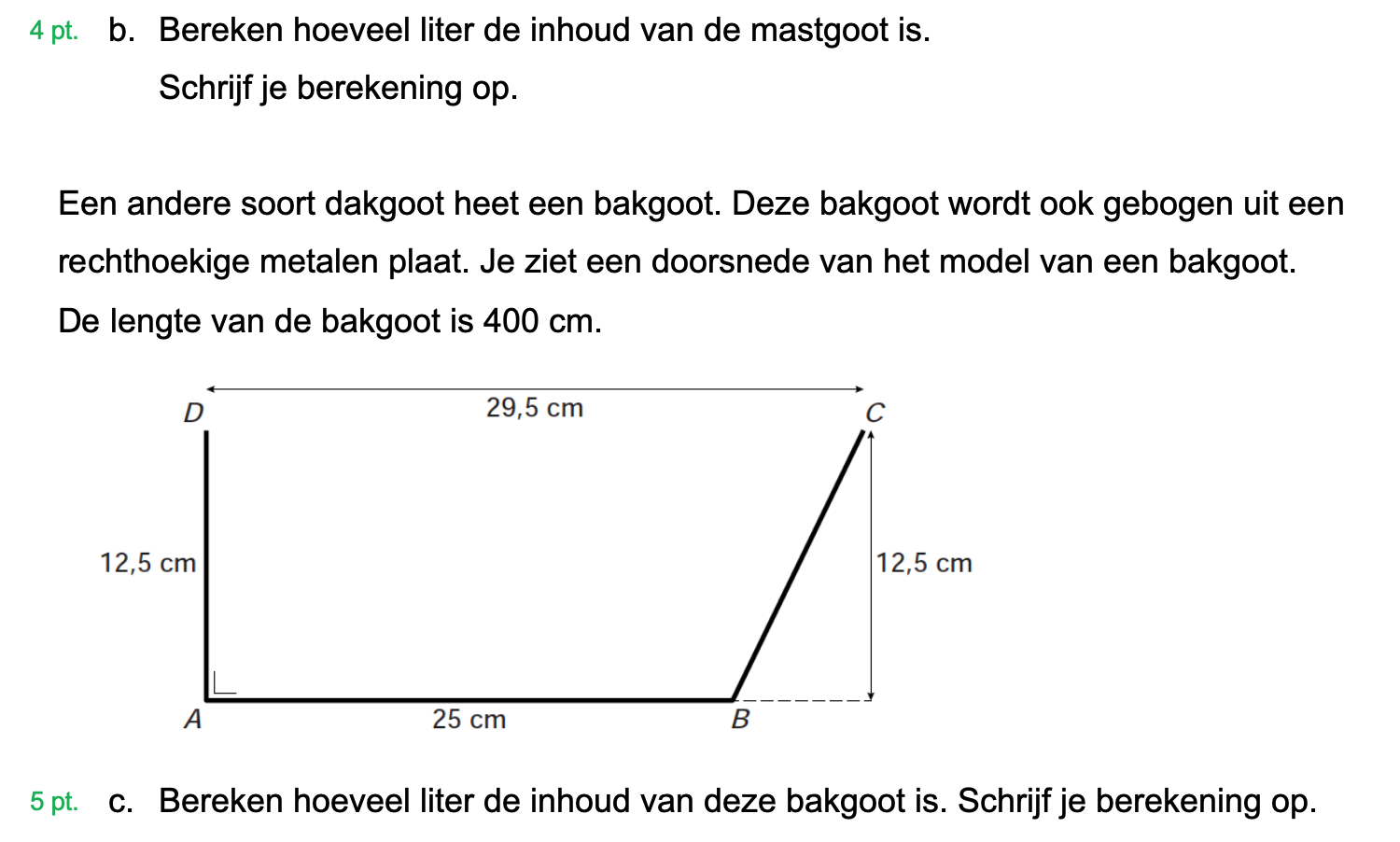
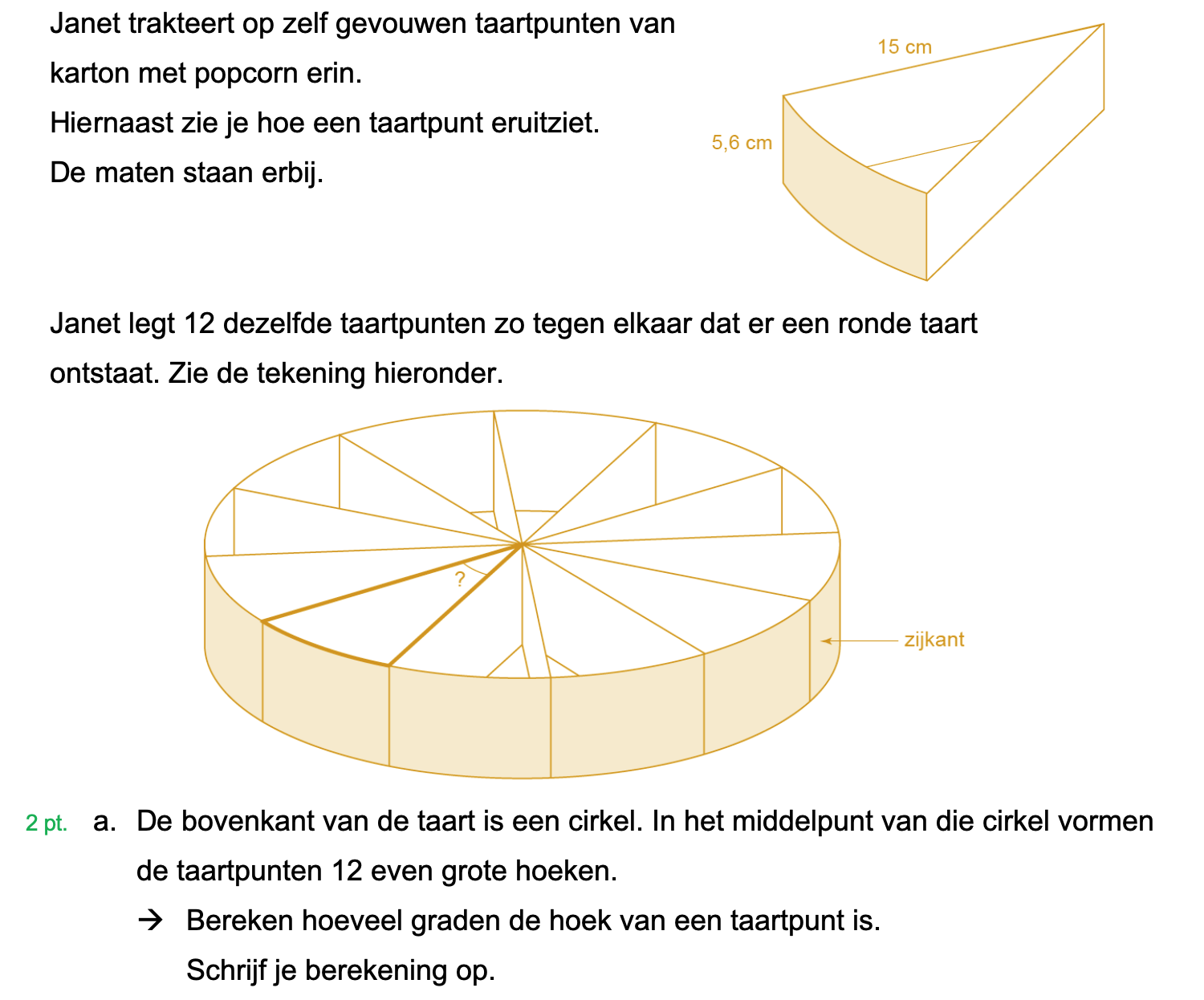
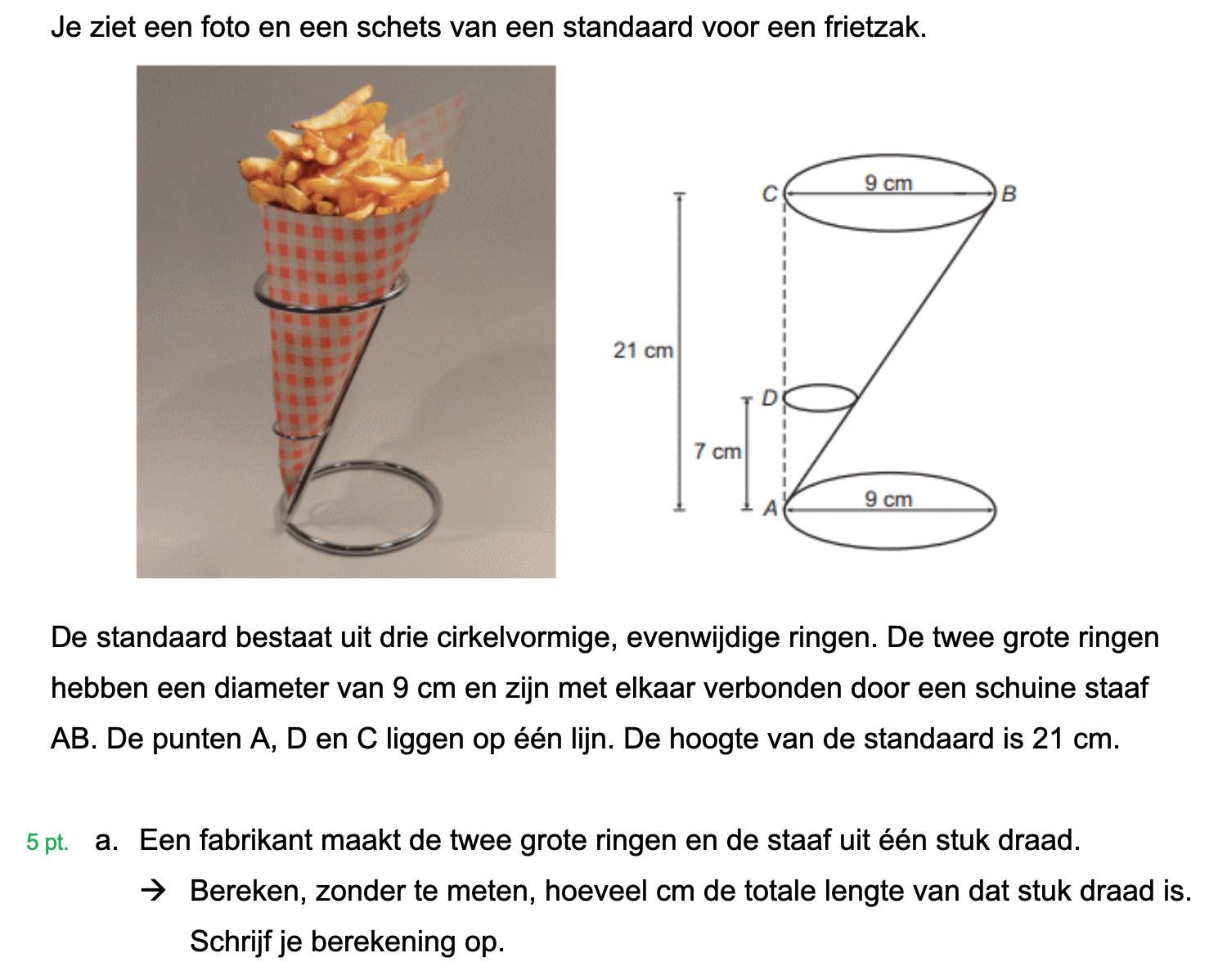
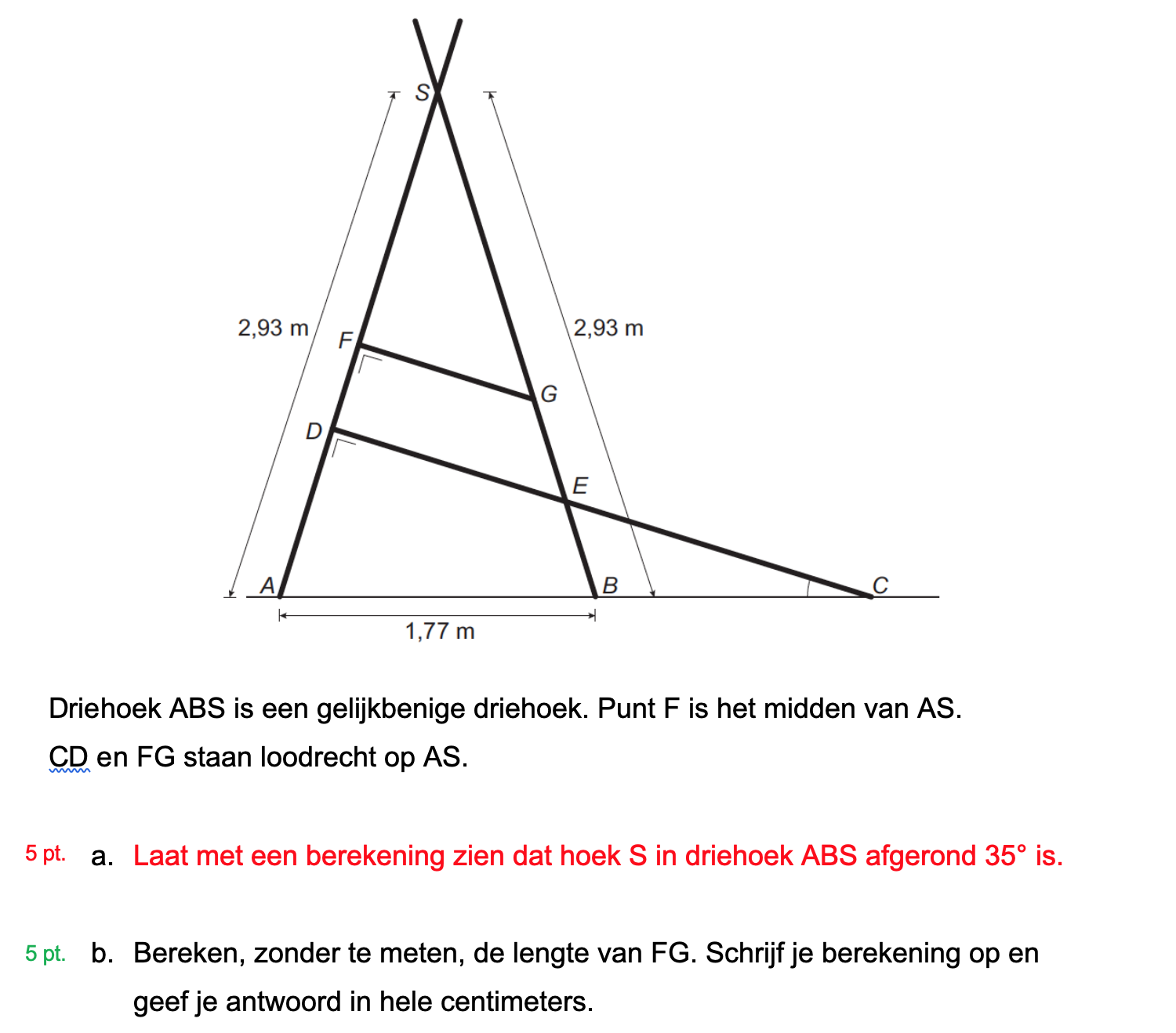
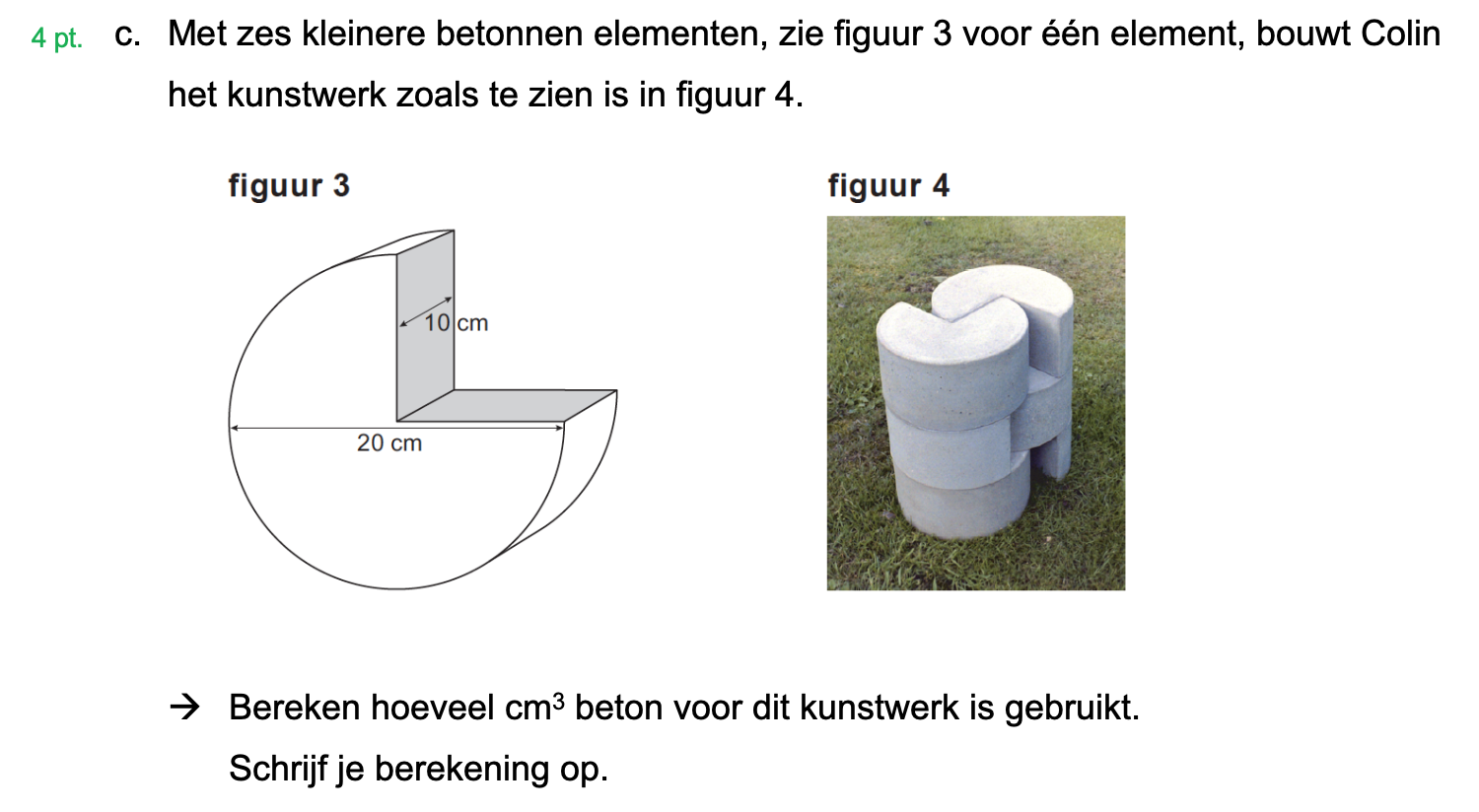
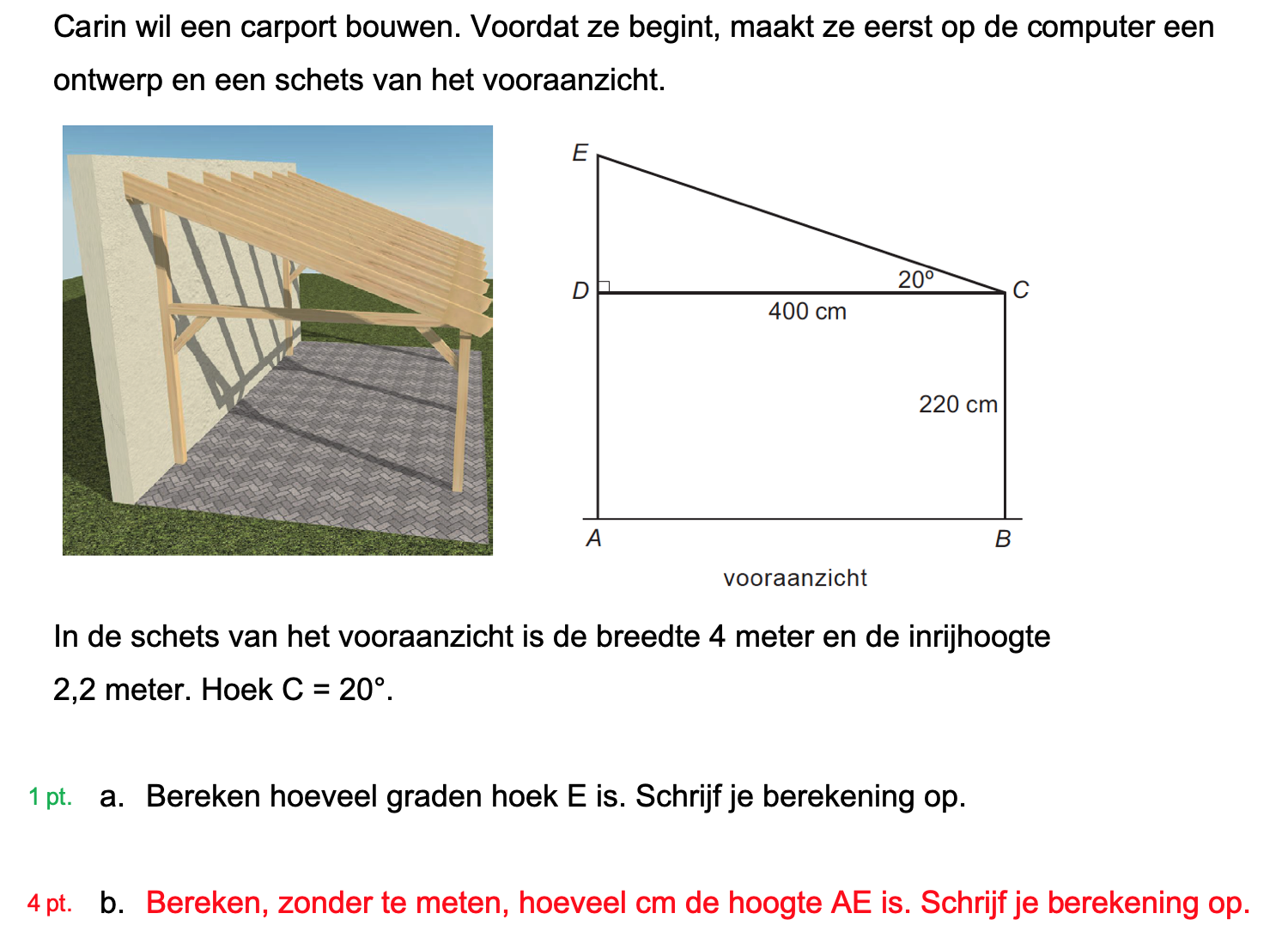
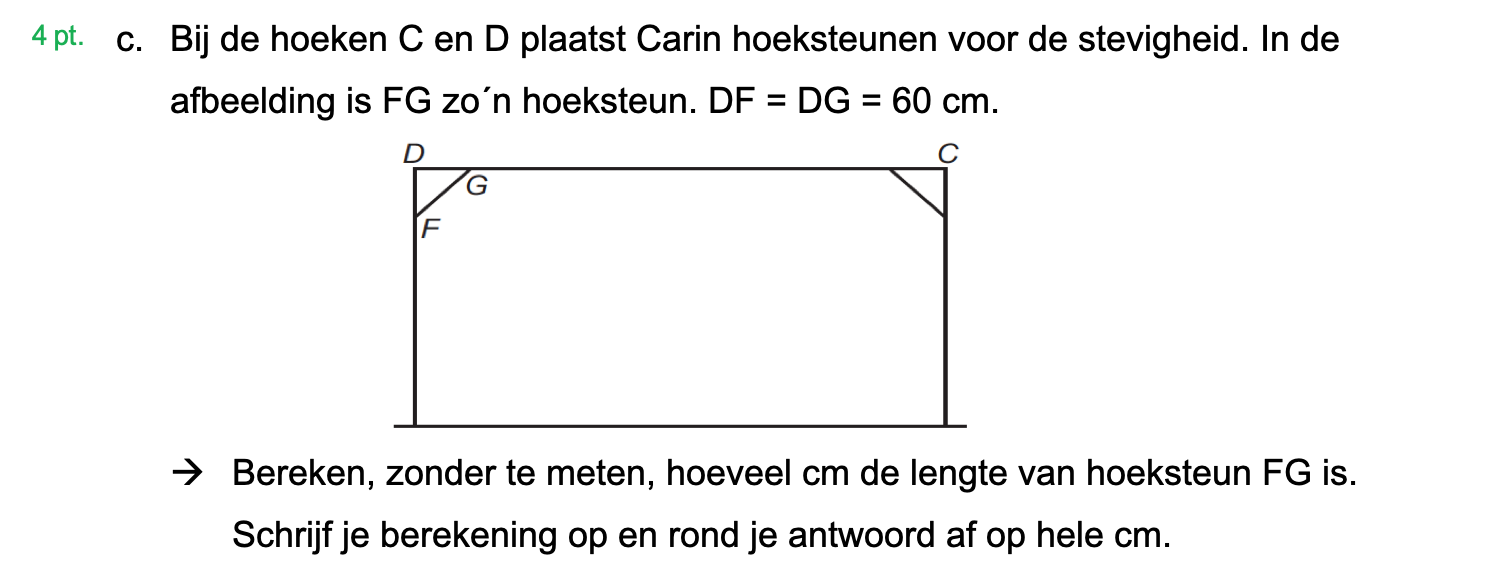
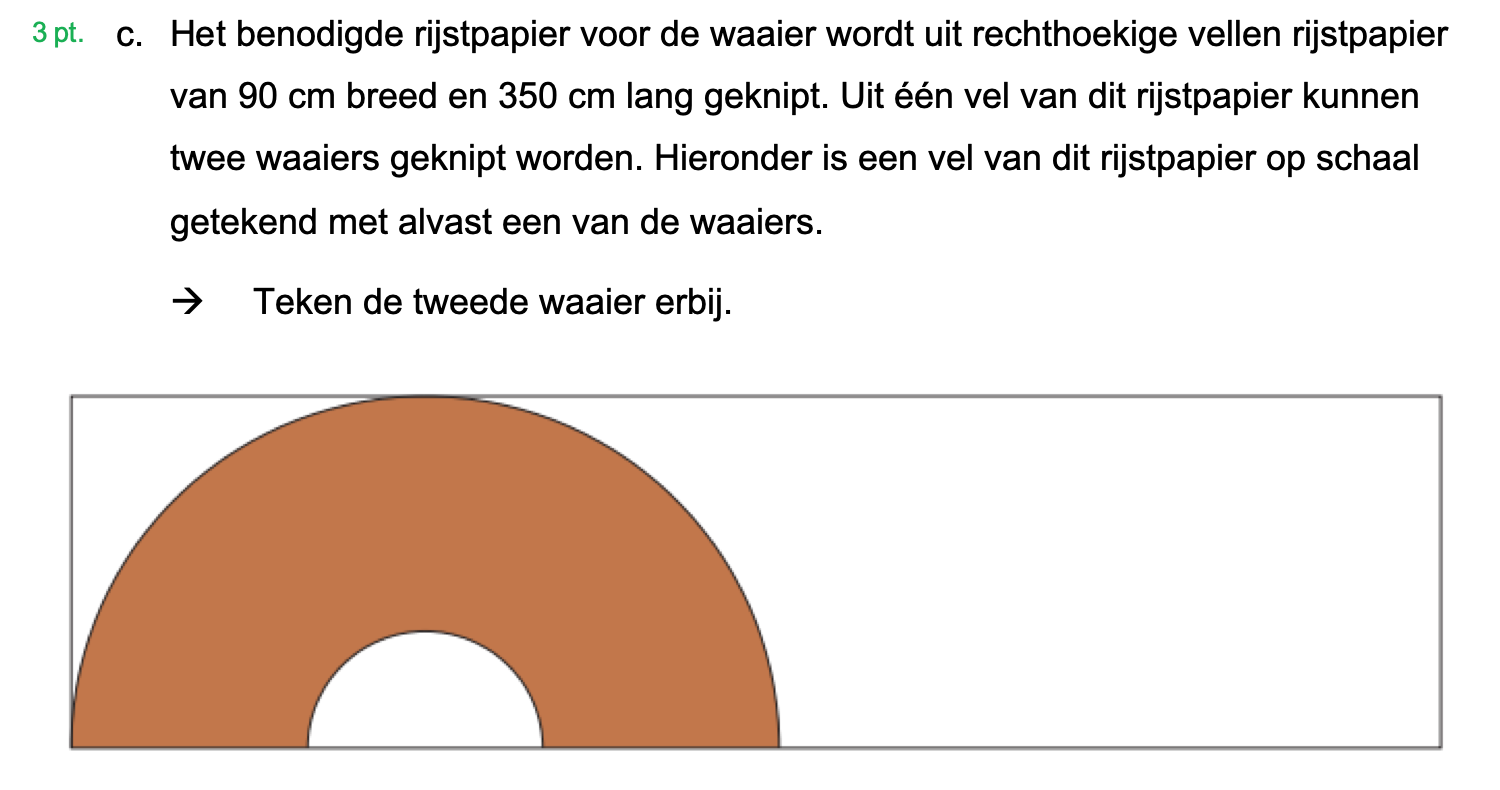
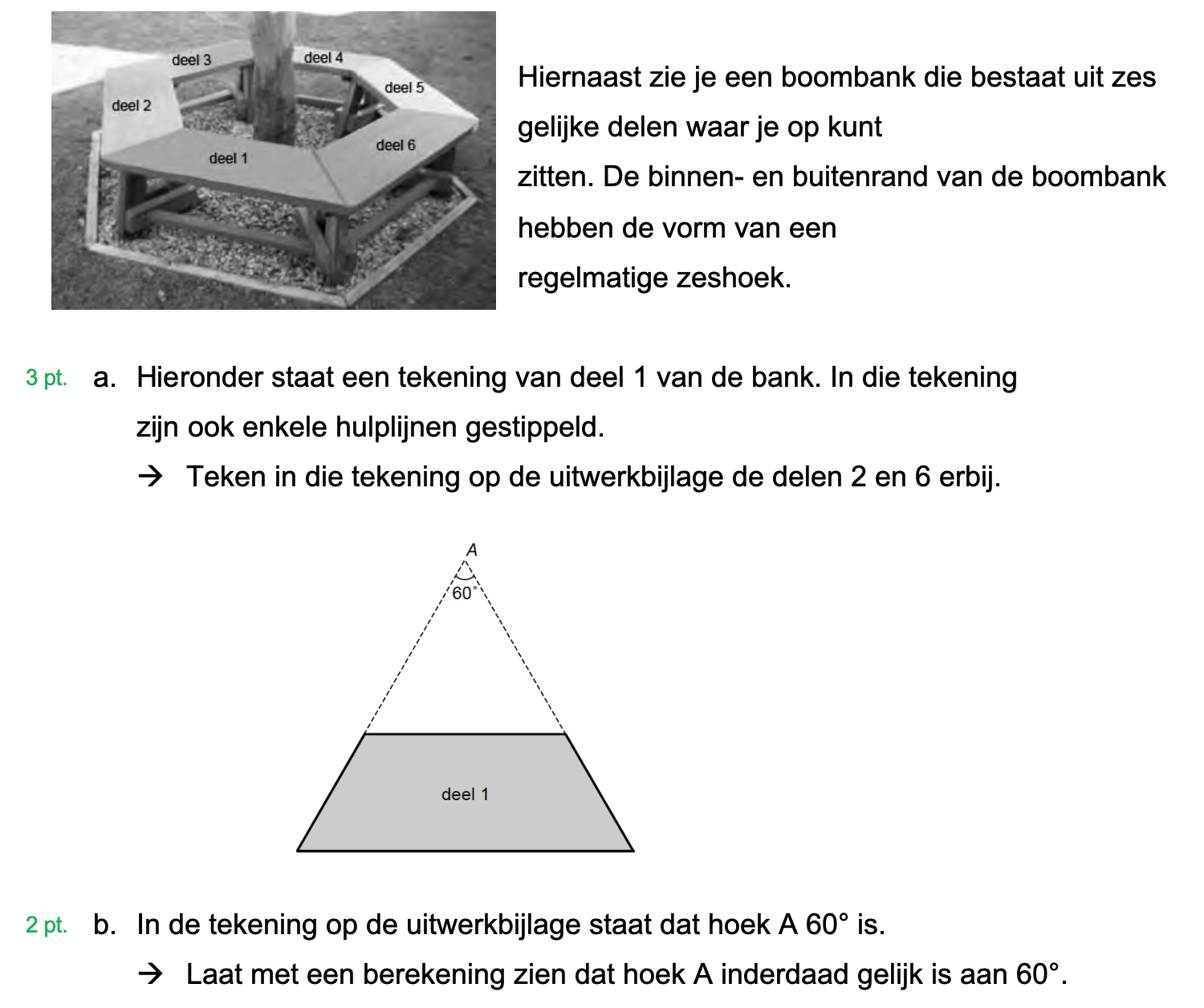
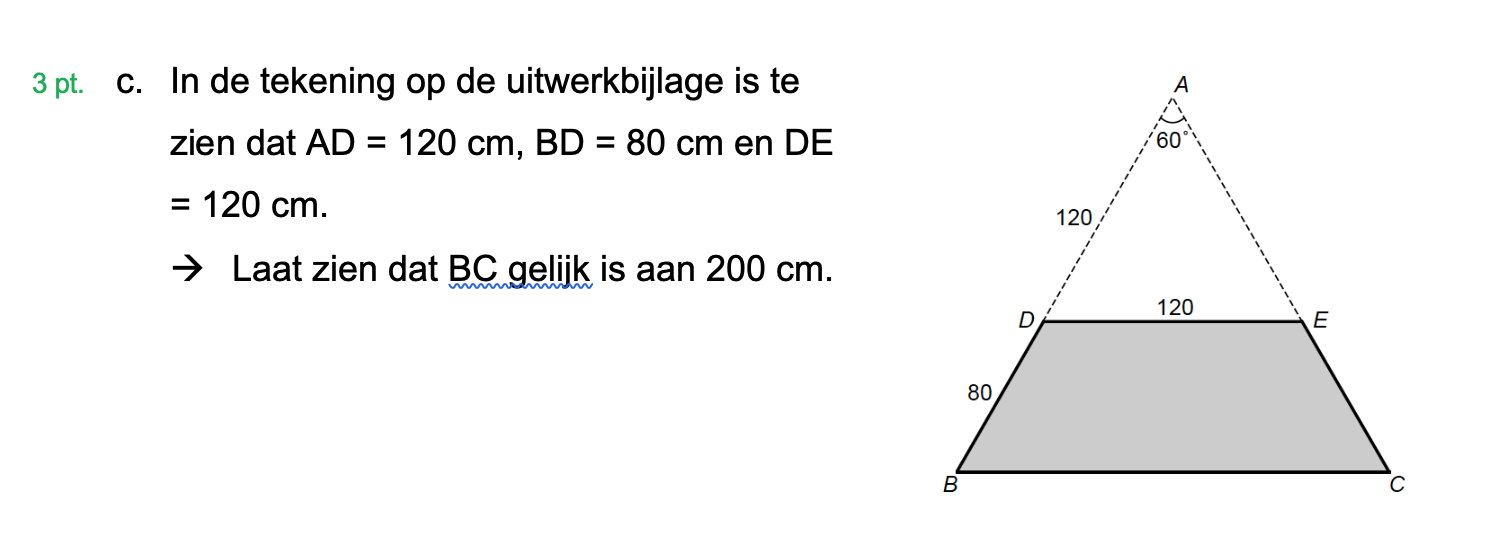
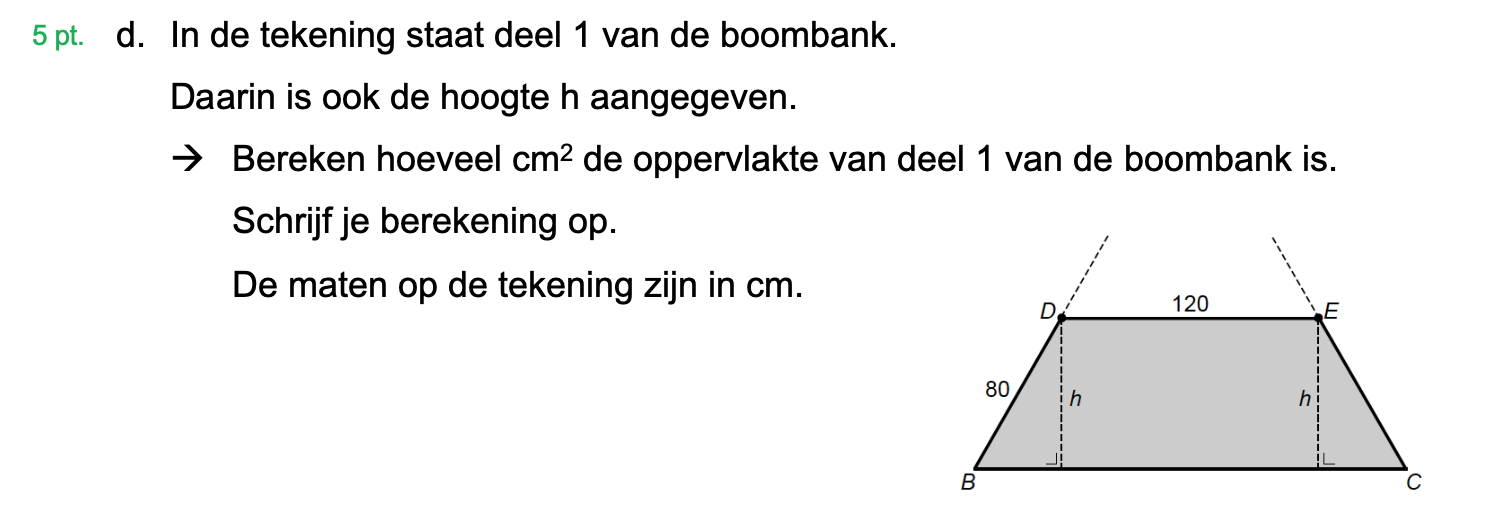
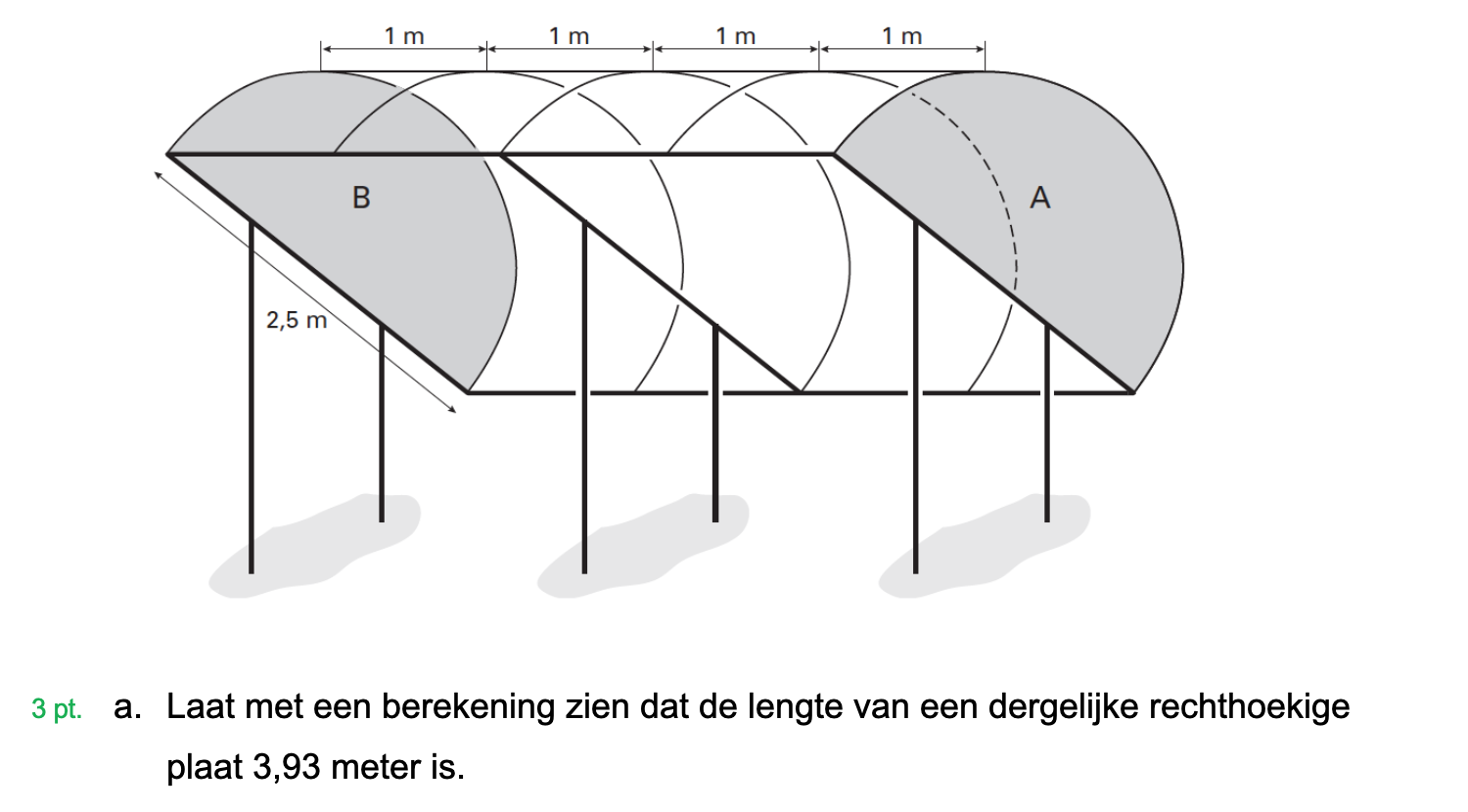
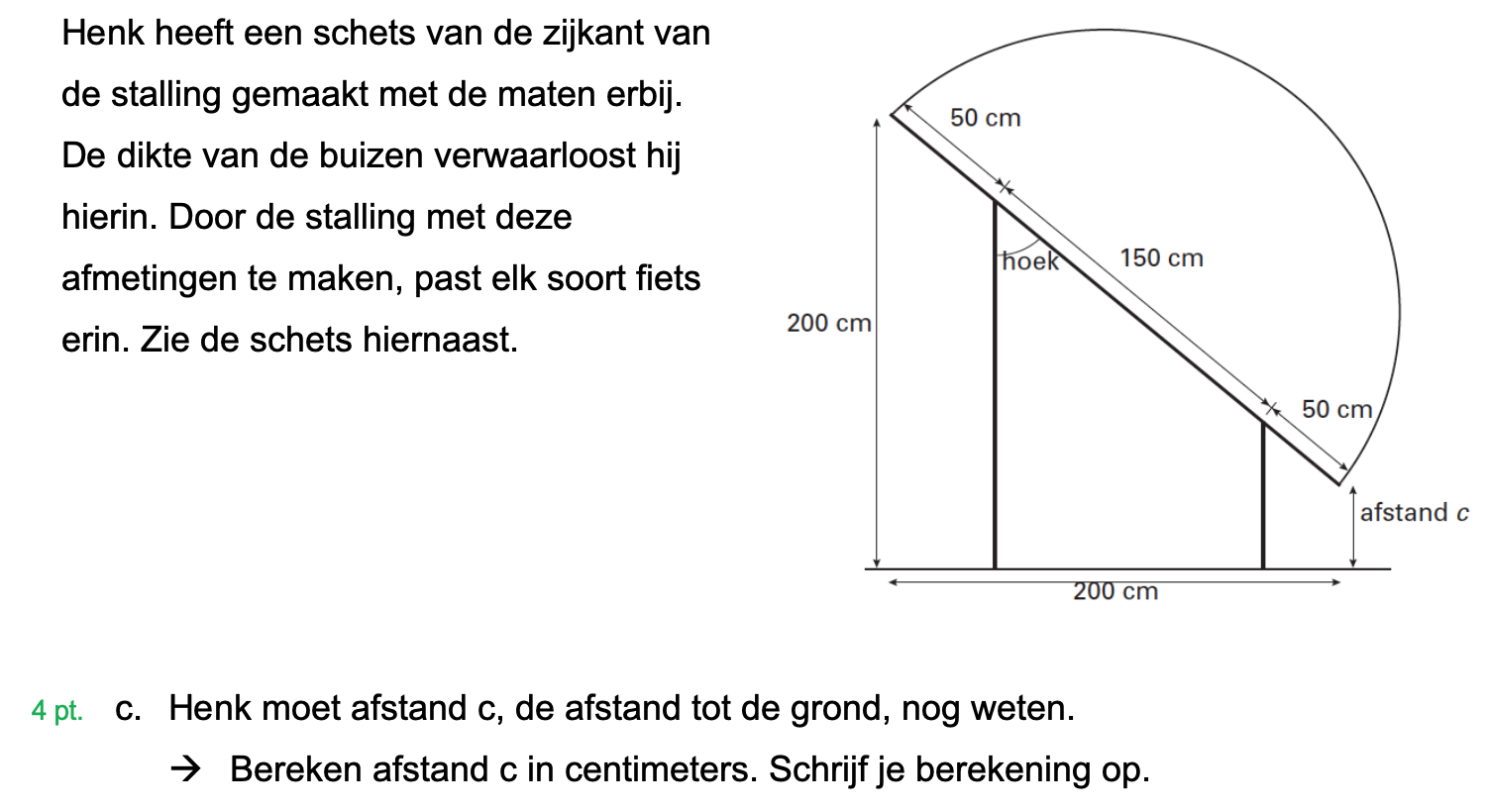
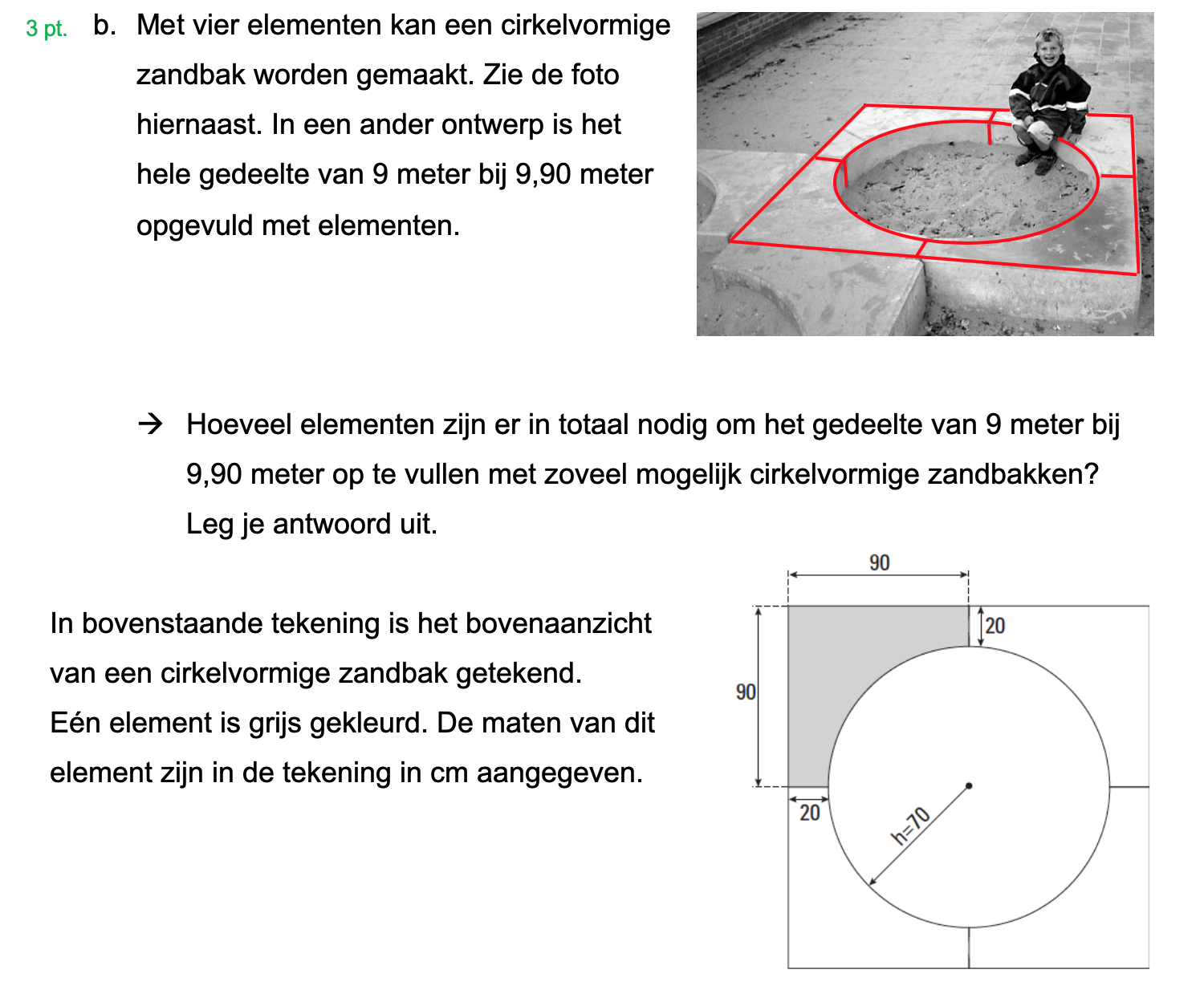
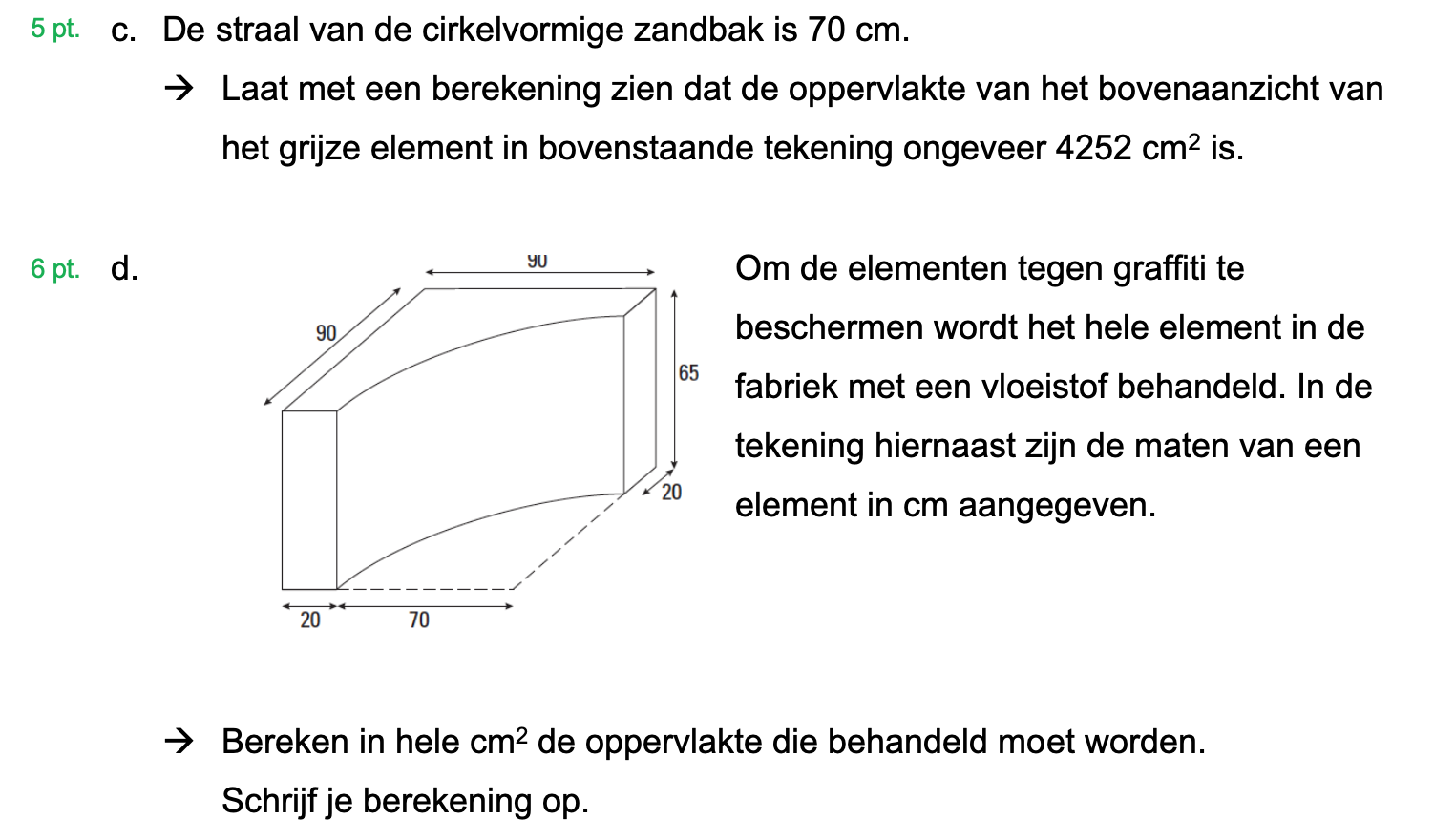
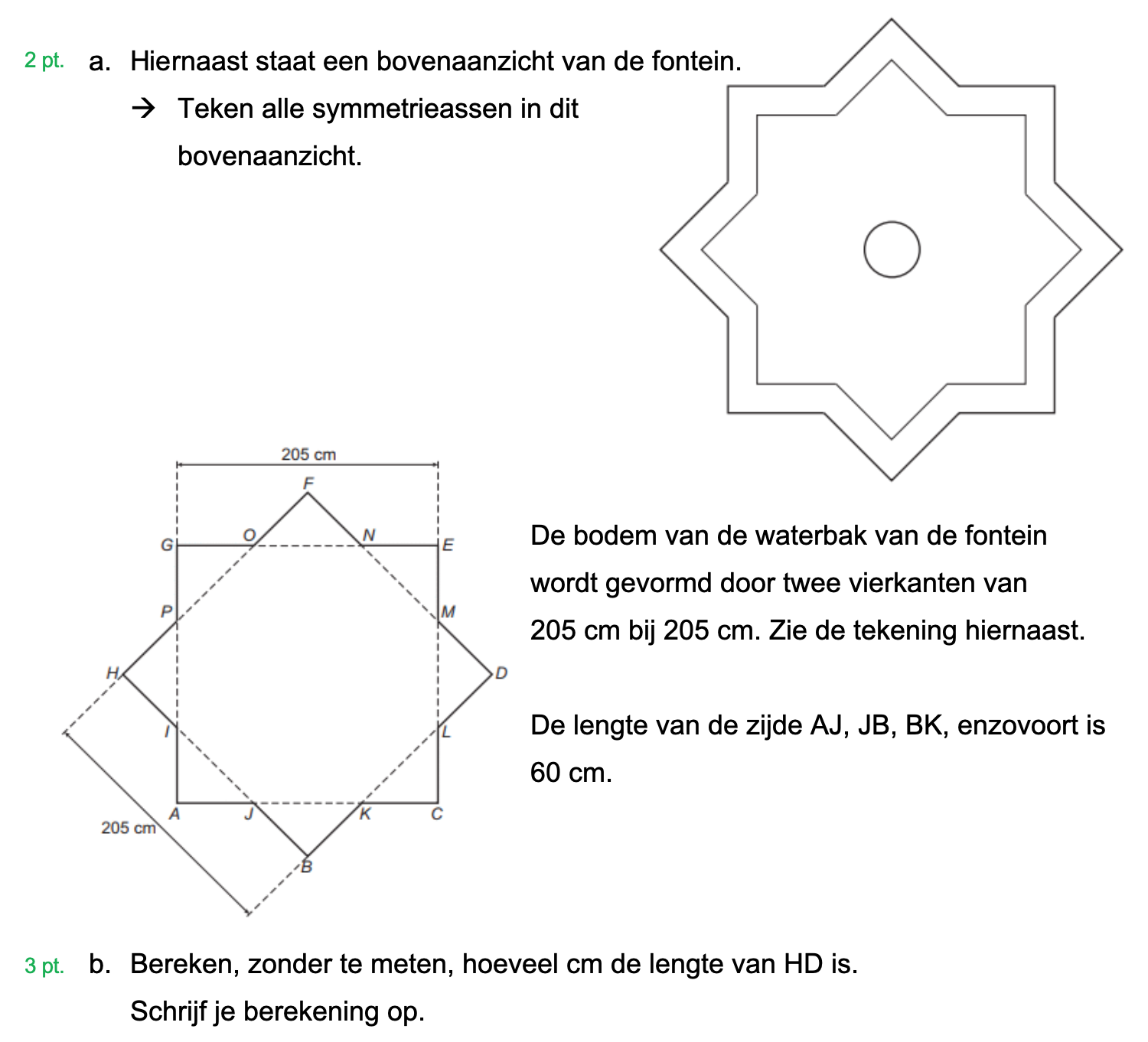
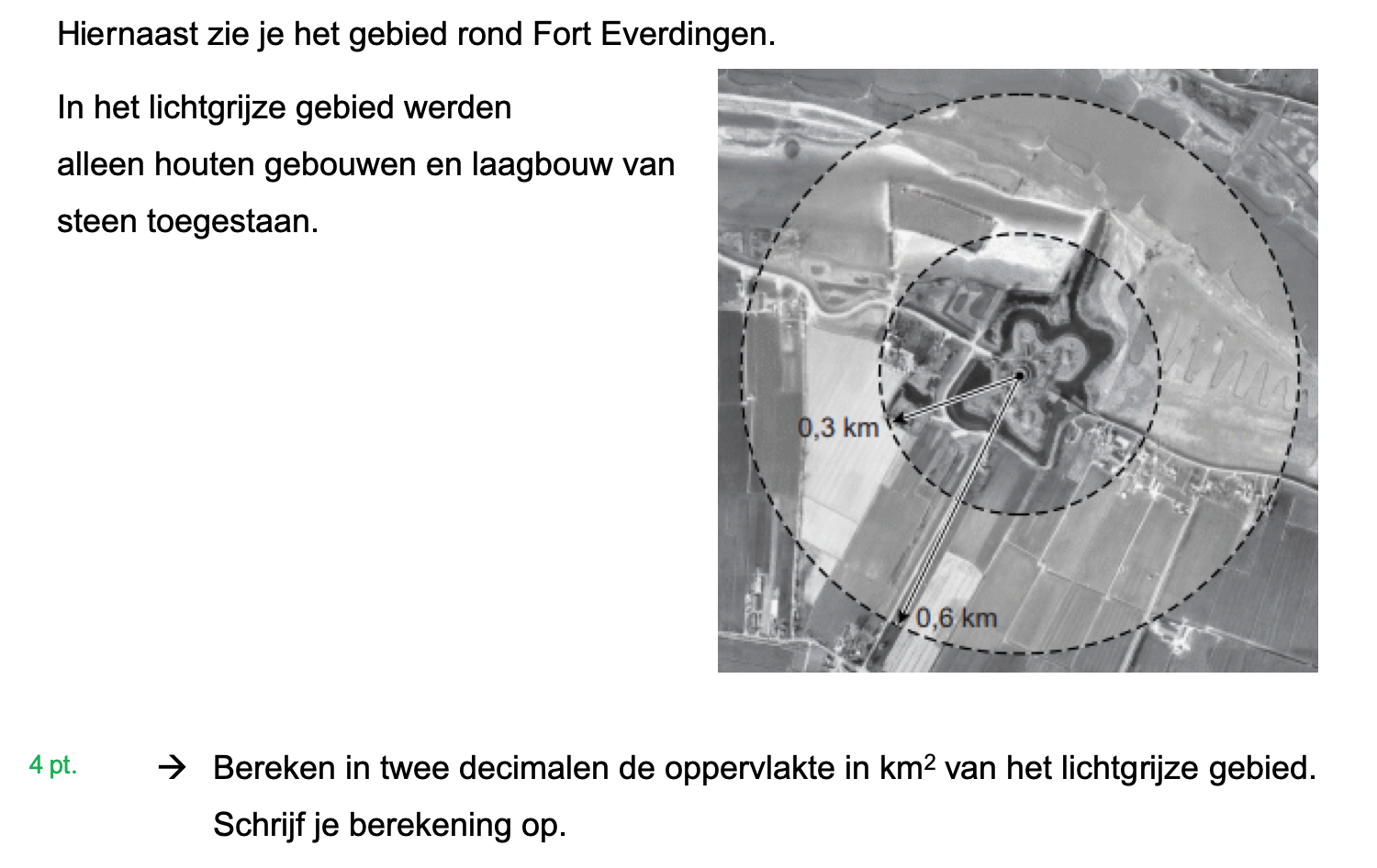
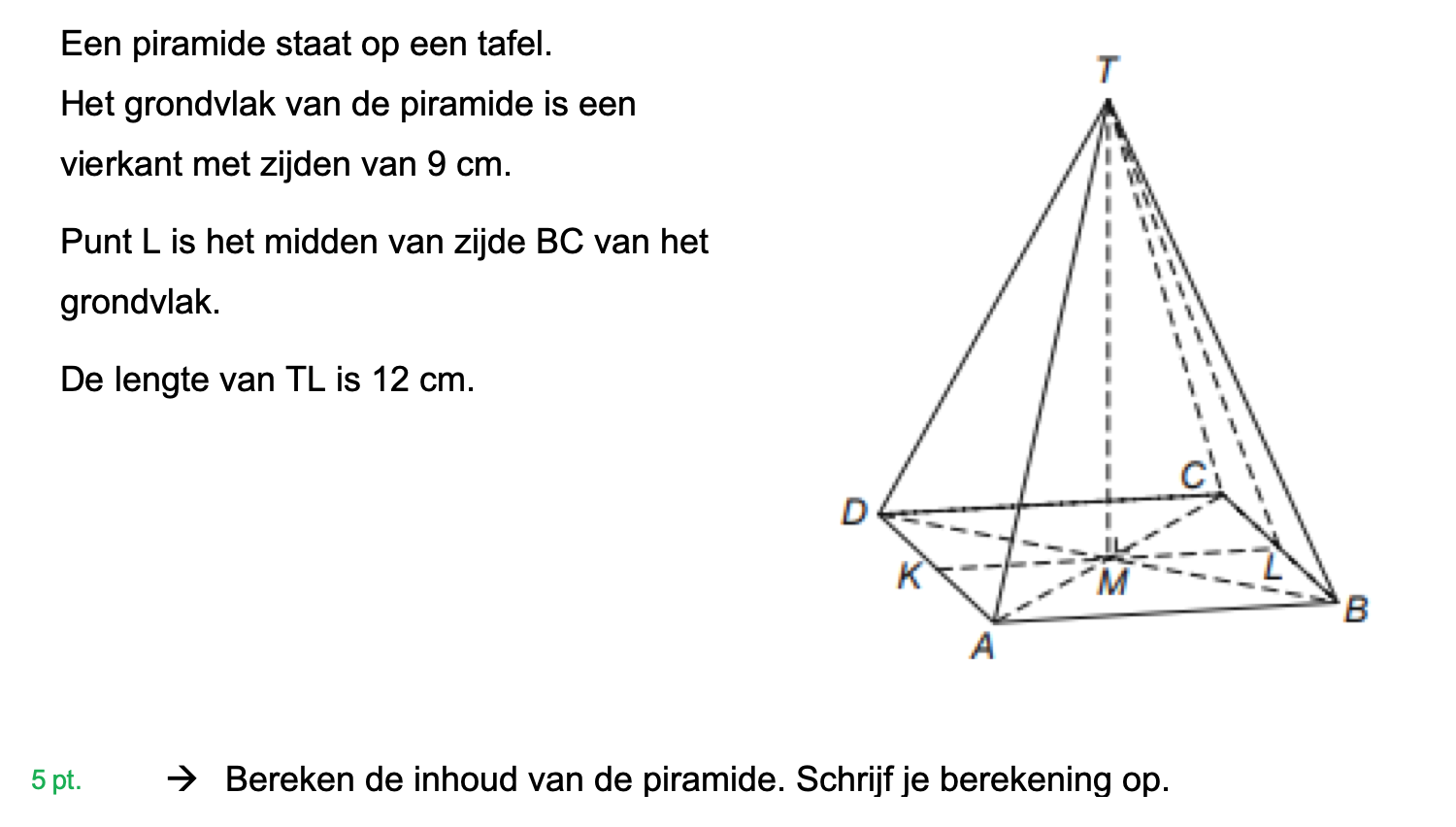
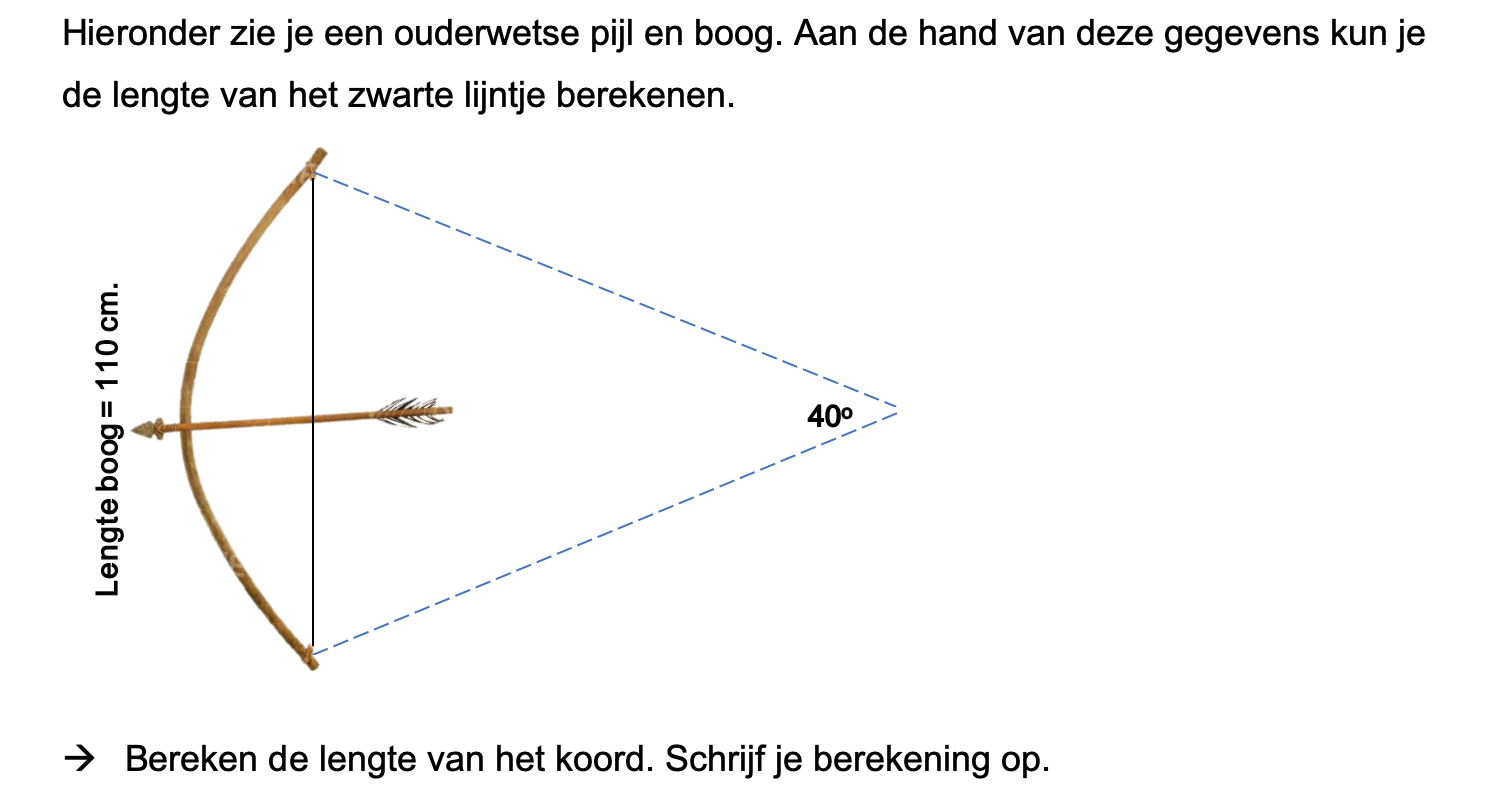
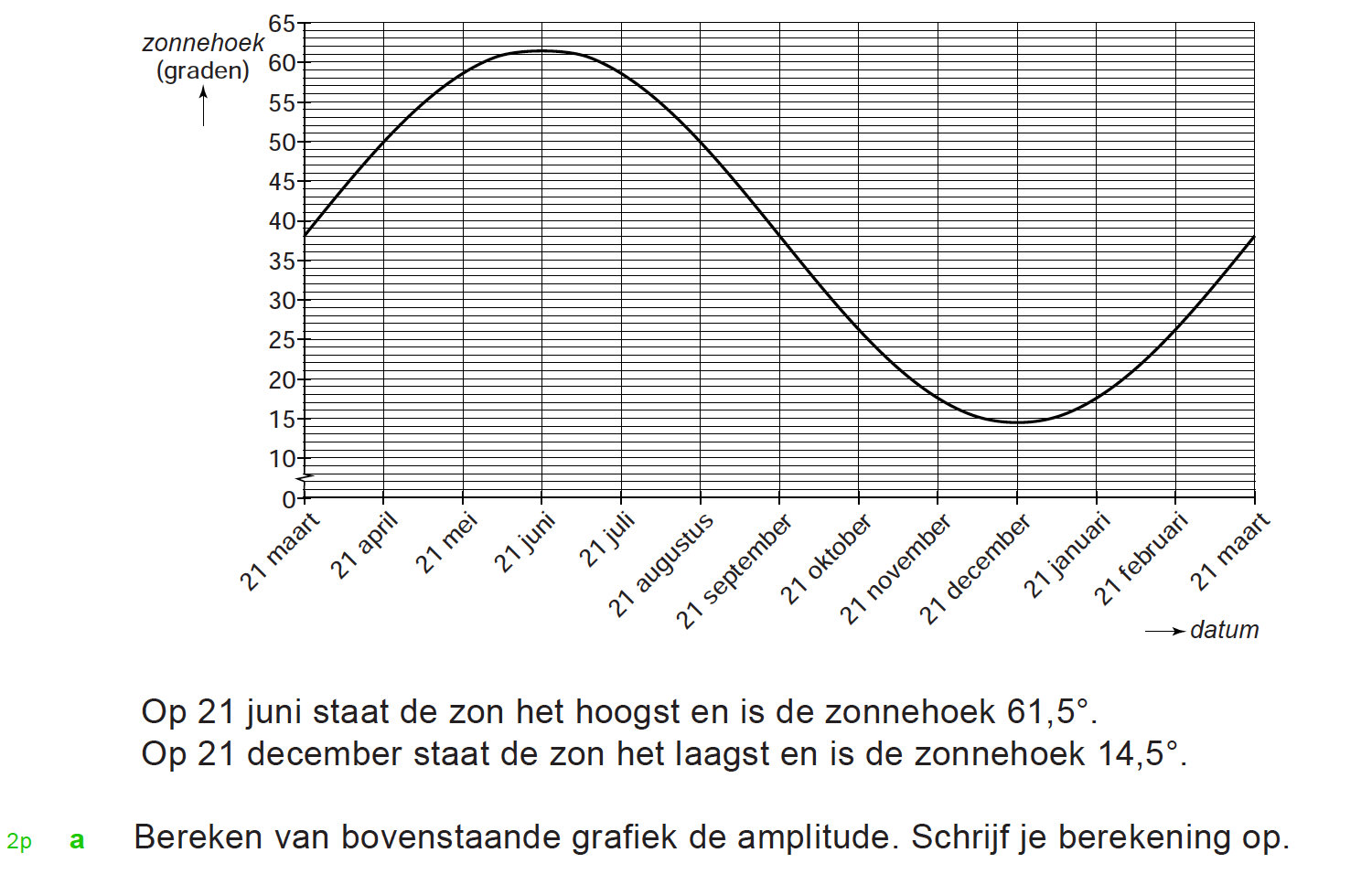
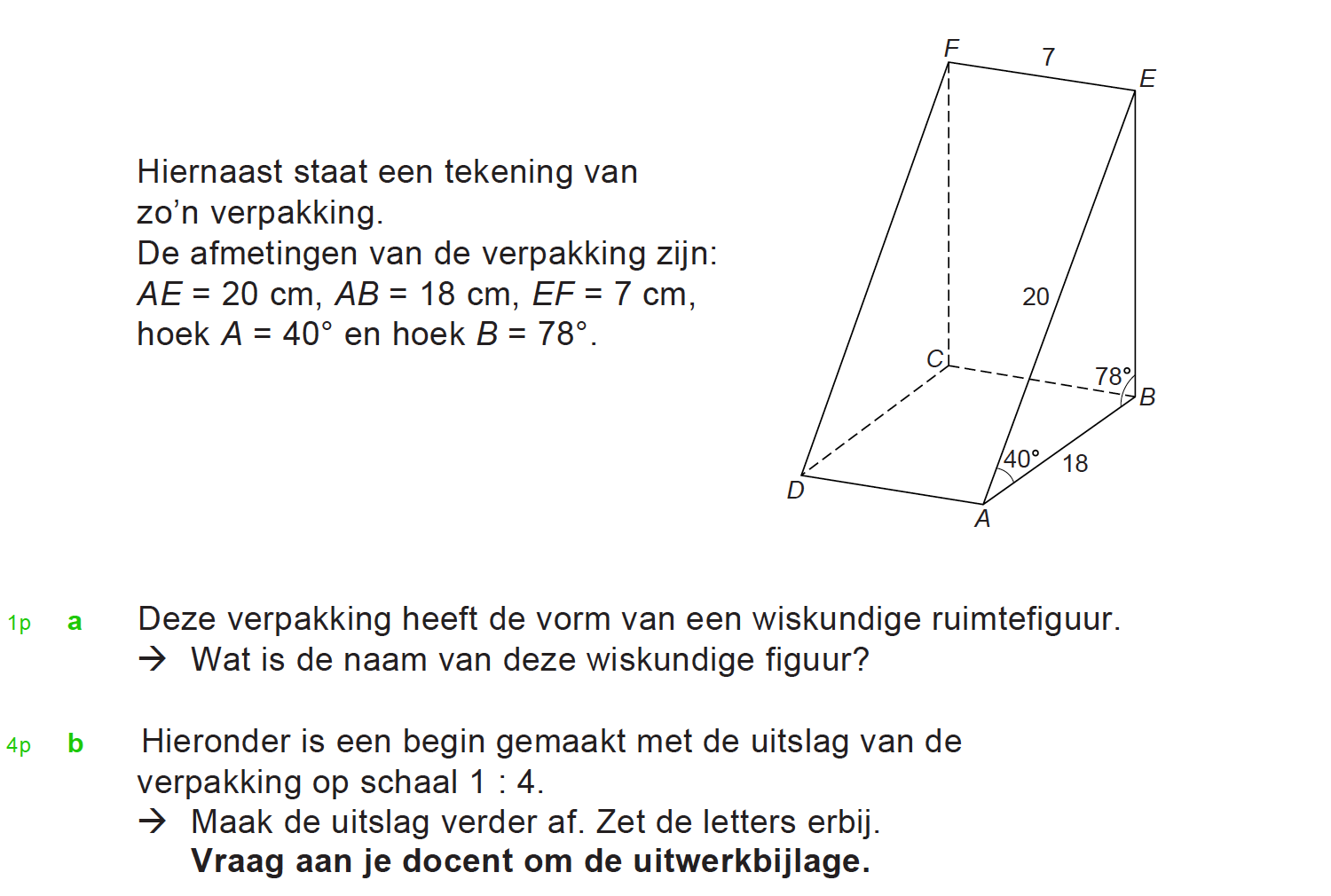
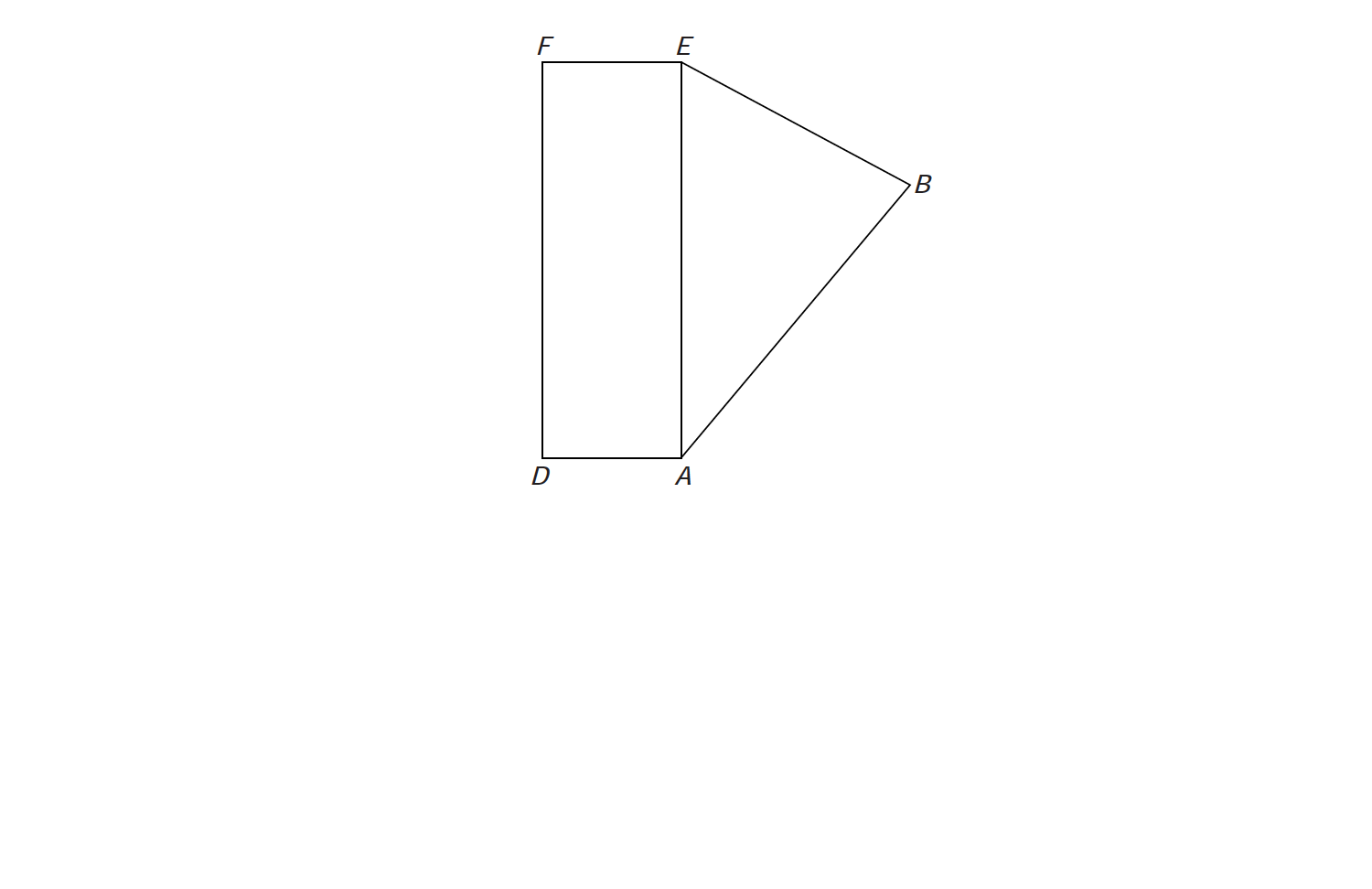
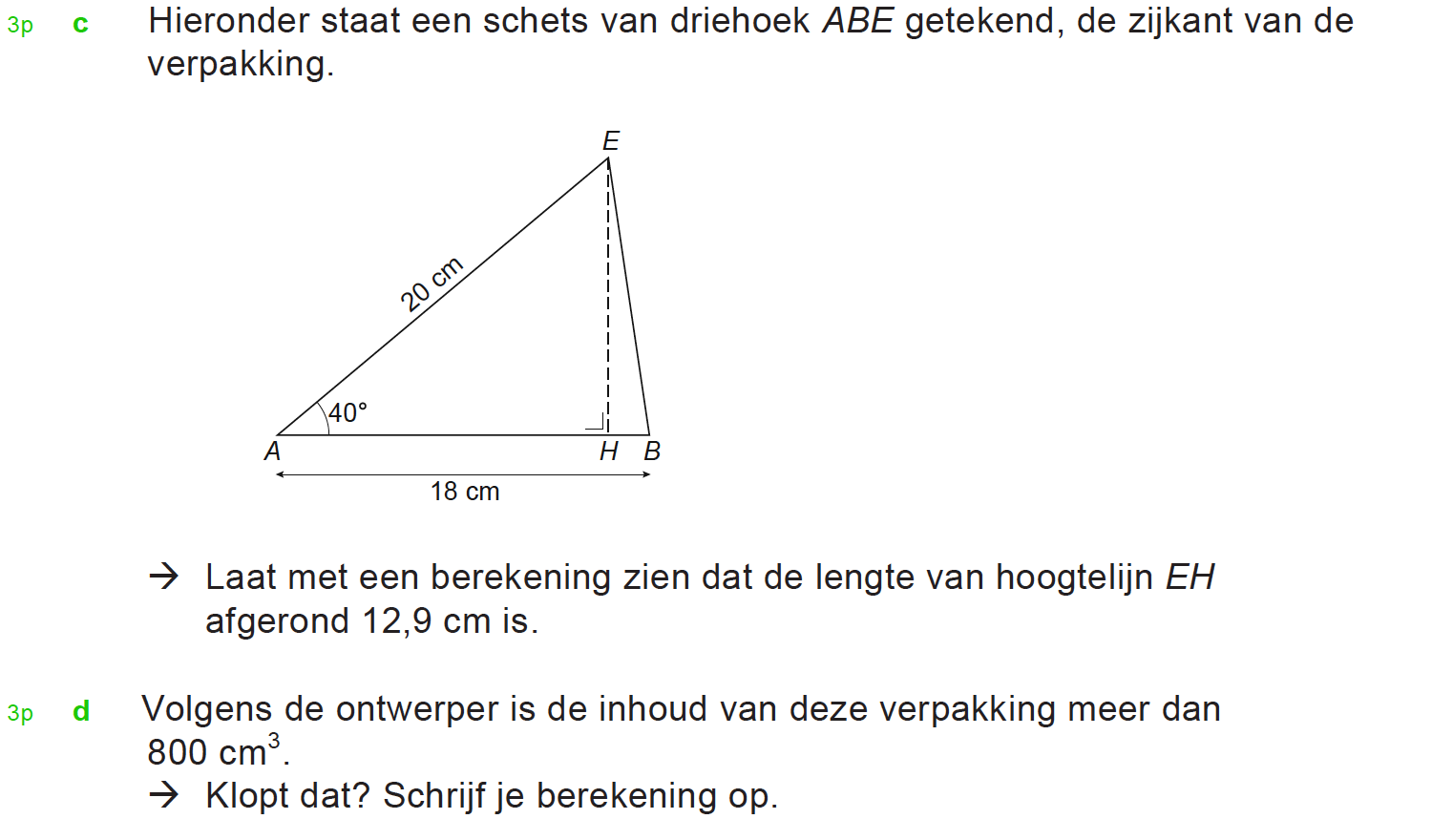
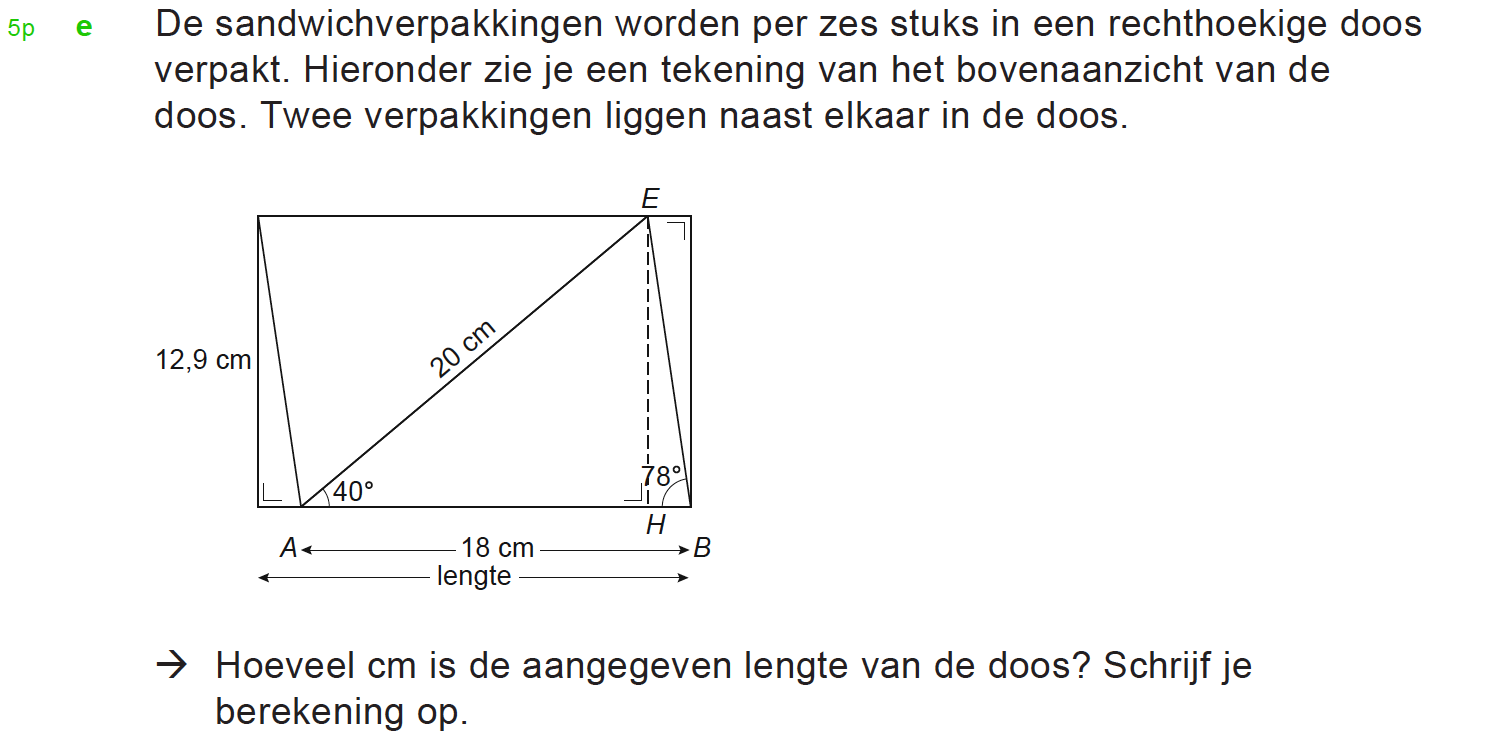
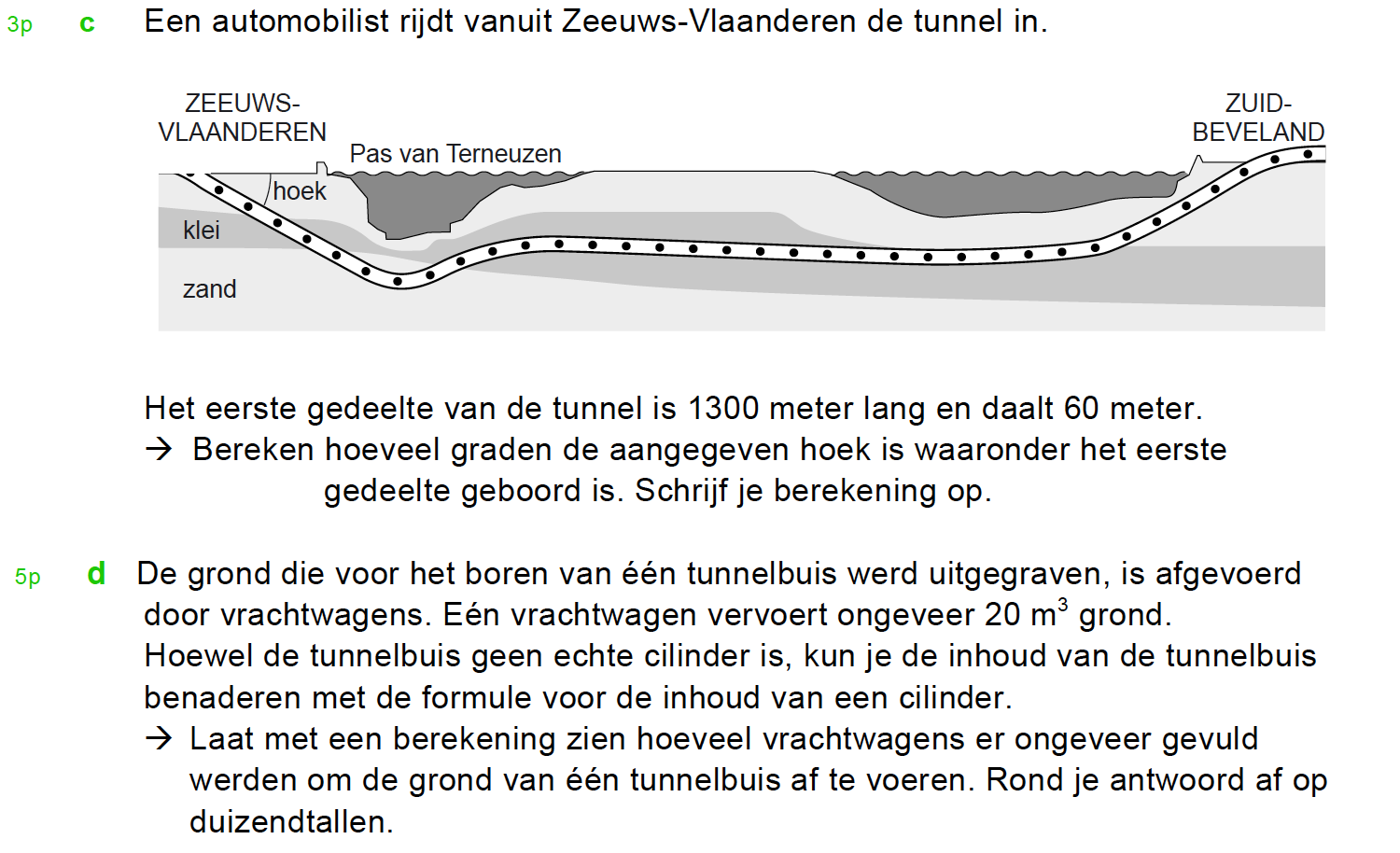
Hieronder een schets van een bouwkavel met een huis. De familie zoekt nog een plek voor de afvalcontainers. Deze willen ze zó op het terras plaatsen dat ze niet zichtbaar zijn vanuit de woonkamer.
Gegeven is de gelijkzijdige driehoek ABC met zijden van 35 cm. In de driehoek zijn de hoogtelijnen getekend. Deze hoogtelijnen snijden elkaar in punt S.
Uitwerkbijlage omgaan met verbanden
Teken in deze figuur op de 
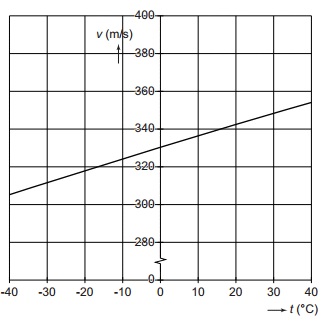
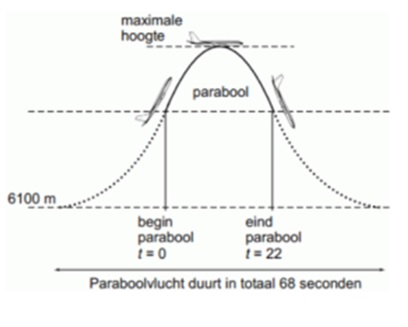
Het KNMI in De Bilt laat elke dag een weerballon op. Zo’n ballon is gevuld met heliumgas. Er hangt een zender aan de ballon, die gegevens over het weer doorgeeft.
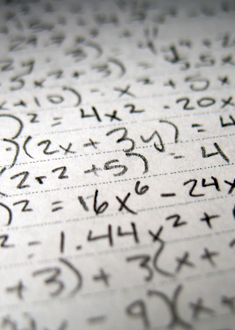
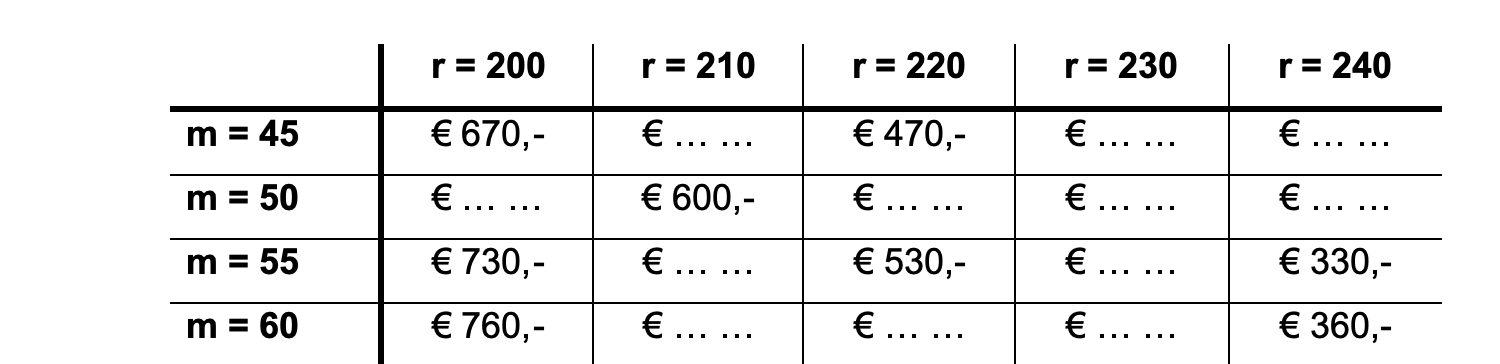
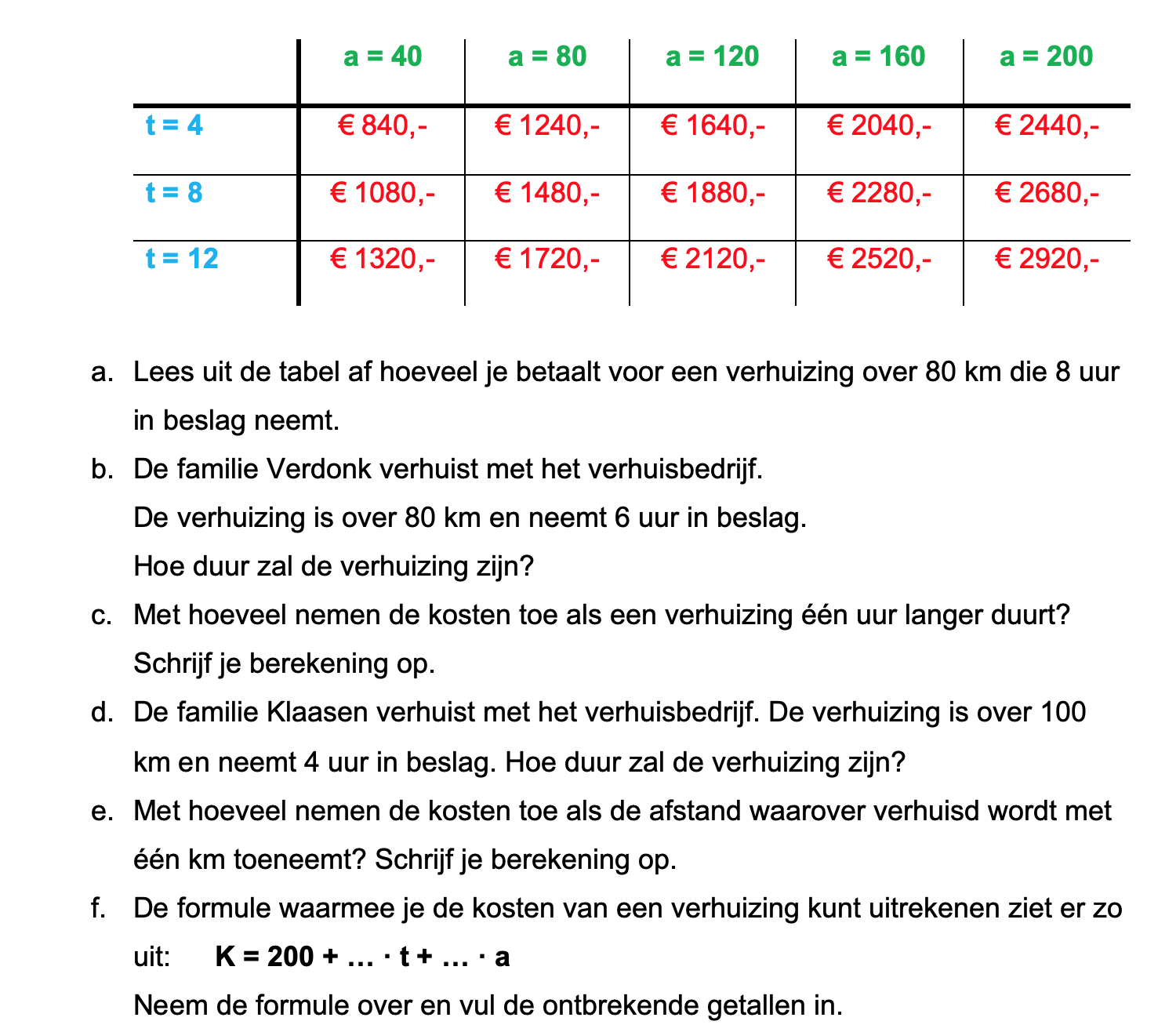
formule bij een tabel/verhaaltje voorbeeld 2
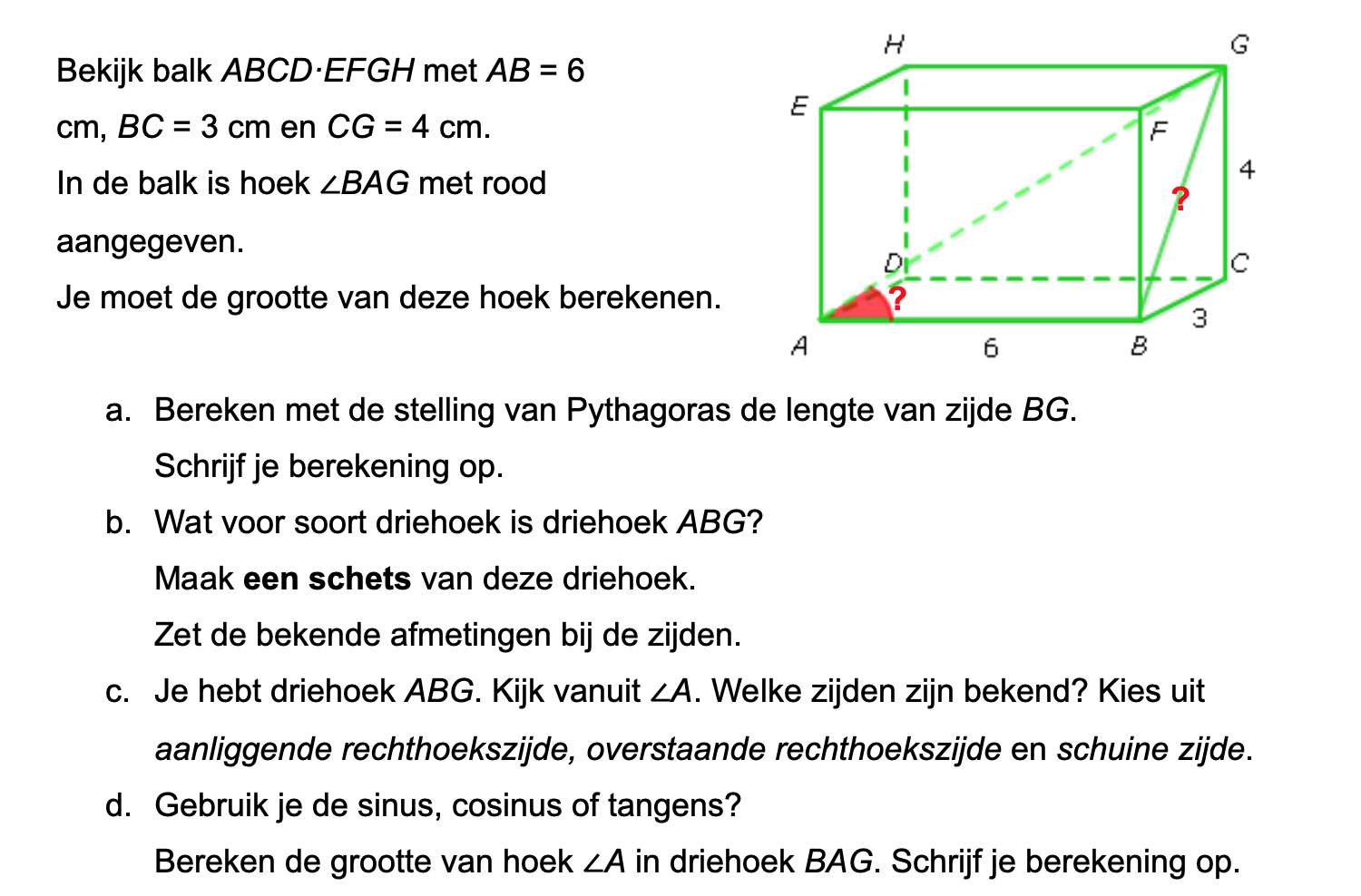
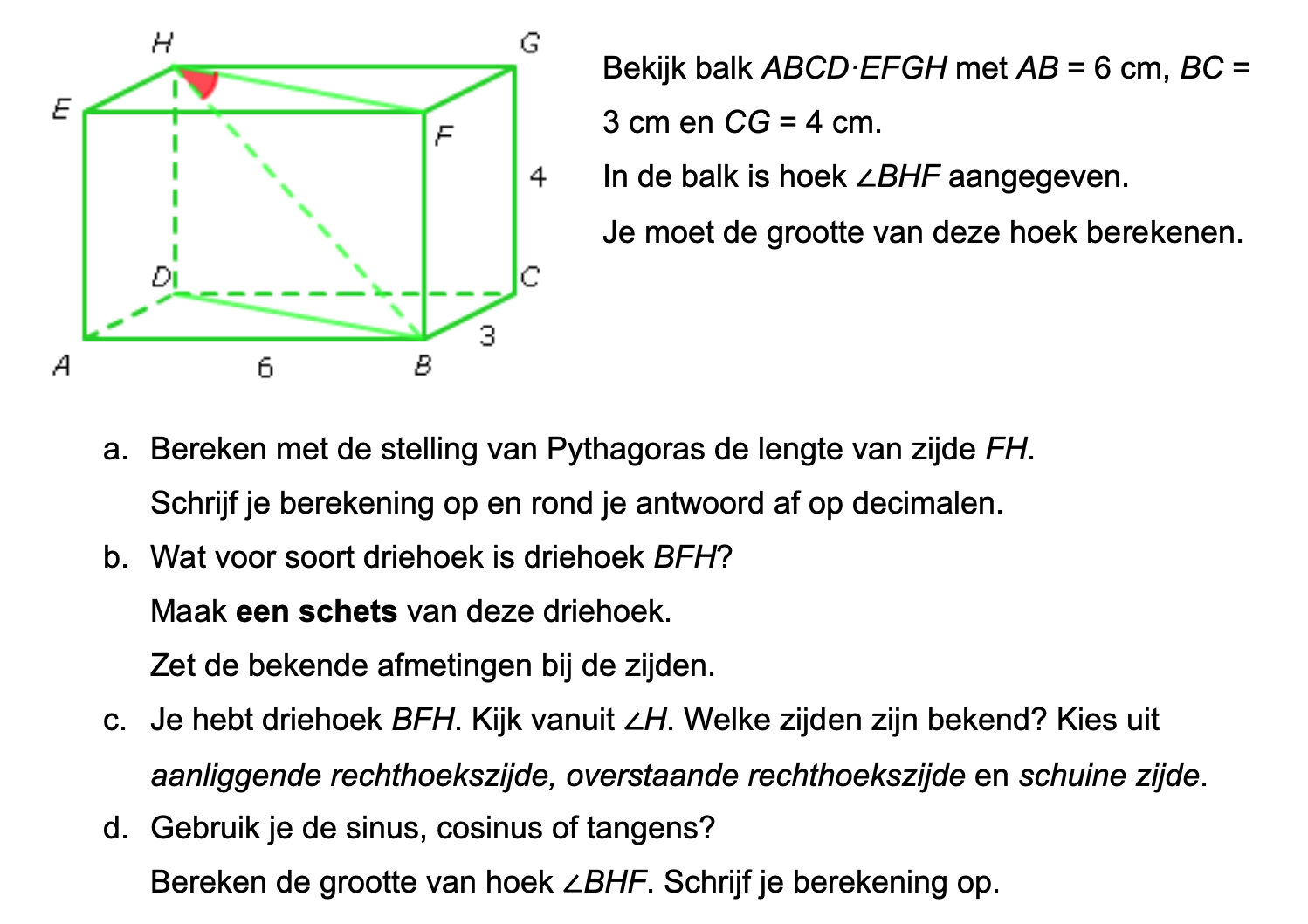
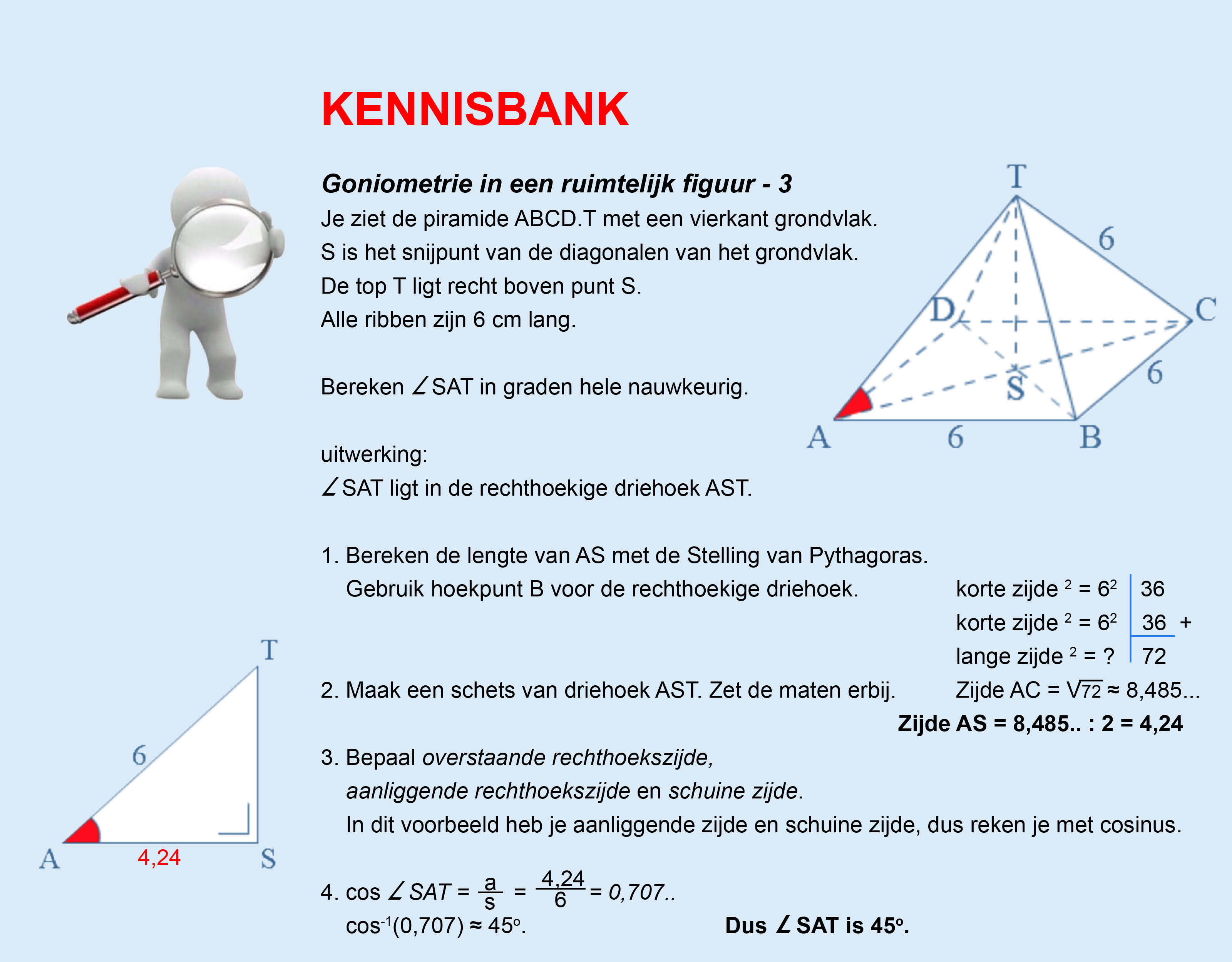
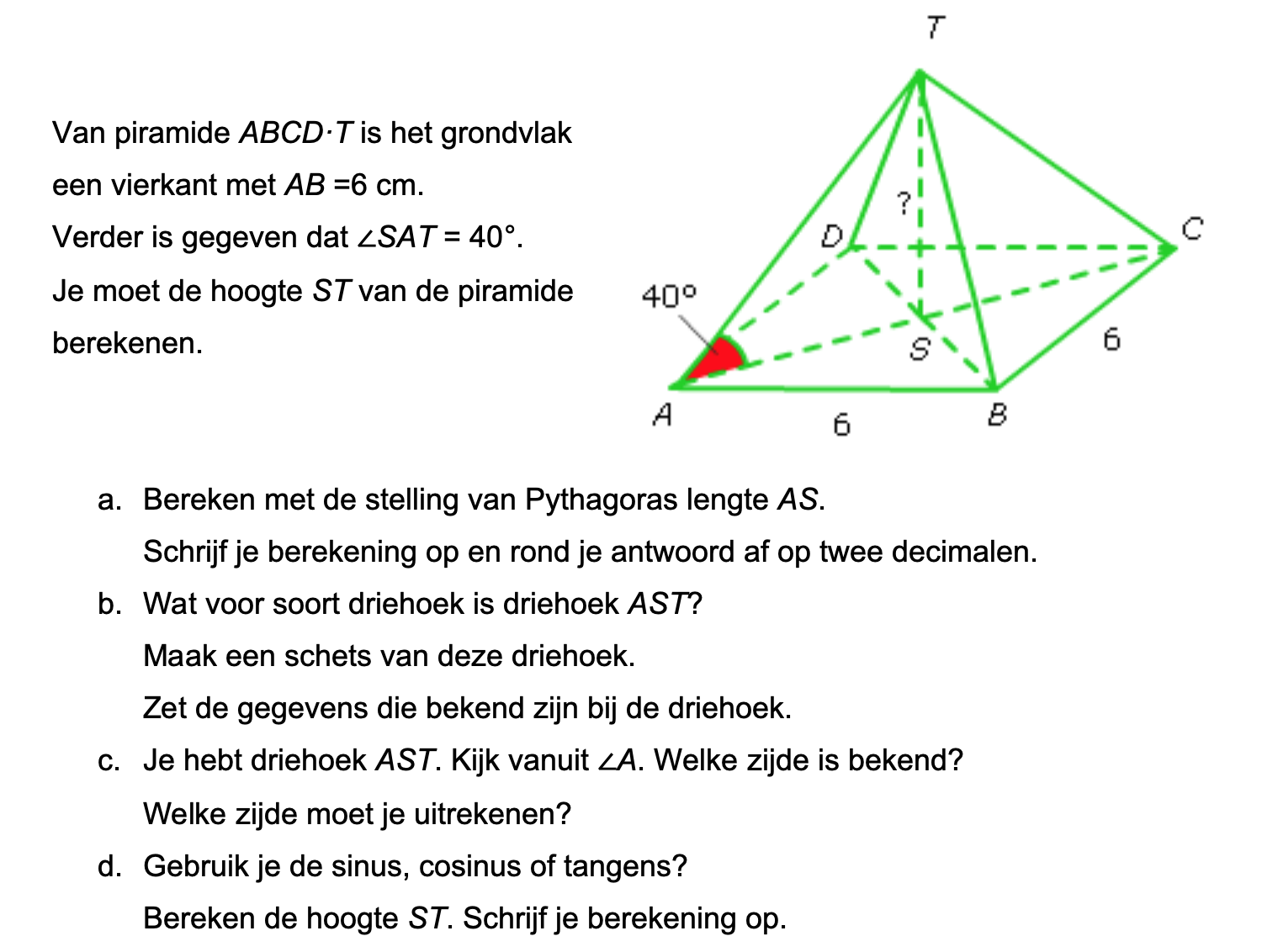
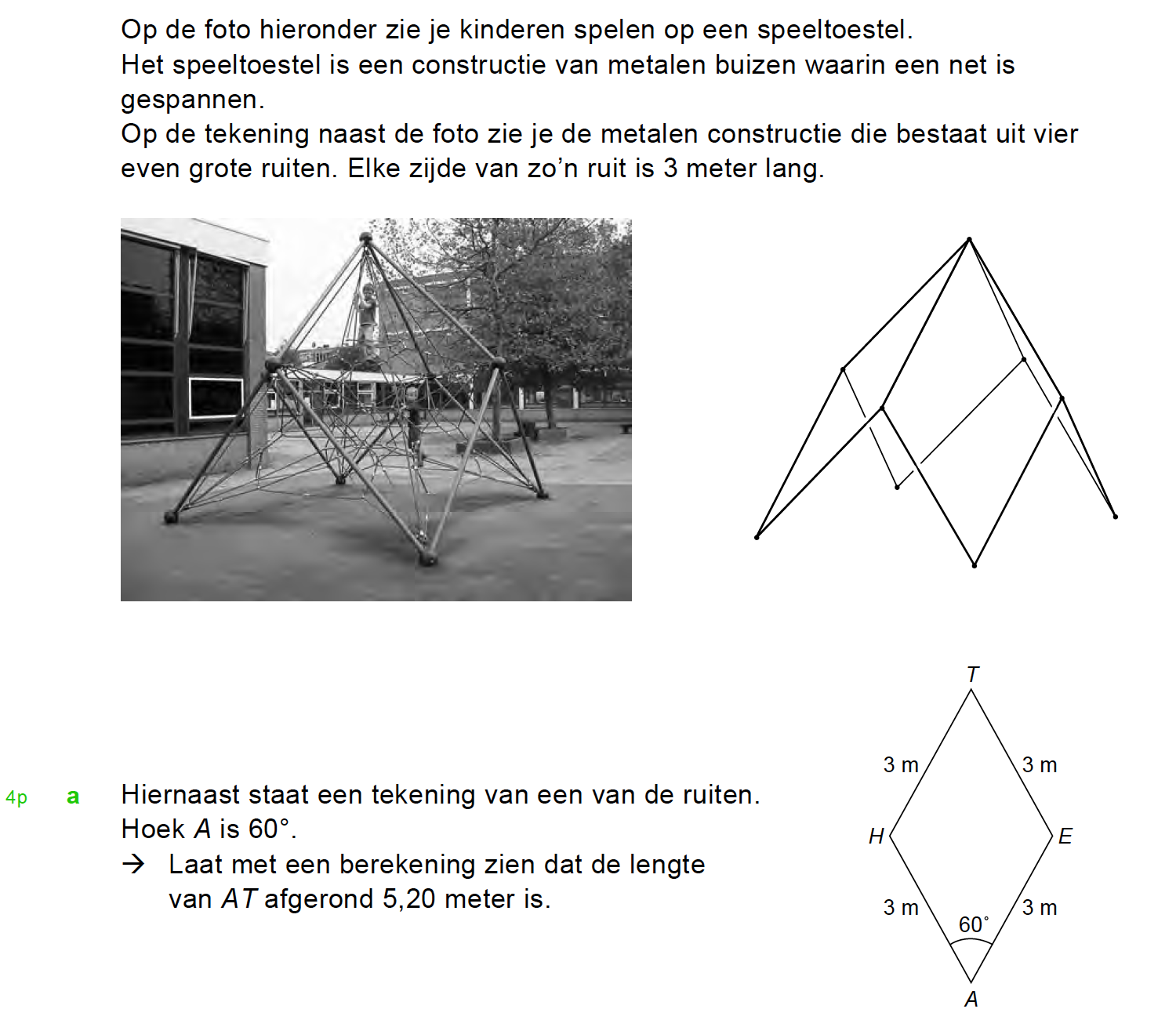
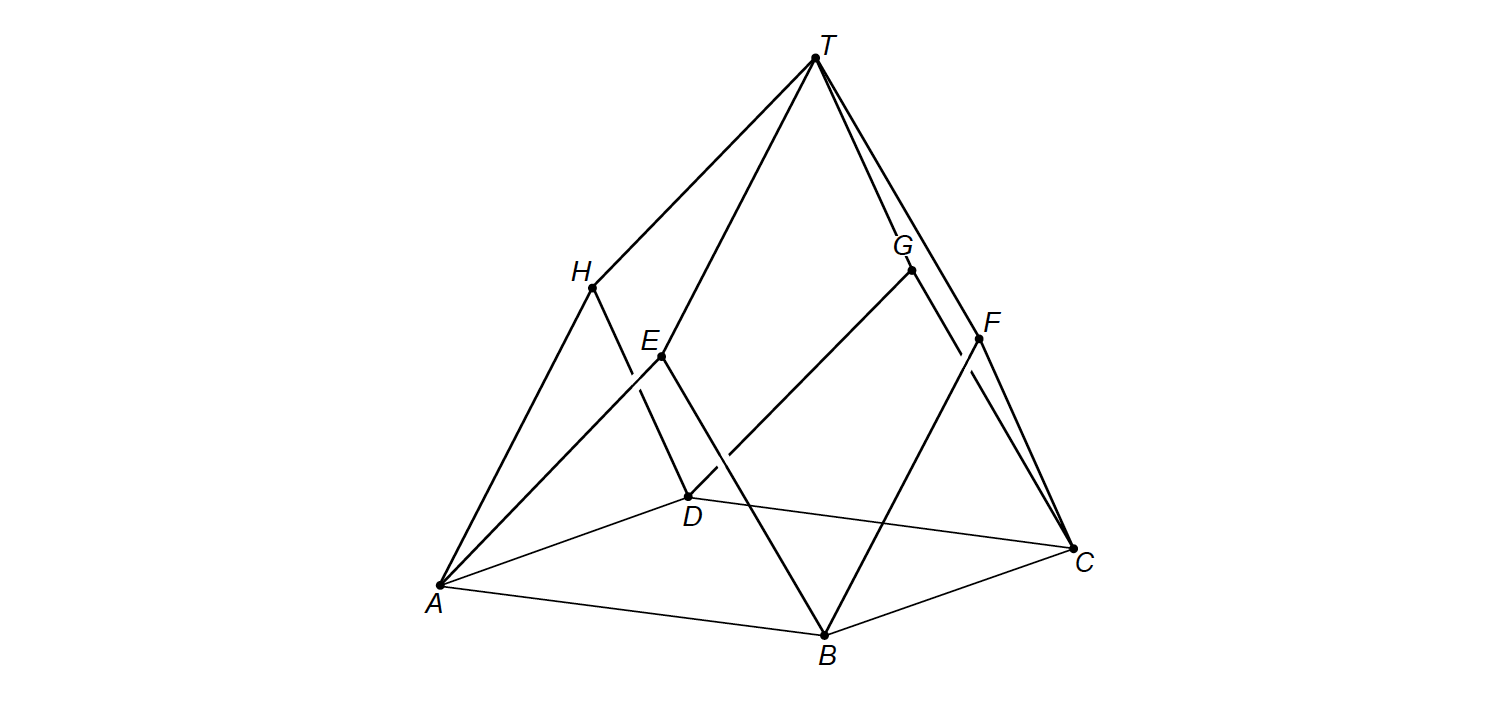
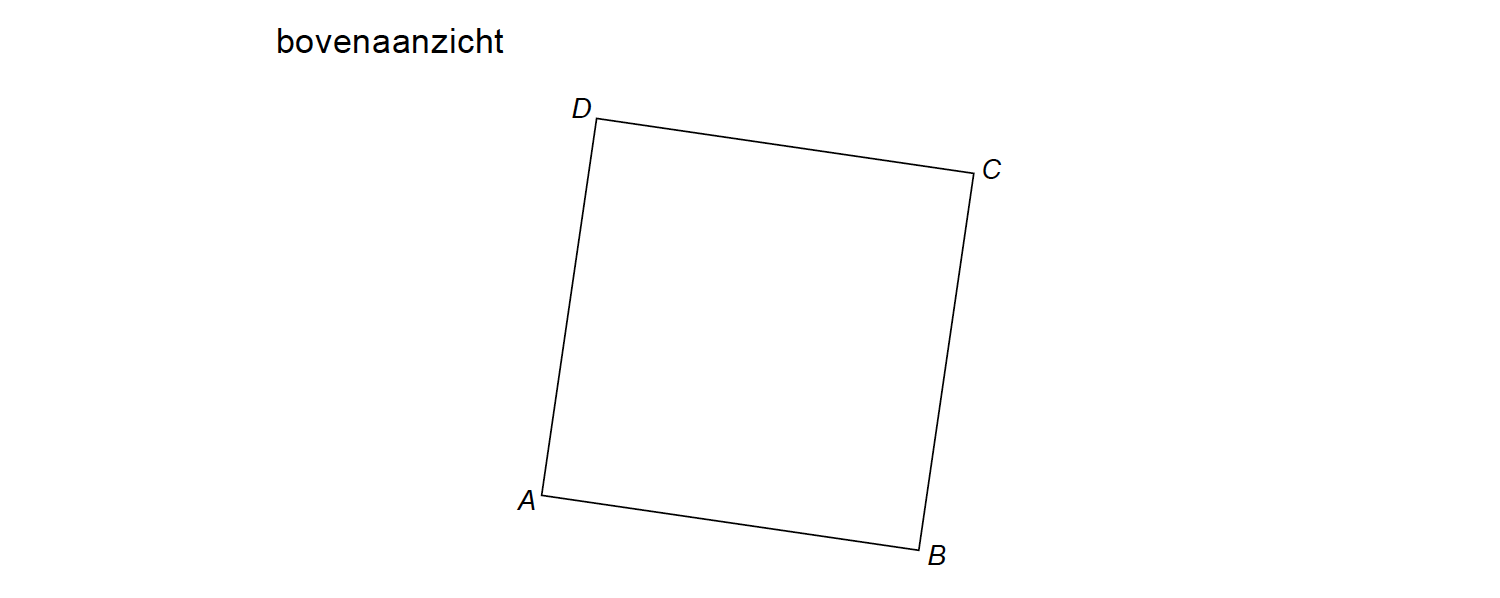
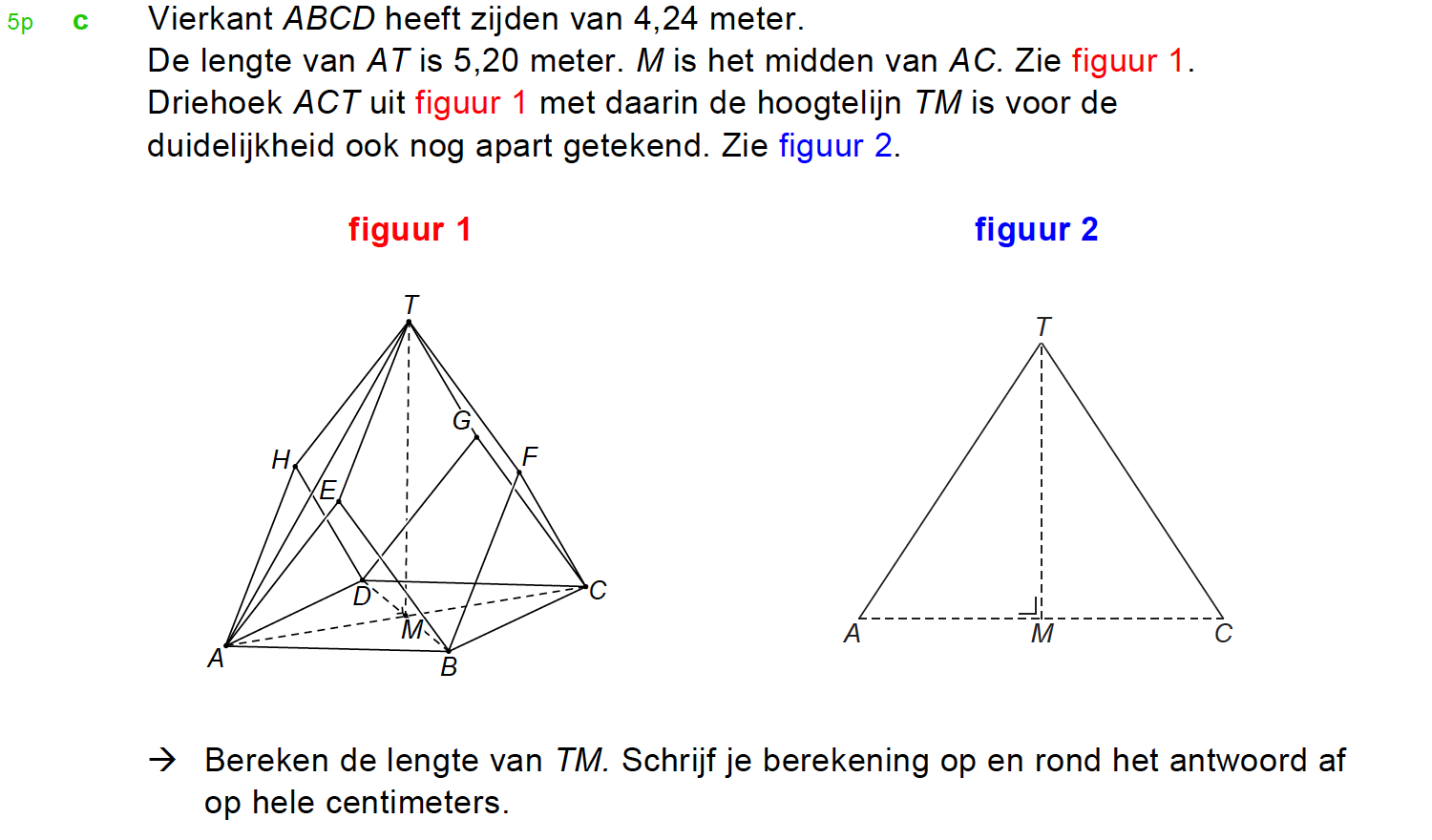
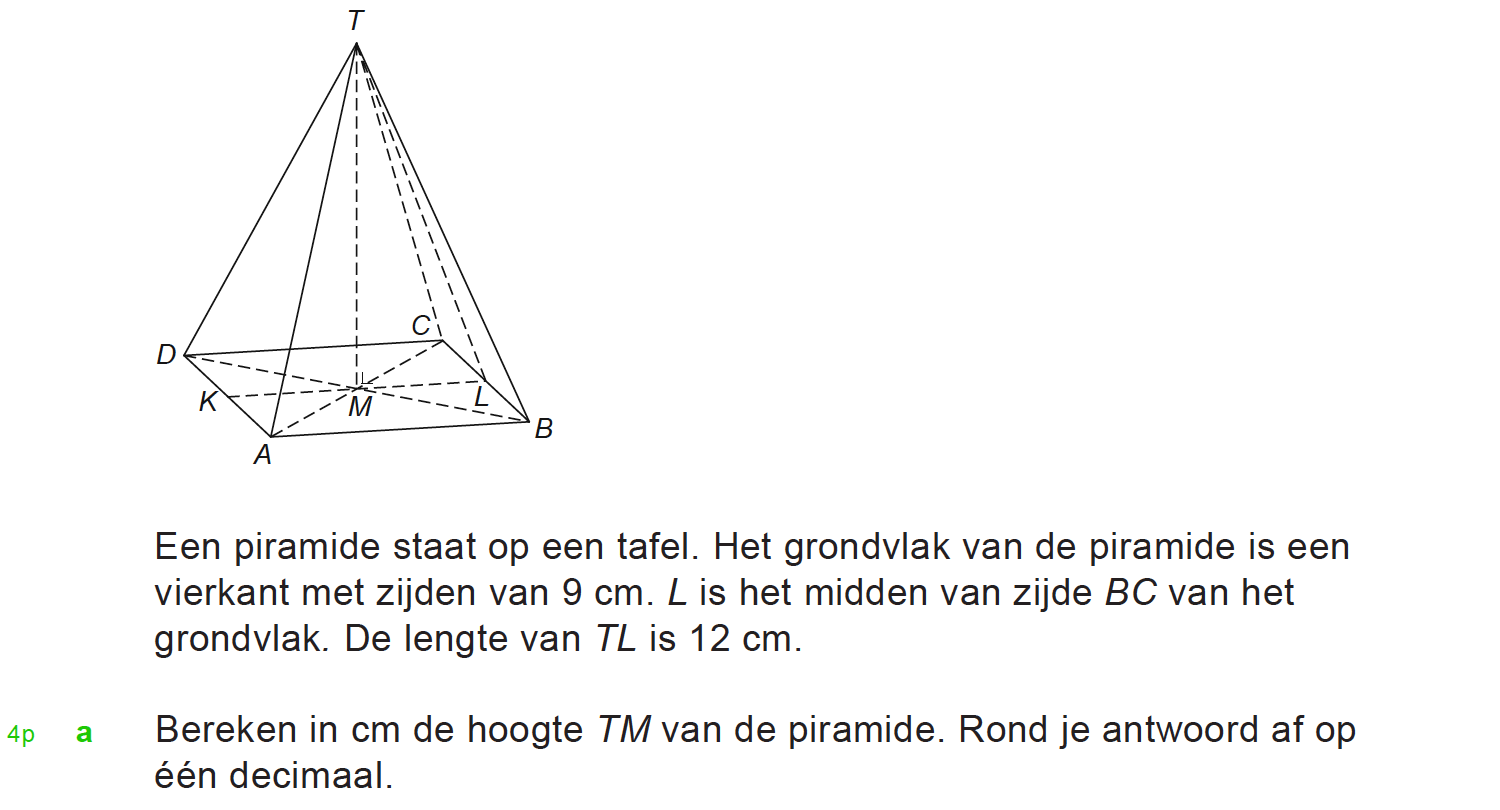
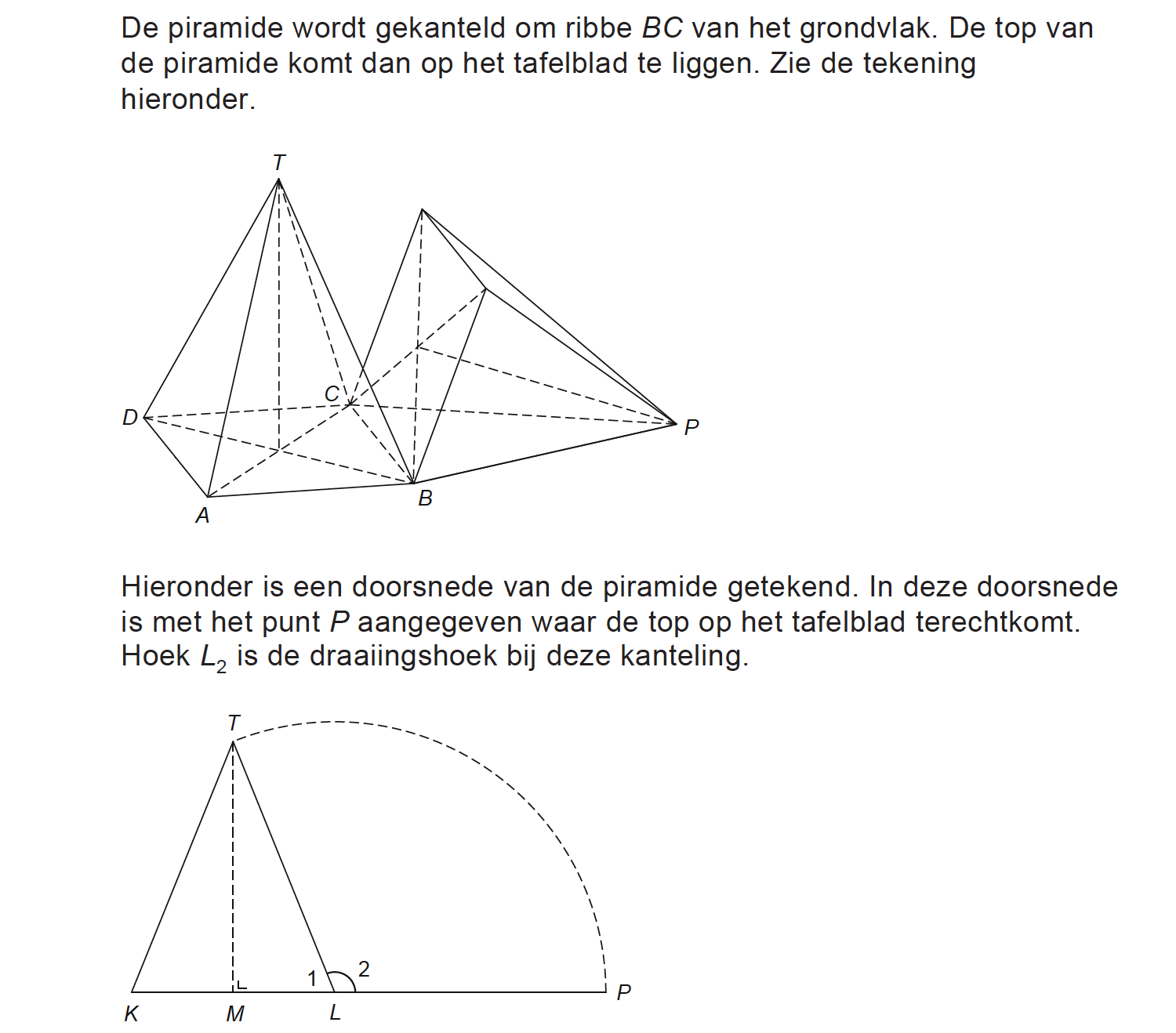
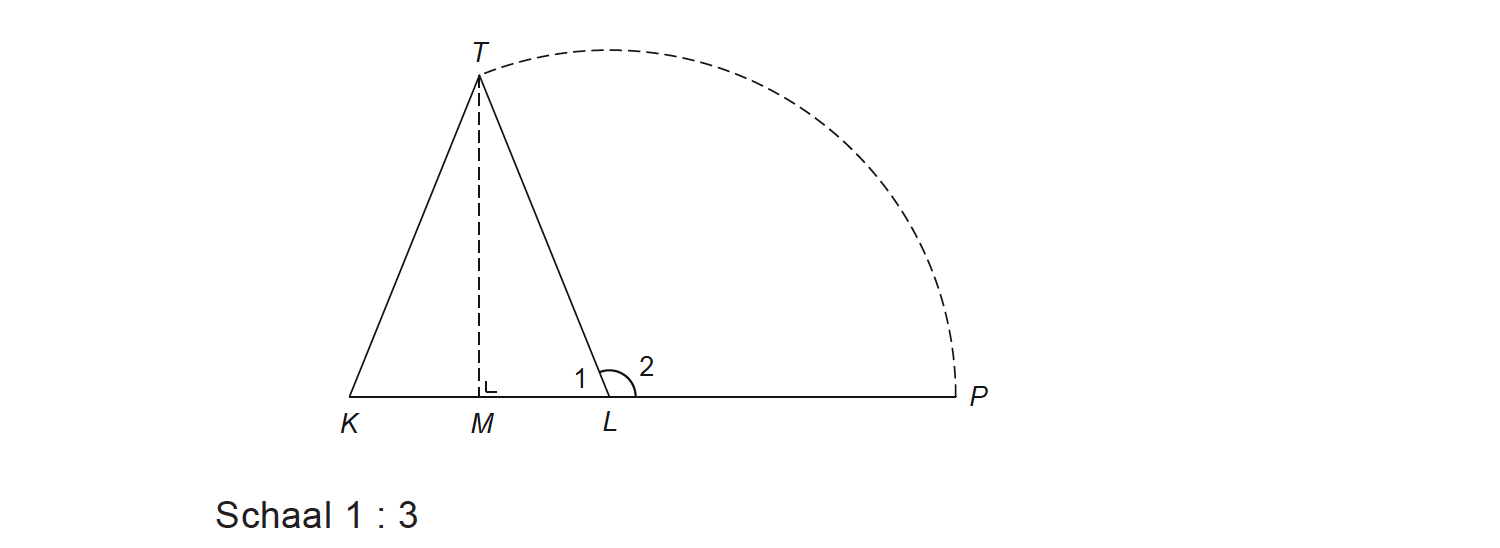
Goniometrie in de ruimte
