Het arrangement Licht is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 2016-04-11 20:56:48
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 3.0 Nederlands licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 3.0 Nederland licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- t.b.v. ROCMN Bouw & Interieur - Bouwkunde
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- breken, invalshoek, lens, licht, pentagonprisma, snellius, solatube, spiegelen

 De komende lessen ga je je bezig houden met licht. Hoe verplaatst het zich, wat gebeurt er bij overgang van de lichtstraal van lucht naar water. Hoe gebruik je het in de bouw, etc. etc.
De komende lessen ga je je bezig houden met licht. Hoe verplaatst het zich, wat gebeurt er bij overgang van de lichtstraal van lucht naar water. Hoe gebruik je het in de bouw, etc. etc.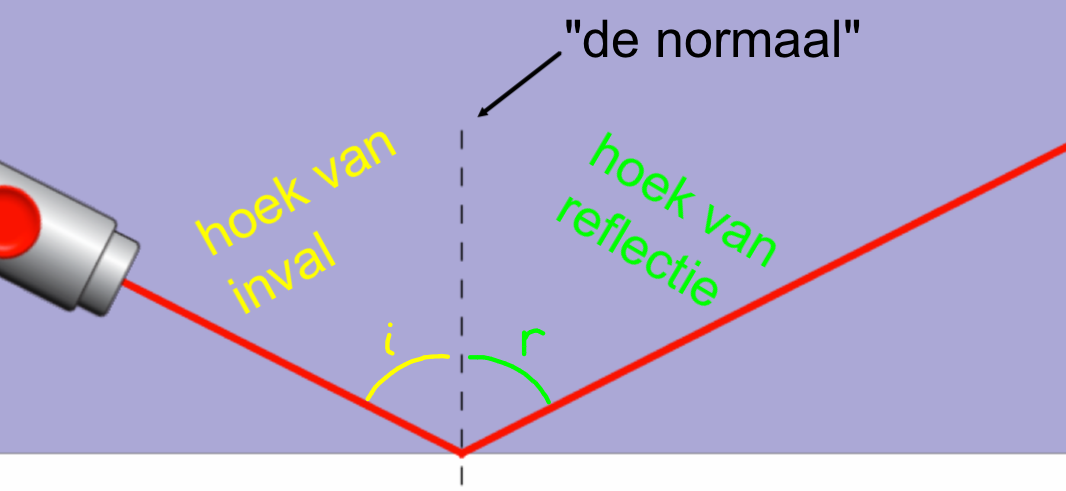 Wanneer lichtstralen zich in een homogeen (overal gelijk) medium voortplanten, doen ze dat volgens een rechte lijn.
Wanneer lichtstralen zich in een homogeen (overal gelijk) medium voortplanten, doen ze dat volgens een rechte lijn. 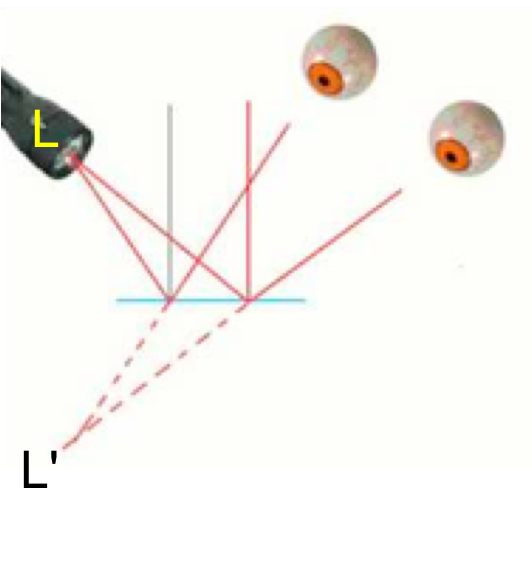 Als de stralen uit één punt komen (lichtpunt L), dan zullen ze na terugkaatsing uit één punt lijken te komen. Dit punt heet het spiegelbeeld L’. Omdat de lichtstralen niet echt uit dit beeld komen, wordt het beeld virtueel genoemd. Het spiegelbeeld ligt bij een vlakke spiegel even ver áchter de spiegel als het voorwerp er vóór staat.
Als de stralen uit één punt komen (lichtpunt L), dan zullen ze na terugkaatsing uit één punt lijken te komen. Dit punt heet het spiegelbeeld L’. Omdat de lichtstralen niet echt uit dit beeld komen, wordt het beeld virtueel genoemd. Het spiegelbeeld ligt bij een vlakke spiegel even ver áchter de spiegel als het voorwerp er vóór staat.
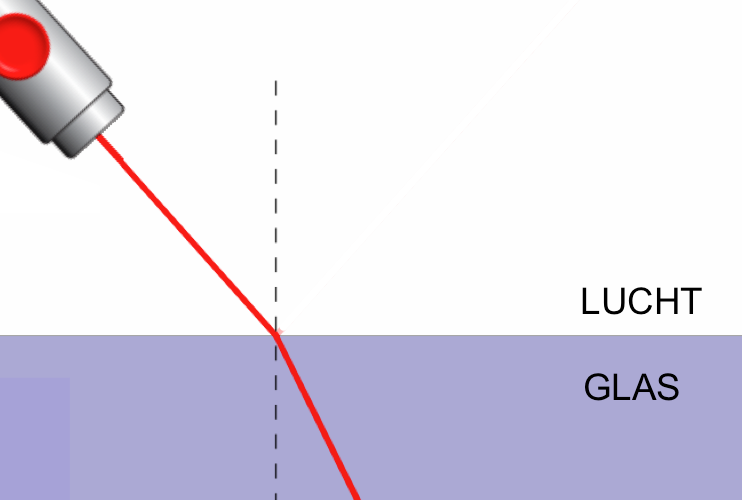

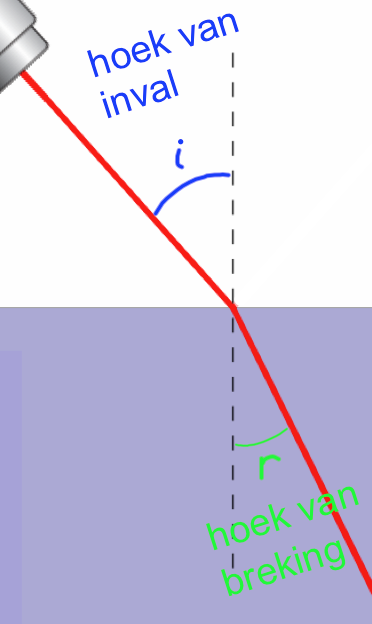
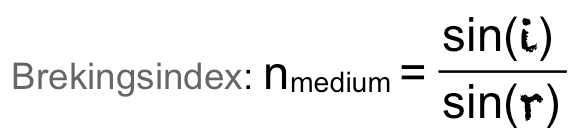

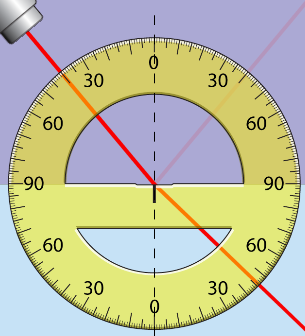
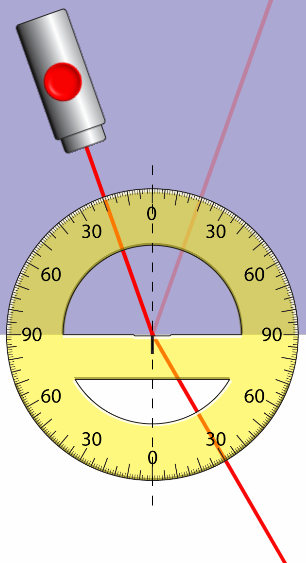 Wanneer een lichtstraal naar een medium met een lagere brekingsindex gaat, zal de hoek met de normaal groter worden. Zie de straal hiernaast die van glas naar lucht gaat.
Wanneer een lichtstraal naar een medium met een lagere brekingsindex gaat, zal de hoek met de normaal groter worden. Zie de straal hiernaast die van glas naar lucht gaat.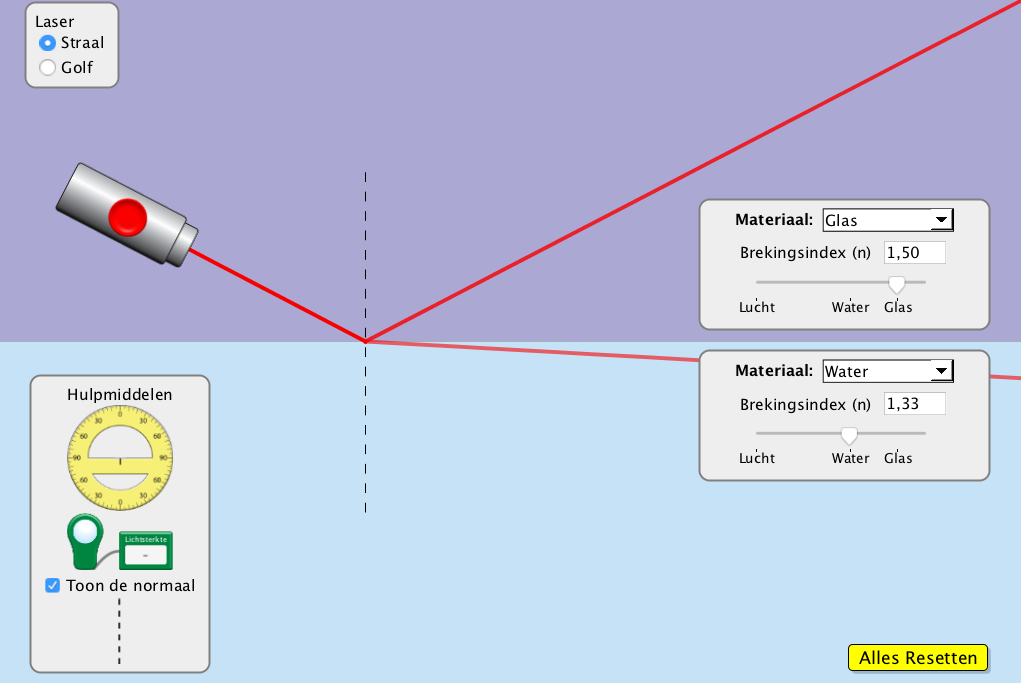


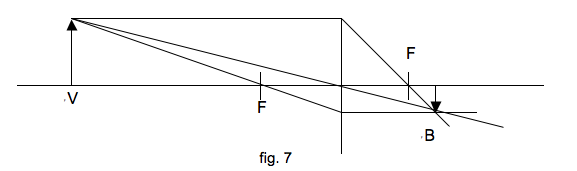
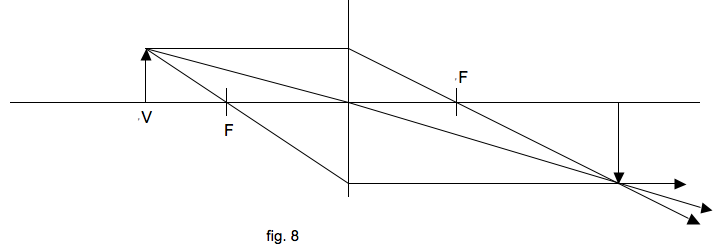
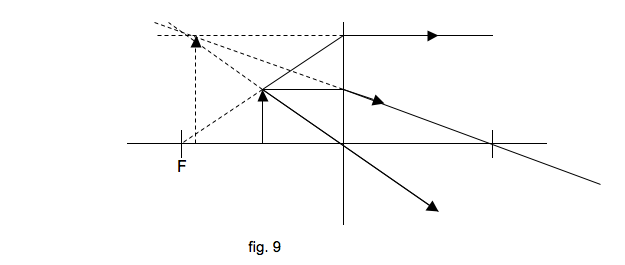

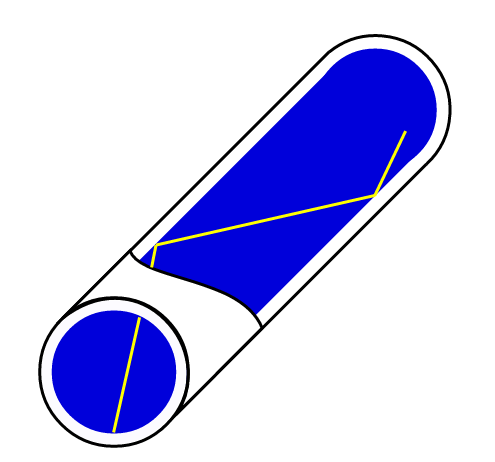
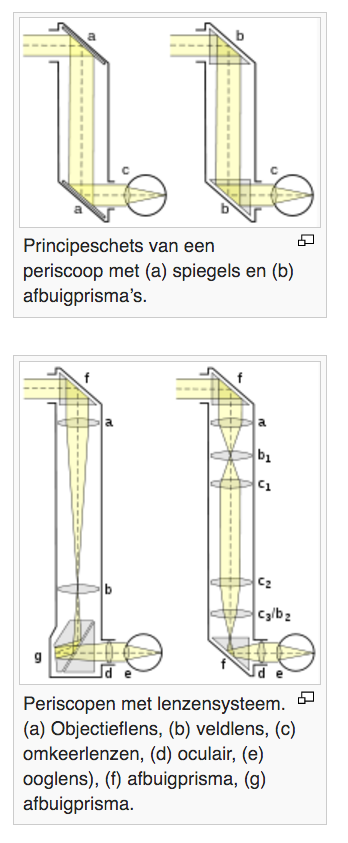 mogelijk in riolen of luchtkanalen te kijken zonder er zelf in te hoeven. Het maakt gebruik van twee prisma’s (elk met twee hoeken van 45º en één van 90º)
mogelijk in riolen of luchtkanalen te kijken zonder er zelf in te hoeven. Het maakt gebruik van twee prisma’s (elk met twee hoeken van 45º en één van 90º)
