Welkom bij de e-klas Medische Beeldvorming! In deze e-klas maak je kennis met medische technieken, en de natuurkunde achter die technieken.
Veel van de technieken die gebruikt worden bij het kijken in je lichaam maken gebruik van eigenschappen van atomen. Veel medische apparaten gebruiken bijvoorbeeld elektromagnetische straling om een beeld te maken. Voorbeelden van deze straling zijn radiogolven, radargolven, infrarood straling, licht, ultraviolet straling, röntgenstraling en gammastraling.
Naast beeldvorming, kan sommige straling ook gebruikt worden voor behandeling. Zulke zogenaamde nucleaire geneeskunde heeft tal van mogelijkheden. Niet alleen kunnen er diagnoses mee worden gesteld, maar het heeft ook een toepassing in het genezen van patiënten. Denk maar aan bestraling bij patiënten met tumoren.
Je zult na deze e-klas exact weten hoe een aantal belangrijke medische technieken werken.
Studiewijzer
Deze e-klas bestaat uit 7 hoofdstukken. De hoofdstukken zijn geordend op inhoud en hebben geen vaste volgorde, afgezien van hoofdstuk 1. Dat is het starthoofdstuk en moet als eerste doorlopen worden.
Daarna kan je in willekeurige volgorde kiezen tussen de hoofdstukken 2 t/m 5. Deze hoofdstukken moeten wel allemaal doorlopen worden.
Heb je dat gedaan, dan volgen de afsluitende hoofdstukken 6 en 7. Heb je die ook afgerond, dan heb je het gehele havo-examenprogramma voor medische beeldvorming doorlopen.
Schema van de cursus:
Leerdoelen
Als je deze e-klas hebt doorgewerkt, moet je:
1. weten welke verschillende soorten ioniserende straling er zijn (hs 2 en 3);
1.1. de soorten straling kunnen benoemen (hs 2 en 3);
1.2. eigenschappen van de verschillende soorten straling kunnen beschrijven (hs 2 en 3);
1.3. weten hoe je de verschillende soorten straling kunt opsporen (hs 6);
2. weten wat ioniserend en doordringend vermogen is (hs 3);
3. de effecten van ioniserende straling op mens en milieu kunnen beschrijven (hs 2 en 3);
4. toepassingen kunnen verklaren van ioniserende straling (hs 2 en 3);
5. weten hoe je je kunt beschermen tegen ioniserende straling (hs 6);
6. weten hoe de verschillende soorten straling worden opgewekt (hs 2 en 3);
7. Weten hoe een atoom is opgebouwd (hs 1);
8. Kunnen rekenen met halveringstijd (hs 3);
9. Een vervalvergelijking kunnen opstellen (hs 3);
10. Kunnen rekenen met eV en Joule (hs 3);
11. Kunnen rekenen met de formules: A = N+Z, H= QD, E= Dm (hs 1 en 6).
Inleiding
Inleiding
In de film zie je de ambulance die na een ongeluk met spoed naar het ziekenhuis gaat. In de ambulance ligt het slachtoffer van een verkeersongeluk. Op de spoedeisende hulp wordt de patient onderzocht. Als niet op het eerste gezicht duidelijk zichtbaar is wat het slachtoffer mankeert, moet er "in het lichaam" gekeken worden. Om in je lijf te kijken, hebben artsen allerlei verschillende technieken tot hun beschikking. Die technieken gaan we in deze lessen nader bekijken. De technieken waar we naar gaan kijken, zijn: röntgenstraling, nucleaire diagnostiek, MRI en echoscopie.
Bij elk van de technieken kijken we naar patiënten die er voor hun genezing afhankelijk van zijn.
H1 Achtergrondkennis
1 Achtergrondkennis
In dit hoofdstuk wordt de atoombouw besproken. We gebruiken hierbij het model dat rond 1910 werd ontwikkeld. Rutherford, Bohr en veel andere mensen hebben aan dit model gewerkt. Hun kennis heeft uiteindelijk ook tot het moderne atoommodel geleidt. Nog steeds is men bezig om atoommodellen te verbeteren en te perfectioneren. Over dit werk kun je lezen in wetenschappelijke tijdschriften. Soms komt wetenschappelijk werk zelfs in het gewone nieuws. Een bekend voorbeeld daarvan is de zoektocht naar het Higgs-deeltje. Dit behoort echter niet tot de examenstof en zal daarom in deze e-klas niet besproken worden.
1.1 Atoombouw
Inleiding
Veel technieken waarmee wordt gekeken in je lichaam, maken gebruik van eigenschappen van atomen. Al heel lang denken mensen na over wat materie is en waaruit het bestaat. De Grieken hadden al voorstellingen van het 'inwendige' van alle materie. Empedocles dacht dat alle materie was opgebouwd uit de vier elementen: vuur, water, lucht en aarde. Plato hield het erop dat je materie tot in het oneindige kon delen. Iemand die al een notie had van hoe het werkelijk zat, was Democritus. Hij ging ervan uit dat je niet verder kon gaan dan een kleinste ondeelbare stukje materie: het atoom, afgeleid van het Griekseatomos, dat ondeelbaar betekent. Na de Grieken hebben nog meer mensen zich met het atoom bezig gehouden, maar pas in de negentiende en twintigste eeuw is het huidige model voor atomen ontstaan. Dit model is nog niet helemaal af en wordt nog steeds bijgesteld door de uitkomsten van allerlei nieuw onderzoek.
Om de werking van apparaten in het ziekenhuis te begrijpen, is het atoommodel van de Deen Niels Bohr voldoende, met enkele aanvullingen over de samenstelling van de atoomkern. Hoewel het niet de perfecte beschrijving van een atoom biedt, is het wel geschikt om verschijnselen als röntgenstraling en radioactiviteit te verklaren.
Opdracht
Er is een lange weg afgelegd voordat we tot een goed model zijn gekomen om de eigenschappen van een atoom te verklaren. Er zijn twee verschillende modellen die veel kunnen verklaren van de eigenschappen die we gebruiken in de geneeskunde: het model van Rutherford en het model van Bohr. Die twee modellen gaan jullie in deze opdracht onderzoeken. Het resultaat van je onderzoek is een verslag.
Zoek op wat de atoommodellen van Rutherford en Bohr precies inhouden. Maak een tekening van beide modellen.
Beschrijf de verschillen tussen de modellen.
Welke problemen heeft het model van Bohr opgelost, vergeleken met het model van Rutherford?
Geef een omschrijving van de volgende begrippen:
* neutron
* elektron
* proton
* elektronvolt
* K-schil
* energieniveau
* aangeslagen toestand
* atomaire massa-eenheid
Leg het verband tussen atoomnummer en massagetal uit aan de hand van de formule A= N + Z. Geef aan wat de letters A, N en Z betekenen.
1.2 Straling
Elektromagnetische straling
Veel medische apparaten gebruiken elektromagnetische straling om een beeld te maken. Voorbeelden van deze straling zijn radiogolven, radargolven, infrarode straling, licht, ultraviolette straling, röntgenstraling en gammastraling. Al deze golven planten zich voort met de lichtsnelheid (in het luchtledige bijna 300 000 km/s). De verschillende vormen van elektromagnetische straling onderscheiden zich van elkaar door hun golflengte.
Het plaatje geeft een overzicht van de elektromagnetische golven. De golflengte van röntgenstraling is bijvoorbeeld tussen de 0,1 en 10 nanometer, veel korter dan die van zichtbaar licht. Een nanometer is 10-9 meter, ofwel een miljoenste millimeter.
Verband tussen golflengte en frequentie
Als je goed naar de afbeelding kijkt, zie je dat de frequentie lager wordt naarmate de golflengte groter wordt. Het verband tussen de golflengte en de frequentie van een golfverschijnsel wordt gegeven door de volgende formule:
λ = c/f
In de formule is c de voortplantingssnelheid (in m/s); λ is de golflengte (in m) en f is de frequentie (in Hz).
Men stelt zich elektromagnetische golven voor als twee loodrecht op elkaar staande golven, de elektrische en de magnetische component. Hun snijlijn geeft de voortplantingsrichting van de golf (zie de figuur hieronder).
Door elektromagnetische straling wordt energie vanuit een bron naar de omgeving overgedragen; hoe hoger de frequentie, des te groter de energie die wordt overgebracht. In het begin van de 20e eeuw bleek uit heel nauwkeurig onderzoek van elektromagnetische golven dat deze golven bestaan uit heel kleine golfdeeltjes die we fotonen noemen. Een foton vertegenwoordigt het kleinst mogelijke brokje (licht)energie van een elektromagnetische golf. De energie van een dergelijk brokje, de fotonenergie, hangt af van de frequentie: hoe groter de frequentie, des te groter de energie. De energie van een foton kun je berekenen met de volgende formule:
E = h · f
In de formule is E de energie van het foton in Joule (J), f is de frequentie in hertz (Hz) en h is de constante van Planck: h = 6,62607.10-34J · s
Fotonen kunnen reageren met geladen deeltjes, zoals de elektronen in een atoom. Op die manier kunnen fotonen van het zichtbare licht chemische reacties veroorzaken (denk aan de fotosynthese bij groene planten, aan zintuigcellen in het oog en aan de werking van fotofilm).
De frequentie van röntgenstraling is zeer hoog. De energie van röntgenfotonen is dus ook veel groter dan die van lichtfotonen. Fotonen van röntgenstraling kunnen daardoor moleculen in ons lichaam beschadigen, wat uiteraard gevaarlijk is voor de gezondheid. Dit bespreken we verder in het hoofdstuk over röntgenstraling.
Waar/Niet waar-vraag
Opdracht
Schrijf de antwoorden in je schrift.
1. Zoek in Binas de tabellen op waar natuurconstanten, grootheden en eenheden in staan.
2. Zoek de waarden en eenheden van de volgende grootheden op:
a. lichtsnelheid (c)
b. constante van Planck (h)
c. elementair ladingsgetal (e)
d. elektronvolt (eV)
3. Reken de energie om: 3 (J) = .... (eV)
4. Bereken de fotonenergie (J en eV) van een röntgenfoto die gebruikt maakt van fotonen met een golflengte van 5,00 nm.
5. Zoek in Binas de tabellen voor het elektromagnetische spectrum op.
1.3 Kernstraling
De Frans-Poolse wetenschapper Marie Curie heeft aan het eind van de 19e eeuw onderzoek gedaan naar onder meer de nieuwe elementen polonium en radium. Zij ontdekte dat er van die elementen straling afkwam in de vorm van deeltjes. Om ze een naam te geven, heeft ze de eerste drie letters van het Griekse alfabet gebruikt. Deze namen zijn blijven bestaan. De eerst ontdekte vorm heet dus alfastraling (of α-straling), de tweede en de derde heten respectievelijk bèta- en gammastraling (of β- en γ-straling).
Deze straling bleek afkomstig uit de atoomkern en wordt daarom ook wel kernstraling genoemd. Eigenschappen van deze stralingssoorten zijn het ioniserende vermogen en het doordringende vermogen.
Opdracht
Zoek aan de hand van de onderstaande tabel informatie op over deze stralingsvormen.
1. Neem de onderstaande tabel over in je schrift, maak hem compleet en beantwoord daarmee de volgende vragen.
Uit welke deeltjes bestaat deze straling?
Welke elektrische lading heeft deze straling?
Hoe groot is het ioniserend vermogen in kwalitatieve termen?
Hoe groot is het doordringende vermogen van deze straling?
bestaat uit
lading
ioniserend vermogen
doordringend vermogen
alfa
bèta
gamma
2. Rangschik de soorten straling op doordringend vermogen. De meest doordringende het eerst.
Doe dit ook voor het ioniserend vermogen. Wat valt je op? Leg uit.
3. Leg uit waardoor alfastraling een veel groter ioniserend vermogen heeft dan bètastraling.
4. Zoek op hoe en waarmee men zich kan beschermen tegen de verschillende soorten straling.
Een kern bestaat uit protonen en neutronen. De atoomsoort (ofwel het element) wordt bepaald door het aantal protonen: helium heeft 2 protonen, uranium heeft er 92. Het aantal protonen wordt atoomnummergenoemd en aangeduid met Z. Voor een bepaald element kan het aantal neutronen nog iets verschillen. De meeste heliumkernen hebben 2 protonen en 2 neutronen, maar heliumkernen met 1 neutron komen ook voor. Een koolstofkern heeft 6 protonen en meestal ook 6 neutronen, maar 8 neutronen komt ook voor (dat noemen we "koolstof 14", dus met 14 kerndeeltjes). Atomen met hetzelfde aantal protonen maar een verschillend aantal neutronen worden isotopen genoemd. Het totale aantal kerndeeltjes, dus protonen en neutronen, wordt massagetal genoemd en aangeduid met A. Het massagetal van gewone koolstof is 12, maar het massagetal van de isotoop met 8 neutronen is 14.
Een van de bijzondere verschijnselen bij straling is dat elke isotoop zijn eigen typerende eigenschappen heeft. Aan het soort straling, de energie, en de halfwaardetijd herkent men de isotoop. We zoeken daarom naar een mechanisme dat dit verklaart of waarmee we de verschijnselen kunnen uitleggen. Voor de eerste 20 elementen van het periodiek systeem geldt dat isotopen met een ongeveer gelijk aantal protonen en neutronen het stabielst zijn. Voor atomen met een hoger atoomnummer zijn er altijd meer neutronen dan protonen.
Stralingsdeeltjes
Wanneer in een kern het aantal neutronen en protonen niet in balans is, is de kern instabiel en kan een alfa- of bètadeeltje worden uitgezonden. Een kern kan ook aangeslagen zijn, in een hogere energietoestand verkeren en de extra energie uitzenden in de vorm van een gammadeeltje. In al deze gevallen zeggen we dat "verval" optreedt. De kern vervalt.
Halfwaardetijd
De tijd waarin een isotoop vervalt, varieert zeer sterk. De ene isotoop zal snel, in bijvoorbeeld 1 ms, vervallen en de andere isotoop doet er miljarden jaren over (bijvoorbeeld uranium-238). De grootheid die wij hieraan verbinden heet de halveringstijd of de halfwaardetijd. Deze halfwaardetijd is dus per isotoop verschillend.
Energie
De energie die vrijkomt bij straling is ook per isotoop verschillend. Bij alfa- en bètastraling is dit de kinetische energie van het alfa- of bètadeeltje. Die kan gemeten worden door bijvoorbeeld de snelheid van het deeltje te bepalen. Bij gammastraling wordt de energie bepaald door de frequentie te meten.
De genoemde eigenschappen vind je terug in de Binas, in tabel 25 van isotopen.
We komen hierop terug in hoofdstuk 3, in de paragraaf over de gammacamera.
H2 Röntgenstraling
2 Röntgenstraling
Röntgenstraling wordt in de medische wereld vaak toegepast, denk maar aan röntgenfoto's bij botbreuken. Ook een CT-scan wordt met behulp van röntgenstraling gemaakt. In dit hoofdstuk maak je kennis met de natuurkundige principes achter de röntgenfoto en de CT-scan, maar eerst kijken we terug in de tijd.
Een stukje geschiedenis
In het jaar 1895 is Wilhelm Röntgen (1845-1923) aan het experimenteren met een kathodestraalbuis. Dit is een buis waarin aan de ene kant een gloeidraad zit (de kathode) en aan de andere kant een metalen plaat (de anode). Als de
gloeidraad wordt verhit, komen daar elektronen vanaf. Die elektronen kunnen met behulp van een hoge spanning naar de anode 'geschoten' worden. Als Röntgen bezig is, ziet hij een lichtflits in de buis. Vervolgens verlaagt hij de druk in de kathodestraalbuis; de lichtflits die hij dan ziet, is blauw. Bij verdere verlaging van de druk, naar bijna vacuüm, verdwijnt de zichtbare lichtflits. Röntgen denkt wel dat er nog energie wordt overgedragen van de kathode naar de anode, maar hij kan er niet precies de vinger op leggen hoe. Wel valt hem op dat een plaat die ingesmeerd is met een bariumplatinacyaanzuur-verbinding 'oplicht.' Het lijkt of er licht van de plaat afkomt, telkens als hij de kathodestraalbuis aanzet. Dit vraagt om nader onderzoek. Röntgen plakt de buis af met zwart karton om er zeker van te zijn dat er geen licht meer op de plaat kan komen, en toch blijft de plaat 'oplichten'. Hiervoor moet een nieuw soort straling verantwoordelijk zijn. Deze straling is niet zichtbaar, maar ligt wel aan de kant van violet in het zichtbare spectrum. Röntgen noemt deze straling "X-stralen". Dit naar analogie met de wiskunde, waarin de onbekende ook altijd x genoemd wordt.
Röntgen experimenteert verder met zijn X-stralen en het blijkt dat de straling door heel veel materialen heen gaat. Zelfs door zijn huid en spieren, als hij zijn hand tussen de kathodestraalbuis en de met bariumplatinacyaanzuur-verbinding geprepareerde plaat houdt. Wat opvalt, is dat de straling niet door zijn botten heen gaat. Hij krijgt een schaduwafbeelding van zijn skelet op de plaat te zien. Hierna maakt hij een foto van de hand van zijn vrouw: de allereerste röntgenfoto!
Opdracht
1. Leg met behulp van een tekening in je schrift uit hoe je een schaduwafbeelding van je skelet op een röntgenfoto krijgt, en niet een 'gewone' foto.
Toepassing
In 1901 krijgt Röntgen de Nobelprijs voor zijn ontdekking.
Nadat de eerste röntgenfoto's zijn gepubliceerd, neemt de toepassing ervan een grote vlucht. Niet alleen in medische kringen wordt het nieuwe middel gebruikt; al snel zijn er allerlei toepassingen van het 'wonderapparaat'. Schoenverkopers schaffen een klein röntgenapparaat aan om de maat van je schoenen goed te kunnen vaststellen en ga zo maar door.
Nu men voor het eerst in een levend lichaam kan kijken, gaat men voor allerlei onderzoek de X-stralen toepassen. Zie het filmpje van het onderzoek van de bewegingen van een schouder van Prof. Dr. R. Janker uit 1930.
Kijkvragen bij de film
1. Als je een röntgenfoto bekijkt, zie je wit gekleurde botten. In de film zijn de botten van de man echter zwart. Leg uit hoe dat komt.
2. De man in beeld wordt eerst gewoon opgenomen, en later zijn dezelfde opnames met röntgenstraling gemaakt. De hele film duurt ongeveer 9 minuten. Vind je dat verstandig? Leg uit.
3. Kan een dergelijke film nu nog een keer gemaakt worden? Zou het mogen?
2.1 Röntgenfotografie
Casus
Johan is bij een voetbalwedstrijd geblesseerd geraakt. Hij heeft iets aan zijn been: het staat scheef en het doet pijn. Het lijkt erop dat zijn been gebroken is.
In het ziekenhuis wordt hij opgevangen door de afdeling spoedeisende hulp. De arts komt bij hem en kijkt naar zijn been. De arts laat een röntgenfoto van zijn been maken.
De arts kijkt naar de foto. Hij kan zien dat beide botten in het onderbeen gebroken zijn.
Johan krijgt de foto ook te zien en is nieuwsgierig geworden. Hij gaat vragen stellen aan de arts. Hij stelt vragen over wat er gaat gebeuren, maar hij stelt ook technische vragen over de röntgenstraling zelf. Voor het medische gedeelte kan de arts hem geruststellen, maar voor de technische vragen moet hij naar de klinisch fysicus. Maar gezien de ernst van de situatie moet Johan eerst geopereerd worden.
Na de operatie, als Johan weer op zaal ligt, komt de radioloog langs om een aantal vragen van Johan te beantwoorden. Johan heeft de volgende vragen:
1. Waar komen röntgenstralen vandaan? Hoe worden ze gemaakt?
2. Kun je met röntgenstraling alleen botten zichtbaar maken, of ook andere delen van je lichaam?
3. Waarom gaan de verplegers bij het nemen van een röntgenfoto achter een muurtje staan? Hoe dik moet dat muurtje zijn?
4. Hoe voorkom je dat het personeel teveel straling krijgt?
De radioloog probeert Johan alles zo goed mogelijk uit te leggen.
Jullie gaan de radioloog helpen om antwoorden op de vragen van Johan te vinden. Schrijf de antwoorden op Johans vragen in je schrift op en laat ze door de docent of PAL controleren.
Om informatie te vinden, kun je gebruik maken van het internet, maar ook van je leerboek of andere bronnen.
Practicum
Practicum - Lichtstralen versus röntgenstralen
Benodigdheden: fotopapier.
Leg zo snel mogelijk nadat je een stuk fotopapier uit de verpakking hebt gehaald je hand met gespreide vingers erop, handpalm naar beneden.
Houd je hand zo stil mogelijk totdat het niet bedekte stuk fotopapier duidelijk donker kleurt. Dit kan enkele minuten duren.
Haal je hand van het papier en kijk wat er langzaam met de afdruk gebeurt.
1. Geef twee overeenkomsten tussen deze foto en een röntgenfoto.
2. Geef twee verschillen tussen deze foto en een röntgenfoto.
3. Waardoor verdwijnt je handafdruk?
4. Wat moet je doen om je handafdruk niet te laten verdwijnen?
2.2 Animaties
Opdracht
Bekijk het bovenstaande filmpje over het ontstaan van röntgenstraling.
Je ziet een atoom uit de anode van een röntgenbuis. In het midden zit de kern en in de cirkelbanen (schillen) eromheen de elektronen. Als je het aantal elektronen van het atoom weet, dan weet je ook hoeveel protonen er zijn. Het aantal protonen geeft het atoomnummer van het element in het periodiek systeem.
1. Welk atoom is afgebeeld?
Je ziet een elektron dat van de kathode af komt. Beschrijf wat dat elektron doet aan de hand van de volgende vragen:
2. Uit welke schil wordt een elektron weggeschoten? Waarom juist uit die schil en niet uit een andere?
3. Het elektron wordt vervangen door een ander elektron uit een verdere schil met hogere energie. Wat gebeurt er als het elektron van de verdere schil terugvalt? Leg uit.
Remstraling
Elektronen van de kathode zullen, aangekomen op de anode, niet allemaal gebruikt worden om elektronen uit atomen weg te stoten. Een deel van de aankomende elektronen zal hun energie afstaan door af te remmen in het anodemateriaal. De energie die vrij komt, wordt omgezet in röntgenstraling die ook wel remstraling wordt genoemd.
De volgende animatie laat zien hoe zulke remstraling ontstaat. Bekijk deze animatie.
Beschrijf wat er gebeurt aan de hand van de volgende vragen:
4. Vergelijk de snelheid van het elektron bij binnenkomst met de snelheid bij het verlaten van het atoom. Leg uit hoe hierdoor energie vrijkomt.
5. Beschrijf de baan van het binnenkomende elektron. Leg uit hoe hierdoor energie vrijkomt.
6. Bedenk en beschrijf wat er gebeurt met het elektron als het eenmaal 'stil' staat in de anode.
Hieronder staat een aantal plaatjes van het spectrum van de röntgenbuis. Rechtsonder in een aantal van de plaatjes zie je de formule E = h · ν, het laatste symbool is geen v, maar een griekse letter ν (spreek uit: nu). Sommige natuurkundigen gebruiken de letter ν voor de frequentie van een foton. De energie van het foton kun je dus uitrekenen met behulp van de constante van Planck en de golflengte. Als je het spectrum van een röntgenbuis bestudeert, zal je het een en ander opvallen.
Er ontstaat een grote bult met daarop pieken. De grote bult wordt de witte berg genoemd en geeft de remstraling weer. De pieken zijn de specifieke golflengten voor een bepaald anodemateriaal.
7. Leg uit waardoor de witte berg een 'continu' deel van het spectrum is.
Afhankelijk van de toepassing zal juist de witte berg of de specifieke piek uit het spectrum gefilterd worden. Dit heeft te maken met de veiligheid van degene die de bestraling ondergaat. Als het bijvoorbeeld om het fotograferen van een beenbreuk gaat, zorgt men ervoor dat de golflengten die de huid en spieren kunnen aantasten uit de röntgenbundel gefilterd zijn. Men streeft naar een zo laag mogelijke 'stralingsbelasting'.
8. Geef in woorden weer wat je ziet op de plaatjes van het röntgenspectrum.
9. Bereken de golflengtes van de fotonen die bij de twee pieken horen. Gebruik hierbij de formule uit hoofdstuk 1 voor de relatie tussen de frequentie en golflengte van een foton, of zoek deze op in Binas. Controleer vervolgens in Binas of de gevonden golflengtes inderdaad binnen het röntgengebied vallen.
Afbeeldingengalerij
2.3 Eindopdracht
De vraag:
Waar komt röntgenstraling vandaan?
Inleiding
Je bent gevraagd om voor de radiologenopleiding een verhaal te verzorgen over de werking van een röntgenapparaat. Dat is best ingewikkelde materie. Om het goed duidelijk te maken, besluit je om een model van een röntgenbuis te maken waarin je alle onderdelen goed kunt laten zien. Met die buis geef je een presentatie waarin je het een en ander duidelijk uitlegt.
Opdracht
Maak een model van een röntgenbuis waarin alle onderdelen goed zichtbaar zijn. Je laat duidelijk zien waar alles zit en kunt de onderdelen benoemen met hun functie. Er is goed te zien waar de straling de buis verlaat.Met dit model geef je een presentatie over de werking van een röntgenbuis. In je presentatie komen de volgende begrippen in ieder geval aan de orde en leg je de begrippen uit:
anode en kathode
elektronenbundel
remstraling
kinetische energie
elektronvolt
foton
Je kunt aan de hand van een grafiek uitleggen welke straling van de röntgenbuis gebruikt wordt voor een foto en waarom.
Bronnen
Voor de werking van een röntgenbuis en het ontstaan van X-stralen kun je de volgende bronnen gebruiken:
Lees de bronnen goed door. Schrijf woorden die je niet kent op en zoek de betekenis op, of vraag het je docent.
Aan het eind van de presentatie geef je een samenvatting van de belangrijkste dingen uit je presentatie en je maakt 5 vragen over röntgenstraling en -apparaten voor de rest van de klas. Zij moeten die vragen kunnen beantwoorden als zij het hoofdstuk hebben doorgewerkt en/of naar je presentatie hebben geluisterd.
H3 Nucleaire geneeskunde
3 Nucleaire geneeskunde
Nucleaire geneeskunde heeft tal van mogelijkheden. Niet alleen kunnen er diagnoses mee worden gesteld, het kan ook worden toegepast in het genezen van patiënten. Denk maar aan bestraling van patiënten met tumoren. We beginnen dit hoofdstuk met een patiënt waarbij de nucleaire geneeskunde ingezet wordt voor de diagnose.
Casus
Mevrouw De Wit heeft een aantal klachten. Zij heeft het snel koud, wordt zwaarder, voelt zich vaak sloom en heeft een vertraagde hartslag. Na verschillende onderzoeken stuurt de huisarts haar door naar de specialist voor verder onderzoek. Deze besluit een scintigram van haar schildklier te maken.
Voor het onderzoek krijgt mevrouw De Wit jodium-123 ingespoten, een radioactief isotoop van jodium.
Dit jodium-123 verzamelt zich in de schildklier, doordat voor de vorming van schildklierhormoon jodium nodig is.
Opdrachten
In hoofdstuk 1 heb je geleerd dat de elementen met een atoomnummer Z en massagetal A worden aangegeven. Zoek het atoomnummer en het massagetal van jodium op.
Jodium-123 heeft hetzelfde atoomnummer als jodium, toch verschilt de massa. Leg uit hoe dat kan. Gebruik in je antwoord het woord neutronen.
In de tekst staat het woord isotoop. Zoek de betekenis hiervan op.
In tabel 25 van je Binas staan alle isotopen van de elementen. Vaak zijn isotopen niet stabiel. Dit betekent dat zij niet lang kunnen bestaan. Jodium-123 bijvoorbeeld heeft een halveringstijd van 13,5 uur. Dat betekent dat na 13,5 uur nog maar de helft van het aantal atomen jodium-123 over is. De jodium-123-deeltjes veranderen in tellurium-123: door het invangen van een elektron verandert een proton in een neutron en wordt gammastraling uitgezonden.
4. Zoek in tabel 25 van je Binas nog meer isotopen van jodium op en schrijf de halveringstijden op.
3.1 Practicum
In paragraaf 1.3 over kernstraling heb je kennis gemaakt met het begrip halfwaardetijd, ook wel halveringstijd genoemd. Dit practicum laat je ervaren wat halveringstijd inhoudt.
Je hebt er 100 muntjes voor nodig met een verschillende boven- en onderkant. Muntjes van 1 of 2 eurocent zijn het gemakkelijkst. Het eerste wat je doet, is een tabel maken. In de tabel zet je een kolom voor het aantal worpen en een kolom voor het aantal munten dat kop is tijdens die worp. De munten met kop stellen de vervallen atomen voor.
Gebruik een bak om de munten in te gooien, anders liggen ze door het hele lokaal.
aantal worpen
munten kop
Je verzamelt de 100 munten en gooit ze in de bak. Alle munten die met kop boven liggen haal je uit de bak en tel je. Leg ze vervolgens weg. Het aantal zet je in de kolom "munten kop".
Nu haal je de resterende munten uit de bak en gooit ze opnieuw in de bak. Weer pak je de munten die kop zijn eruit en zet je hun aantal in de tabel.
Dit herhaal je totdat uiteindelijk alle munten weg zijn.
Maak van je resultaten een diagram.
Je kunt het aantal keer gooien vergelijken met de tijd die verstrijkt om een kern te laten vervallen. Het aantal keer dat je moest gooien om 50 munten kop te krijgen is dan de halfwaardetijd. Lees uit je diagram af na hoeveel keer werpen er 50 munten met kop zijn gevallen. Wat is de halveringstijd van de munten?
Vraag bij het practicum
1. Na het onderzoek moet mevrouw De Wit nog even in het ziekenhuis blijven, omdat zij een radioactieve bron is geworden door het ingespoten middel. Mevrouw De Wit wil graag weten hoelang dat radioactieve jodium-123 in haar lichaam aanwezig blijft. Zoek in Binas op wat de halveringstijd van dit isotoop is en reken uit wanneer mevrouw De Wit nog minder dan 1% radioactieve stof in haar lichaam heeft.
3.2 Applet
Voor het onderzoek van mevrouw De Wit werd gebruik gemaakt van radioactief jodium-123. Dit wordt radioactief genoemd, omdat het straling uitzendt. Onder de straling die radioactieve stoffen kunnen uitzenden, kun je drie verschillende soorten onderscheiden: alfastraling (α-straling), bètastraling (β-straling) en gammastraling (γ-straling). Alfa- en bètastraling bestaan uit deeltjes die uit de kern van een atoom komen en gammastraling zijn fotonen (energiepakketjes). De soorten straling hebben een verschillend doordringend vermogen. Dit betekent dat zij afhankelijk van de stralingsoort meer of minder diep in je lijf kunnen doordringen. De deeltjesstraling gaat aanmerkelijk minder diep dan de gammastralling.
Een arts kan verschillende soorten straling gebruiken, afhankelijk van wat hij of zij te weten wil komen, en hoe diep de organen waar het om gaat in je lijf zitten.
In de volgende applets ga je kijken naar de twee deeltjesstralingen.
We beginnen met de grootste deeltjes, namelijk de alfastraling.
Vraag
1. Heeft alfastraling een groot of klein doordringend vermogen?
Het applet simuleert het verval van een polonium-211-kern.
Opdrachten
Zoek polonium op in Binastabel 25.
Hoeveel isotopen van polonium zijn er?
Schrijf de isotopen met de grootste en kleinste halveringstijd op.
Wat is de vervaltijd van Po-211?
Start het applet en klik op tabblad 1, "Atoom".
Bekijk het Po-211 atoom als het vervalt. Klik daarna op de knop "Herbegin" en laat het atoom minstens 10 keer vervallen.
Schrijf minstens drie verschillen op tussen de kern voor en na het verval.
Wat gebeurt er in de Po-211-kern waardoor hij vervalt?
Klik op de "pauze"-knop meteen nadat de kern is vervallen, zodat je het weggeschoten deeltje nog kan zien. Waar bestaat dat deeltje uit?
Welke atoomkern is het?
Wat heeft het weggeschoten deeltje te maken met het massagetal van het nieuwe atoom?
Hoe heet het nieuwe element?
Geef de vervalvergelijking van Po-211.
Bekijk de grafiek boven in het venster. De halveringstijd is aangegeven. Wat kun je zeggen over de kernen die vervallen zijn, als je kijkt naar de halveringstijd? Is er een patroon aan te geven?
Wat zeg dit over de kans dat een enkele kern vervalt? Kun je dat voorspellen?
Laat je antwoorden controleren.
Klik nu op de tab "Meerdere atomen".
Klik eerst op de pauzeknop onderin en maak dan de emmer met atomen leeg, door een aantal keer op "10 toevoegen" te klikken.
Laat de simulatie lopen. Bovenin het scherm kun je het aantal vervallen atomen en de tijd ertussen zien. Pauzeer de simulatie elke halve minuut. Schrijf telkens de verlopen tijd in de tabel en schrijf daarbij het totaal aantal vervallen kernen op.
Herhaal dit 4 keer.
Je hebt nu 5 verschillende waarnemingen van het verval van polonium-211. Maak van je waarnemingen 1 diagram met 5 lijnen. De lijnen vallen niet precies over elkaar. Geef een verklaring voor het verschil tussen de lijnen.
Het tweede applet gaat over bètastraling, ook deeltjes maar veel kleiner dan alfadeeltjes. De manier waarop de deeltjes ontstaan is ook anders.
Met het applet kun je het verval simuleren van H-3- en C-14-kernen.
Opdrachten:
Zoek op en omschrijf zo kort mogelijk wat de oorzaak is van dit verval en waardoor de bètadeeltjes ontstaan.
Zoek in Binastabel 25 koolstof-14 op.
Hoeveel isotopen van koolstof zijn er?
Wat is de vervaltijd van C-14?
Laat je antwoorden controleren.
Start het applet en klik op tabblad 1, "Atoom".
Bekijk het C-14- en het H-3-atoom als het vervalt.
Schrijf minstens drie verschillen en minstens drie overeenkomsten op tussen de kern voor en de kern na het verval.
Schrijf de vervalvergelijkingen op.
Wat is het verschil met het alfaverval van het applet hierboven?
Klik op de "pauze"-knop meteen nadat de kern is vervallen, zodat je de weggeschoten deeltjes nog kunt zien. Waar bestaan de deeltjes uit?
Welk deeltje komt er behalve een bètadeeltje nog meer vrij? Waar komen de deeltjes van het bètaverval vandaan? Gebruik in je antwoord de termen neutron, proton en elektron.
C-14-koolstof wordt gebruikt bij het bepalen van de ouderdom van archeologische vondsten.
De achterliggende aanname is dat de verhouding tussen C-12 en C-14 in de atmosfeer niet veranderd is in de loop der eeuwen. Dit komt doordat C-14 weliswaar verdwijnt door verval, maar bovenin de atmosfeer tegelijk voortdurend C-14 wordt bijgemaakt door reactie van kosmische straling met stikstof.
Opdrachten
1. Zoek op hoe je met behulp van C-14 kunt bepalen hoe oud een vondst is. Schrijf dit op in je schrift.
2. Maak een grafiek waarin je op de verticale as de hoeveelheid C-14 (in percentage) neerzet. Op de horizontale as zet je de tijd in jaren neer. Teken in de grafiek het verloop van de hoeveelheid C-14.
3. Tijdens opgravingen zijn resten van een prehistorische maaltijd gevonden. De archeologen schatten de leeftijd van de gevonden botten op 12.000 jaar. Bereken of bepaal hoeveel % van de oorspronkelijke C-14 atomen er nog in de vondst zitten.
Voor sommige ouderdomsbepalingen is de C-14 methode niet geschikt, bijvoorbeeld als een voorwerp geen C-atomen bevat. Dan wordt er een ander radioactief element gebruikt, zoals bijvoorbeeld K-40. Men kijkt dan naar de verhouding tussen K-39 en K-40.
De activiteit van een stof is evenredig met het aantal radioactieve deeltjes. We kunnen dus ook de activiteit tegen de tijd uitzetten. Een andere methode is het maken van een tabel, waarbij in de ene kolom de tijd staat en in de andere kolom de activiteit.
4. In een laboratorium wordt een hafniumbron gebruikt. Hafnium is een metaal dat onder andere in atoomonderzeeërs wordt gebruikt.
Op de oorspronkelijke verpakking staat dat de activiteit 28 x 105 Bq is. De laborant meet de activiteit en bepaalt dat deze nu nog 2736 Bq is.
1. Schrijf in je schrift de volgende begrippen op en zoek de betekenis daarvan op:
scintillatiekristal
photo multiplier tubes
collimator
oplossend vermogen.
Een gammacamera maakt gebruik van gammastraling. Deze straling bestaat in tegenstelling tot alfa- en betastraling niet uit deeltjes maar uit energie. Deze energie wordt gebruikt voor het maken van een afbeelding.
Maak na het lezen van het bovenstaande artikel een schematische tekening van een gammacamera in je schrift. Controleer je tekening door op de onderstaande link te klikken:
Om een beeld te maken met een gammacamera gebruikt een radioloog tracers. Dit zijn stoffen die gammastraling uitzenden.
Opdrachten
Schrijf drie eigenschappen op waaraan een tracer moet voldoen.
Een veel gebruikte tracer is technetium-99m. De m achter het massagetal betekent dat het metastabiel is en kan vervallen. Dit betekent dat de protonen en neutronen in de kern zich nog kunnen herschikken tot een toestand met minder energie. Bij terugval naar deze 'grondtoestand' zendt de kern van dit atoom de voor medisch onderzoek bruikbare gammastraling uit. Waarom is Tc-99m een goede tracer?
Tc-99m is een product van het verval van Mo-99. Schrijf de vervalvergelijking van Mo-99 naar Tc-99 op en ook de vergelijking van Tc-99m naar Tc-99.
Hoeveel energie komt er vrij in MeV? Hoeveel J is dat?
Hoe komt het dat het massagetal van Mo en Tc gelijk is? Wat is er veranderd in de kern?
Zoek nog drie andere tracers op die gebruikt worden in de gezondheidszorg. Schrijf voor elk van die tracers op waar ze voor gebruikt worden en wat de vervalvergelijking van die tracer is.
3.4 Eindopdracht
Je docent geeft aan welke van de twee opdrachten je moet doen.
1. Samenwerkingsopdracht
Maak naar aanleiding van dit hoofdstuk 10 vragen. Deze vragen leg je voor aan je docent of de PAL. Als ze zijn goedgekeurd, geef je ze aan een klasgenoot die ze gaat maken. Je krijgt zelf van deze persoon 10 vragen. Zorg dat je de antwoorden op je zelfgemaakte vragen hebt. Samen kijken jullie de gegeven antwoorden na. Bij verschillen leg je elkaar uit wat het goede antwoord is.
Voorbeeldopdrachten
Deze opdrachten zijn voorbeelden. Maak zelf andere.
- Stel de vervalvergelijking op van U-238.
- Bereken de snelheid van een bètadeeltje met een kinetische energie van 31 keV.
2.Individuele opdracht
Schrijf een Wiki-artikel over nucleaire geneeskunde. In dat artikel beschrijf je wat er bij nucleaire geneeskunde allemaal komt kijken. Doe in elk geval het volgende:
- Je beschrijft de vormen van straling die voor nucleaire geneeskunde belangrijk zijn. Je schrijft op
hoe alfa-, bèta- en gammastraling ontstaan;
waaruit de verschillende soorten straling bestaan;
hoe groot het doordringend vermogen van de verschillende soorten is.
- Voor elke vorm van straling geef je een voorbeeld van het gebruik in het ziekenhuis.
- Je beschrijft een patiënt met een aandoening die met nucleaire geneeskunde kan worden opgespoord of behandeld.
H4 MRI
4 MRI
In dit hoofdstuk behandelen we een techniek die voor mooie 3D-plaatjes van het binnenste van je lijf kan zorgen: MRI. MRI maakt ook gebruikt van straling, maar deze straling is niet schadelijk voor je. Verderop in dit hoofdstuk zul je zien welke soort straling dit is. We beginnen, net als in het vorige hoofdstuk, met twee cases.
Casus 1
Meneer De Boer heeft klachten in zijn buik. De internist kan uit bloedonderzoek zien dat er iets in de lever niet helemaal goed is, maar niet precies wat. Om zich een goed beeld van de lever te vormen, laat de internist van meneer De Boer een zogenaamde MRI-scan maken. Dit kan van het hele lichaam, maar ook van een gedeelte. Voor de klachten van meneer De Boer is het niet nodig om zijn hele lichaam te scannen.
Opdracht
Waar staan de letters MRI voor?
Voordat je in het ziekenhuis de ruimte van de MRI-scanner in gaat, wordt er gevraagd of je voorwerpen van ijzer, zoals bijvoorbeeld sleutels, bij je hebt. Die moet je dan eerst afgeven. Leg uit waarom je die sleutels niet mee naar binnen mag nemen.
Op welke manier is MRI belastend voor een patiënt?
De dokter laat maar een gedeelte van meneer de Boer scannen. Leg uit waarom de dokter dat doet.
Casus 2
Op de SEH (spoedeisende hulp) is iemand binnengebracht die een schop tegen zijn knie heeft gekregen.
Een röntgenfoto geeft niet genoeg duidelijkheid over de kwetsuur. Er is besloten een MRI-scan te maken. Het resultaat staat hieronder.
Wat is er met deze knie aan de hand? Als je het niet meteen ziet, kun je MRI-scans van een gezonde knie opzoeken en vergelijken.
Schrijf je antwoord in je schrift.
4.1 Practicum
Practicum 1
MRI maakt gebruik van elektromagneten. Met elektromagneten heb je in de derde klas al kennisgemaakt. Dit practicum laat je zien hoe elektromagneten ook alweer werken.
Je hebt spoelen nodig met verschillende aantallen windingen.
Bedenk een manier waarop je de sterkte van het magneetveld van een spoel kunt meten. Laat dit door je docent, de TOA of de PAL beoordelen. Vinden zij het een goede manier, dan kun je verder.
Meet de sterkte van het magneetveld van de spoelen met verschillende aantallen windingen. Bedenk welke grootheden je niet moet veranderen.
Zet ze in volgorde van sterkte.
Valt je iets op?
Onderzoek hoe je de sterkte van 1 spoel kunt variëren.
Een MRI-scanner moet goed gekoeld worden. Leg aan de hand van je waarnemingen uit waarom dat is.
Wat is de eenheid van magnetische veldsterkte?
Maak van je resultaten een verslag. In je conclusie schrijf je wat voor een spoel jij voor een MRI-toestel zou gebruiken.
Practicum 2
In dit practicum ga je een MRI-scan simuleren.
Je hebt hiervoor een aardappel of een stevige vrucht nodig (bijvoorbeeld een appel), een scherp mes, een digitale fotocamera, liefst met statief, een stuk donker papier en een computer.
Met behulp van het mes snijd je plakjes van je vrucht af. Zo dun mogelijk, maar niet dikker dan ongeveer 5 mm. Dunner is mooier. (Pas op met het mes.)
Fotografeer de plakjes 1 voor 1 op een donkere (liefst zwarte) onderdergrond. Let op dat je de plakjes steeds op dezelfde plek legt.
Zet de foto's op je computer achter elkaar en maak er een filmpje van.
Je kunt nu door je vrucht heen en weer lopen, net als door een MRI-scan.
Mensen scannen met MRI
Auteur: M.P. Huijbregtse, J.H. van der Schee, J.E. Frederik
Een van de grootste medische successen was de ontdekking dat men met behulp van röntgenstraling zicht op het menselijk skelet kon krijgen. Zonder de patiënt te opereren! Het lokaliseren van botbreuken werd zo een fluitje van een cent. Natuurlijk wilde men al snel ook andere delen van het lichaam kunnen bekijken, en zo ging de zoektocht naar nieuwe afbeeldingstechnieken voort.
'Magnetic Resonance Imaging' (MRI) is de naam van zo'n techniek. Met MRI kunnen afbeeldingen van diverse soorten weefsel - waaronder de hersenen - worden gemaakt om bijvoorbeeld tumoren op te sporen. Hoe gaat dat nu in zijn werk?
Om te beginnen moet je weten dat er ontzettend veel waterstofatomen in een lichaam zitten. Deze zijn opgebouwd uit één proton en één elektron. Elektronen hebben een eigenschap die we spin noemen en dat ze daardoor eigenlijk kleine magneetjes zijn. Protonen hebben deze eigenschap ook en daar maakt MRI graag gebruik van.
Eerst wordt er een sterk magnetisch veld rondom het te onderzoeken lichaamsdeel aangelegd (ca. 1 T, dat is 20.000x de sterkte van het aardmagnetisch veld). In dit veld gaan de protonen zich richten, net zoals een kompasnaaldje in een magnetisch veld. De tweede stap is het toevoeren van kortdurende elektromagnetische golven: 'pulsen'. Deze pulsen beïnvloeden de protonen en brengen ze als het ware uit evenwicht en het proton gaat in een andere positie staan.
Als een puls voorbij is, kan het proton weer terugkeren in zijn oude positie. Hierbij zendt het proton zelf echter ook een elektromagnetische puls uit. Deze pulsen worden gedetecteerd. Zo kan men zien hoe de waterstofatomen in het lichaam verdeeld zijn. Aangezien de waterstofdichtheid per weefselsoort verschilt, kan men nu achterhalen op welke plek welk weefsel zit!
Grappig: MRI werd eerst NMR genoemd, Nuclear Magnetic Resonance. Een proton is immers de kern ('nucleus') van een waterstofatoom. Mensen kregen echter zo'n spookbeeld bij het woord 'nuclear', dat er toch maar van deze naam is afgestapt!
Open de applet en maak de opdrachten die eronder staan.
In het hoofdvenster zie je een aantal trillende atoomkernen. Onder het venster staat het bedieningspaneel van de EM-golfgenerator. Hiermee kun je het vermogen ('Power') en de frequentie instellen. In de balk rechts naast het hoofdvenster staat een klein venstertje waarin twee lijnen te zien zijn. Op de bovenste lijn staan de atoomkernen die 'in trilling' zijn gebracht. Op de onderste lijn staan de kernen die geen energie van de EM-bron hebben meegekregen. Ook kun je in de rechterbalk het hoofdmagneetveld instellen. Zet de power op ongeveer 50%, de hoofdmagneet ('main magnet') op ongeveer 1 T en stel de frequentie zo in dat het golfje tussen de 2 lijnen in het kleine venstertje precies tussen die 2 lijnen past.
Beantwoord de volgende vragen.
Welke signalen meet een MRI-apparaat en waar komen deze vandaan?
Wanneer ontvangt de detector de meeste signalen?
Hoe groot is de resonantiefrequentie?
Zet nu de frequentie terug naar 10 MHz en verklaar wat je waarneemt.
Deel II: Tabblad 'Vereenvoudigd MRI'
Stel de MRI in met de waarden waarmee je met de NMR veel resonantie waarnam. Onderaan in de rechter balk kun je onder het kopje 'head' een tumor toevoegen. Doe dit.
De kunst is nu natuurlijk om zoveel mogelijk fotonen uit de tumor te laten komen en zo weinig mogelijk uit de rest van het hoofd. Zoals je ziet, is de concentratie van de gevoelige kernen het grootst in de tumor. Omdat ze dichter bij elkaar liggen, draaien ze iets moeilijker en hebben dus iets meer energie nodig en dus een hogere frequentie. Laat nu de frequentie voorzichtig toenemen totdat er bijna geen fotonen meer uit de kernen in het hoofd komen. Omdat de kernen ook slordiger liggen, reageren ze beter op een magneetveld dat een beetje scheef op de bewegingsrichting van de golven staat. Zet nu de horizontale 'gradient magnet' op vol en probeer het signaal van de tumor zo duidelijk mogelijk te krijgen. Vergelijk jouw resultaat met dat van andere leerlingen en schrijf op wat je opvalt aan de instellingen van deze scanner.
Schrijf de antwoorden in je schrift.
Laat alles door de docent of de PAL controleren.
4.3 Eindopdracht
Groepsopdracht voor maximaal drie personen
Meneer De Boer, waarvan de scan overigens uitwees dat hij een onschuldige cyste bij zijn lever had, is door alle ziekenhuisbezoeken nieuwsgierig geworden. Hij wil nu graag weten hoe dat precies werkt, zo'n MRI-scanner. Hij besluit om contact op te nemen met een bedrijf dat MRI-scanners maakt. Jullie zijn medewerkers van dat bedrijf en nodigen meneer De Boer uit om langs te komen. Daar wordt hem uitgelegd hoe een MRI werkt, welke onderdelen erin zitten, hoe je met een magneet een beeld kunt maken en zo verder.
Jullie maken die presentatie en presenteren hem aan je docent of de klas.
Om de presentatie goed te kunnen maken, is het verstandig om eerst de volgende deelopdrachten te doen:
Zoek op internet een bedrijf dat de scanners maakt en bekijk de specificaties van verschillende scanners.
Bestudeer folders voor dergelijke apparaten.
Aan het eind van de presentatie geef je een samenvatting van de belangrijkste punten uit je presentatie. Maak ook 5 vragen over MRI voor de rest van de klas. Zij moeten die vragen kunnen beantwoorden als zij het hoofdstuk hebben doorgewerkt en/of naar jullie presentatie hebben geluisterd.
H5 Echografie
5 Echografie
Dit hoofdstuk gaat over de minst gevaarlijke techniek om beelden te maken van iemands binnenste. Het is ook een techniek waar jullie allemaal, al wist je het misschien niet, mee te maken hebben gehad. We beginnen weer met een patiënt.
Casus
Marjan van Veenendaal is 12 weken zwanger van haar eerste kindje. Ze gaat een echo laten maken. Best wel spannend. Bij de verloskundige heeft ze het hartje al horen kloppen, maar nu gaat ze voor het eerst haar kindje zien. Is het een jongetje of een meisje? Hoewel ze van alle kanten gerustgesteld is, vindt ze het toch wel spannend. Is het niet gevaarlijk? En dat ultrageluid, is dat niet gevaarljk voor haar kindje, kan het daar doof van worden?
Opdracht
Er zijn meer mensen die zo'n echo, net als Marjan, best spannend vinden. Daarom geeft het ziekenhuis aan iedereen die een echo laat maken een "bijsluiter" mee, als je een afspraak komt maken. De bijsluiter is een A4-tje waarop dingen staan die betrekking hebben op de behandeling. Maak zo'n bijsluiter voor het ziekenhuis. Hierin staan de volgende dingen:
de frequenties die een echo-apparaat gebruikt;
de frequenties waarvoor een mens gevoelig is;
wanneer je gehoorbeschadiging krijgt;
of echografie gevaarlijk is voor het menselijk gehoor.
De bijsluiter lever je aan het eind van de les in.
5.1 Applet
Geluid wordt gemaakt door een geluidsbron te laten trillen. Met de applet hieronder kun je je kennis ophalen van vorig jaar.
Start de applet die hieronder staat. Gebruik de tab "Meten". Hier krijg je een luidspreker te zien, waaruit je geluidsgolven kunt laten komen. Aan de rechterkant kun je de frequentie en de amplitude veranderen. Links staan twee blauwe lijnen die je kunt verplaatsen. Ook de liniaal en de stopwatch zijn verplaatsbaar.
Opdrachten
Laat de applet lopen en kijk wat er gebeurt als je frequentie en amplitude verandert.
Stel de frequentie in op achtereenvolgens 250, 500, 750 en 1000 Hz. De precieze waarden van de frequenties zijn niet heel belangrijk, als je maar 4 verschillende frequenties hebt die over het hele gebied verdeeld zijn.
Meet met de liniaal en de twee hulplijnen de golflengten op. Onderzoek het verband tussen de golflengte en de frequentie.
Stel de frequentie willekeurig in. Meet de tijd op die nodig is voor 10 golven. Bereken de frequentie.
Doe dit met 3 andere frequenties.
Schrijf je antwoorden in je schrift en laat je antwoorden controleren.
Voor het verband tussen golflengte, snelheid en frequentie geldt de volgende formule: v = f · λ.
Gebruik tabel 15 in je Binas. De antwoorden op de volgende opdrachten schrijf je in je schrift en laat je door de PAL of je docent controleren.
1. Bereken de golflengte van een geluidsgolf met een frequentie van 35 kHz, die door een zeeschip wordt gebruikt om de diepte van de zee te peilen.
2. Het vriest 20 graden. Je ziet de bliksem en hoort 5 seconden later de donder. Hoe ver is de onweersbui weg?
3. Een vleermuis gebruikt ultrasoon geluid om zijn prooi te lokaliseren en zijn weg in de ruimte te vinden. De golflengte van dat geluid is ongeveer 4,0 x 10-3 m. Bereken de frequentie.
5.2 Animatie
Echografie wordt niet alleen gebruikt bij zwangerschappen. Er zijn nog veel meer mogelijkheden. Zo heeft mevrouw Van der Veen last van haar darmen. Er wordt een echogram gemaakt. Kijk in de animatie hieronder wat er gebeurt met de geluidspuls. Beantwoord daarna de vragen in je schrift en laat ze weer controleren door je docent of de PAL.
Opdrachten
1. Waarom wordt er gewerkt met geluidspulsen en niet met een constante stroom geluid?
2. Heeft wat je op het filmje ziet overeenkomsten met de manier waarop een vleermuis zijn weg door een ruimte vind? Leg uit.
3. Hoe kunnen we uit de geluidspulsen de dikte van de darm meten?
Echografie werkt met geluidspulsen die worden teruggekaatst en afgebogen in de verschillende weefsels. In de vorige animatie heb je gezien dat een gedeelte van de geluidspuls wordt teruggekaatst naar de transducer en dat een ander gedeelte doorgaat in het weefsel. Terugkaatsing van geluid op snijvlak tussen twee verschillende weefsels gaat hetzelfde als bij licht. Dit betekent dat de hoek i van inval die de geluidspuls maakt met de normaal gelijk is aan de hoek van terugkaatsing t.
De snelheid van geluid is in de verschillende weefsels ook anders. Hierdoor verandert de richting van het geluid. De mate waarin het geluid van richting verandert, is afhankelijk van het verschil in geluidssnelheid tussen de twee stoffen. Net als bij licht is de wet van Snellius hier van toepassing. n = v1 / v2 }= sin i / sin r. In deze formule is n de brekingsindex, v1 de geluidssnelheid in weefsel 1 en v2 de geluidssnelheid in weefsel 2. Sin i is hoek van inval en sin r de hoek van breking.
Opdracht
Bekijk de volgende applet. Neem drie verschillende waarden voor de geluidssnelheid in weefsel 1 en reken de dikte van het weefsel uit. Doe dat ook met drie verschillende geluidssnelheden in weefsel 2. De berekeningen en antwoorden schrijf je in je schrift en laat je controleren door je docent of de PAL.
Casus
Meneer Smit heeft last van zijn benen. De artsen vermoeden dat hij last heeft van vaatvernauwing. Hierdoor komt er minder bloed bij zijn spieren en krijgt hij zogenaamde 'etalagebenen'. Mensen die daar last van hebben, kunnen geen langere tijd lopen. Zij moeten dan af en toe even stilstaan. Met echografie kun je ook de stroomsnelheid van het bloed bepalen.
Vraag
1. Stroomt het bloed bij een vaatvernauwing sneller of langzamer?
Het verschijnsel dat bij het bepalen van de stroomsnelheid wordt gebruikt, is het dopplereffect en de dopplerverschuiving.
Opdracht
2. Zoek op wat we met het dopplereffect en de dopplerverschuiving bedoelen. Schrijf de uitleg in je schrift met een tekening en de formule waarmee je de dopplerverschuiving kunt berekenen.
Als we de stroomsnelheid van het bloed willen bepalen, hebben we te maken met een dubbel dopplereffect. De bloedcel waarvan we de snelheid meten, fungeert eerst als een bewegende waarnemer; en daarna, als hij de geluidspuls terugkaatst, als een bewegende geluidsbron. Dit heeft een dubbele dopplerverschuiving tot gevolg.
De formule waarmee je de snelheid van het bloed kunt berekenen, is:
vbloed= Δf · v/(2 · cos θ · fbron).
In de formule is Δf het frequentieverschil dat de transducer meet, v is de geluidssnelheid in bloed, cos θ de cosinus van de hoek die de transducer maakt met het bloedvat en fbron de frequentie die de transducer uitzendt.
3. Beantwoord de volgende vragen in je schrift:
Bereken de waarde van Δf als de verzonden puls een frequentie fbron heeft van 1,0 · 104 Hz en de ontvangen puls een frequentie heeft van 10.002,8 Hz.
Leg met behulp van je antwoord op bovenstaande vraag uit waarom niet alleen de detectie, maar ook de opwekking van de geluidsgolven heel precies moet gebeuren.
Opdracht
4. In de volgende animatie kun je de snelheid van het bloed veranderen met een schuifje. Je ziet dan onderin het scherm de frequentie die de transducer uitzendt en de opgevangen frequentie. Zet het schuifje eerst helemaal links, dan ongeveer in het midden en tenslotte helemaal rechts en reken voor deze drie situaties de snelheid van het bloed uit.
Schrijf je antwoorden met berekeningen in je schrift en laat ze controleren door je docent of de PAL.
5.3 Practicums
Echoscopie maakt gebruik van ultrasoon geluid, dat is geluid dat niet hoorbaar is voor de mens omdat de frequentie te hoog is. De plaatssensor, of afstandsensor, doet dat ook. Hij zendt een geluidspuls uit en vangt het teruggekaatste signaal op. Uit het tijdsverschil tussen die twee kan een computerprogramma de afstand uitrekenen en weergeven. Dit weergeven kan op verschillende manieren; je kunt een afstandsmeter laten zien of een grafiek. Het eerste is vooral makkelijk als je één afstand wilt weergeven. Met een grafiek kun je een klein beetje een echogram simuleren. Dat laatste gaan jullie doen in dit practicum.
Sluit de afstandsensor aan op de interface van het programma dat bij jullie op school gebruikt wordt. Vaak is dat IP-Coach, maar het kan ook Data Studio zijn.
Start het programma en stel het in voor een afstandmeting. Kies voor weergave als een grafiek.
Plaats een aantal voorwerpen op verschillende afstanden van elkaar en van de afstandsensor.
Start de meting.
Schuif de afstandsensor met een constante snelheid langs de voorwerpen en laat de computer een grafiek tekenen.
Stop de meting als je langs alle voorwerpen gegaan bent.
Print de grafiek uit en laat een medeleerling met behulp van de grafiek proberen te tekenen waar de voorwerpen stonden.
Resolutie is belangrijk als je een echo maakt.
Zoek op wat er wordt bedoeld met "resolutie".
Om een hoge resolutie te krijgen, worden golven met een kleine golflengte gebruikt. Hoe kleiner de golflengte, des te hoger de resolutie van het plaatje. Het nadeel is dat deze golven met kleine golflengte niet zover in het weefsel doordringen. De afstandsensor die je voor het bovenstaande proefje hebt gebruikt, werkt met een frequentie van ongeveer 49 kHz.
Probeer met steeds smallere blokjes tot hoeveel cm de sensor nog kan "zien". Zoek in de specificaties van de door jullie gebruikte afstandsensor op met welke frequentie hij precies werkt.
Laat met een berekening zien of de resolutie van de sensor overeenkomt met de door jullie gevonden waarde van het smalste blokje.
5.4 Eindopdracht
Ultrageluid is een belangrijk hulpmiddel in het diagnostiseren van allerlei aandoeningen. Het is weinig belastend voor de patiënt en niet gevaarlijk. Je kunt niet alles met echografie zichtbaar maken, maar wel veel.
Je hebt de keuze tussen opdracht 1 en opdracht 2. Overleg met je docent welke je gaat doen.
Eindpdracht 1
Maak met een groep van maximaal 4 leerlingen een Klokhuis- of animatiefilm, waarin je laat zien waar ultrageluid in het ziekenhuis voor gebruikt wordt. De film duurt ongeveer 10 minuten.
Wat moet er in de film?
Wat is ultrageluid? Waarom noemen we het zo?
Terugkaatsing/afbuiging van geluid in je lijf. Hoe komt dat? Welke wet geldt hiervoor?
Uitleg van een echografie-apparaat:
Wat is een transponder? Wat doet deze?
Hoe worden verschillende weefsels in beeld gebracht? Gebruik hierbij het verschil in geluidssnelheid in verschillende weefsels en de terugkaatsing.
Voor je film kun je gebruik maken van de volgende bronnen:
Tot de Tweede Wereldoorlog had men eigenlijk geen goede apparatuur om hoeveelheden straling te meten. De meetmethoden waren grof, onnauwkeurig en willekeurig en leverden dus te weinig goede informatie om verantwoorde conclusies te trekken.
Om de schadelijkheid van röntgenstraling te bepalen, hanteerde men bijvoorbeeld de volgende methode: stel een lichaamsdeel bloot aan de straling en kijk wanneer de huid rood wordt. Deze hoeveelheid werd dan door 12 gedeeld (het aantal maanden). Dit laatste werd de norm voor de maximale hoeveelheid straling per jaar.
Wij weten inmiddels meer van straling af dan aan het begin van deze e-klas. Om te zeggen hoe gevaarlijk of juist ongevaarlijk straling is, moeten we deze kunnen meten. Apparaten waarmee je dat kunt doen, zijn onder meer de thermoluminescentiedosismeter, de geiger-müllertelbuis en de scintillatieteller.
Alleen het meten is echter niet voldoende. We willen ook iets kunnen zeggen over de biologische schadelijkheid van straling. Daarvoor gebruiken we de begrippen dosis en dosisequivalent. Dosis is de totale hoeveelheid ontvangen straling en dosisequivalent gaat over de mogelijke biologische schade.
6.1 Meten van straling
Meetmethode 1: TLD of thermoluminescentiedosismeter
De gebruiker, de persoon die in de omgeving van de stralingsbron werkt, draagt de TLD op zijn of haar kleding. Aan het einde van een periode wordt er gemeten hoeveel straling er in totaal op de TLD gekomen is. Dit is een maat voor de hoeveelheid straling, waaraan deze persoon is blootgesteld.
De thermoluminescentiedosismeter wordt in het artikel op deze website beschreven.
Opdrachten
1. Beschrijf uit welke onderdelen de TLD bestaat en waarvoor deze onderdelen dienen.
2. Hoe werkt deze meter?
3. Hoe wordt de meter uitgelezen en gereset?
4. Voor welke stralingssoorten wordt de TLD gebruikt?
Meetmethode 2: de geiger-müllertelbuis
Als er een geladen deeltje de geiger-müllertelbuisinkomt, botst het tegen een van de gasatomen in de buis. Dit gasatoom wordt geioniseerd en verliest elektronen. Doordat er elektrische spanning is tussen de draad in het midden en de wand, komen de elektronen in beweging. Er loopt dan een stroom. Deze stroom wordt gemeten en omgezet in een signaal. De signalen die de buis levert, worden geteld via een elektronisch telsysteem.
Opdrachten
5. Leg uit waarom het gas in de buis een lage druk heeft.
6. Welk soort deeltjes kun je hiermee meten?
7. Welk soort deeltjes kun je niet meten?
Meetmethode 3: scintillatieteller
De scintillatieteller is speciaal gemaakt voor het meten van gammastraling. Hij bestaat uit een kristal met daarachter een beeldversterker. In het kristal wordt een atoom in aangeslagen toestand gebracht door de gammastraling. Dit betekent dat een elektron energie opneemt en in een andere schil gaat zitten. Bij het terugvallen van de elektronen naar de grondtoestand, ontstaan er kleine lichtflitsen die we scintillaties noemen. Deze lichtflitsen worden versterkt door de beeldversterker en elektronisch omgezet naar een meetsignaal.
Opdrachten
8. Teken een model van een scintillatieteller of zoek een plaatje ervan op.
9. Leg uit wat er bedoeld wordt met de grondtoestand en de aangeslagen toestand van een atoom. Maak hierbij een tekening.
10. Leg uit op welke manier de beeldversterker werkt..
6.2 Dosisbepaling
Om te bepalen hoe gevaarlijk straling wel of niet is, moeten we weten wat er met straling in het lichaam gebeurt. Er zijn in principe 4 mogelijke gebeurtenissen denkbaar.
A. Er gebeurt niets. De straling gaat zonder contact door het lichaam heen en beïnvloedt het lichaam niet. Dit kan doordat de ruimte tussen kern en elektronenschillen relatief groot is.
B. Het stralingsdeeltje maakt een ander atoom radioactief. Dit kan alleen als het deeltje door een atoomkern geabsorbeerd wordt. De kans daarop is erg klein vanwege het kleine volume van de kern in het grotendeels lege atoom.
C. De straling wordt geabsorbeerd door atomen en de energie van de straling wordt omgezet in warmte.
D. Het stralingsdeeltje ioniseert atomen en de resulterende vrije elektronen kunnen chemische reacties - en dus schade - veroorzaken in lichaamscellen.
Opdrachten
1. Geef een schatting van de grootte van een atoom, atoomkern, elektronenschillen en een alfadeeltje. Leg hiermee uit dat een stralingsdeeltje eenvoudig door een atoom kan gaan zonder iets te raken.
2. Leg uit dat een atoom door een stralingsdeeltje niet radioactief kan worden. Gebruik hierbij de volgende begrippen: energie, snelheid, elektrische lading, afstoting
3. Leg uit hoe een stralingsdeeltje zijn energie kan afgeven.
4. Hoe kan een atoom of molecuul veranderen als het botst met een stralingsdeeltje? Gebruik hierbij het begrip ioniseren.
Dosisbepaling
Om stralingsrisico's te kunnen bepalen, gebruikt men de begrippen dosis en dosisequivalent. Het blijkt dat verschillende delen van het lichaam verschillende hoeveelheid straling kunnen weerstaan. Delen van het lichaam die nauwelijks groeien, kunnen veel meer straling absorberen zonder dat dit schadelijk wordt, dan delen die snel groeien en waar veel celdeling plaats vindt. Meer informatie hierover is te vinden in Binas.
De dosis is de absolute hoeveelheid stralingsenergie die opgenomen wordt in het weefsel. Het dosisequivalent wordt gebruikt om de verschillende soorten straling met elkaar te kunnen vergelijken. Elke stralingssoort heeft namelijk zijn eigen mogelijke effecten. Een alfadeeltje reageert bijvoorbeeld feller met zijn omgeving dan een röntgenfoton. Om ze met elkaar te kunnen vergelijken, is er een kwaliteitsfactor ingevoerd.
Dosis is hoeveelheid energie per massa ofwel:
D = E / m
In deze formule is E de energie in Joule, m de massa in kilogram en D de dosis in Gray (Gy), een eenheid voor Joule per kilogram.
Voor dosisequivalent H geldt:
H = Q · D
Hierin is Q de eenheidsloze weegfactor, H heeft dus dezelfde eenheid als D, namelijk J/kg, maar we noemen die nu Sievert (Sv) om te laten zien dat rekening is gehouden met de weegfactor.
Merk op dat Gray en Sievert beide de eenheid J/kg zijn, maar toch niet dezelfde betekenis hebben.
Hieronder staat een overzicht van de gevolgen van een bepaalde dosis als deze in korte tijd ontvangen wordt.
Effecten van acute blootstelling over het gehele lichaam
Dosis (Gy)
Effect
<0,05 Gy
Geen direct waarneembaar effect
0,15 - 0,25 Gy
Bij enkele mensen veranderingen in bloedwaarden
0,5
Vrijwel zeker veranderingen in de bloedwaarden
1,0
Vaak acuut stralingssyndroom merkbaar (begint met misselijkheid, overgeven,
vermoeidheid, geen eetlust)
1,5
Overgevoelige mensen overlijden
2
Ooglens begint troebel te worden
3,2-3,6
De helft overlijdt binnen 30 dagen bij minimale medische verzorging
4
Permanente steriliteit bij bestraling van de geslachtsorganen
5
Haaruitval
4,8-5,4
De helft overlijdt binnen 30 dagen bij normale medische verzorging
11
De helft overlijdt binnen 30 dagen, ook bij intensieve medische verzorging, waaronder
beenmergtransplantatie
>20
Vrijwel zekere dood
>50
Centraal zenuwstelsel (hersenen, spieren) bestuurt lichaamsfuncties als ademen en bloedcirculatie
niet meer. Zekere dood binnen enkele uren.
Je ziet in de tabel dat er bij röntgen- en gammastraling onder 0,05 Gy (=0,05 Sv = 50 mSv) geen direct waarneembaar effect is. Dit betekent niet dat een lage dosis straling ongevaarlijk is. Er bestaat altijd een zeer kleine kans op genetische veranderingen en kanker door straling.
Opgaven
5. Zoek op internet of een andere plaats op welke normen er worden gehanteerd voor de dosislimieten in Nederland.
6. Een röntgenfoto van bijvoorbeeld een voet geeft een stralingsbelasting van 1 microsievert (μSv). Als je in een vliegtuig op grote hoogte (10 km) zit, is de belasting veel hoger. Bovendien wordt deze belasting uitgedrukt in Sv/hr. Het strand in Brazilië geeft een belasting van 50 mSv per jaar.
a. Hoe groot is de stralingsbelasting in een vliegtuig?
b. Vergelijk de verschillende stralingsbelastingen en leg uit waarom de Nederlandse limiet veel kleiner is.
7. Een man laat een röntgenfoto van zijn arm maken om te kijken of deze gebroken is. De man legt zijn arm onder het röntgenapparaat en er wordt een foto gemaakt. De arm heeft een massa van 2,4 kg. De hoeveelheid geabsorbeerde energie uit het apparaat is 0,005 J. Voor Q geldt de waarde 1.
a. Bereken de dosis die de man ontvangt.
b. Bereken het dosisequivalent dat de man ontvangt.
8. Een man wordt 10 minuten blootgesteld aan een bron van alfadeeltjes. De bron heeft een vermogen van 0,0025 W. De man heeft een massa van 85 kg. Door absorptie in de omgeving wordt slechts 80% van de hoeveelheid straling door de man geabsorbeerd.
a. Bereken de dosis die de man ontvangt.
b. Bereken het dosisequivalent van deze straling.
c. Gezien de eigenschappen van alfastraling, door welk deel van het lichaam zal deze vooral geabsorbeerd worden?
9. Als een persoon of voorwerp radioactief materiaal in of op zich krijgt, dan wordt hij continu blootgesteld aan straling. Deze persoon of dit voorwerp is dan besmet. Als een stralingsbron zich buiten het lichaam of voorwerp bevindt, ontvangt deze persoon of dit voorwerp alleen straling zolang hij in de buurt van de bron is. De persoon wordt dan alleen bestraald.
a. Leg uit waarom besmetting doorgaans gevaarlijker is dan bestraling.
10. Een moeder doet samen met haar zoon uit havo 5 boodschappen in de supermarkt. De appels komen uit Australië en op het etiket staat dat de appels ter conservering bestraald zijn. Moeder uit haar twijfels over de veiligheid van de appels. Zij is bang dat ze zelf radioactief wordt als ze de appels eet en stralingsziekten kan krijgen. Haar zoon legt uit waarom het niet gevaarlijk is en gebruikt hierbij de termen besmet en bestraald.
a. Leg uit wat de zoon zegt over bemetting en bestraling.
b. Leg uit dat de moeder geen stralingsziekte kan oplopen door het eten van de appels.
Er is een duidelijk onderscheid tussen dosis (Gray) en dosisequivalent (Sievert), hoewel de natuurkundige eenheden gelijk zijn.
11. Leg dit uit.
H7 Eindopdracht
7 Eindopdracht
In dit hoofstuk staan twee eindopdrachten. De eerste opdracht is een ontwerpopdracht waarbij je de nieuwe vleugel voor een ziekenhuis gaat ontwerpen en de tweede opdracht bestaat uit een aantal opgaven die ontleend zijn aan pilotexamens Nieuwe Natuurkunde. Je docent vertelt je welke van de twee opdrachten je moet doen.
Als je de ontwerpopdracht moet maken, is het niet verkeerd om ook 1 of 2 van de examenopgaven te maken. Zo kun je kijken of je de stof van deze e-klas onder de knie hebt.
7.1 Ontwerpopdracht
Het ziekenhuis gaat een nieuwe vleugel bouwen voor de afdeling medische beeldvorming.
Jullie gaan de vleugel ontwerpen en presenteren aan de rest van de groep. Je presenteert het plan namens een architectenbureau aan het personeel van de afdeling en de directie van het ziekenhuis.
Houd rekening met het volgende:
Alle beeldvormende technieken van dit hoofdstuk moeten een plaats hebben.
Sommige beeldvormende technieken geven gevaarliljke straling af. Houd rekening met veiligheid voor personeel en patiënten.
Neem wachtruimtes en balies voor de verschillende technieken op in je ontwerp.
Patiëntenstromen moeten logisch zijn. Mensen moeten elkaar niet in de weg lopen.
De gemaakte beelden moet digitaal en centraal kunnen worden opgeslagen.
De mensen die er werken, moeten een rustruimte hebben.
Het ontwerp maak je met Google Sketch-Up. Eventueel maak je een maquette.
Tijdens de presentaties zijn er verschillende rollen voor iedereen:
De architecten die een plan presenteren (tijdens je eigen presentatie).
Het personeel dat reageert op de plannen (tijdens andere presentaties).
De directie die op basis van argumenten beslist welk bureau de opdracht krijgt.
7.2 Toetsvragen
Opgave 1: Alfadetector
Carla en Harry gaan een experiment uitvoeren, waarbij zij de dracht van alfadeeltjes in lucht willen bepalen. Figuur 1 is een foto van de opstelling die ze gebruiken. Uit een radioactieve bron komen alfadeeltjes die in de richting van een detector bewegen. In figuur 2 is de detector van achteren te zien. De detector bestaat uit een dunne metaaldraad en twee metaalplaten. Tussen de draad en de metaalplaten staat een hoge spanning. Als een alfadeeltje in de buurt van de metaaldraad voldoende moleculen van de lucht ioniseert, vindt er een elektrische ontlading plaats tussen één van de metaalplaten en de dunne metaaldraad, waardoor een vonk ontstaat. In figuur 2 zijn vier vonken te zien. Carla en Harry verschillen van mening over de manier waarop een alfadeeltje de moleculen van de lucht ioniseert.
Carla zegt: “Het alfadeeltje bestraalt de moleculen van
de lucht.”
Harry zegt: “Het alfadeeltje botst tegen de moleculen
van de lucht.”
a. Wie heeft gelijk?
Eén alfadeeltje kan maar één vonk maken. Carla en Harry tellen gemiddeld 24 vonken per minuut. Volgens Harry is de activiteit van de bron gelijk aan 0,40 Bq. Carla is het hiermee oneens en denkt dat de activiteit van de bron groter is.
b. Leg uit wie gelijk heeft.
In figuur 3 is het elektrische gedeelte van de detector schematisch weergegeven. De grootte van de weerstand R is 100 MΩ. Carla en Harry discussiëren over de vraag hoe groot de spanning tussen de metaaldraad en een metaalplaat is op het moment dat er geen vonk is.
Volgens Carla is deze spanning 2,0 kV.
Volgens Harry is deze spanning 4,0 kV.
c. Leg uit wie gelijk heeft.
Als er wel een vonk is, verandert de spanning tussen de draad en één van de metaalplaten. Volgens Carla neemt deze spanning af, volgens Harry neemt deze spanning toe.
d. Leg uit wie gelijk heeft.
De voltmeter in figuur 3 wijst tijdens een elektrische ontlading 250 V aan. e. Bereken de stroomsterkte die de ampèremeter nu aangeeft.
Als radioactieve bron wordt americium-241 gebruikt.
f. Geef de vervalvergelijking van Am-241.
De americium-241-bron is vijf jaar oud.
g. Leg uit of de activiteit in die vijf jaar merkbaar is afgenomen.
Carla en Harry gaan nu met de opstelling van figuur 1 de dracht van de alfadeeltjes in lucht bepalen. In deze opstelling is het mogelijk met de bron te schuiven.
h. Leg uit hoe ze met deze opstelling de dracht van de alfadeeltjes kunnen bepalen.
Opgave 2: Nucleaire microbatterij
Lees eerst onderstaande tekst.
Nucleaire microbatterij
Onderzoekers hebben een kleine batterij ontwikkeld die werkt met behulp van een radioactieve bron. In de figuren hiernaast wordt de werking ervan uitgelegd. Een kunststofstrip is aan één kant ingeklemd. Op de strip zit een plaatje zogenoemd piëzo-elektrisch materiaal. Onder het andere uiteinde zit een koperen plaatje. Tegenover dit plaatje is een plaatje radioactief nikkel (63Ni) geplaatst. Het geheel bevindt zich in vacuüm. Zie figuur (a). 63Ni zendt β-straling uit die door het koper wordt geabsorbeerd. Zie figuur (b). Het nikkel wordt dan positief geladen en het koper negatief. Daardoor trekken de plaatjes elkaar aan waardoor de strip buigt. Zie figuur (c). Wanneer de twee plaatjes elkaar aanraken, schiet de kunststof strip terug en trilt een tijdje na. Zie figuur (d). Dit proces herhaalt zich steeds. Piëzo-elektrisch materiaal heeft de eigenschap dat het een elektrische spanning opwekt wanneer het gebogen wordt. Zo wordt de trillingsenergie van de strip omgezet in elektrische energie
63Ni zendt β-straling uit.
a. Geef de vervalvergelijking van 63Ni.
Het koperen en het nikkelen plaatje krijgen een tegengestelde lading en trekken elkaar aan.
b. Leg uit waarom:
− het koperen plaatje een negatieve lading krijgt;
− het nikkelen plaatje een positieve lading krijgt.
Door de aantrekkende kracht buigt de kunststof strip naar beneden. Als het koperen en nikkelen plaatje elkaar aanraken, schiet de strip meteen terug.
c. Leg uit waarom de strip dan terugschiet.
Het apparaatje is in werkelijkheid slechts enkele millimeters groot. De dikte van het koperen plaatje is maar 60 micrometer. Voor een goede werking van de batterij heeft men radioactief materiaal uitgekozen waarvan de β-deeltjes een betrekkelijk lage energie hebben.
d. Leg uit waarom de batterij minder goed werkt als de uitgezonden β-deeltjes een
hoge energie zouden hebben.
Een tweede eis die men aan het radioactieve materiaal stelt, is dat het naast de β-straling geen γ-straling uitzendt.
e. Leg uit wat het nadeel is van radioactief materiaal dat ook γ-straling uitzendt.
De microbatterij kan worden gebruikt als voeding voor een pacemaker. Het is dan nuttig dat de batterijen niet vaak vervangen hoeven te worden.
f. Leg uit waarom deze microbatterij daar zeer geschikt voor is. Baseer je uitleg op een gegeven uit Binas.
Opgave 3: Radondochters
Radon is een radioactief edelgas dat uit de bodem en uit bouwmaterialen kan ontsnappen en terecht kan komen in kelders en kruipruimtes die slecht geventileerd worden.De meest voorkomende isotoop van radon is radon-222. Radioactieve isotopen met atoomnummers tussen 82 en 90 komen in de natuur voor omdat ze voortdurend aangemaakt worden. Er bestaan in de natuur twee zogenoemde ‘radioactieve reeksen’. De ene reeks begint bij thorium-232, de andere bij uraan-238.
a. Beredeneer of radon-222 ontstaat uit thorium-232 of uit uraan-238. Beschouw daartoe het aantal nucleonen van de kernen.
Hint: het is niet nodig om de vervalvergelijkingen op te schrijven.
In figuur 1 zijn het verval van radon-222 en de daarop volgende vervalstappen weergegeven. Bij elke isotoop is de halfwaardetijd gegeven.
NB: uit de gegevens in Binas zou ook een alternatieve vervalroute kunnen worden afgeleid. Deze komt echter zo weinig voor, dat we hem in deze opgave verwaarlozen.
De vier grijze isotopen worden ‘radondochters’ genoemd. Zij hebben een betrekkelijk kleine halveringstijd: als een radon-222 kern vervalt, vervallen vrij snel daarna ook de radondochters. De radondochters hechten zich aan microscopische stofdeeltjes en blijven in de lucht zweven. De lucht in een gesloten kelderruimte bevat dus radon en radondochters. Ook als er per seconde steeds dezelfde hoeveelheid radon ontsnapt, gaat het ophopen van radon in een gesloten kelderruimte niet eindeloos door. Als er niet geventileerd wordt, bereikt de activiteit (in Becquerel) van het radon een bepaalde constante waarde.
b. Leg uit:
- waarom in dat geval de activiteit van radon-222 uiteindelijk constant wordt;
- dat elk van de radondochters dan dezelfde activiteit heeft als radon-222.
Een persoon die een tijdje in zo’n kelderruimte verblijft, ademt lucht in met de daarin aanwezige isotopen. Stel dat een persoon tijdens zijn verblijf in de kelderruimte 1 m3 lucht inademt. De persoon ademt het radon weer uit omdat het een edelgas is. De microscopische stofdeeltjes met de radondochters blijven achter in de longen. Bij het verval hiervan worden de longen (totale massa van 2,5 kg) bestraald.
In tabel 1 staat het aantal kernen in 1 m3 lucht van elk van de radondochters in de kelderruimte.
Voor de stralingsdosis D geldt: D = Estr / m
Hierin is:
- Estr de stralingsenergie, die geabsorbeerd wordt;
- m de massa van het bestraalde orgaan.
c. Bereken de stralingsdosis die de longen ontvangen ten gevolge van alfa-straling.
d. Bereken de stralingsdosis die de longen ontvangen ten gevolge van alfa-straling.
Tabel 1
Aantal kernen (in 1 m3 lucht) in de kelderruimte
Po-218
2,6·104
Pb-214
2,3·105
Bi-214
1,7·105
Po-214
Opgave 4: Radiotherapie
In de geneeskunde wordt sinds lange tijd gebruik gemaakt van ioniserende straling om tumoren te behandelen. Vroeger gebruikte men daarbij vaak de isotoop radium-226. Een kleine hoeveelheid hiervan bracht men aan op de punt van een naald die in de tumor werd gestoken.
Ra-226 zendt α- en γ-straling uit.
a. Geef de vervalvergelijking van Ra-226.
b. Hieronder staan twee beweringen.
I Het doordringend vermogen van α-straling is groter dan dat van γ-straling.
II Het ioniserend vermogen van α-straling is groter dan dat van γ-straling.
Wat is juist?
A Alleen bewering I is waar.
B Alleen bewering II is waar.
C Beide beweringen zijn waar.
D Geen van beide beweringen is waar.
In plaats van Ra-226 wordt tegenwoordig vaak de radioactieve isotoop iridium-192 gebruikt. Deze isotoop zendt β-straling uit.
c. Hieronder staan twee beweringen.
I De massa van een β-deeltje is groter dan de massa van een α-deeltje.
II De lading van een β-deeltje is groter dan de lading van een α-deeltje.
Wat is juist?
A Alleen bewering I is waar.
B Alleen bewering II is waar.
C Beide beweringen zijn waar.
D Geen van beide beweringen is waar.
Behalve α-, β- en γ-straling wordt in de geneeskunde vaak röntgenstraling toegepast.
d. Hieronder staan twee beweringen.
I Volgens Binas is de energie van een γ-foton groter dan die van een röntgenfoton.
II Volgens Binas is de golflengte van γ-straling groter dan die van röntgenstraling.
Wat is juist?
A Alleen bewering I is waar.
B Alleen bewering II is waar.
C Beide beweringen zijn waar.
D Geen van beide beweringen is waar.
Sinds kort is een nieuwe bestralingsmethode ontwikkeld: bestraling met snelle protonen. Deze methode heeft voordelen ten opzichte van bestraling met γ-fotonen. In figuur 1 is zowel voor γ-fotonen als protonen de (geabsorbeerde) dosis weergegeven als functie van de indringdiepte. Ook is aangegeven op welke diepte de tumor zich bevindt. Kenmerkend voor protonen is de piek in de grafiek. De plaats waar deze piek optreedt, hangt af van de energie van de protonen. Die energie kan men instellen.
e. Noem aan de hand van het diagram in de figuur hiernaast twee voordelen van bestraling met protonen ten opzichte van bestraling met γ-fotonen.
Men wil een oogtumor met een massa van 4,2 mg met protonen bestralen. De protonenbundel die er op gericht wordt, bevat 7,8·103 protonen per seconde.
De energie van elk proton is 70 MeV. De protonen geven 80% van hun energie af aan het weefsel van de tumor. De tumor moet een stralingsdosis (de geabsorbeerde energie per kg) opnemen van 60 Gy, verdeeld over 30 bestralingen.
f. Bereken hoe lang elke bestraling moet duren. Neem daarbij aan dat alle protonen de tumor treffen.
Bij het maken van deze e-klas is gebruik gemaakt van de NLT-modules "Medische Beeldvorming" voor havo en vwo, en van de NiNa-module "Medische Beeldvorming".
De afdeling Medische Beeldvormende Technieken van het Streekziekenhuis Koningin Beatrix in Winterswijk heeft ons enorm geholpen met uitleg over de apparatuur en met foto's.
Verantwoording foto/plaatjes/film/animaties
Inleiding:
Het filmpje van de ambulance komt van YouTube. Het toont een ambulance van de ambulancedienst Noord-West Veluwe
Hoofdstuk 1:
Niels Bohr, Marie Curie en EM-golven: Wikimedia
EM-spectrum: website ErasmusMC
Hoofdstuk 2:
röntgenbuis en lab Röntgen: Wikimedia
gebroken been: Streekziekenhuis Beatrix
röntgenapparaat: www.natuurkunde.nl
film: Torsten Fleisch via Vimeo
animaties: PennStateUniversity/Schuijlkill
Hoofdstuk 3:
gammacamera: Wikimedia
Hoofdstuk 4:
MRI-scanner: Wikimedia
Mensen scannen met MRI: M.P. Huijbregtse, J.H. van der Schee, J.E. Frederik
Voor zover wij hebben kunnen nagaan, zijn alle plaatjes en foto's vrij van rechten en mogen zij met bronvermelding worden gebruikt, afgezien van de afbeeldingen van het Streekziekenhuis Koningin Beatrix. Mochten wij toch wat over het hoofd hebben gezien, dan is dat niet met opzet en bieden wij onze verontschuldigingen aan. Degenen die menen rechten te kunnen doen gelden op opgenomen beelden wordt verzocht zich met ons in verbinding te stellen.
Auteurs: Wim van der Weiden (Alberdingk Thijm College) en Menno Ossekoppele (SG Marianum)
Begeleiding en redactie: Ed van den Berg (VU) en De Praktijk
Het arrangement Medische beeldvorming is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
Bètapartners
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2014-07-21 14:48:25
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 3.0 Nederland licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Veel technieken waarmee wordt gekeken in je lichaam, maken gebruik van eigenschappen van atomen. Al heel lang denken mensen na over wat materie is en waaruit het bestaat. De Grieken hadden al voorstellingen van het 'inwendige' van alle materie. Empedocles dacht dat alle materie was opgebouwd uit de vier elementen: vuur, water, lucht en aarde. Plato hield het erop dat je materie tot in het oneindige kon delen. Iemand die al een notie had van hoe het werkelijk zat, was Democritus. Hij ging ervan uit dat je niet verder kon gaan dan een kleinste ondeelbare stukje materie: het atoom, afgeleid van het Griekseatomos, dat ondeelbaar betekent. Na de Grieken hebben nog meer mensen zich met het atoom bezig gehouden, maar pas in de negentiende en twintigste eeuw is het huidige model voor atomen ontstaan. Dit model is nog niet helemaal af en wordt nog steeds bijgesteld door de uitkomsten van allerlei nieuw onderzoek.
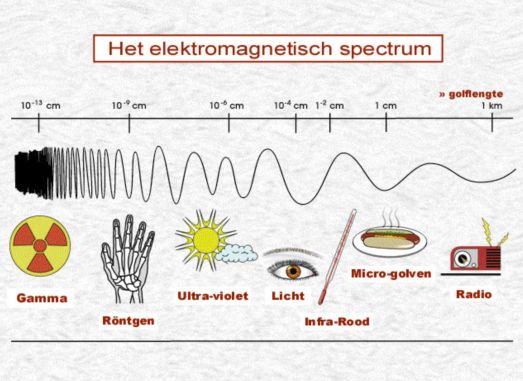
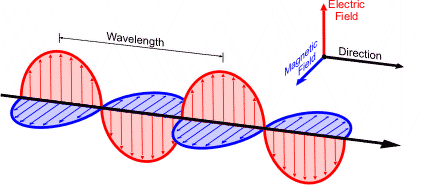
Deze straling bleek afkomstig uit de atoomkern en wordt daarom ook wel kernstraling genoemd. Eigenschappen van deze stralingssoorten zijn het ioniserende vermogen en het doordringende vermogen.
alpha-decay_nl.jnlp
Je hebt spoelen nodig met verschillende aantallen windingen.
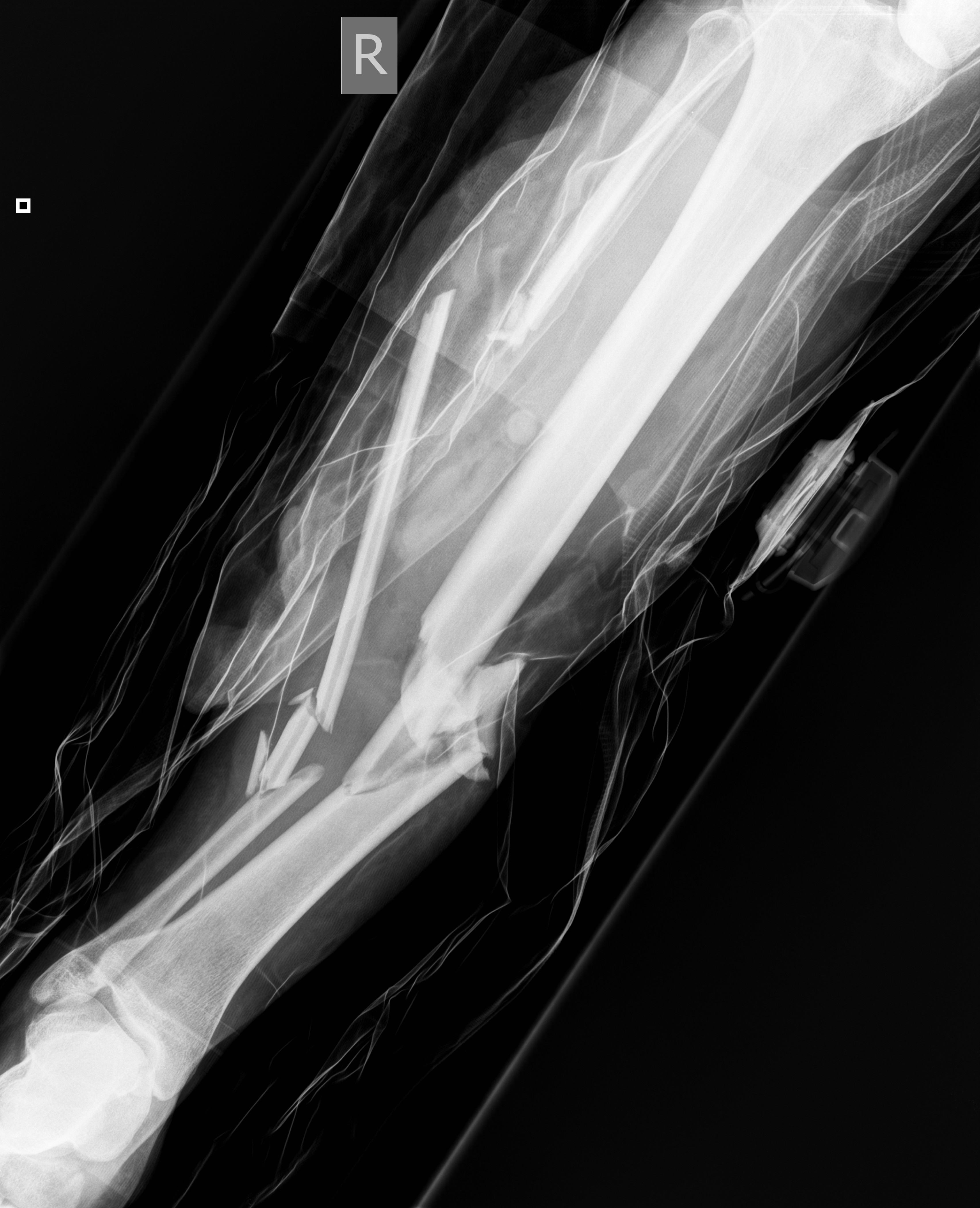
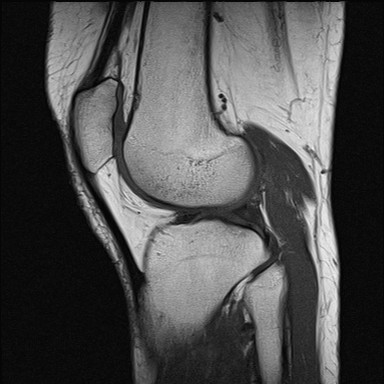
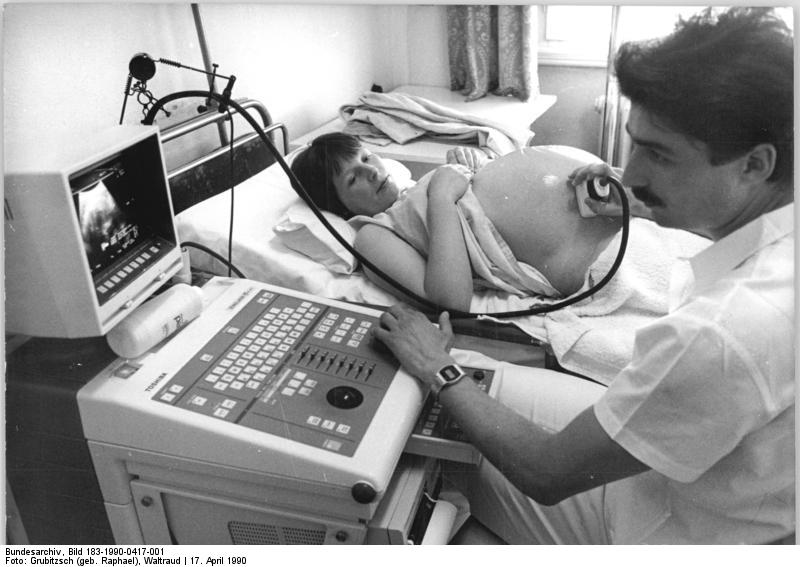Casus
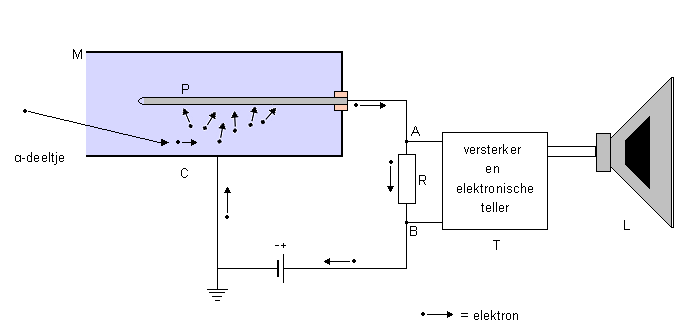
Carla zegt: “Het alfadeeltje bestraalt de moleculen van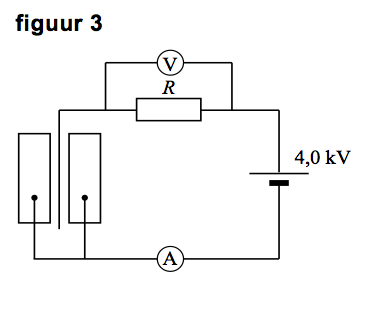
e. Bereken de stroomsterkte die de ampèremeter nu aangeeft.
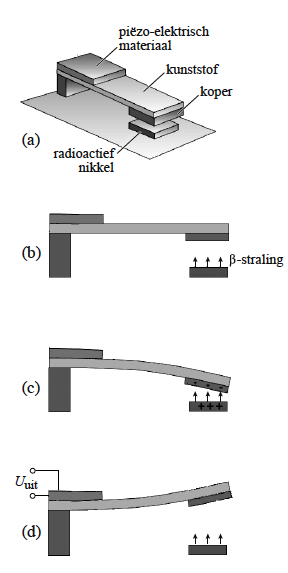Nucleaire microbatterij
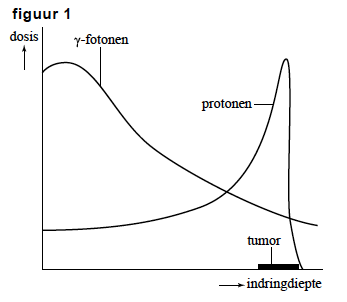Kenmerkend voor protonen is de piek in de grafiek. De plaats waar deze piek optreedt, hangt af van de energie van de protonen. Die energie kan men instellen.
