Het arrangement 09. Les 9 Het Computertijdperk is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 18-12-2014 14:11:13
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 3.0 Nederland licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 3.0 Nederland licentie.
Dit materiaal is achtereenvolgens ontwikkeld en getest in een SURF-project (2008-2011: e-klassen als voertuig voor aansluiting VO-HO) en een IIO-project (2011-2015: e-klassen&PAL-student). In het SURF project zijn in samenwerking met vakdocenten van VO-scholen, universiteiten en hogescholen e-modules ontwikkeld voor Informatica, Wiskunde D en NLT. In het IIO-project (Innovatie Impuls Onderwijs) zijn in zo’n samenwerking modules ontwikkeld voor de vakken Biologie, Natuurkunde en Scheikunde (bovenbouw havo/vwo). Meer dan 40 scholen waren bij deze ontwikkeling betrokken.
Organisatie en begeleiding van uitvoering en ontwikkeling is gecoördineerd vanuit Bètapartners/Its Academy, een samenwerkingsverband tussen scholen en vervolgopleidingen. Zie ook www.itsacademy.nl
De auteurs hebben bij de ontwikkeling van de module gebruik gemaakt van materiaal van derden en daarvoor toestemming verkregen. Bij het achterhalen en voldoen van de rechten op teksten, illustraties, en andere gegevens is de grootst mogelijke zorgvuldigheid betracht. Mochten er desondanks personen of instanties zijn die rechten menen te kunnen doen gelden op tekstgedeeltes, illustraties, enz. van een module, dan worden zij verzocht zich in verbinding te stellen met de programmamanager van de Its Academy (zie website).
Gebruiksvoorwaarden: creative commons cc-by sa 3.0
Handleidingen, toetsen en achtergrondmateriaal zijn voor docenten verkrijgbaar via de bètasteunpunten.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
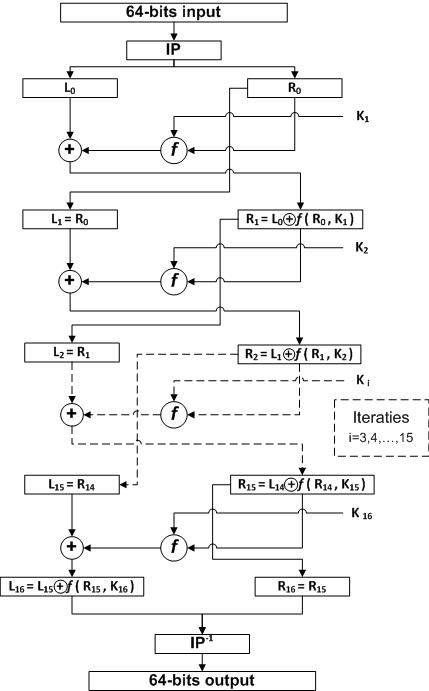
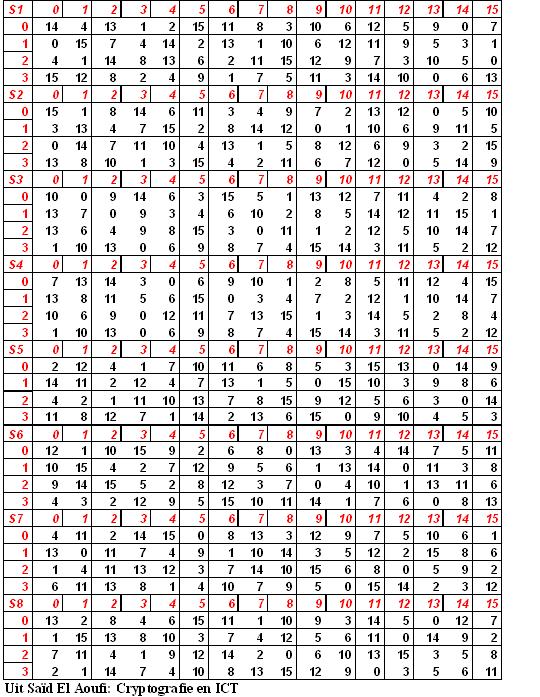
- Deze les maakt onderdeel uit van de e-klas 'Cryptografie' voor Havo 5 voor het vak wiskunde D.
- Leerniveau
- HAVO 5;
- Leerinhoud en doelen
- Wiskunde D; Inzicht en handelen;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- e-klassen rearrangeerbaar