Het arrangement Sk-01 Eenheden en meten is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteurs
- Laatst gewijzigd
- 10-01-2016 19:43:55
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 3.0 Nederland licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 3.0 Nederland licentie.
Vakinhoudelijk deel van een thema over eenheden en meten, omgezet in een Wikiwijs arrangement vanuit een prototype van een kennisbank scheikunde van het voormalige Ruud de Moor Centrum van de OU. Oorspronkelijke auteurs en samenstellers van de kennisbank: Jan de Dobbelaere, Ingrid Holtkamp en Jan Lutgerink. Aanpassingen door Dick Naafs en Jan Lutgerink.
We werken de kennisbank sinds 2010 niet meer bij, maar we doen dit wel voor thema's die we hebben omgezet in Wikiwijs arrangementen. U kunt mailen naar Jan Lutgerink als u voorstellen heeft voor aanpassing, maar u kunt ook een kopie van het arrangement maken om het zelf aan te passen of uit te breiden voor gebruik in de les of voor zelfstudie door leerlingen. In een digitale handleiding kunt u zien hoe u dat moet doen.
De kennisbank is ooit opgezet voor ondersteuning van beginnende docenten scheikunde. Ze bestond ook uit meerdere kennislagen: vakinhoud, vakdidactiek, toetsen, etc. De vakinhoud beschreven we als minimale parate kennis die een beginnend docent moet hebben om het vak te kunnen geven. Daaraan koppelden we didactische aanwijzingen en - waar relevant - kennis over preconcepten en misconcepten bij leerlingen.
Sommige teksten zijn wellicht ook voor leerlingen geschikt, maar dat was niet de opzet van de kennisbank. We laten het aan de docent(e) over of dit materiaal geschikt is voor bijvoorbeeld zelfstudie van zijn/haar leerlingen.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
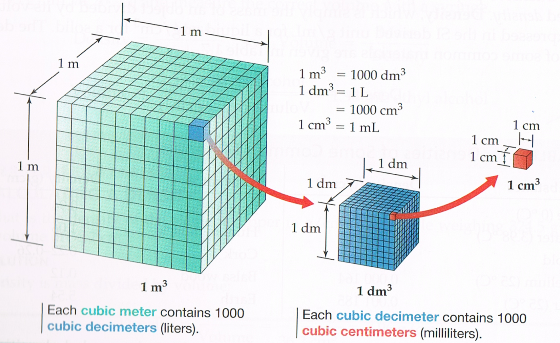
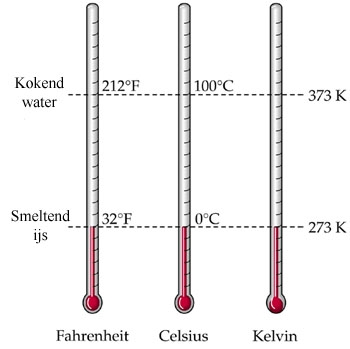
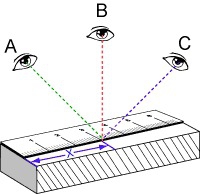
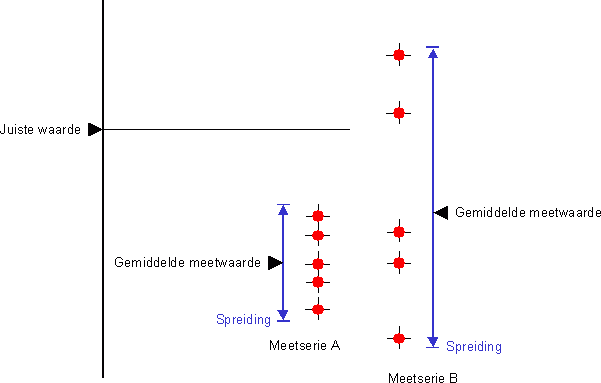
- Dit thema gaat over eenheden en meten.
- Leerniveau
- VMBO gemengde leerweg, 2; VMBO kaderberoepsgerichte leerweg, 1; VWO 2; VO; VMBO kaderberoepsgerichte leerweg, 2; VMBO basisberoepsgerichte leerweg, 4; VMBO gemengde leerweg, 3; VMBO basisberoepsgerichte leerweg, 1; VMBO theoretische leerweg, 1; HAVO 4; HAVO 1; VMBO theoretische leerweg, 4; VWO 6; VMBO gemengde leerweg, 1; VMBO theoretische leerweg, 2; VMBO basisberoepsgerichte leerweg, 2; HAVO; VWO 1; VWO; HAVO 3; VWO 3; VMBO; HAVO 5; VWO 4; VMBO theoretische leerweg, 3; VMBO basisberoepsgerichte leerweg, 3; VMBO kaderberoepsgerichte leerweg, 4; HAVO 2; VMBO gemengde leerweg, 4; VWO 5; VMBO kaderberoepsgerichte leerweg, 3;
- Leerinhoud en doelen
- Scheikunde;
- Eindgebruiker
- leraar
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 0 uur 50 minuten
- Trefwoorden
- absolute meetonzekerheid, absolute nulpunt, afgeleide grootheden, afgeleide grootheid, afleesnauwkeurigheid, afronden, afrondfout, afrondfouten, aftrekken, ampere, analytische balans, balans, basisgrootheden, basisgrootheid, bekerglas, buret, candela, celsius, chemie, delen, dichtheid, druk, eenheden, eenheid, elektronische balans, erlenmeyer, fahrenheit, gasmeetspuit, gemiddelde meetwaarde, glaswerk, graad, graden, grootheden, grootheid, hoeveelheid stof, injectiespuit, interpolatie, interpoleren, kelvin, kilogram, lengte, lichtsterkte, liniaal, maatcilinder, maatgetal, maatgetallen, maatkolf, maatpipet, maatverdeling, massa, meetfout, meetfouten, meetinstrument, meetinstrumenten, meetonzekerheden, meetonzekerheid, meetpipet, meetwaarde, meetwaarden, meten, meter, mol, nanotechnologie, nauwkeurigheid, optellen, parallax, pipet, pipetpomp, pipetteerballon, pipetteren, precisie, reken-/wiskundige vaardigheden, relatieve meetonzekerheid, scheikunde, seconde, si-eenheden, si-eenheid, si-standaard, si-standaarden, si-stelsel, significant, significant cijfer, significante cijfers, significantie, standaardeenheid, stroomsterkte, symbolen, symbool, systematische fout, systematische fouten, tarreren, technisch-instrumentele vaardigheden, temperatuur, temperatuurschaal, temperatuurschalen, thermometer, thomson, tijd, toevallige fout, toevallige fouten, verdeelpipet, vermenigvuldigen, verschilzicht, volpipet, volume, volumetrische pipet, voorvoegsel, voorvoegsels, weegtoestel, wetenschappelijke notatie
Bronnen
| Bron | Type |
|---|---|
|
Water en whiskey (alcohol) hebben verschillende dichtheden. Welke vloeistof heeft de grootste dichtheid? https://youtu.be/NJeLqwhIJ9s?rel=0 |
Video |
|
Significante cijfers bij vermenigvuldigen, delen, optellen en aftrekken. https://youtu.be/DxleIz2BTzk?rel=0 |
Video |
|
Demonstratievideo pipetteren en omgaan met de pipetteerballon. https://youtu.be/tigTIN5ALfM?rel=0 |
Video |
Gebruikte Wikiwijs Arrangementen
Naafs, Dick. (z.d.).
Test significante cijfers