Het arrangement Leerlijn onderzoeken havo/vwo bovenbouw is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 21-08-2025 11:22:00
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Modeldidactiek lessen over leren onderzoeken voor havo/vwo bovenbouw
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Gebruikte Wikiwijs Arrangementen
Modeldidactiek. (z.d.).
Elektrostatica: ontwikkeling van lading en veld begrip
https://maken.wikiwijs.nl/207485/Elektrostatica__ontwikkeling_van_lading_en_veld_begrip
Modeldidactiek. (z.d.).
Leerlijn onderzoek en practicum
https://maken.wikiwijs.nl/207491/Leerlijn_onderzoek_en_practicum
Modeldidactiek. (z.d.).
Practica vaardigheden en trillingen / golven
https://maken.wikiwijs.nl/207530/Practica_vaardigheden_en_trillingen___golven
Modeldidactiek. (z.d.).
Practicum cirkelbeweging en vaardigheden: Ronddraaiende stop
https://maken.wikiwijs.nl/207528/Practicum_cirkelbeweging_en_vaardigheden__Ronddraaiende_stop
Modeldidactiek. (z.d.).
Practicum soortelijke warmte (deel 1)
https://maken.wikiwijs.nl/207490/Practicum_soortelijke_warmte__deel_1_
Modeldidactiek. (z.d.).
Practicum soortelijke warmte (deel 2)
https://maken.wikiwijs.nl/207524/Practicum_soortelijke_warmte__deel_2_
Modeldidactiek. (2024).
Practicum Spaghettibrug - verband tussen belasting en breken
https://maken.wikiwijs.nl/212096/Practicum_Spaghettibrug___verband_tussen_belasting_en_breken
Modeldidactiek. (z.d.).
Practicum vaardigheden en mechanica: Horizontale worp
https://maken.wikiwijs.nl/207527/Practicum_vaardigheden_en_mechanica__Horizontale_worp
Modeldidactiek. (2024).
Practicum Vaardigheden: Meten en rekenen met significante cijfers
https://maken.wikiwijs.nl/212095/Practicum_Vaardigheden__Meten_en_rekenen_met_significante_cijfers
Modeldidactiek. (2024).
Practicum Vaardigheden: Ohmse weerstand
https://maken.wikiwijs.nl/207526/Practicum_Vaardigheden__Ohmse_weerstand
Modeldidactiek. (2024).
Practicum Vaardigheden: Schuivende bekertjes - meetonzekerheid
https://maken.wikiwijs.nl/212098/Practicum_Vaardigheden__Schuivende_bekertjes___meetonzekerheid
Modeldidactiek. (2024).
Practicum vaardigheden: vallende bakjes
https://maken.wikiwijs.nl/212100/Practicum_vaardigheden__vallende_bakjes











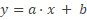
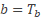
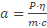
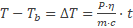
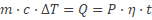
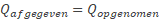
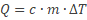


 Knip twee stukjes krantenpapier uit, met dezelfde afmeting als de tapes, en hang er één 15 cm links van het folie aan de rand van een tafel. Label het hangende krantenpapier “P”. Benader het hangende papier met het andere stuk papier.
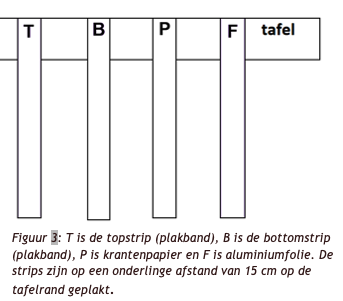
Knip twee stukjes krantenpapier uit, met dezelfde afmeting als de tapes, en hang er één 15 cm links van het folie aan de rand van een tafel. Label het hangende krantenpapier “P”. Benader het hangende papier met het andere stuk papier.  plakkerige kant om eventuele lading te verwijderen. Trek daarna de B- en T-tapes snel uit elkaar. Plak beide strips aan de rand van de tafel, naast het aluminiumfolie en krantenpapier, met minimaal 15 cm ertussen. Zie figuur 3.
plakkerige kant om eventuele lading te verwijderen. Trek daarna de B- en T-tapes snel uit elkaar. Plak beide strips aan de rand van de tafel, naast het aluminiumfolie en krantenpapier, met minimaal 15 cm ertussen. Zie figuur 3.
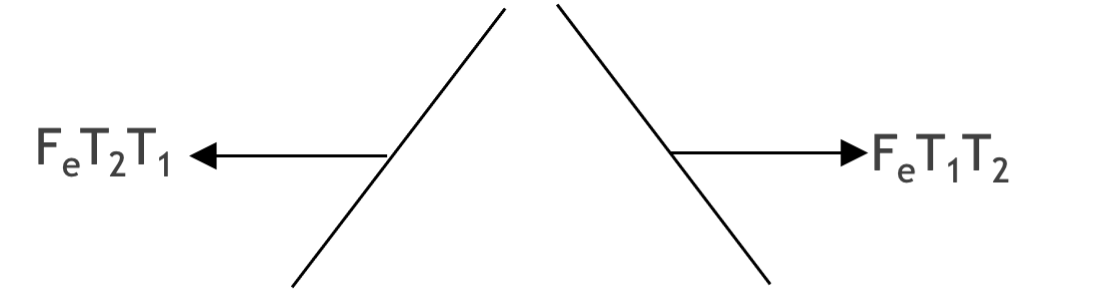
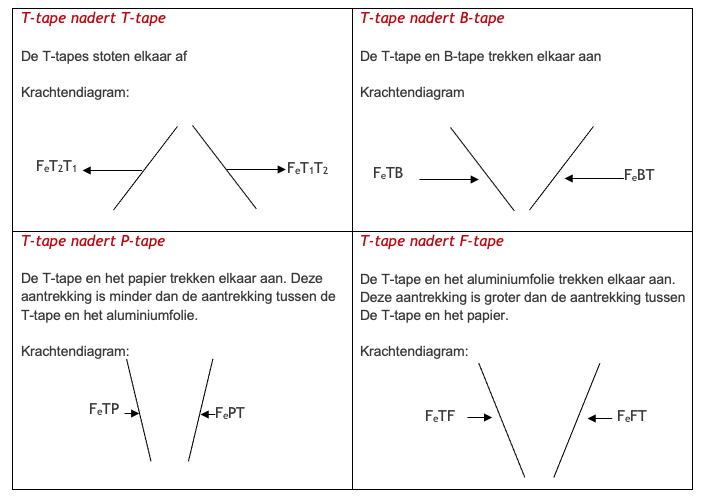
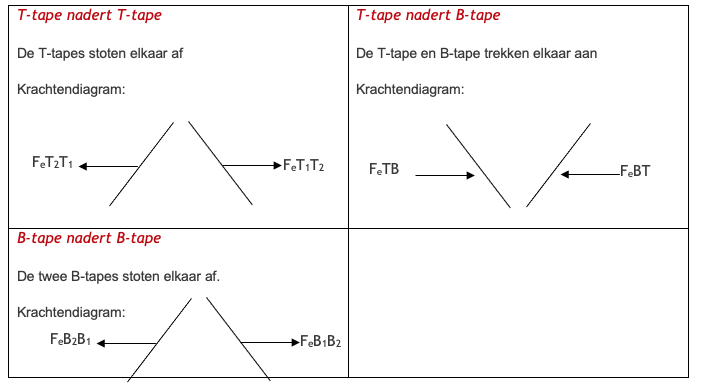
 Werkblad sticky tape
Werkblad sticky tape