Het arrangement Systematisch tellen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 07-04-2025 06:00:52
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Cartoon rok vectorafbeeldingen, illustraties en clipart | Depositphotos
Digitale leeromgeving - Boom beroepsonderwijs
Feesthoedjes Stippen - 6 Stuks - Feestbazaar.nl
Hoe ga je met je leerling op zoek naar een goed leesboek? - ZIEN in de Klas
Ja/nee-vragen zijn veel te makkelijk?! | SBO Blog
Minky Ballenbak met Ballen 200 st Roze Voor Meisjes (kleinbaby.nl)
Moderne Wiskunde havo A deel 1 (MW12.1) - 4, 5 havo
Tips voor unieke en leuke Sinterklaas en Kerst Cadeautjes - Fiets-stoeltje.nl
Weense koffiehuizen en specialiteiten - Tips Op Reis
Zomervakantie 2024 - Bel Lighting
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Systematisch tellen
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Bronnen
| Bron | Type |
|---|---|
|
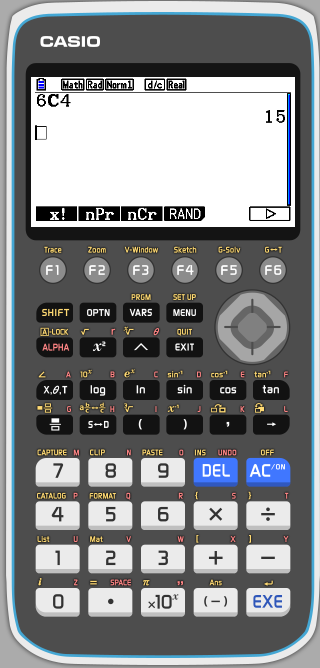
Faculteit berekenen op een grafische rekenmachine https://www.youtube.com/watch?v=lbwNp3NpJCo |
Video |



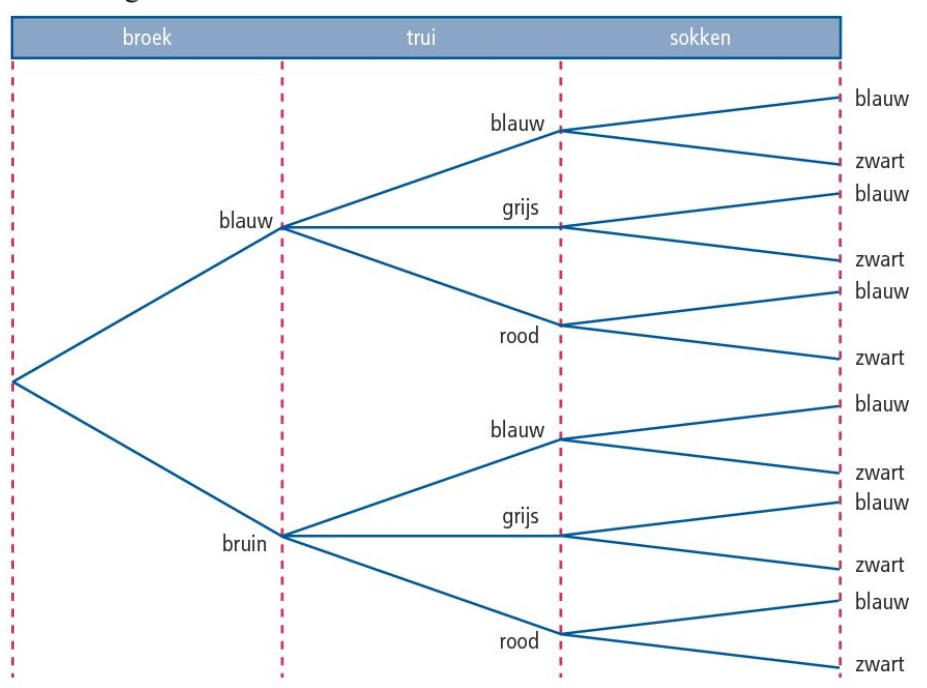

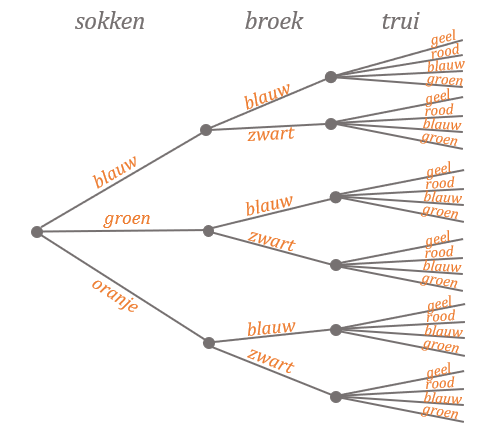
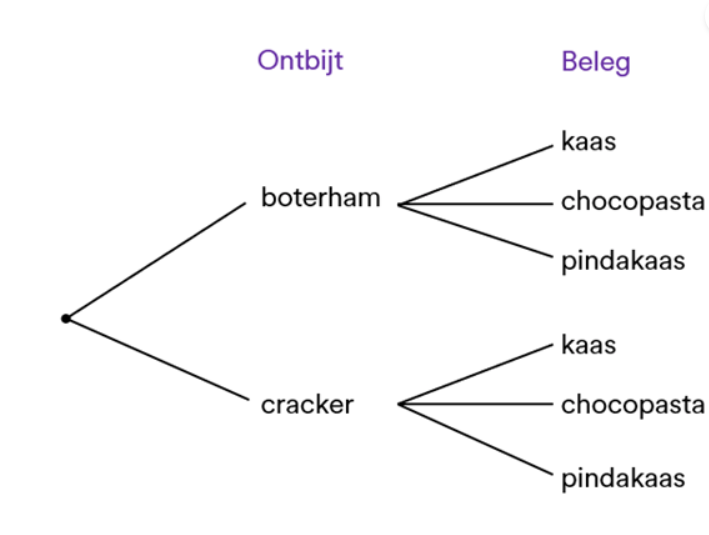
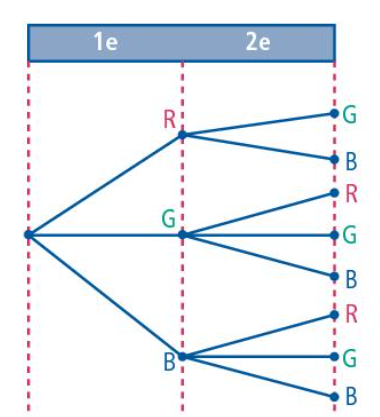
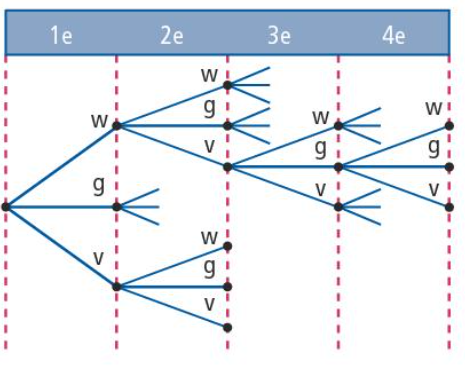
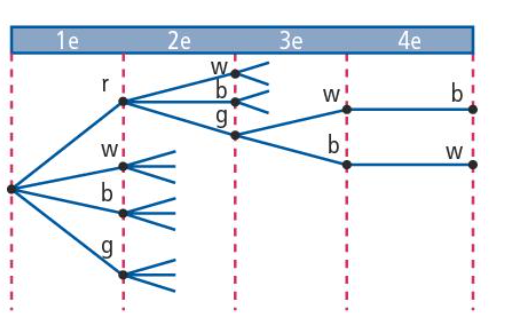

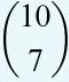 Dit spreek je uit als "10 boven 7".
Dit spreek je uit als "10 boven 7".