Het arrangement De stelling van Pythagoras is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 08-01-2023 21:20:28
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
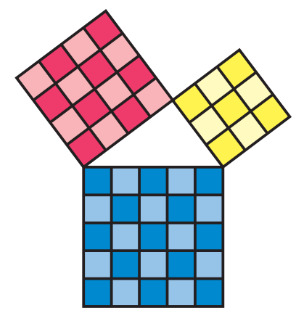
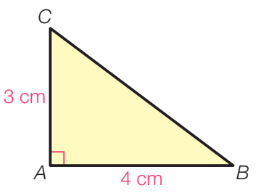
- Je loopt door een parkje heen over het voetpad. Je loopt eerst rechtdoor, en moet vervolgens rechts afslaan. In plaatst van dat je netjes over het voetpad loopt (eerst rechtdoor en dan naar rechts), zie je dat meer mensen de kortere route hebben genomen over het glasveld. Dit heet een olifantenpaadje. Maar, is dit de kortere route? En, hoeveel korter is dit dan? Dit hoofdstuk gaat over de stelling van Pythagoras. De lesdoelen zijn als volgt: - Hoe de stelling van Pythagoras luidt. - Het berekenen van zijden van rechthoekige driehoeken. - Hoe je kunt narekenen of een driehoek rechthoekig is. - Hoe je in ruimtefiguren doorsneden tekent. - De lengten van lijnstukken in ruimtefiguren berekenen. Leerniveau: 2 havo vak: Wiskunde Doelgroep: 2 havo leerlingen op de middelbare school
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 0 uur 45 minuten
Bronnen
| Bron | Type |
|---|---|
|
Stelling van Pythagoras 1 https://www.youtube.com/watch?v=rg2e1dzwCa4 |
Video |
|
Stelling van Pythagoras 2 https://www.youtube.com/watch?v=bZMBWQdl7eg |
Video |
|
Stelling van Pythagoras 3 https://www.youtube.com/watch?v=BhSadWf3Rdw |
Video |
|
Stelling van Pythagoras 4 https://www.youtube.com/watch?v=PAvTC7wbqfg |
Video |
|
QUIZ https://quizlet.com/761457390/flashcards |
Link |
|
Oefentoets https://docs.google.com/forms/d/e/1FAIpQLSdWlA34NK-Wb5mnnGLquF5rv2d1e6q1u0Ha7ietncWFN1qTmQ/viewform |
Link |