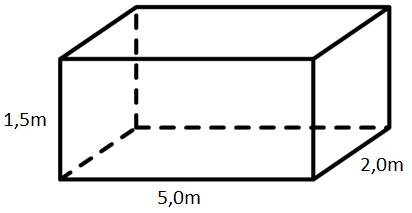
Inleiding
Welkom!
In klas 1 heb je geleerd de inhoud te berekenen van kubusvormige ruimtefiguren. In dit hoofdstuk leer je de inhoud te berekenen van cilinders, prisma's, piramides en kegels.
Daarna leer je de factor te gebruiken bij het berekenen van de inhoud van een vergroting.
Ten slotte leer je de inhoud berekenen van ruimtefiguren die zijn samengesteld uit balken, cilinders, prisma's, piramides en kegels.
Intro
In het dagelijkse leven komen we ruimtefiguren vaak tegen. Herken je ze?
Hiernaast zie je de Rock and Roll Hall of Fame in de Amerikaanse stad Cleveland.
- Welke ruimtefiguren herken je in dit gebouw?
Voorkennis
Een bouwplaat (zonder plakranden) van een ruimtefiguur noemen we een 'uitslag'.
Een bouwplaat is een platte tekening waar je een 3D figuur van kunt maken. Als je de bouwplaat uit zou knippen, dan kun je er een figuur van vouwen. Je hebt dan een driedimensionaal (3D) figuur.
1. Bestudeer de bouwplaat
Kijk goed naar de bouwplaat. Wat is de vorm en welke figuren zie je?
2. Vouw (denkbeeldig) de bouwplaat.
Om te bepalen welke kubus bij de bouwplaat hoort, moet je de bouwplaat (denkbeeldig) vouwen.
3. Uitkomst
Bekijk nu goed de antwoorden. Welke antwoorden vallen in ieder geval al af? Schrijf het juiste antwoord in je schrift.
Kennisclip
https://www.youtube.com/watch?v=wkeOl3gDS6A
Opdracht 1
V1 Vul in.
a. 7 m2 = ...dm2 f. 3500 cm3 = ...dm3
b. 3500 cm2 = ...dm2 g. 0,48 m3 = ...dm3
c. 0,48 m2 = ...cm2 h. 23 000 cm3 = ...m3
d. 0,05 m2 = ...mm2 i. 49 dm3 = ...L
e. 0,94 km2 = ...m2 j. 0,08 L = ...cm3
Opdracht 2
V2 Een aquarium heeft de vorm van een balk. Het aquarium is 40 cm lang en 30 cm breed. De hoogte is 35 cm.
a. Bereken de inhoud van de aquarium in cm3.
b. Geef de inhoud van dit aquarium in liters.
c. In het aquarium zit tot 5 cm onder de rand water. Hoeveel liter water zit er in het aquarium?
Opdracht 3
V3 Een ronde vijver heeft een diameter van 20 meter.
a. Bereken hoeveel meter de omtrek van de vijver is. Rond je antwoord af op één decimaal.
b. Bereken hoeveel m2 de oppervlakte van de vijver is. Rond je antwoord af op helen.
§10.1 Balk en cilinder
Leerdoelen
- Je leert hoe je de inhoud van een balk en de inhoud van een cilinder berekent.
- Je leert hoe je de inhoudsmaten L, dL, cL en mL omrekent.
Theorie
De inhoud van een balk en de inhoud van een cilinder kun je berekenen met de formule:
inhoud = oppervlakte grondvlak x hoogte of korter I = G x h.
Voorbeeld 1 Voorbeeld 2
Bereken hoeveel cm3 de inhoud van deze balk is. Bereken de inhoud van de cilinder.
Oplossing Oplossing
De oppervlakte van het grondvlak van de balk is De straal is 3.
6 x 4 = 24 cm2. De oppervlakte van het grondvlak is
De inhoud van de balk is π x 32 = π x 9.
24 x 4 = 96 cm3. De inhoud van de cilinder is
De balk heeft een inhoud van 96 cm3. π x 9 x 6 = 169,65.
Inhoud balk
De inhoud van een balk is makkelijk te berekenen. Door de oppervlakte grondvlak x hoogte met elkaar te vermenigvuldigen, bereken je de inhoud van een balk.
Wanneer je met eenheden werkt, moet je niet vergeten die er ook bij te zetten. Zet er bijvoorbeeld bij of je in meter, centimeter of millimeters werkt. Voor de inhoud gebruik je een inhoudsmaat, zoals cm3. Bijvoorbeeld een balk van 20 cm x 30 cm x 50 cm heeft een inhoud van 30 000 cm3.
Voorbeeld
Bereken de inhoud van de balk in de onderstaande afbeelding.
Oplossing
De oppervlakte van het grondvlak van de balk is 5,0 x 2,0 = 10 m2.
De inhoud van de balk is 10 x 1,5 = 15 m3.
De balk heeft een inhoud van 15 m3.
Inhoud cilinder
De inhoud van een cilinder is iets lastiger te berekenen dan die van een balk. Een cilinder heeft een cirkelvormig grondvlak en een bepaalde hoogte. Bij het berekenen van de inhoud gaat het bij beide vormen om hetzelfde principe: grondvlak vermenigvuldigen met de hoogte.
Het grondvlak (en het bovenvlak) van een cilinder is een cirkel. De formule om de oppervlakte van een cirkel te te berekenen is π x r2.
Om de inhoud van een cilinder te berekenen moeten we de oppervlakte van deze cirkel (het grondvlak) vermenigvuldigen met de hoogte van de cirkel.
De inhoud kan in verschillende eenheden gevraagd zijn. Onthoudt altijd goed dat 1 liter gelijk is aan 1 dm3 en dat dit weer gelijk is aan 1000 cm3.
Voorbeeld
Bereken de inhoud van een cilinder met een diameter van 14 cm en een hoogte van 45 cm. Rond je antwoord af op twee decimalen.
Oplossing
De straal is 14 : 2 = 7.
De oppervlakte van het grondvlak is π x 72 = π x 49.
De inhoud van de cilinder is π x 49 x 45 = 6927, 21 cm3.
Omrekenen inhoudsmaten
Voor het omrekenen van de inhoudsmaten L, dL, cL en mL kun je de schema's hieronder gebruiken.
1 L = 1 dm3 1 mL = 1 cm3
Voorbeeld
0,02 m3 =...cL
0,02 m3 is gelijk aan 20 000 cm3.
20 000 cm3 is gelijk aan 20 000 mL.
Van mL naar cL is eeen stap naar links.
20 000 : 10 = 2000.
Dus 0,02 m3 = 2000 cL
Quizlet
http://quizlet.com/_bqix67?x=1jqt&i=4i56h7
Oefenen
Oefentoets 1
Toets: Oefentoets 1
Start
Oefentoets 2
Toets: Oefentoets 2
Start
Begrippenlijst
Balk: Een balk is een ruimtelijk figuur dat bestaat uit zes rechthoeken. De uitslag van een balk bestaat uit een grondvlak, een bovenvlak en vier zijvlakken die je in elkaar kunt vouwen als een balk.
Cilinder: Een cilinder is een meetkundig lichaam met een cirkelvormig grondvlak en evenwijdig aan het grondvlak overal dezelfde cirkelvormige doorsnede met alle middelpunten op een rechte, de as.
Cirkel: de meetkundige plaats van de punten in een plat vlak die gelijke afstand r hebben tot een bepaald punt M. Dit punt M heet het middelpunt, de afstand r heet de straal van de cirkel.
Driehoek: Een driehoek is een meetkundige figuur die bestaat uit drie punten die niet op een rechte lijn liggen, en de lijnstukken die die punten met elkaar verbinden.
Inhoudsmaat: maat waarmee de inhoud van een ruimte of voorwerp kan worden aangegeven.
Rechthoekige driehoek: een van de hoeken is 90 graden.
Ruimtefiguur: In de wiskunde wordt een meetkundig figuur in de ruimte een ruimtefiguur ofwel een ruimtelijke figuur genoemd. Dus een driedimensionaal object.
Scherphoekige driehoek: alle hoeken zijn kleiner dan 90 graden.
Stomphoekige driehoek: een van de hoeken is groter dan 90 graden.
Vlakke figuur: gesloten figuren die in een plat vlak liggen. Deze worden begrensd door rechte lijnstukken. Behalve de cirkel, deze wordt begrensd door een gebogen lijnstuk.
Feedback
