Het arrangement Klokken luiden is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 31-05-2022 08:48:48
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Het lesdoel van deze les is
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Bronnen
| Bron | Type |
|---|---|
|
Klokken luiden https://youtu.be/khc-iA0FZEY |
Video |

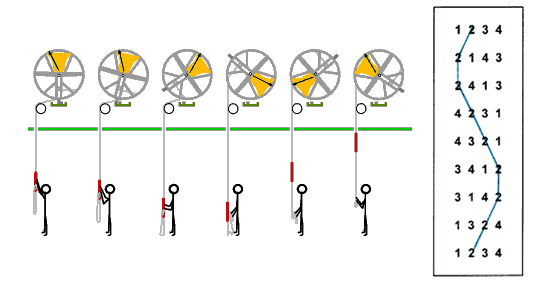
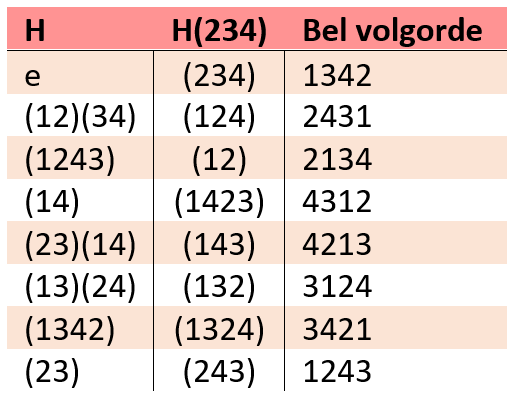
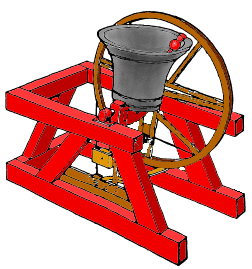 Voor de sport hangen ze met de klokmond omhoog, zo heeft de klokkenluider controle over het moment dat de klok luid. Als de klok luid draait hij 360 graden rond zijn as. Na een klokslag hangt de klok weer in de startpositie maar met de klepel in de tegengestelde richting. Een klokslag duurt ongeveer 2 seconden. Omdat dit even duurt kunnen de klokken niet zomaar in willekeurige volgorde geluid worden. Om ervoor te zorgen dat er nooit dezelfde melodie gespeeld wordt moet er steeds één klok het moment van luiden verwisselen met een klok na of voor de klok in de voorgaande rij tonen.
Voor de sport hangen ze met de klokmond omhoog, zo heeft de klokkenluider controle over het moment dat de klok luid. Als de klok luid draait hij 360 graden rond zijn as. Na een klokslag hangt de klok weer in de startpositie maar met de klepel in de tegengestelde richting. Een klokslag duurt ongeveer 2 seconden. Omdat dit even duurt kunnen de klokken niet zomaar in willekeurige volgorde geluid worden. Om ervoor te zorgen dat er nooit dezelfde melodie gespeeld wordt moet er steeds één klok het moment van luiden verwisselen met een klok na of voor de klok in de voorgaande rij tonen.