Vooraf
Welkom in de Wiki voor Rekenen voor het 1e jaar van de opleiding Verpleegkunde.
Om deze lessenserie goed te kunnen doen heb je het boek "NU Rekenen mbo 2021 leerwerkboek niveau 4" nodig mét de daarbij behorende licentie voor de digitale omgeving.
De digitale omgeving bereik je via de tegel "Bundle" op start.mboutrecht.nl
(m.b.v. een activeringscode die je hebt ontvangen in je privémail, toen je de boeken hebt aangeschaft.)
Les 1 Introductie
Lesdoelen:
- kennismaking en introductie
- Je weet welk rekentype je bent
- Je hebt nagedacht over je sterke en zwakke rekenpunten
- Je kunt inloggen bij de Online versie van Nu Rekenen Online 3e editie, niveau 4
Activiteiten:
- Welkomstgesprek
- Deel van een aflevering van Labyrinth kijken.
- A.d.h.v. de vier rekentypes uit de documentaire vul je de vragenlijst in.
- Via de tegel Bundle op start.mboutrecht.nl ga je inloggen in Nu Rekenen Online. Zorg dat je je activeringscode bij de hand hebt. Deze code heb je ontangen op het mailadres waarmee je de boeken hebt besteld. (prive adres van jou of je ouders/verzorgers)
Les 2 Fotosafari
Lesdoelen:
- Je kunt rekensituaties in je omgeving herkennen
- Je kunt eenvoudige berekeningen mbv rekensituaties oplossen
Activiteiten:
Je gaat op zoek naar rekensituaties buiten de klas/school en maakt daar foto's van, om daar vervolgens opgaves mee te maken.
Tijdens de les krijg je een werkblad. De uitwerking daarvan lever je in bij de opdracht in Teams.
.
Les 3 Instaptoets BV 1
Lesdoelen:
Je weet n.a.v. de instaptoetsuitslag welke leerroute je gaat nemen in Nu Rekenen Online.
Activiteiten:
Tijdens de les maak je de instaptoets m.b.t Basisvaardigheden 1 t/m12.
De toets vind je via start.mboutrecht.nl → Bundle → NUR Online
Les 4 Basisvaardigheden 1 en 2
1. Structuur van getallen
Een getal is opgebouwd uit cijfers. De plaats van het cijfer in het getal geeft de waarde aan van het cijfer in dat getal.
Van rechts af gezien wordt om de drie cijfers een spatie geplaatst om de leesbaarheid van een getal te vergroten.
Bij geldbedragen wordt in plaats van een spatie vaak een punt gebruikt.
In een decimaal getal gebruik je een komma.
De cijfers achter de komma noem je decimalen.
Maken (pag 224 e.v.):
De reguliere route: Opdracht 1, 2, 3 en 4
De verkorte route: Opdracht 2
2. Getallen ordenen
Getallen kun je ordenen door ze van klein naar groot op een getallenlijn te plaatsen. De stappen tussen de streepjes zijn gelijk.
Bij decimale getallen mag je achter de laatste decimaal nullen toevoegen. 2,5 en 2,50 staan op dezelfde plek op de getallenlijn.

Negatieve getallen zijn getallen kleiner dan nul.
Voor het noteren van negatieve getallen gebruik je vaak het minteken.
Op de getallenlijn staan de negatieve getallen links van de 0.
De tijdlijn is een bijzondere getallenlijn. Hierop worden historische gebeurtenissen weergegeven.
Tekens voor het ordenen van getallen
Getallen kun je ook ordenen door de volgende tekens te gebruiken.
< kleiner dan
> groter dan
= is gelijk aan
Maken (pag 226 e.v.):
De reguliere route: Opdracht 1 t/m 15
De verkorte route: Opdracht 4, 11 en 13
Les 5 BV 3, 4, 5 en 6
3. Grote getallen
Grote getallen worden vaak met woorden geschreven.
De woorden van grote getallen gaan met stappen van duizend.
duizend = 1000 (3 nullen)
miljoen = 1 000 000 (6 nullen)
miljard = 1 000 000 000 (9 nullen)
biljoen = 1 000 000 000 000 (12 nullen)
biljard = 1 000 000 000 000 000 (15 nullen)
triljoen = 1 000 000 000 000 000 000 (18 nullen)
5 miljoen = 5 000 000
2,7 miljoen = 2 700 000
4,25 miljard = 4 250 000 000
Bij de uitspraak van grote getallen gebruik je bovenstaande woorden.
Het getal 1 235 475 spreek je uit als:
één miljoen tweehonderdvijfendertig duizend vierhonderdvijfenzeventig
Maken (pag 230 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 3 en 4
Uitspraak van grote getallen
Uitspraak van grote getallen
4. Optellen en aftrekken
Als je twee getallen bij elkaar optelt, noem je het antwoord de som van de getallen.
Als je twee getallen van elkaar aftrekt noem je het antwoord het verschil.
Bij een optelling mag je de volgorde van de getallen wisselen, bij aftrekken mag dat niet.
Je kunt op verschillende manieren optellen en aftrekken:
uit het hoofd, kolomsgewijs of traditioneel.
Maken (pag 232 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 5
5. Optellen en aftrekken: decimale en negatieve getallen
Bij het optellen en aftrekken van decimale getallen moeten de komma’s recht onder elkaar geplaatst worden. Soms moet je getallen met een verschillend aantal decimalen bij elkaar optellen of van elkaar aftrekken. Het is dan handig om extra nullen achter de komma te plaatsen, zodat de getallen evenveel cijfers achter de komma hebben.
Maken (pag 234 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 3
6. Handig rekenen: optellen en aftrekken
Bij het rekenen kijk je eerst naar de getallen waarmee je gaat rekenen. Vaak is er een handige manier om een opdracht te berekenen.
Maken (pag 236 e.v.):
De reguliere route: Opdracht 1 t/m 6
De verkorte route: Opdracht 5

leeftijdmethode

latjesmethode
Les 6 BV 7, 8 en 9
7. Vermenigvuldigen
Vermenigvuldigen is herhaald optellen.
Als je getallen met elkaar vermenigvuldigt, noem je het antwoord het product van de getallen. Bij een vermenigvuldiging mag je de volgorde van de getallen verwisselen.
Je kunt op verschillende manieren vermenigvuldigen:
uit het hoofd, kolomsgewijs of cijferend traditioneel.
Maken (pag 238 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 4
8. Delen
Als je getallen deelt maak je een deling. Het antwoord noem je het quotiënt van de getallen.
Je kunt op verschillende manieren delen:
uit het hoofd, kolomsgewijs delen (herhaald aftrekken) of staartdelen.
Als je eerlijk deelt, houd je soms wat over. Dat noem je de rest.
Maken (pag 240 e.v.):
De reguliere route: Opdracht 1 t/m 6
De verkorte route: Opdracht 4
9. Handig rekenen: vermenigvuldigen en delen
Bij het rekenen kijk je eerst naar de getallen waarmee je gaat rekenen. Vaak is er een handige manier om een opdracht te berekenen.
Maken (pag 242 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 2 en 4
Les 7 BV 10, 11 en 12
10. Handig rekenen met nullen
Bij vermenigvuldigingen van een geheel getal met 10, 100, 1000 enovoort komen er één of meerdere nullen achter het getal. Je telt het aantal nullen voor het juiste aantal nullen in het antwoord.
Bij het vermenigvuldigen van decimale getallen met 10 verschuift de komma 1 plaats naar rechts. Bij vermenigvuldigen met 100 verschuift de komma 2 plaatsen naar rechts.
Bij vermenigvuldigen met 0,1 verschuift de komma 1 plaats naar links.
Bij vermenigvuldigen met 0,01 verschuift de komma 2 plaatsen naar links.
Maken (pag 244 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 3 en 4
11. Machtsverheffen en wortels
Een kwadraat is het product van twee gelijke getallen, ofwel een macht van twee.
Een derdemacht is het product van drie gelijke getallen en zo verder.
De wortel van een getal is het omgekeerde van het kwadraat.
Maken (pag 246 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 3 en 5
12. Volgorde van bewerkingen
Als in een opdracht verschillende bewerkingen voorkomen, houd je een vaste volgorde aan:
1 Alles wat tussen haakjes staat eerst.
2 Kwadrateren en worteltrekken van links naar rechts.
3 Vermenigvuldigen en delen van links naar rechts.
4 Optellen en aftrekken van links naar rechts.
Maken (blz. 248 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 4
Les 8 Eindtoets BV 1
Activiteiten:
Tijdens de les maak je de toets m.b.t Basisvaardigheden 1 t/m12.
De toets vind je via start.mboutrecht.nl → Bundle → NUR Online
Les 9 Instaptoets BV 2
Lesdoelen:
Je weet n.a.v. de instaptoetsuitslag welke leerroute je gaat nemen in Nu Rekenen Online.
Activiteiten:
Tijdens de les maak je de instaptoets m.b.t Basisvaardigheden 13 t/m 25
De toets vind je via start.mboutrecht.nl → Bundle → NUR Online
Les 10 BV 13, 14 en 15
13. Afronden
Bij het afronden op één decimaal kijk je naar de tweede decimaal.
Is het cijfer lager dan 5, dan blijft de eerste decimaal onveranderd.
Is het cijfer een 5 of hoger, dan wordt de eerste decimaal 1 hoger.
Bij het afronden op twee decimalen kijk je naar de derde decimaal.
Bij het afronden op een heel getal kijk je naar het eerste cijfer achter de komma.
Rond pas af bij je eindantwoord en niet tijdens de berekening.
Maken (blz. 250 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 2
14. Mooi en verstandig afronden
Getallen worden afgerond volgens vaste afspraken.
Een cijfer van 5 of hoger wordt naar boven afgerond.
Een cijfer lager dan een 5 wordt naar beneden afgerond.
Het getal 247 527 wordt afgerond op duizendtallen.
Je kijkt dan naar de honderdtallen.
Het getal heeft 5 honderdtallen.
Het duizendtal, de 7, wordt één hoger.
Het getal 247 527 is afgerond op duizendtallen 248 000.
Maken (blz. 252 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 1 en 3
15. Schatten
Je hebt niet altijd het exacte antwoord van een berekening nodig. Je kunt dan door te rekenen met afgeronde getallen de uitkomst schatten.
Maken (blz. 254 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 5
Les 11 TO: Grip op je geld
In deze les begin je aan de themaopdracht Grip op je geld.
- Online vind je deze opdracht bij de Themaopdrachten, onder het kopje "Thema Wonen". In de linkerkolom zie je "Grip op geld*" staan.
- In het boek staat de opdracht op pag. 206.
Wat ga je doen:
- Je werkt deze opdracht individueel uit. (Elkaar helpen mag natuurlijk ;-)
- Maak in een Worddocument een nette, duidelijke uitwerking van de stappen 1 t/m 7 in de opdracht. (Bij 7. mag je ook een andere manier bedenken om een overzicht te maken. Het hoeft niet met Excel)
- Kies 1 van de 3 Extra opdrachten en werk ook deze uit in hetzelfde document.
- De uitwerkingen lever je in als een PDF-bestand via de opdracht in MS Teams.
Beoordeling
Bij de beoordeling wordt gelet op:
- Zijn alle 8 (7+1) opdrachten behandeld.
- Is het ingeleverde duidelijk, overzichtelijk en netjes.
- Zijn de antwoorden geloofwaardig.
(Uitwerkingen worden niet, zonder overleg, gedeeld met anderen.)
Les 12 BV 16, 17 en 18
16. Breuken verkennen
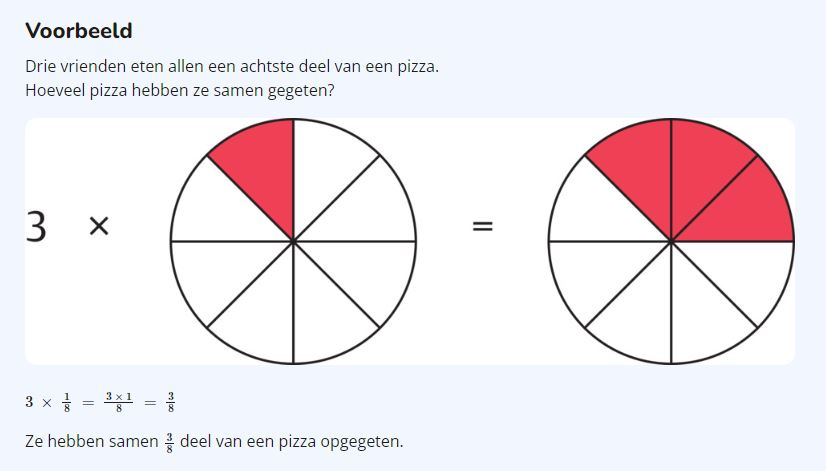
Als je een hele pizza met drie personen deelt, krijgt ieder 1/3 deel.
1/3 deel (één derde) van de pizza is gekleurd. 1/3 is een breuk.


Het getal boven de breukstreep is de teller.
Het getal onder de breukstreep is de noemer.
Van de breuk 1/3 is 1 de teller, en 3 de noemer.
De breuken 1/4 en 3/4 zijn gelijknamig omdat ze dezelfde noemer hebben.
Maken (blz. 256 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 1 en 3
17. Breuken vergelijken
Als breuken niet gelijknamig zijn, kun je ze niet vergelijken.
Je moet ze eerst gelijknamig maken. Je zoekt een getal dat in een vermenigvuldiging van beide noemers voorkomt. Dat wordt de nieuwe noemer.

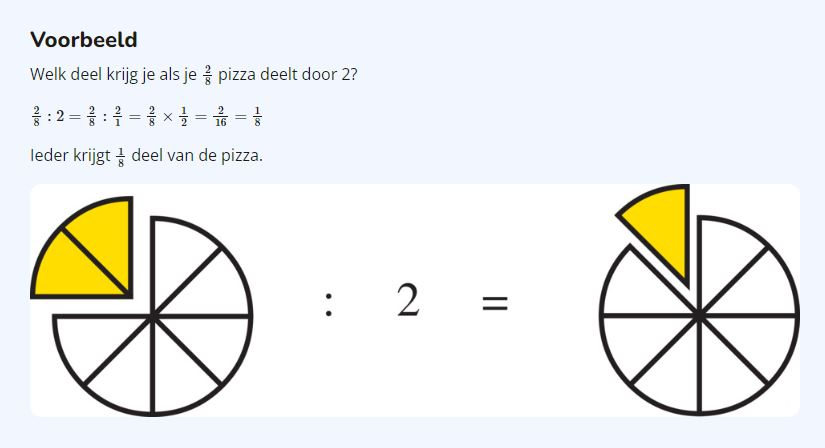
In deze cirkel is 2/8 deel rood gekleurd.
2/8 deel van de cirkel is gelijk aan 1/4 deel.
De breuken 2/8 en 1/4 zijn gelijkwaardig.
De teller en de noemer van een breuk mag je met hetzelfde getal vermenigvuldigen of door hetzelfde getal delen.

Van de linker rij is 1/3 de meest eenvoudige vorm en van de rechter rij is dat 1/4.
Een breuk in de meest eenvoudigste vorm schrijven heet vereenvoudigen.
Maken (blz. 258 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 2 en 4
18. Breuken optellen en aftrekken
Als de teller groter is dan de noemer, is de breuk groter dan één.
Je kunt de ‘helen’ eruit halen.
3/2 = 2/2 + 1/2 = 1 + 1/2 = 1 1/2

Breuken optellen: 3/5 + 2/7
Breuken aftrekken: 3/5 - 1/7
Breuken aftrekken: 2 1/4 - 1/3
Maken (blz. 260 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 5
Les 13 BV 19, 20, 21 en 22
19. Breuken vermenigvuldigen en delen
Bij het vermenigvuldigen van een breuk met een geheel getal vermenigvuldig je de teller van de breuk met het gehele getal:
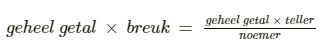
Breuken vermenigvuldigen 2/3 x 3/4 en 2 1/4 x 2 2/5
Breuken vermenigvuldigen 3/8 x 24 en 5/6 x 24
Maken (blz. 262 e.v.):
De reguliere route: Opdracht 1 t/m 4
De verkorte route: Opdracht 2 en 3
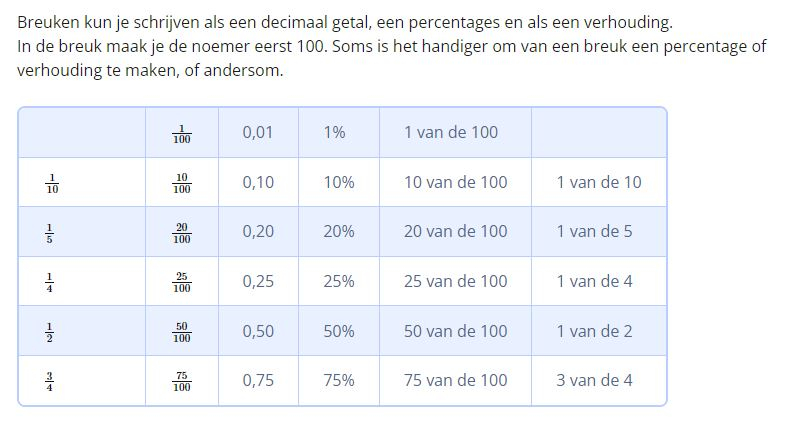
20. Breuken, decimale getallen, procenten en verhoudingen
Een getal met één decimaal spreek je uit als tienden, met twee decimalen als honderdsten en met drie decimalen als duizendsten.
Een decimaal getal kan eenvoudig als breuk worden genoteerd met noemer 10, 100, 1000 en daarna eventueel genoteerd worden in zijn eenvoudigste vorm.

Als je een breuk als een decimaal getal wilt schrijven, maak je van de noemer van de breuk tienden, honderdsten, duizendsten enzovoort.
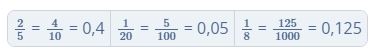
Maken (blz. 264 e.v.):
De reguliere route: Opdracht 1 t/m 15
De verkorte route: Opdracht 2, 9 en 12
21. Verhoudingstabellen
Als je met verhoudingen rekent, kun je een verhoudingstabel gebruiken.
Je mag in een verhoudingstabel zowel horizontaal als verticaal met hetzelfde getal vermenigvuldigen of door hetzelfde getal delen.

Maken (blz. 268 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 3
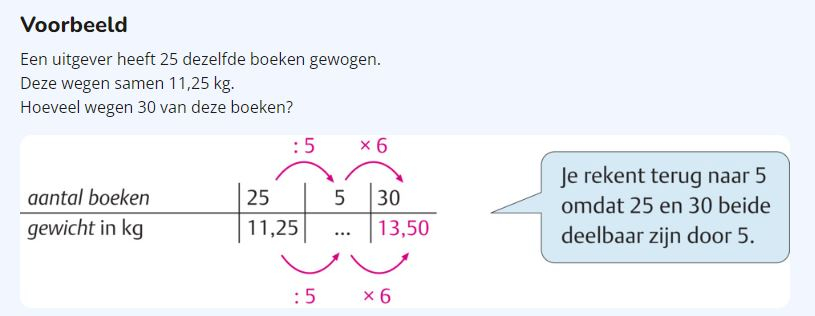
22. Verhoudingstabellen met tussenstap
Bij het rekenen in verhoudingstabellen is het vaak handig om een tussenstap te maken. Je kunt eerst naar 1 rekenen of een ander handig getal. Let er op dat je tussendoor niet afrondt, maar verder rekent met het niet afgeronde getal in je rekenmachine.
Maken (blz. 270 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 5
Les 14 BV 23, 24 en 25
23. Metriek stelsel
Lengtematen omrekenen
De eenheid van lengte is de meter.

Van millimeter naar meter is drie stappen naar links.
600 mm is dus 600 : 10 : 10 : 10 = 600 : 1000 = 0,6 m
Maken (blz. 272 e.v.):
De reguliere route: Opdracht 1 t/m 6
De verkorte route: Opdracht 6
24. Gewicht en digitaal geheugen
Gewichtsmaten omrekenen
Gewichten drukken we uit in kilogram, gram, milligram en ton.

Van kilogram naar gram is drie stappen naar rechts.
0,25 kg is dus 0,25 × 10 × 10 × 10 = 0,25 × 1000 = 250 g
1 ton = 1000 kg
6,5 ton is 6,5 × 1000 = 6500 kg
Maken (blz. 274 e.v.):
De reguliere route: Opdracht 1 t/m 5
De verkorte route: Opdracht 3 en 5
25. Tijd en snelheid
Je kunt tijd uitdrukken in verschillende eenheden zoals: eeuwen, jaren en minuten.
km/u : 3,6 = m/s
15 km/u : 3,6 = 4,167 m/s
m/s x 3,6 = km/u
10 m/s x 3,6 = 36 km/u
Maken (blz. 276 e.v.):
De reguliere route: Opdracht 1 t/m 4
De verkorte route: Opdracht 1 t/m 3
Les 15 Eindtoets BV 2
Activiteiten:
Tijdens de les maak je de toets m.b.t Basisvaardigheden 13 t/m 25.
De toets vind je via start.mboutrecht.nl → Bundle → NUR Online
Les 16 TO Festival
In deze les begin je aan de themaopdracht Festival.
- Online vind je deze opdracht bij de Themaopdrachten, onder het kopje "Thema Vrije tijd". In de linkerkolom zie je "Festival*" staan.
- In het boek staat de opdracht op pag. 218 en 219.
Wat ga je doen:
- Je maakt deze opdracht alleen óf met z'n tweeën.
- Maak in een Worddocument een nette, duidelijke uitwerking van de stappen 1 t/m 6 in de opdracht.
- Kies 1 van de 2 Extra opdrachten en werk ook deze uit in hetzelfde document.
- De uitwerkingen lever je in als een PDF-bestand via de opdracht in MS Teams.
- Als je de opdracht met z'n tweeën hebt gemaakt levert 1 persoon de opdracht in. Vergeet dan niet duidelijk de naam van beide makers te vermelden.
Beoordeling
Bij de beoordeling wordt gelet op:
- Zijn alle 7 (6+1) opdrachten behandeld.
- Is het ingeleverde duidelijk, overzichtelijk en netjes.
- Zijn de antwoorden geloofwaardig.
- Staan de uitwerkingen in een PDF-bestand
(Uitwerkingen worden niet, zonder overleg, gedeeld met anderen.)
Les 17 GYST-les
Deze les kun je gebruiken om de basisvaardigheden op orde te krijgen.
Kijk ook of de drie themaopdrachten af hebt (Fotosafari, Grip op je geld en Festival)
Les 18 Instaptoets D 1 Grootheden en eenheden
1.1 Getallen, grootheden en eenheden
In het dagelijks leven kom je veel getallen tegen, zoals geldbedragen in een winkel, afstanden op een kilometerteller en gewicht. Als iemand 75 kg weegt, dan geef je het gewicht (grootheid) aan in kilogram (eenheid). De waarde van de grootheid kun je bepalen met een meetinstrument, zoals een weegschaal.
In dit domein leer je verschillende grootheden, zoals lengte, gewicht, tijd, temperatuur en snelheid, te gebruiken en ermee te rekenen. Je kiest een passende grootheid en eenheid. Je leest de getallen af van een meetinstrument.
Ook maak je schattingen met referentiematen, zoals een verdieping is ongeveer 3 m hoog en een volwassen man is ongeveer 1,80 m lang.

Activiteiten:
Tijdens de les maak je de instaptoets m.b.t Domein 1 Grootheden en eenheden
De toets vind je via start.mboutrecht.nl → Bundle → NUR Online
Les 19 D1 1.1 1.2 1.3
1.1 Getallen, grootheden en eenheden
1.2 Lengte
1.3 Gewicht
Gewichten drukken we uit in kilogram, gram, milligram en ton.

1 kg = 1 × 10 × 10 × 10 = 1000 g
1 g = 1 × 10 × 10 × 10 = 1000 mg
1000 mg = 1000 : 10 : 10 : 10 = 1 g
1000 g = 1000 : 10 : 10 : 10 = 1 kg
1 ton = 1000 kg
Maken:
De reguliere route: Opdracht 1 t/m 13
De verkorte route: Opdracht 4, 10 en 13
Bij het meten van breedte, dikte, diepte, hoogte en afstand bepaal je de lengte. De eenheid van lengte is de meter.
Bij het omrekenen van lengtematen kun je dit schema gebruiken:

1 km = 1 × 10 × 10 × 10 = 1000 m
1 hm = 1 × 10 × 10 = 100 m
10 dm = 10 : 10 = 1 m
100 cm = 100 : 10 : 10 = 1 m
1000 mm = 1000 : 10 : 10 : 10 = 1 m
Maken:
De reguliere route: Opdracht 1 t/m 13
De verkorte route: Opdracht 4, 8 en 12
Of van 1.2 som 1 t/m 6 via Quizziz: D1 Grootheden en eenheden som 1 t/m 6.
(dit gaat via de docent)
In het dagelijks leven kom je vaak getallen tegen. Een getal kan verschillende dingen voorstellen.
De 11 achter Dordrecht geeft het aantal kilometer tot Dordrecht aan.
De 15 bij A15 stelt het wegnummer voor.
Ook de 31 van E31 is een wegnummer.

Maken:
De reguliere route: Opdracht 1 t/m 12
De verkorte route: Opdracht 8, 11 en 12
Les 20 Niveautest
In deze laatste rekenles maak je de Niveautest.
Met de uitslag van deze test weet je wat je rekenniveau is m.b.t. het rekenexamen.
Blijkt uit de uitslag dat je onder het rekenniveau zit. Maak dan afspraken met je SLB-er voor het 2e en 3e jaar met betrekking tot het rekenen.
Les 21 D1 1.4 1.5 1.6 (1.7)
1.4 Tijd
1.5 Andere maten en voorvoegsels
1.6 Referentiematen
(1.7 Vuistregels en formules)
Vuistregel
Een vuistregel is een rekenregel waarmee je op een gemakkelijke manier een vaak voorkomende berekening kunt uitvoeren.
De uitkomst is een schatting van wat je wilt berekenen.
Voorbeeld
Om snel en eenvoudig te berekenen of je een gezond gewicht hebt, wordt de volgende vuistregel gebruikt:
gezond gewicht in kg = lichaamslengte in cm − 100
Als je 172 cm lang bent is 172 − 100 = 72 kg een gezond gewicht.
Formules
Een formule is een rekenregel waarmee je nauwkeurig een veel voorkomende berekening kunt uitvoeren.
Voorbeeld
Een taxichauffeur berekent de prijs van een taxirit met de formule:
prijs taxirit in € = 3 + aantal kilometer × 2
Bereken de prijs van een taxirit van 9 km.
prijs taxirit in € = 3 + aantal kilometer × 2 = 3 + 9 × 2 = 3 + 18 = € 21,-
De prijs van een taxirit van 9 km is € 21,-.
Maken:
De reguliere route: Opdracht 1 t/m 12
De verkorte route: Opdracht 2, 6 en 11
Referentiematen
Om schattingen te kunnen maken is het belangrijk bekende aantallen en hoeveelheden te weten. Zo’n maat heet een referentiemaat.
Een aantal belangrijke referentiematen zijn:
- Een volwassen man is ongeveer 1,80 m lang.
- De hoogte van een deur is ongeveer 2 m.
- Een verdieping van een gebouw is ongeveer 3 m hoog.
- Je wandelt ongeveer 4 à 6 km/h.
- Je fietst ongeveer 15 à 18 km/h.
- Nederland telt ongeveer 17 miljoen inwoners
Voorbeeld
Hoe hoog is het gebouw op de foto?

Het gebouw heeft vier verdiepingen.
Een verdieping is ongeveer 3 m hoog.
Het gebouw is ongeveer 4 × 3 = 12 m hoog.
Voorbeeld
Hoeveel kilometer wordt er per dag door alle Nederlanders samen afgelegd?

Nederland telt ongeveer 17 miljoen mensen.
Het gemiddeld aantal fietskilometer per Nederlander is 3 km.
3 × 17 miljoen is ongeveer 51 miljoen fietskilometers.
Maken:
De reguliere route: Opdracht 1 t/m 11
De verkorte route: Opdracht 1, 7 en 10
Woorden of voorvoegsels
Grote getallen worden vaak met woorden of voorvoegsels geschreven.
Het woord kilo betekent duizend (1000) en giga wordt gebruikt voor miljard (1 000 000 000).
Voorbeeld
1 kilometer (km) = 1000 meter (m) = duizend meter (m)
1 megahertz (MHz) = 1 000 000 hertz (Hz) = één miljoen hertz (Hz)
1 gigavolt (GV) = 1 000 000 000 volt (V) = één miljard volt (V)
Bijzondere maten
Je komt in de praktijk verschillende eenheden tegen. Een aantal veel voorkomende zijn:
digitaal geheugen
1 kilobyte (kB) = 1000 byte
1 megabyte (MB) = 1000 kilobyte
1 gigabyte (GB) = 1000 megabyte
1 terabyte (TB) = 1000 gigabyte
1 petabyte (PB) = 1000 terabyte
temperatuur
graden Celsius (°C)
geld
1 ton = € 100.000,-
snelheid
kilometer per uur (km/h)
meter per seconde (m/s)
Voorbeeld
Een camera filmt beelden van 200 MB per minuut.
Hoeveel minuten film past op de SD-kaart?

16 GB = 16 000 MB
16 000 : 200 = 80
Op de SD-kaart past 80 minuten film.
Voorbeeld
Tijdens een reis is de gemiddelde snelheid 80 km/h. De reis duurt drie kwartier.
Hoeveel kilometer leg je met deze snelheid af?
|
afstand in km
|
80
|
20
|
60
|
|
tijd in uur
|
1
|
0,25
|
0,75
|
In een uur leg je 80 km af, dus in een kwartier (0,25 uur) 20 km.
In drie kwartier leg je dus een afstand af van 3 × 20 = 60 km.
Maken:
De reguliere route: Opdracht 1 t/m 12
De verkorte route: Opdracht 2, 13 en 14
Je kunt tijd uitdrukken in verschillende eenheden zoals: eeuwen, jaren, minuten en seconden.
Voorbeeld
|
1 eeuw = 100 jaar
|
1 maand = 30 of 31 dagen
|
|
1 jaar = 12 maanden
|
februari = 28 of 29 dagen
|
|
1 jaar = 365 of 366 dagen
|
1 etmaal = 24 uur
|
|
1 jaar = 4 kwartalen
|
1 dag = 24 uur
|
|
1 kwartaal = 3 maanden
|
1 uur = 60 minuten
|
|
1 kwartaal = 13 weken
|
1 kwartier = 15 minuten
|
|
1 week = 7 dagen
|
1 minuut = 60 seconden
|
Rekenen met tijd
Bij het noteren van een tijdsduur gebruik je een dubbele punt tussen uren, minuten en seconden. Een deel van een uur, minuut of seconde noteer je na een komma in tienden, honderdsten of duizendsten.
Voorbeeld
Edwin van der Sar liep de New York Marathon in 04:19:15.
Hoeveel minuten liep hij?
Hij liep 4 uur, 19 minuten en 15 seconden.
Hoeveel minuten is hij onderweg? .........
˙uǝʇnuıɯ 52'952 = 06 : 51 + 91 + 06 × 4
Tijdsaanduiding op een klok
De analoge klok gaat van 0 tot 12 uur.
De digitale klok heeft een 12-uursnotatie of een 24-uursnotatie.
Bij de 12-uursnotatie worden de afkortingen AM (voor de middag) en PM (na de middag) gebruikt.

Analoge tijdsaanduiding
Maken:
De reguliere route: Opdracht 1 t/m 14
De verkorte route: Opdracht 2, 9 en 13 en Extra opdrachten (zie doc)
AM en PM
Het woord AM vaak ook A.M. staat voor Ante Meridiem en is Latijn dat je letterlijk kan vertalen naar “voor de middag“. AM staat daarom voor de tijdaanduiding van voor de middag en loopt van 12 uur ‘s nachts tot 12 uur ‘s middags. Met het volgende ezelsbruggetje kan je het gemakkelijk onthouden; AM staat voor “At morning” of “After midnight“.
Het woord PM vaak ook P.M. staat voor Post Meridiem en is Latijn dat je letterlijk kan vertalen naar “na de middag“. PM staat daarom voor de tijdsaanduiding van na de middag en loopt van 12 uur ‘s middags tot 12 uur ‘s nachts. Een handig ezelsbruggetje om dit te onthouden is door van het woord PM “Post morning” of “Passeert middag” te maken.
Les 22 Eindtoets D1
Activiteiten:
Tijdens de les maak je de toets m.b.t Domein 1 Grootheden en eenheden.
De toets vind je via start.mboutrecht.nl → Bundle → NUR Online
Les 23 GYST
Deze les kun je gebruiken om de basisvaardigheden op orde te krijgen.
Kijk ook of de drie themaopdrachten af hebt (Fotosafari, Grip op je geld en Festival)
Ook om eventuelle een toets te herkansen
Les 24





 De opdracht
De opdracht