Hoeken berekenen met SOS CAS TOA - kopie 1

Hoeken berekenen met SOS CAS TOA - kopie 1

Welkom

Dag allemaal,

Welkom op de pagina over hoeken berekenen met goniometrie.
Op deze pagina kun je uitlegvideo's, theorie, oefentoetsen en nog veel meer vinden over goniometrie.

Onder het kopje 'theorie' vind je de uitleg over het desbetreffende onderwerp. In dit hoofdstuk gaat het over het berekenen van hoeken in een rechthoekige driehoek met behulp van de sinus, cosinus en de tangens. Onder het kopje 'uitlegvideo's' zal er theorie uitgelegd worden over de desbetreffende paragraaf.

Lesdoelen

  • Je kunt benoemen wat de overstaande-, aanliggende-, en schuine zijde is in een rechthoekige driehoek.
  • Je kunt de hoeken berekenen met de sinus, cosinus en de tangens.

Onder het kopje 'Oefentoets kan je je kennis testen door een proeftoets te maken. Je kunt doormiddel van het knopje controleren kijken of je de opdrachten goed hebt gemaakt. Waneer je alle stof goed begrijpt kan je de eindtoets maken die vind je onder het kopje 'Eindtoets'. Als je deze met een voldoende afsluit heb je de doelen behaald.

Heel veel succes en vooral plezier op deze pagina!

Theorie

SOS CAS TOA (ezelbruggetje)

Sinus, cosinus en tangens worden de drie goniometrische verhoudingen genoemd. 

Zet je de letters van elk van de afkortingen achter elkaar, dan vormen ze het woord soscastoa:

  • S inus =
  • O verstaande (rechthoeks)zijde, gedeeld door de
  • S chuine zijde
     
  • C osinus =
  • A anliggende (rechthoeks)zijde, gedeeld door de
  • S chuine zijde
     
  • T angens =
  • O verstaande (rechthoeks)zijde, gedeeld door de
  • A anliggende rechthoekszijde.

 

Tangens

We gebruiken de tangens in rechthoeke driehoeken. Zoals je weet kun je elke zijde van een driehoek een naam geven.
Zie de afbeelding hiernaast. De blauwe hoek a is hier de rechte hoek (90 graden). Daar tegenover ligt altijd de zijde die we de schuine zijde noemen (afgekort s). 

De rode hoek noemen we B en vanuit deze hoek gaan we naar de andere zijden kijken. De zijde die hier recht tegenover ligt is de overstaande (rechthoek) zijde (afgekort met o).
De zijde die ligt aan hoek B is de aanliggende (rechthoek) zijde (afgekort met a).

Wanneer het gaat om de groene hoek y is de schuine zijde hetzelfde, maar de zijde niet bij hoek B de overstaande was is nu de aanliggende en andersom. 

De tangens is de verhouding tussen de overstaande zijde en de aanliggende zijde. 

Voorbeeld opgave:

 

Sinus en Cosinus

Als je het lastig vindt welke goniometrische verhouding moet gebruiken volg dan de stappen die hieronder staan.

Stap 1  Kijk wat de schuine zijde van de driehoek is. Dat is natuurlijk de langste, maar als je dat niet goed kunt zien, kun je het veiligst gebruiken dat het degene tegenover de rechte hoek is.

Stap 2 Beslis om welke hoek het gaat. Dus de hoek die je wilt berekenen of een hoek die gegeven is (als je een lengte wilt berekenen).

Stap 3  De schuine zijde heb je al. Dan zijn er nog twee rechthoekszijden over. Degene daarvan die aan jouw hoek vastzit noem je de aanliggende rechthoekszijde, en degene tegenover jouw hoek heet de overstaande rechthoekszijde.
 

Voorbeeld Cosinus:

 

 

 

 

 

 

 

 

 

 

Voorbeeld Sinus:

Uitlegvideo's

Uitleg schuine, aanliggende en overstaande zijde

Uitleg SOS CAS TOA

Hoeken bereken met de tangens

Hoeken berekenen met SOS CAS TOA

Oefentoets

Eindtoets

  • Het arrangement Hoeken berekenen met SOS CAS TOA - kopie 1 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.

    Auteur
    nabil oudrhiri Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
    Laatst gewijzigd
    Licentie

    Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:

    • het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
    • het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
    • voor alle doeleinden, inclusief commerciële doeleinden.

    Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.

    Aanvullende informatie over dit lesmateriaal

    Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:

    Toelichting
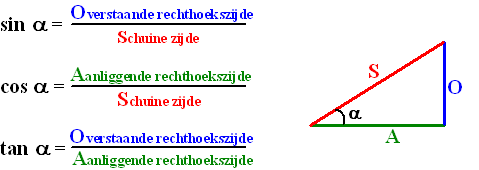
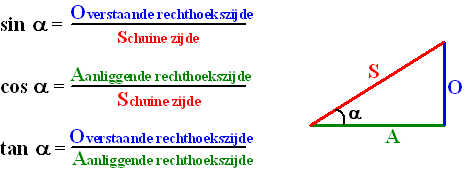
    In dit wikiwijs arrangement kunnen leerlingen de hoeken berekenen met de Sinus, Cosinus en de Tangens in een rechthoekige driehoek. Dit arrangement sluit aan bij hoofdstuk 10 Goniometrie van Getal & Ruimte 3 VMBO KGT.
    Eindgebruiker
    leerling/student
    Moeilijkheidsgraad
    gemiddeld
    Trefwoorden
    cosinus, goniometrie, hoeken berekenen, sinus, tangens

    Bronnen

    Bron Type
    Uitleg schuine, aanliggende en overstaande zijde
    https://www.youtube.com/watch?v=DJkh7uKErGs     		Video
    Uitleg SOS CAS TOA
    https://youtu.be/gpaYdfP89ak     		Video
    Hoeken bereken met de tangens
    https://www.youtube.com/watch?v=PduRZYA9raY&index=4&list=PLAKVMyQ8XDCjnMqZ38YpIxD6kXTsroPgz     		Video
    Hoeken berekenen met SOS CAS TOA
    https://www.youtube.com/watch?v=EWtwQviiPDk     		Video

    Gebruikte Wikiwijs Arrangementen

    Smale, Annelies. (2018).

    Hoeken berekenen met SOS CAS TOA

    https://maken.wikiwijs.nl/124999/Hoeken_berekenen_met_SOS_CAS_TOA

  • Downloaden

    Het volledige arrangement is in de onderstaande formaten te downloaden.

    Metadata

    LTI

    Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI koppeling aan te gaan.

    Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.

    Arrangement

    Oefeningen en toetsen

    Oefentoets

    Eindtoets Goniometrie

    IMSCC package

    Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.

    QTI

    Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat alle informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen punten, etc. Omgevingen met een QTI player kunnen QTI afspelen.

    Versie 2.1 (NL)

    Versie 3.0 bèta

    Meer informatie voor ontwikkelaars

    Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op onze Developers Wiki.

  • Gebruik
    Weergave
  • Wikiwijs is een dienst van