Het arrangement WI - Flow vinden bij wiskunde is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 24-06-2021 13:24:09
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Bronnen
| Bron | Type |
|---|---|
|
Video 1: Positieve en negatieve getallen https://www.youtube.com/watch?v=-PkK9Mo5qDw |
Video |
|
Video 2: letterrekenen, product en som https://www.youtube.com/watch?v=N37vIsFlhBE |
Video |
|
Video 3: lettertekenen verschil https://www.youtube.com/watch?v=WnI7DxkbhrU |
Video |
|
Video 4: grafiek bij een lineaire formule https://www.youtube.com/watch?v=xbuLYgtxhag |
Video |
|
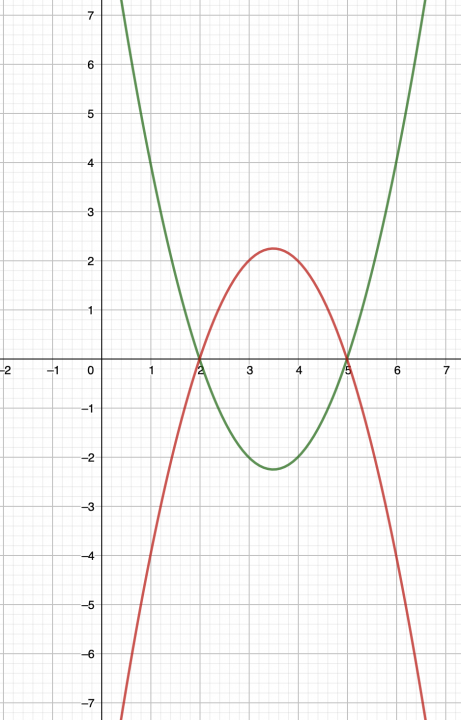
Video 5: grafiek bij een kwadratische formule https://www.youtube.com/watch?v=otvNIrnFJvk |
Video |
|
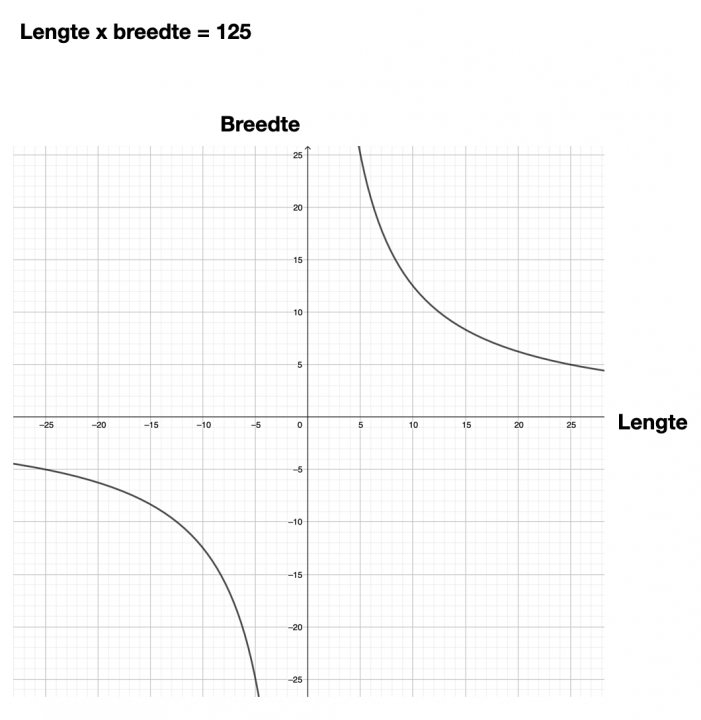
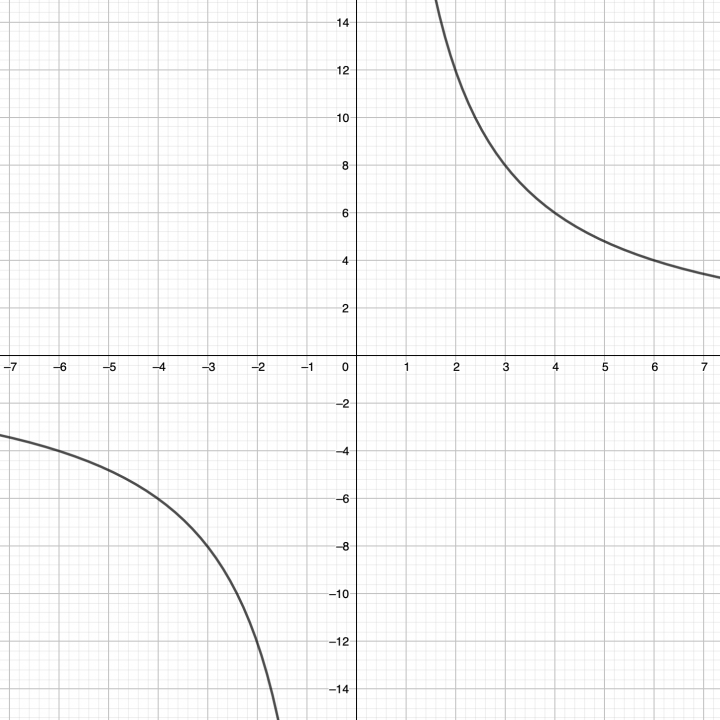
Video 6: grafiek bij een wortelformule https://www.youtube.com/watch?v=Y7OccdtW-ws |
Video |
|
Video 7: merkwaardig product https://www.youtube.com/watch?v=eZWMmFVEF20 |
Video |
|
Video 8: een raaklijn opstellen met de afgeleide https://www.youtube.com/watch?v=4nq_Y_dXhNM |
Video |
Gebruikte Wikiwijs Arrangementen
Herbert Vissers eXplore. (z.d.).
Template quest met cyclus eXplore miles - balans
https://maken.wikiwijs.nl/176776/Template_quest_met_cyclus_eXplore_miles___balans
Herbert Vissers eXplore. (2021).
WI - Flow vinden bij wiskunde
https://maken.wikiwijs.nl/177116/WI___Flow_vinden_bij_wiskunde




 Motivatiemotor
Motivatiemotor Verderkijker
Verderkijker
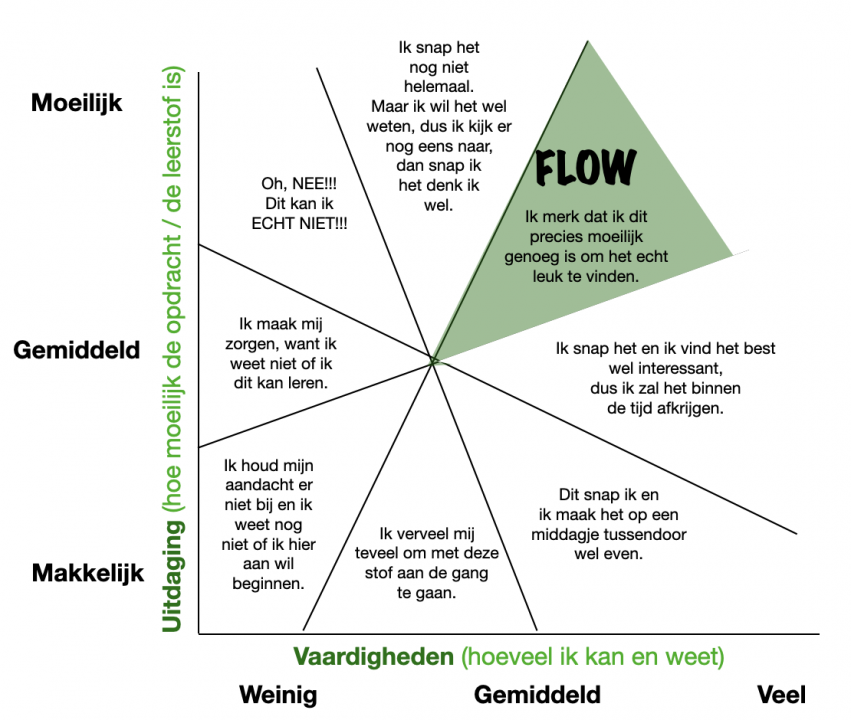
 Onderzoek
Onderzoek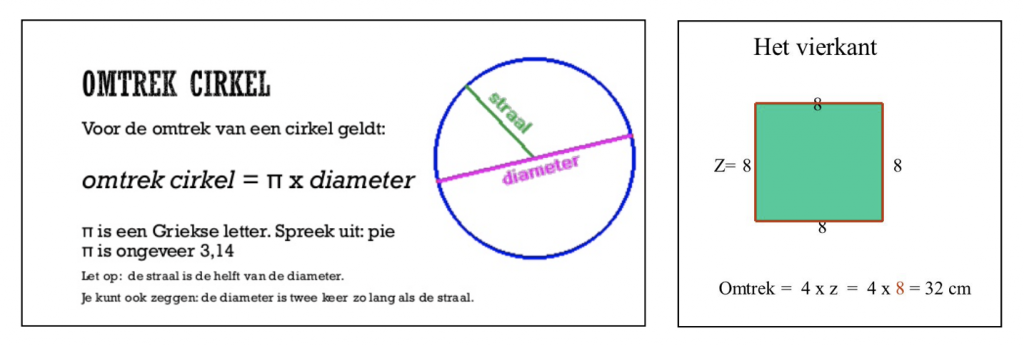
 Verwerking
Verwerking Reflective journal
Reflective journal