Het arrangement Economie SE 6 Rekenen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 04-05-2021 18:54:43
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Bronnen
| Bron | Type |
|---|---|
|
Afronden https://www.lessonup.com/nl/lesson/jevTxoBoeDhwivw2j |
Link |
|
Het afronden van getallen https://youtu.be/ocR6w6giOXc |
Video |
|
Bedragen omrekenen https://www.lessonup.com/nl/lesson/wAHsMQoSQuRMrRzXk |
Link |
|
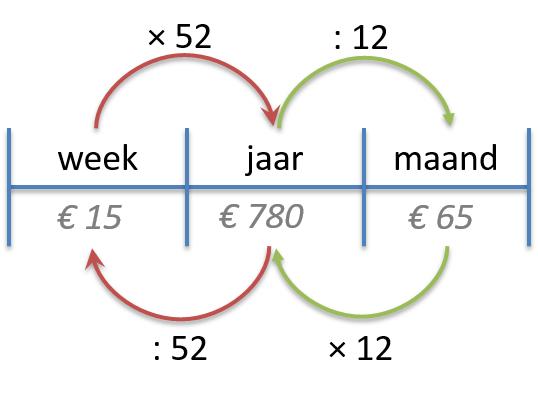
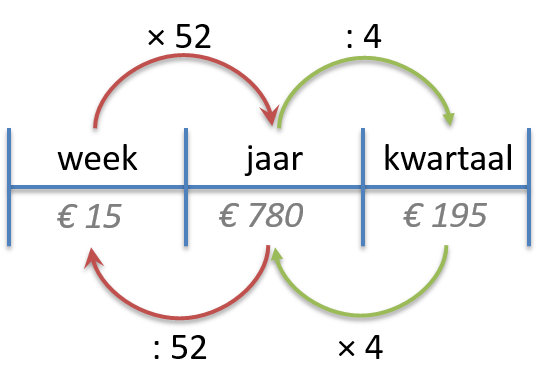
Rekenen van maand naar week en andersom https://youtu.be/eOaLm9xTJ8Q |
Video |
|
Rekenen met grote getallen https://www.lessonup.com/nl/lesson/pqhizwPd392ebqkff |
Link |
|
Het rekenen met miljoenen en miljarden https://youtu.be/omplPDeB5yM |
Video |
|
Rekenen met procenten https://www.lessonup.com/nl/lesson/nw4yddRebHrPiXd9W |
Link |
|
Rekenen met procenten: Los het op met de verhoudingstabel https://youtu.be/36-w8Q7bKm8 |
Video |
|
Een getal berekenen met procenten https://www.lessonup.com/nl/lesson/mELHhLSBFzbYTQTEf |
Link |
|
Rekenen met procenten: een nieuw getal berekenen https://youtu.be/cBMw5tZGa2E |
Video |
|
Rekenen met procenten: De 100% onbekend https://youtu.be/Rfkb45urt4g |
Video |
|
Een percentage berekenen https://www.lessonup.com/nl/lesson/Sqv2XaYSNLtfpdxXz |
Link |
|
Rekenen met procenten: een deel van het geheel berekenen https://youtu.be/pm5-U6UrYj8 |
Video |
|
Een verschil in procenten berekenen https://www.lessonup.com/nl/lesson/XRFQkwmjwHWyKZy2T |
Link |
|
Rekenen met procenten: een stijging/daling berekenen https://youtu.be/hHnqjSMSpZM |
Video |
|
Rekenen met procenten: het procentuele verschil berekenen https://youtu.be/TAcgFHUnS-M |
Video |
|
Rekenen met indexcijfers https://www.lessonup.com/nl/lesson/GJPyxifTGWCvSbvmP |
Link |
|
Indexcijfers berekenen 1 https://youtu.be/0n1uUv9Hkek |
Video |
|
Indexcijfers berekenen 2 https://youtu.be/xwrEXPffcUQ |
Video |
|
CPI en inflatie berekenen https://youtu.be/AFcZMax0Iks |
Video |
|
Prijzen omrekenen https://www.lessonup.com/nl/lesson/NqyberSqcgXperu8X |
Link |
|
BTW https://www.lessonup.com/nl/lesson/v2FxcDeDKgv5SnT6z |
Link |
|
Het berekenen van de btw/omzetbelasting https://youtu.be/3FXmNr2f1Dg |
Video |
|
Wisselkoersen https://www.lessonup.com/nl/lesson/9M5vWhRbwctjyBn2Y |
Link |
|
Vreemde valuta aankopen/verkopen https://youtu.be/Cd6uw5BePiE |
Video |
|
Afschrijving https://www.lessonup.com/nl/lesson/nPG4vzoqqRXxGExwx |
Link |
|
Uitleg over afschrijvingen en reserveringen https://youtu.be/nZas0fwU9qQ |
Video |
|
Inkomen per hoofd van de bevolking berekenen https://youtu.be/XDHEmFFfvZM |
Video |
|
Consumentenprijs berekenen https://youtu.be/A3I4POBVJik |
Video |
|
Het berekenen van enkelvoudige/samengestelde rente https://youtu.be/iOoBuQbM-6Y |
Video |
|
Importquote en exportquote berekenen https://youtu.be/WtpWHx0GK48 |
Video |
|
Box 1: het belastbaar inkomen berekenen https://youtu.be/m2UFNs5Ui0I |
Video |
|
Box 1: Rekenen met de belastingschijven https://youtu.be/QiV836FjiQY |
Video |
|
Box 3: Vermogensrendementsheffing berekenen https://youtu.be/_elZhQUTjPU |
Video |
|
De kostprijs per product berekenen https://youtu.be/rus8Mc6DRSg |
Video |
|
Het berekenen van kredietkosten https://youtu.be/PsCn0V8DIgo |
Video |
|
Van brutoloon naar nettoloon berekenen https://youtu.be/6F3Wl5W7Q6E |
Video |
|
De omzet en het nettoresultaat berekenen https://youtu.be/sc2MbwSyJlo |
Video |
|
Koopkracht/reeele inkomen berekenen https://youtu.be/x33gFuVqMUQ |
Video |
|
Banksaldo berekenen https://youtu.be/pMjMldjTvt8 |
Video |
Gebruikte Wikiwijs Arrangementen
Herbert Vissers eXplore. (z.d.).
Economie SE basis