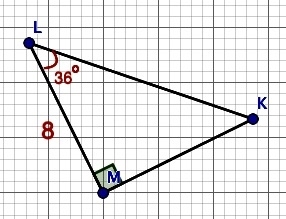
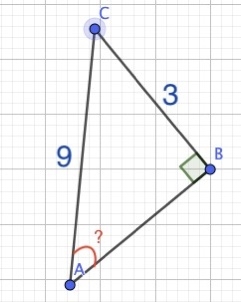
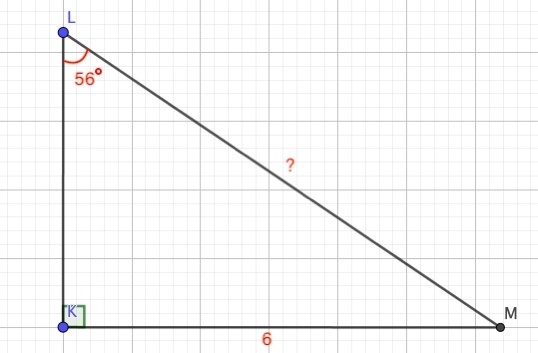
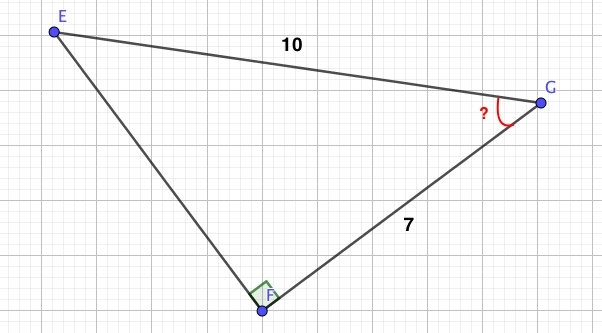
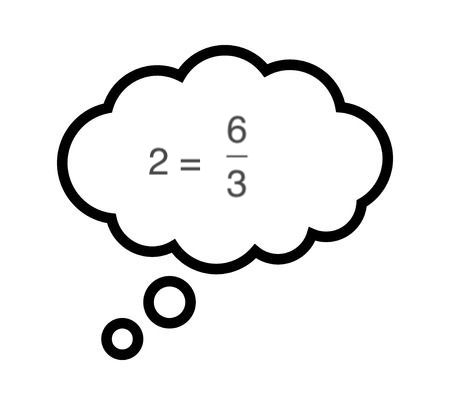Het arrangement SOS CAS TOA is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 01-06-2022 10:41:34
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Bronnen
kopjes
welkom:
Welkom afbeelding van https://images.app.goo.gl/dVeGePpYdSbzReQCA.
voorkennis:
zelf gemaakt en bedacht.
theorie:
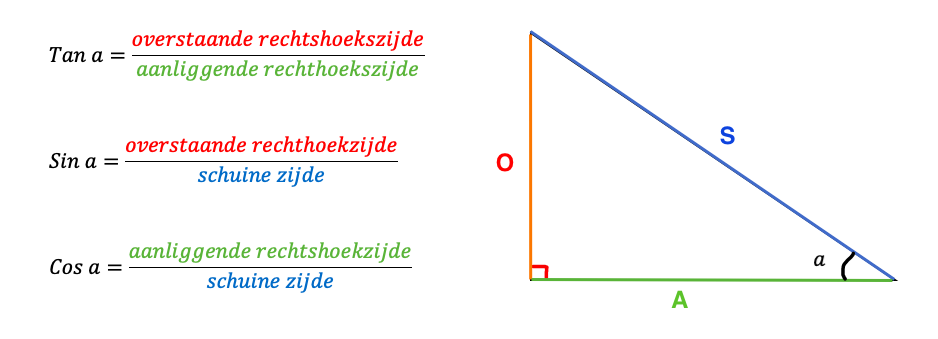
- sos cas toa:
Afbeelding 1 komt van https://images.app.goo.gl/f88JXbkdP4g2pM7H8.
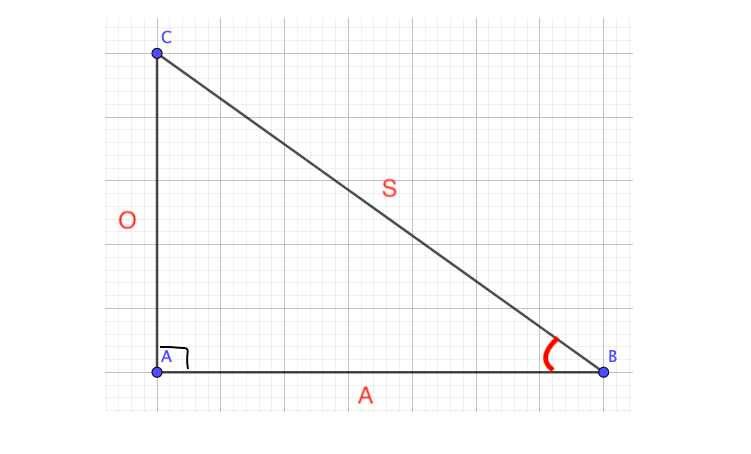
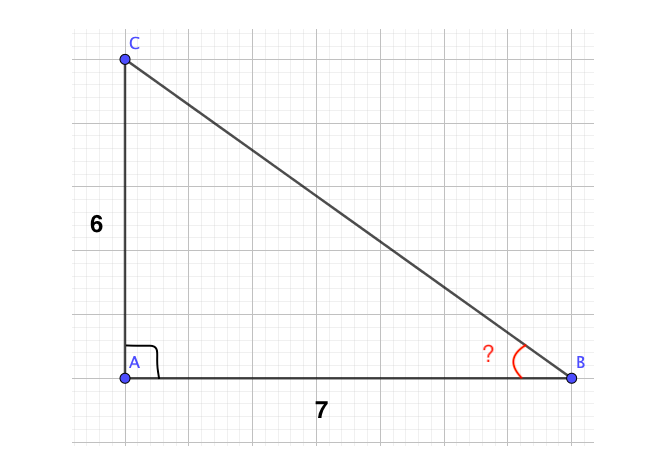
- tangens:
Afbeelding 1 en 2 zelf gemaakt en bedacht.
Afbeelding met het rekenmachine komt van https://images.app.goo.gl/wKVAC1UXamqpjaKw7.
Afbeelding met het denkwolkje zelf gemaakt.
Afbeelding 3 zelf gemaakt en bedacht.
- sinus
Afbeelding 1 en 2 zelf gemaakt en bedacht.
- cosinus
Afbeelding 1 zelf gemaakt en bedacht.
Uitlegfilmpjes:
Het tweede filmpje komt van https://youtu.be/DZ7Fe0Cih9o.
Oefenen:
Vraag 1 t/m 3 van VO-content (wikiwijs)
vraag 8 t/m 14 van Walter Kivits (wikiwijs)
QUIZ time:
Het eerste filmpje is van https://youtu.be/yzYOuJw4wUI.
Extra lesstof:
- Verdieping
Geen bron
- Remediërend
Vraag 1 t/m 3 zijn van Paul Westeneng (wikiwijs)
Oefentoets:
vraag 11: afbeelding van https://images.app.goo.gl/yQxopT71R6wm1DRH6.
vraag 12: afbeelding van https://images.app.goo.gl/4ADvt94QRfha7h8WA.
vraag 14 is een examen vraag van 2019 opgave 16 eerste tijdvak https://www.examenblad.nl/examendocument/2019/cse-1/wiskunde-kb-vmbo/opgaven/2019/vmbo-kb/f=/KB-0153-a-19-1-o.pdf.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Uitgebreid uitleg over goniometrie. Voor VMBO-leerlingen 4 klas kader en kader-gemend\theoretische leerweg. Oefenopdrachten uitleg filmpjes en quiz spelletjes aanwezig!
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- cosinus, goniometrie, sinus, sos cas toa, tangens, wiskunde