Het arrangement 1H09 Ruimtefiguren is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 19-11-2021 13:26:23
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- editie 2020 van dit hoofdstuk
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
- Trefwoorden
- balk, bol, cilinder, kegel, kubus, piramide, prisma, rechthoek, ruimtefiguren, vierkant
Gebruikte Wikiwijs Arrangementen
Wiskundesectie Juliana. (z.d.).
1H09 Ruimtefiguren


 Aan het begin van dit jaar heb je al kennis gemaakt met de vlakkefiguren. Behalve vlakke figuren bestaat de wereld om ons heen ook uit ruimte figuren. De naam zegt het al, ze nemen ruimte in. Je kunt er iets instoppen. Denk maar aan een schoenendoos of een klaslokaal.
Aan het begin van dit jaar heb je al kennis gemaakt met de vlakkefiguren. Behalve vlakke figuren bestaat de wereld om ons heen ook uit ruimte figuren. De naam zegt het al, ze nemen ruimte in. Je kunt er iets instoppen. Denk maar aan een schoenendoos of een klaslokaal. Zo aan het eind van het jaar heb je al heel wat kennis en vaardigheden opgedaan.
Zo aan het eind van het jaar heb je al heel wat kennis en vaardigheden opgedaan.
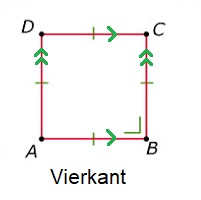
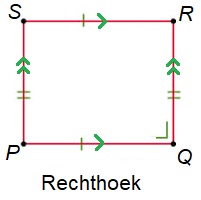
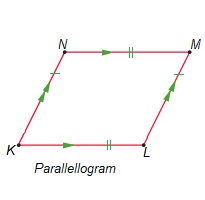
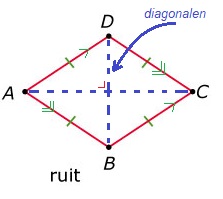



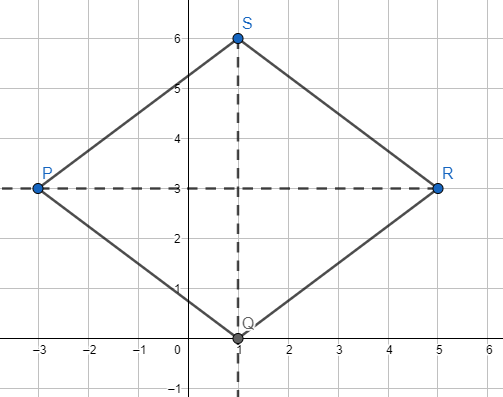
 Bereken de oppervlakte van de ruit KLMN die hiernaast is afgebeeld.
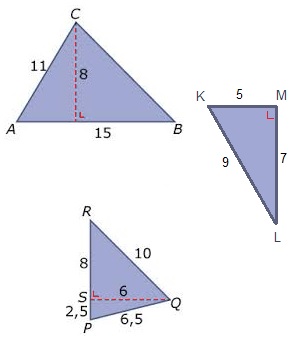
Bereken de oppervlakte van de ruit KLMN die hiernaast is afgebeeld.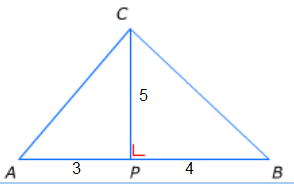 Hiernaast staat driehoek ABC. PC is de hoogtelijn. Deze staat loodrecht op AB. Bereken de oppervlakte van de driehoek. Alle maten zijn in meters.
Hiernaast staat driehoek ABC. PC is de hoogtelijn. Deze staat loodrecht op AB. Bereken de oppervlakte van de driehoek. Alle maten zijn in meters.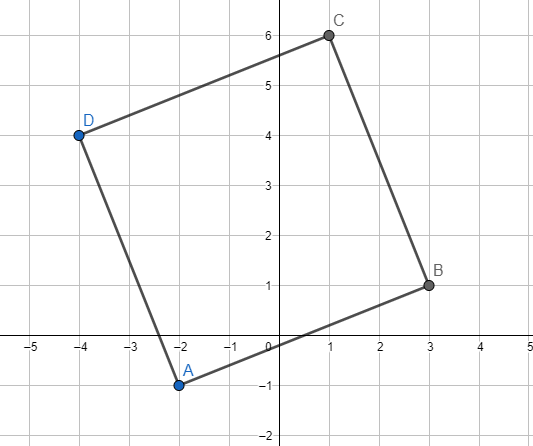
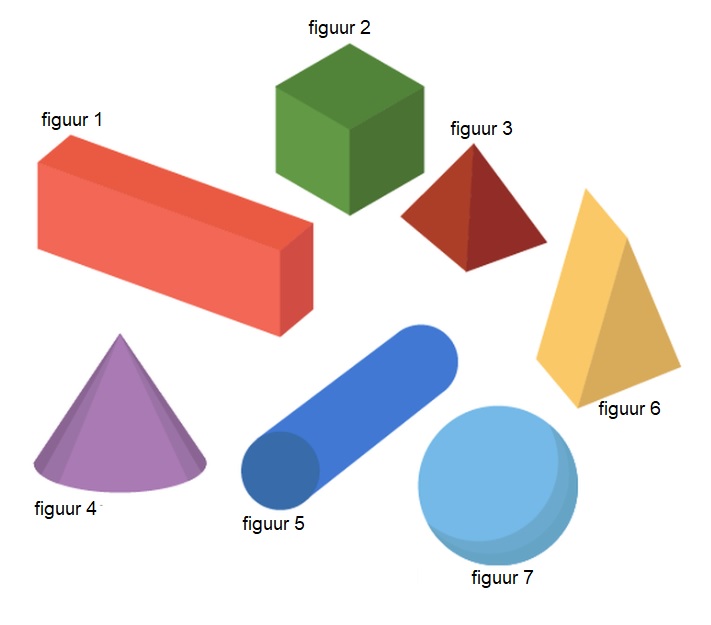
 De kerk hiernaast is opgebouwd uit verschillende ruimtefiguren. Schrijf in je schrift de namen op van de ruimtefiguren waaruit deze kerk bestaat.
De kerk hiernaast is opgebouwd uit verschillende ruimtefiguren. Schrijf in je schrift de namen op van de ruimtefiguren waaruit deze kerk bestaat. Hiernaast zie je de afbeelding van een kasteel. Dit kasteel bestaat uit verschillende ruimtefiguren.
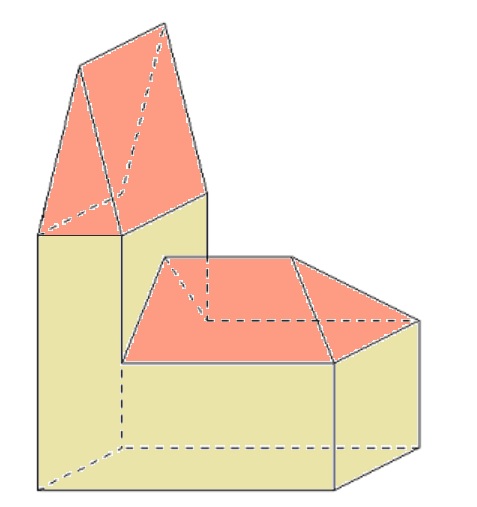
Hiernaast zie je de afbeelding van een kasteel. Dit kasteel bestaat uit verschillende ruimtefiguren.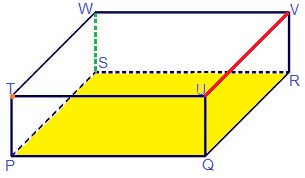 Bekijk de balk hiernaast. Beantwoord daarna de vragen.
Bekijk de balk hiernaast. Beantwoord daarna de vragen.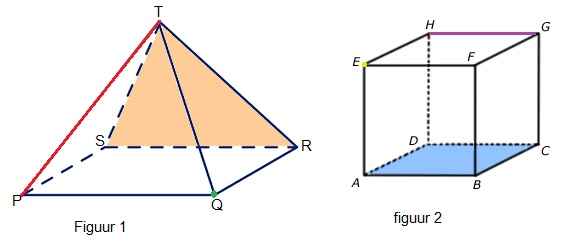
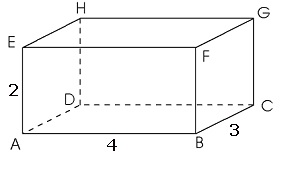 Bekijk balk ABCD EFGH. beantwoord daarna de vragen in je schrift.
Bekijk balk ABCD EFGH. beantwoord daarna de vragen in je schrift. Bekijk het prisma hiernaast. Beantwoord daarna de vragen.
Bekijk het prisma hiernaast. Beantwoord daarna de vragen.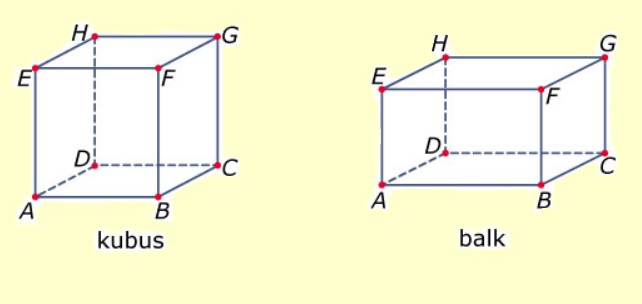
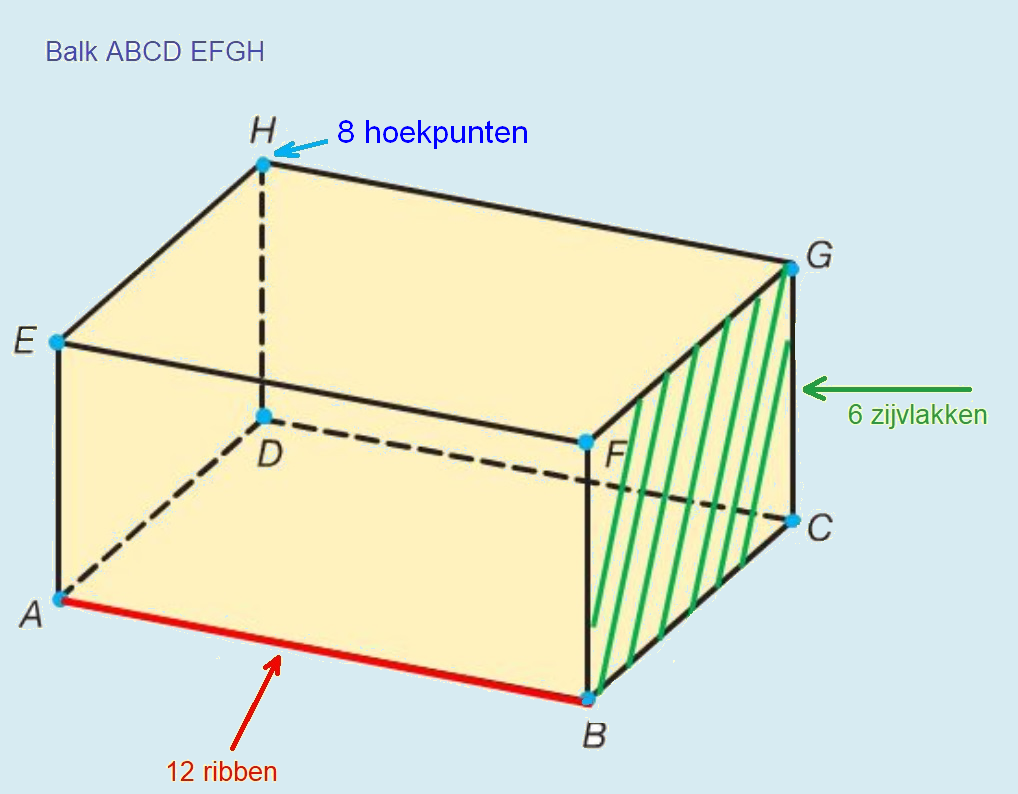
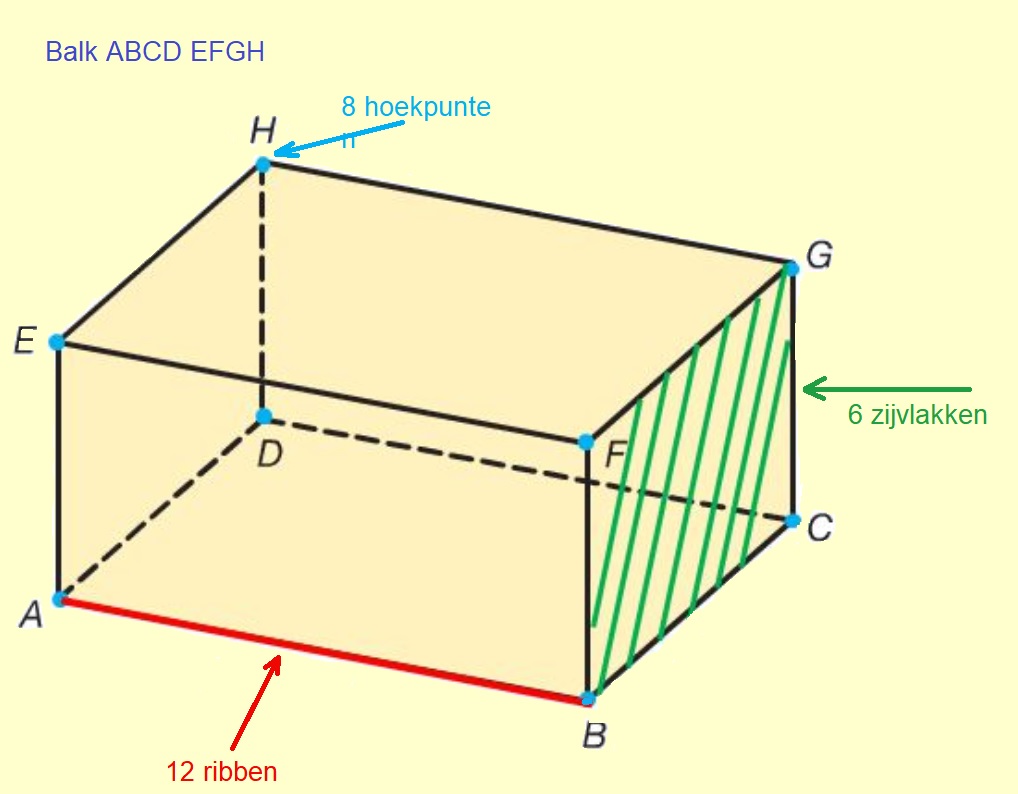 In de opsomming van de eigenschappen worden de begrippen hoekpunt, ribben en zijvlakken genoemd. Maar wat zijn dat nou eigenlijk. Kijk maar eens naar de afbeelding van de balk hiernaast.
In de opsomming van de eigenschappen worden de begrippen hoekpunt, ribben en zijvlakken genoemd. Maar wat zijn dat nou eigenlijk. Kijk maar eens naar de afbeelding van de balk hiernaast. Bekijk de balk PQRS TUVW hiernaast.
Bekijk de balk PQRS TUVW hiernaast.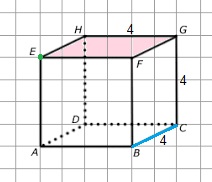 Bekijk de kubus hiernaast.
Bekijk de kubus hiernaast. Hiernaast zie je een afbeelding van een cilinder.
Hiernaast zie je een afbeelding van een cilinder.
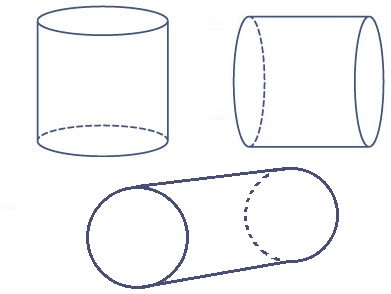 Bekijk de cilinders hiernaast. Deze staat ook op werkblad.
Bekijk de cilinders hiernaast. Deze staat ook op werkblad.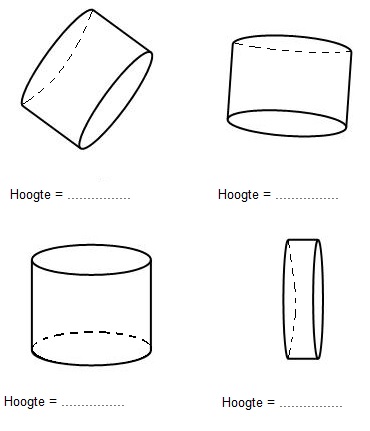 Bekijk de cilinders hiernaast. Deze staat ook op werkblad.
Bekijk de cilinders hiernaast. Deze staat ook op werkblad.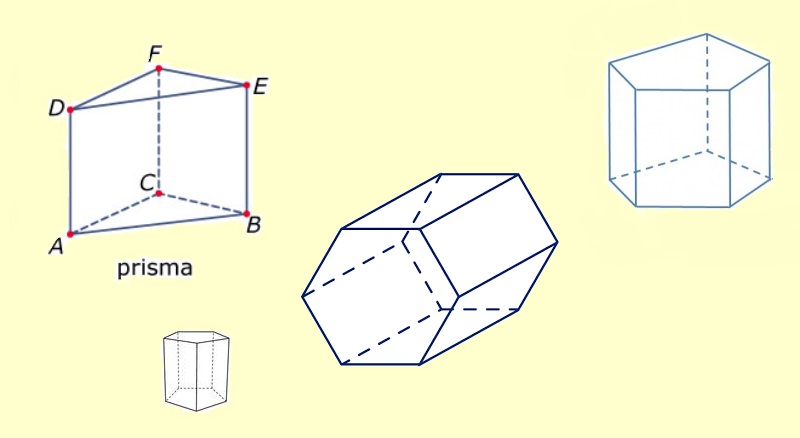
 Bekijk het prisma hiernaast, beantwoord daarna de vragen in je schrift.
Bekijk het prisma hiernaast, beantwoord daarna de vragen in je schrift.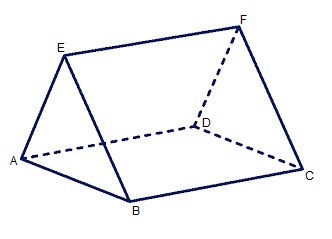
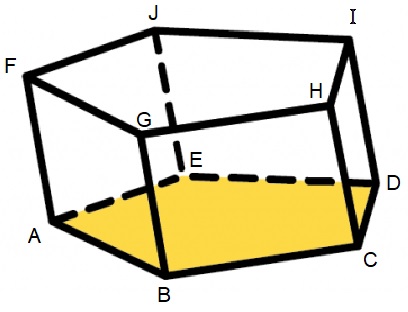
 Bekijk het prisma hiernaast, beantwoord daarna de vragen in je schrift.
Bekijk het prisma hiernaast, beantwoord daarna de vragen in je schrift. Bekijk de afbeelding van de kubus hiernaast.
Bekijk de afbeelding van de kubus hiernaast.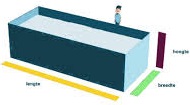 Van een balkvormig zwembad zijn de maten als volgt:
Van een balkvormig zwembad zijn de maten als volgt: Bekijk de afbeelding hiernaast.
Bekijk de afbeelding hiernaast.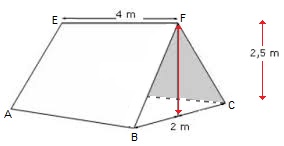 Bekijk de afbeelding van de tent hiernaast.
Bekijk de afbeelding van de tent hiernaast.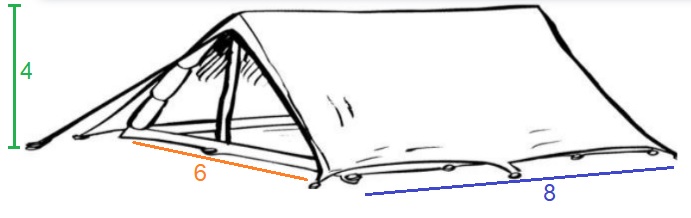 Het gronddoek van deze grote tent is 6 bij 8 meter.
Het gronddoek van deze grote tent is 6 bij 8 meter.
 In de opsomming van de eigenschappen worden de begrippen hoekpunt, ribben en zijvlakken genoemd. Maar wat zijn dat nou eigenlijk. Kijk maar eens naar de afbeelding van de balk hiernaast.
In de opsomming van de eigenschappen worden de begrippen hoekpunt, ribben en zijvlakken genoemd. Maar wat zijn dat nou eigenlijk. Kijk maar eens naar de afbeelding van de balk hiernaast.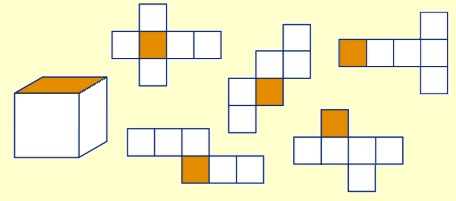
 Bekijk de ruimtefiguur hiernaast.
Bekijk de ruimtefiguur hiernaast. Hiernaast zie je een uitslag van een ruimtefiguur die wordt dichtgevouwen. Van welk ruimtefiguur is dit de uitslag?
Hiernaast zie je een uitslag van een ruimtefiguur die wordt dichtgevouwen. Van welk ruimtefiguur is dit de uitslag?


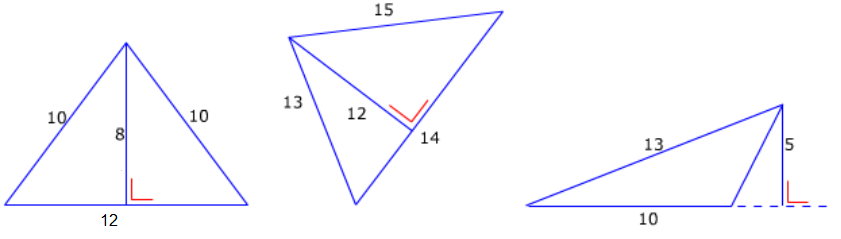
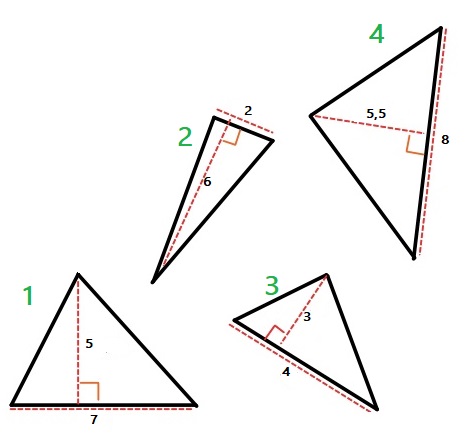 Bereken van de vier driehoeken hiernaast de oppervlakte.
Bereken van de vier driehoeken hiernaast de oppervlakte.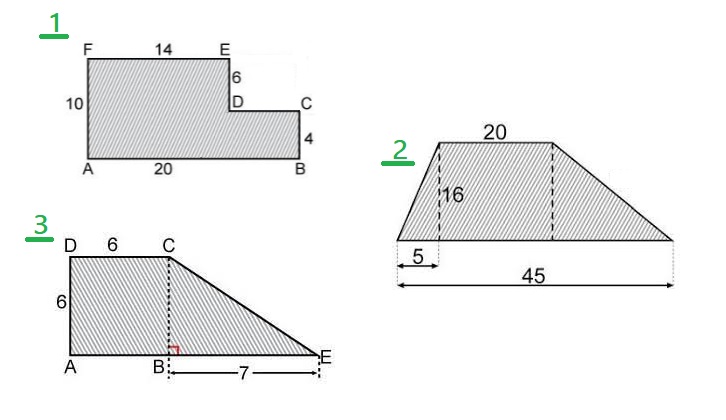 Bereken van deze figuren de oppervlakte.
Bereken van deze figuren de oppervlakte.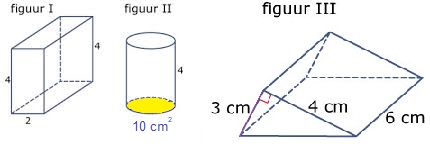 Bereken de inhoud van de figuren hiernaast
Bereken de inhoud van de figuren hiernaast