Het arrangement 1KGT H08 Symmetrie is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 03-07-2020 11:17:52
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten

 Elke ochtend kijk je vast even in de spiegel. Je bent dan met symmetrie bezig zonder dat je het door hebt. Of knipt jou vader of moeder de heg in de tuin ook altijd zo netjes? Ook dan ben je met symmetrie bezig.
Elke ochtend kijk je vast even in de spiegel. Je bent dan met symmetrie bezig zonder dat je het door hebt. Of knipt jou vader of moeder de heg in de tuin ook altijd zo netjes? Ook dan ben je met symmetrie bezig. Aan het eind van dit hoofdstuk kan ik:
Aan het eind van dit hoofdstuk kan ik:

 Maak een schema in je schrift:
Maak een schema in je schrift: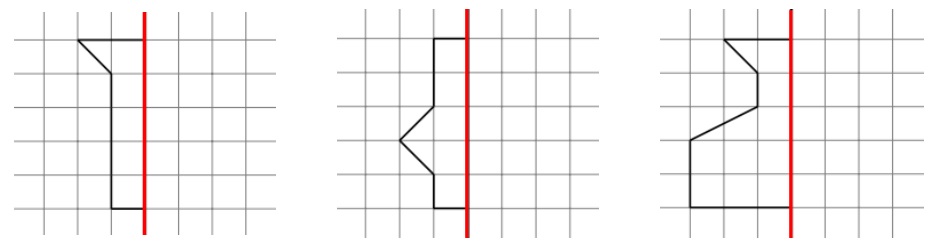
 Op je werkblad zie je de afbeelding zoals die hiernaast staat.
Op je werkblad zie je de afbeelding zoals die hiernaast staat.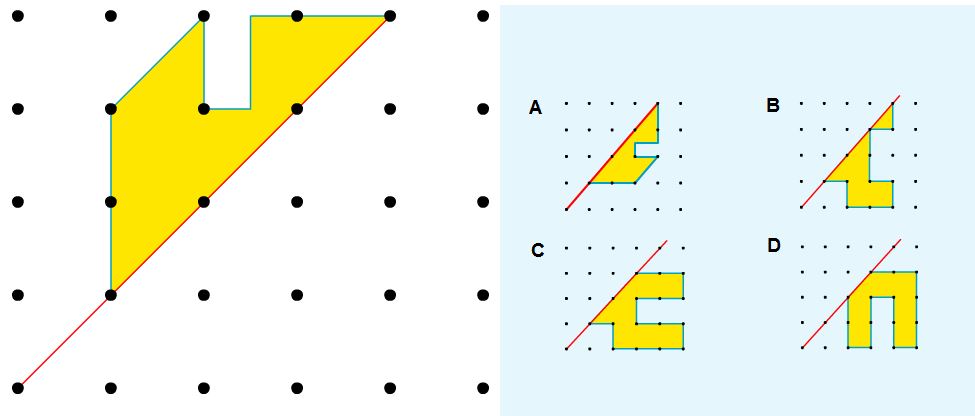
 De vierhoek hiernaast past bij draaiing vier keer op zichzelf.
De vierhoek hiernaast past bij draaiing vier keer op zichzelf. Kijk maar.
Kijk maar.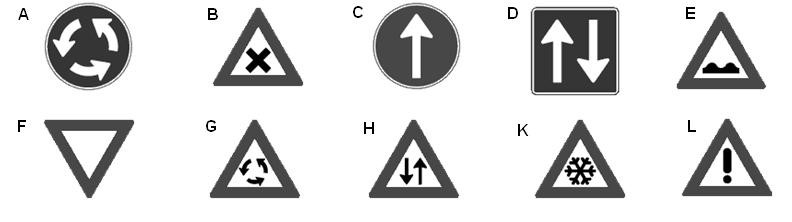
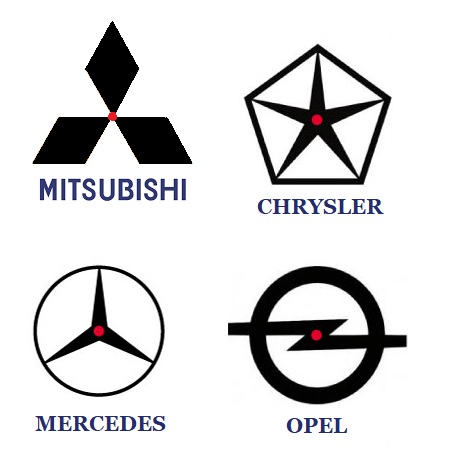 Hiernaast zien we vier logo's van vier verschillende auto merken. De logo's zijn draaisymmetrisch. Bereken van ieder logo de kleinste draaihoek. Schrijf de berekeningen netjes in je schrift.
Hiernaast zien we vier logo's van vier verschillende auto merken. De logo's zijn draaisymmetrisch. Bereken van ieder logo de kleinste draaihoek. Schrijf de berekeningen netjes in je schrift.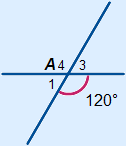
 Bekijk de figuur hiernaast.
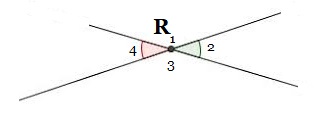
Bekijk de figuur hiernaast.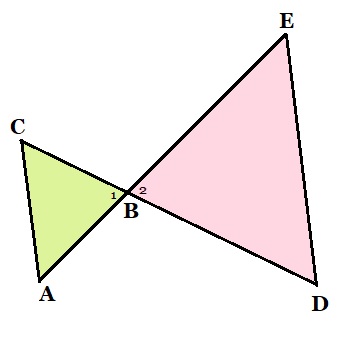 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.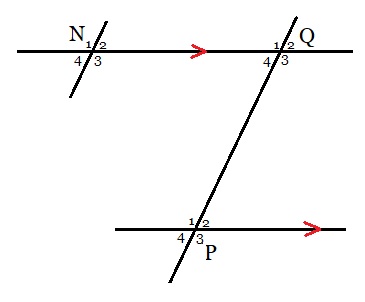 Bekijk de afbeelding hiernaast. Je ziet hier de hoeken N, P en Q. Alle hoeken zijn onderverdeelt in vier stukken.
Bekijk de afbeelding hiernaast. Je ziet hier de hoeken N, P en Q. Alle hoeken zijn onderverdeelt in vier stukken.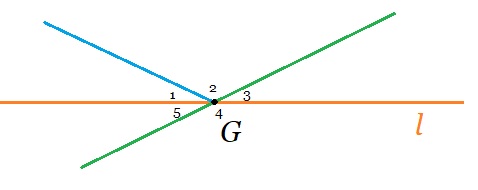 Hiernaast zie je hoek G. Hoek G is verdeeld in 5 stukken.
Hiernaast zie je hoek G. Hoek G is verdeeld in 5 stukken.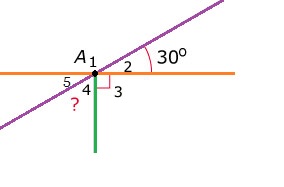 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.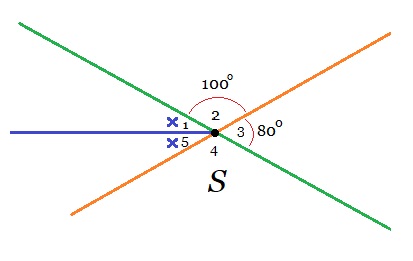 Bekijk de afbeelding hiernaast.
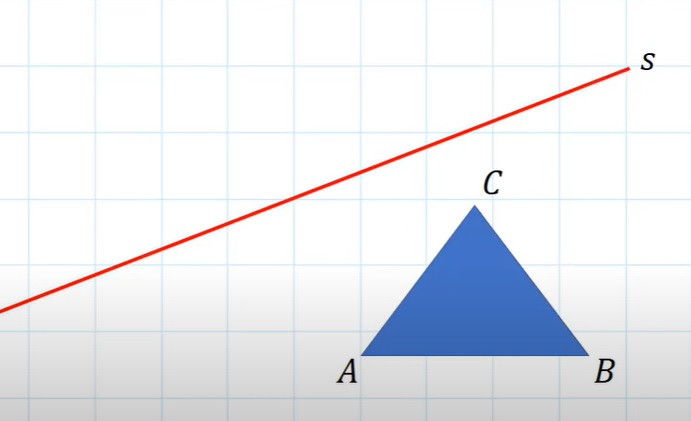
Bekijk de afbeelding hiernaast.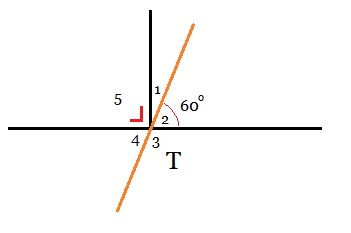
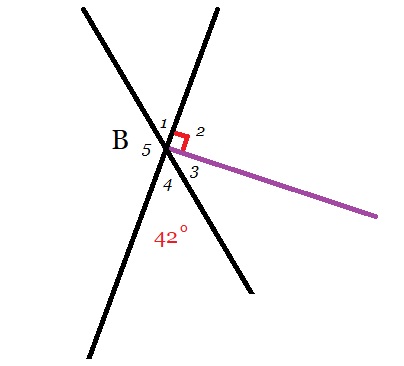 Bekijk de afbeelding hiernaast.
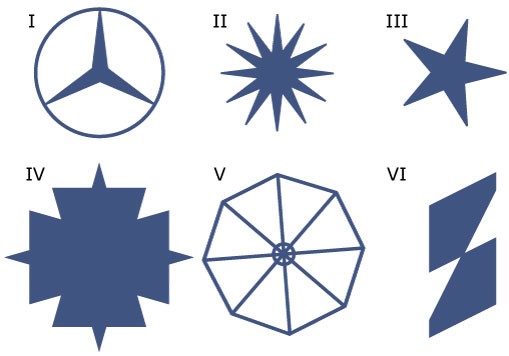
Bekijk de afbeelding hiernaast. Bekijk de acht afbeeldingen hiernaast.
Bekijk de acht afbeeldingen hiernaast.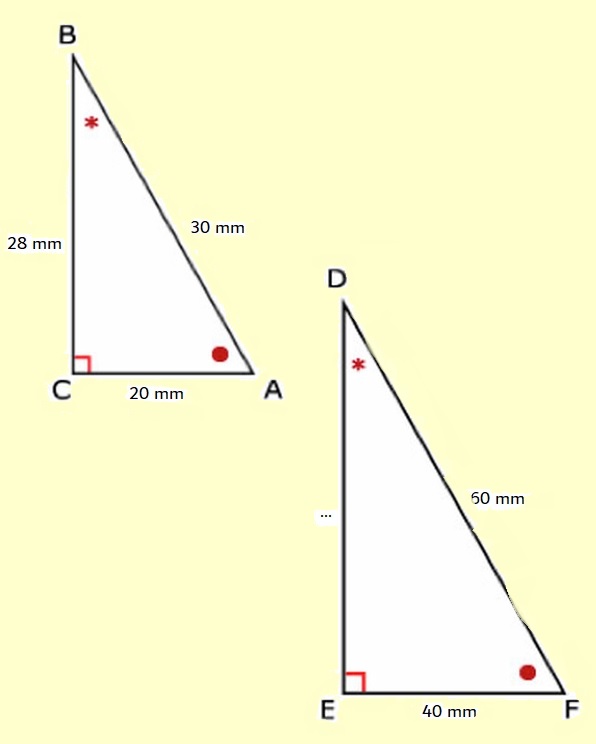
 Bekijk de twee driehoeken hiernaast.
Bekijk de twee driehoeken hiernaast.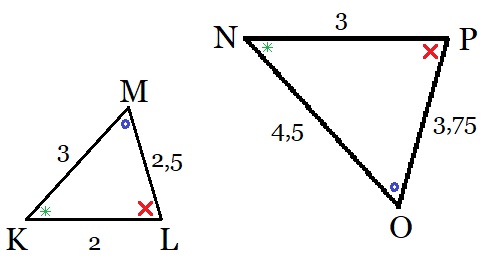 Bekijk de twee driehoeken hiernaast.
Bekijk de twee driehoeken hiernaast.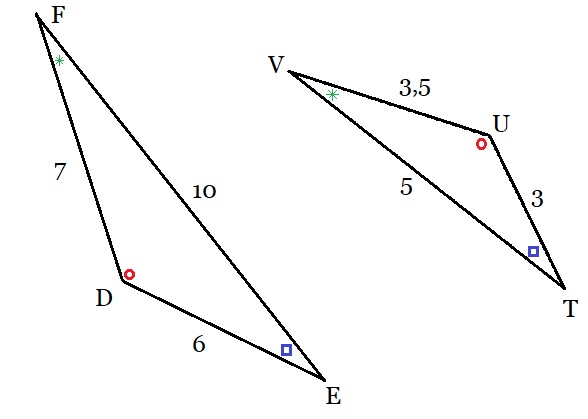 Bekijk de twee driehoeken hiernaast.
Bekijk de twee driehoeken hiernaast.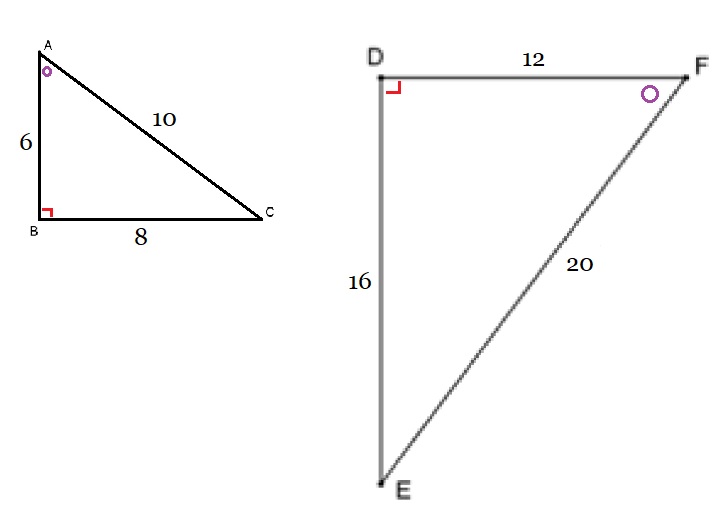
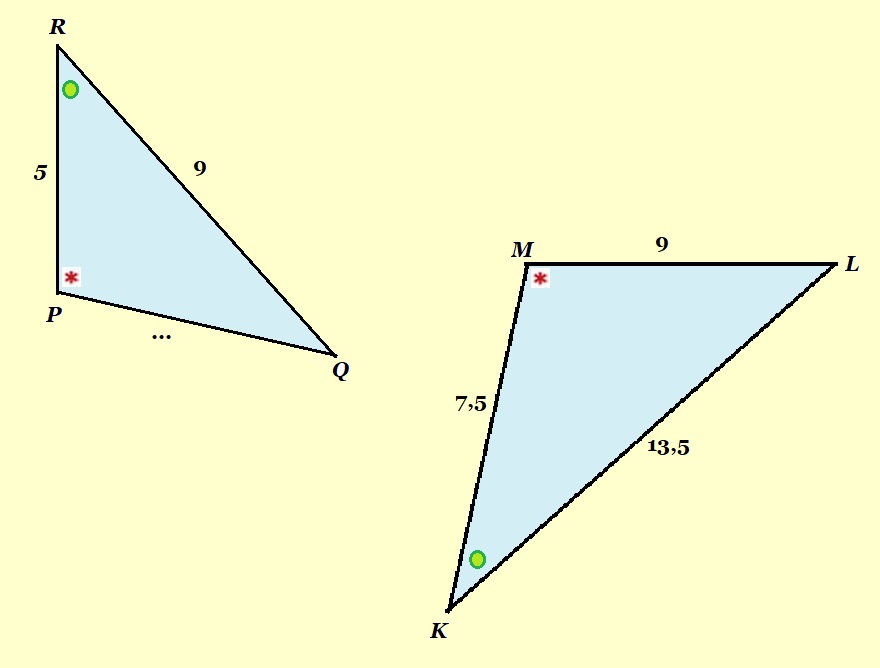
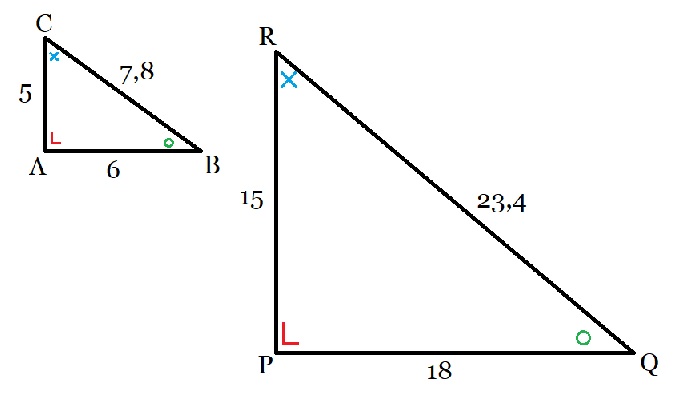
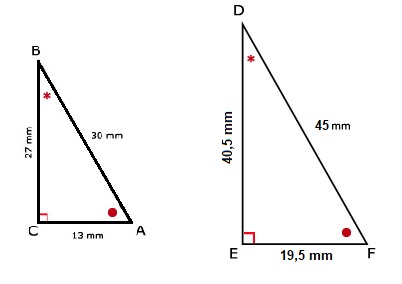 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.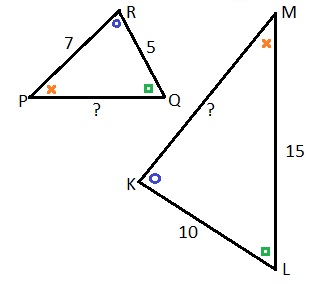 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.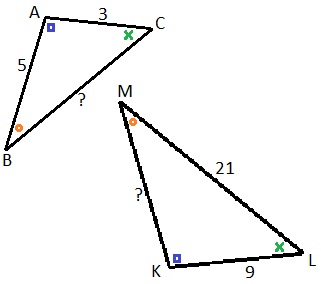 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.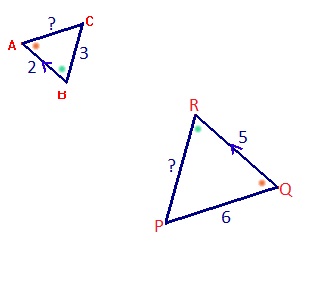 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.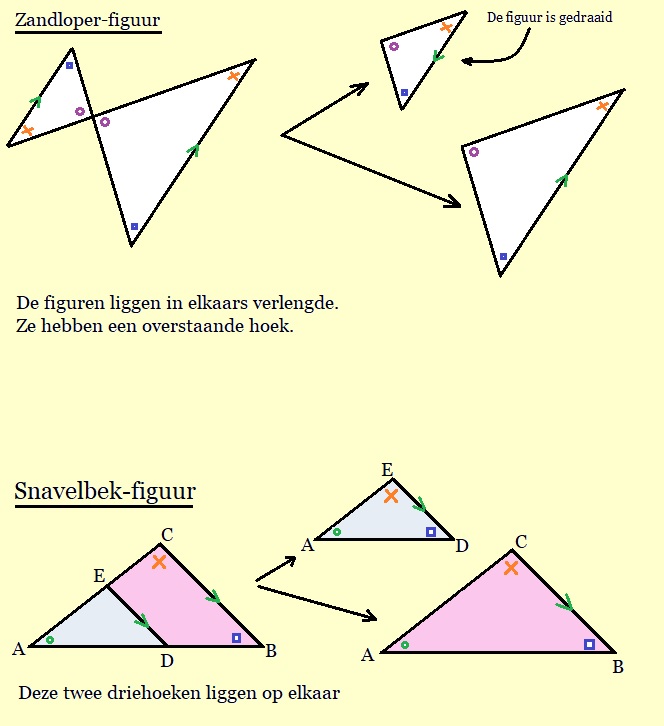
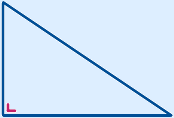 Een driehoek met een rechte hoek.
Een driehoek met een rechte hoek.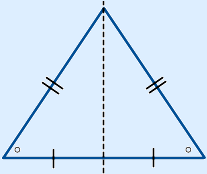 Een driehoek met twee gelijke zijden. Deze driehoek heeft één symmetrieas.
Een driehoek met twee gelijke zijden. Deze driehoek heeft één symmetrieas.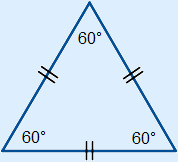 Een driehoek met drie gelijke zijden. Alle zijden van deze driehoek zijn even lang.
Een driehoek met drie gelijke zijden. Alle zijden van deze driehoek zijn even lang.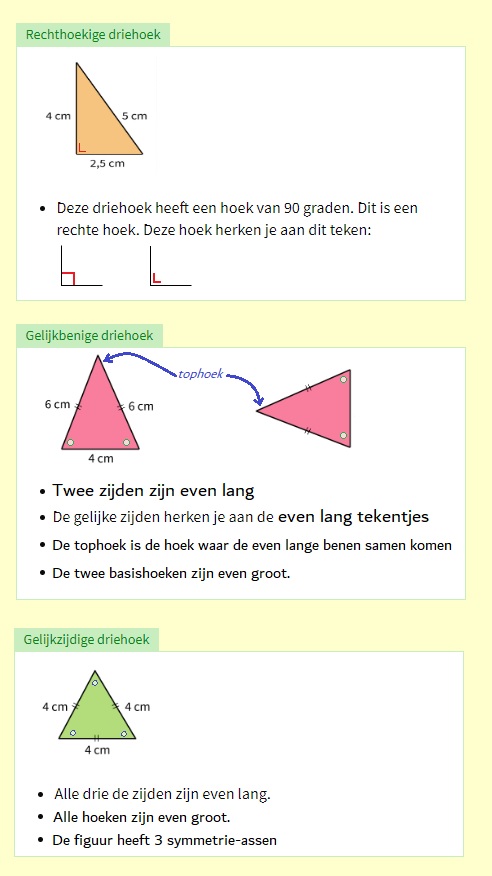
 Bekijk de driehoek op het plaatje. Deze staat ook op je werkblad. Gebruik je geodriehoek om de zijden eventueel op te meten.
Bekijk de driehoek op het plaatje. Deze staat ook op je werkblad. Gebruik je geodriehoek om de zijden eventueel op te meten. Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.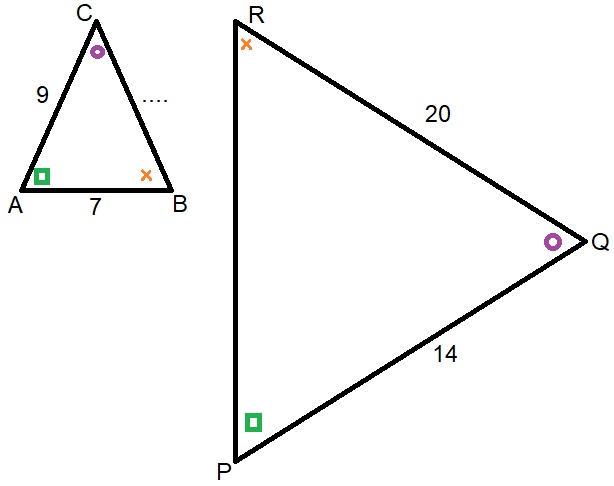 Bekijk de driehoeken hiernaast. Geef daarna antwoord op de vragen.
Bekijk de driehoeken hiernaast. Geef daarna antwoord op de vragen. Bekijk de afbeelding hiernaast.
Bekijk de afbeelding hiernaast. Bekijk de verkeersborden hiernaast. Deze staan ook op je werkblad.
Bekijk de verkeersborden hiernaast. Deze staan ook op je werkblad.