Het arrangement 1H02 Vlakke figuren is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 11-10-2022 10:37:01
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Openingspagina van waaruit alle koppelingen gemaakt worden
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Gebruikte Wikiwijs Arrangementen
Giessen, D.. (z.d.).
1KGT H02 Vlakke figuren
Wiskundesectie Juliana. (z.d.).
1H02 Vlakke figuren







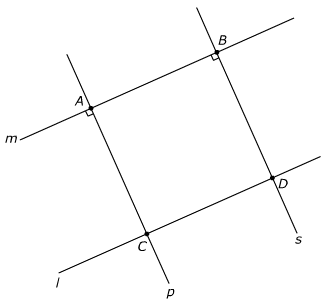
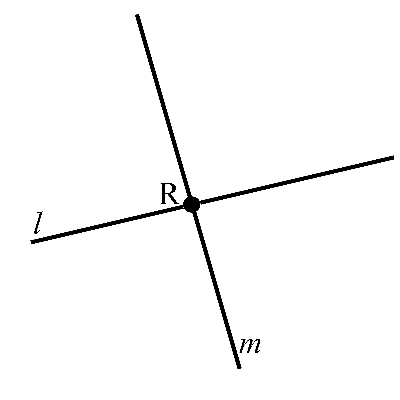
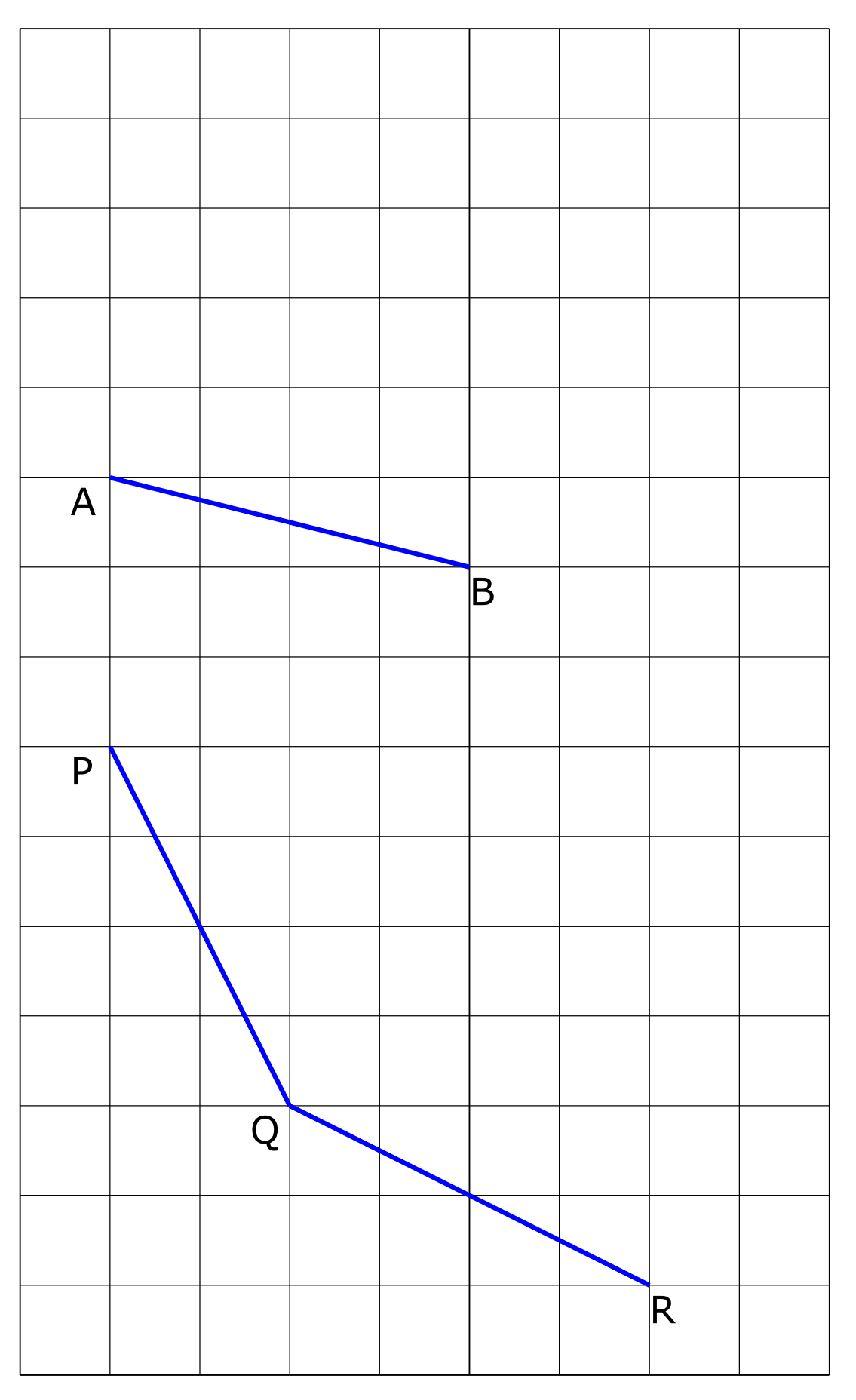
 Bekijk de lijnen hiernaast in de afbeelding.
Bekijk de lijnen hiernaast in de afbeelding.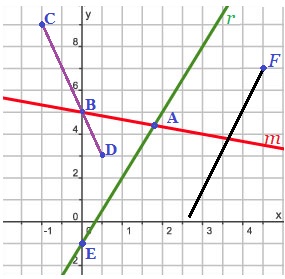 Hiernaast zie je verschillende lijnen, lijnstukken en halve lijnen getekend in een assenstelsel.
Hiernaast zie je verschillende lijnen, lijnstukken en halve lijnen getekend in een assenstelsel.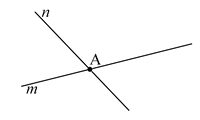
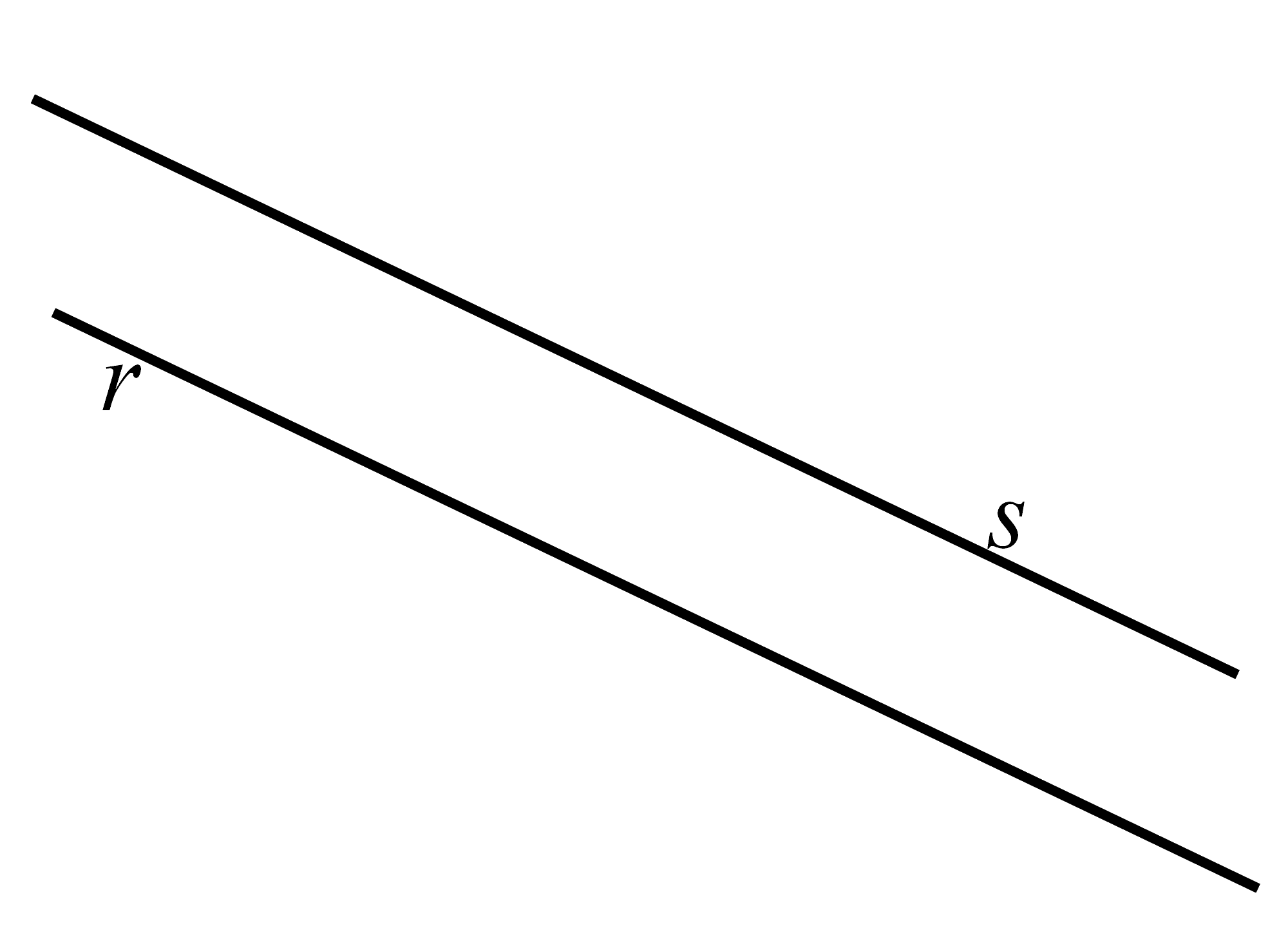
 De lijnen
De lijnen 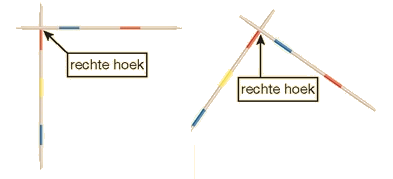
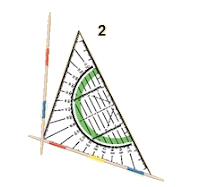
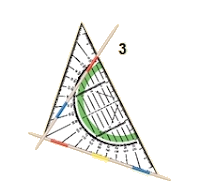
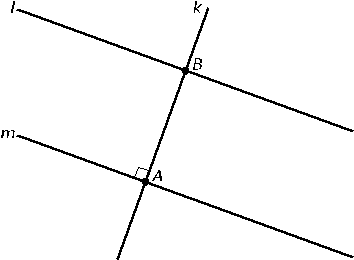
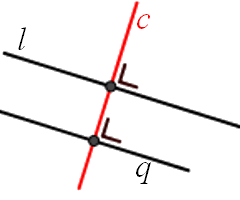
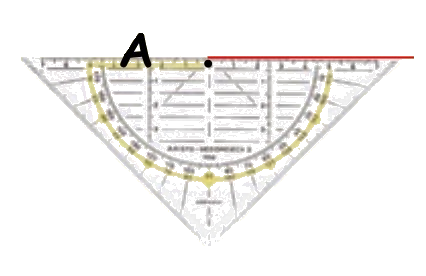
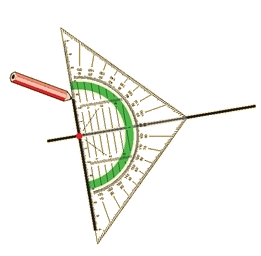 Hiernaast zie je een voorbeeld hoe we loodrecht kunnen tekenen met een geodriehoek. We gebruken daarvoor de ingebouwde loodlijn van je geodriehoek. Deze loopt precies in het midden.
Hiernaast zie je een voorbeeld hoe we loodrecht kunnen tekenen met een geodriehoek. We gebruken daarvoor de ingebouwde loodlijn van je geodriehoek. Deze loopt precies in het midden.




 fstand tussen twee punten meten we altijd met een rechte lijn.
fstand tussen twee punten meten we altijd met een rechte lijn.
 De afstand tussen een punt en een lijn meet je altijd loodrecht.
De afstand tussen een punt en een lijn meet je altijd loodrecht.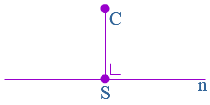
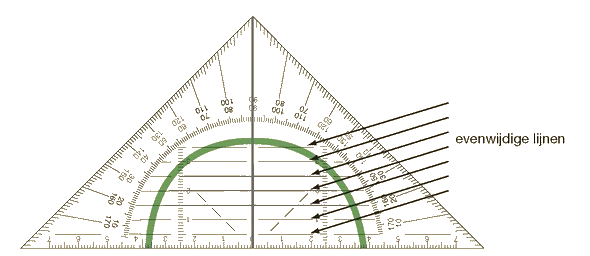
 Ook de kortste afstand tussen twee evenwijdige lijnen meet je loodrecht.
Ook de kortste afstand tussen twee evenwijdige lijnen meet je loodrecht.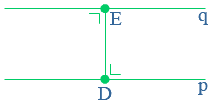
 Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad.
Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad. Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad.
Bekijk de afbeelding hiernaast. Deze afbeelding staat ook op je werkblad.
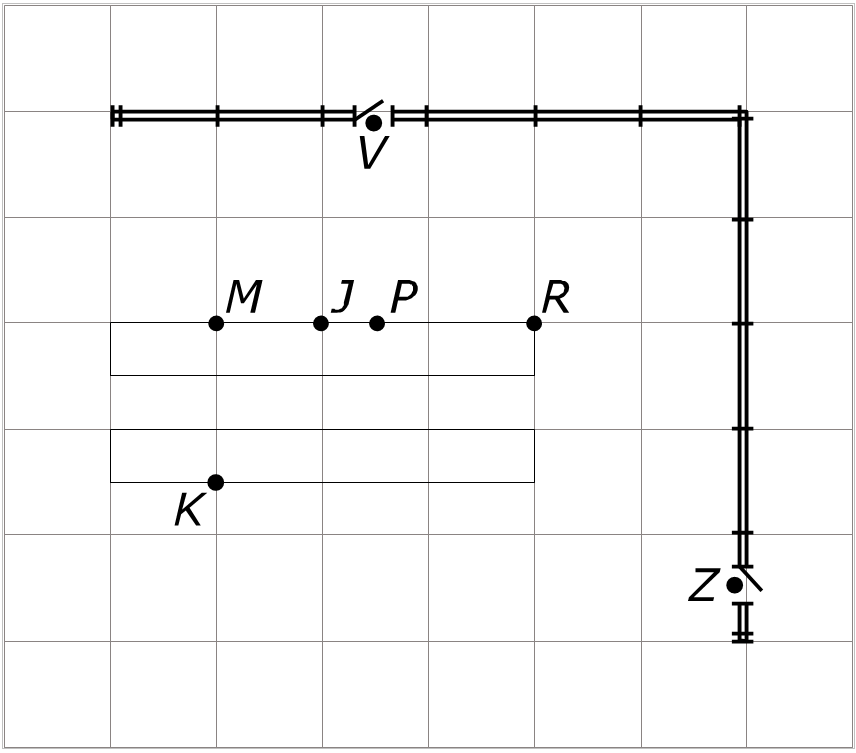 Je ziet een plattegrond van een school en de fietsenstalling.
Je ziet een plattegrond van een school en de fietsenstalling.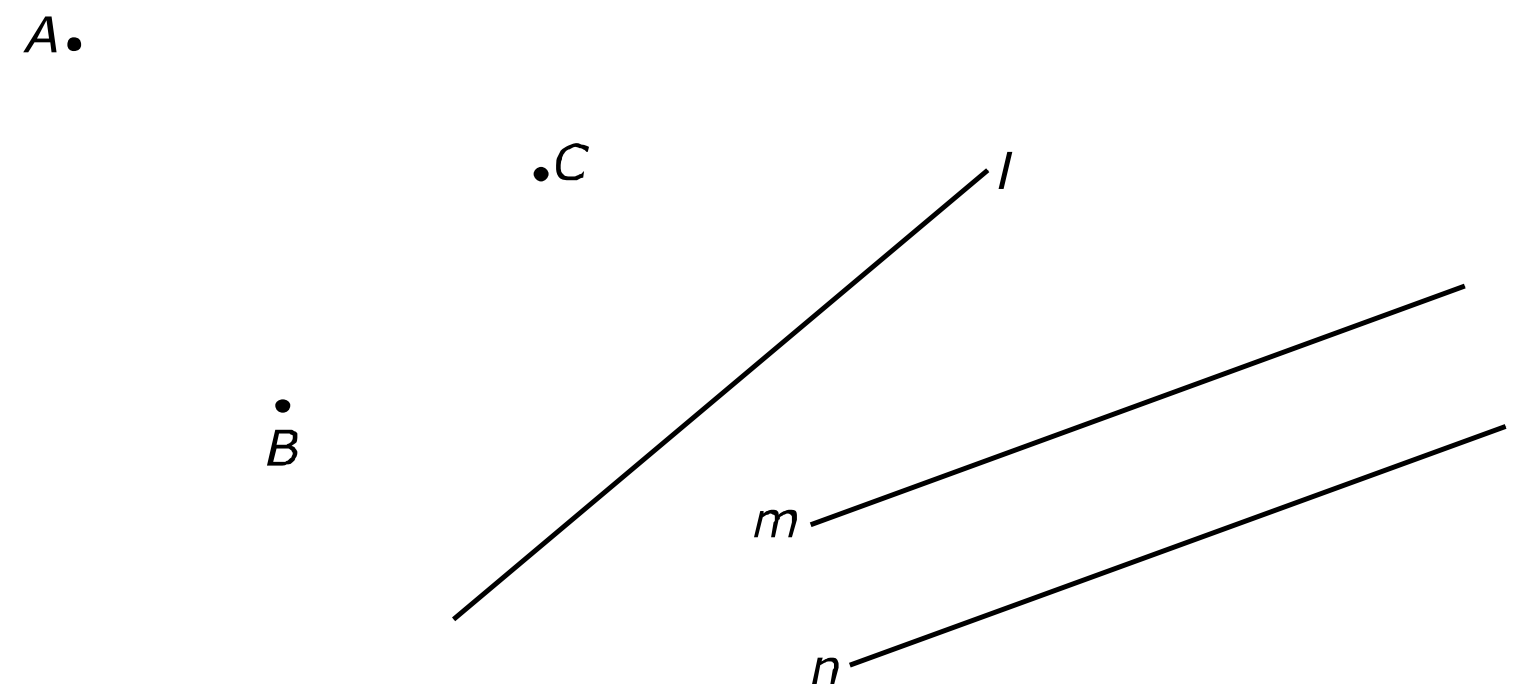
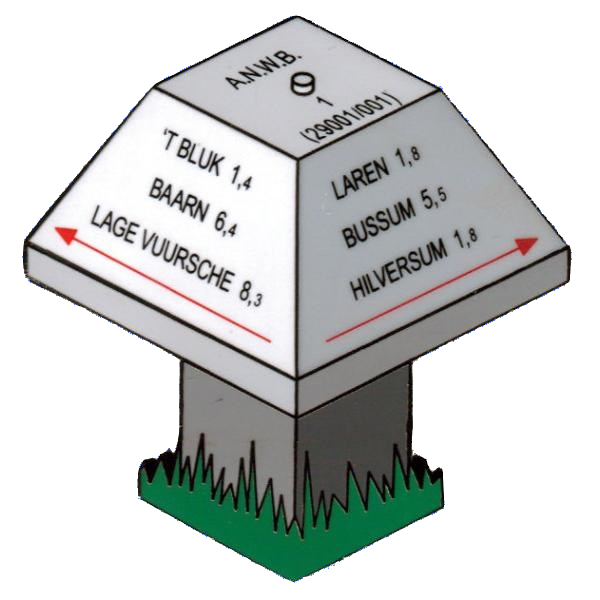
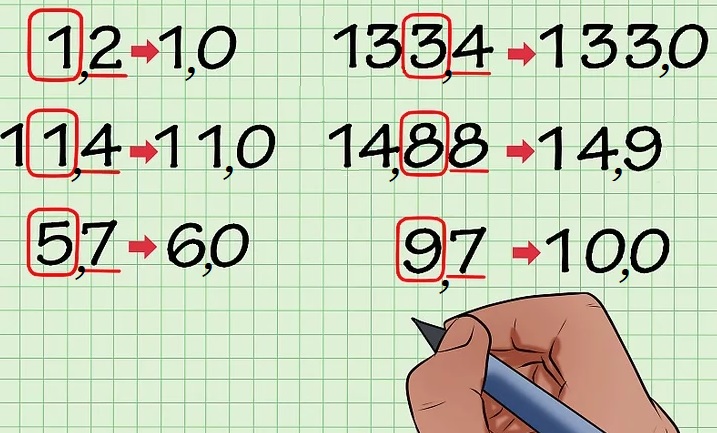

 De afstand naar Harfsen staat op de paddenstoel.
De afstand naar Harfsen staat op de paddenstoel.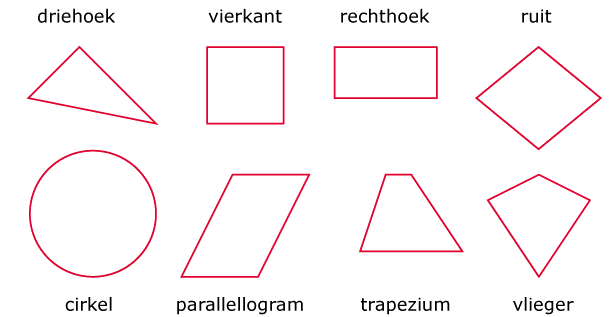
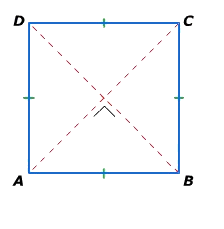 Een vierkant is een vlakke figuur. Het figuur is 2D, plat.
Een vierkant is een vlakke figuur. Het figuur is 2D, plat.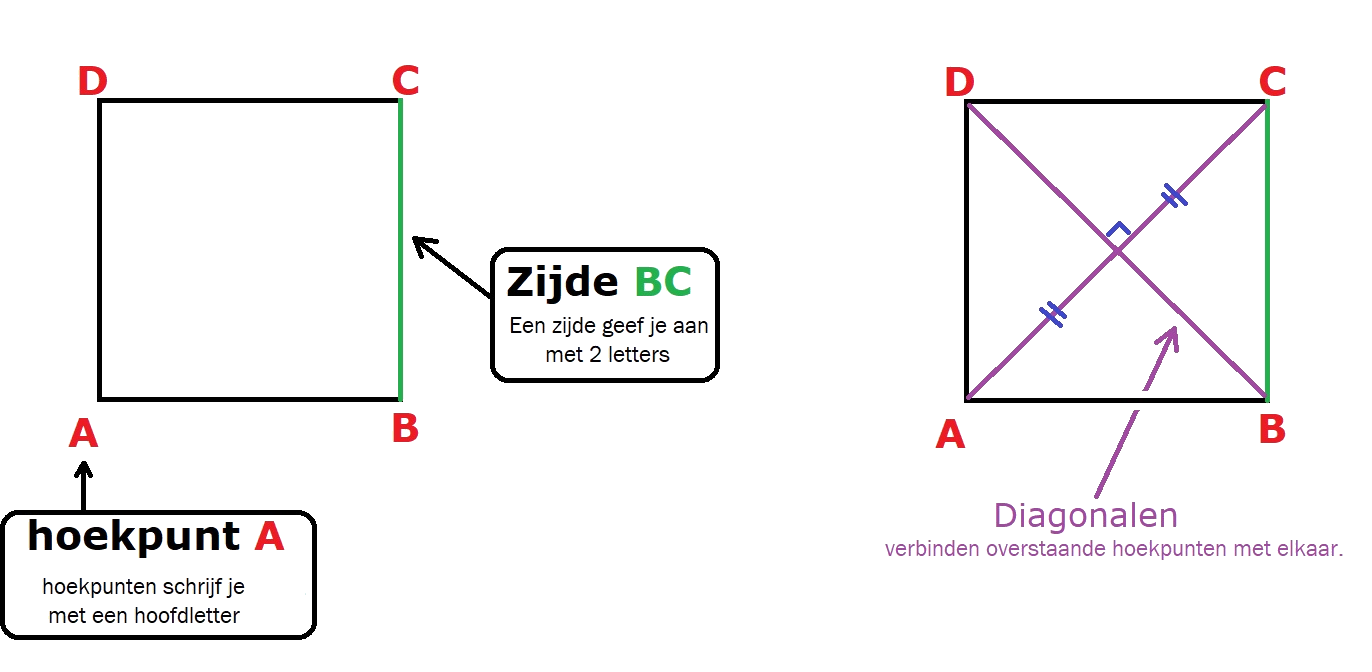
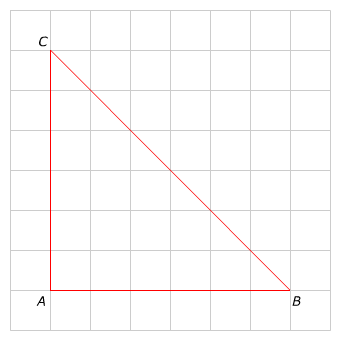
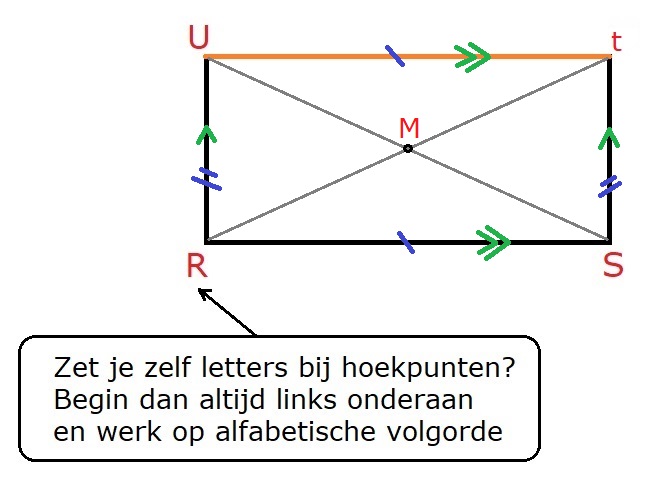 Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.
Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.

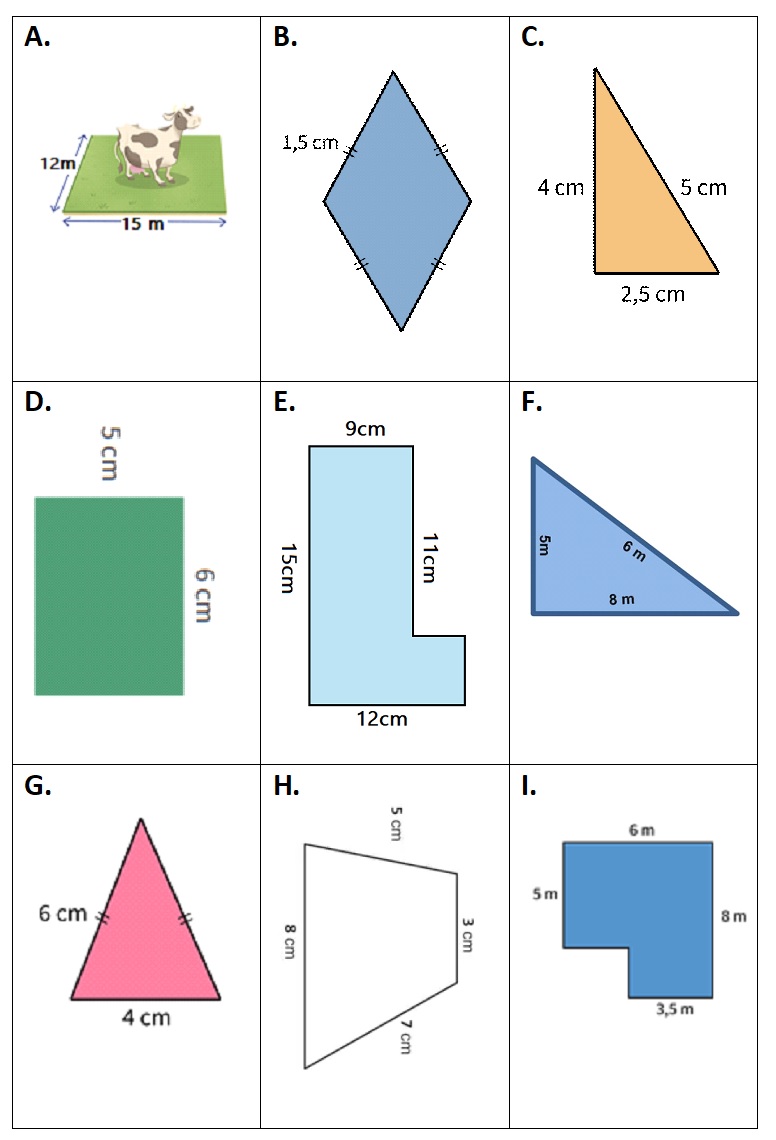



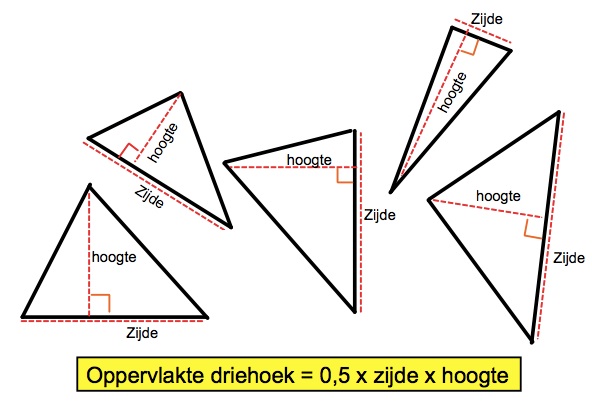
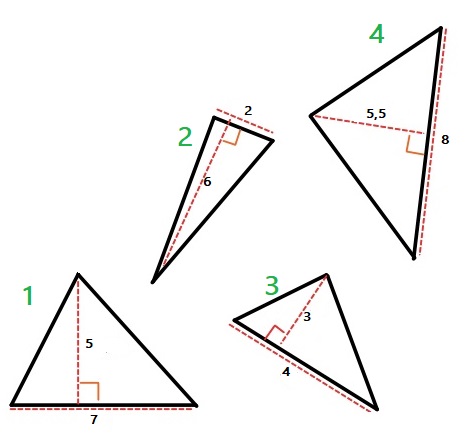

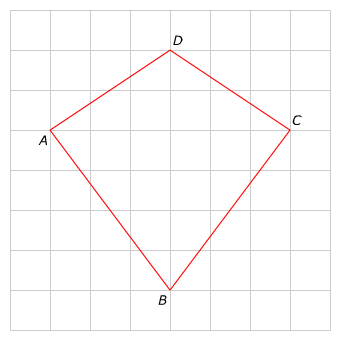
 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.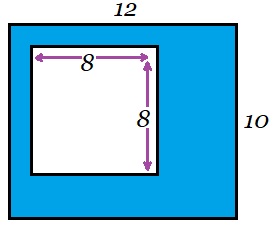 Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.
Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.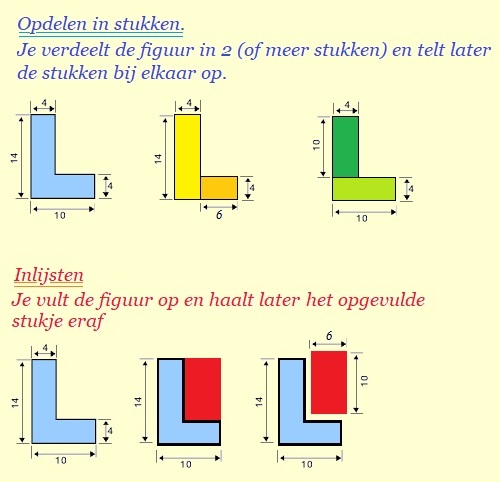
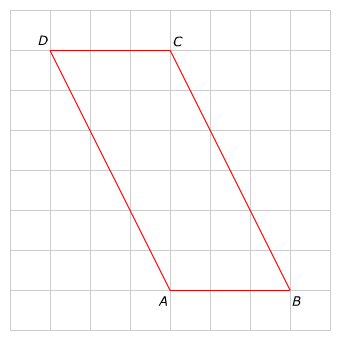
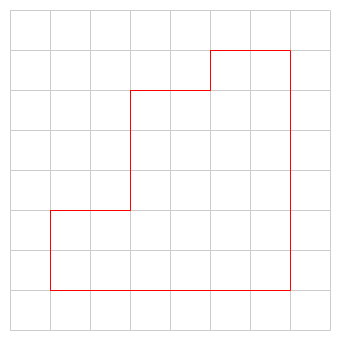
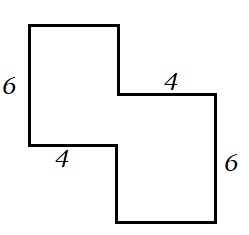
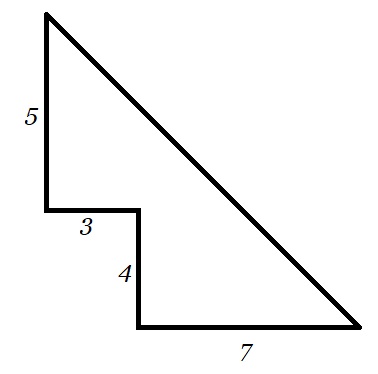 Bekijk de figuur hiernaast. Bereken de oppervlakte van deze figuur.
Bekijk de figuur hiernaast. Bereken de oppervlakte van deze figuur.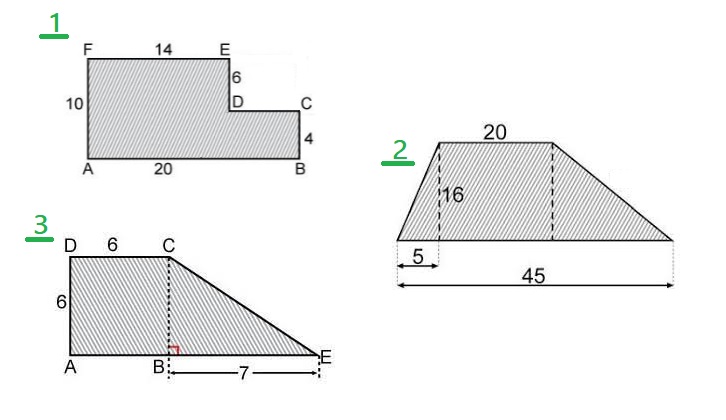
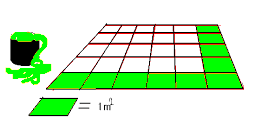 Hoeveel ruimte neemt het vlak ik. Met andere woorden hoeveel verf past er op je figuur.
Hoeveel ruimte neemt het vlak ik. Met andere woorden hoeveel verf past er op je figuur.




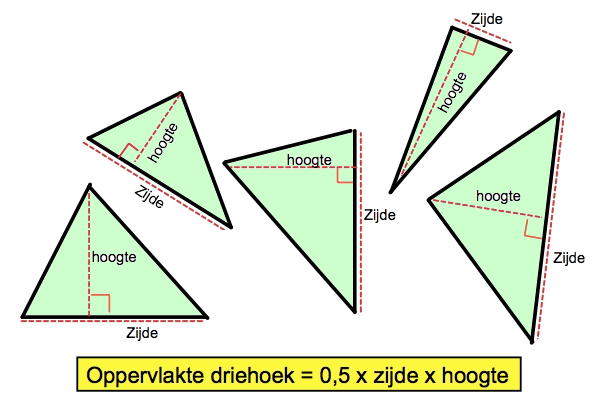
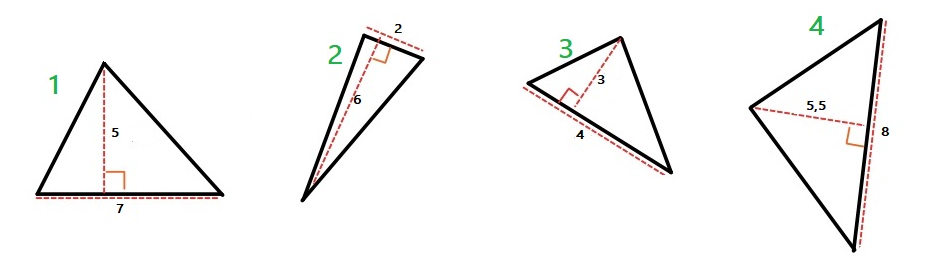
 Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is.
Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is.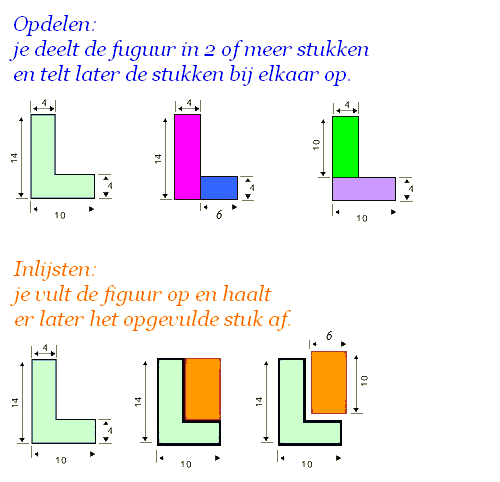
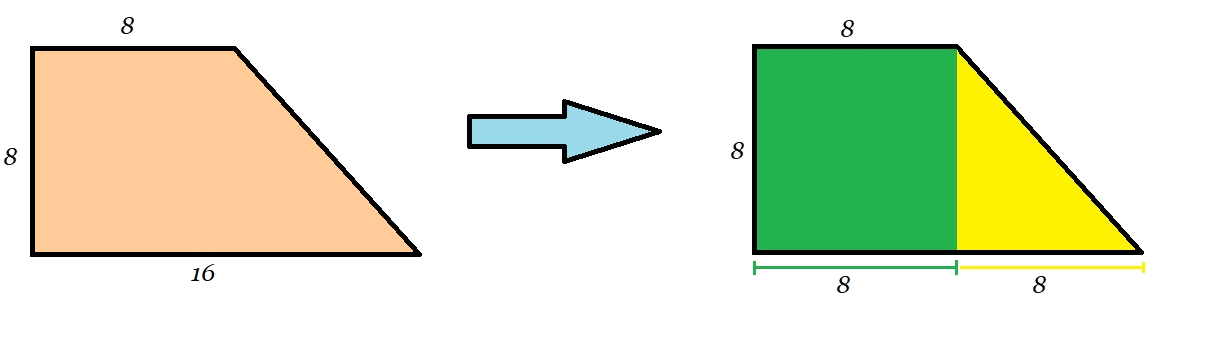
 Bekijk de figuur hiernaast. Bereken de oppervlakte van deze figuur.
Bekijk de figuur hiernaast. Bereken de oppervlakte van deze figuur.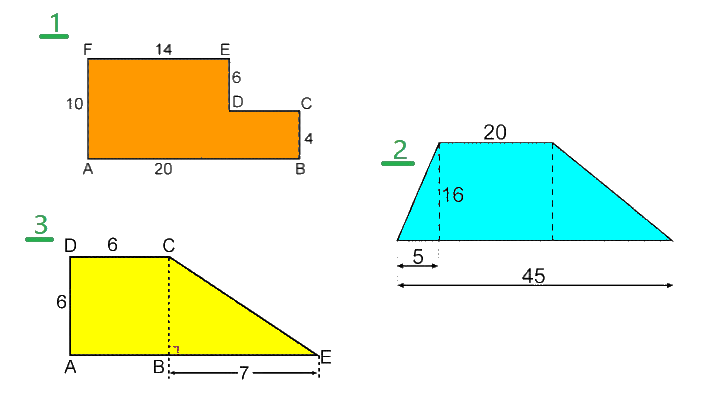

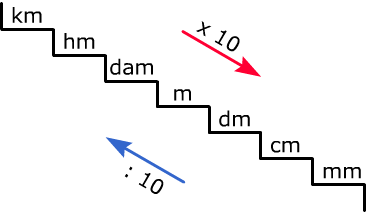
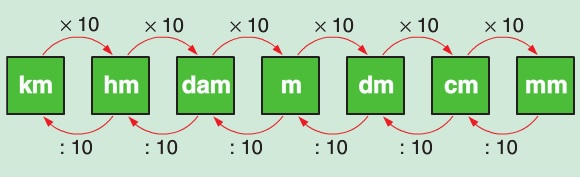
 De lengte van een lesboek is 40 centimeter (cm). Hoeveel decimeter is dat?
De lengte van een lesboek is 40 centimeter (cm). Hoeveel decimeter is dat?

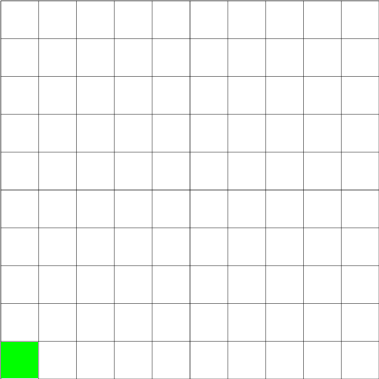
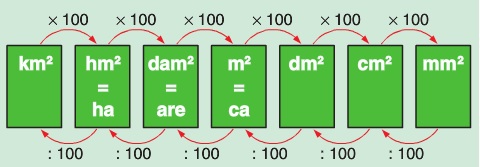

 aat uit twee even grote vakken.
aat uit twee even grote vakken.



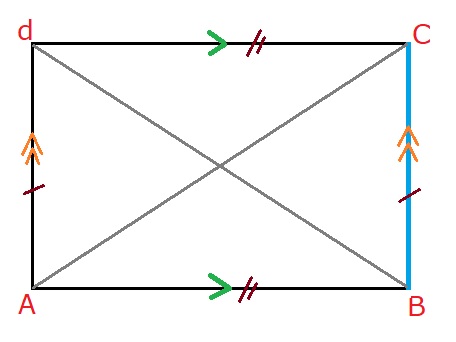 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.