Oppervlakte en Inhoud - kopie 1

Oppervlakte en Inhoud - kopie 1

Inleiding

Welkom allemaal !

Nu de scholen dicht zijn en docenten vanuit huis les moeten geven, worden jullie overvallen met mailtjes met informatie, uitleg en opdrachten. Om dit overzichterlijk te houden, heb ik deze site gemaakt. Hier kun je al het materiaal vinden dat ik heb gemaakt of gevonden heb voor jullie rondom Hoofdstuk 8 en Hoofdstuk 10.

Onder het kopje Daltontaak kun je alle uitleg video's en tips vinden voor Deel 1 en Deel 2 van de Daltontaak.

Onder de kopjes met een weeknummer vindt je alle uitleg video's voor de stof die er in die week gemaakt moet worden. Daarnaast komen er in de loop van die week, afhankelijk van jullie vragen, uitwerkingen van de opdrachten, die jullie dienen te maken als huiswerk, op de site te staan.

Is er iets toch nog niet helemaal duidelijk ? Stuur dan vooral een berichtje via Microsoft Teams, dan beantwoord ik je vraag zo snel mogelijk !

 

Heel veel succes de komende weken en probeer vooral gezond te blijven !

 

Groetjes mevrouw Bos

Daltontaak

De Daltontaak bestaat uit twee delen.

Deel 1

Bewijs de Stelling van Pythagoras in Geogebra.

Deel 2

Maak een vlakvulling of in Geogebra of met de hand.

Creëer een link

Creëren van een link in Geogebra

Week 12

In deze week ga je de stof van paragraaf 10.1 en paragraaf 10.2 verwerken.

Het bijbehorende huiswerk:

Paragraaf 10.1: opdracht 2, 4, 5 en 8

Paragraaf 10.2: opdracht 12, 13, 15 en 16

Paragraaf 10.1

Om even in te komen, kun je het onderstaande filmpje bekijken. In deze video wordt een liedje gezongen, waarin wordt uitgelegd hoe je de inhoud van een kubus en een balk kan berekenen.

De video hieronder is een uitlegfilmpje over het berekenen van de inhoud van een cilinder.

In de volgende video wordt uitgelegd wat een prisma is en hoe je de inhoud van een prisma kan bereken. Deze video is misschien een beetje saai, maar deze meneer weet echt waar hij het over heeft!

In de afbeelding hieronder staat mijn uitwerking van opdracht 4. Wanneer je op de afbeelding klikt, wordt deze vergroot en kan je mijn handschrift misschien wat beter lezen. Wil je de vergroting weer sluiten ? Klik dan ergens in je beeld, dan verschijnt er een kruisje links onderin in je beeld, waarmee je de vergroting kan sluiten en terugkeert naar de site.

Ook opgave 5 heb ik voor jullie uitgewerkt, controleer of jij ook op dit antwoord uitkwam !

 

Paragraaf 10.2

Paragraaf 10.2 gaat over de prisma ! Weet je nou even niet meer wat een prisma is ? Bekijk dan de onderstaande video, waarin wordt uigelegd wat een prisma is en hoe je de inhoud van een prisma kan berekenen.

Opgave 13 bleek ook wel een lastige opgave te zijn, want de juiste vorm zien in 3D vergt wel wat ruimtelijk inzicht. Daarom kun je hieronder de uitwerkingen van deze opgave bekijken.

Opgave 15 en 16 zijn hieronder te vinden. De goudentip bij deze opdrachten is: het grondvlak hoeft niet perse het vlak te zijn dat op de bodem ligt ! De zijkant van het figuur kan dus ook zomaar het grondvlak zijn, waardoor de diepte van het figuur opeens de hoogte wordt. Succes !

Inleveropdracht

Beste leerlingen,

Je dient de inleveropdracht te maken in je schrift of op een blaadje. Schrijf bij de opdracht natuurlijk een berekening op waar dat kan en onderbouw je antwoord als dat van je gevraagd wordt. Wanneer je klaar bent met het maken van de opdracht, scan je je uitwerkingen in of maak je er een foto van. Dit lever je in op Magister à ELO à Opdrachten à a2b wiskunde opdracht week 12 / g2 wiskunde opdracht week 12

Succes !

Je kunt de opdracht vinden in Magister bij 'berichten' of bij 'opdrachten'.

Week 13

In deze week ga je de stof van paragraaf 10.3 en paragraaf 10.4 verwerken.

Het bijbehorende huiswerk:

Paragraaf 10.3: opdracht 19, 21, 22 en 23

Paragraaf 10.4: opdracht 25, 27, 29 en 30

Paragraaf 10.3

In deze paragraaf leer je hoe je de inhoud van een kegel en een piramide kan berekenen. Hoe je dit precies kan doen, wordt uitgelegd in de onderstaande video.

 

Opdracht 20

Om de inhoud van een piramide te berekenen, gebruiken we de formule:

Vpiramide = Agrondvlak x hoogte : 3

Het grondvlak is een gelijkzijdige driehoek, wat betekent dat de 'hoogte' van deze nog uitgerekend moet worden. De hoogte van de driehoek staat loodrecht op één van de zijdes. Vervolgens kun je met de Stelling van Pythagoras de hoogte berekenen, waarmee je de oppervlakte van het grondvlak kunt berekenen, waarmee je de inhoud van de piramide kunt berekenen.

Paragraaf 10.4

In hoofdstuk 2 heb je geleerd hoe je de zijden van figuren kunt vergroten. Weet je nog ? Iets met de originele zijde x de vergrotingsfactor ? In paragraaf 10.4 leer je hoe je oppervlaktes kunt vergroten. Let op ! Dit gaat dus net iets anders dan zijden vergroten...

De onderstaande video geeft uitleg over het berekenen van de vergrotingsfactor bij oppervlakte en het vergroten van oppervlaktes.

Inleveropdracht

Deze opdracht is nog niet beschikbaar

Week 14

Tot nu toe ziet het er naar uit dat dit de laatste week zal zijn dat jullie thuis aan de slag moeten.

Voor deze week staan paragraaf 10.5 en paragraaf 10.6 op het programma. Daarnaast moet je in deze week ook je Daltontaak inleveren. De inleverdatum is 03-04-2020.

Het huiswerk voor deze week:

Paragraaf 10.5: opdracht 32, 33 en 36

Paragraaf 10.6: opdracht 42 en 44

 

Paragraaf 10.5

In deze paragraaf wordt de kennis die je hebt opgedaan in de eerdere paragrafen uit dit hoofdstuk samengevoegd. Je zult meerdere vaardigheden die je hebt geleerd moeten toepassen in één opdracht.

In de onderstaande video wordt aan de hand van een voorbeeld uitgelegd hoe je de inhoud van samengestelde figuren kunt berekenen.

Uitwerkingen

In de foto hieronder staat de uitwerkingen van opdracht 33. In het groen staan de stapjes en in het blauw de uitwerking zelf.

In de foto's hieronder staan de uitwerkingen van opdracht 36. In de ene foto staan de berekeningen en in de andere foto staat een schets van het afgesneden stuk. De zwarte pijl wijst naar hetzelfde afgesneden stuk alleen dan 180graden gedraaid. Het groen gearceerde deel in beide schetsen is het grondvlak van de piramide.

Paragraaf 10.6

Deze paragraaf bevat de gemengde opgaven van dit hoofdstuk.

Uitwerkingen

In de foto hieronder staat de uitwerking van opgave 42. Bij opdracht c zijn er twee opties om tot je antwoord te komen. In het groen staat aangegeven wat de twee opties zijn. De eindantwoorden zijn voor de duidelijkheid onderstreept met rood.

In de foto hiernaast staat de uitwerkingen van opgave 44.

Uitleg PowerPoint H10

Wanneer je op het bestand hieronder klikt, kom je terecht op een PowerPoint, waarin kort de theorie van H10 wordt doorgenomen. Ieder ruimtefiguur dat aanbod komt in het hoofdstuk heeft zijn eigen dia. In deze dia staat de formule van de inhoud en daarbij een uitgewerkt voorbeeld.

Samenvatting H8 en H10

De letters die we in dit hoofdstuk gebruiken zijn:

r           =          Straal

d          =          Diameter

A         =          Oppervlakte

P          =         Omtrek

G         =         Oppervlakte grondvlak

V         =         Inhoud

k          =         Vergrotingsfactor

 

Eventueel kun je ook nog gebruiken:

h          =          Hoogte

l           =          Lengte

b          =          Breedte

Kennen- en Kunnenlijstje

In het zogenoemde Kennen- en Kunnenlijstje staan alle vaardigheden en begrippen die je nodig hebt om de toets van H8 en H10 te kunnen maken. Het is een flinke lijst, maar de lijst is dan ook erg gedetailleerd en uitgebreid, dus schrik vooral niet!

Hoofdstuk 8

Kennen

  • Je kent de verschillende vormen die een driehoek kan aannemen.
    • Scherphoekige-, stomphoekige- en rechthoekige driehoek
  • Je kent de begrippen basis en bijbehorende hoogte en je kunt deze in verschillende driehoeken en parallellogrammen herkennen.
  • Je kent de begrippen diameter, middellijn en straal en kunt deze in eigen woorden omschrijven.
  • Je kent de formules voor het berekenen van de oppervlakte van een driehoek, parallellogram en cirkel.

 

Kunnen

  • Je kunt de oppervlakte van alle soorten driehoeken berekenen.
  • Je kunt de oppervlakte van een parallellogram berekenen.
  • Je kunt de omtrek en de oppervlakte van een cirkel berekenen.
  • Je kunt de oppervlakte van samengestelde figuren berekenen.
  • Je kunt de stelling van Pythagoras toepassen in de bovengenoemde figuren om een ontbrekende zijde te berekenen.
  • Je kunt de diameter van een cirkel berekenen met een gegeven omtrek/oppervlakte.
  • Je kunt de straal van een cirkel berekenen met een gegeven omtrek/oppervlakte.
  • Je kunt de hoogte van een driehoek/parallellogram berekenen m.b.v. de oppervlakte & basis en je kunt de basis berekenen m.b.v. de oppervlakte & hoogte.

 

Hoofdstuk 10

Hoofdstuk 8 is de basis van hoofdstuk 10. Dit houdt in dat je de vaardigheden van hoofdstuk 8 nodig zult hebben om de vaardigheden van hoofdstuk 10 onder de knie te krijgen.

 

Kennen

  • Je kent de ruimtefiguren kubus, balk, cilinder, prisma, piramide en kegel en kunt deze herkennen in een samengesteld ruimtefiguur.
  • Je kent de formules voor de inhoud van de bovengenoemde ruimtefiguren.
  • Je kent de definitie van een prisma en je kunt dit uitleggen in je eigen woorden.
    • Hiermee kun je aantonen of een ruimtefiguur wel/niet een prisma is.
  • Je kent het begrip uitslag van een ruimtefiguur.
  • Je kent het begrip vergrotingsfactor en kunt herkennen uit een verhaaltjessom.

 

Kunnen

  • Je kunt de inhoud van een balk en een cilinder berekenen.
  • Je kunt het grondvlak van een prisma herkennen en hiervan de oppervlakte berekenen.
  • Je kunt de inhoud van een prisma berekenen.
  • Je kunt de inhoud van een piramide en een kegel berekenen.
  • Je kunt de inhoud van een samengesteld ruimtefiguur berekenen.
  • Je kunt de oppervlakte van een kubus, balk, cilinder, prisma en piramide berekenen (eventueel m.b.v. de uitslag van het ruimtefiguur).
  • Je kunt de vergrootte lengte van de zijde van een (ruimte)figuur berekenen met de vergrotingsfactor.
  • Je kunt de vergrootte oppervlakte van een (ruimte)figuur berekenen met de vergrotingsfactor.
  • Je kunt de vergrootte inhoud van een (ruimte)figuur berekenen met de vergrotingsfactor.
  • Je kunt de vergrotingsfactor berekenen m.b.v. originele lengte/oppervlakte/inhoud en de vergrootte lengte/oppervlakte/inhoud.
  • Je kunt de originele lengte/oppervlakte/inhoud berekenen m.b.v. de vergrotingsfactor en de vergrootte lengte/oppervlakte/inhoud.

Als laatst is het de bedoeling dat je de afkortingen kent die we gebruiken voor woorden als inhoud, oppervlakte en straal.

H8

H10

De onderstaande video is een samenvattingsvideo van H10. Hierin worden vooral veel inzichtsvragen behandeld, waardoor het van belang is dat je de vaardigheden van H8 onder de knie hebt, voordat je deze video gaat bekijken en de stappen probeert te volgen.

In de samenvattingsvideo zit geen samengesteld figuur. Daarom heb ik de opdracht van de wcrollen uitgewerkt in een video. Deze video kun je hieronder vinden.

Paragraaf 9.3 & 9.4

Uitlegvideo

Paragraaf 9.5

Uitlegvideo's

Herleiden van een formule

Substitueren

Herhaling H9

Extra PowerPoints

In deze PowerPoint kun je al het huiswerk van hoofdstuk 9 vinden. Daarnaast staat er ook per paragraaf een stappenplan dat je kunt gebruiken bij de bijbehorende theorie. Let op! Soms wordt er in een opgave een extra stap van je verwacht, die niet in het stappenplan staat, zoals haakjes uitwerken of gelijksoortige termen bij elkaar optellen of van elkaar afhalen.

Paragraaf 11.1 & 11.2

Uitlegmateriaal

De bovenstaande PowerPoint is de PowerPoint die ik heb gebruikt tijdens het geven van de wiskunde les over Paragraaf 11.1 en Paragraaf 11.2

Priemgetallen & GGD

Paragraaf 11.3 en 11.4

Uitlegmateriaal

De bovenstaande PowerPoint is de PowerPoint die ik heb gebruikt tijdens het geven van de wiskunde les over Paragraaf 11.3 en Paragraaf 11.4

De onderstaande PowerPoint is de PowerPoint die ik heb gebruikt tijdens het extra uitleg uur. Hierin staan Stappenplannen, die a.d.h.v. voorbeelden opgaven worden toegelicht. Ook staat er een uitwerking van Opgave 25 uit Paragraaf 11.3 in. 

Tijdens het uitleguur zijn Paragraaf 11.2 t/m 11.4 aanbod gekomen.

Oplossen van Kwadratische vergelijkingen

De bovenstaande PowerPoint is de PowerPoint van de les van g2 en de extrauitlegles van a2b.

Paragraaf 11.5

Uitlegmateriaal

Herhaling H11

Uitlegmateriaal

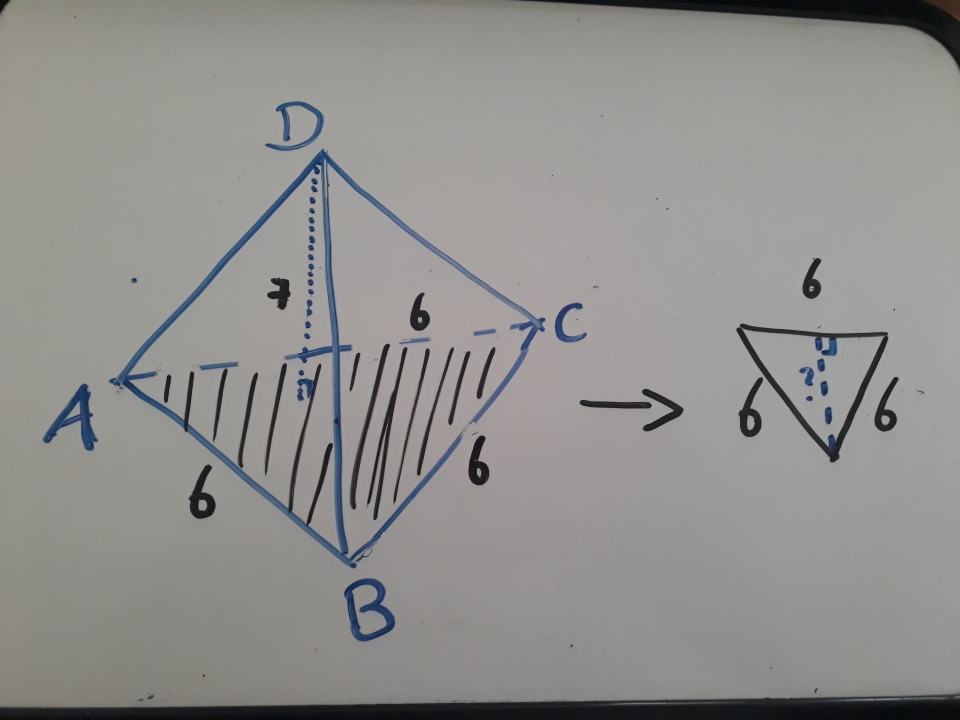
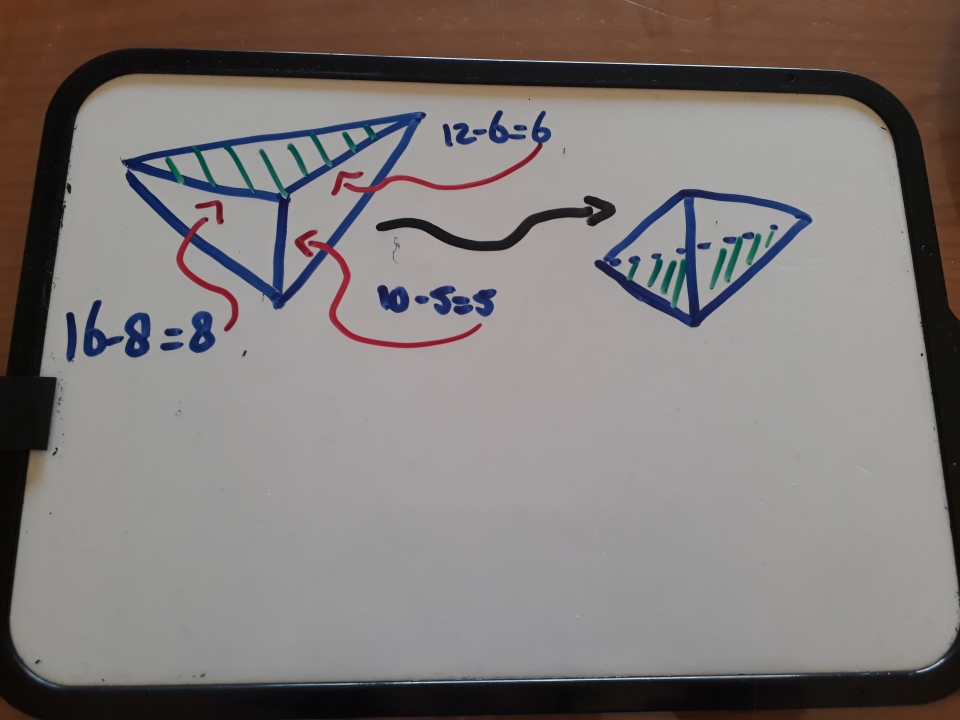
  • Het arrangement Oppervlakte en Inhoud - kopie 1 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.

    Auteur
    Nienke Bos
    Laatst gewijzigd
    15-06-2020 11:53:33
    Licentie

    Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:

    • het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
    • het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
    • voor alle doeleinden, inclusief commerciële doeleinden.

    Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.

    Aanvullende informatie over dit lesmateriaal

    Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:

    Toelichting
    Na het doorwerken van de opdrachten en filmpjes op deze site heb je alle stof doorgenomen van Hoofdstuk 8 en Hoofdstuk 10 van de tweede klas atheneum/gymnasium.
    Leerniveau
    VWO 2;
    Leerinhoud en doelen
    Rekenen/wiskunde; Vormen en figuren; Meten en meetkunde; Vlakke en ruimtelijke figuren herkennen;
    Eindgebruiker
    leerling/student
    Moeilijkheidsgraad
    gemiddeld

    Bronnen

    Bron Type
    Creëren van een link in Geogebra
    https://www.youtube.com/watch?v=bwHv7Ap37nQ&t=25s     		Video
    https://www.youtube.com/watch?v=WA2oj1gx7vs
    https://www.youtube.com/watch?v=WA2oj1gx7vs     		Video
    https://www.youtube.com/watch?v=AR5BKP-xa4c
    https://www.youtube.com/watch?v=AR5BKP-xa4c     		Video
    https://www.youtube.com/watch?v=1OK2MulTT_w
    https://www.youtube.com/watch?v=1OK2MulTT_w     		Video
    https://www.youtube.com/watch?v=1OK2MulTT_w
    https://www.youtube.com/watch?v=1OK2MulTT_w     		Video
    https://www.youtube.com/watch?v=BZOrd73KFBg
    https://www.youtube.com/watch?v=BZOrd73KFBg     		Video
    https://www.youtube.com/watch?v=YaTaNJg7Vy0
    https://www.youtube.com/watch?v=YaTaNJg7Vy0     		Video
    https://www.youtube.com/watch?v=O8PMzZ3mXxs
    https://www.youtube.com/watch?v=O8PMzZ3mXxs     		Video
    https://www.youtube.com/watch?v=XZUR0OwtPyQ
    https://www.youtube.com/watch?v=XZUR0OwtPyQ     		Video
    https://www.youtube.com/watch?v=HWQqjqvC1gI
    https://www.youtube.com/watch?v=HWQqjqvC1gI     		Video
    https://www.youtube.com/watch?v=eWIq3FLUodc&feature=youtu.be
    https://www.youtube.com/watch?v=eWIq3FLUodc&feature=youtu.be     		Video
    https://www.youtube.com/watch?v=dObb4Iu360I
    https://www.youtube.com/watch?v=dObb4Iu360I     		Video
    https://www.youtube.com/watch?v=ZsYIrK4Rj5Y
    https://www.youtube.com/watch?v=ZsYIrK4Rj5Y     		Video
    https://www.youtube.com/watch?v=98pNI5sFWa0
    https://www.youtube.com/watch?v=98pNI5sFWa0     		Video
    Priemgetallen & GGD
    https://youtu.be/Q06ro4u8NHA     		Video
    Oplossen van Kwadratische vergelijkingen
    https://youtu.be/7uwKL0q0YN8     		Video

    Gebruikte Wikiwijs Arrangementen

    Bos, Nienke. (2020).

    Oppervlakte en Inhoud

    https://maken.wikiwijs.nl/158776/Oppervlakte_en_Inhoud

  • Downloaden

    Het volledige arrangement is in de onderstaande formaten te downloaden.

    Metadata

    LTI

    Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI koppeling aan te gaan.

    Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.

    Arrangement

    IMSCC package

    Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.

    Voor developers

    Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op onze Developers Wiki.

  • Wikiwijs is een dienst van