In deze interactieve module leer je hoe te werken met binaire getallen en hoe hexadecimale getallen omgezet worden naar een decimaal getal en omgekeerd.
Vervolgens worden de logische operaties behandeld en leer je daarmee eenvoudige schakelingen te maken.
In het binair talstelsel is net als in het decimale talstelsel de positie van het cijfer bepalend voor de waarde van het cijfer in het getal.
Het verschil tussen beide talstelsels is dat in het binaire talstelsel een getal wordt voorgesteld door een rijtje van twee verschillende symbolen, 0 en 1, terwijl in het decimale talstelsel 10 symbolen gebruikt worden:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Leerdoelen
Na verwerking van deze interactieve module kun je:
getallen van het binaire stelsel naar het decimaal stelsel omzetten;
getallen van het decimaal stelsel naar het binaire stelsel omzetten;
rekenen met binaire getallen;
getallen van het hexadecimaal stelsel naar het decimaal stelsel omzetten;
getallen van het decimaal stelsel naar het hexadecimaal stelsel omzetten;
de functie uitleggen van de logische poorten AND, OR, NOT en XOR;
de waarheidstabellen bij logische poorten invullen;
de waarheidstabel van een eenvoudige schakeling invullen;
de werking van een vergelijker uitleggen;
de werking van een éénbits opteller (half adder) uitleggen;
de werking van een full adder uitleggen;
een tweebits opteller bouwen.
Zo werkt het
Je bent begonnen in de module Elementaire bewerkingen.
Naast een inleiding bestaat de module uit vier onderdelen: “Binaire getallen”, “Hexadecimaal”, “Logische operaties” en “Chips”. In ieder onderdeel vind je, verdeeld over verschillende pagina's, informatie in de vorm van teksten, afbeeldingen en video's.
Daarnaast ga je zelf aan de slag. Onder het kopje "Aan de slag" vind je steeds toepassingsopdrachten. Deze opdrachten maak je alleen of met een klasgenoot.
De antwoorden op deze opdrachten bespreek je met elkaar of in de klas.
Er zijn ook toetsen. Deze herken je aan de blauwe knop met daarop "Adaptieve Toets".
Een toets bestaat uit meerdere vragen. Dat kunnen gesloten vragen zijn, die door de computer worden nagekeken, of open vragen, die moet je zelf nakijken.
Bij een enkele vraag moet je een bestand uploaden.
Van de toetsen wordt, als je ingelogd bent, de voortgang bijgehouden.
Het resultaat vind je onder de knop "Voortgang". Deze voortgang is ook door je docent te bekijken.
Succes met de module Elementaire bewerkingen.
Bijlagen
De bijlagen bij deze module vindt u in dit zip-bestand:
In het decimale stelsel is de positie van het cijfer bepalend voor de waarde.
Het decimale stelsel is gebaseerd op machten van 10. In het getal 514 heeft het cijfer 4 de waarde 4, het cijfer 1 de waarde 10 en het cijfer 5 de waarde 500.
Anders gezegd:
Het binaire stelsel is gebaseerd op machten van 2.
Ook in dit stelsel is de positie van het cijfer bepalend voor de waarde.
Bekijk de animatie om te zien hoe je een binair getal kunt omzetten naar een decimaal getal:
Decimaal > binair
Om een decimaal getal om te zetten naar een binair getal deel je het getal door 2 en noteer je de rest van de deling.
Dit herhaal je totdat de uitkomst gelijk is aan 0.
Bekijk de afbeelding.
Je schrijft de bewerking van rechts naar links.
Het resultaat lees je van links naar rechts: decimaal 29 is binair 11101.
Bekijk de animatie om te zien hoe je een decimaal getal kunt omzetten naar een binair getal:
Toets 1
In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp Elementaire bewerkingen.
Klik op de link en maak de toets.
Van binair naar decimaal
Optellen
Als je de getallen 29 en 57 bij elkaar optelt, schrijf je de getallen eerst onder elkaar op. Dan tel je eerst de eenheden, 9 en 7, op. De som van 9 en 7 is 16, ofwel 6 eenheden en 1 tiental. De 6 schrijf je op. Het tiental moet je 'onthouden'; de 1 wordt bij de tientallen opgeteld: 2 + 5 + 1 = 8 tientallen. De uitkomst is dus 86.
Optellen in het binaire stelsel gaat eigenlijk hetzelfde. Je telt eerst de eenheden op, dan de tweetallen, dan de viertallen, enzovoorts. In de animatie en afbeelding zie je hoe je de binaire getallen 11101 en 111001 optelt:
Aftrekken
Aftrekken van binaire getallen gaat op dezelfde manier als optellen:
In de laatste twee gevallen moet je bij een hogere macht lenen.
Andere bewerkingen
Vermenigvuldigen en delen
Het vermenigvuldigen en delen van binaire getallen gaat op dezelfde manier als bij decimale getallen.
Bekijk de twee animaties:
Toets 2
In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp Elementaire bewerkingen.
Optellen, aftrekken, vermenigvuldigen en delen
Negatieve getallen VWO
Het eindresultaat van een aftrekking kan negatief zijn. Je zou dan tot in de eeuwigheid moeten blijven lenen. Eigenlijk hebben negatieve binaire getallen oneindig veel 'voorloop-enen', zoals positieve getallen oneindig veel 'voorloop-nullen'hebben. Dit heeft geleid tot een afspraak die bekend staat als de complementmethode.
Het meest linkse bit van een bitrij is daarbij een soort tekenbit. Is het meest linkse bit een 1, dan is het getal negatief. Positieve getallen hebben een 0 als meest linkse bit.
In de tekst hieronder zie je welke acht getallen je met de complementmethode kunt maken als je drie bits gebruikt. Je ziet dat het anders werkt dan met het minteken dat we bij decimale getallen gebruiken. Hieronder zie je uitgelegd hoe je van -13 een binair getal maakt.
Schrijf eerst 13 als binair getal. Vergeet het tekenbit niet: 01101
Verander iedere 0 in een 1 en iedere 1 in een 0: 10010
Tel bij het resultaat 1 op: 10011
Oefening 1
De volgende oefening gaat over het omzetten van negatieve getallen naar binaire getallen.
Negatieve getallen
C Hexadecimaal
Inleiding
Je hebt geleerd hoe je getallen kunt omzetten van het binaire stelsel naar het decimale stelsel en omgekeerd.
Op dezelfde manier kun je ook getallen in andere talstelsels schrijven.
Een ander talstelsel dat veel gebruikt wordt in bijvoorbeeld HTML-code en tekenprogramma's is het hexadecimaal stelsel (het zestientallig stelsel).
Ook in het hexadecimaal stelsel is de positie van het cijfer bepalend voor de waarde van het cijfer in het getal.
Je hebt natuurlijk 16 verschillende symbolen nodig om de getallen te noteren.
Daarvoor worden de cijfers 0 tot en met 9 en de letters A tot en met F gebruikt.
Hexadecimaal > decimaal
Het hexadecimaal stelsel is gebaseerd op machten van 16.
Bekijk in de animatie hoe je een hexadecimaal getal omzet naar een decimaal getal:
Decimaal > hexadecimaal
Om een decimaal getal om te zetten naar een hexadecimaal getal deel je het getal door 16 en noteer je de rest van de deling.
Dit herhaal je totdat de uitkomst gelijk is aan 0.
Je schrijft de bewerking van rechts naar links.
Het resultaat lees je van links naar rechts: decimaal 178 is hexadecimaal B2.
Toets 3
In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp Elementaire bewerkingen.
Hexadecimaal decimaal
D Logische operaties
Inleiding
Je hebt gezien dat een computer in het binair stelsel rekent. Je kunt je afvragen hoe dit gaat. In een computer wordt gebruik gemaakt van digitale schakelaars, waarin maar twee waarden kunnen voorkomen: de 0 en 1. Een digitale schakelaar kan zo de waarde van een bit vastleggen. Deze schakelaars heten transistoren en daarvan zitten er miljoenen op een chip.
Om de werking duidelijk te maken kun je kijken hoe je een lamp met behulp van gewone schakelaars aan en uit kunt zetten. Zowel de lamp als de schakelaars stellen een bit voor.
De AND-poort
Je ziet in de popup een schakeling met twee schakelaars en een lampje. Als de schakelaars in positie 0 staan, brandt de lamp niet. Alleen als de schakelaars A én B in positie 1 staan, gaat de lamp branden.
Probeer maar. Klik in de afbeelding in de popup en kijk wanneer de lamp brandt.
Kijk ook naar alle mogelijke varianten in wat ook wel een waarheidstabel wordt genoemd.
Deze schakeling wordt een AND-poort genoemd.
Een AND-poort wordt weergegeven met het symbool:
Je ziet in de popup een schakeling met twee schakelaars en een lampje. Als de schakelaars in positie 0 staan, brandt de lamp niet. Als alleen schakelaar A aan wordt gezet, gaat het lampje branden.
Ook als alleen schakelaar B aan wordt gezet gaat het lampje branden. Ook als beide schakelaars aan staan, brandt het lampje.
Probeer maar.
Kijk ook naar alle mogelijke varianten in de tabel. Deze schakeling wordt een OR-poort genoemd. Een OR-poort wordt weergegeven met het symbool:
De XOR-poort
Je ziet in de popup een schakeling met twee schakelaars en een lampje.
Als beide schakelaars in positie 0 staat, brandt de lamp niet.
Staan beide schakelaars in positie 1 dan brandt de lamp ook niet.
De lamp brandt alleen als schakelaars in verschillende posities staan.
Probeer maar. Kijk ook naar de getallen in de waarheidstabel.
Deze schakeling wordt een XOR-poort genoemd.
Een XOR-poort wordt weergegeven met het symbool:
De NOT-poort
Je ziet een schakeling met een schakelaar en een lampje. Als de schakelaar in positie 0 staat, brandt de lamp. Staat de schakelaar in positie 1 dan brandt de lamp niet.
De stand van de schakelaar is dus omgekeerd aan de toetstand van de lamp.
Probeer maar.
Kijk ook naar de getallen in de waarheidstabel.
Deze schakeling wordt een NOT-poort of Inverter (keert de invoer om) genoemd.
Een NOT-poort wordt weergegeven met het symbool:
Inverters
In de tot nu toe behandelde poorten is alleen de NOT-poort een voorbeeld van een zogenaamde inverter. Een inverter keert de ingevoerde waarde telkens om. Bij de NOT- poort wordt de ingevoerde waarde 0 omgekeerd in de waarde 1. Een invoer van de waarde 1 levert als uitvoer de waarde 0 op. Je herkent een inverter aan het ronde open cirkeltje in het gebruikte symbool voor de poort.
Voorbeelden van andere inverters zijn de NAND-poort, de NOR-poort en de NXOR-poort.
Bekijk de volgende video.
Toets 4
In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp Elementaire bewerkingen.
Logische operaties
E Chips
Inleiding
In de praktijk kom je geen losse poorten tegen, maar zijn ze geintegreerd in een chip. Chips of IC's (geintegreerde circuits) bestaan uit een stukje silicium waarop enkele poorten zijn aangebracht. Ze worden gemonteerd in een plastic of keramische behuizing. Langs de rand bevinden zich rijen pinnen, waarmee de chip wordt bevestigd op een printkaart.
Ga over de verschillende poorten heen voor een toelichting.
Chips worden in vier klassen ingedeeld:
SSI-chips (Small Scale Integrated):
1 tot 10 poorten
MSI-chips (Medium Scale Integrated):
10 tot 100 poorten
LSI-chips (Large Scale Integrated):
100 tot 100.000 poorten
VLSI-chips (Very Large Scale Integrated):
meer dan 100.000 poorten
We gaan het ontwerp van twee relatief eenvoudige chips bekijken: de vergelijker uit het voorbeeld en de opteller.
★ Aan de slag 1
Lees de bijlage werken met MMLogic .
Maak de schakeling van de vergelijker hieronder na in MMLogic en controleer of die goed werkt.
★ Aan de slag 2
Maak de schakeling van de vergelijker hieronder in MMLocig en controleer of ze correct werkt. Een NOR-poort met vier ingangen maak je door de Properties van een OR-poort te wijzigen.
De opteller
Met behulp van deze logische schakelingen kun je een eenvoudige 'opteller' bouwen. Kijk eerst naar het optellen van 1 bits getallen:
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Je kunt deze bewerkingen ook in een tabel zetten:
A
B
2-tallen
eenheden
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
Wanneer je de uitkomst vergelijkt met de waarheidstabellen van de verschillende poorten, dan zie je dat de eenheden worden bepaald door een XOR-poort en dat de tweetallen worden bepaald door een AND-poort.
Met behulp van één XOR-poort en één AND-poort kun je de rekenmachine bouwen voor het optellen van 1 bits getallen.
Deze schakeling wordt een half adder (adder=opteller) genoemd.
Ga over de verschillende poorten heen voor een toelichting.
Met een half adder kun je alleen twee 1-bits getallen bij elkaar optellen.
In de praktijk wil je grotere getallen kunnen optellen. In dat geval heb je het probleem van de overdracht.
Met een full adder, die bestaat uit twee half adders achter elkaar en een extra OR-poort kun je de tweetallen plus de overdracht optellen.
★ Aan de slag 3
Maak de schakeling van de half adder hieronder met MMLogic en test de schakeling aan de hand van de tabel.
★ Aan de slag 4
Maak de schakeling van de full adder met MMLogic en controleer of alles werkt.
★ Aan de slag 5
Ontwerp en maak een schakeling voor een drie-bits opteller.
Sla het bestand in MMLogic op als driebitsopteller.lgi
Controleer of alles werkt.
Open in MMLogic de schakeling van de drie-bits opteller die je hebt gemaakt en al eerder hebt moeten inleveren.
Vervang de switches door twee hexadecimale keypads.
Gebruik twee 7 segment LED’s om de invoerwaardes te tonen.
Vervang de vier LED’s voor de uitvoer door een 7 segment LED.
Controleer of alles werkt.
Oefening 2
De volgende oefening gaat over twee-bits en drie-bits optellers.
Maak de oefening.
2 en 3 bits optellers
Projectopdracht
Download de projectopdracht .
Sluit de module af met dit project.
Voortgang
Bekijk hier je voortgang
Kernprogramma
Docent kan groepen aanmaken en leerlingen volgen
Een docent kan op de profielpagina groepen aanmaken. Als een docent dat gedaan heeft, kunnen de leerlingen zich aan de groep koppelen. Als de leerlingen dat gedaan hebben, kan de docent de voortgang van de leerlingen volgen.
Om toegang te krijgen tot Portfolio-site, log je in bij Mijn VO-content en klik je op Entree.
Log in met je SCHOOLACCOUNT
Profielpagina
Als je ingelogd bent, vul je profielpagina verder in. Je kunt de niveaus aanklikken (waar je lesmateriaal van wilt zien voor de andere programma's) en ook de vakken. De profielpagina werkt voor alle Extra Programma's van VO-content.
Je kunt deze keuzes achteraf ook altijd aanpassen.
Let op: verifieer je e-mailadres na de eerste keer inloggen. Als je dat gedaan hebt kan je bij een storing van de ELO of Entree alsnog met je e-mailadres inloggen.
Het arrangement Module: Enigma - Elementaire bewerkingen is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Het thema 'Elementaire bewerkingen' is ontwikkeld door auteurs en medewerkers van Enigma-online.
Fair Use
In de modules van Enigma-online wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
Deze module is onderdeel van de arrangeerbare leerlijn van de Stercollecties voor het keuzedeel van Informatica voor hv456. In deze interactieve module leer je hoe te werken met binaire getallen en hoe hexadecimale getallen omgezet worden naar een decimaal getal en omgekeerd. Vervolgens worden de logische operaties behandeld en leer je daarmee eenvoudige schakelingen te maken.
In ieder onderdeel vind je, verdeeld over verschillende pagina's, informatie in de vorm van teksten, afbeeldingen en video's. Daarnaast ga je zelf aan de slag met toepassingsopdrachten en toetsen. Van de toetsen wordt je voortgang bijgehouden en deze voortgang zal zowel door jou als je docent te bekijken zijn. Veel succes!
Deze module is onderdeel van de arrangeerbare leerlijn van de Stercollecties voor het keuzedeel van Informatica voor hv456. In deze interactieve module leer je hoe te werken met binaire getallen en hoe hexadecimale getallen omgezet worden naar een decimaal getal en omgekeerd. Vervolgens worden de logische operaties behandeld en leer je daarmee eenvoudige schakelingen te maken.
In ieder onderdeel vind je, verdeeld over verschillende pagina's, informatie in de vorm van teksten, afbeeldingen en video's. Daarnaast ga je zelf aan de slag met toepassingsopdrachten en toetsen. Van de toetsen wordt je voortgang bijgehouden en deze voortgang zal zowel door jou als je docent te bekijken zijn. Veel succes!
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
De bijlagen bij deze module vindt u in dit zip-bestand:
In het decimale stelsel is de positie van het cijfer bepalend voor de waarde.
Om een decimaal getal om te zetten naar een binair getal deel je het getal door 2 en noteer je de rest van de deling.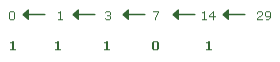
In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp Elementaire bewerkingen.
Als je de getallen 29 en 57 bij elkaar optelt, schrijf je de getallen eerst onder elkaar op. Dan tel je eerst de eenheden, 9 en 7, op. De som van 9 en 7 is 16, ofwel 6 eenheden en 1 tiental. De 6 schrijf je op. Het tiental moet je 'onthouden'; de 1 wordt bij de tientallen opgeteld: 2 + 5 + 1 = 8 tientallen. De uitkomst is dus 86.
Aftrekken van binaire getallen gaat op dezelfde manier als optellen: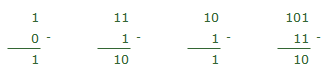
Vermenigvuldigen en delen
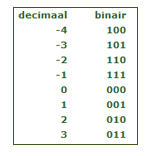
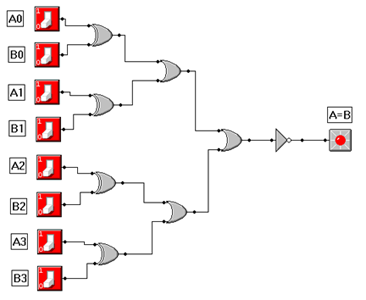
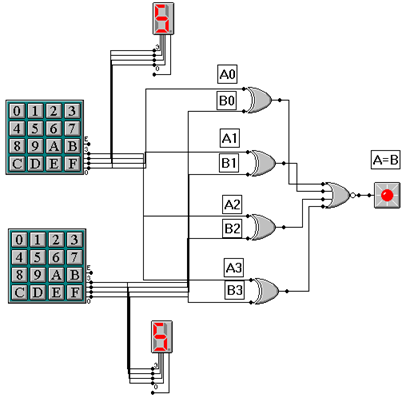
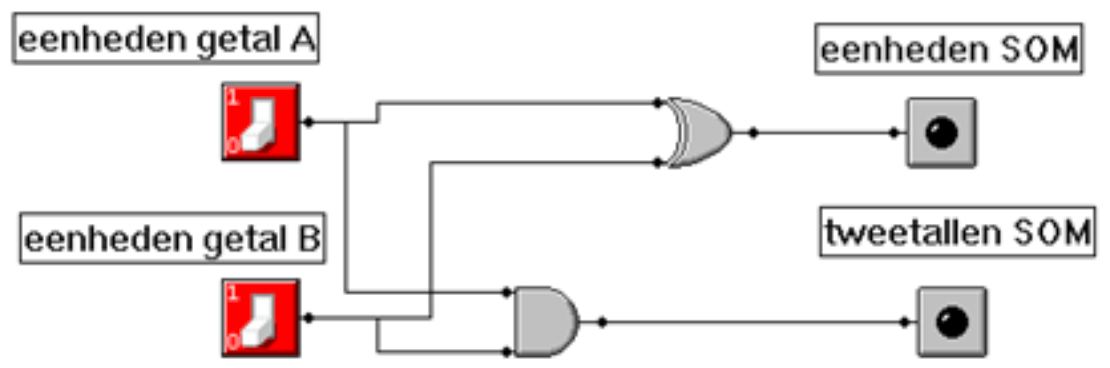
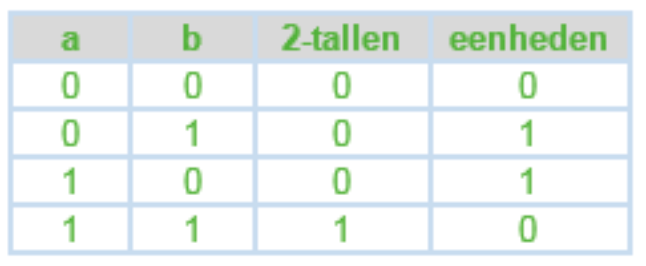
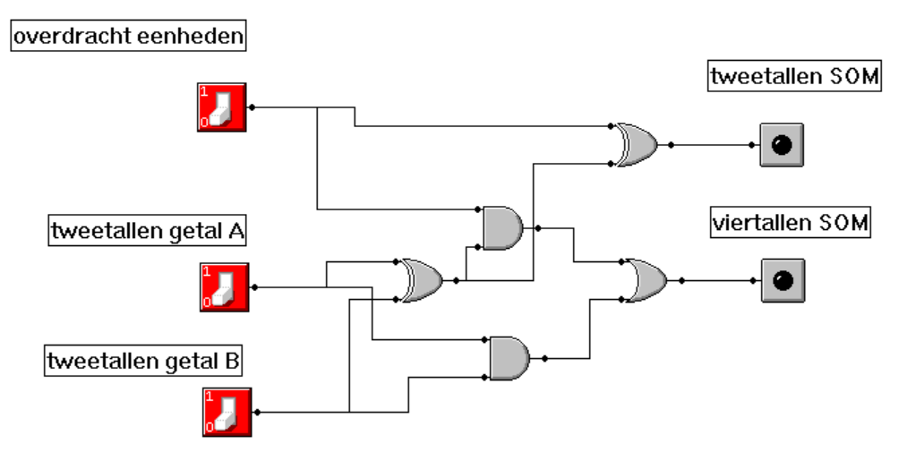
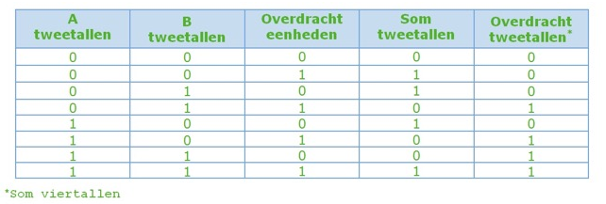
Ontwerp en maak een schakeling voor een drie-bits opteller.
Download de 
Bekijk hier je voortgang
