Vandaag gaan we beginnen aan het onderdeel Algebra.
Algebra is het deel van de wiskunde dat zich bezig houdt met formules, letters en rekenregels.
Binnen het VMBO-KGT is dit het grootste onderwerp. Dat wil zeggen dat je dit onderwerp meerdere keren per jaar terug komt.
Dit jaar heb je al iets geleerd over voorrangregels, het tekenen van een tabel en het tekenen van een grafiek.
In dit hoofdstuk leer je wat een verband is (werken met formules). We maken kennis met het lineaire verband, hier speelt regelmaat een belangrijke rol bij.
De komende jaren ga je allerlei verschillende verbanden leren herkennen.
Lineair verband
Kwadratisch verband
Machtsverband
Wortelverband
Exponentiël verband.
Periodiek verband.
Omgekeerd evenredig verband.
In dit hoofdstuk leggen we de basis voor je kennis over de algebra. Een belangrijk hoofdstuk dus.
Houdt je werk daarom extra goed bij. Kijk je werk goed na en kom je er nadat je het eerst zelf hebt geprobeerd of hulp hebt gevraagd bij een klasgenootje echt niet uit? Stel dan vragen in de les!
Veel succes!
Leerdoelen
Aan het eind van dit hoofdstuk kan ik:
Werkbladen
§1 Voorkennis
Uitleg & opgaven
Inleiding.
In de voorkennis herhalen we de vaardigheden en kennis die we in voorgaande hoofdstukken of jaren hebben opgedaan. Deze vaardigheden en kennis zijn voor het maken van dit hoofdstuk essentieel.
Kijk je werk dus goed na en stel vast welke onderdelen goed gaan en met welke onderdelen je nog moeite hebt. Succes!
Voorrangregels
Moet je een berekeningen maken waar verschillende rekentekens (bewerkingen +, -, :, x , ...−−√... en ...2) in worden gebruikt? Houd dan rekening met de voorrangsregel. Dit houdt in dat je de opgave niet zomaar in volgorde van links naar rechts moet uitrekenen. Sommige bewerkingen moet je namelijk eerder uitrekenen en hebben dus voorrang. Denk maar aan het verkeer. Hier moet je ook de regels goed toepassen, anders vallen er ongelukken.
En vergeet niet, zie je het woordje bereken staan, dan moet je de volledige berekening opschrijven. Alleen een antwoord is dan niet genoeg.
Volgorde van bewerkingen
1. Bereken eerst wat tussen haakjes staat.
(ook binnen haakjes voorrangregels toepassen)
2. Bereken de machten en wortels
(van links naar rechts!)
3. Bereken keer en delen
(van links naar rechts!)
4. Als laatste optellen en eraf.
(van links naar rechts!)
Voorbeeld:
2 x ( 8 + 2 ) - 32 = Eerst tussen haakjes uitrekenen.
2 x 10 - 32 = kwadraten en wortels berekenen.
2 x 10 - 9 = keer en delen.
20 - 9 = 11 plus en min.
Je ziet ook hoe we een bewerking met voorrangregels uitschrijven. Onderstreep het deel dat je uitrekent, zet onder dat deel de uitkomst en ga daarna verder met de volgende bewerking.
In het filmpje hiernaast wordt het allemaal nog eens stapje voor stapje voorgedaan.
Doe hier je voordeel mee. Kijk, zet stop en probeer. Kijk opnieuw, zet eens op pauze en spoel terug. Op deze manier leer jij jezelf deze techniek aan.
..1.
Voorrang regels toepassen 1
Bereken, schrijf dus netjes de hele berekening op.
a 9 - 2 + 7 =
b 4 + 2 - 10 =
c 5 - -7 + - 8 =
d -3 - 5 - - 6 + 2 + - 4 =
..2.
Voorrang regels toepassen 2
Bereken, schrijf dus netjes de hele berekening op
a 6 × 3 : 3 =
b 16 : 4 × 2 =
c -16 : -2 × -4 =
d -12 × 4 : -3 =
..3.
Voorrang regels toepassen 3
Bereken. Schrijf de tussenstappen op!
a 25 + 4 × -4 - -18 : -9 =
b (15 : -3 + -24 : 8) × -3 + -6 =
c 15 : -5 × 16 : -8 + -6 × -3 : -2 =
..4.
Voorrangregels met wortels en kwadraten
Bereken.
2 + 32 - 6 =
3 x 2 + -32 =
3 + 49−−\(\sqrt{49} \) x - 2 =
42 - 81−−\(\sqrt{81} \) - 10 =
..5.
Verhaaltjes opgave
Bereken, schrijf dus ook netjes de berekening op die je gebruikt.
a.
Samantha is jarig geweest. Van haar broer heeft zij 2 briefjes van €10,- gekregen. Van haar ouders een briefje van €50,- en aan het eind van zijn feestje heeft zij 5 keer een munt van €2,- , 3 briefjes van € 5,- en een briefje van €10,- . Bereken het totaal bedrag dat Samantha tijdens haar verjaardag heeft gekregen.
b.
Nina denkt aan het getal 7, ze telt er 4 bij op en daarna doet ze het antwoord keer 2, dan haalt ze er 4 vanaf en en tot slot deelt ze het door 6.
Noteer de berekening die bij deze opgave hoort, denk aan de voorrangregels dus gebruik haakjes. Los daarna de opgave op.
Uitleg.
Grafieken tekenen.
Overbodig om natuurlijk te zeggen, maar tekenen doen we met potlood en rechte lijnen tekenen we met behulp van een geodriehoek.
Zo nu we de eerste afspraak hebben herhaalt kunnen we verder met het herhalen van onze vaardigheden en kennis.
Het tekenen van een grafiek is een vaardigheid, je kunt het dus niet uit je hoofd leren. Je leert dit door te doen, te proberen en als je het fout doet het opnieuw te proberen. Denk maar aan het trainen voor een sport. Behalve de spelregels moet je vooral veel oefenen en doen.
Een grafiek is een erg mooie manier om een "plaatje" te maken van een tabel met getallen. In de uitleg hieronder vind je hier een goed voorbeeld van.
Goed om te onthouden:
Zet bij de assen van je grafiek altijd waar het over gaat;
Gaat het in het verhaaltje over het aantal gegooide ballen en het aantal punten, zet dat dan bij de juiste as, gaat het over het aantal bezoekers en de inkomsten? Zet dat dan bij de assen. Heb je geen idee waar het overgaat? Dan zetten we de woordjes x-as en y-as bij de assen.
Een scheurlijntje gebruik je alleen als de eerste stap groter is dan de rest!
We kunnen het niet vaak genoeg zeggen: Teken met potlood, ja ook de lijntjes van je assen moeten dus met potlood!
Op de assen maak je gelijke stapjes: Kijk hieronder maar eens naar de 4 voorbeelden.
..6.
Grafiek tekenen bij de tabel
Teken de grafiek bij onderstaande tabel hoort in je schrift.
Denk er aan, teken met potlood, rechte lijnen met een geodriehoek en zet bij de assen de juiste woordjes neer.
Lukt het niet, begrijp je het niet? kijk dan even naar het filmpje
..7.
Grafiek bij tabel
Teken de grafiek bij onderstaande tabel hoort op het werkblad.
Denk er aan; teken met potlood, rechte lijnen met een geodriehoek en zet bij de assen de juiste woordjes neer.
..8.
Grafiek tekenen bij de tabel
Teken de grafiek bij onderstaande tabel hoort in je schrift.
Denk er aan, teken met potlood, rechte lijnen met een geodriehoek en zet bij de assen de juiste woordjes neer.
..9.
Kies de juiste grafiek
Bekijk de afbeelding hieronder.
Welke grafiek past bij de tabel, je hoeft alleen de letter te noteren.
..10.
Zoek de fout in de grafiek.
Hieronder zie je een grafiek staan.
Er is een foutje gemaakt met het tekenen van de grafiek.
Noteer de fout in je schrift.
..11.
Zoek de fout
Hieronder zie je een grafiek staan.
Er is een foutje gemaakt met het tekenen van de grafiek.
Noteer de fout in je schrift.
Antwoorden
Let op! Schrijf altijd je volledige berekening op. Aan alleen een antwoord worden geen punten toegekend. Heb je alleen je antwoorden opgeschreven dan is je huiswerk niet af!
..1.
a.9 - 2 + 7 = b.4 + 2 - 10 =
7 + 7 = 14 6 - 10 = - 4
Zie je een + - of - - achter elkaar, vervang ze dan!
+ - wordt - en - - wordt +
c. 5 - -7 + - 8 = d. -3 - 5 - - 6 + 2 + - 4 =
5 + 7 - 8 = -3 - 5 + 6 + 2 - 4 =
12 - 8 = 4 - 8 + 6 + 2 - 4 =
- 2 + 2 - 4 =
0 - 4 = - 4
..2.
Denk aan de regels voor keer en delen!
Neg : Neg = pos - x - = +
Pos x neg = neg + x - = -
Neg x pos = neg - x + = -
Pos : pos = pos + : + = +
a 6 × 3 : 3 =
c-16 : -2 × -4 =
18 : 3 = 6
8 x - 4 = - 32
b16 : 4 × 2 =
d -12 × 4 : -3 =
4 x 2 = 8
- 3 : - 3 = 1
..3.
a 25 + 4 × -4 - -18 : -9 =
25 + 4 × -4 + 18 : -9 =
25 - 16 + 18 : -9 =
25 - 16 - 2 =
9 - 2 = 7
b (15 : -3 + - 24 : 8) × -3 + - 6 =
(15 : -3 - 24 : 8) × -3 - 6 =
( - 5 - 24 : 8) × -3 - 6 =
(- 5 - 3) × -3 - 6 =
-8 × -3 - 6 =
24 - 6 = 18
c 15 : -5 × 16 : -8 + - 6 × -3 : -2 =
15 : -5 × 16 : -8 - 6 × -3 : -2 =
-3 × 16 : -8 - 6 × -3 : -2 =
-48 : -8 - 6 × -3 : -2 =
6 - 6 x - 3 : -2 =
6 + 18 : - 2 =
6 - 9 = - 3
Vanaf hier volgen alleen antwoorden. Let op, je schrijft altijd de volledige berekening in je schrift. Zonder berekening is je huiswerk niet af!
..4.
a. 2 + 32 - 6 = 5
b. 3 x 2 + -32 = -3
c. 3 + 49 −−√49 x - 2 = 38
d. 42 - 81 −−√81 - 10 = - 66
..5.
2 x 10 + 50 + 5 x 2 + 3 x 5 + 10 =
20 + 50 + 5 x 2 + 3 x 5 + 10 =
20 + 50 + 10 + 3 x 5 + 10 =
20 + 50 + 10 + 15 + 10 =
70 + 10 + 15 + 10 =
80 + 15 + 10 =
95 + 10 = 105
((7 + 4) x 2 - 4) - 6 =
( 11 x 2 - 4) - 6 =
( 22 - 4) - 6 =
18 - 6 = 12
..6.
..7.
..8.
..9.
De tabel hoort bij grafiek B
(Bij grafiek A is het scheurlijntje fout, er is een getal onder 40 dus kan het scheurlijntje dan niet)
(Bij grafiek C kloppen de punten niet, het laagste punt is op de x-as bij 4, en niet bij 3)
..10.
De getallen bij de x-as staan midden in de hokjes, zo is het niet goed afleesbaar
..11.
De woordjes van de x-as staan er niet bij.
Op de x-as zijn de stapjes niet allemaal even groot!
§2 Regelmaat
Uitleg & Opgaven
Inleiding.
Hoe sneller je fietst, hoe eerder je thuis bent.
Hoe langer een kaars brand, hoe korter de kaars wordt.
Allerlei situaties die je vast wel kent. De ene actie heeft gevolgen voor de uitkomst. Het ene heeft verband met het andere. Wanneer we praten over een verband hebben we het dus over een oorzaak -> gevolg reactie.
Deze verbanden hebben te maken met twee variabele. Variabele kun je het beste voorstellen als grootheden en eenheden. Later zeggen we ook wel eens dat variabele de woordjes of letters in je formule zijn. Met deze woordjes of letter bedoelen we altijd grootheden/eenheden.
Voorbeeld: Hoe langer een kaars brand, hoe korter de kaars wordt.
Hier heeft de brandtijd van de kaars iets te maken met de lengte. De variabele zijn dus de brandtijd en de lengte.
Hoe sneller je fietst, hoe eerder je thuis bent.
Hier heeft je snelheid iets te maken met de tijd die je er over doet. De variabele zijn dus snelheid en tijd.
..1.
Hoe-hoe zinnen.
Bij een verband kun je vaak een ‘Hoe-hoe-zin’ maken.
Vul in:
‘Hoe langer je loopt, hoe …………………… de afstand die je hebt aflegt.’
‘Hoe verder je reist met de trein, hoe …………………… je betaalt.
..2.
Hoe-hoe zinnen bedenken
Bedenk zelf eens drie hoe-hoe zinnen. Dus:
Hoe later ik op sta, hoe ...
Hoe ..
..3.
Variabele in een hoe-hoe zin.
Zinnen zoals hieronder kom je bijna dagelijks tegen.
Hoe meer uur je werkt, hoe meer je verdient.
Hoe langer je slaapt, hoe beter je bent uitgerust.
Hoe langer je fietst, hoe dichter je bij huis komt.
Hoe meer uur je televisie kijkt, hoe minder uur je aan je huiswerk kunt besteden.
Elk van deze zinnen geeft een verband tussen twee variabelen weer.
Schrijf telkens de twee variabelen op.
Uitleg.
Regelmaat.
Een eenvoudig te herkennen verband is een verband waarbij we spreken over regelmaat. Regelmaat is een vorm van herhaling. Er gebeurt telkens precies hetzelfde. Bijvoorbeeld
In de kast liggen kaarsen. De kaarsen zijn 32 cm lang. Op de verpakking staat dat elk uur dat een kaars brand deze 4 cm korter wordt.
De variabele in dit voorbeeld zijn: De lengte van de kaars en de brandtijd
De regelmaat in dit voorbeeld herken je vast snel. Elk uur 4 cm korter. Dit stukje herhaalt zich tot de kaars op is.
En het getal 32? Dat is het begingetal, zo lang was de kaars aan het begin.
..4.
Regelmaat in situaties
Noteer van onderstaande situatie telkens de: Variabele, het begingetal ende regelmaat
Je kunt dit overzichtelijk in een tabel weergeven:
Variabele
begingetal
regelmaat
A.
B.
...
Je trekt de stop van het bad eruit. In het bad zat 150 liter water. Elke minuut loopt er 50 liter water weg.
Van rotterdam naar groningen is het 250 km rijden. Een auto kan gemiddeld 80 km/u rijden. Hoe lang duurt de reis van rotterdam naar groningen?
Jochem spaart voor een nieuwe spelcomputer. Hij moet nog €70,- bij elkaar sparen, daarom werkt hij in de supermarkt. Per uur verdient hij daar €2,50 mee. Hoeveel uur moet Jochem nu werken om de spelcomputer te kunnen kopen?
In een zeecontainer passen 1500 dozen. Er staan al 600 dozen in. Per uur kan een werknemer 250 dozen in de container zetten. Hoeveel uur moet de werknemer nu werken om de container te vullen?
Uitleg.
Regelmaat in een tabel.
Regelmaat (herhaling) komt natuurlijk niet alleen voor in de context (in het verhaaltje). Regelmaat kun je ook herkennen in een tabel. Kijk maar eens naar de tabel hieronder.
Je kunt de regelmaat gemakkelijk met boogjes laten zien:
Je ziet dat wanneer de tijd met één uur toe neemt, de inhoud van de tank met 7 liter afneemt.
Omdat de inhoud steeds minder wordt spreken we hier van regelmatige afname. Regelmatig omdat er elke stap hetzelfde gebeurt en afname omdat het minder wordt.
Neemt de onderste regel telkens toe (wordt het meer), dan spreken we over toename.
..5.
Regelmaat herkennen 1
HIeronder zie je zes tabellen. Alle tabellen zijn regelmatig.
Geef met boogjes de regelmaat van de tabellen aan. Doe dit op je werkblad.
..6.
Regelmaat herkennen 2
Bekijk onderstaande tabellen.
Noteer per tabel of er sprake is van regelmatige toename, regelmatige afname of dat er geen regelmaat is.
Controleer de tabellen op regelmaat. (de tabellen staan ook op het werkblad.)
Noteer de stapgrootte van iedere tabel in je schrift. Zet ook de berekening die je gebruikt hebt in je schrift erbij.
..11.
Hieronder zie je zes tabbelen. (de tabellen staan ook op je werkblad.)
Controleer de tabellen op regelmaat.
Noteer de stapgrootte van iedere tabel in je schrift. Zet ook de berekening die je gebruikt hebt in je schrift erbij.
Antwoorden
..1.
‘Hoe langer je loopt, hoe groter de afstand die je hebt aflegt.’
‘Hoe verder je reist met de trein, hoe meer je betaalt.
..2.
Allerlei antwoorden zijn mogelijk. Zolang er maar een oorzaak gevolg is.
Voorbeelden:
Hoe langer je werkt, hoe meer je verdient.
Hoe harder je fietst, hoe groter de afstand.
Hoe groter het glas, hoe meer er in past.
enz..
..3.
Uren en verdiensten (euro's).
Uren en uitgerustheid (fitheid).
Tijd en afstand.
Tv-tijd en huiswerk-tijd.
..4.
Variabele
begingetal
regelmaat
A.
Inhoud en tijd
150
50
B.
Tijd en afstand
250
80
C.
Tijd en verdiensten
70
2,50
D.
Tijd en dozen
900*
250
* 900 want 1500 - 600 = 900 Zoveel moet hij er nog
..5.
..6.
Tabel 1: Dalen met een luchtballon.
Regelmatige afnamen. Neemt de tijd met één toe, dan neemt de hoogte met 80 af.
Tabel 2: Gitaarlessen.
Regelmatige toenamen. Nemen de lessen met één toe, dan nemen de kosten met 15 toe.
Tabel 3: Vliegreis.
Geen regelmaat, de stapjes worden niet gelijk.
..7.
A. Regelmatige toename. D. Regelmatige afname.
B. Regelmatige afname. E. Geen regelmaat.
C. Geen regelmaat. F. Regelmatige toename.
..8.
..9.
..10.
..11.
Tabel 1 is regelmatig, de stapgrootte is: \(1 \over 7\) = 7
Tabel 2 is niet regelmatig!
Tabel 3 is regelmatig, de stapgrootte is: \(-20 \over 2\) = -10
Tabel 4 is niet regelmatig!
Tabel 5 is regelmatig, de stapgrootte is: \(5 \over 1\) = 5, \(10 \over 2\) = 5 en \(15 \over 3\) = 5 alle uitkomsten zijn gelijk
Tabel 5 is regelmatig, de stapgrootte is: \(2 \over 1\) = 2
§3 Rekenen met verbanden
Uitleg & Opgaven
Inleiding.
In een verband hebben twee onderdelen een oorzaak -> gevolg reactie met elkaar: de invoer en de uitvoer.
Denk maar aan de hoe- hoe zinnen. Hoe langer je werkt, hoe meer je verdient. Er is een verband tussen de uren die je werkt en je verdiensten.
Of het branden van een kaars, hoe langer de kaars brand, hoe korter deze wordt.
er is hier een verband tussen de tijd en de lengte.
Een verband vindt altijd plaats tussen 2 (of meer) grootheden.
*grootheden zijn dingen die je kunt meten zoals de tijd, de afstand, de lengte, de inhoud, de hoogte enz..
Voor invoer wordt er binnen wiskunde vaak de letter X gebruikt, voor de uitvoer de letter Y. Deze letters zie je dan ook vaak in tabellen of verbanden terug komen.
Een ander woord voor een verband is een formule, in havo noemen ze het ook wel een functie.
Uitleg.
In het machientje hieronder zie je dat wanneer je iets invoert, je de invoer eerst vermenigvuldigd met 3 en er daarna nog 4 bij op telt.
Vul je voor invoer (x) het getal 2 in dan krijg je:
Vul je voor invoer (x) het getal 7 in dan krijg je
2×3+4= 10
7×3+4= 25
Je kunt een verband (een formule) als het ware voor je zien als een machientje dat een berekening uitvoert.
..1.
Machientje
Bekijk het machientje hieronder. Schrijf daarna netjes jeberekeningenop.
In het machientje hierboven zie je dat wanneer je iets invoer (x) je dat eerst x2 doet en daarna van het antwoord 1 aftrekt.
Voer het getal 2 in, bereken de uitkomst.
Voer het getal 5 in, bereken de uitkomst.
Voer het getal 9 in, bereken de uitkomst.
Neem de tabel over in je schrift en vul deze netjes in.
Teken de boogjes met de stapjes bij je tabel, net als in de vorige paragraaf.
..2.
Machientje 2
Bekijk het machientje hieronder. Schrijf daarna netjes je berekeningen op.
In dit macheintje deel je de invoer (x) eerst door twee, daarna tel je er 6 bij op.
Voer het getal 8 in, bereken de uitkomst.
Voer het getal 12 in, bereken de uitkomst.
Neem de tabel over in je schrift en vul deze netjes in.
Teken de boogjes met de stapjes bij je tabel, net als in de vorige paragraaf.
..3.
Machientje 3
Bekijk het machientje hieronder. Schrijf daarna netjes je berekeningen op.
In dit macheintje deel je de invoer (x) eerst door twee, daarna tel je er 6 bij op.
Voer het getal 5 in, bereken de uitkomst.
Voer het getal 11 in, bereken de uitkomst.
Neem de tabel over in je schrift en vul deze netjes in.
Teken de boogjes met de stapjes bij je tabel, net als in de vorige paragraaf.
..4.
Machientje 4
Bekijk het machientje hieronder. Schrijf daarna netjes je berekeningen op.
In dit macheintje deel je de invoer (x) eerst door twee, daarna tel je er 6 bij op.
Voer het getal -2 in, bereken de uitkomst.
Voer het getal 1,5 in, bereken de uitkomst.
Neem de tabel over in je schrift en vul deze netjes in.
Teken de boogjes met de stapjes bij je tabel, net als in de vorige paragraaf.
..5.
Tabel invullen
Je kunt natuurlijk ook tabellen invullen wanneer je niet werkt met een machientje maar bijvoorbeeld met een formule
Vul nu eens het getal 2 in het pijlenschema in, bereken de uitkomst (y)
Voer het getal -4 in, bereken de uitkomst.
Voer voor x het getal 0 in, bereken de uitkomst.
..11.
Formule
En tot slot kun je in plaats van werken met het machientje of de pijlen het natuurlijk ook als een formule opschrijven:
De formule geeft het verband tussen de lengte van de plant boven de grond en het aantal dagen dat de plant groeit weer.
Lengte plant = -3 + 5 x aantal dagen.
Vul nu eens het getal 2 op de plek van het aantal dagen in, bereken de lengte van de plant.
Waarom heeft het invullen van het getal -4 nu opeens iets raars?
Voer voor het aantal dagen (x) het getal 0 in, bereken de lengte van de plant (y).
Uitleg
In de wiskunde wordt er veel gewerkt met formules. Maar wat is een formule nou eigenlijk?
Een formule beschrijft een verband. Dus een oorzaak -> gevolg.
De eerste formule die we gaan leren herkennen en maken is de lineaire formule.
Dit type formule heeft te maken met regelmaat. Dat betekent dat als de waarde van de ene variabele met even grote stapjes omhoog/omlaag gaat, dat de waarde van de andere variabele dan ook met even grote stapjes ) omhoog/omlaag gaat.
In de tabel zie je dus regelmaat, gelijke stapjes boven en onder. We leren deze regelmaat in een latere paragaaf nog beter herkennen en berekenen.
Teken je de grafiek van een lineaire formule, dan wordt dat een rechte lijn. Vandaar de naam lineair, komt van het woordje lineaal, een rechte lijn dus.
Ook in de formule zie je de regelmaat terug. De formule heeft namelijk altijd dezelfde opbouw. We noemen dit het formule voorschrift.
Leer het formule voorschrift uit het hoofd: Uitvoer (y) = begingetal +/- stapgrootte x invoer (x)
..12.
Machientje
Bekijk het machientje hieronder.
Wanneer je voor x (invoer) het getal6 invult krijg je de volgende berekening.
6x 2+ 4 = 16
Vul nu voor x het getal 2 in, bereken de uitkomst (y). Schrijf ook nu weer je berekening op.
Vul voor x het getal - 4 in, bereken de uitkomst (y).
Vul voor x het getal 0 in, bereken y
..13.
pijlen
Bij het machientjesschema uit vraag 1 kan je natuurlijk ook een pijlenschema maken kijk maar.
Vul nu eens het getal 2 in het pijlenschema in, bereken de uitkomst (y)
Voer het getal -4 in, bereken de uitkomst.
Voer voor x het getal 0 in, bereken de uitkomst.
..14.
Formule
En tot slot kun je in plaats van werken met het machientje of de pijlen het natuurlijk ook als een formule opschrijven:
De formule geeft het verband tussen het aantal schepen in de haven en het aantal uren
Aantal schepen = 4 + 2 x aantal uren.
Vul nu eens het getal 2 op de plek van het aantal uren in, bereken het aantal schepen in de haven.
Waarom heeft het invullen van het getal -4 nu opeens iets raars?
Voer voor het aantal uren (x) het getal 0 in, bereken het aantal schepen (y).
..15.
Berekeningen met een formule
Gegeven is de formule: Verdiensten = 5 + 3 x aantal gewerkte uren
Vul voor het aantal gewerkte uren (u) het getal 6 in, welke verdiensten geeft dat, noteer de berekening in je schrift.
Waarom heeft het invullen van het aantal uren -2 nu opeens iets raars?
Vul voor u het getal 0 in, bereken de verdiensten.
Vul voor u het getal 3 in, bereken de verdiensten.
..16.
Werken met lineaire formules
Gegeven is de formule: Aantal broden op voorraad = 100 - 2 x aantal klanten
Vul voor het aantal klanten (k) het getal 4 in, welke hoeveelheid broden op voorraad geeft dat, noteer de berekening in je schrift.
Vul voor het aantal klanten (k) het getal 25 in, bereken aantal broden.
Vul voor k het getal 0 in, bereken het aantal broden.
Vul voor k het getal 8 in, bereken de aantal broden.
Waarom is het raar als je voor het aantal klanten een negatief getal invult?
..17.
Gegeven formule
Gegeven is de formule: Inhoud = 50 - 3 x aantal minuten
Vul voor het aantal minuten (m) het getal 1 in, welke Inhoud geeft dat, noteer de berekening in je schrift.
Vul voor het aantal minuten (m) het getal 10 in, bereken de Inhoud.
Vul voor m het getal 0 in, bereken de Inhoud.
Vul voor m het getal 15 in, bereken I.
Ook nu weer, waarom is het invullen van een negatief getal voor het aantal minunten zo raar?
..18.
Bereken
Gegeven is de formule: Kosten = 25 + 10 x aantal nachten
Vul voor het aantal nachten (a) het getal 8 in, welke uitkomst geeft dat, noteer de berekening in je schrift.
Vul voor het aantal nachten (a) het getal 4 in, bereken de kosten.
Vul voor a het getal 0 in, bereken de kosten.
Vul voor a het getal 7 in, bereken de kosten.
Famke heeft een kamer geboekt in het hotel. Aan het eind van haar verblijf moet zij 55 euro betalen. Bereken het aantal nachten dat zij in het hotel heeft gelogeerd
Antwoorden
§4 Lineaire verbanden maken.
Uitleg & Opgaven
Inleiding.
Tot op heden:
Weten we dat een formule het verband tussen verschillende variabele weer geeft. (Een hoe- hoe zin, een oorzaak -> gevolg) .
Weten we dat een lineaire formule te maken heeft met regelmaat.
Weten we dat een lineaire formule bestaat uit een begingetal en een stapgrootte.
In de vorige paragraaf heb je geoefend met het herkennen van regelmaat. Dit is belangrijk omdat je bij tabellen, grafieken en contexten (verhaaltjes) met herhaling (regelmaat) één type formule gaat leren maken.
We noemen de formules waarbij regelmaat een belangrijke rolspeelt lineaire formule. Als je paragraaf 5 van dit hoofdstuk af hebt begrijp je vast waarom we die naam gekozen hebben.
Uitleg.
Wanneer we de regelmaat herkennen in de context, de grafiek of in de tabel kunnen we gebruik maken van een vast schema:
uitvoer (y) = begingetal + stapgrootte x invoer (x)
Voorbeeld:
Formule maken bij een context (verhaaltje) met regelmaat.
Sandra heeft een bezorgdienst. Bestel je iets online, dan bezorgt Sandra dit bij je thuis. Hoe zwaarder het pakket, hoe groter de kosten voor het bezorgen. Sandra rekent €2,- voor het ontvangen van het pakket. Elke kilo dat het pakket zwaar is, rekent Sandra nog eens €1,-.
Je bestelt een pakketje van 2kg. Bereken hoeveel het kost om dit door Sandra thuis te laten bezorgen.
Stap 1. Schrijf het vaste invulschema in je schrift op. uitvoer (y) = begingetal + stapgrootte x invoer (x)
Stap 2. Zoek de juiste grootheden in de context (het verhaaltje) en vul deze in.
uitvoer: Wat bereken je? Zoek hier de grootheid bij (in het verhaaltje de bezorgkosten)
invoer: Wat moet je weten om een berekening te maken (in het verhaaltje het gewicht)
Stap 3. Lees de beginhoeveelheid af en vul het op de plek van het begingetal in. (€2,-)
Stap 4. Lees het bedrag dat zich herhaalt af en vul het op de plek van het stapgrootte in. (€1,-)
Je formule ziet er nu dus zo uit:
uitvoer (y) = begingetal + stapgrootte x invoer (x)
Bezorgkosten = 2 + 1 x aantal kg
..1.
Taxi service
Serena bestelt een taxi. Het instaptarief van deze taxi is €3. Dus wanneer je instapt kost het al €3,-
Per gereden kilometer komt daar nog eens €2,- bij.
Serena moet in totaal 6 km rijden. Daarom maken we voor Serena een formule waarmee zij kan berekenen hoeveel zij voor de taxirit moet betalen.
Neem het schema uitvoer (y) = begingetal + stapgrootte x invoer (x) over in je schrift. .
Bedenk welke grootheden op de plek van de uitvoer en welke woordjes op de plek van de invoer moeten komen. .
Lees uit het verhaaltje het begingetal af en vul die in. (welke kosten maak je zo ie zo zonder ook maar een kilometer gereden te hebben?) .
Lees uit het verhaaltje de stapgrootte af en vul die in.
(welk getal herhaalt zich per kilometer?)
Je formule is nu klaar. Je kunt nu voor elk aantal kilomter de kosten berekenen.
Bereken wat een taxirit van 6 kilometer moet kosten.
..2.
Silvio vaart met een zeilbootje een rondje op een meer. Hij heeft al 10 km gevaren. Elk uur dat hij met het bootje vraart legt Silvio 5 km af. Silvio wil weten hoeveel kilometer hij over 3 uur heeft gevaren. Daarom maken we voor Silvio een formule waarmee hij zijn afgelegde afstand kan berekenen.
Neem het schema uitvoer (y) = begingetal + stapgrootte x invoer (x) over in je schrift. .
Bedenk welke grootheden op de plek van de uitvoer en welke woordjes op de plek van de invoer moeten komen. .
Lees uit het verhaaltje het begingetal af en vul die in. (welke kosten maak je zo ie zo zonder ook maar een kilometer gereden te hebben?) .
Lees uit het verhaaltje de stapgrootte af en vul die in.
(welk getal herhaalt zich per kilometer?) .
Bereken hoeveel kilometer Silvio na 3 uur varen in totaal heeft afgelegd.
..3.
Noura heeft twee katten. Deze krijgen natuurlijk elke dag een beetje voer.
In een grote zak voer zit 8 kg.
Per dag krijgen de katten in totaal 0,5 kg voer.
Noura wil graag weten hoeveel voer zij nog over heeft na 10 dagen, daarom maken we een formule voor Noura waarmee ze per dag kan berekenen hoeveel voer er nog over is.
Neem het schema uitvoer (y) = begingetal - stapgrootte x invoer (x) over in je schrift. .
Bedenk welke grootheden op de plek van de uitvoer en welke woordjes op de plek van de invoer moeten komen. .
Lees uit het verhaaltje het begingetal af en vul die in. (welke kosten maak je zo ie zo zonder ook maar een kilometer gereden te hebben?) .
Lees uit het verhaaltje de stapgrootte af en vul die in.
(welk getal herhaalt zich per kilometer?) .
Bereken voor Noura hoeveel kg voer er nog in de zak zit na 10 dagen.
..4.
Aquarium met goudvissen
Kimberley wil graag een goudvis in een aquarium op haar kamer. De verkoper in de dierenwinkel heeft een mooi starters aquarium voor haar. Dit kost €20,- Nu moet Kimberley alleen nog goudvissen komen. Deze kosten €1,50 per stuk
Maak een formule bij het verhaaltje. Bereken daarna voor 5 goudvissen en voor 8 goudvissen de kosten.
Schrijf beide berekeningen op.
..5.
Parkeerkosten
Joan gaat een dagje winkelen. Ze kiest er voor haar auto te parkeren in een parkeergarage.
Het inrij-tarief voor de garage is €2,-
Per uur kost het parkeren nog €3,50
Maak een formule bij het verhaaltje.
Bereken daarna voor 3 uur en voor 6 uur de parkeerkosten.
..6.
Bijbaantje
Kevin werkt in een restaurant. Hij is daar ober. Iedere maand krijgt hij een vastbedrag van de baas uit de fooien pot. Ook krijgt hij natuurlijk per uur nog salaris.
Iedere maand krijgt Kevin van zijn baas € 25,- uit de fooien pot.
Per gewerkt uur krijgt Kevin €2,50 uitbetaald.
Kevin heeft in de maand Februari 12 uur gewerkt, in Maart 10 uur gewerkt en in April 16 uur gewerkt.
Maak een formule voor kevin.
Bereken voor Kevin zijn verdiensten voor de maand Februari.
Bereken ook zijn verdiensten voor de maand Maart.
Bereken zijn verdiensten voor de maand April.
Uitleg.
Hoe maak je een formule bij een tabel?
In dit filmpje wordt dat voorgedaan.
Let op! In dit filmpje gebruiken ze de afkorting R.C. in plaats van het woordje stapgrootte
De letter x en het keerteken lijken wel heel erg op elkaar. Daarom laten we dit in formules weg, of we zetten er een zwevende punt tussen (een vermenigvuldigingspunt) ·
..7.
In de tabel hieronder zie je het verband tussen je verdiensten in € en het aantal uren dat je hebt gewerkt.
Neem het schema uitvoer (y) = begingetal + stapgrootte x invoer (x) over in je schrift. .
Lees de grootheden die horen bij de y-as (onder in je tabel) en de woordjes die horen bij je x-as (boven in je tabel) af en vul deze in je schema in. .
Lees in de tabel het begingetal af. (dit kun je vinden onder de nul in je tabel) en vul dit in je schema in. .
Teken de boogjes bij je tabel en bereken de stapgrootte: \(onderste\space verschil \over bovenste \space verschil \)
Vul de uitkomst in je schema in
..8.
In de tabel hieronder zie je het verband tussen de afstand die je op de fiets aflegt en het aantal uren dat je aan het fietsen bent
Neem het schema uitvoer (y) = begingetal + stapgrootte x invoer (x) over in je schrift. .
Lees de grootheden die horen bij de y-as (onder in je tabel) en de woordjes die horen bij je x-as (boven in je tabel) af en vul deze in je schema in. .
Lees in de tabel het begingetal af. (dit kun je vinden onder de nul in je tabel) en vul dit in je schema in. .
Teken de boogjes bij je tabel en bereken de stapgrootte: \(onderste\space verschil \over bovenste \space verschil \)
Vul de uitkomst in je schema in
..9.
In de tabel hieronder zie je het verband tussen Het aantal keren dat een stuiterbal stuitert en de hoogte van de bal.
Neem het schema uitvoer (y) = begingetal - stapgrootte x invoer (x) over in je schrift. .
Lees de grootheden die horen bij de y-as (onder in je tabel) en de woordjes die horen bij je x-as (boven in je tabel) af en vul deze in je schema in. .
Lees in de tabel het begingetal af. (dit kun je vinden onder de nul in je tabel) en vul dit in je schema in. .
Teken de boogjes bij je tabel en bereken de stapgrootte: \(onderste\space verschil \over bovenste \space verschil \)
Vul de uitkomst in je schema in
..10.
In de tabel hieronder zie je het verband tussen de inhoud van het bad en het aantal minuten dat de stop eruit is
Maak een formule bij de tabel.
..11.
In de tabel hieronder zie je het verband tussen de verdiensten en het aantal gewerkte uren.
Maak een formule bij de tabel.
..12.
In de tabel hieronder zie je het verband tussen de inhoud van de bezine tank en de afgelegde afstand.
Maak een formule bij de tabel.
Antwoorden
§5 Lineaire grafieken
Uitleg & Opgaven
Inleiding.
Bij een verband kun je ook een grafiek tekenen.
Een grafiek is een grafische weergave van gegevens. Je maakt dus een plaatje bij je berekeningen.
Hoe je dat moet doen wordt in deze paragraaf behandeld.
Uitleg.
Zodra je een formule (een verband) gekregen hebt of zelf gemaakt hebt kun je er een grafiek bij tekenen. Voor een grafiek heb je wel informatie nodig. Je moet dus een aantal berekeningen gemaakt hebben. Bij de invoer en uitkomst van deze berekeningen kun je een grafiek tekenen.
Voorbeeld.
Gegeven is de formule: y = 3x + 4
1. Neem de formule over in je schrift.
2. Teken een tabel bij de formule, bereken minimaal 3 getallen.
3. Teken een passend assenstelsel bij je tabel.
4. Teken de grafiek in je assenstelsel.
In dit filmpje kun je alles nog eens rustig nakijken als het je te snel ging.
Van formule; naar een tabel; naar een grafiek.
..1.
Formule, tabel grafiek.
Gegeven is de formule: y = 2x + 6
Neem de formule over in je schrift. (zet ook het keerteken tussen het cijfer en de letter)
Maak een tabel met de getallen 0, 3 en 6.
Teken een passend assenstelsel
(maak de x-as van 0 t/m 6 en de y-as tot 18, maak stapjes van 3 op je y-as)
Teken de grafiek in je assenstelsel. Zet eerst de punten (coördinaten) uit je tabel in je
assenstelsel en verbind die met een lijn.
..2.
Formule, tabel grafiek.
Emre heeft een eigen kledingwinkel. Bij hem in de zaak werken verschillende weekendhulpen. Het loon van een weekendhulp berekent hij met de formule: Loon = 5 + 2,50 x aantal gewerkte uren.
Eén van de weekendhulpen heeft op zaterdag 6 uur gewerkt. Maak een tabel waarin de verdiensten van de weekendhulp staan.
Teken het assenstelsel dat pas bij de tabel van vraag a.
Teken met rood kleurpotlood de grafiek die hoort bij de tabel van vraag a in het assenstelsel van vraag b.
..3.
Formule, tabel grafiek.
Op een pak kaarsen van 24 cm lang staat geschreven dat deze elk uur 4 cm korter worden.
Maak op het werkblad een formule bij dit verhaaltje. het begin is al voor je gemaakt: Lengte kaars = ... - ... x aantal branduren.
Vul op het werkblad te tabel in.
Teken in het assenstelsel op het werkblad de grafiek die bij de formule past. Vergeet de woordjes die horen bij x-as en de y-as niet op te schrijven.
..4.
Formule, tabel grafiek.
Gegeven is de formule: Inhoud = 800 - 50 x aantal minuten.
Teken de grafiek bij de formule.
*denk aan de vier stappen.
..5.
Formule, tabel grafiek.
Chantal werkt bij coolblue in het distributiecentrum. Hier is zij verantwoordelijk voor het bijhouden van de voorraad. In het distributiecentrum is plaats voor 20000 artikelen. Per week verkoopt coolblue gemiddeld zo'n 4000 artikelen.
Chantal gebruikt de formule: Voorraad = 20000 - 4000 x aantal weken.
Teken voor Chantal een grafiek die bij de voorraad past.
..6.
Formule, tabel grafiek.
Joshua spaart voor een nieuwe spelcomputer. Hij heeft al 135 euro gespaard. Om sneller te kunnen sparen werkt Joshua elke week bij Emre in de kledingzaak. Hier verdient hij €25,- per dag mee.
Maak op het werkblad een formule bij dit verhaaltje. het begin is al voor je gemaakt: Spaargeld = ... - ... x aantal werkdagen.
Vul op het werkblad te tabel in.
Teken in het assenstelsel op het werkblad de grafiek die bij de formule past. Vergeet de woordjes die horen bij x-as en de y-as niet op te schrijven.
..7.
Formule, tabel grafiek.
Gegeven is de formule: y = 15 - 2,5x.
Neem de formule over in je schrift. (zet ook het keerteken tussen het cijfer en de letter)
Maak een tabel met de getallen 0, 2 en 4.
Teken een passend assenstelsel
(maak de x-as van 0 t/m 4 en de y-as tot 15, maak stapjes van 2,5 op je y-as)
Teken de grafiek in je assenstelsel. Zet eerst de punten (coördinaten) uit je tabel in je
assenstelsel en verbind die met een lijn.
..8.
Formule, tabel grafiek.
Jillian doet mee aan een sponsorloop voor het goede doel. Met onderstaande formule kan hij zijn opbrengsten uitrekenen:
Opbrengst = 20 + 5 x aantal rondjes
Maak voor Jullian een grafiek waarin zij haar verdiensten kan laten zien. Jillian loopt maximaal 8 rondjes.
..9.
Formule, tabel grafiek.
Féline speelt graag spelletjes op haar telefoon. Dit kost haar wanneer ze niet op de wifi zit heel wat MB's. Per kwartier kost dit 250 MB. Gelukkig heeft Féline een 5 Gb (5000MB) abonnement.
Maak op het werkblad een formule bij dit verhaaltje. het begin is al voor je gemaakt: Aantal MB = 5000 - ... x aantal kwartier.
Vul op het werkblad te tabel in.
Teken in het assenstelsel op het werkblad de grafiek die bij de formule past. Vergeet de woordjes die horen bij x-as en de y-as niet op te schrijven.
Antwoorden
§6 Gemengde opgaven
Opgaven
Zoals je inmiddels wel gewend bent, start vandaag de toetsvoorbereiding. Wiskunde is vooral een doe-vak, net als met je sport is behalve de kennis over de spelregels het vooral belangrijk dat je veel getraind hebt. Bij wiskunde is dat net zo. Leer de begrippen, zorg dat je weet wat het woordje variabele betekent, maar oefen met toepassen. Maak dus veel verschillende opgaven.
Je leert vooral van het maken van opgaven, vragenstellen en vragen beantoorden. Ook van foutjes leer je een hoop, bij het oefenen is een foutje maken dus ook helemaal niet erg. Begrijp je niet wat er fout gaat, vraag dan hulp.
..1.
Werken met formules
Gegeven is de volgende formule:
verdiensten = 12 + 3 x aantal klanten
Bereken de verdiensten bij 5 klanten.
Bereken de verdiensten bij 10 klanten.
Wanneer je het dubbele aantal klanten invult in de formule worden de verdiensten niet verdubbelt, kun jij uitleggen hoe dat kan. Schrijf je uitleg in je schrift.
Neem onderstaande tabel over in je schrift en vul de ontbrekende gegevens in.
.
Teken de grafiek die bij de tabel en de formule past. Weet je het nog? De woordjes onder in je tabel horen bij de y-as.
..2.
Machientjes schema
Hieronder zie je een machientje. In dit machientje doe je de invoer eerst x 4, daarna haal je 2 van het antwoord af.
Voer het getal 5 in, bereken de uitkomst. .
Voer het getal 17 in, bereken de uitkomst. .
Neem de tabel over in je schrift en vul deze netjes in.
.
Teken de boogjes met de stapjes bij je tabel, net als in de vorige paragraaf.
..3.
Regelmaat
Bekijk de drie tabellen hieronder.
Schrijf van elke tabel op of er sprake is van regelmatige toename, regelmatige afnamen of geen regelmaat in de tabel.
..4.
Grafiek bij tabel tekenen
Teken in je schrift de grafiek die past bij onderstaande tabel.
..5.
Een grafiek tekenen
Om te meten wanneer het bubbelbad op de juiste temperatuur is gebruikt het zwembad de volgende formule:
Temperatuur bubbelbad = 20 + 1,5 x aantal minunten
Bereken de temperatuur na 10 minunten verwarmen.
Bereken de temperatuur bij 15 minunten verwarmen.
Maak een tabel die bij de formule past. Hieronder zie je al een beginnetje.
Teken de grafiek die bij te tabel past. Weet je het nog? De woordjes boven in je tabel horen bij de x-as.
..6.
Ijsjes kopen
Bij de ijskar die wel eens op het pleintje staat kun je schepijs kopen.
Een hoorntje kost €0,50.
Een bolletje kost €0,75.
Een ijsje met drie bolletje kost dus 0,50 + 0,75 x 3 = €2,75
We gaan voor de ijskar een formule maken waarmee kan worden uitrekenen hoeveel er betaalt moet worden voor een willekeurig ijsje.
Neem het schema uitvoer (y) = begingetal + stapgrootte x invoer (x) over in je schrift. .
Bedenk welke woordjes op de plek van de uitvoer en welke woordjes op de plek van de invoer moeten komen. .
Lees uit het verhaaltje het begingetal af en vul die in. (welke kosten maak je zo ie zo zonder ook maar één bolletje ijs te krijgen?) .
Lees uit het verhaaltje de stapgrootte af en vul die in.
(welk getal herhaalt zich per bolletje?)
Je formule is nu klaar. Je kunt nu voor elk aantal bolletjes de kosten berekenen.
..7.
Regelmaat in tabellen
Hieronder zien we drie regelmatige tabellen. In elke tabel ontbreken twee getallen. Op die plek staat een letter. In de eerste tabel zie je de letter A en B.
Neem de letters A, B, C, D, E,en F over in je schrift en schrijf er achter welke getallen daar in de tabel horen te staan.
..8.
Werken met formules
Een dagje naar de Kermis in Tilburg met de trein
Als je een dagje naar de Kermis in Tilburg wilt moet je naast reiskosten natuurlijk ook nog per attractie betalen.
Jan berekent met de volgende formule wat het hem gaat kosten: Kosten = 15 + 3 x aantal attracties
Bereken wat het Jan kost als hij in totaal 7 attracties doet.
Bereken de kosten voor Jan bij 14 attracties.
Welk getal in de formule zijn de kosten voor de trein?
Hoeveel kost een losse attractie?
Jan heeft in totaal 48 euro uitgegeven. Hoeveel attracties heeft Jan gedaan?
..9.
Formule maken bij de tabel.
In de tabel hieronder zie je het verband tussen de afstand die je op de fiets aflegt en het aantal uren dat je aan het fietsen bent
Neem het schema uitvoer (y) = begingetal + stapgrootte x invoer (x) over in je schrift. .
Lees de woordjes die horen bij de y-as (onder in je tabel) en de woordjes die horen bij je x-as (boven in je tabel) af en vul deze in je schema in. .
Lees in de tabel het begingetal af. (dit kun je vinden onder de nul in je tabel) en vul dit in je schema in. .
Teken de boogjes bij je tabel en bereken de stapgrootte: \(onderste \space boogje \over bovenste \space boogje\)
Vul de uitkomst in je schema in
..10.
Volgorde van bewerkingen
Pas de voorrangregels toe. Schrijf je volledige berekening op! Alleen een antwoord is niet genoeg.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Wanneer je een grafiek ziet die bestaat uit een rechte lijn, dan kunnen we hier een formule bij maken.
We gebruiken natuurlijk weer het schema dat we al eerder geleerd hebben:
uitvoer (y) = begingetal + stapgrootte x invoer (x)
De uitvoer (y) en invoer (x) zijn het gemakkelijkst terug te vinden in je grafiek. Dat zijn namelijk de woordjes of letters (variabele) die bij de x-as en y-as staan. Deze kun je dus in één oogopslag invullen.
..1.
Vul de juiste woordjes in.
Bekijk de grafiek hiernaast. Zoals je kunt zien is deze grafiek een rechte lijn. Er hoort dus een lineaire formule bij.
Noteer het schema dat hoort bij het maken van een lineaire formule in je schrift.
Kijk nu eens goed naar de y-as. Zet de variabele die hoort bij de y-as op de goede plek in je schema.
Kijk dan nu naar de x-as. Zet de variabele die hoort bij de x-as op de goede plek in je schema.
..2.
Variabele invullen
Bekijk de grafiek hiernaast. Zoals je kunt zien is deze grafiek een rechte lijn. Er hoort dus een lineaire formule bij.
Noteer het schema dat hoort bij het maken van een lineaire formule in je schrift en vul direct de goede variabele in.
..3.
Y-variabele en x-variabele
Bekijk de grafiek hiernaast. Zoals je kunt zien is deze grafiek een rechte lijn. Er hoort dus een lineaire formule bij.
Noteer het schema dat hoort bij het maken van een lineaire formule in je schrift en vul direct de goede variabele in.
Hoe vind je het begingetal in een lineaire grafiek?
Dit onderwerp hebben we al eens eerder benoemd. Het begingetal is het getal dat je overhoudt wanneer je voor de x-variabele (de woordjes die horen bij de x-as) het getal nul in voert in je formule. Kijk maar naar het voorbeeld hieronder
In de tabel keken we onder het getal nul.
En in de grafiek? Ook nu kijken we weer bij x = 0 dus we kijken waar de grafiek (de lijn) de y-as raakt. Bekijk de voorbeelden hieronder maar.
..4.
Aflezen begingetal
Bekijk de grafiek hiernaast. Zoals je kunt zien is deze grafiek een rechte lijn. Er hoort dus een lineaire formule bij.
Noteer het schema dat hoort bij het maken van een lineaire formule in je schrift en vul direct de goede variabele in.
Kijk nu op de x-as bij het getal nul. Dus daar waar de grafiek (de lijn) de y-as raakt. Vul het getal waar de grafiek de y-as raakt op de goede plek in je schema in.
..5.
Variabele + begingetal.
Bekijk de grafiek hiernaast. Zoals je kunt zien is deze grafiek een rechte lijn. Er hoort dus een lineaire formule bij.
Noteer het schema dat hoort bij het maken van een lineaire formule in je schrift en vul direct de goede variabele en het begingetal in
..6.
Maak de juiste combinaties
Hieronder zie je drie grafieken (A, B en C). Er staan hier ook drie (begin)getallen. Zoek het juiste begingetal bij de juiste grafiek. Noteer de combinaties in je schrift.
Bijvoorbeeld: A - 3 , B - 2, enz...
Stapgrootte/richtingscoëfficient berekenen
Je ziet het al, we gaan op zoek naar de stapgrootte van je grafiek. Een ander woord voor stapgrootte is richtingscoëfficient. We noemen het ook wel de richtingscoëfficient (r.c.) omdat dit getal de richting van je grafiek aan geeft. Kijk maar naar de drie grafieken hieronder.
Hoe vindt je de richtingscoëfficient (r.c.)? (De stapgrootte)
Het arrangement 1KGT H07 Verbanden is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-07-02 10:38:06
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Diagnostische toets hoofdstuk 7
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Algebra is het deel van de wiskunde dat zich bezig houdt met formules, letters en rekenregels.
Aan het eind van dit hoofdstuk kan ik: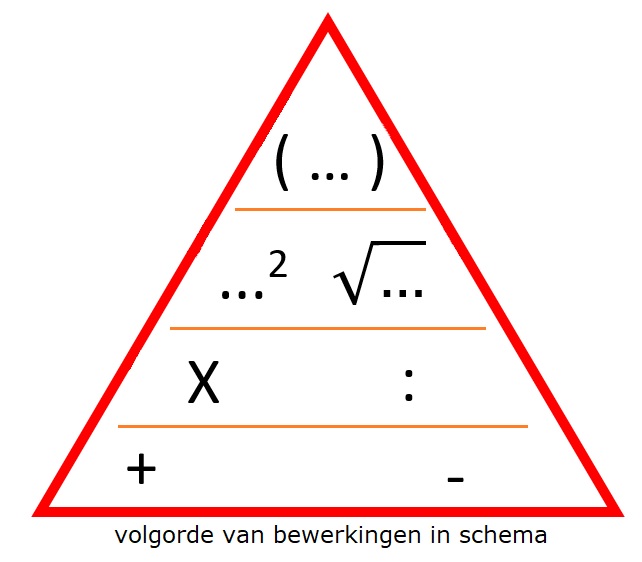
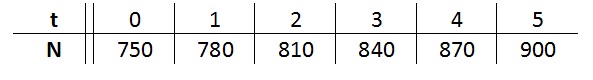
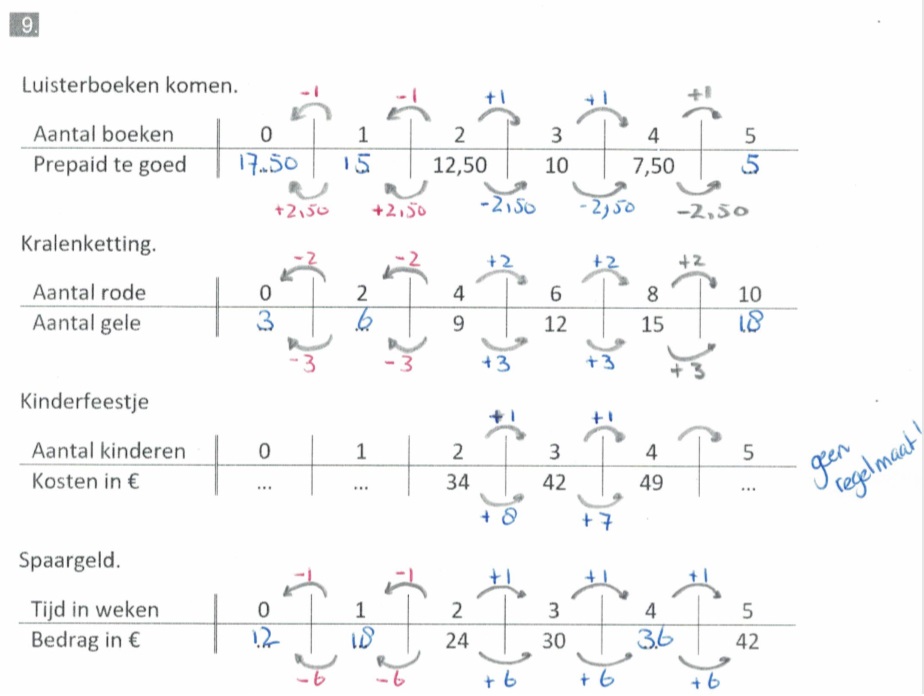
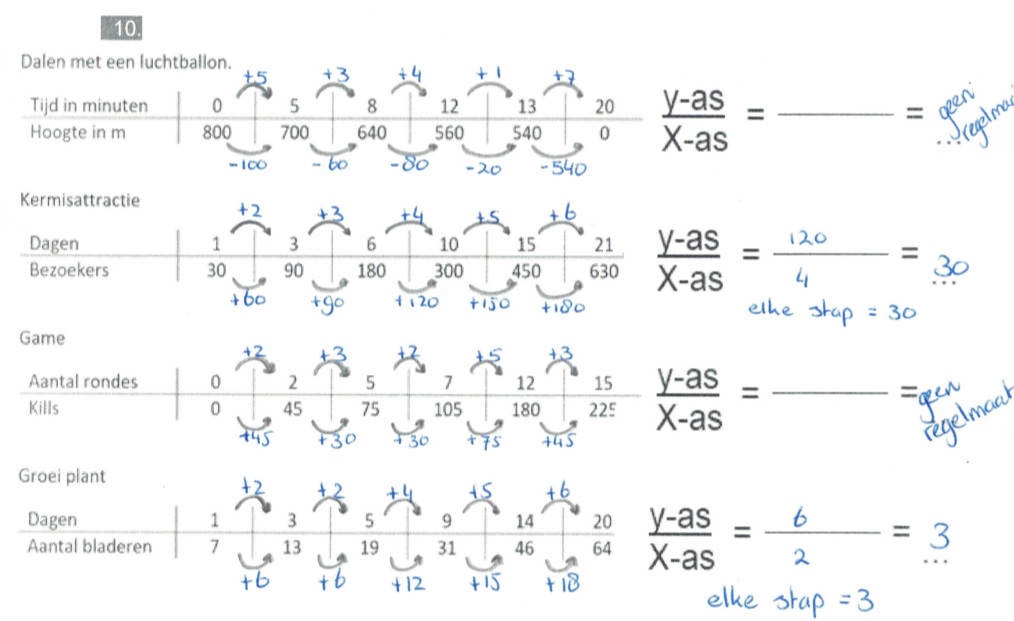
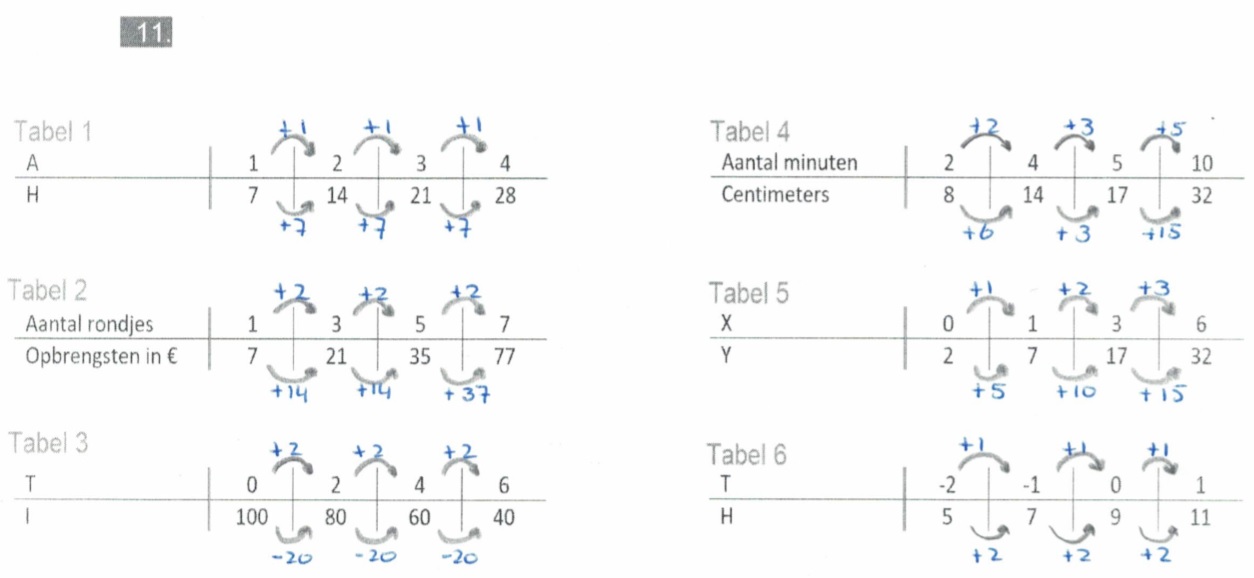
Inleiding.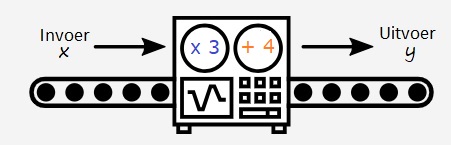
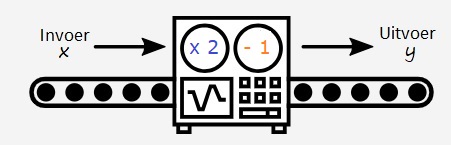
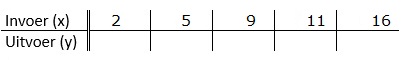
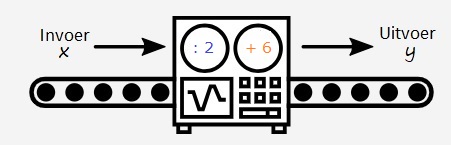
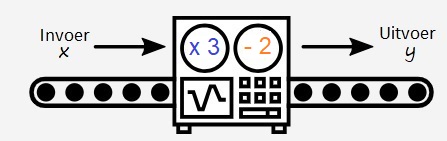
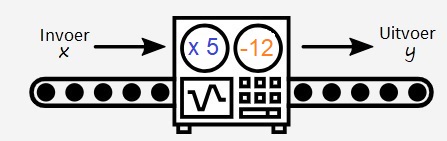
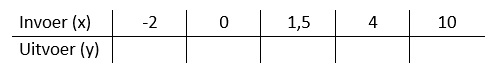
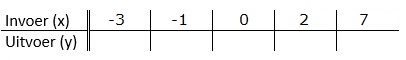
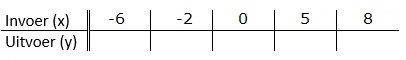
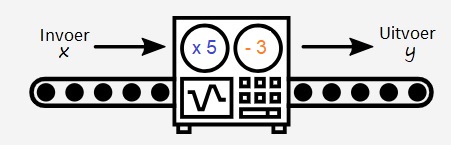
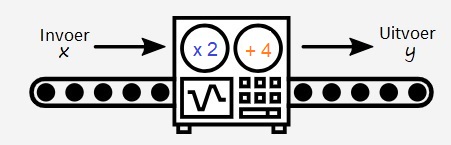
Gegeven is de formule: 
Gegeven is de formule: 
Serena bestelt een taxi. Het instaptarief van deze taxi is €3. Dus wanneer je instapt kost het al €3,-
Silvio vaart met een zeilbootje een rondje op een meer. Hij heeft al 10 km gevaren. Elk uur dat hij met het bootje vraart legt Silvio 5 km af. Silvio wil weten hoeveel kilometer hij over 3 uur heeft gevaren. Daarom maken we voor Silvio een formule waarmee hij zijn afgelegde afstand kan berekenen.
Noura heeft twee katten. Deze krijgen natuurlijk elke dag een beetje voer.
Kimberley wil graag een goudvis in een aquarium op haar kamer. De verkoper in de dierenwinkel heeft een mooi starters aquarium voor haar. Dit kost €20,- Nu moet Kimberley alleen nog goudvissen komen. Deze kosten €1,50 per stuk
Joan gaat een dagje winkelen. Ze kiest er voor haar auto te parkeren in een parkeergarage.
Kevin werkt in een restaurant. Hij is daar ober. Iedere maand krijgt hij een vastbedrag van de baas uit de fooien pot. Ook krijgt hij natuurlijk per uur nog salaris.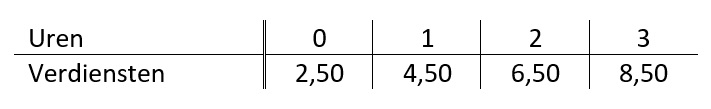
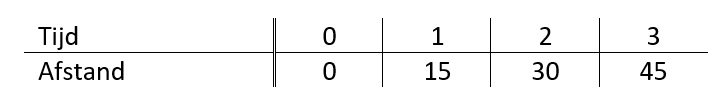
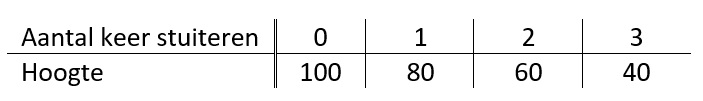
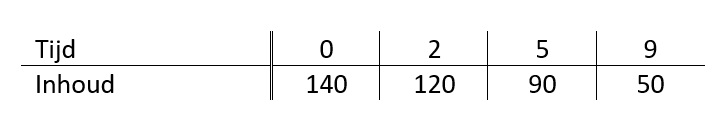
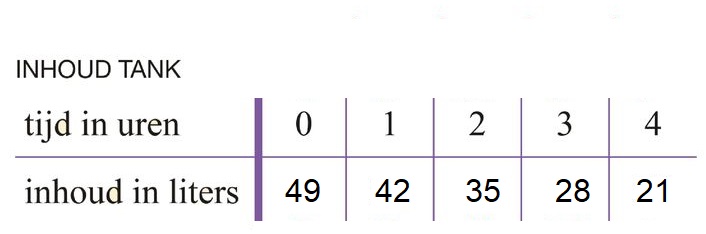
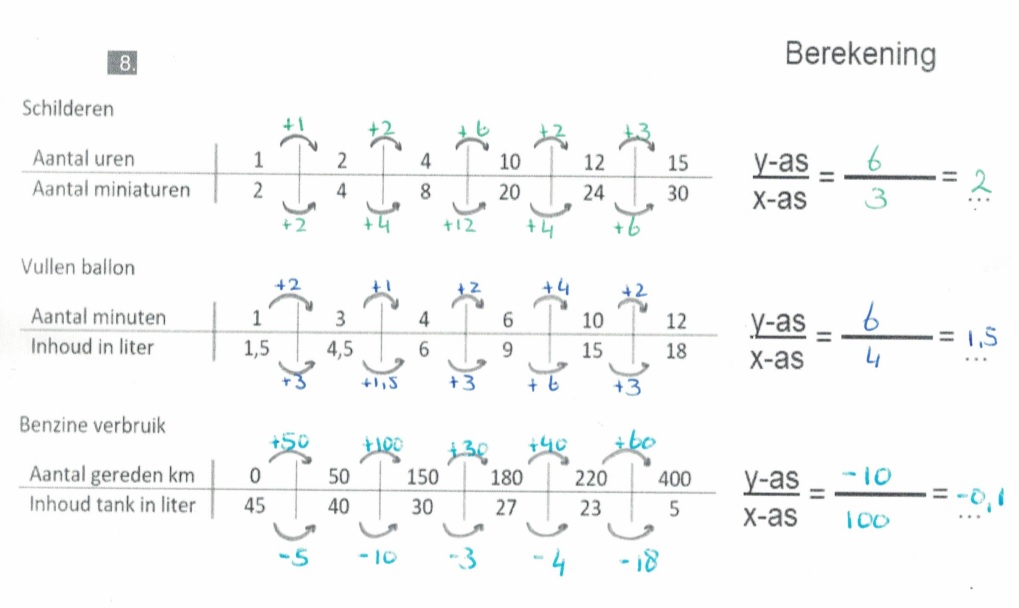
In de tabel hieronder zie je het verband tussen de inhoud van de bezine tank en de afgelegde afstand.
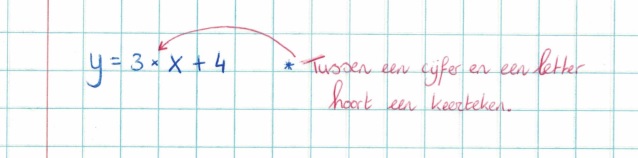
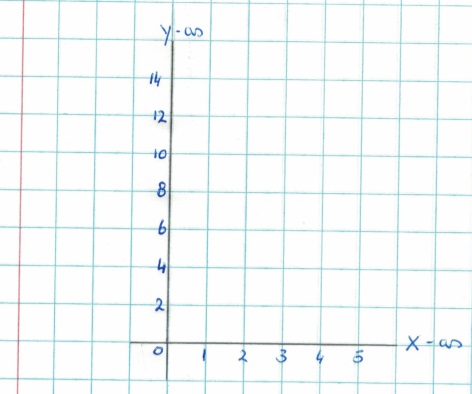
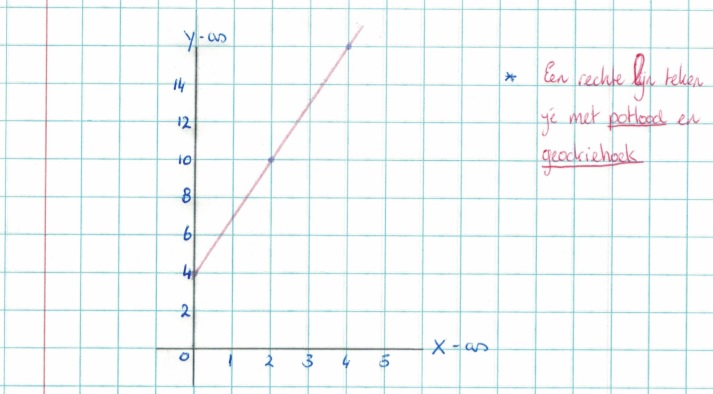
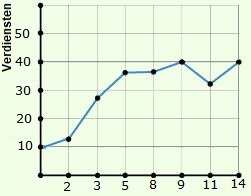
Op een pak kaarsen van 24 cm lang staat geschreven dat deze elk uur 4 cm korter worden.
Joshua spaart voor een nieuwe spelcomputer. Hij heeft al 135 euro gespaard. Om sneller te kunnen sparen werkt Joshua elke week bij Emre in de kledingzaak. Hier verdient hij €25,- per dag mee.
Jillian doet mee aan een sponsorloop voor het goede doel. Met onderstaande formule kan hij zijn opbrengsten uitrekenen:
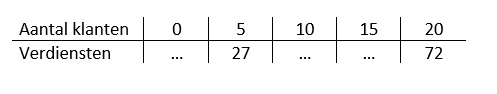
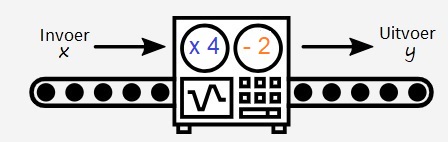
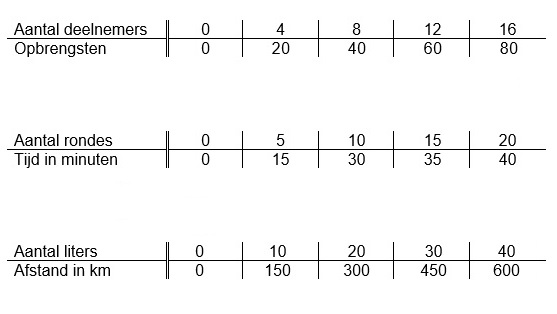
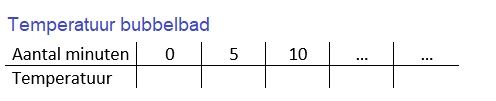
Een dagje naar de Kermis in Tilburg met de trein
