Na de Middeleeuwen kwam in Europa het wetenschappelijke denken weer op gang. De oude Grieken werden bestudeerd, met name de werken van Archimedes. Allerlei problemen stonden in de belangstelling, meestal mechanische of meetkundig van aard.
Vaak kwamen de vragen neer op het berekenen van de steilte van een grafiek, de lengte van een grafiek of de oppervlakte onder een grafiek. Uiteindelijk is hier in de zeventiende eeuw een mooie theorie uit ontstaan: de differentiaal- en integraalrekening.
We stellen de drie typen vragen die hierboven werden genoemd voor het eenvoudige voorbeeld van de parabool \(\small y=x^2\).
Hoe steil loopt de parabool in het punt \(\small (\frac{1}{2},\frac{1}{4})\)?
Hoe lang is de parabool tussen \(\small (0,0)\) en \(\small (1,1)\)?
Hoe groot is de oppervlakte onder de parabool tussen \(\small x=0\) en \(\small x=1\)?
Dit soort vragen hoort thuis in de Analyse. In de zeventiende eeuw hielden zich maar enkele intellectuelen daarmee bezig. Tegenwoordig is dit een groot onderdeel van wiskunde B voor het vwo. Een groot verschil tussen toen en nu is de rekenkracht waarover we nu kunnen beschikken: computer, grafische rekenmachine. Dankzij deze snelle rekenapparatuur hebben wij niet de rekenproblemen van de wetenschappers van 3 à 4 eeuwen geleden. Zo kunnen wij gemakkelijk (?) antwoorden op de drie vragen over de parabool vinden. Maar dat zijn wel benaderingen. Het is belangrijk dat je leert hoe en vooral waarom die werken. In die benaderingsmethoden zit de sleutel tot de exacte antwoorden, en daar gaat het ons om. In dit hoofdstuk houden we ons met vragen van het eerste type bezig. De andere vragen komen in vwo5 en vwo6 aan bod.
Opgaven
Trajectcontrole
Twee foto's
Wandeling
Autorit
De skipiste
Zonnebloem
De helling in een punt
Gegeven een functie \(\small f\). De gemiddelde helling van \(\small f\) tussen \(\small a\) en \(\small b\) (of op het interval \(\small [a,b]\)) is: \(\small \frac{{f(b) - f(a)}}{{b - a}}\).
In plaats van gemiddelde helling spreken we ook van gemiddelde steilheid of van gemiddelde groeisnelheid.
Helling in 4 punten
Helling in punt P
GeoGebra applet "auto1"
Groeisnelheid
figuur 1
figuur 2
Een voorwerp beweegt. De afgelegde weg \(\small s\) is een functie van de tijd \(\small t\). Neem voor het gemak maar even aan dat \(\small s\) in meters en \(\small t\) in seconden is gegeven. We willen de snelheid van het voorwerp op een zeker moment bepalen.
Als de grafiek van \(\small s\) een rechte lijn is, zoals in figuur 1, dan is dat niet zo moeilijk: de snelheid is dan de richtingscoëfficiënt oftewel de helling van die lijn. Een snelheid van \(\small 3\) m/s betekent dat de afgelegde afstand \(\small 3\) keer zo snel toeneemt als de tijd. (In \(\small t\) seconden wordt \(\small 3t\) meter afgelegd.)
Als de grafiek gebogen is, zoals in figuur 2, is het veel moeilijker: de snelheid verandert dan steeds. In de grafiek kun je de snelheid op bijvoorbeeld \(\small t=1\) bepalen door in het punt bij \(\small t=1\) de helling van de raaklijn te meten.
Dat de snelheid op \(\small t=1\) bijvoorbeeld \(\small 2\) is, betekent dat op dat moment de afstand \(\small 2\) keer zo snel toeneemt als de tijd.
Plaats, tijd en snelheid zijn begrippen uit de natuurkunde.
In de wiskunde werken we meestal met functies zonder fysische betekenis. We willen het begrip (gemiddelde) snelheid ook op dit soort functies overdragen en spreken over de (gemiddelde) groeisnelheid van een functie.
GeoGebra-applet "groeisnelheid"
De groeisnelheid van de functie \(\small f\) in het punt met eerste coördinaat \(\small a\) is de helling van de raaklijn aan de grafiek in dat punt.
Als je een formule van \(\small f(x)\) hebt, dan kun je de helling in het punt met eerste coördinaat \(\small a\) goed benaderen door de gemiddelde groei van de functie op een klein interval waar \(\small a\) in ligt uit te rekenen.
In plaats van groeisnelheid kun je ook spreken van helling of van steilheid.
Opmerking:
Met de \(\small Δ\)-notatie kunnen we dit ook zó zeggen: \(\small Δx=b−a\) en \(\small Δy=f(b)−f(a)\) en dus \(\small \frac{{f(b) - f(a)}}{{b - a}} = \frac{{\Delta y}}{{\Delta x}}\).
De gemiddelde helling van een functie \(\small f\) op het interval \(\small [a,b]\) is een quotiënt van twee verschillen namelijk \(\small Δy=f(b)−f(a)\) gedeeld door \(\small Δx=b−a\).
Daarom noemt men \(\small \frac{{f(b) - f(a)}}{{b - a}} = \frac{{\Delta y}}{{\Delta x}}\) ook wel een differentiequotiënt.
Rekenschema
We werken verder met de functie B
Gegeven de functie \(\small B\) met \(\small B(t) = \frac{1}{2}{t^2} + 2t\).
Om de helling van de grafiek van \(\small B\) in het punt met \(\small t=3\) te benaderen, kun je een rekenschema gebruiken:
\(\small t=3\)
\(\small →\)
\(\small B=10,5\)
\(\small \underline {t=3,1}\)
\(\small →\)
\(\small \underline {B=11,005}\)
\(\small Δt=0,1\)
\(\small →\)
\(\small ΔB=0,505\)
dus \(\small \frac{{\Delta B}}{{\Delta t}} = 5,05\).
Vier keer hetzelfde gezegd voor het geval \(\small t=3\).
\(\small \frac{{\Delta B}}{{\Delta t}}\) nadert tot de limiet \(\small 5\), als \(\small Δt\) nadert tot \(\small 0\);
Anders geschreven: \(\small \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta B}}{{\Delta t}} = 5\).
De oppervlakte \(\small B\) neemt toe met snelheid \(\small 5\) cm2/s.
De groeisnelheid van \(\small B\) is \(\small 5\) cm2/s.
De raaklijn aan de grafiek van \(\small B\) heeft richtingscoëfficiënt \(\small 5\).
Opmerking:
Je kunt de waarde van de groeisnelheid voor \(\small t=3\) bepalen met een rekenschema:
met een concrete waarde voor \(\small Δt\), bijvoorbeeld \(\small 0,01\):
\(\small t=3\)
\(\small →\)
\(\small B=10,5\)
\(\small \underline {t=3,01}\)
\(\small →\)
\(\small \underline {B=10,05005}\)
\(\small Δt=0,01\)
\(\small →\)
\(\small ΔB=0,05005\)
dus \(\small \frac{{\Delta B}}{{\Delta t}} = 5,005 \approx 5\).
Je krijgt een benadering.
\(\small \Delta B = 5\Delta t + \frac{1}{2}{(\Delta t)^2}\)
\(\small \frac{{\Delta B}}{{\Delta t}} = 5 + \frac{1}{2}\Delta t\) en dit nadert tot \(\small 5\) als \(\small Δt\) nadert tot \(\small 0\).
Je krijgt de exacte waarde.
Groeisnelheid
Helling van de raaklijn in een punt
De helling van een functie \(f\) in een punt met eerste coördinaat \(a\) bereken je met een rekenschema:
\(\small x=a\)
\(\small →\)
\(\small y=f(a)\)
\(\small \underline {x = a + \Delta x} \)
\(\small →\)
\(\small \underline {y = f(a + \Delta x)}\)
\(\small Δx\)
\(\small →\)
\(\small Δy=f(a+Δx)−f(a)\)
De gemiddelde helling is dan \(\small \frac{{\Delta y}}{{\Delta x}} = \frac{{f(a + \Delta x) - f(a)}}{{\Delta x}}\).
De helling van de functie \(\small f\) in het punt met eerste coördinaat \(\small a\) is: \(\small \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(a + \Delta x) - f(a)}}{{\Delta x}}\) of \(\small \mathop {\lim }\limits_{x \to a} \frac{{f(x) - f(a)}}{{x - a}}\).
Dat de twee limieten hierboven op hetzelfde neerkomen zie je als je \(\small a+Δx\) vervangt door \(\small x\).
Als \(\small Δx→0\), dan \(\small x→a\).
Voorbeeld:
Gegeven is de functie \(\small f\) met \(\small f(x) = \frac{1}{2}{x^2} + 2x\) (dat is de functie van opgave "Strook papier").
De helling in het punt met eerste coördinaat \(\small 3\) is: \(\small \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(3 + \Delta x) - f(3)}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\frac{1}{2}{{(\Delta x)}^2} + 5\Delta x}}{{\Delta x}} =\) \(\small \mathop {\lim }\limits_{\Delta x \to 0} \frac{1}{2}\Delta x + 5 = 5\)
of anders:
de helling in het punt met eerste coördinaat \(3\) is: \(\small \mathop {\lim }\limits_{x \to 3} \frac{{f(x) - f(3)}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{\frac{1}{2}{x^2} + 2x - 10\frac{1}{2}}}{{x - 3}} =\) \(\small \mathop {\lim }\limits_{x \to 3} \frac{{\frac{1}{2}(x + 7)(x - 3)}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{1}{2}(x + 7) = 5\)
Voorbeeld:
Gegeven is de functie \(\small f\) met \(\small f(x) = {x^2} - 3x + 3\).
Dan is de helling in het punt met eerste coördinaat \(\small 5\): \(\small \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(5 + \Delta x) - f(5)}}{{\Delta x}} =\) \(\small \mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{(\Delta x + 5)}^2} - 3(\Delta x + 5) - 13}}{{\Delta x}} =\) \(\small \mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{(\Delta x)}^2} + 7\Delta x}}{{\Delta x}} =\)
\(\small \mathop {\lim }\limits_{\Delta x \to 0} \Delta x + 7 = 7\).
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
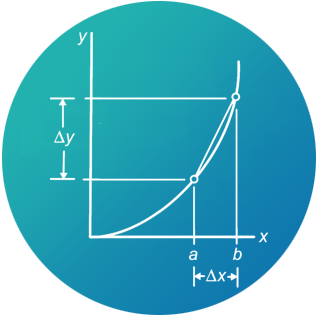
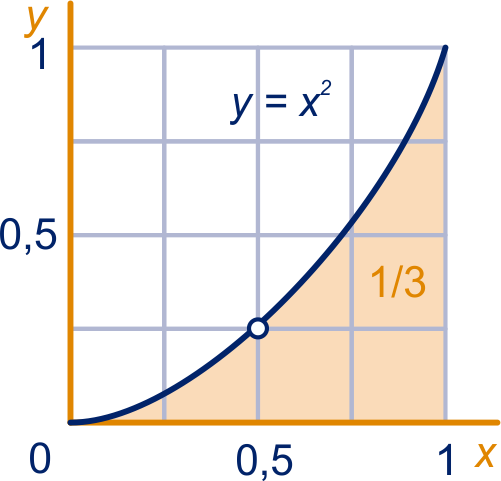We stellen de drie typen vragen die hierboven werden genoemd voor het eenvoudige voorbeeld van de parabool 
Dit soort vragen hoort thuis in de Analyse. In de zeventiende eeuw hielden zich maar enkele intellectuelen daarmee bezig. Tegenwoordig is dit een groot onderdeel van wiskunde B voor het vwo. Een groot verschil tussen toen en nu is de rekenkracht waarover we nu kunnen beschikken: computer, grafische rekenmachine. Dankzij deze snelle rekenapparatuur hebben wij niet de rekenproblemen van de wetenschappers van 3 à 4 eeuwen geleden. Zo kunnen wij gemakkelijk (?) antwoorden op de drie vragen over de parabool vinden. Maar dat zijn wel benaderingen. Het is belangrijk dat je leert hoe en vooral waarom die werken. In die benaderingsmethoden zit de sleutel tot de exacte antwoorden, en daar gaat het ons om. In dit hoofdstuk houden we ons met vragen van het eerste type bezig. De andere vragen komen in vwo5 en vwo6 aan bod.
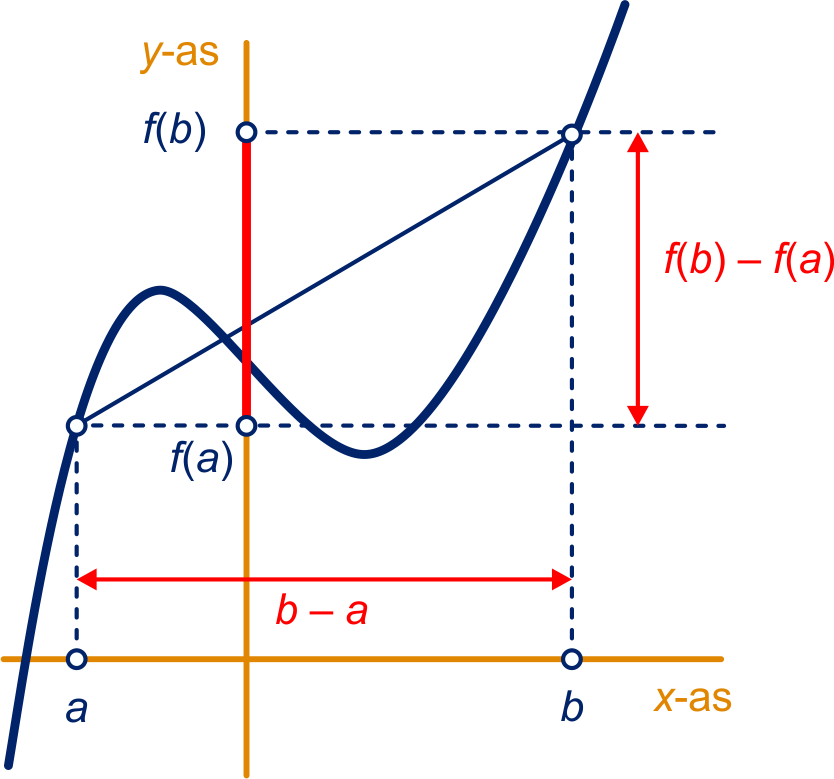
Gegeven is de functie 
