Welkom bij deze lessenserie over de verzamelingenleer!
Op deze website vind je uitgebreide informatie en uitleg over onder andere het ontstaan, de basis en de toepassing van de verzamelingenleer. Bij elke paragraaf staat ook een filmpje waarin een korte uitleg wordt gegeven. Daarnaast worden bij veel paragraven oefeningen gegeven om te kijken of je de stof goed hebt begrepen. Tot slot is er nog een diagnostische toets, waarin alle besproken onderwerpen voorbij komen. Aan het eind van deze lessenserie zal je onder andere weten waarom de verzamelingenleer zo belangrijk is, hoe deze is toe te passen en zal je er van verschillende kanten naar gekeken hebben.
Veel leerplezier!
2. Het ontstaan
Verzamelingenleer het ontstaan
2.1 Verzamelingen in de klassieke oudheid
Al een erg lange tijd wordt de verzamelingenleer gebruikt door wiskundigen; ook de Grieken gebruikten het. De Grieken definieerden bijvoorbeeld een cirkel als een verzameling van punten op een vaste afstand r van een vast punt P. Het begon met het werk van Zeno van Elea (een Griekse filosoof) rond 450 voor Christus, omdat wiskundigen in die tijd (zo ook Zeno) veel moeite hadden met het concept van de oneindigheid. Zo bleven wiskundigen door de tijd heen altijd bezig met verzamelingen.
Rond 1870 gaf Georg Cantor een nieuwe draai aan de ontwikkeling van de verzamelingenleer door zijn onderzoek naar oneindige verzamelingen. Cantor wordt gezien als de grondlegger van de verzamelingenleer met zijn artikel: “Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen” (Over een eigenschap van de belichaming van alle reële algebraïsche getallen) uit 1874. Hierin staat zijn grote ontdekking dat alle reële getallen ontelbaar zijn en oneindig. Cantor´s theorie werd niet gelijk geaccepteerd door zijn tijdgenoten en er werd erg sceptisch naar gekeken. Pas later, in de jaren 90 (van de 19e eeuw) werden delen van zijn theorie veel gebruikt, omdat ze een praktisch raamwerk boden voor een grote verscheidenheid aan wiskundige theorieën. Wiskundigen ontdekten de waarde van de verzamelingenleer (vooral in de analyse), waardoor de theorie door velen werd geaccepteerd.
Ironisch dat rond de tijd dat Cantor´s theorie eindelijk geaccepteerd leek, er paradoxen werden gevonden in zijn werk. Het russellparadox is een beroemd paradox van Bertrand Russell uit 1902 dat gaat over verzamelingen waarvan de elementen zelf ook weer verzamelingen zijn. Deze paradox zorgde voor een enorme schok in de wereld van de grondslagen van de wiskunde. De grondslagen van de wiskunde zijn de aannames, de grondbeginselen en de uitgangspunten van de wiskunde. Daarom bloeiden gedurende de vroege jaren 1900 verschillende bewegingen op met het doel het bestaan van de verzamelingen te herzien.
Een verzameling pannen, een verzameling glazen, een verzameling borden, kan je allemaal vinden in een keuken. Maar wat is nou eigenlijk een verzameling? Een verzameling is een collectie van verschillende 'dingen'. In de verzamelingenleer noem je de 'collectie' een verzameling en de 'dingen' elementen. Dus een verzameling bestaat uit verschillende elementen. De verzameling van pannen kan dus bestaan uit de elementen: koekenpan, wokpan en soeppan. Een verzameling wordt altijd weergegeven met een hoofdletter. Als we de verzameling pannen weergeven met een P en de elementen benoemen met a, b en c geldt het volgende:
P = {a,b,c}
Met een verzamelingaccolade {...} kan je een verzameling weergeven. Dus de verzameling P bestaat uit de elementen a, b en c.
De volgorde van de verzameling is niet per se van belang. Dus de verzameling Q = {b,c,a} is ook correct en gelijk aan P. Toch worden verzamelingen vaak eerder weergegeven zoals in verzameling P.
De verzameling R = {a,a,b,c,c} is wel incorrect aangezien een verzameling alleen kan bestaan uit allemaal verschillende elementen.
3.2 Eindig of Oneindig?
In de vorige paragraaf werd er besproken hoe je de verzamelingenleer kan toepassen op een verzameling pannen. Die verzameling: P = {a,b,c} is een eindige verzameling, want het aantal elementen staat vast. Maar in deze verzameling A = {1,4,9,16,25,36,...} staat het aantal elementen niet vast. Mat de puntjes na 36 wordt aangeven dat er oneindig veel elementen zijn in A. Met de genoemde elementen kan je de daarop volgende elementen zelf verder invullen.
3.3 Hoe beschrijf je een verzameling?
De beschrijvende notaties: { : } en { | } betekenen allebei hetzelfde. Met deze notatie kan je een eigenschap geven aan de verzameling.
verzameling pannen = {koekenpan, wokpan, soeppan | de pan heeft een steel)
Dit lees je als: De verzameling pannen, die bestaat uit een koekenpan, een wokpan en een soeppan, waarvoor geldt dat ze een steel hebben.
Dus uiteindelijk zou deze verzameling alleen bestaan uit een wokpan en een koekenpan
3.4 Wat is een deelverzameling? (vergelijken)
Een deelverzameling is een een verzameling uit een andere verzameling. Stel je hebt weer een verzameling van pannen. Deze verzameling kan je weer verdelen in deelverzamelingen. Bijvoorbeeld in de deelverzamelingen: keramische pannen, gietijzeren pannen en kopere pannen. Dit kan je weergeven met het teken ⊆. Met dit teken kan je verzamelingen met elkaar vergelijken.
Dus:
{kopere pannen} ⊆ {pannen}
Als A ⊆ B, is elk element van A ook een element van B.
Een ander teken dat je kan gebruiken voor een deelverzameling is ⊂. Stel: A ⊂ B. Hierbij ga je ervanuit dat B minimaal een element meer heeft dan A en dat A geen lege verzameling is.
Er zijn twee verzamelingen die worden weergegeven met speciale symbolen. Namelijk de lege verzameling: de verzameling die geen elementen bevat. En de universele verzameling: de verzameling die juist alle elementen bevat.
De lege verzameling kan worden weergegeven met het teken ∅ of met het teken {} wat letterlijk een verzameling zonder elementen voorstelt. Deze verzameling is eindig.
De universele verzameling wordt weergegeven met een U.
Nu vraag je je misschien af: Wat kan ik met deze verzamelingen?
De verzameling H= {bananen met pootjes} = ∅. Je kan dus met dit symbool aangeven dat die verzameling niet bestaat of in een bepaalde context niet van toepassing is.
Een universele verzameling is eigenlijk altijd context gebonden. Dus als je bijvoorbeeld onderzoek naar verschillende soorten guppies doet, zou je de verzameling van U kunnen beschrijven als de verzameling van van alle verzamelingen guppies. Hierin zijn de verschillende soorten guppies deelverzamelingen van U.
3.6 Waar horen de elementen bij?
Om duidelijk te maken welk element bij welke verzameling hoort, maakt men gebruik van het teken ∈.
Voorbeeld:
Je hebt weer een verzameling pannen die bestaat uit de elementen: koekenpan, wokpan en soeppan.
Hierbij geldt: soeppan ∈ {pannen}. Hier staat dan dus de soeppan is een element van de verzameling pannen.
Met het teken ∉ duid je juist het omgekeerde aan.
'braadpan ∉ {pannen}' betekent dus: een braadpan is geen element van de verzameling pannen.
4. Verdieping
4.1 Wat is een vereniging?
Verzamelingenleer verdieping deel 1
Een vereniging, ookwel een een unie genoemd, is een collectie van verzamelingen. Dat betekent dat alle elementen uit de verzamelingen in de vereniging zitten. Stel je hebt drie verzamelingen: frambozen, kiwis, en sinaasappels. De vereniging van deze drie verzamelingen bestaat dan uit alle elementen. Dus alle soorten fruit zitten dan samen in een verzameling.
Een vereniging geef je weer met een ∪. Als er staat A ∪ B dan lees je: de verzameling die bestaat uit alle element van A en van B. Kort: de vereniging van A en van B.
A ∪ B kan je in de beschrijvende notatie noteren als: {x | x ∈ A of x ∈ B}
Een doorsnede, ookwel een intersectie genoemd, is een verzameling die bestaat uit de gemeenschappelijke elementen uit verschillende verzamelingen. Stel je hebt twee verzamelingen met fruit:
Verzameling 1: Kiwi, banaan, appel, peer, sinaasappel, framboos en aardbei
Verzameling 2: Mango, ananas, framboos, kiwi, pruim, nectarine en sinaasappel
De doorsnede van deze twee verzamelingen zou dan de verzameling van een framboos een kiwi en een sinaasappel zijn.
Een doorsnede geef je weer met het symbool ∩.
A ∩ B betekent de verzameling, die bestaat uit alle element die zowel in A als in B zitten. In het kort: de doorsnede van A en B. In de beschrijvende notatie zou je dit noteren als: A ∩ B = {x | x ∈ A en x ∈ B}
Een verschil, ookwel een verschilsverzameling of een relatief complement genoemd, is een verzamling die bestaat alleen uit de element die niet ook in een andere verzameling zitten.
Bijvoorbeeld:
Je hebt weer de twee verzamelingen fruit:
Verzameling 1: Kiwi, banaan, appel, peer, sinaasappel, framboos en aardbei
Verzameling 2: Mango, ananas, framboos, kiwi, pruim, nectarine en sinaasappel
Het verschil van verzameling 1 en 2 bestaat dan uit alleen de elementen uit verzameling 1 die niet in verzameling 2 zitten, dus: banaan, appel, peer en aardbei.
Er zijn twee symbolen waarmee je een verschil weer kan geven, namelijk: - en \
A \ B lees je als: de verzameling van alle elementen uit A, die niet in B zitten. In het kort: Het verschil van A en B.
In de beschrijvende notatie kan je A \ B weergeven als {x | x ∈ A en x ∉ B}
Het verschil is altijd asymmetrisch behalve wanneer beide verzamelingen gelijk zijn aan elkaar, want dan is de verzameling van het verschil leeg.
Het symmetrisch verschil is de verzameling van elementen uit twee verzamelingen, waarvoor geldt dat de elementen uit een van de verzamelingen komt, maar niet uit beide.
Bijvoorbeeld:
We maken weer gebruik van dezelfde twee fruit verzamelingen:
Verzameling 1: Kiwi, banaan, appel, peer, sinaasappel, framboos en aardbei
Verzameling 2: Mango, ananas, framboos, kiwi, pruim, nectarine en sinaasappel
Het symmetrisch verschil zou dan bestaan uit slechts de elementen: banaan, appel, peer, aardbei, mango, ananas, pruim en nectarine
Om een symmetrisch verschil aan te geven tussen twee verzamelingen maakt men gebruik van het symbool Δ .
A Δ B lees je als de verzameling van alle elementen die in A of B zitten, maar niet in A en B.
Kardinaliteit is het aantal elementen waaruit een verzameling bestaat. Dus als je een verzameling fruit hebt:
Verzameling 1: Kiwi, banaan, appel, peer, sinaasappel, framboos en aardbei
Deze verzameling bestaat uit zeven elementen dus de kardinaliteit van deze verzameling is 7.
Als je een lege verzameling hebt is de kardinaliteit natuurlijk 0.
Dit is best simpel in een een eindige verzameling, maar hoe pas je dit toe in een oneindige verzameling?
Je kan geen letterlijk getal geven van de kardinaliteit van een oneindige verzameling, maar je kan wel iets zeggen over de kardinaliteit van de ene verzameling ten opzichte van de kardinaliteit van een andere verzameling
A = {1,4,9,16,25,36,...}
B = {2,5,10,17,26,37,...}
Hierover kan je zeggen dat de kardinaliteit van A gelijk is aan de kardinaliteit van B, aangezien B bestaat uit de element van A, maar +1.
Kardinaliteit geef je weer met het teken van de absolute waarde: |...| of met een ander teken: #
Een ander voorbeeld van de kardinaliteit van oneindige verzamelingen is:
Met het cartesisch product, ookwel productsverzameling genoemd, kan je verzamelingen vermenigvuldigen. Als je een verzameling veremenigvuldigt, doe je dit door middel van geordende paren. Geordende paren zijn combinaties van elementen, die een bepaalde volgorde hebben. Hieruit volgt dan ook dat het cartesisch product niet omkeerbaar is.
Het cartesisch product van twee verzamelingen geef je weer met het symbool: ×
Bijvoorbeeld:
Je hebt twee verzamelingen (zie de afbeelding/tabel).
De paren hebben allemaal het element uit de eerste verzameling A eerst en dan het element uit de verzameling B. B×A is dus niet hetzelfde aangezien alle paren dan omgedraaid zouden zijn.
Hierbij is elk geordend paar een element uit de verzameling van A×B. Daarom geldt er voor de kardinaliteit van het cartesisch product dat dus in dit geval zou 3*3=9 de kardinaliteit van A×B zijn.
Daarnaast geldt voor het cartesisch product dat als een van de verzamelingen oneindig is en de ander niet leeg het cartesisch product automatisch ook oneindig is.
Als je een lege verzameling keer een willekeurige andere verzameling doet is het cartesisch product ook leeg.
In de beschrijvende notatie kan je het cartesisch product weergeven als:
Zonder dat je het misschien wist maak je in de wiskunde nu al heel erg veel gebruik van het cartesisch product van ×. Aangezien de verzameling van alle reële getallen oneindig is kan je van het cartesisch product geen tabel maken. Daarvoor is een vlak gemaakt, waarbij voor elk punt op het vlak een geordend paar bestaat. Dit noemen wij ook wel een assenstelsel. Later in dit hoofdstuk komt er nog meer over reele getallen en andere bekende verzamelingen van getallen.
4.7 Wat is een machtsverzameling?
Een machtsverzameling is een verzameling die bestaat uit alle mogelijke deelverzameling van een bepaalde verzameling.
Stel je hebt een verzameling van fruit, die bestaat uit een: kiwi, framboos en een sinaasappel.
Dan zou de machtsverzameling zijn: {{},{kiwi},{sinaasappel},{framboos},{kiwi,sinaasappel},{sinaasappel,framboos},{kiwi,framboos},{kiwi,framboos,sinaasappel}}
Merk hierbij op dat er de hele verzameling en een lege verzameling bijzitten.
Een machtsverzameling noteer je met P(...), hierbij staat de P voor het Engelse woord power wat in het Nederlands macht betekent.
De kardinaliteit van een machtsverzameling is |P(A)| = \(2^n\), hierin is n de kardinaliteit in verzameling A
Als we nu weer kijken naar de verzameling fruit dan klopt dit ook, aangezien de verzameling fruit een kardinaliteit heeft van 3 en \(2^3=8\)
De kardinaliteit van een machtsverzameling is dus ook altijd groter dan de kardinaliteit van de oorspronkelijke verzameling. Dit geldt ook voor oneindige verzamelingen.
4.8 Wat zijn voorbeelden van bekende verzamelingen?
Verzamelingenleer verdieping deel 3
Natuurlijke getallen: een getal dat resulteert in een eindig aantal dingen, maar niet negatief. Het getal 0 wordt er soms wel onder geschaard en soms niet. Het wordt weergegeven met = {(0),1,2,3,4,5,...}. In deze lessenserie scharen wij het getal 0 wel onder natuurlijke getallen.
Gehele getallen: alle hele getallen rond het getal 0, dus ook negatieve getallen. Het wordt weergegeven met het symbool = {...,-3,-2,-1,0,1,2,3,...}.
Rationale getallen: de verhouding van twee getallen, waarvan het onderste getal niet 0 is. Het is altijd een repeterende breuk. Het wordt weergegeven met het symbool .
Irrationele getallen: Alle getallen, die niet te schrijven zijn in een breuk. Een bekend voorbeeld van irrationale getallen is de constante van pi.
Reële getallen: Alle irrationale en rationale getallen samen. Het wordt weergegeven met het symbool .
Complexe getallen: Een getal dat bestaat uit twee reële getallen, waarvan één getal een imaginair getal is. Als het imaginaire gedeelte 0 is, is het een reëel getal. Complexe getallen bevinden zich dus op een ander cartesisch vlak, namelijk het complexe vlak, waarbij de horizontale as de reële as is en de verticale as de imaginaire as. Het wordt weergeven met het symbool .
De relatie tussen natuurlijke getallen, gehele getallen, rationale getallen, reële getallen en complexe getallen zijn deelverzamelingen:
⊂ ⊂
Verzamelingen worden zo toegepast om getallen te kunnen sorteren in verschillende groepen.
Een complement van een bepaalde verzameling is de deelverzameling van U (universele verzameling), die bestaat uit alle elementen uit U behalve de elementen uit die bepaalde verzameling.
Stel je doet een onderzoek naar verschillende soorten fruit, dan zou de universele verzameling bestaan uit: Kiwi's, bananen, appels, peren, sinaasappels, frambozen en aardbeien.
Nu zou het complement van de verzameling van appels bestaan uit alle deelverzamelingen en losse elementen behalve uit appels.
Het complement van A geef je weer als of als\(A^c\) . De universele verzameling hoef je dus niet weer te geven in de notatie.
In de beschrijvende notatie geef je complement weer als:
Het complement is eigenlijk het verschil tussen een verzameling en de universele verzameling.
Als je het complement van het complement van een bepaalde verzameling neem krijg je weer dezelfde verzameling.
Het complement van \(U\) is leeg aangezien er niets is buiten het universum en het complement van een lege verzameling is dan dus ook gelijk aan \(U\).
Verzamelingenleer toepassing: propositielogica deel 1
Een van de toepassingen van de verzamelingenleer is te zien in de logica.
De logica is erg belangrijk in de filosofie. Het is een manier om de geldigheid van redeneringen en argumentatie te controleren. In de logica worden de onderliggende structuren van argumenten bestudeerd.
We zullen de basis van de propositielogica kort uitleggen:
Neem het voorbeeld:
1. Als het bewolkt is, dan regent het Premisse 1
2. Het is bewolkt Premisse 2
3. Dus: het regent Conclusie
Regels 1 en twee noem je de premissen. Regel 3 wordt de conclusie genoemd.
Je kunt de logische geldigheid van een redenering controleren aan de hand van de volgende regel:
Een argument is alleen geldig als het onmogelijk is dat alle premissen waar zijn en de conclusie onwaar.
Dit zegt dus niets over de feitelijke waarheid van de conclusie. Stel:
1. Als mensen zoogdieren zijn, dan zijn ze warmbloedig Premisse 1
2. Mensen zijn niet warmbloedig Premisse 2
3. Dus: mensen zijn niet zoogdieren Conclusie
Feitelijk gezien klopt dit natuurlijk niet; mensen zijn wel warmbloedig en ze zijn wel zoogdieren. Toch is de onderliggende redenatie wel logisch geldig. In het eerste voorbeeld zie je ook dat het niet om de feitelijke waarheid gaat. Het is natuurlijk niet zo dat het altijd regent als het bewolkt is. Maar omdat dit een premisse is, nemen we dit als waar aan.
Vervolgens kan je de componentzinnen vervangen door een letter. ‘(Als) het bewolkt is’ vervang je door de letter ‘p’. ‘(Dan) regent het’ vervang je door de letter ‘q’. Je krijgt dan:
1. Als p, dan q Premisse 1
2. p Premisse 2
3. Dus q Conclusie
Daarna kun je nog als p dan q weergeven zonder woorden. Dit wordt gedaan met de logische connectieven:
p en q: p ∧ q conjunctie
p of q: p ∨ q disjunctie
als p dan q: p ⊃ q materiële implicatie
niet p: ¬p negatie
p als en alleen dan als q: p ↔ q dubbele implicatie
Je krijgt dan:
1. p ⊃ q Premisse 1
2. p Premisse 2
3. Dus: q Conclusie
Er bestaan verschillende vormen van syllogismen zoals:
Modus ponens:
p ⊃ q
p
Dus: q
Modus tollens:
p ⊃ q
¬q
Dus: ¬p
Disjunctief syllogisme:
p ∨ q
¬p
Dus: q
Deze vormen zijn geldig. Wanneer een argumentatie op deze manier is opgebouwd, weet je dus meteen al dat deze geldig is.
5.2 waarheidstabellen
Verzamelingenleer de toepassing: propositielogica deel 2.1
Verzamelingenleer de toepassing: propositielogica deel 2.2
De letters p en q, maar bijvoorbeeld ook r, s, t, u ,v etc., zijn atomaire zinnen. We gaan nu kijken naar de waarheidstabellen. Hierbij worden de symbolen A en B gebruikt. Deze staan voor een willekeurige zin, die atomair (p, q, r) kan zijn of complex (p ⊃ q, p ∨ q).
Als de A voor p ∨ q staat en de B voor p ∧ q, dan staat A ⊃ B dus voor (p ∨ q) ⊃ (p ∧ q). Hierin is '⊃' de hoofdconnectief, omdat deze als laatste wordt toegevoegd.
A ⊃ B kan dus ook zijn: ((p ∧ q) ⊃ r). Hierin is het hoofdconnectief ‘⊃’. In de zin: (p ∧ q) ∨ (r ∧ s) is ‘∨’ het hoofdconnectief.
In de zin ((p ∧ (q ⊃ r)) ∨ (¬((p ∧ q) ⊃ r))) is ‘∨’ de hoofdconnectief.
In een waarheidstabel kan je de waarheidswaardes van een zin zien.
Bij negatie ziet de tabel er als volgt uit:
¬
A
¬A
waar
onwaar
onwaar
waar
Als A waar is, dan is ‘niet A’ dus niet waar. En omgekeerd: als A onwaar is, dan is ‘niet A’ waar. Stel dat A staat voor: het regent. Als A waar is, regent het dus. 'Niet A', dus het regent niet, is dan dus niet waar.
Je kan ‘waar’ weergeven met 1 en ‘onwaar’ met 0:
¬
A
¬A
1
0
0
1
Dit kan je ook voor de andere connectieven doen. Deze waarheidstabellen zien er als volgt uit:
conjunctie
∧
A
B
(A ∧ B)
1
1
1
1
0
0
0
1
0
0
0
0
'A en B' is alleen waar als A en B allebei waar zijn. Stel A is: 'ik draag een rode trui'; en B is 'ik draag blauwe schoenen'. 'Ik draag een rode trui en blauwe schoenen' (A en B) klopt dan dus alleen als ik zowel een rode trui (A) als blauwe schoenen (B) draag.
Disjunctie (let op: hier betekent ‘A ∨ B’ A en/of B):
∨
A
B
(A ∨ B)
1
1
1
1
0
1
0
1
1
0
0
0
'A en/of B' is alleen onwaar als A en B allebei onwaar zijn. Omdat 'A ∨ B' zowel 'A en B' als 'A of B' betekent, is het waar niet alleen waar als een van beiden waar is (of), maar ook wanneer ze allebei waar zijn (en).
Materiële implicatie:
⊃
A
B
(A ⊃ B)
1
1
1
1
0
0
0
1
1
0
0
1
De materiële implicatie is alleen onwaar wanneer A waar is en B onwaar is. Wanneer A waar is volgt hier namelijk meteen uit dat B ook waar is, want als A dan B.
Als A onwaar is en B waar is, klopt de materiële implicatie echter wel. A is namelijk niet het enige dat tot B kan leiden. Neem het voorbeeld:
Als robots slim zijn, dan zijn ze gevaarlijk (p ⊃ q)
Robots zijn gevaarlijk (q)
Dus: robots zijn slim (p)
Deze redenering is niet geldig. Dat robots gevaarlijk zijn, betekent niet dat ze ook slim zijn. Ze kunnen bijvoorbeeld ook gevaarlijk zijn omdat ze sterk zijn.
Dubbele implicatie:
↔
A
B
(A ↔ B)
1
1
1
1
0
0
0
1
0
0
0
1
Deze is waar als A en B dezelfde waarde hebben. A en B zijn hierbij namelijk gelijkwaardig.
Met behulp van waarheidstabellen kun je testen of een argumentvorm geldig is. We nemen als voorbeeld de Modus Tollens:
p ⊃ q
¬q
Dus: ¬p
De regel is: Een argument is alleen geldig als het onmogelijk is dat alle premissen waar zijn en de conclusie onwaar.
We maken eerst van de premissen een conjunctie:
(p ⊃ q) ∧ (¬q)
Vervolgens zetten we dit samen met de conclusie in een tabel:
(p ⊃ q) ∧ (¬q)
¬p
We stellen nu de premissen op door een 1 onder de hoofdconnectief (∧) te zetten. De conclusie stellen we op onwaar door een 0 onder de hoofdconnectief (¬) te zetten.
(p ⊃ q) ∧ (¬q)
¬p
1
0
Nu kan je de waarheidstabellen die we eerder hebben gezien gebruiken om de waarheidswaardes verder in te vullen. We zien in de waarheidstabel van negatie dat ¬p alleen onwaar is als p waar is. Onder de p vul je dus 1 in. Dit doe je vervolgens voor elke p in de tabel:
(p ⊃ q) ∧ (¬q)
¬p
1 1
01
We zien in de waarheidstabel van een conjunctie dat de conjunctie alleen waar is, als beide zinnen waar zijn. Onder de hoofdconnectieven van de zinnen (p ⊃ q) en (¬q) (⊃ en ¬) kun je dus een 1 zetten:
(p ⊃ q) ∧ (¬q)
¬p
1 1 1 1
01
In de waarheidstabel van een materiële implicatie zie je dat als p waar is, q ook waar moet zijn.
(p ⊃ q) ∧ (¬q)
¬p
1 1 1 1 1
01
En in de waarheidstabel van een negatie zie je dat als ¬q waar is, q onwaar moet zijn. Dit leidt dus tot een probleem: q moet zowel waar als onwaar zijn. Dit is onmogelijk.
Het voldoet dus aan de regel:Een argument is alleen geldig als het onmogelijk is dat alle premissen waar zijn en de conclusie onwaar.
De argumentvorm Modus Tollens is dus logisch geldig.
Deze methode kun je ook gebruiken voor andere redeneringen om erachter te komen of ze logisch geldig zijn.
6. Het nut (venndiagrammen)
Verzamelingenleer het nut
6.1 Wat is een venndiagram?
Een venndiagram is een grafische voorstelling van de logische relaties tussen meerdere verzamelingen. Bij de venndiagrammen komen ook verzamelingen die geen elementen bevatten voor (dat is niet zo bij de Euler diagrammen).
Venndiagrammen worden veel gebruikt in de kansrekening en de statistiek, de logica, de informatica en de linguïstiek. Het is de meest gebruikte methode om syllogismen (logica) op te lossen.
Informatie visueel weergeven
Het is een manier van visuele communicatie waarbij relaties worden aangetoond tussen de verzamelingen. Ze zijn erg praktisch voor presentaties en rapporten, omdat de data op een heldere, krachtige manier wordt gevisualiseerd door gebruikers.
Twee of meer keuzes vergelijken
Het spreekt wel enigszins voor zich. Venndiagrammen geven duidelijk weer wat de verzamelingen gemeenschappelijk hebben tegenover wat ze verschillend maakt. Dit kan gebruikt worden voor de selectie van een product of dienst.
Datasets vergelijken
De verzamelingenleer (en de venndiagrammen) kan worden gebruikt om correlaties te ontdekken en de waarschijnlijkheid dat iets zal gebeuren te voorspellen. Correlatie is de statistische samenhang tussen twee grootheden. Correlaties kunnen op vele manieren in de praktijk worden gebruikt, zo wordt het veel gebruikt in de economie en in de statistiek. In paragraaf 6.5 wordt uitgelegd hoe aan de hand van de verzamelingenleer de waarschijnlijkheid van een bepaalde situatie kan worden voorspeld.
Logica beredeneren
De logica is erg belangrijk in de filosofie. Het is een manier om de geldigheid van redeneringen en argumentatie te controleren. In de logica worden de onderliggende structuren van argumenten bestudeerd. Hierbij wordt de verzamelingenleer toegepast.
6.3 Gebruik in verschillende vakgebieden
Handel
Producten, processen, diensten etc. worden in een verzameling geplaatst waardoor ze makkelijker te vergelijken en te onderscheiden zijn. Zo worden kasten, banken, bedden en ga zo maar door onderverdeeld in verzamelingen, zoals in een IKEA-catalogus.
Computerwetenschap
Computertalen en hiërarchieën (classificatie) worden door middel van venndiagrammen gevisualiseerd. De wortels van de computerwetenschap zit bij de logica die onscheidbaar is van de verzamelingenleer. De data op de computers kan worden geordend en onderverdeeld in verzamelingen. De computerwetenschappen worden voor enorm veel dingen gebruikt in het dagelijks leven (in de 21e eeuw).
Taalkunde
De overeenkomsten en verschillen tussen talen worden onderzocht met behulp van de verzamelingenleer en venndiagrammen. Het wordt gebruikt om de aard van bepaalde soorten uitdrukkingen en de interactie met elkaar te beschrijven.
Er zijn in totaal 89 leerlingen in het leerjaar, waarvan 45 mensen geen biologie en geen natuurkunde hebben. 30 leerlingen hebben biologie, 27 leerlingen hebben natuurkunde en 13 leerlingen hebben biologie en natuurkunde. Deze gegevens zijn verwerkt in het onderstaande venndiagram.
De P staat voor probability, het Engelse woord voor waarschijnlijkheid.
De B staat voor biologie.
De C staat voor natuurkunde.
P (B) is de kans dat een willekeurige leerling biologie heeft.
P (B) = \({30} \over {78}\)
Voowaardelijke kansen
P (B | C) is de kans op B onder voorwaarde C, dus de kans dat een leerling biologie heeft als diegene ook natuurkunde heeft.
P (B | C) = \({P (B ∩ C)}\over {P (C)} \) = \({13}\over {27}\)
Het arrangement Verzamelingenleer is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteurs
Hera Stallmann
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-01-31 09:52:18
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
verzamelingenleer
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
| < |
|
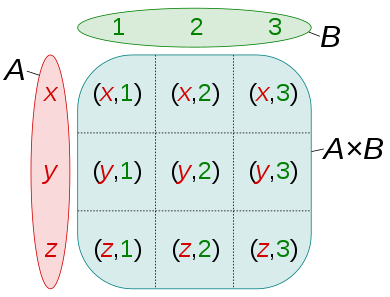
dus in dit geval zou 3*3=9 de kardinaliteit van A×B zijn.
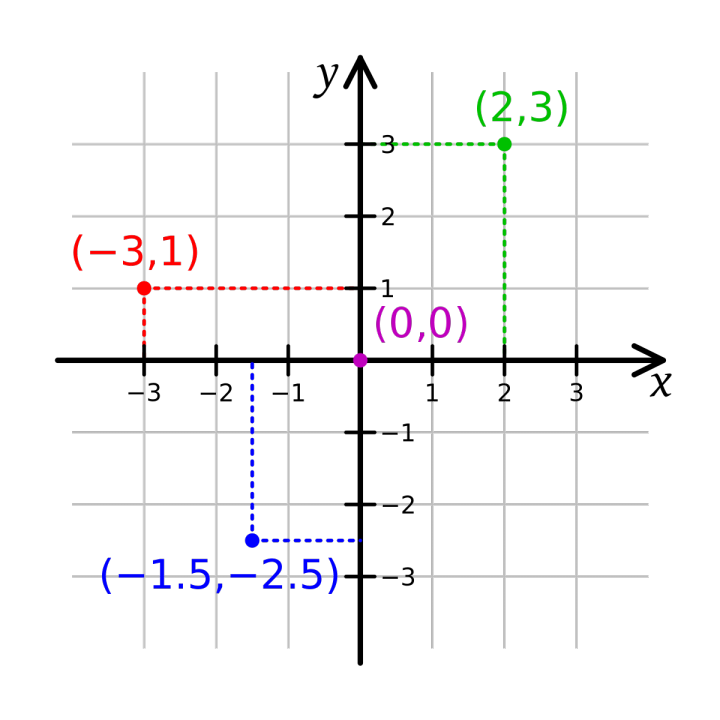
= {...,-3,-2,-1,0,1,2,3,...}.
.
.
⊂ 
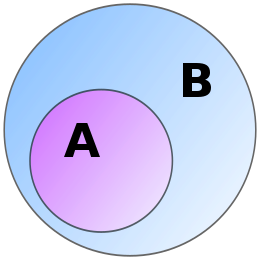
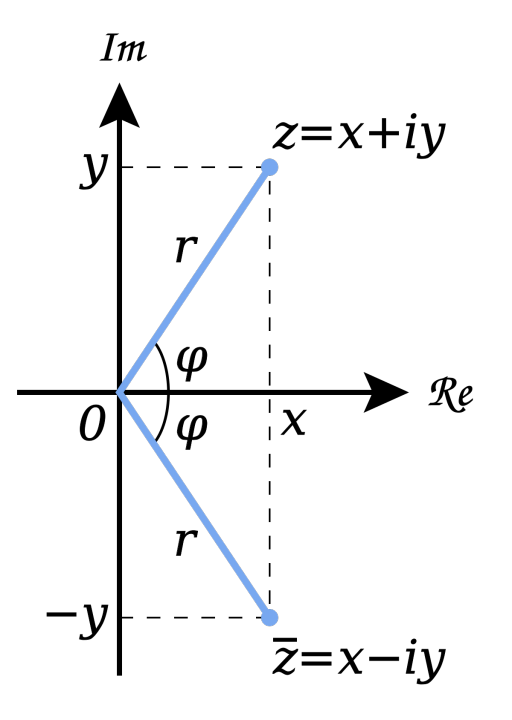
of als
