Ja, behalve hoeken meten en tekenen kun je ook hoeken berekenen. Dit doe je in vlakke figuren of in ruimte figuren. We hebben in hoofdstuk 2 al een aantal vlakke figuren behandeld.
Voor deze paragraaf kijken we naar driehoeken. We berekenen de hoeken binnen een driehoek.
1. De hoekensom.
Eerst leren we iets over de hoekjes van een driehoek. Er is namelijk een regel. Deze regel ontdekken we door samen met elkaar een opdracht uit te voeren.
Stap 1. Teken een driehoek. Het maakt niet uit hoe groot deze is, als hij maar netjes drie hoekpunten heeft.
Stap 2. Geef de hoekpunten van je driehoek een kleurtje.
Stap 3. Scheur nu de hoekjes af.
Stap 4. Puzzel er een gestrekte hoek van. (de hoekjes samen vormen een halve cirkel)
Stap 5. Conclusie. Je hebt nu bewezen dat de drie hoekjes van een driehoek samen een halve cirkel vormen. Een halve cirkel is 180o. Net als een gestrekte hoek. De hoeken van een driehoek zijn samen altijd 180o
Bekijk het filmpje hieronder nog maar eens als verduidelijking.
2. Hoeken binnen een driehoek berekenen
Nu je geleerd hebt dat de driehoeken van een driehoek samen altijd 180o zijn, kunnen we hier mooi gebruik van maken. Want weet je twee hoekjes van een een driehoek, dan kun je dus de derde berekenen. En dat is veel sneller (en soms preciezer) dan opmeten.
Bekijk het onderstaande filmpje maar eens.
Nog niet helemaal duidelijk? Bekijk dan dit filmpje even.
3. Samengestelde driehoeken
En een stapje lastiger.
Opgaven
..1.
Hoek in twee stukken gesplitst
Hiernaast zie je een rechte hoek.
Deze hoek wordt in twee stukken gedeeld.
Bereken het ontbrekende stuk van de hoek.
Schrijf de berekening netjes in je schrift.
..2.
Hoek in drie stukken gesplitst
Hiernaast zie je een gestrekte hoek. Deze wordt in drie stukken gedeeld.
Bereken het ontbrekende stuk.
Schrijf de berekening netjes in je schrift.
..3.
Hoeken binnen een driehoek berekenen.
Wanneer je de drie hoekjes van een driehoek bij elkaar optelt is dit samen altijd .... graden
Bekijk de driehoek hiernaast en bereken de ontbrekende hoek. Schrijf de berekening netjes in je schrift.
..4.
Hoeken van driehoeken berekenen
Bekijk de driehoek hiernaast.
Bereken \(\angle \space m\)
..5.
Hoeken van driehoeken berekenen
Bekijk de driehoek hiernaast.
Bereken de ontbrekende hoek. Schrijf de berekening netjes in je schrift.
..6.
Hoeken van driehoeken berekenen
Hierboven zie je drie driehoeken. In elke driehoek is één hoek nog niet berekend.
Het arrangement §5 Hoeken berekenen is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-04-06 11:13:51
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Stap 1. Teken een driehoek. Het maakt niet uit hoe groot deze is, als hij maar netjes drie hoekpunten heeft.
Nu je geleerd hebt dat de driehoeken van een driehoek samen altijd 180o zijn, kunnen we hier mooi gebruik van maken. Want weet je twee hoekjes van een een driehoek, dan kun je dus de derde berekenen. En dat is veel sneller (en soms preciezer) dan opmeten.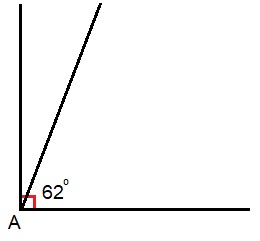
Hiernaast zie je een rechte hoek.
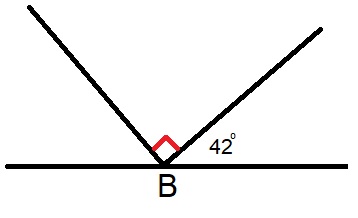Hiernaast zie je een gestrekte hoek. Deze wordt in drie stukken gedeeld.
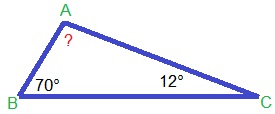Wanneer je de drie hoekjes van een driehoek bij elkaar optelt is dit samen altijd .... graden
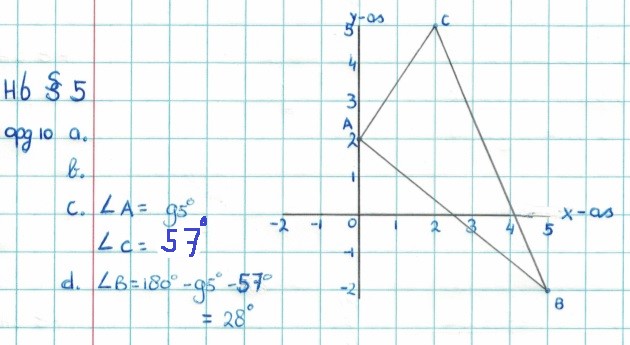
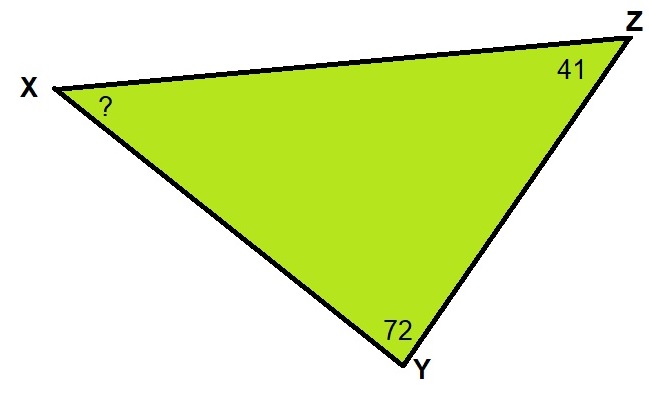Bekijk de driehoek hiernaast.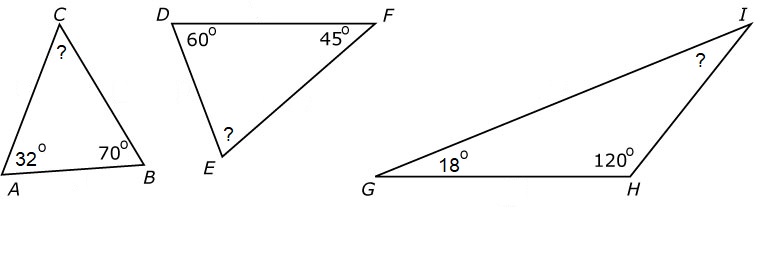
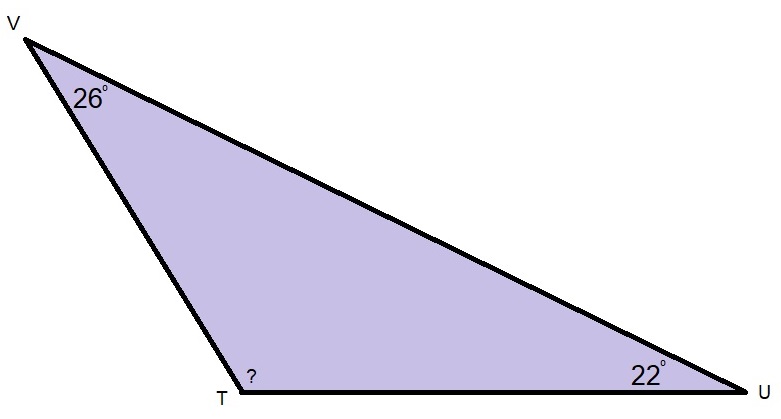
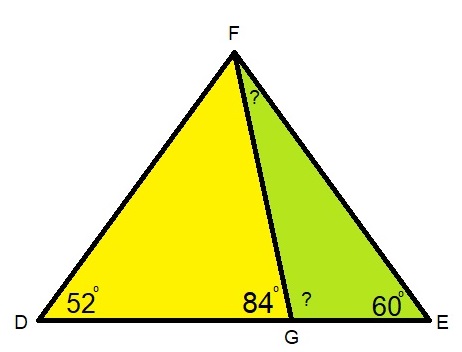
Ook hier weer een samengestelde driehoek.
