In dit thema gaan we allerlei problemen oplossen: je krijgt (woord)problemen die je leert om te zetten naar een formule. En dan kan je het probleem met wiskunde oplossen.
Maar we beginnen eerst met een antal puzzels. Probeer maar of je het antwoord kunt vinden.
Het is niet erg als je niet elke puzzel op kunt lossen. Later in dit hoofdstuk ga je juist leren hoe je dit soort puzzels systematisch kunt aanpakken. Dat hoeft nu nog niet.
Wat kan ik straks?
Aan het einde van dit thema kan je:
een vergelijking opstellen bij een beschrijving van een probleem of situatie in woorden
uitleggen wat wordt bedoeld met de oplossing van een vergelijking
de balansmethode gebruiken bij het oplossen van vergelijkingen
grafieken met vergelijkingen tekenen en aflezen
een vergelijking ook met breuken erin oplossen.
Wat kan ik al?
Je bent in de brugklas al veel formules tegengekomen.
Bijvoorbeeld bij het opstellen van een formule bij stippenpatronen, of bij een stroomschema. Ook heb je al geleerd hoe je met haakjes kunt werken.
In dit thema gaan we hiermee verder. Het is dus van groot belang om de basiskennis over formules van vorig jaar weer te herhalen.
Door deze test te maken kom je erachter wat je nog allemaal weet van vorig jaar.
Het thema Vergelijkingen bestaat uit de volgende onderdelen:
Onderdeel
Tijd in lesuren
Start
Inleiding
0,5 uur
Wat kan ik straks?
Wat kan ik al?
Wat ga ik doen?
Paragrafen
Wat is het getal x?
0,5 uur
De weegschaalmethode
0,5 uur
Vergelijkingen en grafieken
1 uur
Meer vergelijkingen
1,5 uur
Vergelijkingen opstellen
2 uur
Balansen
0,5 uur
Afsluiting
Samenvatting
Thema-opdracht
2 uur
Diagnostische toets
0,5 uur
Extra opgaven
0,5 uur
Terugblik
Totaal
9,5 uur
Gewone opgaven en Super opgaven
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
Die Super variant is wel wat moeilijker. Let op: Je hoeft dan niet ook de 'normale' variant te maken.
Je herkent de opgaven waar een Super variant van is aan dit teken
Als je op dit teken klikt, dan ga je naar de Super variant.
In de Super variant staat dit teken
Als je daarop klikt, ga je weer terug naar de gewone opgave.
De Super opgaven staan ook steeds bij elkaar onder aan iedere paragraaf.
Paragrafen
In dit thema gaan we aan de slag met Vergelijkingen.
In de volgende paragrafen leer je stap voor stap steeds moeilijkere vergelijkingen oplossen. Je leert ook om vergelijkingen op te stellen op basis van een verhaal en deze vervolgens systematischop te lossen.
Conclusie: als \(\small x=\frac{1}{4} \) zijn linker- en rechterlid gelijk, dus \(\small x= \frac{1}{4}\) is de oplossing van deze vergelijking.
Vergelijkingen opstellen en grafieken
Een energiezuinige koelkast \(\small EK\) kost € 710,-- en verbruikt € 60,-- aan stroom per jaar. Een goedkope koelkast \(\small GK\) kost € 390,-- en verbruikt € 100,-- aan stroom per jaar.
Als je de gebruikskosten wilt vergelijken met grafieken, is het handig om de volgende tabel te maken.
aantal jaren
0
5
10
15
kosten \(\small EK\)
710
1010
1310
1610
kosten \(\small GK\)
390
890
1390
1890
Bij de tabel horen twee grafieken.
Denk aan de namen bij de assen en dat elk stapje op de horizontale as hetzelfde is. Dit geldt ook voor de verticale as.
Stel dat we het aantal jaren \(\small a\) noemen. Dan zijn de kosten na \(\small a\) jaar voor \(\small EK\) gelijk aan \(\small 710+60a\) en voor \(\small GK\) gelijk aan \(\small 390+100a\).
Met een vergelijking kunnen we nu het aantal jaren uitrekenen waarbij de kosten voor \(\small EK\) en \(\small GK\) gelijk zijn.
Die vergelijking is: \(\small 710+60a=390+100a\).
De oplossing is \(\small a=8\), dus na 8 jaar.
Check in de grafiek of het antwoord kan kloppen (anders heb je misschien een rekenfoutje gemaakt).
Je kunt het antwoord controleren door de kosten van \(\small EK\) en \(\small GK\) na 8 jaar uit te rekenen.
Kosten \(\small EK\) na 8 jaar = \(710+8\times60=€1190,-\small \).
Kosten \(\small GK\) na 8 jaar = \(\small 390+8\times100=€1190,-\).
Je ziet dat de kosten na 8 jaar inderdaad gelijk zijn.
Vergelijkingen opstellen
Ton is één jaar jonger dan Janneke en elf jaar ouder dan Gerd. Samen zijn ze 92 jaar. Hoe oud is ieder?
Noem de leeftijd van Ton \(\small x\). Dan is Janneke \(\small x+1\) jaar en Gerd \(\small x-11\) jaar.
Een vergelijking voor \(x\) is dan \(\small x+(x+1)+(x-11)=92\).
De oplossing is \(\small x=34\).
Dus Ton is 34, Janneke is 35 en Gerd is 23 jaar oud.
Balansen
Als een balans in evenwicht is, dan is het product \(\small \text {plaats × aantal gewichtjes}\) links en rechts gelijk.
De balans hiernaast is in evenwicht.
De vergelijking die er bij hoort is: \(\small 2(3x+4)=3(4x+1\frac{1}{3})\)
Het arrangement Thema: Vergelijkingen - 2V is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Dit thema is ontwikkeld door auteurs en medewerkers van de Wageningse Methode.
Fair Use
In de Stercollecties van VO-content wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Wat kan ik al?
Diagnostische toets Vergelijkingen
Extra oefening Basis
Extra oefening Plus
Terugblik
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
In dit thema gaan we allerlei problemen oplossen: je krijgt (woord)problemen die je leert om te zetten naar een formule. En dan kan je het probleem met wiskunde oplossen.
Je bent in de brugklas al veel formules tegengekomen.
Het thema Vergelijkingen bestaat uit de volgende onderdelen:
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
In dit thema gaan we aan de slag met Vergelijkingen.
Voorbeeld:
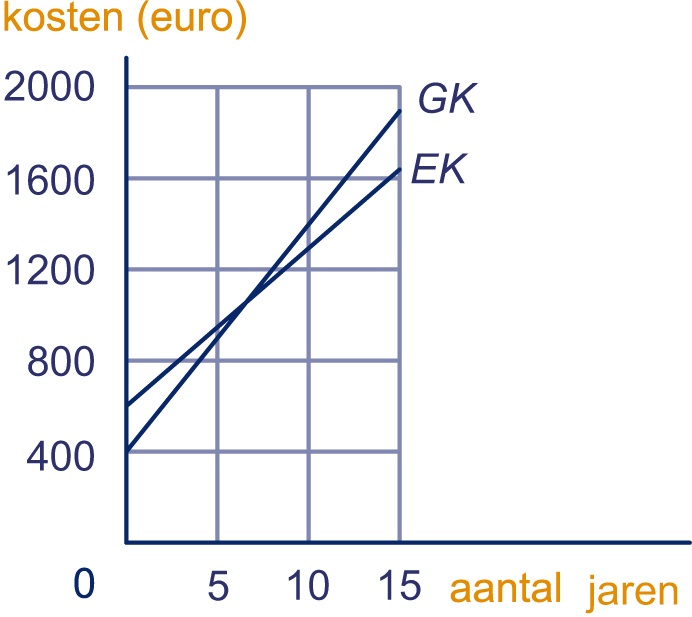Bij de tabel horen twee grafieken.
Korte, uitnodigende tekst waarin wordt uitgelegd wat in de opdracht gaat gebeuren.
Je gaat nu een aantal gevarieerde opgaven maken waarin je kunt laten zien of je de geleerde stof uit de voorgaande paragrafen beheerst.
Je ziet hier twee Extra oefeningen. Je hoeft er maar één te doen.
