Er is eigenlijk niemand in Nederland die nog nooit heeft gehoord van de stelling van Pythagoras.
Wanneer je het over wiskunde hebt, hoor je veel mensen dan ook al snel a2 + b2 = c2 roepen.
zonder dat je het door hebt heb je nu de stelling van Pythagoras gehoord. Maar ja zonder enige kennis of vaardigheden weet je natuurlijk nog niet wat dit dan precies betekent en hoe je dan een berekening maakt met die stelling.
In dit hoofdstuk leer je betekenis geven aan a2 + b2 = c2. Al zullen wij het eerder noteren als
rhz2 + rhz2 = sz2 deze afkortingen geven al veel meer betekenis aan de stelling.
De stelling van Pythagoras
Iedere middelbare scholier moet ‘m leren: de stelling van Pythagoras. Deze stelling laat zien wat het verband is tussen de zijden van een rechthoekige driehoek, namelijk: A² + B² = C². In woorden: de lengte van de korte rechthoekszijde in het kwadraad plus de lengte van de lange rechthoekszijde in het kwadraat is de lengte van de schuine zijde in het kwadraat.
Wist je dat…..
Over Pythagoras zelf zijn ook een heleboel interessante dingen te vertellen, en dat leert bijna niemand tijdens wiskunde. Daarom hier opgesomd, vijf interessante weetjes over de beste man en zijn wiskunde:
Pythagoras was de eerste echte wiskundige en filosoof met een eigen groep volgelingen. Pythagoras leefde in de zesde eeuw voor Christus was afkomstig van het Griekse eiland Samos. Zijn volgelingen, de Pythagoreeërs, werden mathematikoi genoemd. .
Pythagoras en zijn volgelingen dachten dat getallen de bouwstenen van het heelal waren, dat filosofie kan helpen bij het bereiken van geestelijke zuiverheid en dat bepaalde symbolen een mystieke betekenis hebben. .
Daarnaast hadden de Pythagoreeërs heel strikte leefregels. Ze aten geen bonen, ze raapten niets op wat gevallen was, ze raakten geen witte hanen aan, ze aten geen hele broden, ze maakten geen bloemenslingers, ze keken niet in een spiegel waar een lamp naast staat en ze wandelden niet over hoofdwegen. .
Vegetariërs werden vroeger Pythagoreërs genoemd. Het woord vegetariër werd in 1847 pas een officieel woord, toen in Engeland de Vegetarian Society werd opgericht. .
De stelling van Pythagoras is ook in de praktijk heel handig, bijvoorbeeld in de bouw. Met de stelling kun je namelijk berekeken hoe lang een ladder moet zijn bij een bepaalde hoogte te komen, of hoe veel dakpannen er op een dak gelegd moeten worden.
Leerdoelen
Aan het eind van dit hoofdstuk kan ik:
...de bekende wortels en kwadraten uit het hoofd berekenen.
...de gelijkzijdige, de gelijkbenige en rechthoekige driehoek van elkaar onderscheiden.
...de twee rechthoekszijden en de schuine zijde in een rechthoekige driehoek herkennen en benoemen. De stelling van Pythagoras erbij kunnen opschrijven.
...de onbekende lengte van de schuine zijde berekenen met de Stelling van Pythagoras.
...de onbekende lengte van een rechthoekszijde berekenen met de Stelling van Pythagoras.
...de stelling van Pythagoras toepassen in situaties, door hulplijnen te tekenen.
Werkbladen
§1 Voorkennis
Uitleg & opgaven
Inleiding
Een belangrijk onderdeel bij het kunnen werken met de stelling van pythagoras is het berekenen van kwadraten. Vandaar dat we in de voorkennis jou kennis en vaardigheden over kwadraten weer even opfrissen.
Leerdoelen
Aan het eind van deze paragraaf kan ik:
Uitleggen hoe ik een kwadraat uitreken.
Uitleggen hoe ik wortels berekenen.
De voorrangregels toepassen bij bewerkingen.
..1.
Wanneer je naar de reeks figuren hierboven kijkt, dan kun je het aantal sterren met de hand tellen. Maar het kan ook sneller. Welke berekening moet je dan maken?
Uit hoeveel sterren bestaat figuur nummer 7?
En uit hoeveel sterren bestaat figuur nummer 10?
Er is een figuur die uit 225 sterren bestaat, welk figuur nummer heeft deze figuur?
Uitleg.
Kwadraten en wortels
Als je naar opdracht 1 kijkt, dan kun je het aantal sterren vinden door deze te tellen, maar je kunt het ook berekenen met bijvoorbeeld 6 x 6 = 36 of 4 x 4 = 16 sterren.
Voor 6 x 6 kun je ook 62. Dat spreek je uit als zes in het kwadraat.
Het kwadraat van 4 is 42 = 4 x 4 = 16.
Weet jij dat 42 = 16 dan weet je ook \(\sqrt{16}\) = 4 want 4 x 4 = 16
en weet je dat 72 = 49, dan is \(\sqrt{49}\)= 7 want 7 x 7 = 49
\(\sqrt{25}\) spreek je uit als de wortel van 25
en \(\sqrt{196}\) spreek je uit als de wortel van 196
Het kwadraat en de wortel zijn elkaars tegengestelde.
Je rekenmachine heeft daar speciale knoppen voor.
..2.
Bereken zonder rekenmachine.
a.
82
c.
102
e.
142
g.
92
b.
62
d.
42
f.
72
h.
22
..3.
Bereken zonder rekenmachine
a.
\(\sqrt{64}\)
c.
\(\sqrt{121}\)
e.
\(\sqrt{225}\)
g.
\(\sqrt{49}\)
b.
\(\sqrt{9}\)
d.
\(\sqrt{81}\)
f.
\(\sqrt{4}\)
h.
\(\sqrt{144}\)
..4.
Je merkt wel dat het heel handig is om een aantal kwadraten uit het hoofd te leren. Je hoeft dan niet telkens op nieuw de berekening op te schrijven. Het scheelt je veel tijd, tijd die je kunt gebruiken om andere opgaven te maken.
Op je werkblad vindt je een tabel. Vul deze tabel in en leer de kwadraten en bijbehorende wortels uit het hoofd.
..5.
Bereken telkens de uitkomst van de opgaven hieronder. Je hoeft alleen het antwoord op te schrijven in je ruitjesschrift.
32 = ...
\(\sqrt{36}\)= ...
42 = ...
...2 = 81
\(\sqrt{...}\)= 12
52 = ...
92 = ...
\(\sqrt{196}\) = ...
\(\sqrt{4}\) = ...
...2 = 36
\(\sqrt{-81}\) = ...
\(\sqrt{...}\) = 10
132 =
...2 = 49
152 = ...
152 =
142 =
...2 = 100
\(\sqrt{25}\) =
\(\sqrt{...}\)= 25
Uitleg.
voorrangregels
Moet je een berekeningen maken waar verschillende rekentekens (bewerkingen +, -, :, x , \( \sqrt{...}\) en ...2) in worden gebruikt? Houd dan rekening met de voorrangsregel. Dit houdt in dat je de opgave niet zomaar in volgorde van links naar rechts moet uitrekenen. Sommige bewerkingen moet je namelijk eerder uitrekenen en hebben dus voorrang. Denk maar aan het verkeer. Hier moet je ook de regels goed toepassen, anders gebeuren er ongelukken
Volgorde van bewerkingen
Bereken eerst wat tussen haakjes staat.
Bereken de machten en wortels
Bereken keer en delen
Als laatste optellen en eraf.
Let wel op, we werken natuurlijk wel van links naar rechts.
Wat bedoelen we hier nu mee?
voorbeeld:
6 - 4 + 10 =
We zien hier een opgave met daarin - en + , deze bewerkingen staan op dezelfde hoogte in ons schema, ze zijn dus gelijkwaardig. In dat geval werken we van links naar rechts, dus wat we het eerste tegen komen.
6 - 4 + 10 =
2 + 10 = 12
Je ziet ook hoe we een bewerking met voorrangregels uitschrijven.
In het filmpje hiernaast wordt het allemaal nog eens stapje voor stapje voorgedaan.
Doe hier je voordeel mee. Kijk, zet stop en probeer. Kijk opnieuw, zet eens op pauze en spoel terug. Op deze manier leer jij jezelf deze techniek aan.
..6.
Weet je de afspraken nog?
Trek een kantlijn van minimaal 2 hokjes.
Schrijf de opgave hieronder over in je schrift, bereken stap voor stap de uitkomst.
-72 : -9 x -4 =
-16 : 8 x -5 + -16=
94 - -45 : 9 x 4 =
3 x -3 - 6 x -5 =
-21 : 7 + 8 x -3 =
..7.
Hieronder zie je de opgave 14 + 16 : 8 x 2 op twee manieren uitgewerkt.
Welke manier is goed?
Manier 1
Manier 2
14 + 16 : 8 x 2 =
14 + 16 : 16 =
14 + 1 = 15
14 + 16 : 8 x 2 =
14 + 2 x 2 =
14 + 4 = 18
..8.
( 5 + 8 ) x 4 =
6 x 3 + √25 =
26 − 12 : 6 =
14 + 24 : 8 x 2 =
2 + ( 2 + 5 ) x 32 =
..9.
Hieronder zie je de opgave (-6 + 10) x 5 : \(\sqrt{4}\) = op twee manieren uitgewerkt.
Welke manier is goed?
Manier 1
Manier 2
(-6 + 10) x 5 : \(\sqrt{4}\) =
4 x 5 : \( \underline {\sqrt{4}}\) =
4 x 5 : 2 =
20 : 2 = 10
(-6 + 10) x 5 : \(\sqrt{4}\) =
4 x 5 : \(\sqrt{4}\) =
20 : \( \underline {\sqrt{4}}\) =
20 : 2 = 10
..10.
(8 + 3)² - 54 : 9 - \(\sqrt{16} \) =
46 - 4² + 42 : \(\sqrt{36}\) =
(-4)² - 32 : 8 + 2 + (8 - 3)² =
(52 - 7) : 5 - 4² : 2 =
56 - 10² + \(\sqrt{36}\) x 5 - 4² =
Extra herhaling.
Onderstreep het deel dat je uitrekent, zet onder dat deel de uitkomst en ga daarna verder met de volgende bewerking.
Voorbeeld:
2 x ( 8 + 2 ) - 32 = Eerst tussen haakjes uitrekenen.
2 x 10 - 32 = kwadraten en wortels berekenen.
2 x 10 - 9 = keer en delen.
20 - 9 = 11 plus en min.
..11.
-5 x \(\sqrt{81}\) + - 12 : -2 - -8 =
-3 x (5 + 4) - -14 : -2 - -6 =
36 : \(\sqrt{9}\) x (-2 + -3) - 6 =
(-37 - -10) : -3 - - 48 : -8 =
- 3 x (3 - 4) + \(\sqrt{144}\) : -3 =
..12.
Hieronder zie je de opgave 3 x 8 - 42 : 2 op twee manieren uitgewerkt.
Welke manier is goed?
Manier 1
Manier 2
3 x 8 - 42 : 2 =
3 x 8 - 16 : 2 =
3 x 8 - 8 =
24 - 8 = 16
3 x 8 - 42 : 2 =
3 x 8 - 16 : 2 =
24 - 16 : 2 =
24 - 8 = 16
Antwoorden
§2 Driehoeken
Uitleg & opgaven
Inleiding.
De stelling van pythagoras passen we toe in een driehoek, niet zomaar in elke driehoek, maar in een bijzondere driehoek. Deze paragraaf gaat dan ook over verschillende soorten driehoeken.
Leerdoelen.
Ik kan een rechthoekige- gelijkbenige- of gelijkzijdige driehoek herkennen.
Ik kan de eigenschappen van een rechthoekige- gelijkbenige- of gelijkzijdige driehoek benoemen.
Ik kan een rechthoekige- gelijkbenige- of gelijkzijdige driehoek tekenen.
Uitleg.
Soorten driehoeken
Elke figuur met driehoekpunten hoort tot de driehoeken. Driehoeken kunnen dus in allerlei soorten en maten voorkomen. Toch kunnen we een aantal driehoeken indelen in catergorieën
Gelijkbenige driehoek
Gelijkzijdige driehoek
Rechthoekige driehoek
Een gelijkbenige driehoek is een driehoek met:
twee gelijke zijden
PR en QR
twee gelijke hoeken \(\angle\)P en \(\angle\)Q
de basishoeken
één symmetrieas
de symmetrieas gaat door detophoek\(\angle\)R
Een gelijkzijdige driehoek is een driehoek met:drie gelijke zijden
drie gelijke hoeken
drie symmetrieassen
De drie hoeken van een gelijkzijdige driehoek zijn 180o : 3 = 60o
Een rechthoekige driehoek is een driehoek waarvan één van de hoeken 90o is.
Je herkent de rechthoek aan het loodrechttekentje
( of )
Een symmetrieas is de lijn waarlangs je de figuur kunt dubbelvouwen. We noemen dit ook wel lijnsymmetrie of vouwsymmetrie.
..1.
Bekijk de driehoeken op je werkblad.
Zet tekentjes in zijden die even lang zijn.
Zet een rechte hoek teken in de rechte hoek.
Zet een • of een ο in hoeken die even groot zijn.
Teken met rood kleurpotlood de symmetrieas(sen) in de driehoeken.
Zet de juiste naam onder de driehoek.
..2.
Bekijk de driehoek op je werkblad. Dit is een gelijkbenige driehoek.
Zet het woordje tophoek bij de juiste hoek.
Teken de symmetrieas in de driehoek.
Welke twee hoeken zijn even groot?
Hoe noemen we de hoeken die even groot zijn bij een gelijkbenige driehoek?
..3.
Bekijk de driehoek op je werkblad. Dit is een gelijkzijdige driehoek.
Zet even lang tekentjes in zijden die even lang zijn.
Teken de symmetrieassen in de driehoek.
Zet even groot tekentjes in hoeken die even groot zijn.
Schrijf onder de driehoek de eigenschappen uit de uitleg over die bij deze driehoek horen.
..4.
Bekijk de figuur. ΔPQR is een gelijkbenige driehoek.
Welke hoek is de tophoek?
Welke benen zijn even lang?
Welke hoeken zijn even groot?
..5.
Teken in een passend assenstelsel de punten A(1 , 1), B(1 , 7) en C(4 , 5).
Verbind punt A met punt B, punt B met punt C en punt A met punt C zodat ΔABC ontstaat.
Meet de zijden van je driehoek met je geodriehoek.
Wat voor soort driehoek is ΔABC?
Zet even lang tekentjes in benen die even lang zijn.
Zet het woordje tophoek bij de juiste hoek.
Zet even groot tekentjes in hoeken die even groot zijn.
Uitleg.
Zijden benoemen
Wanneer we beter naar een rechthoekige driehoek kijken dan kunnen we de verschillende zijden van de driehoek een naam geven.
De twee zijden die vast zitten aan de rechte hoek, noemen we de rechthoekszijden.(rhz)
De zijde tegenover de rechtehoek, noemen we de schuine zijde (hypotenusa). (sz)
Waarom je de zijden moet kunnen benoemen? Dit heeft te maken met het hoofdonderwerp van dit hoofdstuk: de stelling van Pythagoras en het onderwerp goniometrie dat we in klas 3 behandelen.
..6.
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
Zijde PQ is een ...............zijde.
Zijde QR is een ........... zijde.
...... is de rechte hoek
De letter .... komt niet voor in de schuine zijde.
De schuine zijde is ............. .
..7.
Bekijk de driehoek op je werkblad.
Zet de juiste afkortingen bij de zijden:
Rechthoekzijde - rhz en schuine zijde - sz
..8.
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
De twee rechthoekzijden zijn ......... en .......... .
\(\angle\)S is de ...........
QR is de ........ zijde.
..9.
Bekijk de driehoek hiernaast. Beantwoord daarna de vragen in je schrift.
Zijde BC is een ...............zijde.
Zijde AC is de .................zijde.
...... is de rechte hoek
Zijde AB is een ........... zijde.
De letter .... komt niet voor in de schuine zijde.
..10.
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
De twee rechthoekzijden zijn ......... en .......... .
\(\angle\)S is de ...........
QR is de ........ zijde.
..11.
Bekijk de driehoek hiernaast, de driehoek is een samengestelde driehoek.
Welke drie rechthoekige driehoeken herken je?
Bekijk ΔKRM. Welke zijde is nu de schuine zijde?
Bekijk ΔKLM. Welke twee zijden zijn nu de rechthoekszijden?
Bekijk ΔRLM. Welke hoek is de rechte hoek?
Neem je werkblad voor je en vul het schema in.
Uitleg.
Soorten driehoeken tekenen.
Tot slot, hoe teken je nu eigenlijk een gelijkbenige- of een gelijkzijdige driehoek.
Voor het tekenen van een driehoek waarvan je de lengte van 2 benen of van alle zijden al weet, gebruik je de passer.
Hoe je precies met je geodriehoek, potlood en passer te werk gaat wordt in het filmpje hieronder voor gedaan.
..12.
Teken met behulp van je potlood, geodriehoek en passer een gelijkzijdige driehoek met zijden van 5 cm. Noem de driehoek PQR
Teken met rood kleurpotlood de drie symmetrieassen in je driehoek.
..13.
Teken met behulp van je potlood, geodriehoek en passer een gelijkbenige driehoek met benen van 4 cm. Noem de driehoek ABC
Teken met rood kleurpotlood de symmetrieas in je driehoek.
Zet tekentjes in de basishoeken.
Zet met een pijltje de tophoek erbij.
..14.
Op je werkblad is het begin van een gelijkbenige driehoek ABC getekend en het begin van een gelijkzijdige driehoek PQR getekend. Maak deze driehoeken af. Laat de lijntjes van je passer staan. Dus niet weggummen.
..15.
Teken met behulp van je potlood, geodriehoek en passer:
Een gelijkbenige driehoek ΔKLM met benen van 6 cm.
Een gelijkzijdige driehoek ΔABC met zijden van 4 cm.
Een gelijkbenige driehoek ΔPQR met benen van 4,5 cm.
Een gelijkzijdige driehoek ΔXYZ met zijden van 3,5 cm.
Antwoorden
§3 De stelling van Pythagoras
Uitleg & opgaven
Inleiding.
Leerdoelen:
Bewijs
Nu je weet wat de stelling van Pythagoras is laat ik je het bewijs zien,
want we nemen het niet alleen maar aan. Bij wiskunde wil je (door middel van) met de berekening altijd laten zien dat jouw gevonden antwoord klopt. Hieronder dus een filmpje met het bewijs van de stelling.
In de animatie hieronder zie je dat de oppervlakte van de twee kleine vierkanten (de vierkanten die vast zitten aan de rechte hoek) even groot zijn als de oppervlakte van het grote vierkant (die vast zit aan de schuine zijde)
Het arrangement 2KGT H03 Pythagoras is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-07-16 19:29:07
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Iedere middelbare scholier moet ‘m leren: de stelling van Pythagoras. Deze stelling laat zien wat het verband is tussen de zijden van een rechthoekige driehoek, namelijk: A² + B² = C². In woorden: de lengte van de korte rechthoekszijde in het kwadraad plus de lengte van de lange rechthoekszijde in het kwadraat is de lengte van de schuine zijde in het kwadraat.
De stelling van pythagoras passen we toe in een driehoek, niet zomaar in elke driehoek, maar in een bijzondere driehoek. Deze paragraaf gaat dan ook over verschillende soorten driehoeken.
of 
)
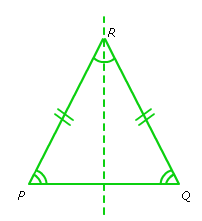
Bekijk de figuur. ΔPQR is een gelijkbenige driehoek.
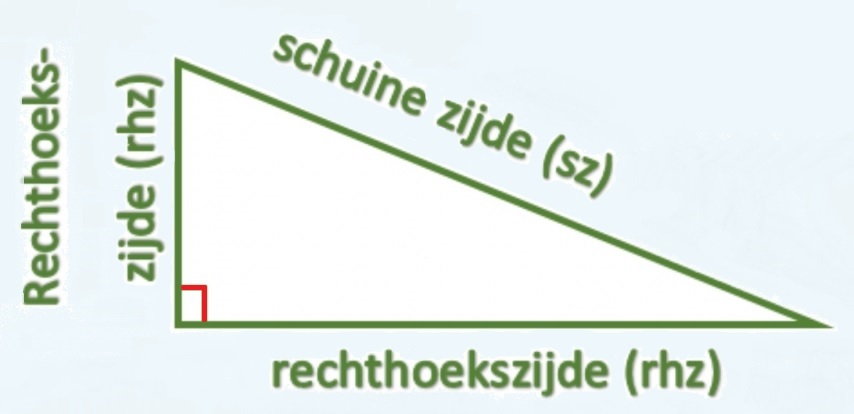
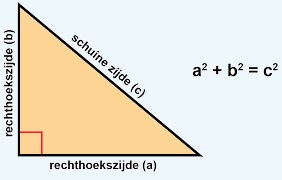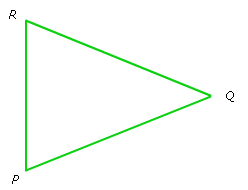
Waarom je de zijden moet kunnen benoemen? Dit heeft te maken met het hoofdonderwerp van dit hoofdstuk: de stelling van Pythagoras en het onderwerp goniometrie dat we in klas 3 behandelen.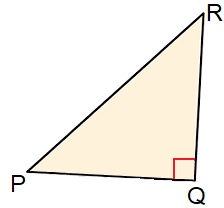
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
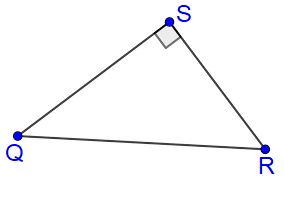Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
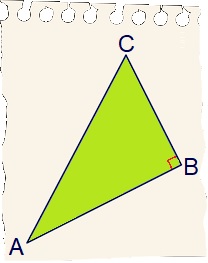Bekijk de driehoek hiernaast. Beantwoord daarna de vragen in je schrift.
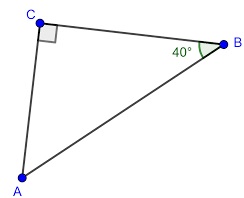Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
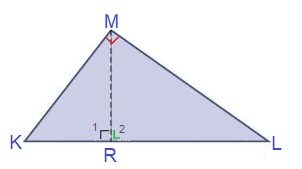Bekijk de driehoek hiernaast, de driehoek is een samengestelde driehoek.
