Wiskunde houdt zich niet alleen bezig met getallen, figuren, regeltjes of afspraken maar ook met lijnen en vormen. In hoofdstuk 2 heb je al eens gewerkt met lijnen, in hoofdstuk 6 kijken we wat er gebeurt wanneer twee lijnen elkaar raken.
Wanneer twee lijnen elkaar raken, ontstaat er namelijk een hoek. Er zit een bepaalde ruimte tussen die twee lijnen. Die ruimte tussen de twee snijdende lijnen noemen we een hoek. Deze kunnen we meten, tekenen en berekenen.
Hoofdstuk 6 gaat dus over hoeken. Een belangrijk stuk gereedschap dat we nagenoeg iedere les gebruiken is de geodriehoek. Zorg er dus voor dat je deze op een handige plek opbergt zodat je deze niet kwijt raakt en de geodriehoek niet beschadigd.
Veel plezier en veel succes.
Leerdoelen
Aan het eind van dit hoofdstuk kan ik:
In een assenstelsel verschillende punten tekenen.
Kan ik loodrechte en evenwijdige lijnen benoemen en tekenen (door een aangegeven punt)
De hoek tussen de wijzers van een klok berekenen.
Kijklijntjes bij een aangegeven figuur tekenen.
Met kijklijntjes het zichtsveld van iemand bepalen.
Vier verschillende soorten hoeken benoemen.
Met behulp van een geodriehoek een hoek meten.
Met behulp van een geodriehoek een hoek tekenen.
In een enkelvoudige driehoek de hoeken berekenen.
In een samengestelde driehoek de hoeken berekenen.
Werkbladen
De werkbladen worden altijd aan het begin van het hoofdstuk uitgedeeld.
Zorg er voor dat je deze netjes in een multomap of in een snelhechter bewaard, zo is je werk netjes verzorg en raak je niet snel iets kwijt.
Toch kwijt geraakt? Bekijk hieronder het werkblad en teken het in je schrift na!
Of, print de werkbladen opnieuw uit.
§1 Voorkennis
Uitleg & opgaven
Inleiding
In de voorkennis herhalen we stukje van de wiskunde die je op de basisschool al geleerd hebt of een stukje van de wiskunde dat al eens in een voorgaand hoofdstuk behandeld is.
Zie het maar als het afstoffen van je boekenplanken. Je verfrist weer wat je weet en je hebt je kennis weer paraat.
We frissen vandaag onze kennis over lijnen op.
Uitleg.
En in hoofdstuk 1 heb je kennis gemaakt met het assenstelsel, heb je geleerd wat de x-as en y-as is en hoe je een punt in het assenstelsel moet noteren.
In dit filmpje wordt je kennis over assenstelsels en coördinaten nog eens verfrist
.1.
Assenstelsel
Hoe noemen we de verticale as van het assenstelsel?
Bij het punt waar de twee assen elkaar raken staat de letter O. deze staat voor ....
Teken in je schrift een x-as van -4 tot 4 en een y-as van -3 tot 5.
Zet in het getekende assenstelsel de volgende punten: A(3, 5), B(-2 , -3), C(0 , 2), D( 3, -2) en E( -1,5 ; 0)
Welk van bovenstaande punten is geen roosterpunt?
Welke punt ligt op de y-as?
En welk punt ligt op de x-as?
4 hokjes links en twee hokjes naar beneden van punt A ligt punt F. Teken punt F in je assenstelsel erbij.
Uitleg
Ook weet je wat loodrecht, even lang en evenwijdig betekend en dat we dit aangeven met verschillende tekentjes.
In het filmpje hiernaast wordt het allemaal nog eens herhaald.
..2.
Mikadostokjes
Bekijk het spelletje mikado hiernaast.
Noteer de antwoorden op de vragen hieronder in je ruitjesschrift.
Liggen stokje 1 en 3 loodrecht op elkaar?
Liggen stokje 4 en 8 evenwijdig aan elkaar?
Maken stokje 2 en 4 een loodrechte hoek met elkaar?
Liggen stokje 2 en 8 evenwijdig aan elkaar?
Liggen stokje 1 en 4 loodrecht op elkaar?
Liggen stokje 3 en 6 evenwijdig aan elkaar?
Welke twee stokjes liggen nog meer evenwijdig aan elkaar?
..3.
Mikadospel
Bekijk de afbeelding hiernaast.
Noteer een paar evenwijdige lijnen.
Noteer twee paar loodrechte lijnen.
..4.
Evenwijdig tekenen
Op het werkblad zie je lijn r met daarbij de punten A en B.
Teken door A de lijn j evenwijdig aan r.
Teken door B de lijn e evenwijdig aan lijn r.
..5.
Loodrecht tekenen
Op het werkblad zie je lijn m met daarbij de punten K en H.
Teken door punt K de lijn f loodrecht op lijn m.
Teken door punt H de lijn p loodrecht op lijn m.
..6.
Bij Barendrecht wordt een nieuwe wijk gebouwd.
Op je werkblad zie je een kaartje waar de wijk moet komen. De hoofdwegen zijn al getekend in het kaartje.
Teken bij punt A een loodrechte weg op de IJzerweg.
Teken bij punt B een evenwijdige weg aan de plastikdijk.
Uitleg.
Weet je het nog? In hoofdstuk 2 van dit jaar heb je het verschil geleerd tussen een lijn, een halve lijn en een lijnstuk.
..7.
lijnen tekenen
Teken in je schrift lijnstuk PQ van 6 cm lang.
Teken een loodrechte lijn op lijnstuk PQ in je schrift. Vergeet het loodrechttekentje niet.
Teken een evenwijdige lijn aan lijnstuk PQ in je schrift. Vergeet het evenwijdig tekentje niet.
..8.
Assenstelsel
Teken de volgende punten in een assenstelsel.
A( 4 , 2), B( -4 , 2), C( 1, -2) en D( -2 , 4)
Verbind punt A met punt B zodat lijnstuk AB ontstaat.
Teken door C de lijn g evenwijdig aan lijnstuk AB.
Teken door D de lijn k loodrecht op lijnstuk AB.
..9.
Teken een lijn a met een punt R op die lijn. Teken een punt S dat niet op lijn a ligt. Teken een lijn door punt S loodrecht op lijn a . Noem die lijn n .
Teken een lijn door punt R loodrecht op lijn a . Noem die lijn t.
Wat weet je nu van de lijnen n en t ?
Antwoorden
§2 Hoeken
Uitleg & opgaven
Inleiding
In de tweede paragraaf van dit hoofdstuk gaat het over hoeken.
Wist jij dat wanneer je om je heen kijkt je te maken krijgt met een hoek.
We leren dus het een en ander over je zichtsveld maar ook over de hoek tussen de wijzers van een klok. Hoeken kom je namelijk op allerlei plaatsten tegen.
Tot slot leren we verschillende hoeken herkennen en benoemen.
Wijzers van de klok.
Een analoge klok heeft wijzers. Deze wijzers draaien rond. Met behulp van de wijzers kun je de tijd aflezen.
Wanneer een wijzer helemaal ronddraait legt deze 360o af.
Op de klok hiernaast staat de grote wijzer boven aan (op de twaalf) en de kleine wijzer op twee. We kunnen nu de ruimte tussen de wijzers berekenen.
De ruimte tussen de wijzers noemen we de hoek van de wijzers. Deze bereken je in graden. Je weet immers dat wanneer een wijzer helemaal ronddraaid deze 360o aflegt.
Leer het volgende feitje uit het hoofd: Een hele cirkel is 360o.
De cijfers op de klok, dus de 1 en 2 en 3 enzovoorts, verdelen de klok in 12 gelijke stukken.
Om de grootte van 1 zo’n stuk te berekenen, moet je 360o delen door 12. Je komt dan uit op 30o.
Om 2 uur is die hoek 2 keer zo groot, dus 30o x 2 =60o.
En om 5 uur is de hoek 5 keer zo groot, dus 30o x 5 =150o.
Om 8 uur is de hoek KLEINER dan om 5 uur. We gaan namelijk altijd uit van de kleinste hoek tussen de wijzers.
Van 8 naar 12 zijn 4 stukjes van 30o, dus 30o x 4 =120o
..1.
Wijzers van de klok
Over hoeveel graden draait de grote wijzer van een klok in:
één uur?
tien minuten?
één minuut?
..2.
Hoek tussen de wijzers
Bereken hoe groot de hoek is tussen de wijzers van een klok om.
4 uur
10 uur
..3.
Wijzers van de klok
Bereken de hoek tussen de wijzers van de klok om
5 uur
8 uur
..4.
Wijzers van de klok
Wanneer de klok niet op een heel uur staat maar bijvoorbeeld op een half uur of op een kwartier (een kwart) dan wijst de kleine wijzer ook niet meer precies het getal aan.
Om kwart over 4 staat de grote wijzer op kwart over (15) en de kleine wijzer is een klein stukje voorbij de vier geschoven. Ook dan kun je berekenen hoeveel graden er tussen de kleine en grote wijzer past.
Tussen de grote en de kleine wijzer zit één heel uurstreepje dat is 360o : 12 = 30o
De kleine wijzer is een kwart van een heel uur streepje verschoven dus:
30o : 4 = 7,5o.
In totaal zit er dus 30o +7,5o = 37,5o tussen de kleine en grote wijzer.
Bereken nu zelf bij de volgende twee klokken hoeveel graden er tussen de wijzers zit.
Kijkhoek en gezichtsveld.
Wanneer je om je heen kijkt heb je ook te maken met hoeken. Je kunt bijvoorbeeld niet om de hoek van het lokaal kijken of door een muur heen. Sommige objecten (spullen, dingen) zorgen er voor dat je delen niet kunt zien. Net als wanneer er een heel groot persoon voor je staat.
In de voorbeelden hierboven spreken we over je gezichtsveld. Dat is het gebied dat je kunt zien zonder je hoofd of je ogen te bewegen. Wanneer iets of iemand voor je staat dan beneemt deze een deel van je zicht.
Onze ogen zitten voor in ons hoofd. Daarom kunnen we het gebied dat recht voor je neus is goed waarnemen Dit gebied (blauw in het plaatje) wordt door bijde ogen gezien. Nadert er iets van de zijkant dan zie je het minder scherp. Het wordt dan maar waargenomen door 1 oog.
Wanneer je het gezichtsveld gaat tekenen, teken je dus twee lijnen vanuit het puntje van je neus. Je neus zit namelijk midden tussen je ogen.
Je kunt niet door muren heen kijken dus de kijklijnen teken je langs de puntjes van de muur.
Houdt ook rekening met de plaats waar je staat. Dit bepaald namelijk wat je wel en niet kunt zien en hoe groot je kijkhoek is.
Hoe verder je van de opening in de muur staat, hoe kleiner de hoek wordt die je kunt zien.
..5.
Kijklijnen
Bekijk de afbeelding. Deze staat ook op je werkblad.
Teken het zichtveld dat je hebt vanuit punt A.
Teken ook het zichtveld uit punt B.
Vanuit welk punt kun je de meeste schapen zien? Noteer de letter in je ruitjesschrift
..6.
Kijklijnen
Bekijk de afbeelding. De afbeelding staat ook op het werkblad afgedrukt.
Geef met kijklijnen aan welke fietser wel en welke fietser niet gezien wordt door de automobilist.
Bekijk de afbeelding. De afbeelding staat ook op het werkblad.
Je ziet de plattegrond van een huis. Achter elk raam is een stip getekend. Dat is het punt van waar je door het raam naar buitenkijkt. Vier van deze punten zijn genummerd met de cijfer 1, 2, 3 en 4. Teken vanuit deze punten de kijklijnen die horen bij het van het zichtveld.
Herhaling uitleg.
Hieronder zie je een voorbeeld van iemand die door twee ramen kijkt. Je kan goed zien wat Jan wel en niet kan zien. Myrthe en Mathijs ziet hij wel staan, Merel ziet hij niet staan.
..7.
Kijklijnen
Bekijk de afbeelding. Deze staat ook op het werkblad.
Je ziet hier een plattegrond van een supermarkt. De supermarkt wordt beveiligd met camera's en beveiligers. Teken in elke kamer de kijklijnen. Doe hetzelfde met de bewakers.
Welke klanten worden niet door een bewaker of camera gezien? Noteer het aantal in je schrift.
..8.
Beveiliging
Bekijk de afbeelding. Deze is ook afgedrukt op het werkblad.
Op deze plattegrond zie je een museum. In de ruimte rechtboven is een gouden ster tentoongesteld. Het is aan jou de taak om ongezien (door de camera's) bij de gouden ster te komen. Teken in iedere camera de kijklijnen en stippel daarna je route naar de gouden ster uit.
Van twee camera's is het zichtveld al getekend.
Een hoek.
Wanneer we spreken over een hoek, dan bedoelen we de ruimte tussen twee snijdende lijnen.
Een hoek bestaat dus uit twee lijnen. Deze lijnen noemen we de benen van de hoek.
Een hoek meet je in graden. Dit doe je met je geodriehoek.
hoe precies? dat leren we in een andere paragraaf. Voor nu concentreren we ons eerst op de vorm van de hoek.
We kennen verschillende soorten hoeken.
In het filmpje hiernaast wordt dat perfect uitgelegd.
Het plaatje hieronder is een samenvatting van de uitleg uit het filmpje.
Handig om over te nemen in je schrift en te leren.
..9.
Benoem de hoeken.
Bekijk de afbeelding hiernaast. Schrijf in je wiskunde schrift van ieder hoek op of het een gestrekte hoek, stompe hoek, rechte hoek of scherpe hoek is.
\(\angle \space A =\)
\(\angle \space B=\)
\(\angle \space C=\)
..10.
Hoeken in een bootje.
Hiernaast zie je een bootje. In dit bootje zijn 7 hoeken verstopt. De hoeken hebben allemaal een hoofdletter.
Welke hoeken zijn scherp, noteer de letters in je schrift.
Welke hoeken zijn stomp, noteer de letters in je schrift.
Zijn er ook rechte hoeken? Noteer de letters in je schrift.
Kun je ook gestrekte hoeken vinden, noteer dan de letters in je schrift.
..11.
Hoeken tussen de wijzers van de klok
Als je naar een analoge klok kijkt, een analoge klok is een klok met wijzers, dan maken de wijzers van de klok ook een hoek met elkaar. Bekijk het plaatje van de zes klokken hiernaast.
Noteer in je schrift van iedere tijd of de wijzers een scherpe, stomp, rechte of gestrekte hoek met elkaar maken.
..12.
Hoeken zonder klok
Bedenk nu zelf, als het je echt niet lukt, schets het dan in je schrift of gebruik het klokje
a. Wat voor soort hoek maken de wijzers van de klok om 2 uur 's middags?
b. Wat voor soort hoek maken de wijzers van de klok om 7 uur 's ochtends?
c. Wat voor soort hoek maken de wijzers van de klok om 9 uur 's avonds?
d. Wat voor soort hoek maken de wijzers van de klok om 5 uur 's middags?
e. Wat voor soort hoek maken de wijzers van de klok om 6 uur 's ochtends?
..13.
Benoem de hoeken.
In de figuur hierboven zijn verschillende hoeken aangegeven. In hoekpunt A komen twee hoeken samen. Als van hoek A wordt gesproken, is niet duidelijk welke hoek bedoeld wordt: de hoek met het ruitje of de hoek met het bolletje. Daarom worden hoeken met drie letters genoteerd.
De hoek met het ruitje noteer je als ∠DAS.
De middelste letter is het hoekpunt. De buitenste letters komen in alfabetische volgorde.
De hoek met het bolletje noteer je als ∠BAS.
Noteer nu zelf de hoek met het sterretje.
Noteer ook de hoek met het klavertje.
Noteer nog één andere hoek, wanneer je buur klaar is laat je hem of haar opzoeken welke hoek jij hebt genoteerd.
..14.
Benoem de hoeken.
Bekijk de figuur hiernaast.
Noteer drie scherpe hoeken.
Noteer de letter van de rechte hoek.
Noteer de letter van de stompe hoek.
Antwoorden
Let op, hier vindt je alleen antwoorden. Je kunt dus alleen je eindantwoord nakijken.
In je schrift schrijf je altijd de volledige berekening op!
..1.
a. 3600 : 12 x 1 = 300
b. 3600 : 60 x 10 = 600
c. 3600 : 60 x 1 = 60
..2.
a. 3600 : 12 x 1 = 1200
b. 3600 : 12 x 2 = 600
..3.
a. 3600 : 12 x 5 = 1500
b. 3600 : 12 x 4 = 1200
..4.
a. 5 x 300 + 300 : 4 = 157,50
b. 4 x 300 + \(1\over 2\) x 300 = 1350
c. 2 x 300 + \(1 \over 4\) x 300 = 67,50
..5.
c. Je ziet de meeste schapen vanuit punt C.
..6.
..7.
..8.
..9.
∠ A = scherp ∠ D= stomp
∠ B = stomp ∠ E = recht
∠ C = scherp ∠ F = stomp
..10.
a. ∠ A, ∠ D, en ∠ E zijn scherp.
b. ∠ C en ∠ G zijn stomp.
c. ∠ B is een rechte hoek.
d. ∠ F is een gestrekte hoek.
..11.
*We meten altijd de kleinste hoek tussen de wijzers!
*We meten altijd de kleinste hoek tussen de wijzers!
a. Scherpe hoek
b. Stompe hoek
c. Rechte hoek
d. Stompe hoek
e. Gestrekte hoek
..13.
a. ∠BSC.
b. ∠DCS.
c. * allerlei hoeken zijn mogelijk, laat diegene die naast je zit dit controleren.
..14.
a. ∠ABE, ∠AEB, ∠BED, ∠DBE, ∠CBD of ∠BDC.
b. ∠D is recht. (er staat een loodrechtteken in!)
c. ∠A.
§3 Hoeken meten
Uitleg & opgaven
Inleiding
In deze paragraaf leer je hoeken opmeten.
Voor het opmeten van een hoek gebruiken we een stuk gereedschap namelijk je geodriehoek.
Net als een kok zonder keuken, of een schilder zonder kwast begin jij niet veel zonder geodriehoek.
Wees dus zuinig op je gereedschappen. (je geodriehoek!)
Uitleg
In de vorige paragraaf heb je de namen en eigenschappen van verschillende hoeken geleerd. We sommen de hoeken en hun eigenschappen hieronder nog eens op.
..1.
Kennis over hoeken
Neem onderstaande zinnen over in je schrift en vul op .... het juiste begrip of aantal graden in.
Een hoek tussen 0o en 90o noemen we een ....
Een gestrekte hoek is precies .....o
Een hoek van 90o noemen we een .....
Een hoek tussen ... en .... noemen we een stompe hoek
..2.
Kennis over hoeken
Je ziet driehoek ABC.
Welke hoek is stomp?
..3.
Kennis over hoeken
Bekijk de afbeelding hier naast.
Bij het meten van deze hoek wordt een fout gemaakt.
Schrijf in je schrift wat deze persoon verkeerd doet bij het meten van deze hoek.
Gebruik in je antwoord het begrip scherpe hoek of het begrip stompe hoek. Beide mag ook.
..4.
Aflezen van de driehoek
Hier zie je een hoek A met daarop een geodriehoek.
Wat voor soort driehoek is hoek a? Kies uit: Rechte hoek, gestrekte hoek, scherpe hoek of stompe hoek.
Nu je de vorm van de hoek heb bepaalt, weet je welk getal je van de driehoek moet aflezen. Hoeveel graden is de hoek?
.5.
Aflezen van de driehoek
Lees de grootte van de volgende hoeken af, denk eerst na over de vorm van de hoek.
Driehoek A Lees het aantal graden af
Driehoek B Lees het aantal graden af
Hoeken meten
In deze paragraaf leer je hoe je met behulp van je geodriehoek een hoek kunt meten.
Het kunnen meten van een hoek is een vaardigheid. Het is dus niet iets wat je uit je hoofd kunt leren, het is iets dat je moet kunnen voordoen net zoals hooghouden met een bal bijvoorbeeld.
Net als met het leren hoog houden van een bal moet je dus veel oefenen en doorzetten als het even tegen zit.
Dit onderwerp leer je het gemakkelijkst door te kijken naar filmpjes op youtube van mensen die voor doen hoe je een hoek moet meten. Hieronder zie je een voorbeeld filmpje.
In de volgende applets zie je nog eens hoe je hoeken kunt meten:
..6.
Hoeken meten
Op het werkblad is de volgende afbeelding afgedrukt.
Meet de hoek op. Noteer het antwoord in je schrift.
Maak gebruik van het hoekteken \(\angle \space A =\space ...\)
..7.
Hoeken meten
Op het werkblad is de volgende afbeelding afgedrukt.
Meet de hoek op en noteer het antwoord in je schrift.
Maak gebruik van het hoekteken \(\angle \space B=\space...\)
..8.
Hoek in een assenstelsel
Teken in je schrift een x-as van -4 tot 6 en een y-as van -3 tot 4. Zet er ook de woordjes x-as en y-as bij.
Teken de punten A(-4 , -1), B(0 , -3) en C(-2 , 0).
Verbind A met C en B met C.
Meet nu de ruimte (de hoek) tussen lijnstuk AC en BC. Noteer het aantal graden in je schrift.
Teken ook de punten P(-2, 4), Q(0 , 1) en R( 6 , 1)
Verbind P met Q en Q met R
Meet de ruimte (de hoek) tussen lijnstuk PQ en QR. Noteer het aantal graden in je schrift.
Samenvatting van de stappen.
..9.
hoeken meten
Op het werkblad is de volgende afbeelding afgedrukt.
Meet in deze afbeelding alle hoeken op en noteer dit netjes in je schrift.
Maak ook nu weer gebruik van het hoekteken
..10.
Hoeken meten in een driehoek
Op het werkblad zie je de afbeelding van een driehoek.
Om je te helpen hebben we enkele zijden van de driehoek alvast verlengd met een stippellijntje zo kun je gemakkelijker meten.
Meet hoek A.
Meet hoek B.
Meet hoek C.
* Als je alle graden van de hoeken van je driehoek bij elkaar optelt moet je tot 180o. Dit is een handigheidje om te controleren of je het goed hebt gedaan.
..11.
Hoeken meten in een driehoek
Op het werkblad zie je de afbeelding van een driehoek.
Lijn CD deelt deze driehoek in twee stukken. Daardoor worden hoek C en hoek D ook in twee stukken gesneden. Je kunt dit zien aan \(\angle \space D_1\) en \(\angle \space D_2\)
Meet alle hoeken met een * noteer de graden netjes in je schrift.
Maak weer gebruik van het hoektekentje.
..12.
Kijkhoek meten
Op de afbeelding op het werkblad zie je Feline op het schoolplein staan.
Feline kijkt richting haar vrienden. Teken de kijklijnen van Feliné.
Welke vrienden worden niet door Feline gezien. Noteer de namen in je schrift.
Meet de kijkhoek van Feliné op en noteer het aantal graden in je schrift.
..13.
Auto rijden
Op de afbeelding op het werkblad zie je een verkeerssituatie. Het zicht van de taxichauffeur wordt voor een deel geblokkeerd door de rode vrachtauto
Teken de kijklijnen vanuit de taxi. langs de vrachtauto.
Meet de kijkhoek van de taxi op en noteer het aantal graden in je schrift.
Kan de taxi boven aan het plaatje de politieauto zien?
Extra filmpje
Het fijne aan filmpjes is dat je deze kunt stop zetten en nog eens opnieuw kunt afspelen.
Je kunt dus altijd meetekenen en meedoen met een filmpje.
..14.
Kijkhoek meten
Op de afbeelding op het werkblad zie je een verkeerssituatie.
Teken het zichtveld van beide fietsers
Meet de hoeken van het zichtveld op en noteer de graden in je schrift
..15.
Hoek in een assenstelsel
Op de afbeelding op het werkblad zie je een assenstelsel.
Noteer de coördinaten van punt C
Meet hoeveel graden \(\angle \space B \) is en noteer het antwoord in je schrift.
Meet ook de andere hoek op en noteer het antwoord in je schrift.
..16.
Hoek in een assenstelsel
Teken een assenstelsel met daarin de punten K(1, 2), L(7, 4) en M(4, 8)
Teken driehoek KLM.
Meet de hoeken in driehoek KLM.
Antwoorden
Schrijf altijd de volledige berekening in je schrift.
Hier vindt je alleen de eindantwoorden zodat je kunt controleren of je oplossing goed is.
..1.
a. Scherpe hoek
b. 180o
c. Rechte hoek
d. 90o en 180o
..2.
Op het plaatje zie je een scherpe hoek. Een scherpe hoek is tussen 0o en 90o.
Deze persoon leest 105o af, dat hoort bij een stompe hoek en dat is nu dus fout.
..3.
∠ A= 650 ( je mag er met meten 2 graden naast zitten dus 630, 640, 660 en 670 ook goed)
..4.
∠ B= 1170 (je mag er met meten 2 graden naast zitten dus 1150, 1160, 1180 en 1190 ook goed)
..5.
..6.
* je mag er per hoek 2 graden naast zitten. Behalve ∠ E= 900, dit moet je herkennen aan het tekentje van loodrecht!
..7.
..8.
..9.
De kijkhoek van Feliné is 640 ( je mag er 2 graden boven of onder zitten met meten)
..10.
De kijkhoek van de taxi richting de politieauto is 220 ( je mag er 2 graden boven of onder zitten met meten)
..11.
De bovenste fietser heeft een kijkhoek van 1280
De onderste fietser heeft een kijkhoek van 1280
..12.
∠ B= 960
∠ D= 1420
§4 Hoeken tekenen
Uitleg & opgaven
Inleiding.
In de vorige paragraaf heb je geleerd hoe je een hoek kunt opmeten.
Je hebt geleerd hoe je de geodriehoek neer legt en dat je heel precies moet werken.
Met het tekenen van een hoek ga je op dezelfde manier te werk. Een groot deel van je techniek heb je dus in de vorige paragraaf al geoefend. Daar gaan we nu op verder.
Uitleg.
Net als met hoeken meten is hoeken tekenen een vaardigheid. Iets dat je doet. In de filmpjes wordt voorgedaan hoe je een hoek tekent. Kijk eerst het filmpje als geheel, in één keer achter elkaar zonder pauze.
In het filmpje wordt gewerkt met een stappenplan.
Teken een \(\angle\) K van 60o
1. Teken een punt in je schrift, zet er de hoofdletter K bij.
2. Teken één been van de hoek aan punt K vast.
3. Leg de geo met de nul bij het hoekpunt, zorg er voor dat de lineaalkant langs het
getekende been ligt.
4. Meet de graden af, tel vanaf je lineaal kant. *Denk ook even na over scherp of stomp.
5. Teken het tweede been nu aan je hoek vast.
Klaar. Je hebt nu een hoek van 60o getekend.
Door het filmpje een tweede keer af te spelen, maar nu met pauzes. Je pauzeert het filmpje elke stap, en tekent meteen mee oefen je jouw vaardigheden met je geodriehoek. Oefen het maar eens. Je kunt het filmpje zo vaak starten en terug spoelen tot het je gelukt.
Om hoeken te meten gebruik je je geodriehoek. We doen dit in kleine stapjes.
Leg je geodriehoek met de nul op het hoekpunt en de lineaal kant langs één van de benen van je hoek.
Tel vanaf de lineaal kant van de geodriehoek het aantal graden af.
Noteer het aantal graden netjes in je schrift. \(\angle A = \space ...\)
Let op: als de driehoek die je wilt opnemen een stuk kleiner is dan je geodriehoek, dan kun je de grootte van de hoek niet goed aflezen. Je moet dan de lijnen van de driehoek doortrekken, zodat je wel goed het aantal graden van de hoeken kunt aflezen.
Teken de gegeven coördinaten in een assenstelsel in je schrift.
Verbind B met D zodat lijnstuk BD ontstaat.
Teken bij punt B een hoek van 18o
Teken bij punt A een hoek van 132o zorg er voor dat de benen van de hoek niet buiten je assenstelsel komen.
Teken bij E een hoek van 42o. Gebruik de y-as als één van de twee benen van de hoek.
Antwoorden
Je vindt hier alleen de eindantwoorden. Zo kan je controleren of je met een berekening tot het goede antwoord bent gekomen.
Noteer in je schrift altijd de volledige berekening. Noteer je alleen het eindantwoord, dan is je werk niet voldoende gemaakt.
..1.
..2.
..3.
..4.
..5.
..6.
..7.
..8.
§5 Hoeken berekenen
Uitleg & opgaven
Inleiding.
In paragraaf 5 van dit hoofdstuk leer je hoe je de hoeken binnen een driehoek kunt berekenen.
Weet je hoe groot twee hoeken van een driehoek zijn, dan kun je met behulp van de hoekensom berekenen hoe groot de derde hoek is.
Leerdoelen:
Aan het eind van deze paragraaf kan ik:
binnen een driehoek een gevraagde hoek berekenen met de hoekensom.
Kan ik de berekening die we gebruiken bij het berekenen van hoeken opschrijven.
Kan ik met behulp van gestrekte hoeken in een samengestelde driehoek de hoeken berekenen.
Uitleg
Hoeken berekenen? Ja, behalve hoeken meten en tekenen kun je ook hoeken berekenen. Dit doe je in vlakke figuren of in ruimte figuren. We hebben in hoofdstuk 2 al een aantal vlakke figuren behandeld.
Voor deze paragraaf kijken we naar driehoeken. We berekenen de hoeken binnen een driehoek.
1. De hoekensom.
Eerst leren we iets over de hoekjes van een driehoek. Er is namelijk een regel. Deze regel ontdekken we door samen met elkaar een opdracht uit te voeren.
Stap 1. Teken een driehoek. Het maakt niet uit hoe groot deze is, als hij maar netjes drie hoekpunten heeft.
Stap 2. Geef de hoekpunten van je driehoek een kleurtje.
Stap 3. Scheur nu de hoekjes af.
Stap 4. Puzzel er een gestrekte hoek van. (de hoekjes samen vormen een halve cirkel)
Stap 5. Conclusie. Je hebt nu bewezen dat de drie hoekjes van een driehoek samen een halve cirkel vormen. Een halve cirkel is 180o. Net als een gestrekte hoek. De hoeken van een driehoek zijn samen altijd 180o
Bekijk het filmpje hieronder nog maar eens als verduidelijking.
..1.
Hoek in twee stukken gesplitst
Hiernaast zie je een rechte hoek.
Deze hoek wordt in twee stukken gedeeld.
Bereken het ontbrekende stuk van de hoek.
Schrijf de berekening netjes in je schrift.
..2.
Hoek in drie stukken gesplitst
Hiernaast zie je een gestrekte hoek. Deze wordt in drie stukken gedeeld.
Bereken het ontbrekende stuk.
Schrijf de berekening netjes in je schrift.
..3.
Hoeken binnen een driehoek berekenen.
Wanneer je de drie hoekjes van een driehoek bij elkaar optelt is dit samen altijd .... graden
Bekijk de driehoek hiernaast en bereken de ontbrekende hoek. Schrijf de berekening netjes in je schrift.
Uitleg.
Hoeken binnen een driehoek berekenen
Nu je geleerd hebt dat de driehoeken van een driehoek samen altijd 180o zijn, kunnen we hier mooi gebruik van maken. Want weet je twee hoekjes van een een driehoek, dan kun je dus de derde berekenen. En dat is veel sneller (en soms preciezer) dan opmeten.
Bekijk het onderstaande filmpje maar eens.
Nog niet helemaal duidelijk? Bekijk dan dit filmpje even.
..4.
Hoeken van driehoeken berekenen
Bekijk de driehoek hiernaast.
Bereken \(\angle \space m\)
..5.
Hoeken van driehoeken berekenen
Bekijk de driehoek hiernaast.
Bereken de ontbrekende hoek. Schrijf de berekening netjes in je schrift.
..6.
Hoeken van driehoeken berekenen
Hierboven zie je drie driehoeken. In elke driehoek is één hoek nog niet berekend.
En een stapje lastiger. In het filmpje hieronder wordt voorgedaan hoe je in een samengestelde driehoek de hoekjes kunt berekenen.
In een samengestelde driehoek zijn 2 of meer driehoeken aan elkaar geplakt tot één grote driehoek.
Zoek in een samengestelde driehoek naar gestrekte hoeken. Dit helpt je vaak verder.
*tip: Maak een schets van je samengestelde driehoek, heb je een hoekje berekend, zet je berekende aantal graden dan in je driehoek, dit helpt je verder.
..10.
Hoeken van driehoeken berekenen
De driehoek hiernaast is samengesteld uit twee driehoeken. Bereken van deze driehoeken alle hoeken met een vraagteken.
Schrijf de berekeningen netjes in je schrift.
..11.
Hoeken van driehoeken berekenen
Ook hier weer een samengestelde driehoek.
Bereken de ontbrekende hoeken en noteer de berekeningen netjes in je schrift.
*tip: Maak eerst een schets van de driehoek in je schrift.
..12.
Hoeken van driehoeken berekenen
Ook hier weer een samengestelde driehoek
..13.
Hoeken van driehoeken berekenen
Ook hier weer een samengestelde driehoek
..14.
Hoeken van driehoeken berekenen
Ook hier weer een samengestelde driehoek
..15.
Hoeken van driehoeken berekenen
Teken de punten A(0 , 2), B(5 , -2) en C( 2 , 5).
Verbind A met B, B met C en C met A zodat driehoek ABC ontstaat.
Meet hoek A en hoek C op. Noteer de graden in de hoeken van je driehoek.
Bereken hoek B. Schrijf de berekening netjes in je schrift.
..16.
Hoeken van driehoeken berekenen
Teken de punten A(0 , 2), B(5 , -2) en C( 2 , 5).
..17.
Hoeken van driehoeken berekenen
..18.
Hoeken van driehoeken berekenen
Teken de punten A(0 , 2), B(5 , -2) en C( 2 , 5).
..19.
Hoeken van driehoeken berekenen
Teken de punten A(0 , 2), B(5 , -2) en C( 2 , 5).
..20.
Hoeken van driehoeken berekenen
Teken de punten A(0 , 2), B(5 , -2) en C( 2 , 5).
Antwoorden
Hier vindt je alleen de eindantwoorden.
Let op, in je schrift werk je altijd de hele opgave uit. Niet alleen een antwoord opschrijven maar de volledige berekening.
..1.
∠ A = 90o - 62o = 28o.
..2.
∠ B = 180o - 42o - 90o= 48o.
..3.
a. 180o
b. ∠ A = 180o - 70o - 12o = 98o
..4.
∠ M = 180o - 114o - 40o = 26o
..5.
∠ X = 180o - 72o - 41o = 67o
..6.
* Let op je vindt hier alleen de antwoorden, in je schrift schrijf je altijd de volledige berekening op.
∠ C = 78o
∠ E = 75o
∠ I = 42o
..7.
∠ T = 132o
..8.
..9.
..10.
∠ G = 96o ( je maakt gebruik van de gestrekte hoek!)
∠ F = 44o
..11.
∠ Q = 30o
∠ S = 73o ( je maakt gebruik van de gestrekte hoek!)
∠ R = 67o
..12.
.13.
..14.
..15.
§6 Gemengde opgaven
Uitleg & opgaven
Inleiding
Het is al weer tijd voor de gemengde opgaven.
Er volgend nu uit iedere paragraaf nog een aantal opgaven kris kras door elkaar heen.
We testen of jij alle vaardigheden hebt om ook dit onderdeel (en dus het hele hoofdstuk) tot een goed einde te brengen.
Zijn er vragen die nog niet willen lukken, lees dan de uitleg van de bijbehorende paragraaf nog eens door en kijk het bijbehorende uitlegfilmpje. Stel ook vragen in de volgende lessen zodat jij de ontbrekende vaardigheden alsnog eigen maakt. Veel succes!
..1.
Loodrecht en evenwijdig
Bekijk de lijnen hiernaast.
Maken lijn b en lijn e een rechte hoek met elkaar?
Zijn lijn e en lijn g evenwijdig aan elkaar?
Maken lijn d en lijn f een rechte hoek met elkaar?
Noteer één paar evenwijdige lijnen.
Noteer één paar lijnen die een samen een rechte hoek maken.
..2.
Kennis over hoeken
Hiernaast zie je een hoek. Teken deze na in je schrift.
Zet bij het hoekpunt de letter R
Kleur de benen blauw.
Teken een boogje in de hoek.
Teken een hoek die groter is dan hoek R. Noem deze hoek S
..3.
Kennis over hoeken
Bekijk de afbeelding hiernaast, beantwoord daarna de vragen.
Noteer de letters van alle stompe hoeken in je schrift.
Noteer de letters van de hoeken op volgorde van klein naar groot.
Meet iedere hoek op en noteer het aantal graden in je schrift.
..8.
Hoeken meten
Meet van driehoek PQR alle hoeken op en noteer het aantal graden telkens in je schrift.
..9.
Hoeken meten
Op je werkblad zie je een trapezium afgebeeld.
Meet van dit trapezium alle hoeken met een boogje op.
Zijn de lijntjes te kort, maak ze dan zelf langer met potlood.
..10.
Hoeken tekenen
Hiernaast zie je hoek R van 50o.
Teken de hoek na in je schrift.
Teken een hoek vast aan hoek R zodat de hoeken samen precies 180o zijn.
Hoeveel graden is de hoek die je aan hoek R hebt vast getekend?
..11.
Hoeken tekenen
Teken een hoek van 30o noem de hoek A.
Teken aan hoek A een hoek vast zodat deze samen een rechte hoek vormen.
..12.
Hoeken tekenen
Teken de volgende hoeken in je schrift:
\(\angle \space A = 72 ^o\)
\(\angle \space B = 118 ^o\)
\(\angle \space C = 140 ^o\)
Verdeel hoek C in twee gelijke stukken. Zet in het onderste deel een 1 en in het bovenste deel een 2 zodat \(\angle \space C_1 = 70 ^o\)
..13.
Hoeken berekenen
Bekijk de driehoek hiernaast.
Bereken de ontbrekende hoek
Schrijf de berekening netjes in je schrift.
..14.
Hoeken berekenen
Bekijk die driehoek hiernaast.
Bereken de ontbrekende hoek.
Schrijf de berekening netjes in je schrift.
..15.
Hoeken berekenen
Bekijk de driehoek hiernaast.
Bereken alle ontbrekende hoeken.
Noteer je berekeningen netjes in je schrift.
Antwoorden
D-toets
1H06.D Diagnostische toets ................................................................................................
Je sluit het thema Hoeken af met de eindtoets.
De eindtoets bestaat uit vier vragen.
Na het beantwoorden van de vragen lever je de antwoorden in.
Vervolgens kun je kijken hoe hoog je score is en kun je jouw antwoorden vergelijken met de goede antwoorden.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De herhaling van het hoofdstuk is de laatste oefening voor je toets.
Je haalt je kennis en vaardigheden nog één laatste keer op. Je test of je alle onderdelen van het hoofdstuk hebt begrepen en of je deze ook echt zelfstandig kunt maken.
Nog beter, of je de onderdelen van het hoofdstuk ook aan iemand anders zou kunnen uitleggen.
Zoals je inmiddels wel gewend bent vind je hier bij iedere onderwerp nog een laatste instructiefilmpje. Lukt een opgave uit een bepaalde paragraaf niet, bekijk dan het filmpje. Oefen daarna de opgave uit herhaling.
1. Verschillende lijnen
..1.
Verschillende lijnen
..2.
Mikado
..3.
Lijnen tekenen
..4.
Lijnen in een assenstelsel
2. Hoeken
..5.
Hoeken benoemen
..6.
Kennis over hoeken.
..7.
Hoeken benoemen.
3. Hoeken meten
..8.
Hoeken meten
..9.
Hoeken meten
.10.
Hoeken meten
.11.
Hoeken meten in een driehoek
4. Hoeken tekenen
.12.
Hoeken tekenen
.13.
Hoeken tekenen
.14.
Driehoek tekenen
.15.
Driehoek tekenen
5. Hoeken berekenen.
.16.
Hoeken berekenen binnen een driehoek
.17.
Hoeken berekenen binnen een driehoek
.18.
Hoeken berekenen binnen een driehoek
.19.
Hoeken berekenen binnen een driehoek
.20.
Hoeken berekenen binnen een samengestelde driehoek
.21.
Hoeken berekenen binnen een samengestelde driehoek
.22.
Hoeken berekenen binnen een samengestelde driehoek
Antwoorden
Extra stof
Uitleg & opgaven
Inleiding.
In deze paragraaf blikken we vast vooruit op de toekomst. We oefenen alvast een vaardigheid en breiden onze kennis over soorten hoeken uit. Dit komt later in het jaar en in klas 2 nog een keer aan bod.
Uitleg
Overstaande hoeken
Wanneer twee lijnen elkaar raken (snijden) ontstaan er verschillende hoeken.
In de figuur hierboven zien we 2 lijnen die elkaar snijden. Er ontstaan dan 4 hoeken bij punt A. Een aantal van deze hoeken zijn even groot. Dit zijn de hoeken die tegenover elkaar liggen. We noemen het overstaande hoeken.
Om het makkelijker te maken hebben we de hoeken een nummer gegeven.
Hoek A1 is even groot als hoek A3. Dat noteren we zo:\(\angle\)A1 = \(\angle\)A3
En zo is \(\angle\)A2 = \(\angle\)A4
Pas wel op. Hieronder zien we een voorbeeld waarbij de hoeken niet allemaal even groot zijn.
Er zit als het ware een knik in de groen lijn! Hierdoor zijn de hoeken natuurlijk niet even groot.
..1.
Overstaande hoeken kleuren.
..2.
Overstaande hoeken herkennen.
..3.
Overstaande hoeken noteren.
..4.
Overstaande hoeken berekenen.
..5.
Berekeningen met overstaande hoeken.
Uitleg.
F - en Z - hoeken.
Wanneer je in een figuur twee evenwijdige lijnen ziet staan, dan moet je extra opletten. Je zou zo maar eens F-hoeken of Z-hoeken kunnen herkennen.
Je ziet in de plaatjes hierboven dan F- en Z- hoeken alle kanten op kunnen voor komen. Kijk dus goed naar je figuur en zoek bij evenwijdige lijnen of je een F of Z kunt vormen.
Het arrangement 1KGT H06 Hoeken is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-07-06 11:10:35
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Hoeken
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Aan het eind van dit hoofdstuk kan ik:
In de voorkennis herhalen we stukje van de wiskunde die je op de basisschool al geleerd hebt of een stukje van de wiskunde dat al eens in een voorgaand hoofdstuk behandeld is.
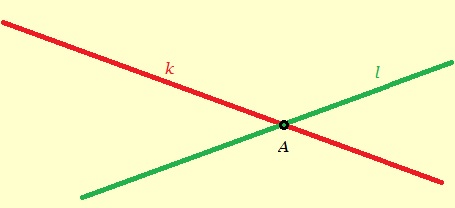
Liggen stokje 1 en 3 loodrecht op elkaar?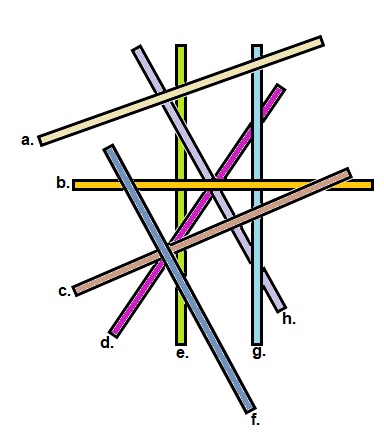
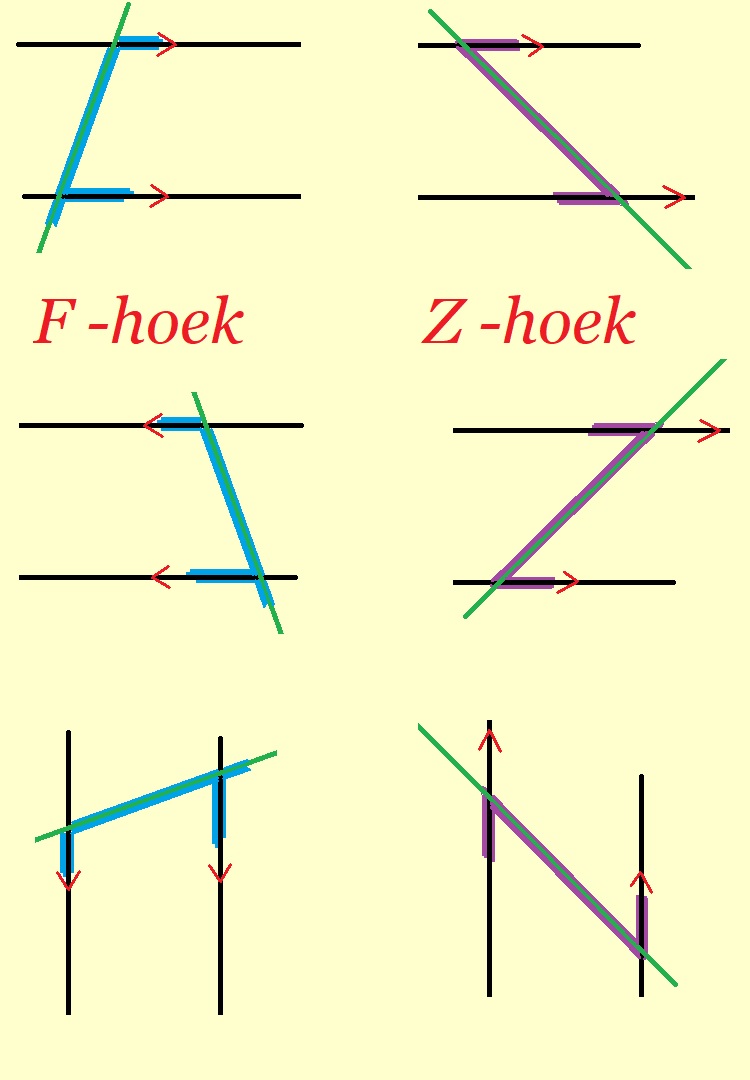
In de tweede paragraaf van dit hoofdstuk gaat het over hoeken.
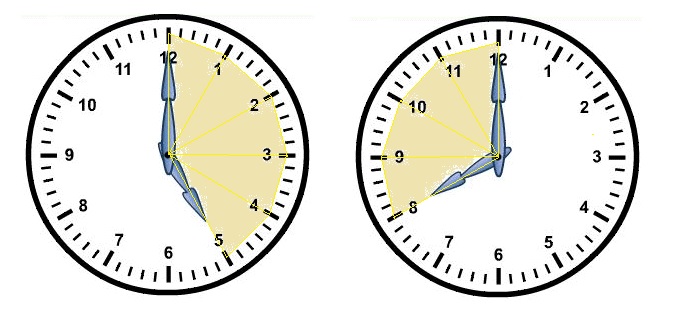
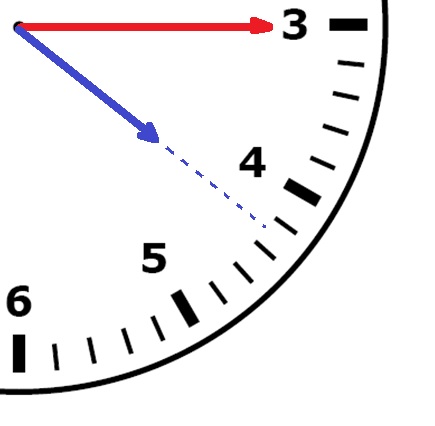
Over hoeveel graden draait de grote wijzer van een klok in: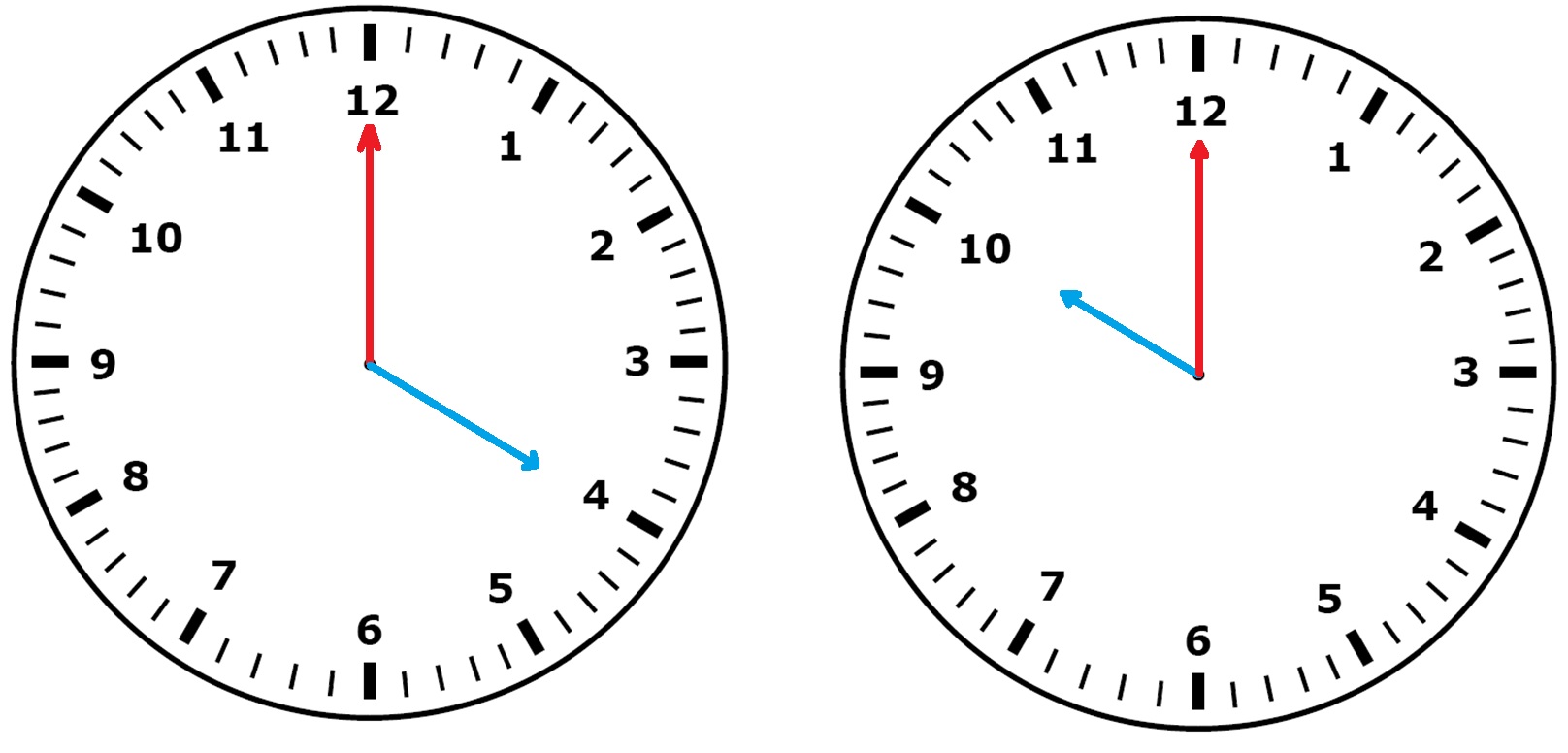
Wanneer de klok niet op een heel uur staat maar bijvoorbeeld op een half uur of op een kwartier (een kwart) dan wijst de kleine wijzer ook niet meer precies het getal aan.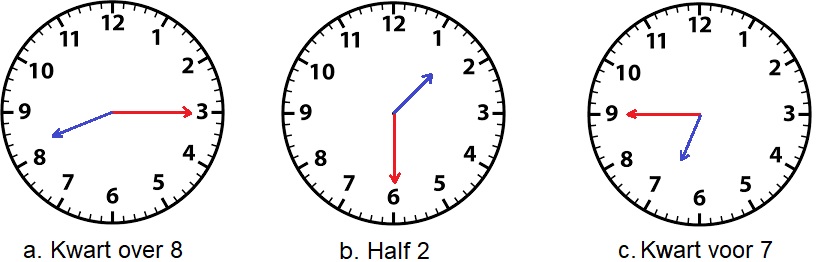
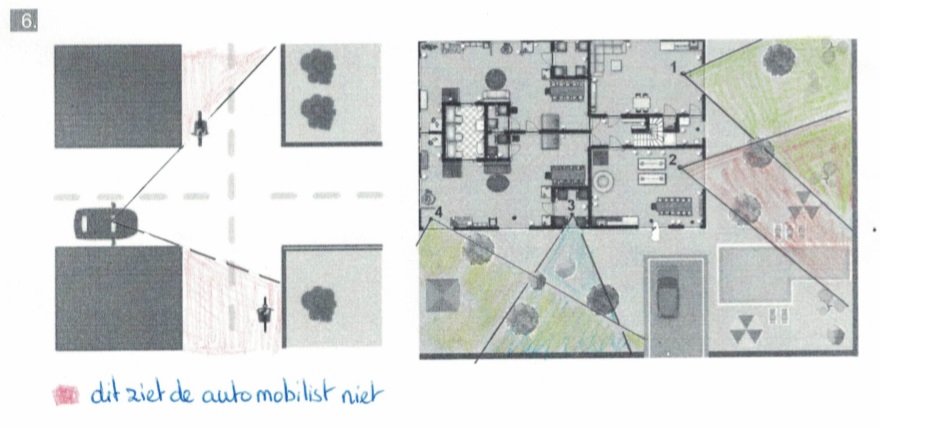
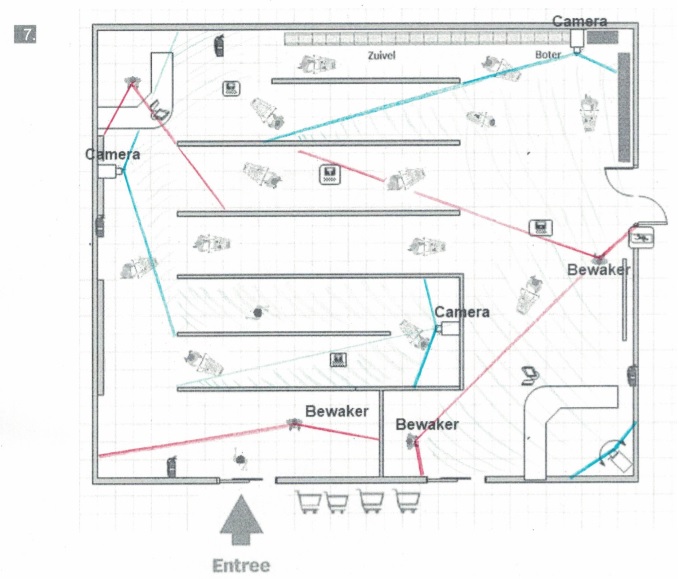
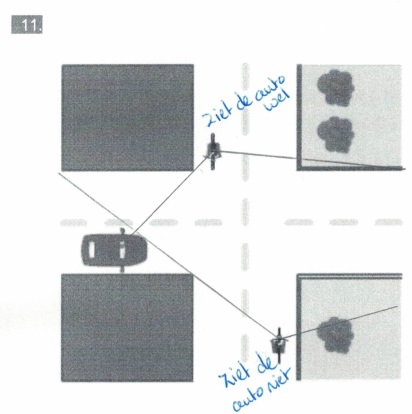
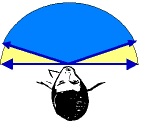In de voorbeelden hierboven spreken we over je gezichtsveld. Dat is het gebied dat je kunt zien zonder je hoofd of je ogen te bewegen. Wanneer iets of iemand voor je staat dan beneemt deze een deel van je zicht.
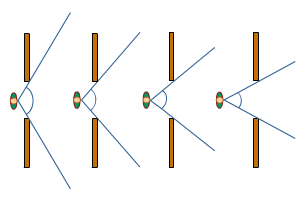
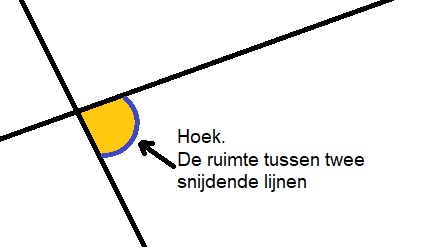
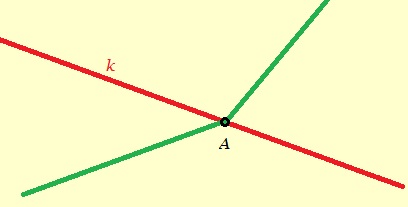
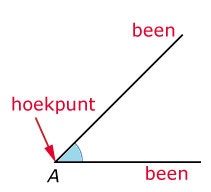Een hoek bestaat dus uit twee lijnen. Deze lijnen noemen we de benen van de hoek.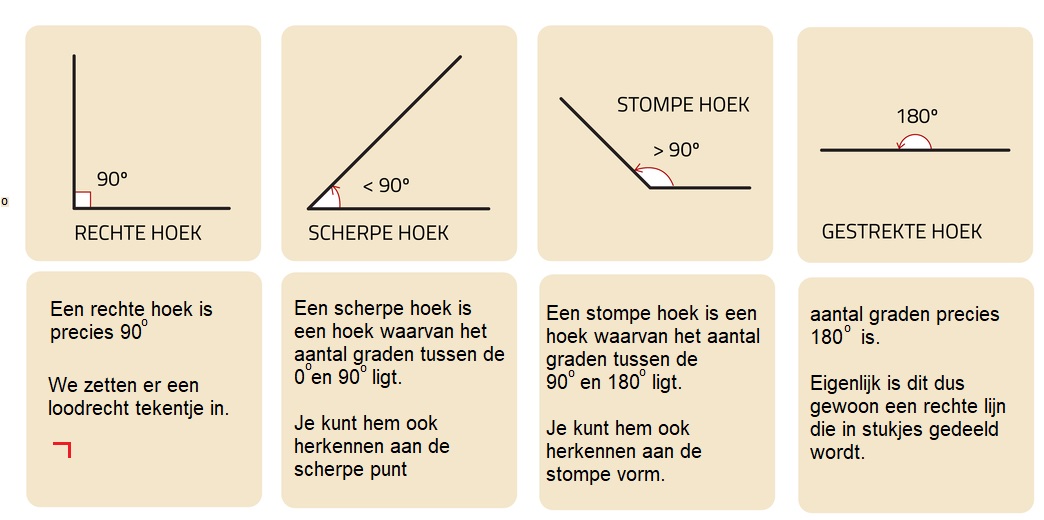
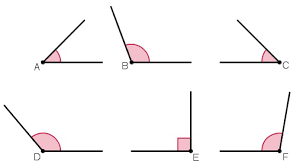
Hiernaast zie je een bootje. In dit bootje zijn 7 hoeken verstopt. De hoeken hebben allemaal een hoofdletter.
Als je naar een analoge klok kijkt, een analoge klok is een klok met wijzers, dan maken de wijzers van de klok ook een hoek met elkaar. Bekijk het plaatje van de zes klokken hiernaast.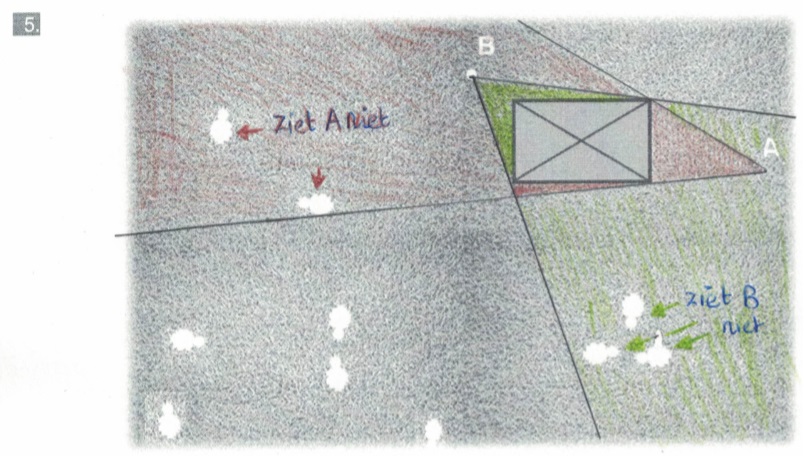
In deze paragraaf leer je hoeken opmeten.
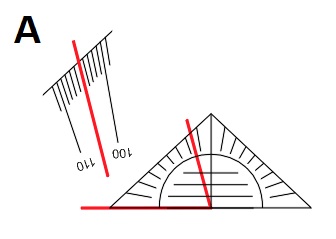
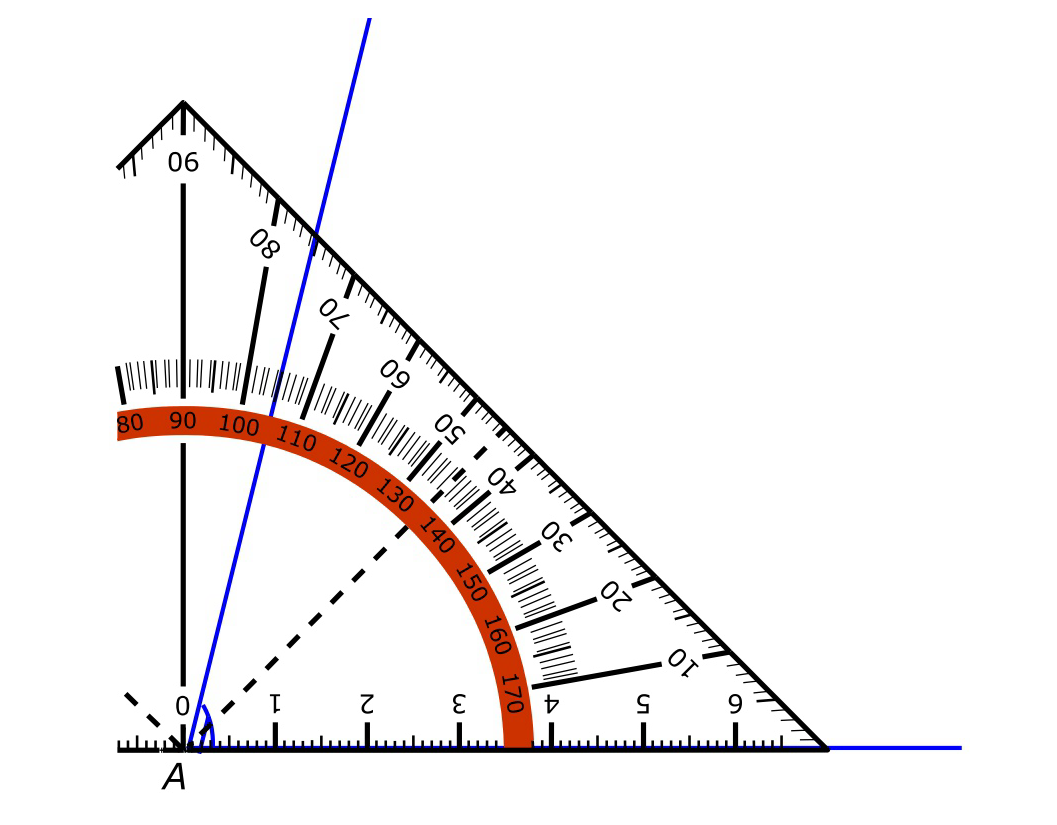
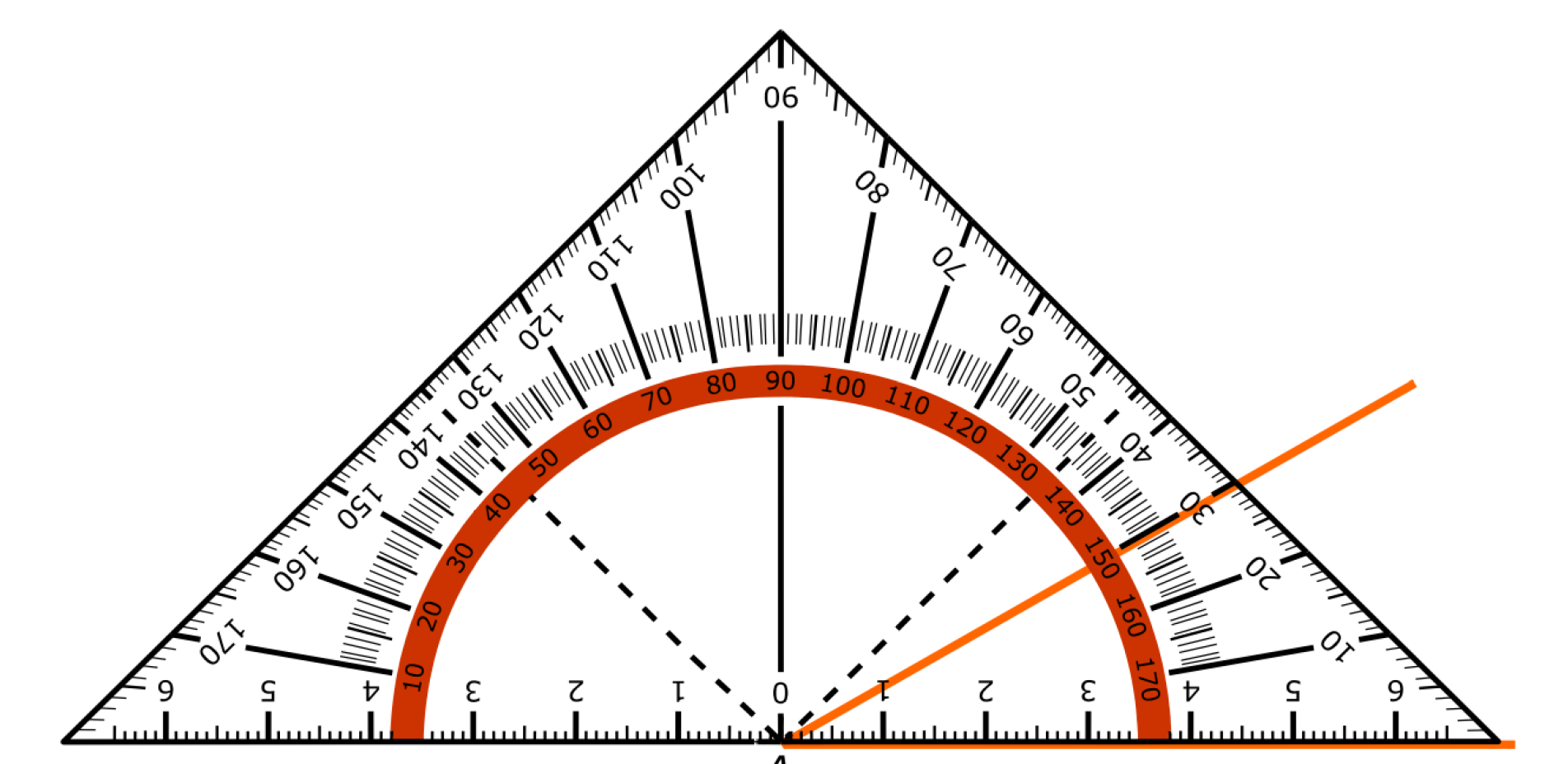
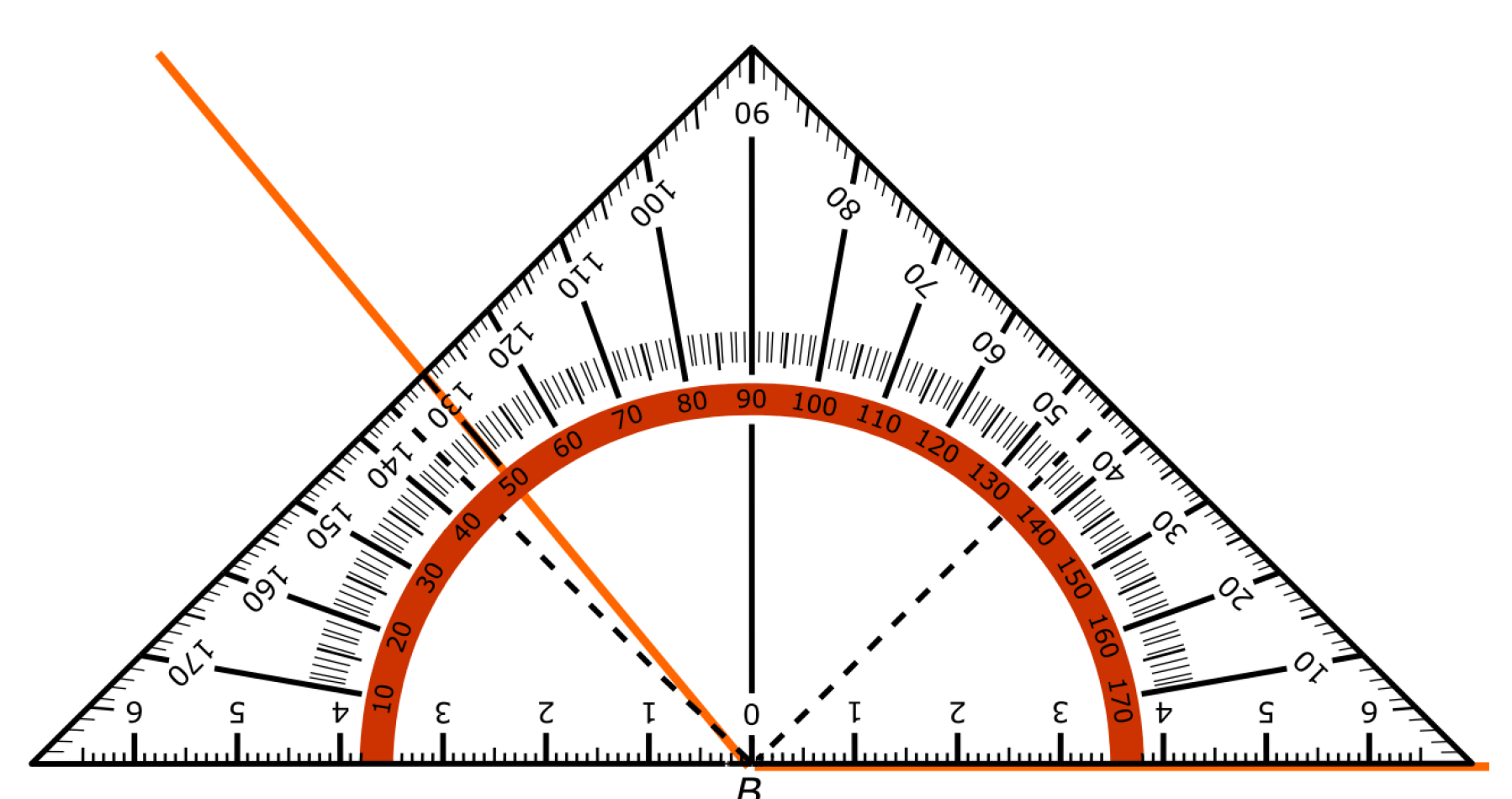
Het kunnen meten van een hoek is een vaardigheid. Het is dus niet iets wat je uit je hoofd kunt leren, het is iets dat je moet kunnen voordoen net zoals hooghouden met een bal bijvoorbeeld.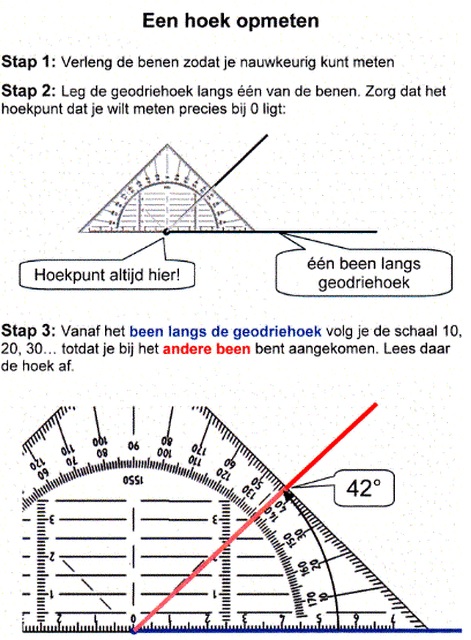
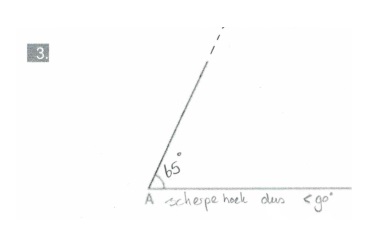
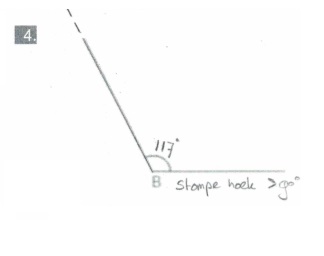
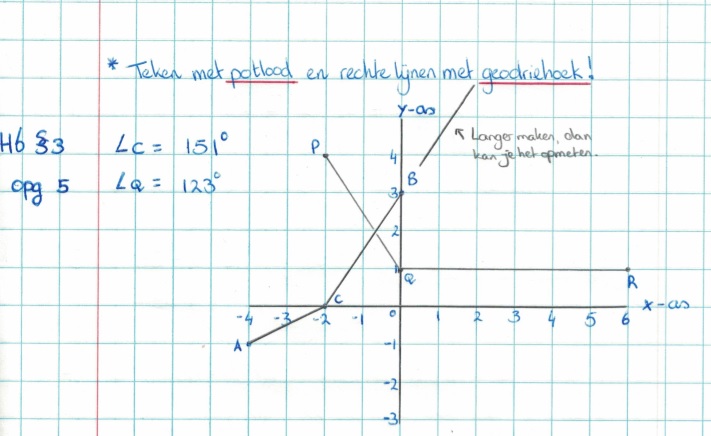
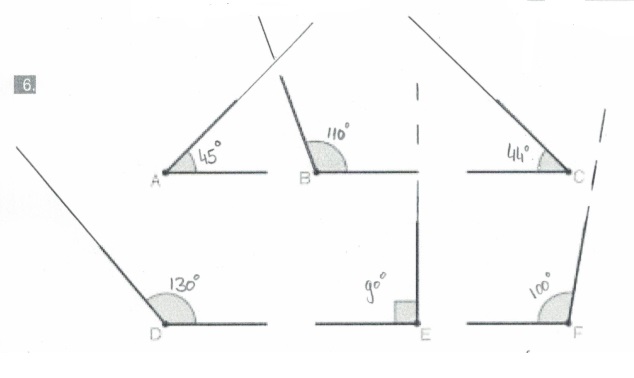
In de vorige paragraaf heb je geleerd hoe je een hoek kunt opmeten.
In paragraaf 5 van dit hoofdstuk leer je hoe je de hoeken binnen een driehoek kunt berekenen.
Stap 1. Teken een driehoek. Het maakt niet uit hoe groot deze is, als hij maar netjes drie hoekpunten heeft.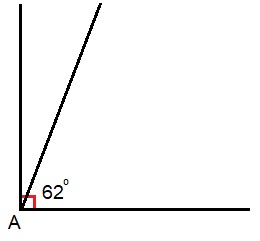
Hiernaast zie je een rechte hoek.
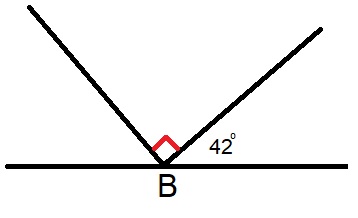Hiernaast zie je een gestrekte hoek. Deze wordt in drie stukken gedeeld.
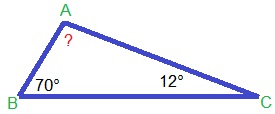Wanneer je de drie hoekjes van een driehoek bij elkaar optelt is dit samen altijd .... graden
Nu je geleerd hebt dat de driehoeken van een driehoek samen altijd 180o zijn, kunnen we hier mooi gebruik van maken. Want weet je twee hoekjes van een een driehoek, dan kun je dus de derde berekenen. En dat is veel sneller (en soms preciezer) dan opmeten.
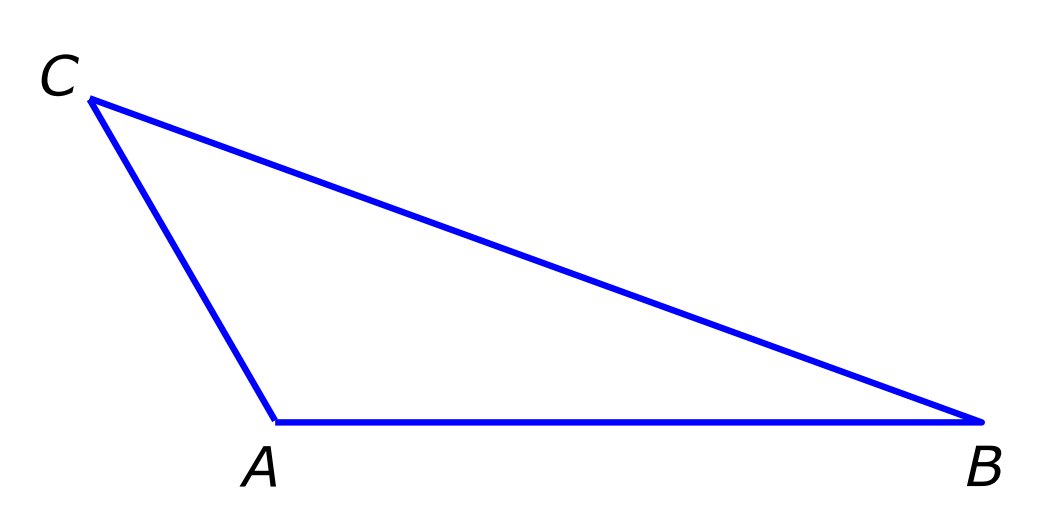
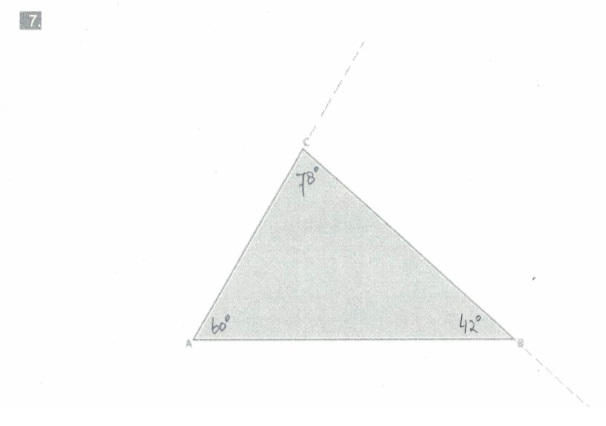
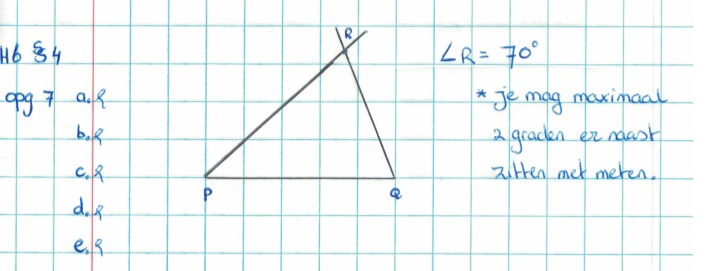
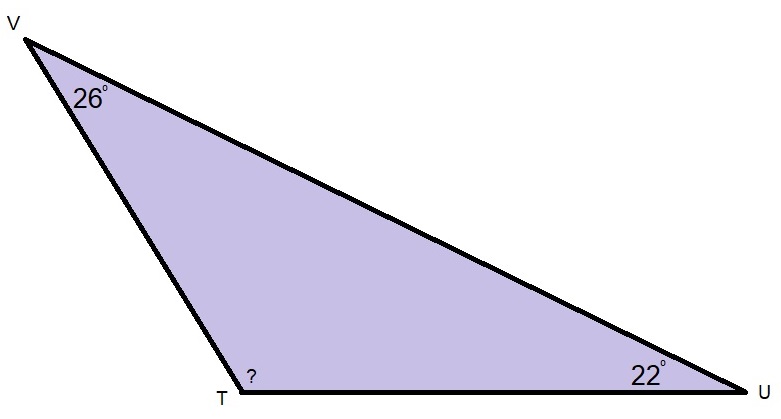
Bekijk de driehoek hiernaast.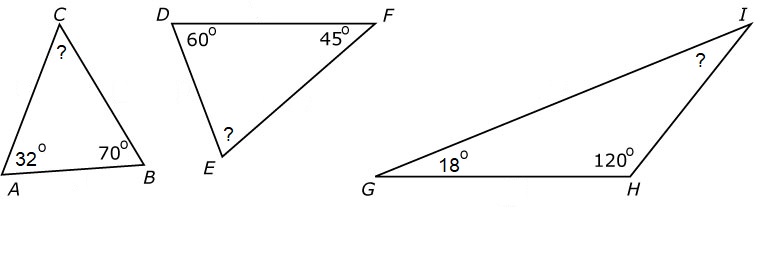
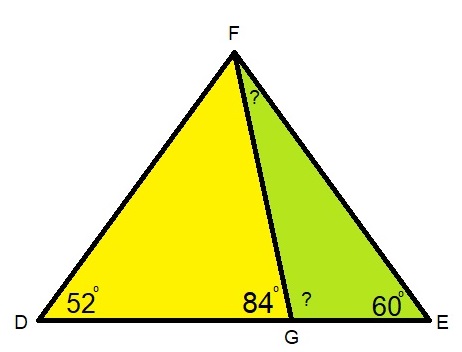
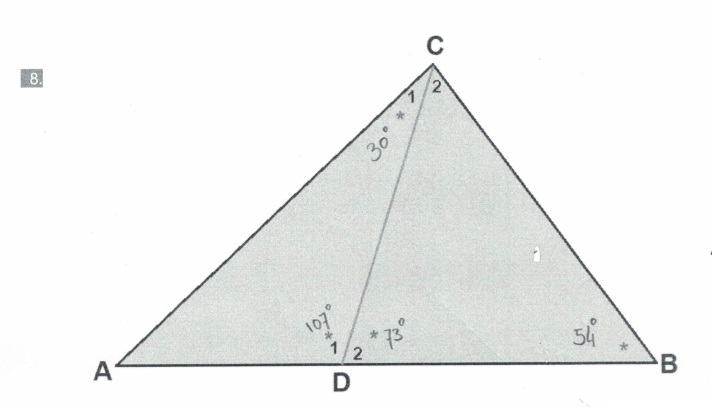
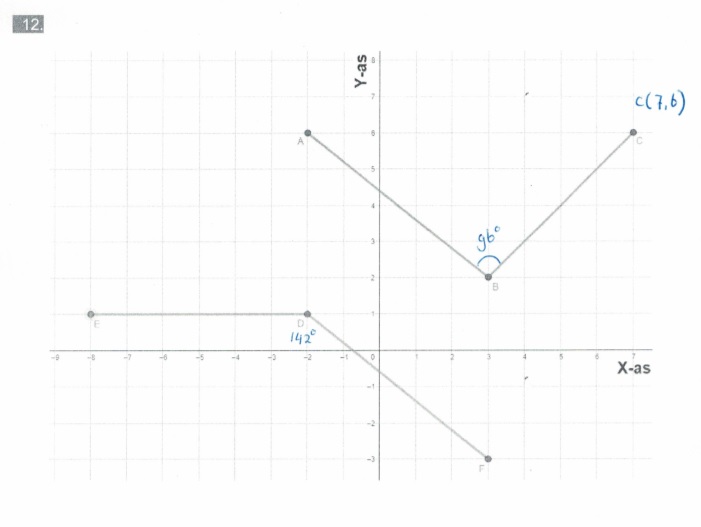
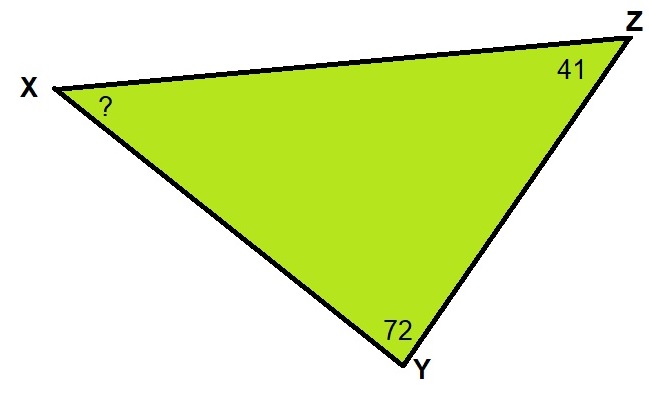
Ook hier weer een samengestelde driehoek.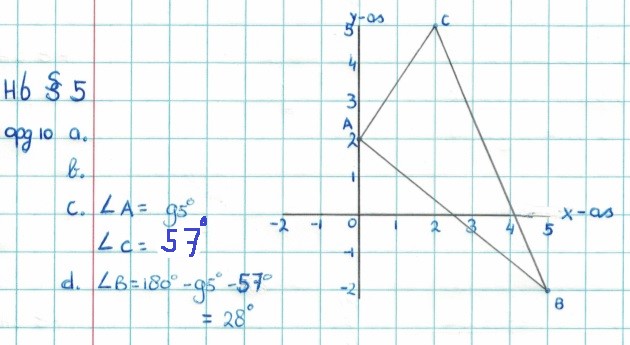
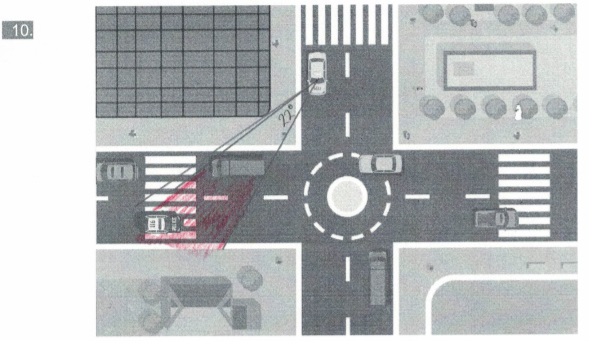
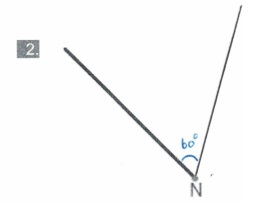
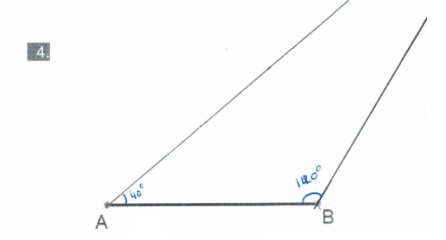
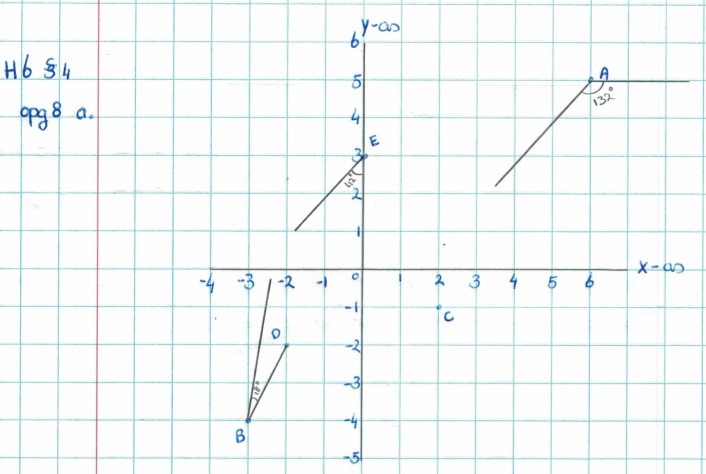
Het is al weer tijd voor de gemengde opgaven.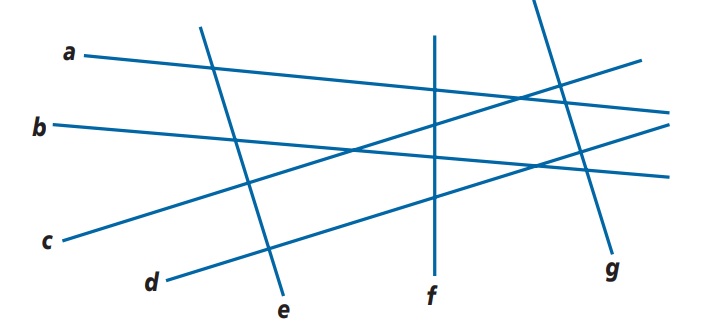
Bekijk de lijnen hiernaast.
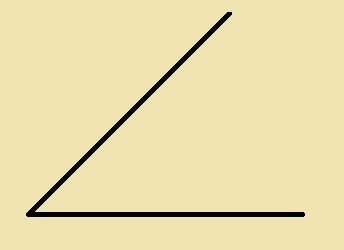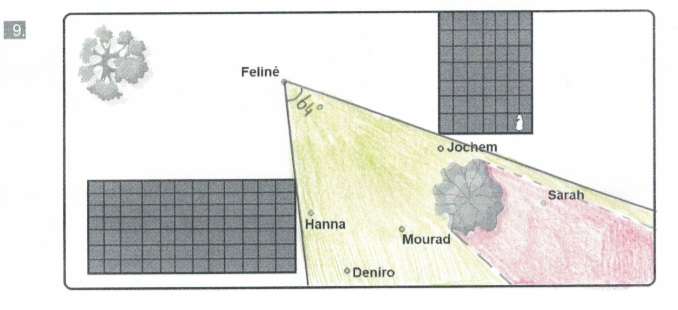
Hiernaast zie je een hoek. Teken deze na in je schrift.
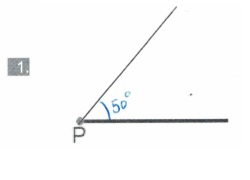
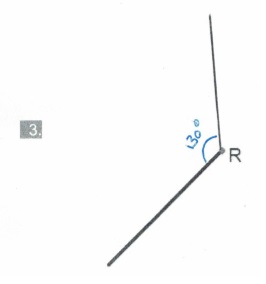
Bekijk de afbeelding hiernaast, beantwoord daarna de vragen.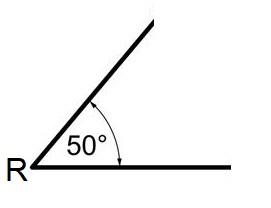
Hiernaast zie je hoek R van 50o.
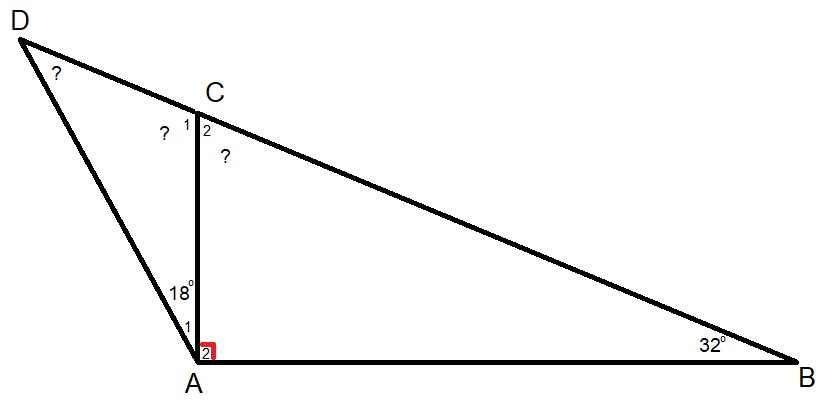Bekijk de driehoek hiernaast.
De herhaling van het hoofdstuk is de laatste oefening voor je toets.
