Het arrangement 1KGT H03 Bewerkingen en getallen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 02-07-2020 10:39:40
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Gebruikte Wikiwijs Arrangementen
Giessen, D.. (z.d.).
§2 Negatieve getallen som & verschil
https://maken.wikiwijs.nl/150498/_2_Negatieve_getallen_som___verschil
Giessen, D.. (z.d.).
§3 Negatieve getallen product & quotiënt
https://maken.wikiwijs.nl/150499/_3_Negatieve_getallen_product___quoti_nt
Giessen, D.. (z.d.).
§4 Kwadraten en wortels
Wiskundesectie Juliana. (z.d.).
1H07 Negatieve getallen


 Aan het eind van dit thema:
Aan het eind van dit thema: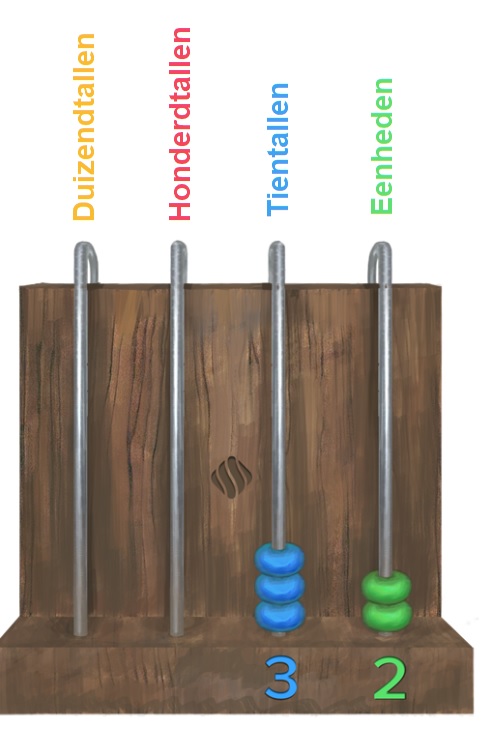 Op een telraam kun je dit goed duidelijk maken.
Op een telraam kun je dit goed duidelijk maken.



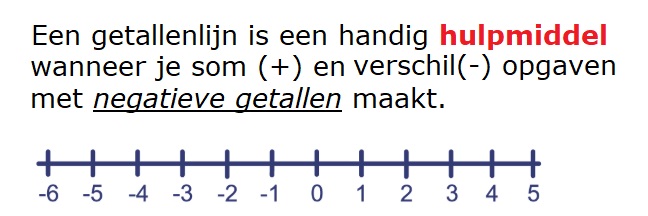
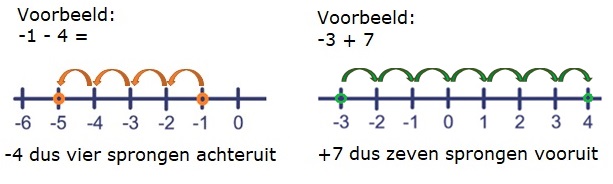
 In het eerste deel van werken met negatieve getallen leer je wat een negatief getal is,
In het eerste deel van werken met negatieve getallen leer je wat een negatief getal is, Een voorbeeld:
Een voorbeeld: Hiernaast zie je een flatgebouw met 11 verdiepingen.
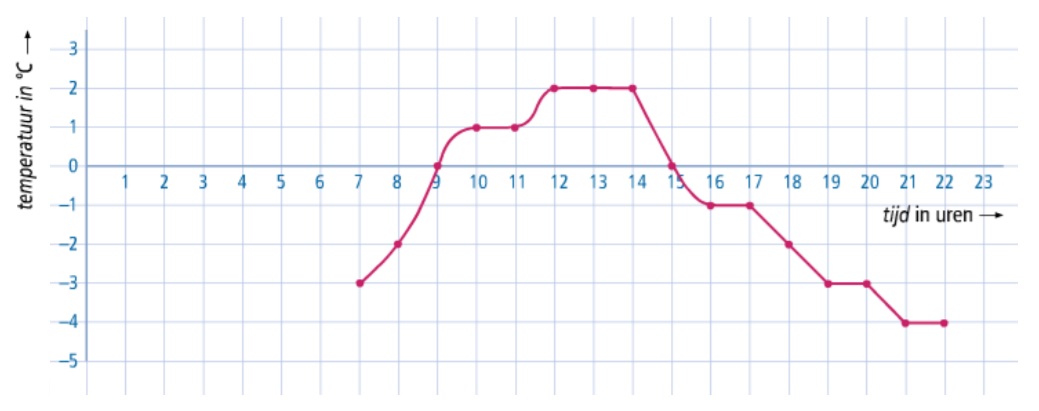
Hiernaast zie je een flatgebouw met 11 verdiepingen. Temperaturen meet je in graden Celcius. Je schrijft ℃. Hiernaast zie je hoe je temperaturen onder 0 ℃ opschrijft.
Temperaturen meet je in graden Celcius. Je schrijft ℃. Hiernaast zie je hoe je temperaturen onder 0 ℃ opschrijft.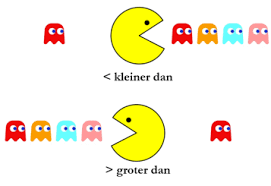
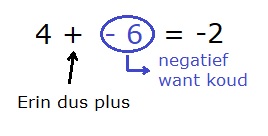
 Denk er aan:
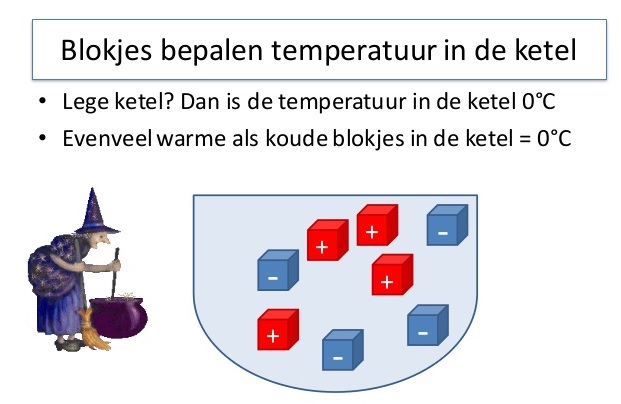
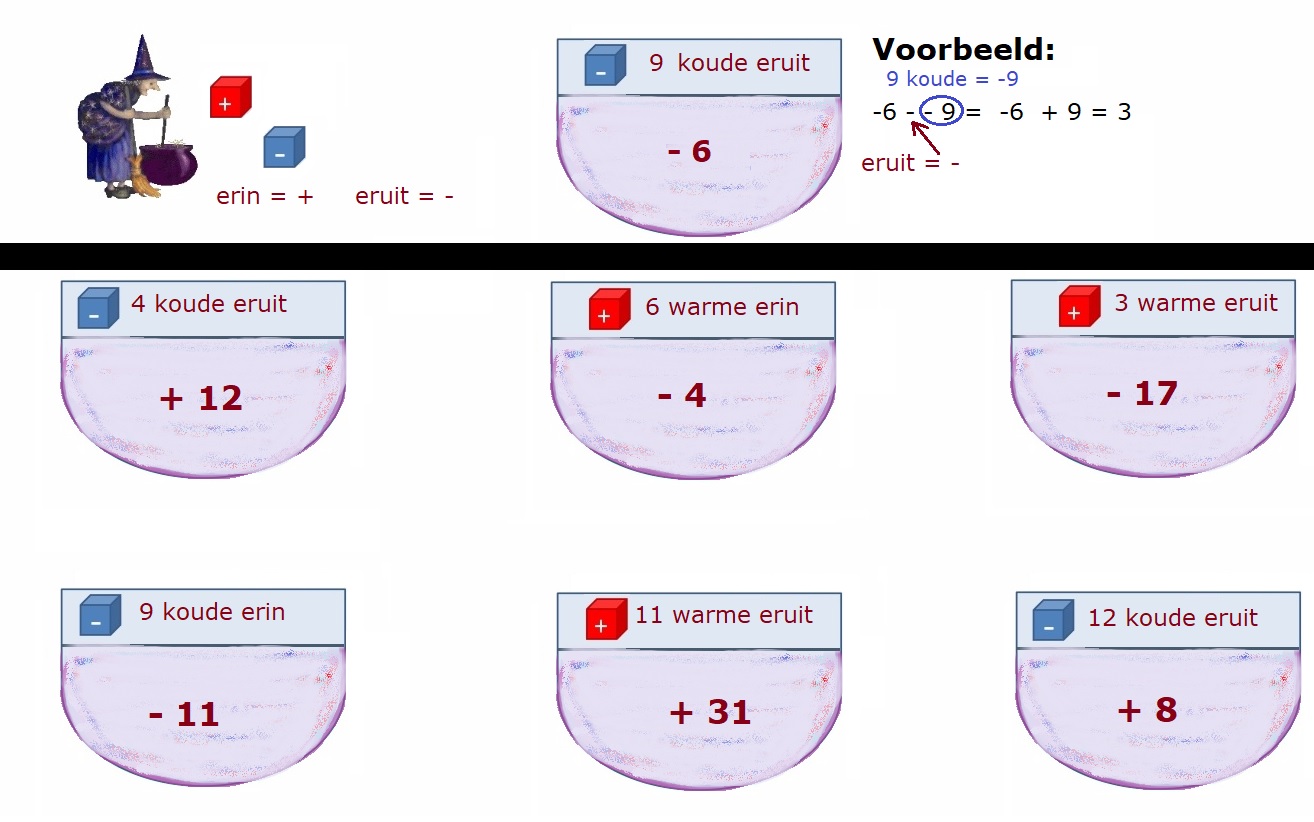
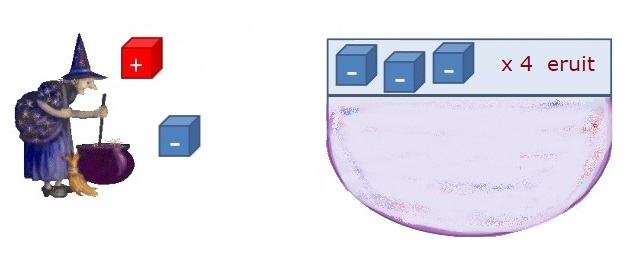
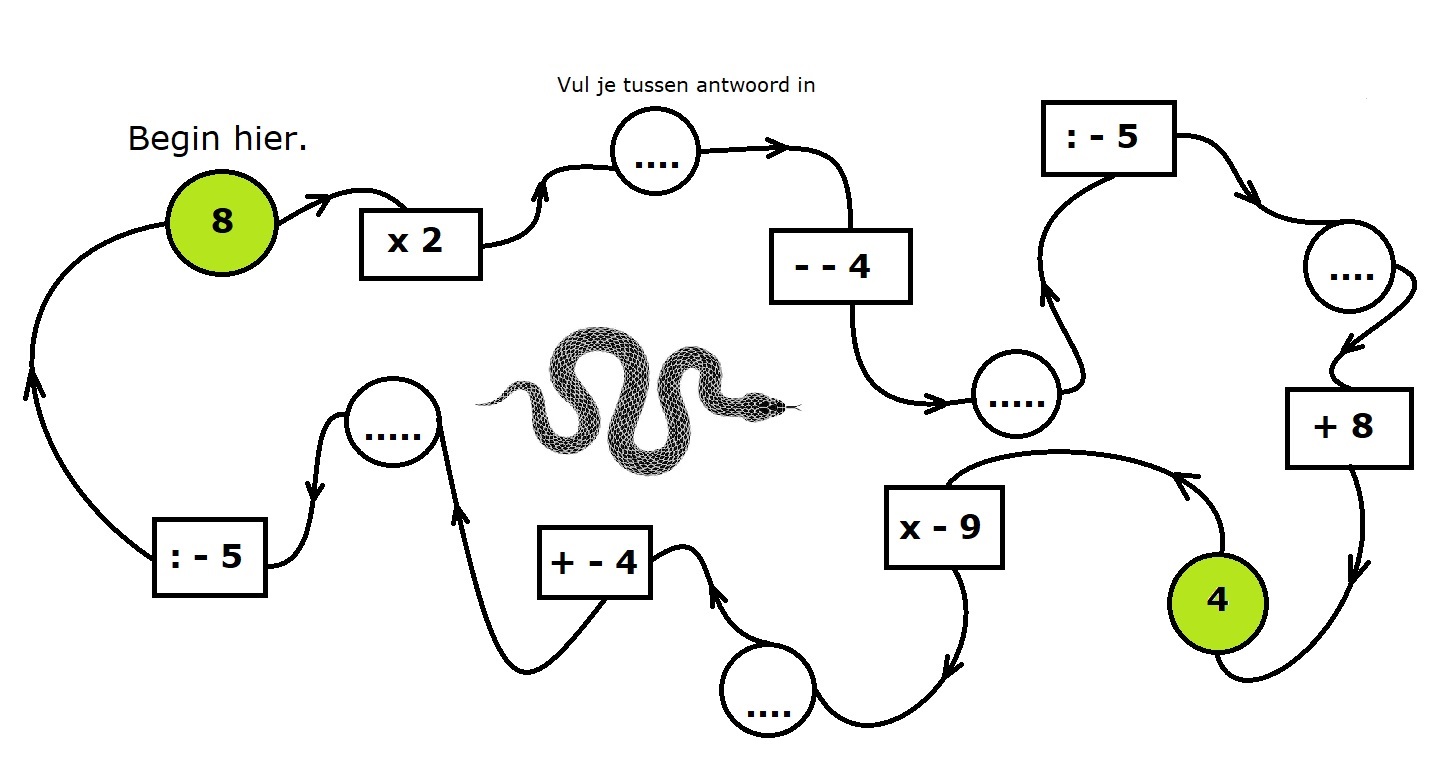
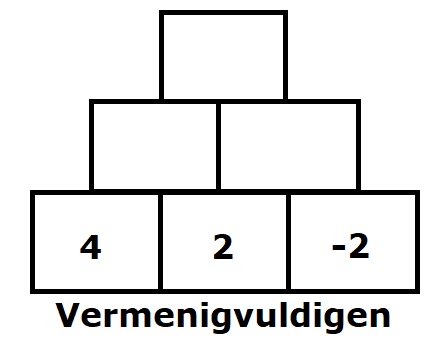
Denk er aan: In het tweede deel van bewerkingen met negatieve getallen leer je negatieve getallen vermenigvuldigen en delen. Je leert een stukje theorie (uitleg) uit het hoofd en oefent met het toepassen hiervan.
In het tweede deel van bewerkingen met negatieve getallen leer je negatieve getallen vermenigvuldigen en delen. Je leert een stukje theorie (uitleg) uit het hoofd en oefent met het toepassen hiervan.


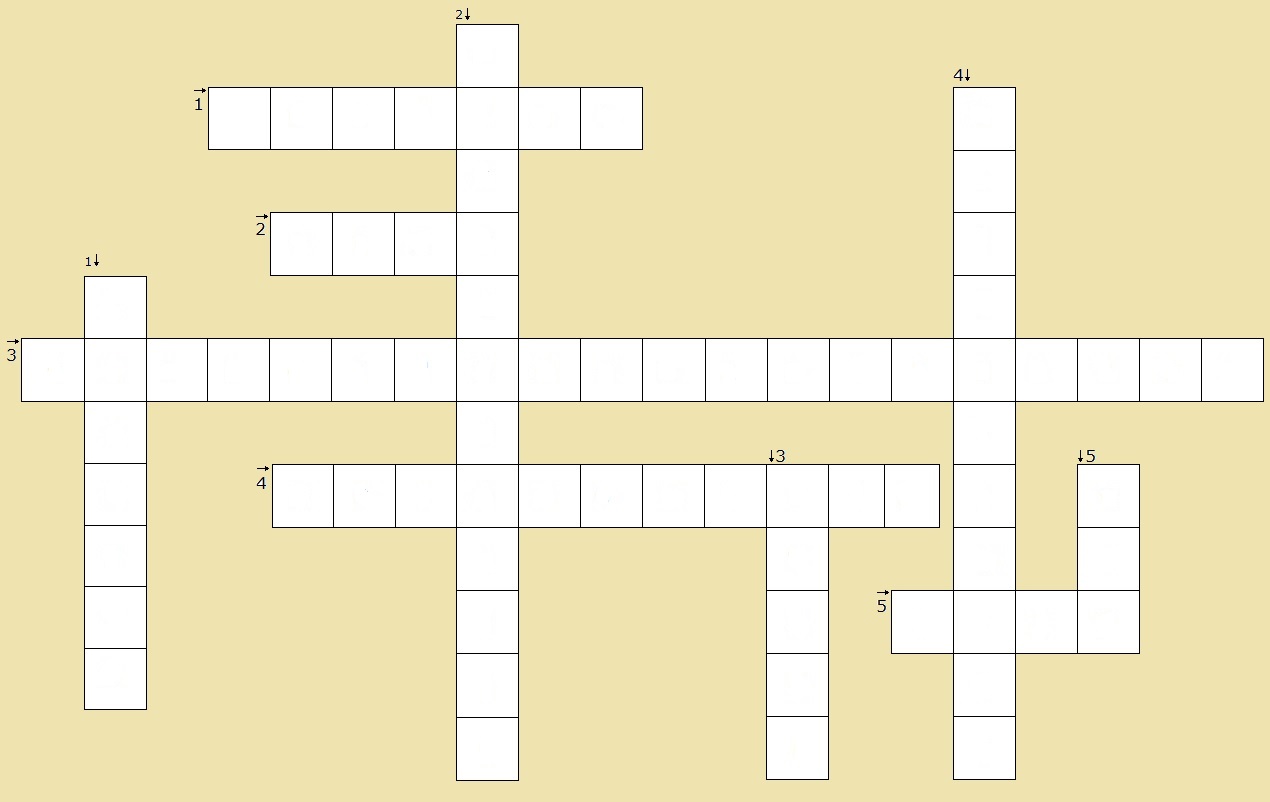
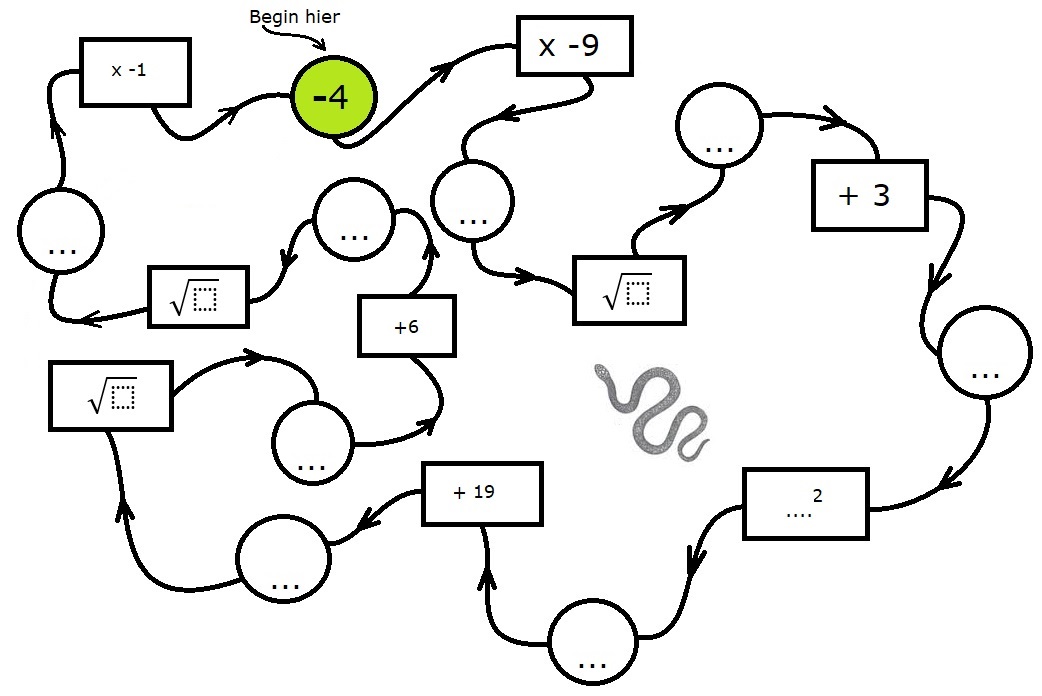
 In deze paragraaf leer je over machten en wortels.
In deze paragraaf leer je over machten en wortels.

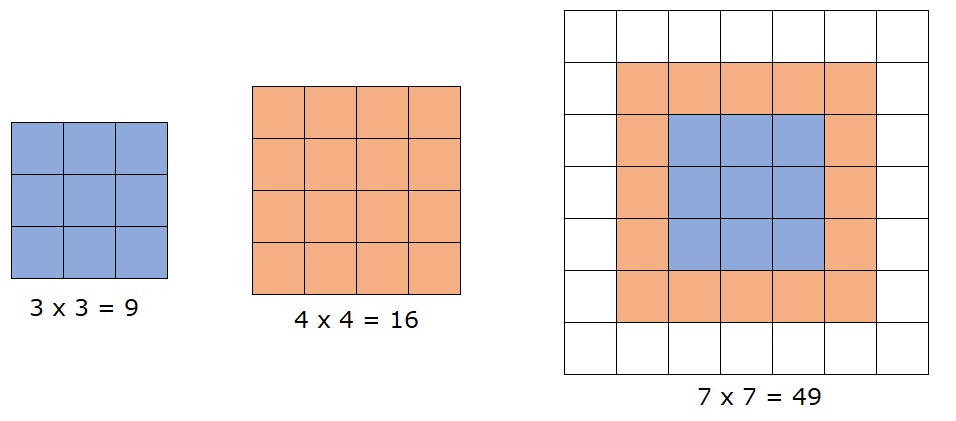
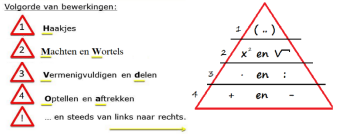 Je wist vast al dat er een bepaalde volgorde bij het berekenen van opgaven wordt gehanteerd.
Je wist vast al dat er een bepaalde volgorde bij het berekenen van opgaven wordt gehanteerd.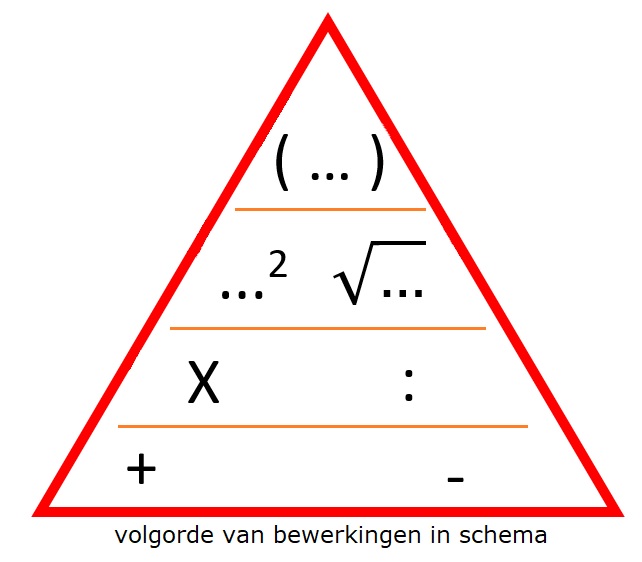
 Je gaat bij de patatzaak om de hoek samen met je vrienden wat eten.
Je gaat bij de patatzaak om de hoek samen met je vrienden wat eten.
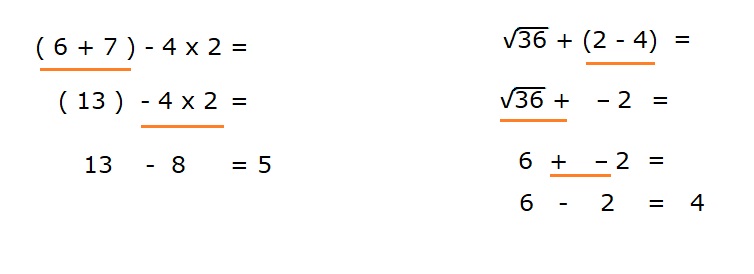

 Met welke toets zet je de rekenmachine eigenlijk aan.
Met welke toets zet je de rekenmachine eigenlijk aan.



 Door op de link te klikken opent er telkens een ander uitlegfilmpje.
Door op de link te klikken opent er telkens een ander uitlegfilmpje.