2KGT H01 Figuren

2KGT H01 Figuren

H1 Figuren

Inleiding

Welkom in leerjaar 2.

ijsbergmetafoor rekenen - Google zoeken (met afbeeldingen ...Een nieuw jaar, een nieuwe start en weer heel wat wiskundige onderwerpen om te ontdekken. Want, na één jaar wiskunde heb je pas het topje van de ijsberg ontdekt, er is nog veel meer wiskunde in de wereld om je heen. Zoals je inmiddels wel weet is wiskunde helaas niet altijd meteen zichtbaar. Door de wiskundelessen leer jij langzaam steeds meer wiskunde in de wereld om je heen te ontdekken.

 

 

 

Het eerste onderwerp van leerjaar 2 is de wereld van de figuren. We gaan het hebben over vlakke figuren (2d) en over ruimtefiguren (3d). De kennis die je vorig jaar al hebt opgedaan komt meteen mooi van pas. Je weet namelijk al het één en ander over vierhoeken en driehoeken. Ook komen de termen loodrecht en evenwijdig weer terug. Kun jij nog uitleggen wat loodrecht ook al weer was? En hoe teken je twee evenwijdige lijnen? Allemaal kennis en vaardigheden die je snel weer beheerst.

4 MAVO Wiskunde - Lesmateriaal - Wikiwijs

Leerdoelen

In dit hoofdstuk:

 

  • Leer je de eigenschappen van de vlakke figuren opnieuw herkennen.
  • Leer je wat ruimtefiguren zijn en welke eigenschappen deze hebben.
  • Leer je ruimtefiguren tekenen.
  • Leer je de oppervlakte en inhoud van ruimtefiguren berekenen.
  • Maak je kennis met \(\pi\).
  • Leer je wat de uitslag van een ruimtefiguur is.

 

Werkbladen

§1 Voorkennis

Uitleg & opgaven

Inleiding.

Over competenties – De kracht van mensenHet afgelopen schooljaar heb je al veel onderwerpen van wiskunde behandeld. Je komt dus niet helemaal nieuw binnen. Je bent geen onbeschreven blad, maar beschikt al over wiskundige kennis en vaardigheden.

 

Wiskunde is een vak dat een combinatie maakt tussen kennis (denk aan begrippen en formules uit je hoofd leren) en vaardigheden (iets kunnen voor doen, het tekenen van evenwijdige lijnen bijvoorbeeld). Dit betekent dus dat je niet alleen moet lezen en leren, maar vooral veel moet doen en oefenen.

 

In deze paragraaf frissen we je kennis en vaardigheden over vierhoeken en driehoeken op. Voordat we weer aan de slag gaan met deze vlakke figuren herhalen we eerst nog even loodrecht en evenwijdig. Dit zijn namelijk twee kenmerken die je moet weten voordat we met de vlakke figuren verder aan de slag kunnen.

 

Uitleg.

Loodrecht.

Wanneer je twee lijnen tekent, dan kunnen deze lijnen elkaar raken. Er onstaat dan een snijpunt.

 

Snijpunt

De lijnen m en n snijden elkaar in punt A.
Punt A is het snijpunt van m en n.

 

Loodrecht

Wanneer twee lijnen elkaar raken dan kan dit onder een hoek van 90o gebeuren. We noemen dat loodrecht

Lijn q staat loodrecht op lijn t.

WisFaq!

 

 

 

 

 

 

 

Loodrecht tekenen met je geodriehoek.

 

 

..1.   Loodrecht tekenen.

Op het werkblad zie je de volgende afbeelding.

  • Teken door punt A de lijn g loodrecht op r

 

..2.   Loodrecht tekenen.

Op het werkblad zie je de volgende afbeelding.

  1. Teken door punt A de lijn k loodrecht op n.
  2. Teken door B de lijn q loodrecht op n.

 

..3.   Loodrecht in een assenstelsel.
  1. Teken de punten: A(4 , 3), B(-2 , 1) en C(-1 , 5).
  2. Verbind punt A met punt B zodat lijnstuk AB ontstaat.
  3. Teken door punt C de lijn s loodrecht op lijnstuk AB.

 

Uitleg.

evenwijdig.

 

Twee getekende lijnen hoeven elkaar natuurlijk niet te raken. Je kunt ze ook beide in dezelfde richting tekenen.

 

De lijnen r en s snijden elkaar niet.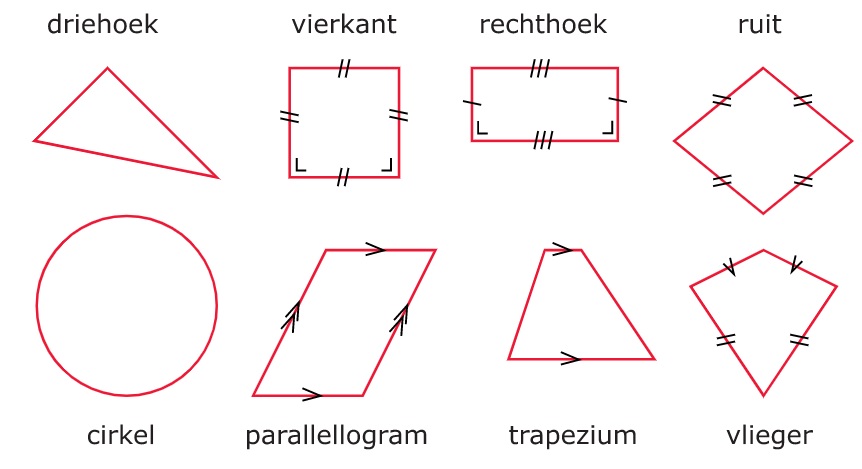
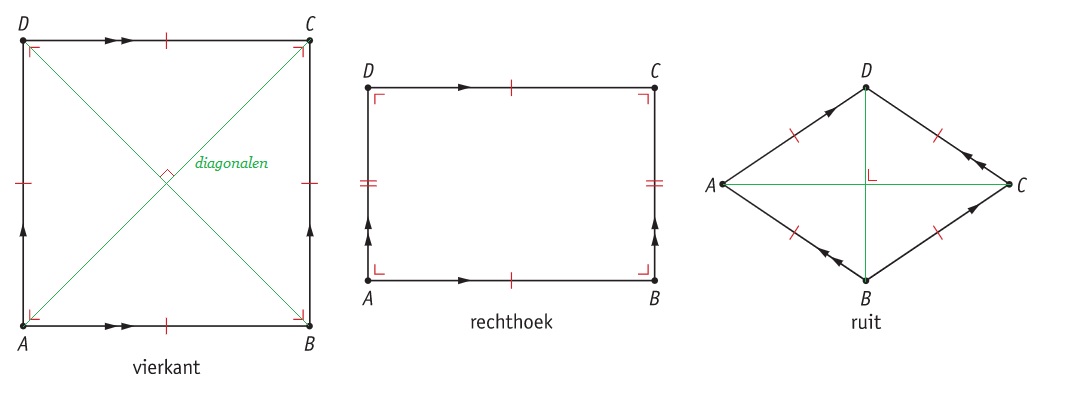
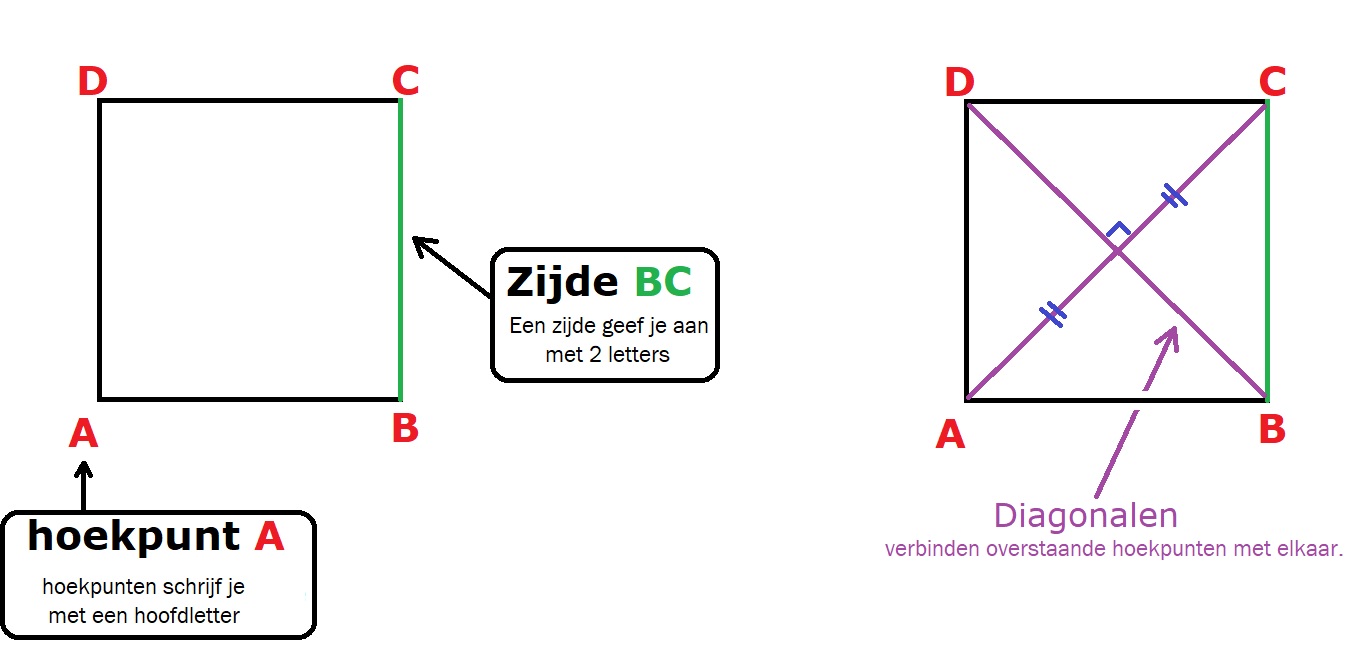
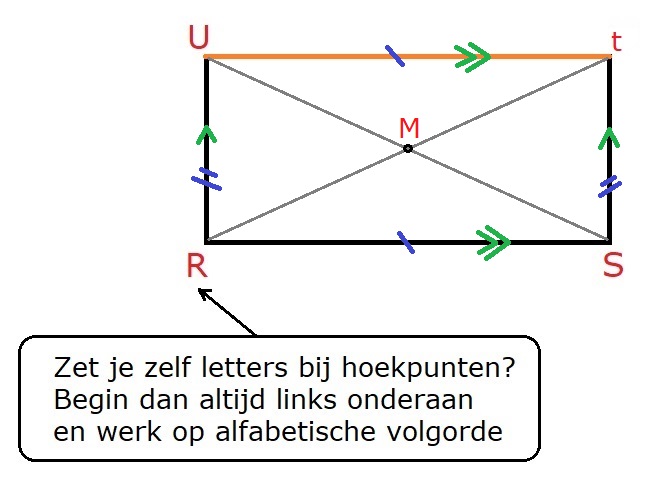Lijn r ligt evenwijdig aan lijn s.
een ander woord voor evenwijdig is parallel.

 

Kijk je naar Lijn r en lijn s dan zijn deze lijnen overal even ver van elkaar af. Of je dit nu aan het begin, in het midden of aan het einde meet. De afstand tussen de lijnen is overal gelijk. De lijnen gaan niet naar elkaar toe, niet van elkaar af maar gaan dezelfde richting op.

 

Evenwijdige lijnen tekenen:

 

 

..4.   Evenwijdig tekenen

Op het werkblad zie je de volgende afbeelding.

  • Teken door punt P de lijn l evenwijdig aan lijn w

 

..5.    

Op het werkblad zie je de volgende afbeelding.

  1. Teken door R de lijn a evenwijdig aan lijn d.
  2. Teken door N de lijn b evenwijdig aan lijn d. Denk je ook aan de tekentjes?

 

..6.   Loodrecht en evenwijdig in een assenstelsel.

a. Teken D(1 , 4) E(6 , 2) en F(8 , 7).

b. Teken door punt E de lijn  r evenwijdig aan lijnstuk DF. (vergeet de tekentjes er niet bij te zetten)

c. Teken door punt F de lijn v evenwijdig aan de y-as.

 

..7.   Loodrecht en evenwijdig in een assenstelsel.
  1. Teken een assenstelsel met een x-as van -2 tot 5 en een y-as van -3 tot 3.
  2. Teken de volgende punten P(-2 , 3), Q(3 , -1) R(5 , 3), S(-1 , -2) en T(2 , 2).
  3. Teken met groenpotlood lijnstuk PQ.
  4. Teken met blauwpotlood een lijn a evenwijdig aan de x-as door punt T.
  5. Teken door R de lijn b loodrecht op lijnstuk PQ

 

 

Uitleg.

Vlakke figuren

In de wiskunde heb je te maken met vlakke figuren. Vlakke figuren zijn figuren die bestaan in een plat vlak. In 2D (twee dimensionaal).

 

Hieronder zie je een aantal vlakke figuren. Je ziet bijvoorbeeld een driehoek en een cirkel. De overige vlakke figuren zijn bijzondere vierhoeken: een vierkant, een rechthoek, een ruit, een parallellogram, een trapezium en een vlieger.

De tekentjes in de figuren hebben natuurlijk een doel; dezelfde pijltjes in de zijden betekent dat die evenwijdig zijn; evenveel streepjes of v-tjes betekent dat de zijden even lang zijn.

 

Onder een diagonaal versta je een lijnstuk dat twee hoekpunten verbindt die niet op dezelfde zijde liggen. Bijvoorbeeld lijnstuk BE.

 

 

 

 

Vierkant, rechthoek en ruit.

Drie vlakke figuren die we al in leerjaar één hebben leren herkennen zijn het vierkant, de rechthoek en een ruit.

Een vierkant, een rechthoek en een ruit lijken op elkaar. Toch zijn er verschillen. Dankzij de eigenschappen van deze figuren kunnen we ze goed uit elkaar houden. Kijk maar eens goed naar de drie figuren en let op de kleine tekentjes in de figuren.

 

De eigenshappen: (leer deze uit het hoofd)

Vierkant   Rechthoek   Ruit
Alle zijden even lang   Overstaande zijden even lang   Alle zijden even lang
Overstaande zijden evenwijdig   Overstaande zijden evenwijdig   Overstaande zijden evenwijdig
Alle hoeken loodrecht   Alle hoeken loodrecht   Overstaande hoeken even groot
Diagonalen loodrecht op elkaar   Diagonalen loodrecht op elkaar   Diagonalen loodrecht op elkaar
        De diagonalen zijn even lang.


Tot slot

 

..8.   Een vierkant tekenen.
  1. Teken op je ruitjespapier een vierkant waarvan de zijde 5 cm zijn.
    Zorg er voor dat alle hoeken netjes recht zijn.
  2. Zet de letters P Q R S bij de hoekpunten. (je vierkant heet nu vierkant PQRS).
  3. Welke zijde ligt tegenover zijde PQ, noteer de letters van die zijde op je ruitjespapier.
  4. Welk hoekpunt is het overliggende hoekpunt van R?
  5. Zet even lang tekentjes in zijden die even lang zijn.
  6. Zet evenwijdig tekentjes in zijden die evenwijdig zijn.
  7. Teken de diagonalen in je vierkant.

 

..9.   Een rechthoek bekijken.

Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.

  1. Welke zijde is gekleurd?
  2. Welke zijden zijn evenwijdig, noteer 2 paren.
  3. Er is een foutje gemaakt bij deze rechthoek. Schrijf op wat er fout is gegaan.
  4. Welke zijde is even lang als zijde RU, hoe kun je dit in één oogopslag zien?
  5. Welke letter staat er bij het snijpunt van de diagonalen?

 

..10.   Benoem de figuren.

Bekijk de afbeelding op je werkblad.

Schrijf bij iedere figuur de juiste wiskundige naam.

 

 

..11.   Een ruit tekenen.
  1. Teken in je schrift een lijnstuk AC. Het lijnstuk moet 4 cm lang zijn.
  2. Zet een punt precies in het midden van lijnstuk AB. Noem dit punt R.
  3. Teken door R een loodrechte lijn op AC. Zorg er voor dat de lijn 2 cm boven en onder lijnstuk AB uitsteekt.
  4. Maak van je tekening een Ruit, Zet de letters B en D bij de ontbrekende hoekpunten.

 

..12.   Waarom is een rechthoek geen vierkant?

Probeer nu eens uit te leggen waarom een vierkant wel behoort tot de rechthoeken, maar een rechthoek geen vierkant is. Maak gebruik van het woordje eigenschappen in je antwoord.

 

..13.   Ruit in een assenstelsel

Teken nu de punten A(-1 , -1), B(-4 , -2) en D(-2 , -4) in je schrift.

  1. AB en AD zijn de zijden van de ruit ABCD. Teken AB en AD.

  2. Teken de ruit.

  3. Teken met rood kleurpotlood de diagonalen in de ruit.

 

..14.    

Teken het vierkant op je werkblad af.

Zorg er voor dat alle zijden even lang zijn en de hoeken netjes recht.

 

 

Driehoeken.

Een ander vlak figuur waar je al veel over geleerd hebt is de driehoek.

De driehoek met de hoekpunten A, B en C wordt genoteerd als {\displaystyle \triangle ABC}.
Als je letters bij een driehoek zet, begin dan altijd links onder.

Driehoek ABC kleurplaat | Gratis Kleurplaten printen

 

 

 

Omtrek en oppervlakte.

De oppervlakte van een rechthoek of vierkant bereken je met de volgende formule:

Oppervlakte rechthoek = lengte x breedte.

 

Ruit (meetkunde) - WikipediaDe oppervlakte van een ruit berekenen we net iets anders.

Oppervlakte ruit: Diagonaal x  diagonaal : 2

 

Voor de omtrek geldt: Tel alle zijde van het figuur bij elkaar op.

 

 

Ook voor het berekenen van de oppervlakte van een driehoek hebben we een formule geleerd:

Oppervlakte driehoek = zijde x bijb. hoogte : 2

 

 

Hoe herken je de hoogte van een driehoek?

Dit is niet zo heel moeilijk. De hoogte van een driehoek staat altijd loodrecht op de zijde waar deze bij hoort. Het loodrechttekentje laat goed welke zijde en hoogte lijn bij elkaar horen.

 

 

 

 

 

..15.   Oppevlakte driehoek berekenen

StudioWiskunde | Kennisbank WiskundeBekijk de groene driehoek hiernaast.

  1. Schrijf de formule die we gebruiken om de oppervlakte van een driehoek te berekenen in je schrift.
  2. Bereken nu de oppervlakte van de driehoek hiernaast.
    Rond je antwoord af op één decimaal (één cijfer achter de komma).

 

 

 

 

..16.   Oppervlakte vierhoek berekenen

De oppervlakte berekenen [1]Bekijk de rechthoek hiernaast.

Bereken de oppervlakte van de rechthoek.

 

 

 

 

 

..17.   Oppervlakte berekenen

Meten is WetenHier rechts zien we een plattegrond van de oppervlakte van de kamer van Jaqueline.
Jaqueline wil graag nieuwe vloerbedekking. Daarvoor moet zij weten hoe groot de oppervlakte van haar kamer in totaal is.

  1. Bereken de oppervlakte van de kamer van Jaqueline, schrijf natuurlijk netjes je berekening op.
    .
  2. De vloerbedekking die Jaqueline heeft uitgezocht kost €11,- per m2. Bereken wat de vloerbedekking in totaal gaat kosten.

 

 

..18.   Oppervlakte berekenen

StudioWiskunde | Kennisbank WiskundeBekijk de driehoek hiernaast.

  1. Schrijf de formule waarmee je de oppervlakte van een driehoek kunt berekenen in je schriftt.
  2. Vul de lengte van de zijde en de bijbehorende hoogte in je formule in en schrijf op.
  3. Bereken nu de oppervlakte van de driehoek.

 

 

 

 

..19.   Oppervlakte ruit berekenen.

Bekijk de twee ruiten hieronder, bereken van iedere ruit de oppervlakte. Schrijf de berekeningen netjes in je schrift.

5.2 Oppervlakte vierhoeken | Wiskunde H5 S2MB

 

 

..20.   Bereken de oppervlakte van het samengestelde figuur

Bekijk de figuur hiernaast. De maten van deze figuur zijn in centimeter.

  1. Teken de figuur na in je schrift.
  2. Verdeel de figuur nu in stukjes. Kleur de stukjes met kleurpotlood in.
  3. Schrijf de namen van de verschillende figuren op, zet er ook de formule voor oppervlakte onder.
  4. Vul de maten in de formule voor oppervlakte in en reken uit.
  5. Tel vervolgens de oppervlakte van losse figuren bij elkaar op.

 

..21.   Bereken de oppervlakte van de ruimte die overblijft.

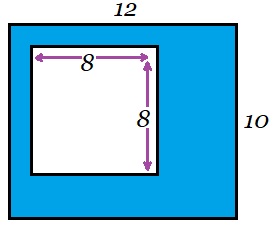Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.

 

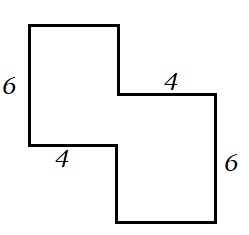Bereken de oppervlakte van de blauwe figuur, voer zelf de stappen van het stappenplan uit.

 

 

 

 

 

..22.   Bereken de oppervlakte van het samengestelde figuur

Bekijk de figuur hiernaast.

  1. Teken de figuur na in je schrift.
  2. Verdeel de figuur nu in stukjes. Kleur de stukjes met kleurpotlood in.
  3. Schrijf de namen van de verschillende figuren op, zet er ook de formule voor oppervlakte onder.
  4. Vul de maten in de formule voor oppervlakte in en reken uit.
  5. Tel vervolgens de oppervlakte van losse figuren bij elkaar op.

 

Antwoorden

§2 Cirkel

Uitleg & opgaven

Inleiding.

Deze paragraaf gaat helemaal over cirkels. Deze platte figuur hebben we in klas 1 namelijk nog niet behandeld. Gek eigenlijk, want cirkels kom je veel tegen in de wereld om je heen. In deze paragraaf leer je onder andere hoe je met je passer een cirkel tekent. En wat het getal \(\pi\) is

Veel succes.

 

Leerdoelen:

Aan het eind van deze paragraaf kan ik:

  • met behulp van mijn passen een cirkel tekenen.
  • Een omschrijving geven van de begrippen diameter en straal.
  • Kan ik de formule voor het berekenen van de oppervlakte van een cirkel opschrijven.
  • Kan ik de oppervlakte en omtrek van gegeven cirkels berekenen.

 

Uitleg.

Omtrek en oppervlakte

Zoals in de inleiding al geschreven staat is een cirkel een vlakke figuur.

De cirkel heeft geen zijden of hoekpunten, maar bestaat uit één enkel gebogen vlak. Dit gebogen vlak gaat 360o in de rondte.

 

De omtrek van een cirkel.

De omtrek van een cirkel bereken je met behulp van een formule:

Omtrek cirkel = diameter x \(\pi\)

 

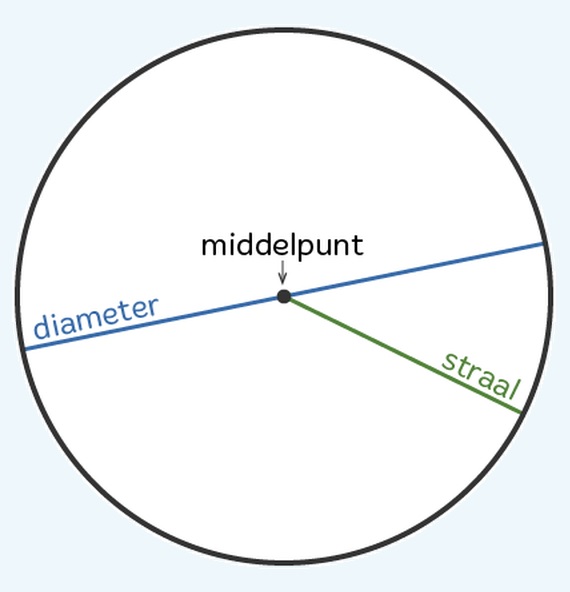Om de omtrek te kunnen bereken van een cirkel moet je dus wel weten wat een diameter (en wat een straal) is. Kijk maar eens naar de afbeelding hiernaast. Dan wordt dat waarschijnlijk snel duidelijk.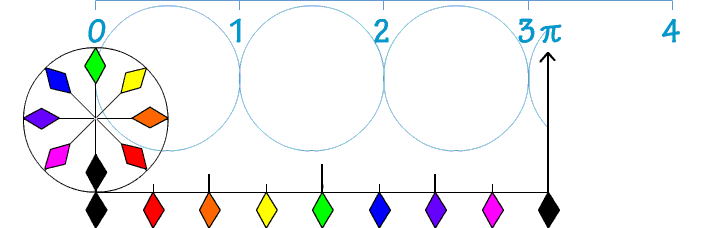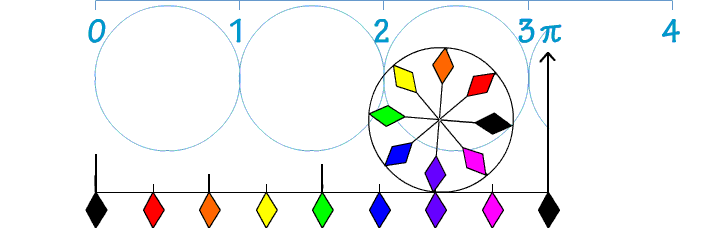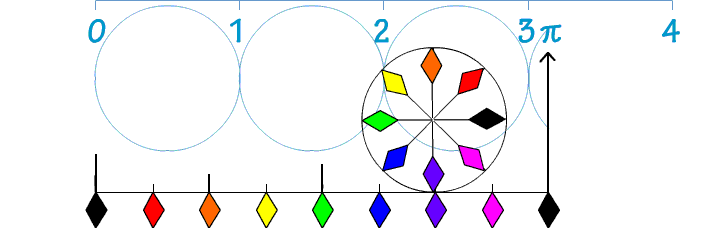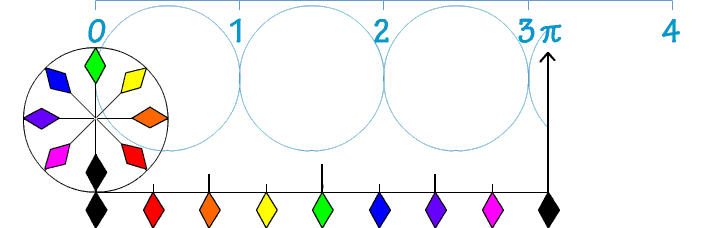

 

Een ander woordt voor diameter is middellijn. De diameter is de lijn die de cirkel in twee gelijke stukken deelt.

 

De straal teken je altijd vanuit het middelpunt naar de rand van je cirkel. De straal is precies de helft van je diameter.

 

En \(\pi\) (pi)

Dit is een ontdekking die heel ver terug gaat. De egyptenaren, oude grieken en zelfs in bijbelse teksten komt dit teken (getal) al voor.

 

\(\pi\) is de uitkomst wanneer je de omtrek van de cirkel deelt door de diameter.
De uitkomst is dan afgerond 3,14      \(\pi\) ≈3,14

Insight: PI day

 

..1.   Omtrek berekenen

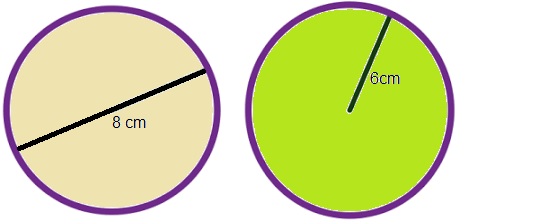Oppervlakte cirkel - Lesmateriaal - WikiwijsBekijk de afbeelding hiernaast.

  1. Wat is de lengte van de diameter van deze cirkel?
  2. Bereken de omtrek van de cirkel op het plaatje. Schrijf de berekening in je schrift.

 

 

 

 

 

..2.    

Bekijk de afbeelding hiernaast.

Bereken van beide cirkels de omtrek.

 

 

 

..3.    

Hoe een suikerrand of crustarand maken?Wie wat te vieren heeft, geeft een feestje. En wat is er feestelijker dan een leuk versierd glas?

Zo'n suikerrandje om een glas heen is niet eesn zo moeilijk te maken. 

 

Het glas dat je op de afbeelding ziet heeft een diameter van 8 cm. Bereken de lengte van het suikerrandje.

 

 

 

..4.   Omtrek zwembad

WISCAT oefenen?| GRATIS oefenen (+Uitleg en Tips) | Rekentoetspabo.nlOm een zwembad komen speciale tegels te liggen. Deze tegels zorgen er voor dat je minder snel uitglijdt.  Op het plaatje zie je het zwembad met daarom heen de rand van speciale tegels.

 

Hoeveel meter aan tegels moeten er gekocht worden? Schrijf je berekening in je schrift.

 

 

 

Uitleg.

oppervlakte van een cirkel.

Natuurlijk heeft een cirkel ook een oppervlakte. Een cirkel neemt tenslotte ruimte in, je kunt hem inkleuren.

 

Om de oppervlakte van een cirkel te berekenen gebruiken we een formule:

oppervlakte cirkel = straal2 x \(\pi\)         spreek uit als: {straal kwadraat keer pi}

H1 - Ruimtefiguren / Klas 1 | Lowik Wiskunde

De straal is de helft van de diameter. Je tekent een straal vanuit het middelpunt van je cirkel naar de rand.

 

Samenvatting:

Leer de volgende twee formules uit het hoofd:

Omtrek cirkel = diameter x \(\pi\)

Oppervlakte cirkel = straal2 x \(\pi\)

 

 

 

..5.    

WISCAT oefenen?| GRATIS oefenen (+Uitleg en Tips) | Rekentoetspabo.nlBekijk de afbeelding hiernaast.

  1. Hoe lang is de straal van deze cirkel.
  2. Bereken nu de oppervlakte van de cirkel.

 

 

 

 

..6.    

Bekijk de afbeelding hiernaast. Op het plaatje zie je twee cirkels.

Bereken van beide cirkels de oppervlakte.

 

 

 

 

 

..7.    

Bereken:

  1. De oppervlakte van een cirkel met een diameter van 10 cm.
  2. De oppervlakte van een cirkel met een straal van 4 cm.
  3. De omtrek van een cirkel met een straal van 3 cm.
  4. De oppervlakte en omtrek van een cirkel met een diameter van 14 cm.

 

 

..8.    

Een ring is eigenlijk een soort holle cirkel. Er is een grote cirkel waar een kleine cirkel uitgehaald wordt. Hiernaast zie je de schets van een ring. Bereken de oppervlakte van het gele gedeelte.

 

 

 

 

 

 

 

Uitleg.

Cirkels tekenen

Een cirkel teken je met behulp van een passer. In het begin is het best lastig om met dit stuk gereedschap een mooie cirkel te tekenen. Het is een vaardigheid die je met veel oefenen al snel onder de knie zult hebben. Dus lukt het je niet in één keer om een mooie cirkel te tekenen, blijf dan oefenen.

 

Hieronder wordt in een video voorgedaan hoe je met je passer een nette cikel tekent.

 

 

 

..9.   Cirkel tekenen
  1. Zet de metale passerpunt in je papier.
  2. Zet de potloodpunt 3 cm verder op, op het papier.
  3. Teken nu een cirkel.
  4. Meet de diameter van je cirkel op
  5. Schrijf de volgende zin over in je schrift:
    Als de passerbenen 3 cm uit elkaar staan, dan wordt de diameter .... cm lang.

 

 

..10.    
  1. Zet de metale passerpunt in je papier.
  2. Zet de potloodpunt 4 cm verder op, op het papier.
  3. Teken nu een cirkel.
  4. Meet de diameter van je cirkel op
  5. Schrijf de volgende zin over in je schrift:
    Als de diameter van de cirkel 8 cm moet worden, dan zet ik de passerbenen ... cm uit elkaar.

 

..11.    
  1. Zet de metale passerpunt in je papier.
  2. Zet de potloodpunt 5 cm verder op, op het papier.
  3. Teken nu een cirkel.
  4. Meet de diameter van je cirkel op
  5. Schrijf de volgende zin over in je schrift:
    Als de passerbenen 5 cm uit elkaar staan, dan wordt de diameter .... cm lang.

 

..12.    
  1. Teken een cirkel met een straal van 2,5 cm.
  2. Hoe veel centimeter is de diameter nu?

 

..13.    
  1. Teken een vierkant met zijden van vier cm in je schrift.
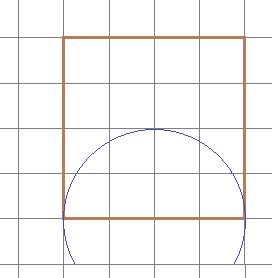  2. Zet de metalen punt in het midden van één van de zijde en de potloodpunt op een hoekpunt. Teken nu een halve cirkel. Als je het goed gedaan hebt, krijg je de figuur die je hiernaast ziet in je schrift.
    .
  3. Maak nu de figuur verder af zodat je figuur lijkt op het plaatje hieronder.

 

 

 

 

 

 

 

 

 

 

 

..14.    

Genesis Patroon | symbolen.jouwweb.nlHiernaast zie je hoe je met je passer het Genesis patroon kunt tekenen.

Maak het genesispatroon in je schrift.
werk netjes, als je het patroon af hebt mag je het patroon met kleurpotlood kleuren.

 

 

 

 

..15.    

Maak de figuur die je hiernaast ziet na in je schrift.

Gebruik alleen je passer.

Ben je klaar? Kleur dan de figuur in met kleurpotlood.

 

 

 

 

 

 

 

 

 

 

..16.    

De figuur hieronder bestaat uit allemaal cirkels.

Probeer deze figuur maar eens na te maken in je schrift. Met kleurpotloden kun je hem daarna netjes in kleuren

 

Antwoorden

§3 Balk & kubus

Uitleg & opgaven

Inleiding.

 

Leerdoelen:

 

Uitleg.

Eigenschappen van een balk en een kubus.

 

 

 

 

 

Uitleg.

Oppervlakte en inhoudsmaten.

 

 

 

 

 

 

Uitleg.

oppervlakte van een kubus of balk

 

 

 

 

 

 

Uitleg.

 

Inhoud van een kubus of balk berekenen

 

 

 

 

 

 

 

 

Uitleg.

Een balk of kubus tekenen.

 

 

 

 

 

 

 

 

Antwoorden

§4 Cilinder en prisma

Uitleg & opgaven

Inleiding.

 

Leerdoelen:

 

Uitleg.

Inhoud en uitslag van een cilinder.

 

 

 

 

Uitleg.

Inhoud en uitslag van een prisma.

 

 

 

Antwoorden

§5 Piramide en kegel

Uitleg & opgaven

Inleiding.

 

Leerdoelen:

 

 

 

Uitleg.

Inhoud en uitslag piramide

 

 

 

Uitleg.

Inhoud en uitslag kegel

 

 

 

 

 

Uitleg.

 

 

Antwoorden

§6 Samengestelde figuren

Uitleg & opgaven

Inleiding.

We hebben inmiddels de namen van de verschillende ruimtefiguren geleerd. We hebben onze kennis over de zijvlakken, hoekpunten en ribben van de ruimtefiguren herhaald en we kunnen de inhoud van een aantal ruimtefiguren berekenen. Maar in de wereld om je heen zie je ook vaak lichamen (ruimtefiguren) die samengesteld zijn uit 2 of meer losse figuren. Er zijn er als het ware 2 of 3 aan elkaar geplakt. Hoe je de inhoud van die figuren moet berekenen leer je in deze paragraaf.

 

Leerdoelen:

Aan het eind van deze paragraaf kan ik:

  • De inhoud van een samengestelde ruimtefiguur berekenen d.m.v opvullen.
  • De inhoud van een samengestelde ruimtefiguur berekenen dm.v. splitsen.

 

 

Uitleg.

De inhoud van een samengestelde figuur berekenen

Kennisbank WiskundeDe wereld om ons heen bestaat niet enkel uit losse ruimtefiguren (lichamen). Heel veel objecten zijn opgebouwd uit twee of meer ruimtefiguren samen. Kijk maar naar het huis hiernaast. Dit huis bestaat uit twee balken en een prisma als dak.

 

Hoe je de inhoud van een samengestelde figuur het gemakkelijkst kunt berekenen zie je in de video hier onder.

 

 

In deze video komen twee manieren aan bod.

  • Opvullen, je stopt er een stukje extra bij en haalt dat er later vanaf.
  • Splitsen, je deelt de figuur in 2 of meer losse figuren en rekent die afzondelijk uit, daarna tel je de stukken bij elkaar op

 

 

 

..1.    

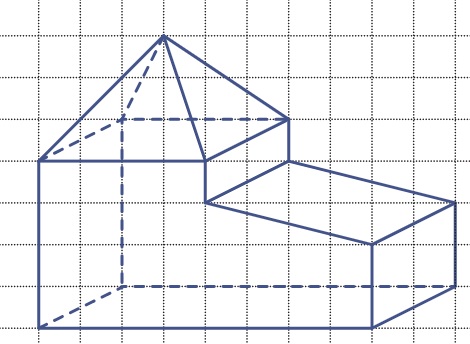Bekijk de afbeelding hiernaast.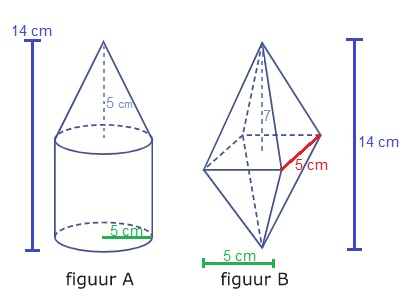

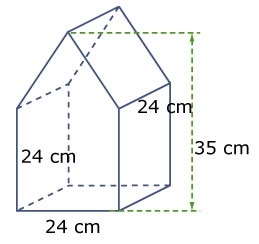Gebruik het roosterpapier om de maten van de figuur te tellen.

 

Bereken de inhoud van de totale figuur.

 

 

 

 

..2.    

Hiernaast zie je twee samengestelde ruimtefiguren.

Bereken van iedere samengestelde ruimtefiguur de inhoud.

 

Schrijf natuurlijk je berekeningen op, rond je antwoord telkens af op 1 decimaal. (Eén cijfer achter de komma).

 

 

 

..3.    

Hiernaast zien we de contouren van een huisje.
Bereken de inhoud van het totale huisje.

Rond je antwoord af op één decimaal.

 

 

 

 

 

 

 

Uitleg.

In het filmpje hieronder wordt nog eens voorgedaan hoe je de inhoud van een samengestelde ruimtefiguur berekend.

 

 

..4.    

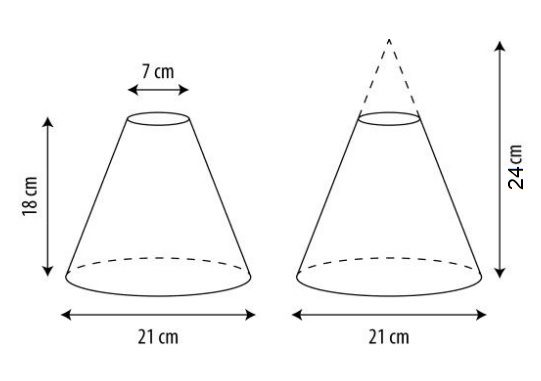Hiernaast zien we een afgeknotte kegel. Voor het gemak is ernaast gezet welk stukje er afgesneden is.

 

Bereken de inhoud van de afgeknotte kegel. Rond je eindantwoord af op één decimaal. En schrijf natuurlijk de berekening weer in je schrift.

 

 

 

..5.    

Bereken de inhoud van het huis hiernaast.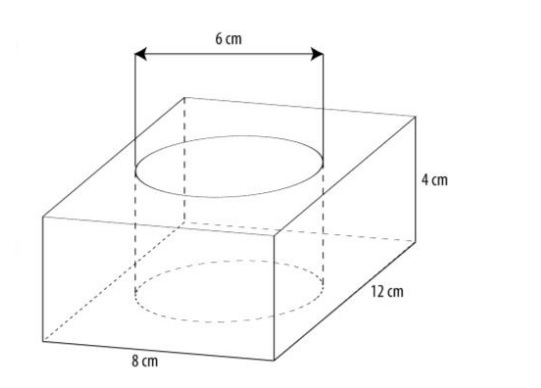

Je mag de ruimte van de ramen en deuren vergeten.

Rond je antwoord af op één decimaal en laat duidelijk zien welke berekeningen je gemaakt hebt.

 

 

 

 

 

..6.    

Hiernaast zien we een kaarsenhouder. Deze balkvormige houder heeft in het midden een cilindervormig gat waar de kaars precies in past.

 

Bereken de totale inhoud van de kaarsenhouder. Rond indien nodig je antwoord af op één decimaal.

 

 

 

 

..7.    

Hiernaast zie je hou handdoekrollen worden vervoert. Op het plaatje kun je zien dat er zes rollen in één doos passen, twee naast elkaar en drie achter elkaar.

 

Wanneer je zes rollen in een doos stopt blijft er natuurlijk nog wat ruimte tussen de rollen over.

 

Bereken hoeveel liter ruimte er nog over is in de doos. Rond je antwoord af op twee decimalen.

Antwoorden

§7 Gemengde opgaven

Opgaven

 

..8.    

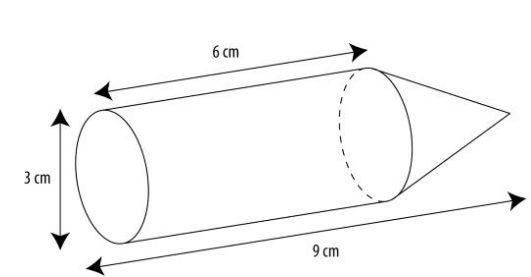De figuur hiernaast is samengesteld uit twee ruimtefiguren.

  1. Schrijf de namen van de ruimtefiguren op die je op het plaatje ziet.
  2. Bereken de inhoud van de totale ruimtefiguur.
    Rond je antwoord af op 1 decimaal.

 

 

 

 

 

..11.    

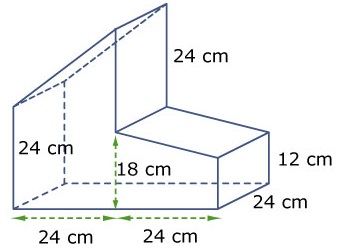Hiernaast zien we een draadmodel van een huisje. De architect wil graag weten wat de inhoud van dit modelhuis is.

 

bereken de inhoud van het modelhuis. Rond je antwoord af op hele cm3.

 

Antwoorden

D-toets

Diagnostische toets

Een diagnostische toets is een onderzoek naar eventuele gaten in jouw kennis of vaardigheden. Het doel van de diagnostische toets is het vaststellen wat je al kan, en waar je de komende tijd nog wat extra aandacht aan moet besteden.

Wanneer je een diagnostische toets maakt is het dus goed om je fouten bij te houden. Met deze fouten ga je de komende dagen extra aan de slag. Je herhaalt de uitleg, vraagt aan andere of ze je kunnen helpen als je de opgaven niet begrijpt of je vraagt aan je docent nog eens extra uitleg.

Op deze manier kom je voorbereid naar een toets. Je weet wat je kan, dit heb je voor de zekerheid nog één keer herhaald, de d-toets heeft je laten zien welke onderdelen je nog niet goed beheerst en deze heb je dan ook extra geoefend en extra uitleg gevraagd. Je weet nu dat je alles beheerst en je de toets goed kunt maken.

Herhaling

Uitleg & opgaven

 

 

Uitleg

§6 Samengestelde ruimtefiguren.

 

 

..14.    

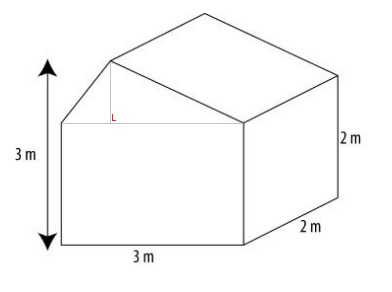Hiernaast zien we een samengestelde ruimtefiguur.

We willen graag dat jij de inhoud van deze figuur berekent

  1. Uit welke twee ruimtefiguur is dit figuur samengesteld? Noteer de namen in je schrift.
  2. Welke formules voor inhoud gebruiken we bij deze twee figuren. Noteer beide formules in je schrift.
  3. Bereken de inhoud van de onderkant van deze samengestelde figuur.
  4. Bereken de inhoud van de bovenkant van deze samengestelde figuur.
  5. Bereken de totale inhoud van de samengestelde ruimtefiguur.

 

..15.    

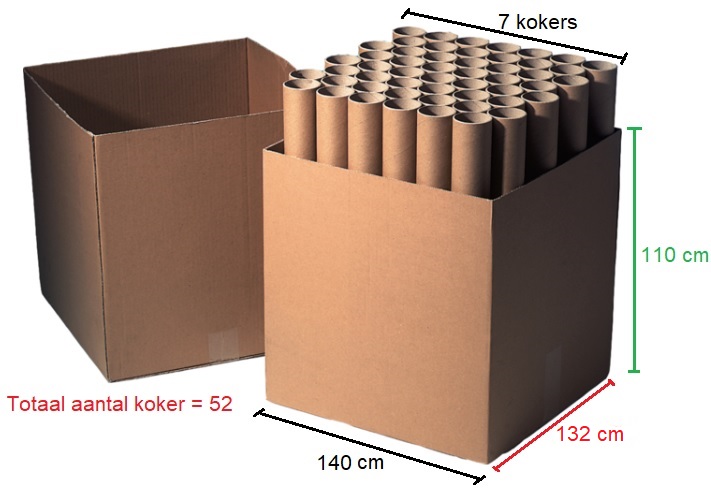Wanneer je een grote hoeveelheid posters besteld worden deze in apparte kokers naar je toegezonden. Een koker heeft een diameter van 20 cm en is net zo hoog als de doos.

 

De kokers worden in een grote kartonnendoos gestopt. In de ruimte tussen de kokers wordt opvulmateriaal zoals piepschuimbolletjes gestopt.

 

De fabrikant van de posters wil graag weten hoeveel liter piepschuimbolletjes hij nog in de ruimte tussen de kokers moet stoppen.

 

Bereken voor de fabrikant de inhoud van de ruimte tussen de kokers. Rond je antwoord af op 1 decimaal. Denk er aan, je antwoord moet in liters gegeven worden.

Antwoorden

Extra stof

Uitleg & opgaven

Het laatste ruimtefiguur waar we de inhoud van leren berekenen is de bol.

Een bol is een driedimensionale figuur waarvan alle punten even ver van een punt, het middelpunt, liggen. Hieronder staat een bol getekend; de rode lijnen zijn diameters.

 

Eigenschappen

De Bol is een ruimtefiguur. De bol heeft geen hoeken of ribben. Het heeft alleen één gebogen vlak. De bol is aan alle kanten rond. Voorbeelden van bolvormige dingen zijn, een voetbal en een globe. In het midden heeft de bol een middelpunt. Vanaf het middelpunt lopen oneindig veel diameters en stralen.

 

Oppervlakte

De oppervlakte van de bol is eenvoudig te berekenen. Voor de oppervlakte heb je alleen de lengte van de straal nodig. Hiervoor gebruiken we de volgende formule:

4 x \(\pi\) x straal² = oppervlakte.

De straal loopt van het middelpunt in een bol naar de buitenkant. Het ²-tekentje staat voor kwadraat.

 

Inhoud

Een bol heeft net als elk ander ruimtefiguur een inhoud. Net als bij de oppervlakte moet je eerst het middelpunt weten. vervolgens teken je twee diameters. Een van boven naar beneden en een van links naar rechts. De diameters moeten loodrecht op elk staan. Je meet nu de lengte van één diameter en deelt het door twee. Nu heb je de lengte van de straal. Vervolgens doe je deze formule:

\(4\over 3\) x \(\pi\) x straal³ = inhoud.

 

De \(\pi\) is een Pi, dit is een getal dat nooit op lijkt te houden. Op de plaats van het woordje straal vul je de lengte van de straal in. Het ³-tekentje betekend derde macht.

 

Antwoorden

  • Het arrangement 2KGT H01 Figuren is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.

    Auteur
    D. Giessen
    Laatst gewijzigd
    2020-07-16 21:39:10
    Licentie

    Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:

    • het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
    • het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
    • voor alle doeleinden, inclusief commerciële doeleinden.

    Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.

    Aanvullende informatie over dit lesmateriaal

    Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:

    Eindgebruiker
    leerling/student
    Moeilijkheidsgraad
    gemiddeld

  • Downloaden

    Het volledige arrangement is in de onderstaande formaten te downloaden.

    Metadata

    LTI

    Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI koppeling aan te gaan.

    Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.

    Arrangement

    IMSCC package

    Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.

    Voor developers

    Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op onze Developers Wiki.

  • Gebruik
    Weergave
  • Wikiwijs is een dienst van