Het arrangement 2H06 §5 Vergelijkingen oplossen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 02-02-2020 09:25:00
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld

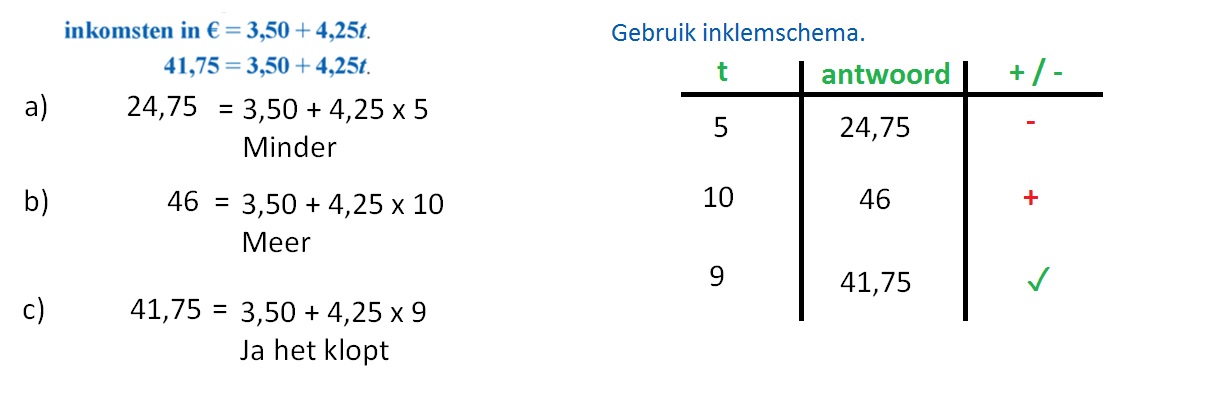
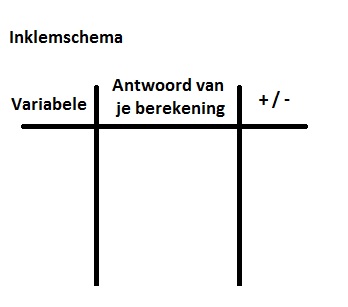 Is de formule waarmee je werkt niet-lineair, dan kun je een vergelijking oplossen met de inklem-methode. De inklem-methode is als het ware gokken. Je vult net zo lang getallen in tot je het goede antwoord hebt gevonden. Bij inklemmen houdt je in een schema bij wat je allemaal geprobeerd hebt.
Is de formule waarmee je werkt niet-lineair, dan kun je een vergelijking oplossen met de inklem-methode. De inklem-methode is als het ware gokken. Je vult net zo lang getallen in tot je het goede antwoord hebt gevonden. Bij inklemmen houdt je in een schema bij wat je allemaal geprobeerd hebt.
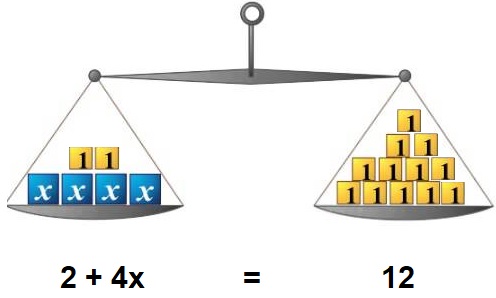
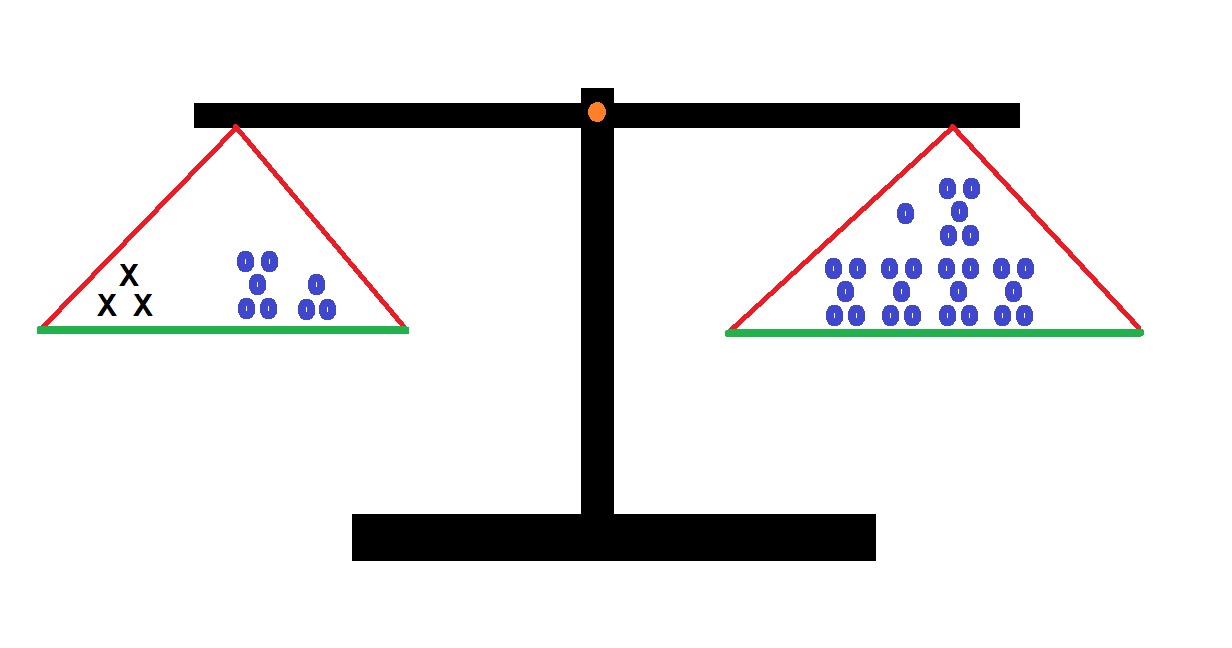 Hiernaast zie je een balans getekend.
Hiernaast zie je een balans getekend.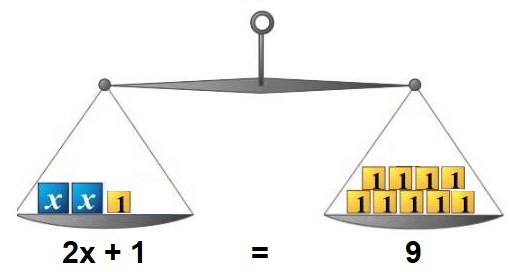

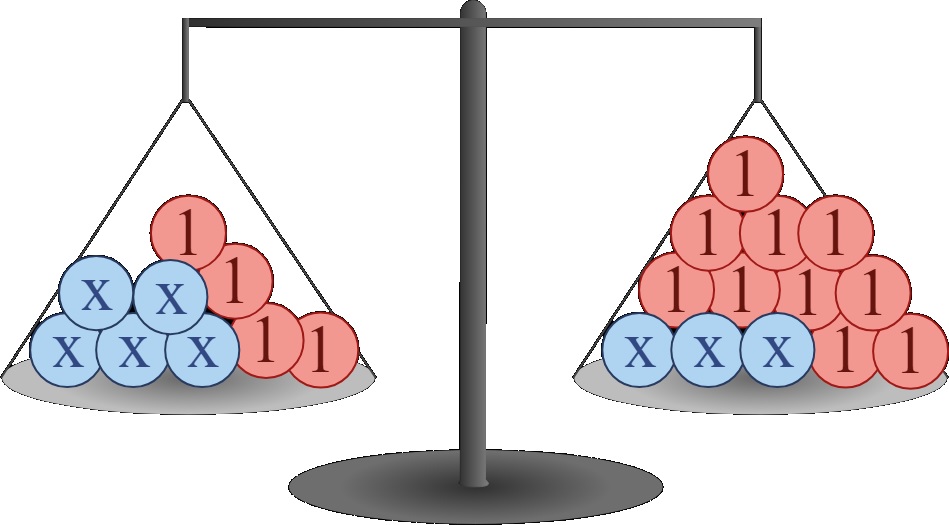

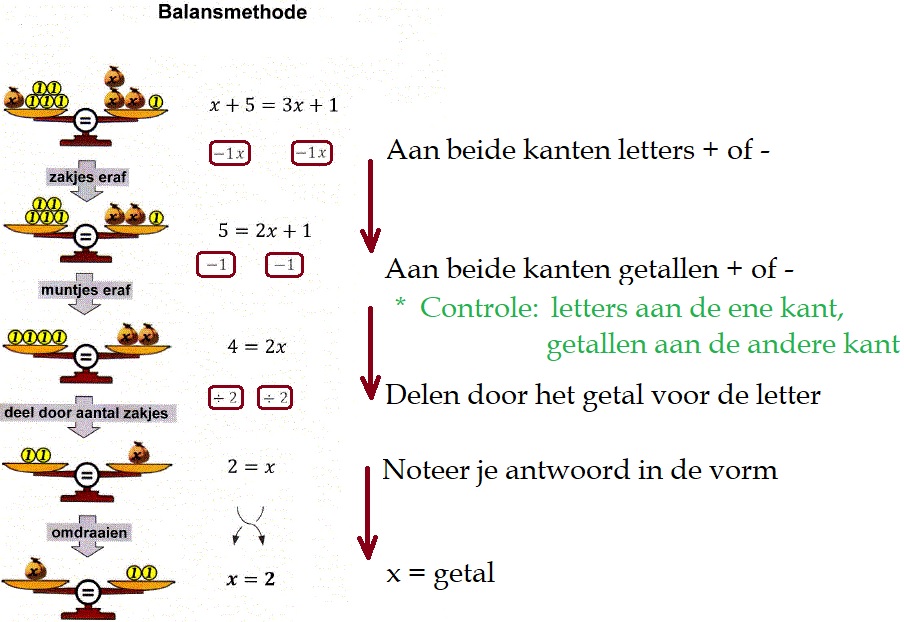
 In opgave 1 t/m 5 heb je jouw kennis over de balansmethode weer even herhaalt. Je werkte in al die opgaven met lineaire formule. Is de formule niet-lineair, dan kun je de balansmethode niet gebruiken, je gebruikt dan de inklemmethode.
In opgave 1 t/m 5 heb je jouw kennis over de balansmethode weer even herhaalt. Je werkte in al die opgaven met lineaire formule. Is de formule niet-lineair, dan kun je de balansmethode niet gebruiken, je gebruikt dan de inklemmethode.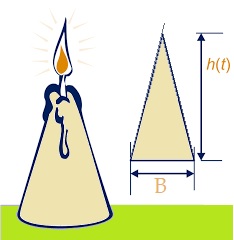 Hiernaast zie je een kaars. Een formule die ongeveer het verband tussen de hoogte van deze kaars en de brandtijd aangeeft, is:
Hiernaast zie je een kaars. Een formule die ongeveer het verband tussen de hoogte van deze kaars en de brandtijd aangeeft, is: Hiernaast zie je een foto van de Red-Bull Cliffdive competitie. Hierbij hoort een verband tussen de hoogte van het plateau en de tijdsduur van de sprong in seconden. Voor dit verband geldt de volgende formule
Hiernaast zie je een foto van de Red-Bull Cliffdive competitie. Hierbij hoort een verband tussen de hoogte van het plateau en de tijdsduur van de sprong in seconden. Voor dit verband geldt de volgende formule Sarah is bloemiste, zij heeft een eigen bloemenzaak.
Sarah is bloemiste, zij heeft een eigen bloemenzaak.
