Thema: Getallen en grafieken hv
Inleiding
In dit thema ga je twee verschillende dingen leren:
- Grafieken kom je overal om je heen tegen: je gaat leren wat je allemaal in grafieken kunt aflezen
- Je gaat ook zelf grafieken tekenen
- Je leert hoe een grafiek bij een evenredig verband eruit ziet
- Je leert hoe je van breuken decimale getallen kunt maken, en omgekeerd
- Je leert wat de rationale getallen zijn: dat zijn de gehele getallen en de getallen die je als een breuk kunt schrijven
- Je gaat leren dat er getallen zijn die je niet als breuk kunt schrijven: je maakt kennis met de irrationale getallen
Wat kan ik straks?
Aan het einde van dit thema:
- kan je een grafiek tekenen bij een tabel
- benoemen wat de eenheden en grootheden zijn bij een verband
- kun je kritisch naar grafieken kijken en daar allerlei gegevens uit aflezen
- weet je een evenredig verband is en kun je daar de kenmerken van benoemen en herkennen
- weet je hoe je van een breuk een decimaal getal kunt maken, en omgekeerd
- weet je wat rationale getallen zijn en weet je hoe je die aan de decimale schrijfwijze kunt herkennen
- weet je dat er ook getallen zijn die niet als breuk zijn te schrijven: de irrationale getallen
Wat kan ik al?
Je kan al eenvoudige grafieken aflezen.
En je weet natuurlijk wat decimale getallen zijn.
Je krijgt nu een paar vragen om te kijken wat je allemaal nog weet.
Toets: Wat kan ik al?
Start
Wat ga ik doen?
Het thema 'Getallen en grafieken' bestaat uit de volgende onderdelen:
| Onderdeel |
Tijd (u:min) |
| Inleiding |
0:35 |
| § Grafieken |
2:00 |
| § Evenredige verbanden |
0:55 |
| § Decimale breuken |
1:25 |
| § Decimalen uitrekenen |
0:50 |
| § Irrationale getallen |
0:50 |
| § Bij een vierkant |
1:40 |
| Afsluiting |
|
| Samenvatting (goed doornemen) |
0:15 |
| Diagnostische toets |
0:50 |
| Extra opgaven (keuze) |
0:50 |
| Thema-opdracht (keuze) |
2:00 |
| Totaal |
±12:00 |
Gewone opgaven en Super opgaven
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
Die Super variant is wel wat moeilijker.
Let op: Je hoeft dan niet ook de 'normale' variant te maken.
Je herkent de opgaven waar een Super variant van is aan dit teken 
Als je op dit teken klikt, dan ga je naar de Super variant.
In de Super variant staat dit teken 
Als je daarop klikt, ga je weer terug naar de gewone opgave.
De Super opgaven staan ook steeds bij elkaar onder aan iedere paragraaf.
Paragrafen
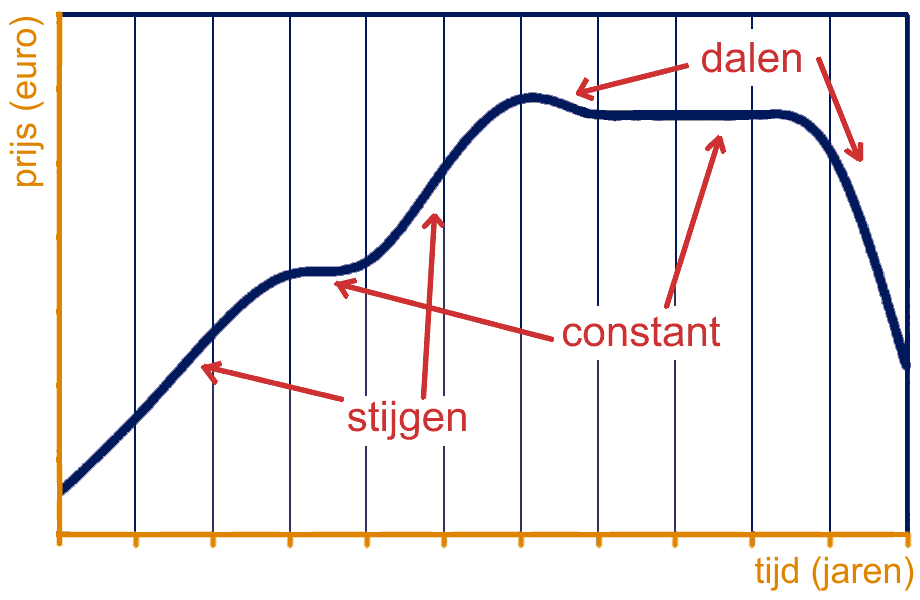
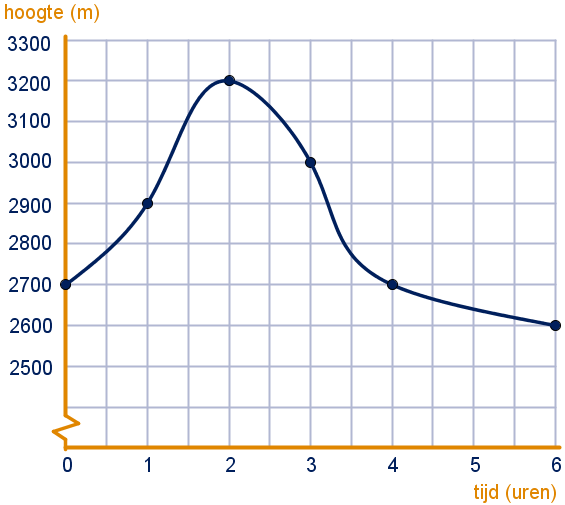In dit thema getallen en grafieken leer je eerst van alles over grafieken en soorten van grafieken. Daarna leer je hoe je een breuk in decimale getallen kunt schrijven en maak je kennis met een nieuw soort getallen die je niet als breuk kunt schrijven!
Afsluiting
Samenvatting
Grafieken
In een grafiek wordt het verband tussen twee grootheden weergegeven.
- Een grootheid is iets wat je kunt meten.
Voorbeelden zijn lengte, oppervlakte, temperatuur, tijd, inhoud en snelheid.
- De bijbehorende eenheid is de maat waar je de grootheden in meet.
Voorbeelden zijn meter, m2, °C, jaar, liter en km/u.
Door het verband van twee grootheden in een grafiek weer te geven, kun je aflezen hoe de twee grootheden met elkaar samenhangen.
Zie bijvoorbeeld hieronder een grafiek van de totale hoeveelheid gereden kilometers met de auto in Italië.
Deze grafiek kun je opdelen in verschillende stukken:
-
stukken waar de grafiek stijgt;
-
stukken waar de grafiek daalt;
-
stukken waar de grafiek constant is.
Grafieken tekenen
Een grafiek heeft een assenstelsel, bestaande uit een horizontale as en een verticale as.
Bij de assen moet altijd staan wat de grootheid en de bijbehorende eenheid is.
Bij een grafiek kun je een tabel maken.
Natuurlijk kun je omgekeerd bij een tabel ook een grafiek maken:
-
Teken een assenstelsel;
-
De horizontale as komt altijd overeen met de bovenste rij van de tabel, de verticale as met de onderste rij van de tabel;
-
Kijk naar het grootste en kleinste getal van de bovenste rij: deze moeten in gelijke stappen over de horizontale as verdeeld worden; Kies een geschikte stapgrootte, zodat de horizontale as tussen 6 tot 10 cm lang is;
-
Kijk naar het grootste en kleinste getal van de onderste rij: deze moeten in gelijke stappen over de verticale as verdeeld worden; Kies ook nu een geschikte stapgrootte, zodat de verticale as tussen 6 tot 12 cm lang is;
-
Zet de namen van de grootheden en de eenheden bij de beide assen;
-
Elk tweetal getallen uit de tabel geeft een punt in de grafiek. Teken ze allemaal;
-
Teken een vloeiende lijn door de punten.
(Er bestaan ook grafieken waarbij de punten met rechte lijnstukken verbonden moeten worden.)
Soms kan je op de verticale as beter een zogenaamde scheurlijn of zaagtand gebruiken, als alle waarden ver van nul afliggen.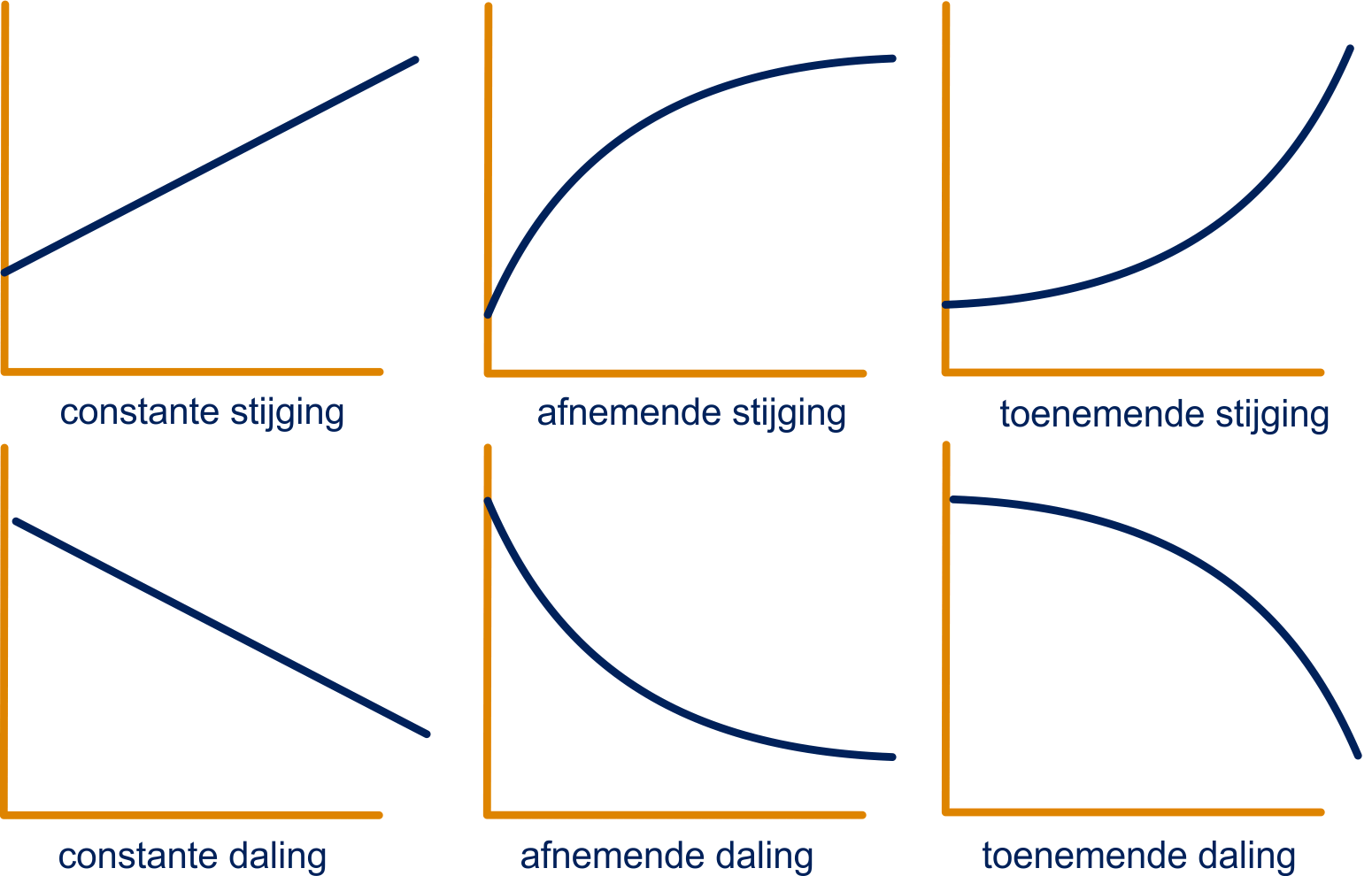
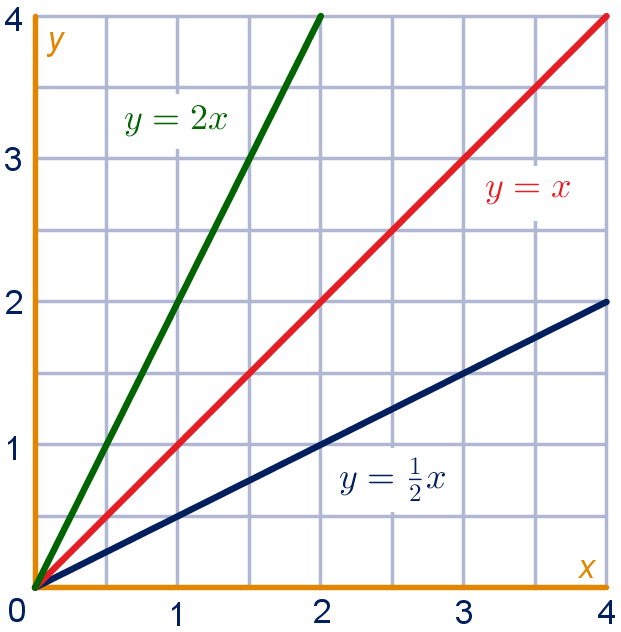Zie figuur hiernaast.
Anders zou je een heel stuk ongebruikte as krijgen.
Je krijgt dan een grafiek die je nauwkeuriger kan tekenen en aflezen.
Let op: Je mag nooit naast de zaagtand nog iets in de grafiek tekenen. En de zaagtand is één keer naar links en één keer naar rechts. Een zaagtand op de horizontale as is vrij ongebruikelijk.
Globale grafieken
Grafieken waarbij de schaalverdeling ontbreekt, noemen we globale grafieken.
We onderscheiden zes manieren waarop een grafiek zich kan ontwikkelen:
Evenredige verbanden
Het verband tussen twee grootheden \(\small x\) en \(\small y\) heet evenredig als er een constante verhouding is tussen \(\small x\) en \(\small y\).
Als \(\small x\) bijvoorbeeld \(\small 2\) keer zo groot wordt, wordt \(\small y\) ook \(\small 2\) keer zo groot.
De grafiek is dan een rechte lijn die door \(\small (0,0)\) gaat.
Een formule is dan \(\small y=c⋅x\).
De waarde van \(\small c\) is voor elk verband anders. Het getal \(\small c\) heet de evenredigheidsconstante.
Decimale breuken op de getallenlijn
Voorbeeld:
\(\small 3,14159 = 3\) eenheden \(\small + 1\) tiende \(\small + 4\) honderdsten \(\small + 1\) duizendste \(\small + 5\) tienduizendsten \(\small + 9\) honderdduizendsten
Het stuk van de getallenlijn tussen \(\small 3\) en \(\small 4\) moet worden verdeeld in honderdduizend gelijke stukjes om dit getal te plaatsen.
Waar ongeveer ligt \(\small 3,14159\)?
Welk getal ligt precies midden tussen \(\small 3,141\) en \(\small 3,1415\)?
Diameter en omtrek
regelmatige zeshoek
De diameter (diagonaal) \(d\), de zijde \(z\) en de omtrek \(p\) van een regelmatige zeshoek zijn evenredig.
\(d=2z\) , \(p=3d\) , \(p=6z\) |
 |
vierkant
De diameter (diagonaal) \(d\) en de zijde \(z\) van een vierkant zijn evenredig.
\(d=di⋅z\), waarbij \(di≈1,41\). |
 |
cirkel
De omtrek \(p\) en de diameter \(d\) van een cirkel zijn evenredig.
\(p=π⋅d\), waarbij \(π≈3,14\). |
 |
Van breuk naar decimale breuk
Voorbeeld:
we bepalen de decimale breuk van \(\frac {35}{54}\).
-
stap 1
\(35 = 350\) tienden; dit gedeeld door \(54\) is \(6\) tienden, met rest \(26\) tienden. Die rest moeten we nog verder verdelen.
-
stap 2
\(26\) tienden \(= 260\) honderdsten; dit gedeeld door \(54\) is \(4\) honderdsten, met rest \(44\) honderdsten. Die rest moeten we verder verdelen.
-
stap 3
\(44\) honderdsten \(= 440\) duizendsten; dit gedeeld door \(54\) is \(8\) duizendsten, met rest \(8\) duizendsten. Die rest moeten we verder verdelen.
-
stap 4
\(8\) duizendsten \(= 80\) tienduizendsten; gedeeld door \(54\) is \(1\) tienduizendste, met rest \(26\) tienduizendsten. Die rest moeten we verder verdelen.
-
stap 5
We zitten nu in de situatie van stap 2: we moeten \(260\) delen door \(54\). Dus krijgen we weer als decimaal \(4\) met als rest \(44\).
-
stap 6
We zitten nu in de situatie van stap 3: we moeten \(440\) delen door \(54\). Dus krijgen we weer als decimaal \(8\) met als rest \(8\).
-
Enzovoort
Dus \(\frac{35}{54}=0,64814848…\)
Rationaal en irrationaal
Rationale getallen zijn de getallen die je kunt schrijven als breuk. Als decimale breuk geschreven zijn ze repeterend: een vast groepje decimalen blijft zich herhalen.
Voorbeelden:
\(\frac{17}{125}=0,136(00000…)\)
\(\frac{567}{370}=1,5324324324…\)
Deze twee decimale breuken hebben periode \(1\) en \(3\).
Irrationale getallen zijn de getallen die niet als breuk kunnen worden geschreven. Als decimale breuk zijn ze niet repeterend.
Voorbeelden:
\(0,12312231222312222312222…\)
\(1,414213562373095048801688…\)
\(π=3,14159265358979323846264…\)
Thema-opdracht
Het weer is één van de meest besproken onderwerpen in Nederland. Dat komt vooral doordat we in Nederland vaak wisselende weersomstandigheden hebben.
Het weer bestaat uit verschillende aspecten zoals temperatuur, neerslag en wind.
In deze opdracht ga je gedurende een periode de temperatuur meten in een bepaalde plaats in Nederland; maar je kijkt ook naar andere aspecten van het weer.
Aan het einde van de opdracht zet je alles netjes uit in een grafiek.
Diagnostische toets
Je gaat nu een aantal gevarieerde opgaven maken waarin je kunt laten zien of je de geleerde stof uit de voorgaande paragrafen beheerst.
Dit zijn voorbeeldopgaven die een goed beeld geven van de opgaven die in een eindtoets over dit thema 'hoeken' voor kunnen komen.
Als je een score van 70% haalt, heb je een voldoende.
Toets: Diagnostische toets
Start
Extra opgaven
Je ziet hier twee Extra oefeningen. Je hoeft er maar één te doen.
- Extra oefening Basis is bedoeld voor leerlingen die de Diagnostische toets NIET goed gemaakt hebben.
- Extra oefening Plus is bedoeld voor de leerlingen die de Diagnostische toets WEL goed gemaakt hebben.
Je moet dus sowieso eerst de Diagostische toets af hebben vóórdat je aan de Extra oefening begint.
Vraag bij twijfel aan je docent wat je moet doen.
Oefening: Extra oefening Basis
Start
Oefening: Extra oefening Plus
Start
Terugblik
Evaluatie: Terugblik
Start
