Tijdens de wiskundelessen heb je de volgende materialen nodig:
- Schrift met een kantlijn van 2/3 hokjes
- Pen, potlood, puntenslijper en gum
- geodriehoek
- rekenmachine
- passer
- drie kleurpotloden
- 2 markeerstiften
Werken met de examensite.
Hoe werk je met de examensite.nl
Voordat je kunt gaan beginnen met het oefenen van de onderwerpen van periode 3 Log je eerst in bij SOMTODAY, daarna moeten we ons eerst aanmelden bij de eindexamensite.nl
Hoe je dit doet, vindt je in het filmpje hier onder.
Een fabrikant wil sandwiches op een mooie manier verpakken. Hiernaast zie je drie sandwichverpakkingen die hij als voorbeeld heeft gebruikt. De zijvlakken van de verpakkingen zijn rechthoeken en driehoeken.
Hieronder staat een tekening van zo’n verpakking.
De afmetingen van de verpakking zijn: AE = 20 cm, AB = 18 cm, EF = 7 cm, hoek A = 40° en hoek B = 78°.
Op de uitwerkbijlage is een begin gemaakt met de uitslag van de verpakking op schaal 1 : 4.
Verfblikken zijn er in allerlei maten. Zie de foto hieronder. In deze opgave gaan we steeds uit van een wiskundig model van een verfblik: een cilinder met een cirkel als bodem en een cirkel als deksel. We houden geen rekening met de dikte van het blik.
Een verfblik heeft een hoogte van 14 cm en een straal van 8 cm.
Teken op schaal 1:4 de uitslag van dit verfblik. Schrijf op hoe je de maten van je tekening gevonden hebt.
Hieronder een schets van een bouwkavel met een huis. De familie zoekt nog een plek voor de afvalcontainers. Deze willen ze zó op het terras plaatsen dat ze niet zichtbaar zijn vanuit de woonkamer.
Kleur op de uitwerkbijlage het hele gebied van het terras dat niet zichtbaar is vanuit de woonkamer. Laat zien hoe je aan je antwoord komt.
De NieuweHollandseWaterlinie was een verdedigingslinie met water als verdedigingswapen. Als de vijand eraan kwam, kon weiland tussen Muiden en de Biesbosch onder water gezet worden. Het land werd daardoor moeilijk begaanbaar.
Op de kaart is te zien welke delen onder water gezet konden worden. Dit is het grijze gedeelte. De stippen zijn forten. Een fort is een versterkt gebouw waarin militairen konden verblijven, zie de foto.
De Waterlinie was ongeveer 85 km lang.
Op deze kaart is de Waterlinie ongeveer 17 cm lang.
Bereken de schaal die bij de kaart hoort. Schrijf je berekening op.
Op de uitwerkbijlage staat een kaart van de Grote Oceaan. Op deze kaart ligt Paaseiland op een afstand van 3,2 cm van de Galapagoseilanden, op 1,5 cm van het eiland Pitcairn en op 4,8 cm van het eiland Kiribati.
Geef op de uitwerkbijlage met punt P aan waar Paaseiland ligt. Laat duidelijk zien hoe je aan je antwoord gekomen bent.
In een pretpark staat een zweefmolen die Vertical Swing wordt genoemd.
In de tekening zie je een gedeelte van de zweefmolen met twee armen en aan één arm een kabel en een stoeltje. De kabel KS heeft een lengte van 8 meter. Als de zweefmolen op een bepaalde snelheid is, maakt de kabel met de arm een hoek van 132°.
Als de zweefmolen op topsnelheid is , is de afstand van het midden van de zweefmolen (M) tot het stoeltje (S) 12,6 meter. Als de zweefmolen één keer ronddraait, legt het stoeltje een bepaalde afstand af.
Bereken hoeveel meter deze afgelegde afstand is. Schrijf je berekening op.
In een pretpark staat een zweefmolen die Vertical Swing wordt genoemd.
De zweefmolen heeft 12 armen op gelijke afstand van elkaar, waaraan kabels met stoeltjes hangen.
In het bovenaanzicht zie je de armen A en B aangegeven.
Bereken hoeveel graden de hoek tussen arm A en arm B is. Schrijf je berekening op.
De puzzelstukken passen in elkaar zoals afgebeeld.
Het zwarte puzzelstuk uit afbeelding c staat ook op de uitwerkbijlage. Onder de afbeelding staat een tabel, waarin je gegevens over de symmetrie van het puzzelstuk kunt invullen.
Tijdens een fietstocht heeft Laurens een poort gezien. Zie de foto. Laurens wil zo’n poort metselen voor in zijn tuin. Het pad waar de poort overheen moet komen is 1,5 meter breed.
Hij heeft een ontwerp gemaakt, zie de schets naast de foto.
De twee pilaren zijn 2 meter hoog. Het punt M ligt op een hoogte van 1,75 meter en op gelijke afstand van de punten A en B. Voor de duidelijkheid is er een aantal hulplijntjes getekend.
Bereken, zonder te meten, hoeveel cm AM is. Schrijf je berekening op.
.
..19.
Pythagoras
2015 -2 vr 15
De eigenaar van een dennenbos laat een aantal bomen kappen. Ze worden verwerkt in de houtindustrie. De bomen worden na het kappen in even lange stukken gezaagd en op een stapel gelegd. De stukken boomstam op de stapel hebben verschillende diameters.
Ga er van uit dat de doorsnede van een boomstam een cirkel is met een diameter van 34 cm.
Alleen het middelste stuk van de boomstam is bruikbaar voor het zagen van mooie rechte planken. Dit stuk is in de tekening hieronder aangegeven met vierkantABCD.
Bereken, zonder te meten, hoeveel cm2 de oppervlakte van vierkant ABCD is. Schrijf je berekening op.
Gegeven is de gelijkzijdige driehoek ABC met zijden van 35 cm. In de driehoek zijn de hoogtelijnen getekend. Deze hoogtelijnen snijden elkaar in punt S.
Bereken hoeveel cm2 de oppervlakte van driehoek ABC is.
Schrijf je berekening op.
Skispringen is een sport waarbij op ski’s van een helling (de schans) gesprongen wordt. Het doel daarbij is om zo ver mogelijk te springen.
Je ziet een schets van de schans. De maten staan erbij in meters. De skispringer begint bij het startpunt S en maakt snelheid op de schans van S tot T. Dit deel van de schans noemt men de aanloophelling. Hoe meer snelheid je maakt op de aanloophelling, hoe verder je kunt springen.
Bereken hoeveel graden de hellingshoek T in driehoek RST is. Schrijf je berekening op.
In een pretpark staat een zweefmolen die Vertical Swing wordt genoemd.
In de tekening zie je een gedeelte van de zweefmolen met twee armen en aan één arm een kabel en een stoeltje. De kabel KS heeft een lengte van 8 meter. Als de zweefmolen op een bepaalde snelheid is, maakt de kabel met de arm een hoek van 132°.
Bereken, zonder te meten, hoeveel meter de afstand van het midden van de zweefmolen (M) tot het stoeltje (S) is in deze situatie. Schrijf je berekening op en geef je antwoord in twee decimalen.
Op de foto zie je een leerling in Kenia in zijn schoolbank zitten.
Het tafelblad is voor deze leerling te hoog. De school wil daarom banken in verschillende maten gaan maken die goed passen bij de leerlingen. In de tabel hieronder zie je welke maat schoolbank bij welke leerling past.
Deze tabel kan zo voortgezet worden.
Welke maat schoolbank heeft een leerling met een lengte van 1,90 m nodig? Leg je antwoord uit.
Bij elke maat schoolbank hoort een bepaalde zithoogte. Hieronder zie je een tabel, waarin de maat van de schoolbank en de bijbehorende zithoogte in cm staat.
Leg met een berekening uit waarom er geen schoolbanken met maat 30 gemaakt zullen worden.
Op 1 mei wordt een zaadje in de grond gestopt. Na 12 dagen komt er een blad boven de grond. Neem aan dat er daarna om de 6 dagen een nieuw blad bijkomt.
Onderstaande foto’s zijn om de 6 dagen genomen.
Op de derde foto kun je zien dat het vijfde blad erbij is gekomen.
Bepaal met de gegevens op welke datum deze foto gemaakt is.
Leg uit hoe je aan je antwoord komt.
In figuur 1 zie je een vierkant. Dit vierkant wordt in tweeën gedeeld, dan ontstaat figuur 2. Daarna wordt een helft weer in tweeën gedeeld (figuur 3) enzovoort. Dit kan eindeloos zo doorgaan. Eén driehoek wordt steeds grijsgekleurd.
Het vierkant heeft een zijde van 32 cm.
Er is een verband tussen de oppervlakte van de grijze driehoek O en het figuurnummer f.
Bij elke maat schoolbank hoort een bepaalde zithoogte. Hieronder zie je een tabel, waarin de maat van de schoolbank en de bijbehorende zithoogte in cm staat.
Er is een lineair verband tussen de zithoogte en de maat van de schoolbank.
De landen waarin olie geproduceerd wordt, gebruiken een deel van de olie zelf. In de grafiek zie je het eigen gebruik van olie van één van deze landen in de afgelopen jaren. Bij deze grafiek hoort een lineair verband.
Geef een formule die hoort bij de grafiek.
Neem voor het aantal jaren na 2000 de letter t en voor het eigen gebruik in duizend tonnen de letter G.
De prijs van een taxirit wordt bepaald door een instaptarief en een kilometertarief. Een rit tot twee kilometer kost alleen het instaptarief. Is de rit langer dan twee kilometer, dan komt er nog een bedrag bij voor elke extra kilometer.
Het taxibedrijf heeft een dagtarief en een nachttarief.
In de tabel hieronder staan deze tarieven voor personentaxi’s.
Hieronder is de grafiek voor het nachttarief getekend.
Bepaal vanaf hoeveel hele kilometers een taxirit volgens het nachttarief bij Pentax meer dan € 25,00 kost.
Laat zien hoe je aan je antwoord komt. Je mag de grafiek gebruiken.
Een museum heeft extra geld nodig voor een speciale tentoonstelling. Dat geld willen ze ophalen met een e-mailactie. Ze sturen een e-mail naar 4 mensen. Aan deze mensen wordt gevraagd om 10 euro te schenken aan het museum en de e-mail door te sturen naar 4 andere mensen en hen ook te vragen om 10 euro te schenken aan het museum. Dit noemen we een kettingmail.
We gaan er in deze opgave vanuit dat iedereen die zo’n e-mail ontvangt, de 10 euro schenkt en de e-mail aan 4 andere mensen doorstuurt. De eerste 4 mensen die de e-mail ontvangen horen bij ronde 1.
Het verband tussen het aantal e-mails en de (bijbehorende) ronde wordt gegeven door de formule
\(A= 4^R\)
Hierin is A het aantal e-mails dat verstuurt wordt in ronde R.
Bereken in welke ronde er 1024 e-mails verstuurd worden. Schrijf je berekening op.
Het kijkbereik is de afstand die je bij helder weer kunt kijken. Het kijkbereik hangt af van de hoogte waarop je staat. De formule die bij benadering het verband aangeeft tussen de hoogte waarop je staat en het kijkbereik is.
\(K= 2 \times \sqrt{\pi \times H}\)
Hierin is k het kijkbereik in kilometer en H de hoogte waarop je staat in meter.
Nynke denkt dat als de hoogte waarop je staat tweemaal zo groot is, het kijkbereik dan ook tweemaal zo groot is.
Heeft Nynke gelijk? Laat zien hoe je aan je antwoord komt.
Om te oefenen met gewichtloosheid maken astronauten paraboolvluchten.
Het vliegtuig vliegt op een hoogte van 6100 meter. Op een zeker moment zet de piloot de motoren op vol vermogen en gaat het vliegtuig steil omhoog. Op een bepaalde hoogte zet de piloot de motoren uit (in de tekening bij t = 0). Het vliegtuig volgt vanaf dat moment een baan in de vorm van een bergparabool. We noemen dat de parabolische baan. In die parabolische baan heerst er in het vliegtuig gewichtloosheid.
Na 22 seconden verlaat het vliegtuig die parabolische baan en daalt dan weer naar 6100 meter.
De hoogte van het vliegtuig tijdens de parabolische baan kan worden berekend met de volgende formule:
\(Hoogte = - 4,91 \times (t - 11)^2 +8500\)
Hierin is de hoogte in meters en t de tijd in seconden.
Bij t = 0 begint de parabool en bij t = 22 eindigt de parabool.
Bereken hoeveel meter de maximale hoogte van het vliegtuig is tijdens het vliegen van de parabolische baan. Schrijf je berekening op.
Na de 68 seconden van de eerste paraboolvlucht vliegt het vliegtuig 15 seconden verder op een hoogte van 6100 meter en dan begint de tweede paraboolvlucht. In de uitwerkbijlage is de grafiek getekend van de hoogte van het vliegtuig in meters tijdens de eerste paraboolvlucht en de 15 seconden erna.
Teken in deze figuur op de uitwerkbijlage de grafiek van de tweede paraboolvlucht erbij. Geef duidelijk het beginpunt, toppunt en eindpunt van de paraboolvlucht aan.
James wil een kippenren aanleggen in de vorm van een rechthoek. Hij gebruikt 15 meter gaas om de kippenren rondom af te zetten. De oppervlakte van de kippenren kan James berekenen met de formule:
\(Oppervlakte = 7,5 \times lengte - lengte^2\)
Hierin is lengte in meter en oppervlakte in m2.
De grafiek die bij de formule hoort is een parabool. James denkt dat bij de top van de parabool de lengte precies gelijk is aan 4.
Geluiden zijn trillingen in de lucht. Een geluid verplaatst zich door de lucht. We spreken dan over geluidsgolven.
Geluid kan zichtbaar worden gemaakt met een apparaat dat een geluidstrilling omzet in een elektrische trilling.
Hierboven zie je wat het apparaat weergeeft bij twee verschillende geluiden. Elk van deze plaatjes geeft een aantal trillingen weer in een bepaalde tijd (bijvoorbeeld 1 milliseconde).
Het aantal trillingen per seconde noemen we de frequentie van het geluid.
Bij welke figuur hoort een hogere frequentie? Leg uit hoe je aan je antwoord komt
Het vermogen van een houtkachel is de hoeveelheid warmte die de kachel kan produceren. Dit vermogen wordt aangegeven in kilowatt (kW).
Er is een verband tussen het benodigde vermogen van een houtkachel en de inhoud van de te verwarmen ruimte. Ook hangt het benodigde vermogen af van de isolatie van de ruimte.
Hieronder zijn in een assenstelsel drie grafieken getekend die dit verband weegeven.
De familie Van Dam heeft een redelijk geïsoleerd huis. Hun woonkamer heeft een inhoud van 60 m3. Zij hebben een houtkachel waarvan het vermogen goed bij de inhoud van de kamer past.
Lees uit de grafiek af hoeveel kW vermogen deze houtkachel heeft. Laat in de grafiek zien hoe je aan je antwoord komt.
In een niet geïsoleerde kamer met een inhoud van 80 m3 staat een houtkachel die, wat betreft vermogen, goed bij deze kamer past. Deze kamer wil men groter maken en daarna goed isoleren. Men wil dezelfde houtkachel behouden.
Met hoeveel m3 kan de inhoud van de kamer maximaal worden vergroot zonder dat het vermogen van de houtkachel hoeft te veranderen? Gebruik de grafieken en laat zien hoe je aan je antwoord komt.
IJsbergen ontstaan doordat grote stukken ijs afbreken van een gletsjer en dan de zee in drijven.
Een ijsberg die naar het zuiden drijft, wordt kleiner doordat hij langzaam smelt. Onderzoekers hebben het gewicht van zo’n ijsberg geschat, zie de tabel.
T (maanden)
0
2
4
6
8
10
G (tonnen)
80 000
70 000
62 000
55 000
48 000
41000
In de tabel is t de tijd in maanden na het afbreken van de ijsberg en G het geschatte gewicht van de ijsberg in ton.
De onderzoekers hebben een formule gemaakt die goed bij de tabel past:
Op de uitwerkbijlage staat een assenstelsel getekend.
Teken in het assenstelsel de grafiek die bij de formule hoort. Gebruik hierbij de tabel. Maak zelf een juiste verdeling bij de verticale as.
.25.
Houtkachel (grafieken aflezen)
2016 -1 vr 3
Windkracht wordt uitgedrukt in Beaufort (Bft).
Een windkracht van 6 Bft wordt een krachtige wind genoemd.
De windkracht is afhankelijk van de gemiddelde windsnelheid. Bij benadering kun je de gemiddelde windsnelheid berekenen met de formule
\(S=k\times(1+0,14\times k)\)
Hierin is s de gemiddelde windsnelheid in m/s en k de windkracht in Bft.
Teken in het assenstelsel op de uitwerkbijlage de grafiek die bij de formule hoort. Vul eerst de tabel op de uitwerkbijlage in.
.26.
Huizenprijzen (grafieken aflezen)
2015 -1 vr 7
Hieronder zie je een grafiek van het verloop van de gemiddelde huizenprijs in Duitsland tussen 1996 en 2008.
In Duitsland kostte een huis op 1 januari 1996 gemiddeld 190 000 euro.
Op 1 januari 2008 was deze prijs gedaald tot 160 000 euro.
De huizenprijzen in Nederland zijn in de periode van 1996 tot 2008 juist gestegen.
Op 1 januari 1996 was de gemiddelde huizenprijs afgerond 100 000 euro. Bij benadering steeg de gemiddelde huizenprijs in Nederland in deze periode elk jaar met 12 500 euro.
In welk jaar was de gemiddelde huizenprijs in Nederland op 1 januari voor het eerst hoger dan in Duitsland?
Gebruik de grafiek op de uitwerkbijlage om je antwoord uit te leggen.
.27.
Huizenprijzen (grafieken aflezen)
2015 -2 vr 2
Nynke staat op een uitkijktoren.
Het kijkbereik is de afstand die je bij helder weer kunt kijken. Het kijkbereik hangt af van de hoogte waarop je staat. De formule die bij benadering het verband aangeeft tussen de hoogte waarop je staat en het kijkbereik is:
\(k = 2\times \sqrt{\pi \times H}\)
Hierin is k het kijkbereik in kilometer en h de hoogte waarop je staat in meter.
Op de uitwerkbijlage staat een assenstelsel. Teken de grafiek die bij de formule hoort. Vul hiervoor eerst de tabel in.
.28.
Aflezen grafieken
2014 -1 vr 7
De landen waarin die geproduceerd wordt gebruiken een deel van de olie zelf. In de grafiek zie je de hoeveelheid olie die het land geproduceerd heeft en het eigen verbruik. Bij beide grafieken hoort een lineair verband.
De geproduceerde olie die overbleef na eigen gebruik werd door dit land verkocht aan het buitenland.
Teken op de uitwerkbijlage de grafiek van de hoeveelheid olie die tussen 2000 en 2008 aan het buitenland verkocht werd.
.29.
Exponentiële formules.
2016 -1 vr 9
In 1900 waren er in Nederland 200 auto’s. In 1938 waren er al 80 000 auto’s. De groei was in deze jaren exponentieel volgens de formule
\(A=200 \times 1,17^t\)
Hierbij is A het aantal auto’s in Nederland en t het aantal jaren na 1900.
Klopte deze formule voor het aantal auto’s in 2014? Laat zien hoe je aan je antwoord komt.
.30.
Aflezen grafieken
2016 -1 vr 2
Jsbergen ontstaan doordat grote stukken ijs afbreken van een gletsjer en dan de zee in drijven.
Een ijsberg die naar het zuiden drijft, wordt kleiner doordat hij langzaam smelt. Onderzoekers hebben het gewicht van zo’n ijsberg geschat, zie de tabel.
In de tabel is t de tijd in maanden na het afbreken van de ijsberg en G het geschatte gewicht van de ijsberg in ton.
De onderzoekers hebben een formule gemaakt die goed bij de tabel past:
Laat met een berekening zien dat in de twintigste maand volgens de formule ongeveer 1600 ton ijs gesmolten is.
.31.
Aflezen grafieken
2016 -2 vr 6
Het KNMI in De Bilt laat elke dag een weerballon op. Zo’n ballon is gevuld met heliumgas. Er hangt een zender aan de ballon, die gegevens over het weer doorgeeft.
De hoogte van de stijgende ballon wordt gegeven door de formule
Hierin is de hoogte in km en de tijd het aantal minuten nadat de ballon is losgelaten.
Bereken hoeveel km de ballon tijdens het tweede half uur is gestegen. Schrijf je berekening op.
.32.
Aflezen grafieken
2016 -2 vr 25
Windkracht wordt uitgedrukt in Beaufort (Bft).
Een windkracht van 6 Bft wordt een krachtige wind genoemd.
De windkracht is afhankelijk van de gemiddelde windsnelheid. Bij benadering kun je de gemiddelde windsnelheid berekenen met de formule
s = k × (1 + 0,14 × k)
Hierin is s de gemiddelde windsnelheid in m/s en k de windkracht in Bft.
De gevoelstemperatuur is afhankelijk van de windsnelheid en de luchttemperatuur. De gevoelstemperatuur kun je berekenen met de formule
g = 1,41 – 1,162 × s + 0,98 × l + 0,0124 × s2 + 0,0185 × s × l
Hierin is g de gevoelstemperatuur in graden Celsius, s de windsnelheid in m/s en l de luchttemperatuur in graden Celsius.
Op een bepaald moment is de luchttemperatuur 3 graden Celsius en is er een windkracht van 5 Bft.
Bereken hoeveel graden Celsius de gevoelstemperatuur op dat moment is. Schrijf je berekening op.
.33.
Aflezen grafieken
2016 -1 vr 4
Jsbergen ontstaan doordat grote stukken ijs afbreken van een gletsjer en dan de zee in drijven.
Een ijsberg die naar het zuiden drijft, wordt kleiner doordat hij langzaam smelt. Onderzoekers hebben het gewicht van zo’n ijsberg geschat, zie de tabel.
In de tabel is t de tijd in maanden na het afbreken van de ijsberg en G het geschatte gewicht van de ijsberg in ton.
De onderzoekers hebben een formule gemaakt die goed bij de tabel past:
G = 80 000 – 4900 x t + 113 x t2 - t3
Bereken in de hoeveelste maand na het afbreken van de ijsberg het laatste stukje van de ijsberg volgens de formule gesmolten moet zijn. Schrijf je berekening op.
34.
Ketting e-mail
2016 -1 vr 23
Een museum heeft extra geld nodig voor een speciale tentoonstelling. Dat geld willen ze ophalen met een e-mailactie. Ze sturen een e-mail naar 4 mensen. Aan deze mensen wordt gevraagd om 10 euro te schenken aan het museum en de e-mail door te sturen naar 4 andere mensen en hen ook te vragen om 10 euro te schenken aan het museum. Dit noemen we een kettingmail.
We gaan er in deze opgave vanuit dat iedereen die zo’n e-mail ontvangt, de 10 euro schenkt en de e-mail aan 4 andere mensen doorstuurt. De eerste 4 mensen die de e-mail ontvangen horen bij ronde 1.
Het verband tussen het aantal e-mails en de (bijbehorende) ronde wordt gegeven door de formule
\(A = 4^R\)
Hierin is A het aantal e-mails dat verstuurd wordt in ronde r.
In totaal moet er 50 000 euro opgehaald worden om de tentoonstelling door te laten gaan. Omdat iedereen meedoet, is er na de eerste ronde 40 euro binnen, na de tweede ronde 40 + 160 = 200 euro, enzovoort.
Na welke ronde is er 50 000 euro opgehaald? Schrijf je berekening op.
35.
discuswerpen
2016 -1 vr 23
De Nederlandse atleet Erik Cadée werpt een discus. Bij deze worp van Erik hoort de formule
h = –0,009a2 + 0,55a + 1
Hierin is h de hoogte van de discus boven de grond in meter en a de horizontale afstand vanaf Erik in meter.
Voor de veiligheid van de toeschouwers zijn er om een gedeelte van de werpcirkel netten gespannen met een hoogte van 4,5 meter.
Bereken hoeveel meter de horizontale afstand vanaf Erik is op het moment dat de discus voor de eerste keer op een hoogte van 4,5 meter is. Geef je antwoord in één decimaal en schrijf je berekening op.
Antwoorden
Uitwerkbijlage
Ben je de uitwerkbijlage kwijt geraakt?
Je kunt hem hier downloaden en opnieuw uitprinten.
Het arrangement 4KGT is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-03-05 14:47:48
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Hieronder een schets van een bouwkavel met een huis. De familie zoekt nog een plek voor de afvalcontainers. Deze willen ze zó op het terras plaatsen dat ze niet zichtbaar zijn vanuit de woonkamer.
De Nieuwe Hollandse Waterlinie was een verdedigingslinie met water als verdedigingswapen. Als de vijand eraan kwam, kon weiland tussen Muiden en de Biesbosch onder water gezet worden. Het land werd daardoor moeilijk begaanbaar.
Ga er van uit dat de doorsnede van een boomstam een cirkel is met een diameter van 34 cm.
Gegeven is de gelijkzijdige driehoek ABC met zijden van 35 cm. In de driehoek zijn de hoogtelijnen getekend. Deze hoogtelijnen snijden elkaar in punt S.
Een museum heeft extra geld nodig voor een speciale tentoonstelling. Dat geld willen ze ophalen met een e-mailactie. Ze sturen een e-mail naar 4 mensen. Aan deze mensen wordt gevraagd om 10 euro te schenken aan het museum en de e-mail door te sturen naar 4 andere mensen en hen ook te vragen om 10 euro te schenken aan het museum. Dit noemen we een kettingmail.
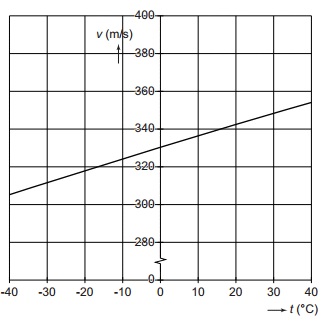
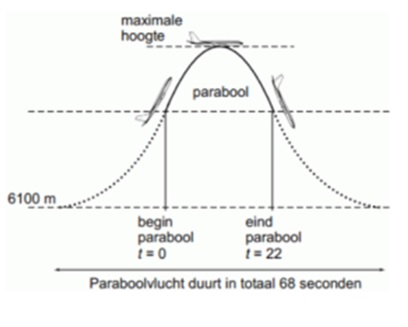
Teken in deze figuur op de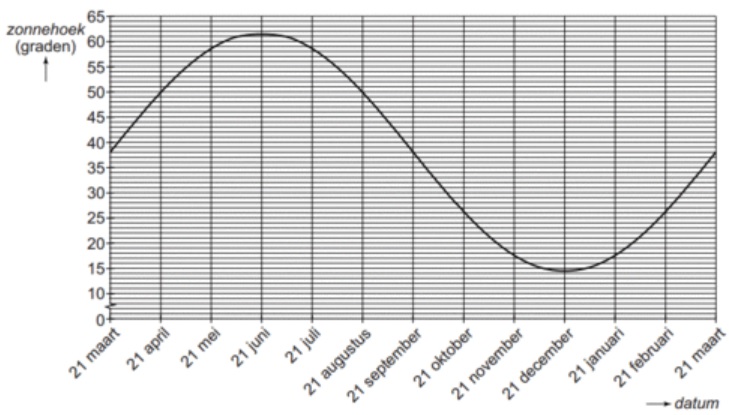 
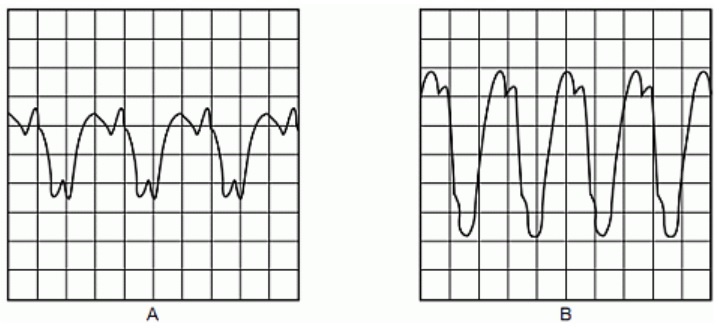
Het KNMI in De Bilt laat elke dag een weerballon op. Zo’n ballon is gevuld met heliumgas. Er hangt een zender aan de ballon, die gegevens over het weer doorgeeft.
Uitwerkbijlage bij boekje 2
