Het arrangement Goniometrie opgaven is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 22-01-2019 14:30:38
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Opgaven bij het onderwerp goniometrie op VMBO-TL/GL niveau
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- 4vmbo-kgt, gonio, goniometrie 4 vmbo kgt, goniometrie opgaven, goniometrische verhoudingen
Gebruikte Wikiwijs Arrangementen
VO-content Wiskunde. (2020).
Thema: Goniometrie vmbo-kgt34
https://maken.wikiwijs.nl/74210/Thema__Goniometrie__vmbo_kgt34

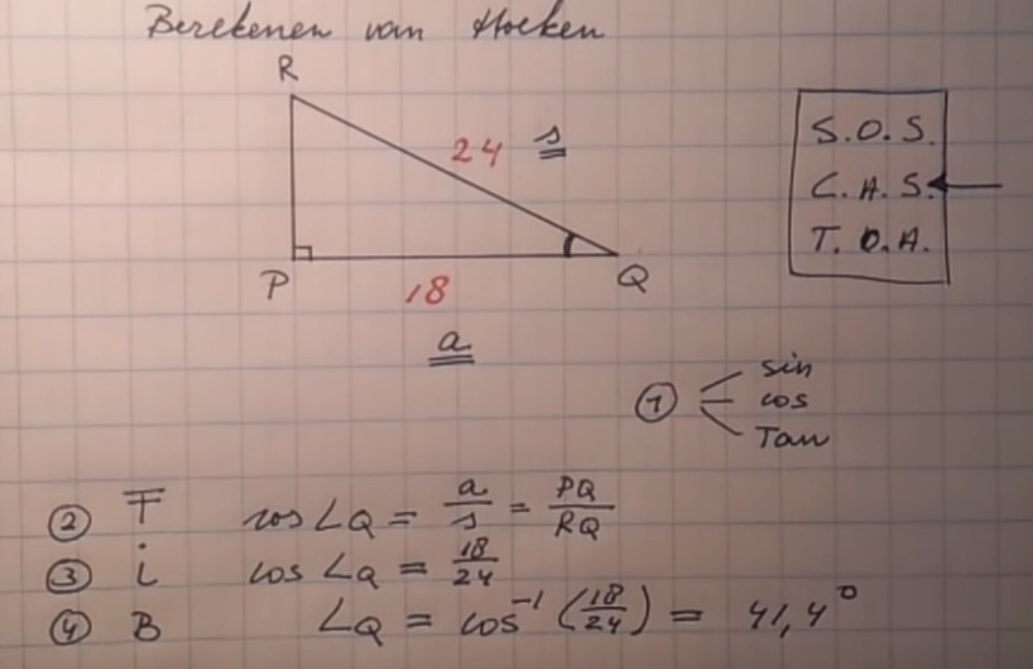
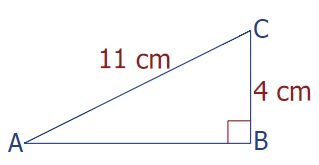
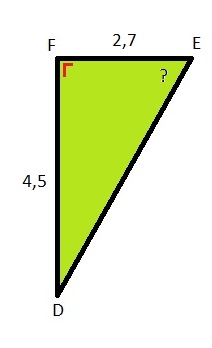
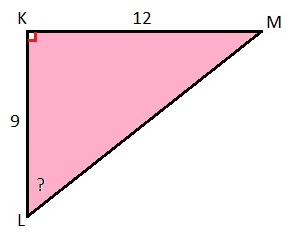
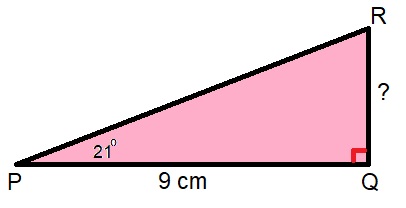
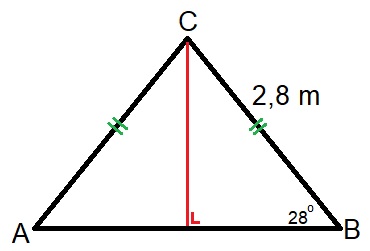
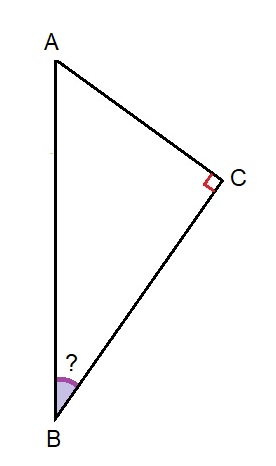 Hiernaast zie je een afbeelding van een rechthoekige driehoek. Bekijk het plaatje en beantwoord daarna de vragen.
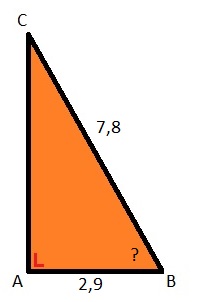
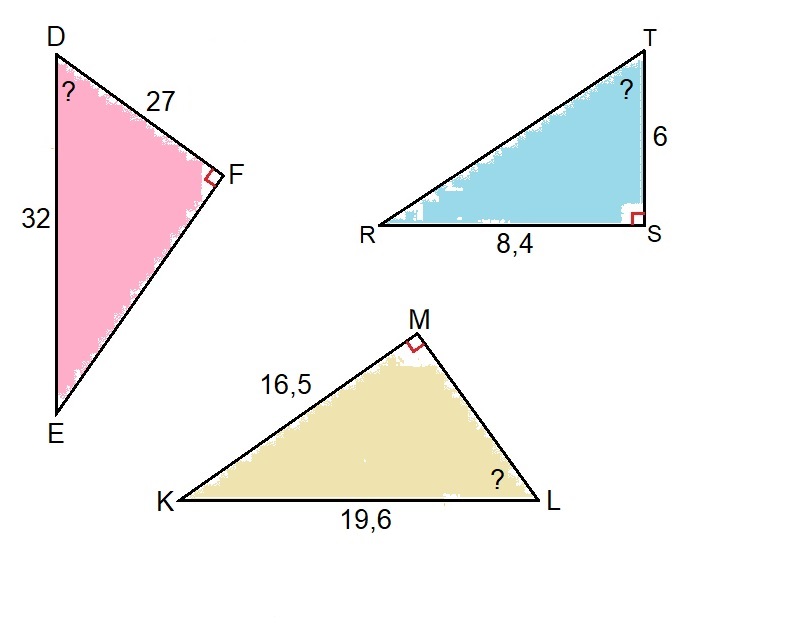
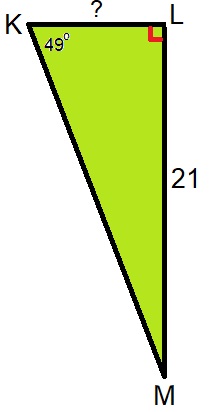
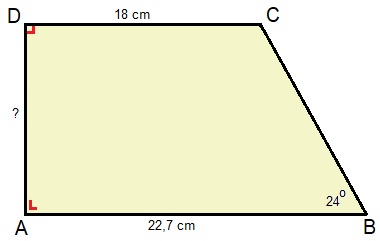
Hiernaast zie je een afbeelding van een rechthoekige driehoek. Bekijk het plaatje en beantwoord daarna de vragen.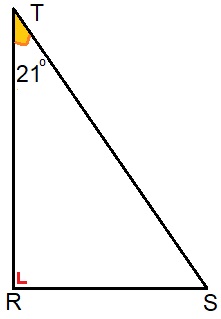 Bekijk de driehoek hiernaast. Beantwoord daarna de vragen. Noteer de antwoorden netjes in je schrift.
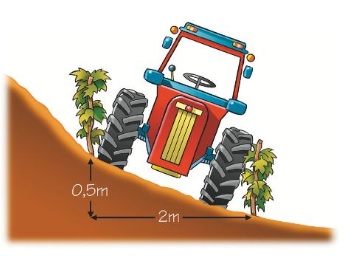
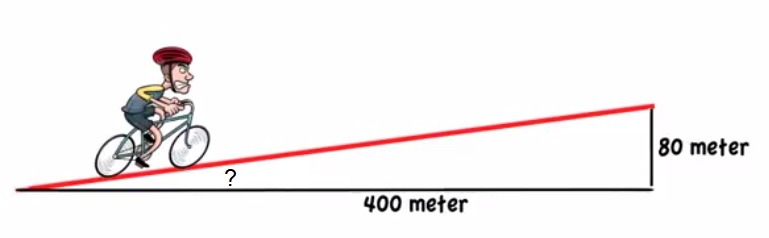
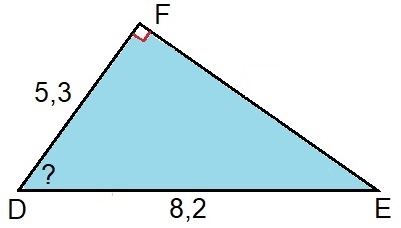
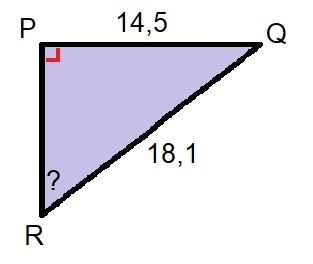
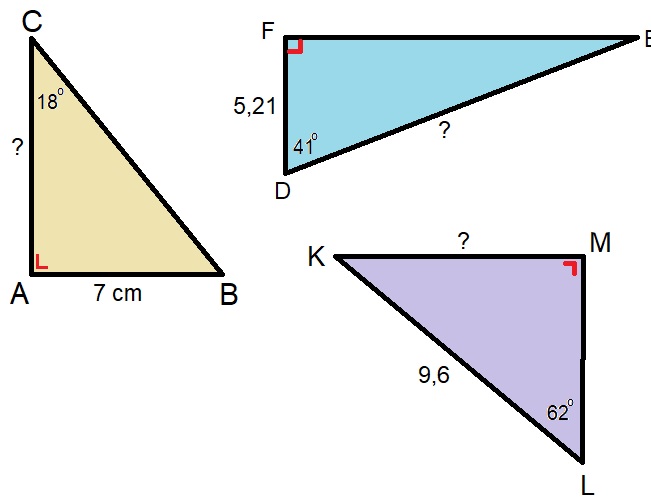
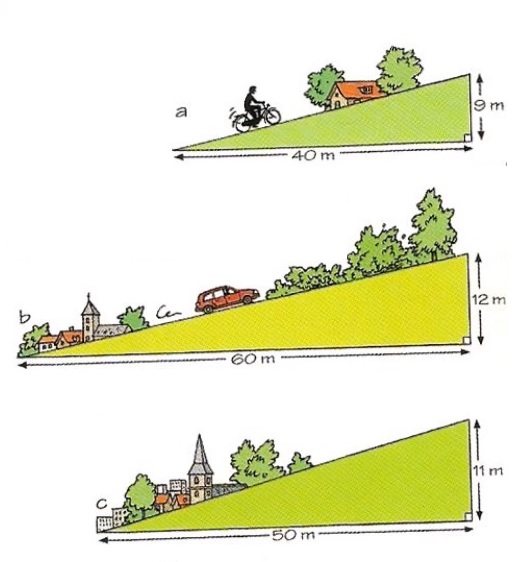
Bekijk de driehoek hiernaast. Beantwoord daarna de vragen. Noteer de antwoorden netjes in je schrift.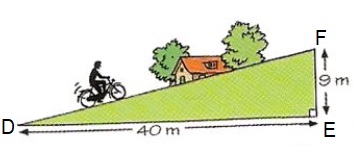 In de afbeelding van de fietser hiernaast herken je
In de afbeelding van de fietser hiernaast herken je  Jeroen en Nataly gaan oefenen voor hun wintersport vakantie. Ze besluiten een dagje naar Snowworld in Zoetermeer te gaan.
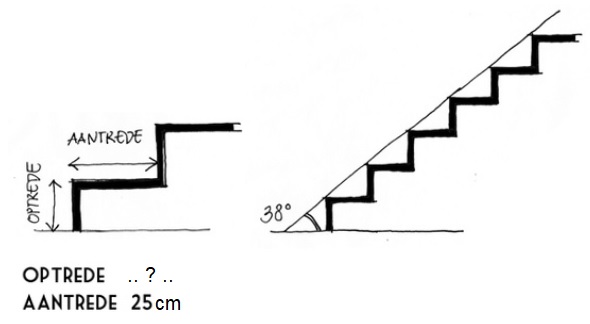
Jeroen en Nataly gaan oefenen voor hun wintersport vakantie. Ze besluiten een dagje naar Snowworld in Zoetermeer te gaan.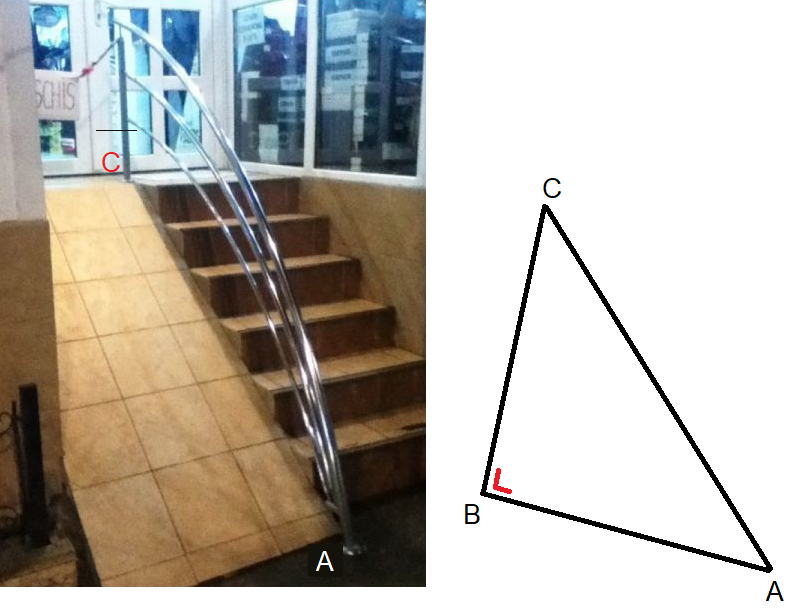 Je kan het je misschien niet goed voorstellen, maar wanneer je slecht ter been bent is een rolstoel een handig hulpmiddel. Echter niet elke architect houdt hier voldoende rekening mee. Je wilt de helling natuurlijk niet te schuin maken.
Je kan het je misschien niet goed voorstellen, maar wanneer je slecht ter been bent is een rolstoel een handig hulpmiddel. Echter niet elke architect houdt hier voldoende rekening mee. Je wilt de helling natuurlijk niet te schuin maken.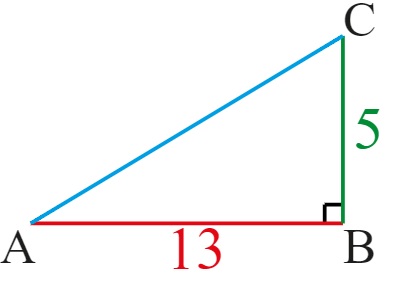






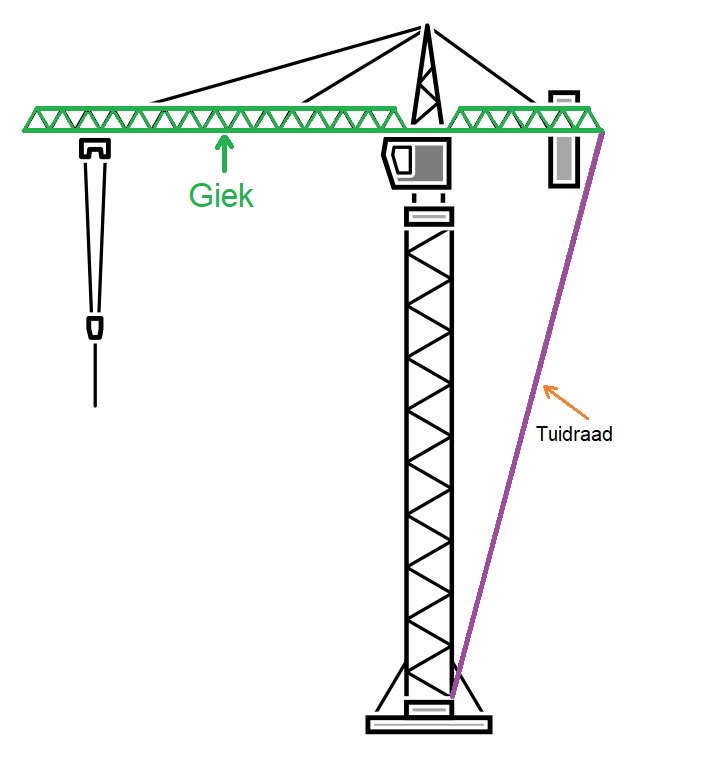
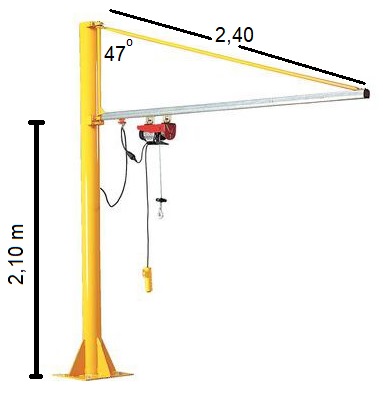 In een garage wordt vaak met zwaar materiaal gewerkt. Een til-lift is dan geen overbodig hulpmiddel. Hiernaast zie je een plaatje van een til-lift.
In een garage wordt vaak met zwaar materiaal gewerkt. Een til-lift is dan geen overbodig hulpmiddel. Hiernaast zie je een plaatje van een til-lift.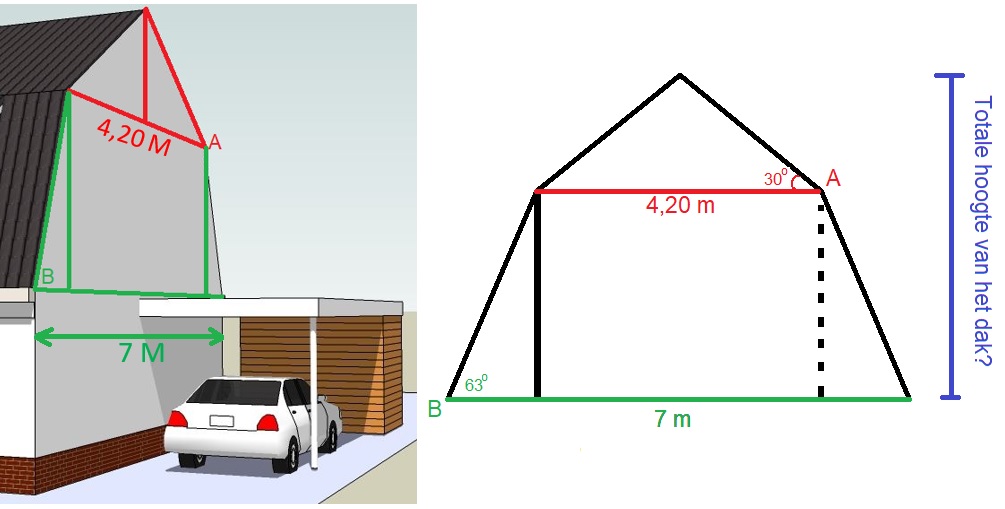 Hiernaast zie je de zijgevel van het hoekhuis van een rij nieuw te bouwen huizen. De onderste verdieping van het huis is 2,62 meter hoog. Daarna volgt verdieping één (aangegeven in groen) boven op verdieping één is nog een bergzolder. (aangeven in rood).
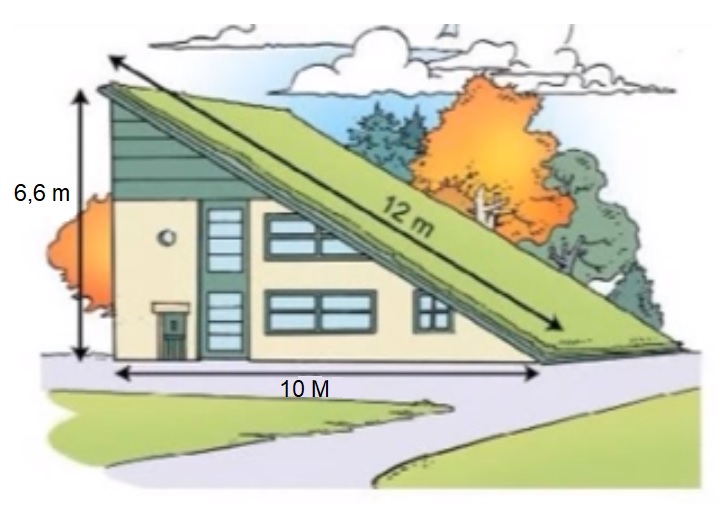
Hiernaast zie je de zijgevel van het hoekhuis van een rij nieuw te bouwen huizen. De onderste verdieping van het huis is 2,62 meter hoog. Daarna volgt verdieping één (aangegeven in groen) boven op verdieping één is nog een bergzolder. (aangeven in rood). Joachim heeft nog een tweede nieuwebouw huis gezien. In een folder ziet Joachim de afbeelding die je hier naast ziet staan.
Joachim heeft nog een tweede nieuwebouw huis gezien. In een folder ziet Joachim de afbeelding die je hier naast ziet staan.
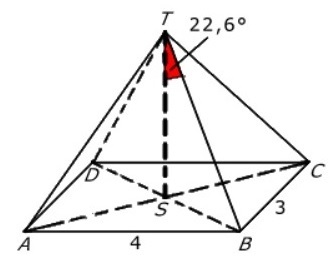
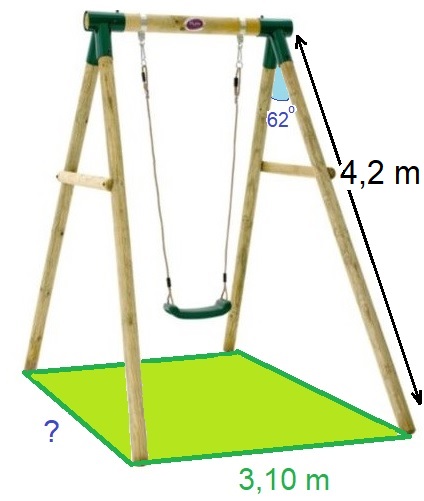
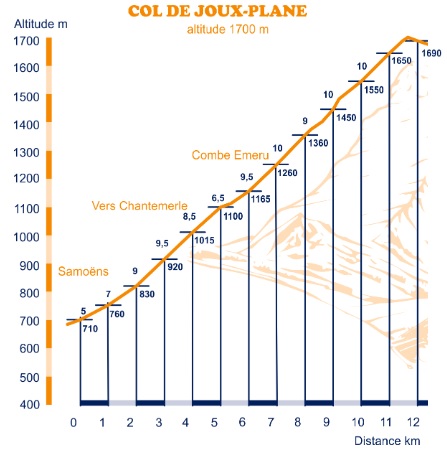
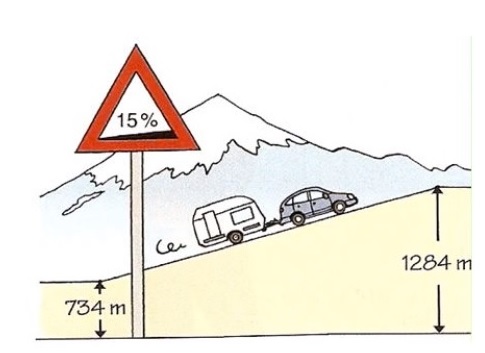 Ze trekken met hun caravan de bergen in. Op een hoogte van 734m komt de familie een 15% steile weg tegen. Het eindpunt van dit steile stuk bevindt zich op een hoogte van 1284m.
Ze trekken met hun caravan de bergen in. Op een hoogte van 734m komt de familie een 15% steile weg tegen. Het eindpunt van dit steile stuk bevindt zich op een hoogte van 1284m.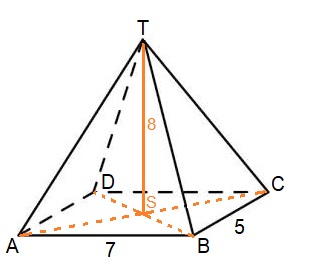
 Hieronder vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.
Hieronder vind je een aantal examenvragen uit examens van vorige jaren. De vragen sluiten zo goed mogelijk aan bij het thema dat je net afgerond hebt. Het zal echter ook wel voorkomen dat je kennis nodig hebt die niet in het thema behandeld is. Gebruik dan je gezonde verstand.

