Het arrangement Goniometrie uitleg is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 20-01-2019 16:04:23
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- In deze module vindt je uitleg over goniometrie op het Vmbo GL/TL niveau
- Leerniveau
- VMBO gemengde leerweg, 3; VMBO theoretische leerweg, 4; VMBO theoretische leerweg, 3; VMBO gemengde leerweg, 4;
- Leerinhoud en doelen
- Rekenen/wiskunde; Meten en meetkunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
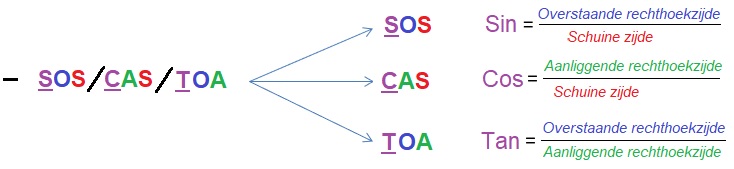
- goniometrie, hoeken bereken met goniometrie, mavo 4, sos cas toa, uitleg goniometrie, vmbo tl, zijden berekenen met goniometrie
Bronnen
| Bron | Type |
|---|---|
|
Hoeken berekenen in een balk https://www.youtube.com/watch?v=I6f2iBoHe_M |
Video |
|
Hoeken berekenen in een balk (2) https://www.youtube.com/watch?v=VU1mBbeBG7Y |
Video |
|
Hoeken berekenen in een piramide https://www.youtube.com/watch?v=TTv6xCv76nI |
Video |

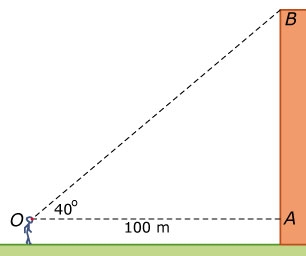
 Hoe steil een helling is, kun je aangeven met het hellingsgetal.
Hoe steil een helling is, kun je aangeven met het hellingsgetal.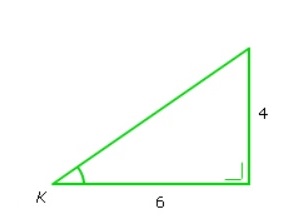 Voorbeeld
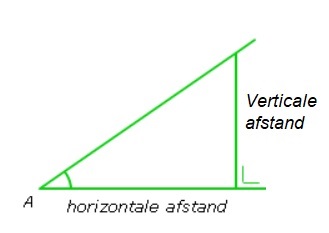
Voorbeeld In de afbeelding hiernaast zie je een berg. De verticale afstand is 210 meter en de horizontale afstand is 840 meter. We gaan het hellingspercentage berekenen
In de afbeelding hiernaast zie je een berg. De verticale afstand is 210 meter en de horizontale afstand is 840 meter. We gaan het hellingspercentage berekenen