Stelling van Pythagoras

Stelling van Pythagoras

Wat is de stelling van Pythagoras?

De stelling van Pythagoras is een wiskundige stelling die de naam van de Griekse wiskundige Pythagoras heeft gekregen. 'Zijn' stelling was overigens alleen maar nieuw voor de Grieken. In Soemer was het resultaat al veel langer bekend en ook in Babylonië en het oude Egyptewerd ze al eerder toegepast. In het bijzonder werd de verhouding {\displaystyle a:b:c=3:4:5} al vroeg gebruikt om rechte hoeken uit te meten, zoals dat tot op de dag van vandaag door sommigen nog wordt gedaan. Naast kennis van de stelling om haar toe te kunnen passen, is ook het leveren van een bewijs belangrijk. Wat dat betreft waren de Grieken (Pythagoras of een van zijn leerlingen) wel de eersten. Zij wisten niet alleen dat de stelling waar was, maar konden ook in algemene termen (abstracties) aantonen waarom zij waar was.

Hoe werk je met de stelling van Pythagoras?

De stelling van Pythagoras geeft een verband tussen de lengten van de zijden van een rechthoekige driehoek. In woorden luidt de stelling:

In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde.

De zijden die aan de hoek van 90° liggen noemen we rechthoekszijden ( a en b ). De overige zijde wordt de schuine zijde genoemd (de zijde die niet aan de rechte hoek grenst, c) 

De bekende wiskundige vorm van de stelling:

a^{2}+b^{2}=c^{2}

Een voorbeeld.

Een rechthoekige driehoek heeft rechthoekszijden met lengten {\displaystyle a=3} en {\displaystyle b=4}. Volgens de stelling van Pythagoras geldt dan voor de lengte c van de schuine zijde:

{\displaystyle c^{2}=a^{2}+b^{2}=3^{2}+4^{2}=9+16=25}

Omdat de lengte c niet negatief kan zijn, is

c=\sqrt {25}=5

 

Controle:

Als van dezelfde driehoek de lengten {\displaystyle b=4} en {\displaystyle c=5} gegeven zijn, volgt de lengte a van de overgebleven zijde uit:

{\displaystyle a^{2}=c^{2}-b^{2}=5^{2}-4^{2}=25-16=9}

Omdat de lengte a niet negatief kan zijn, is

a=\sqrt {9}=3

 

Bewijs voor de stelling.

Er bestaan meer dan 350 bewijzen voor de stelling van Pythagoras. Onder deze bewijzen zijn er die zijn ontdekt of mogelijk herontdekt door prominenten, zoals James Garfield, de 20e president van de Verenigde Staten, en Multatuli.

Hieronder zullen een aantal bewijzen uitgelegd worden. 

 

Bewijs met opdelen in vierkant

Een van de meer eenvoudige bewijzen deelt een vierkant met zijde {\displaystyle a+b}op twee manieren in. In de figuur hieronder is het vierkant opgebouwd uit een vierkant met zijde a, een vierkant met zijde b, en 4 rechthoekige driehoeken. De rechterfiguur is een vierkant opgebouwd uit een vierkant met zijde cen dezelfde 4 rechthoekige driehoeken.

Beide figuren tonen een vierkant met zijde {\displaystyle a+b}, dus beide vierkanten hebben dezelfde oppervlakte. Laat men nu zowel links als rechts de vier rechthoekige driehoeken weg, dan hebben de figuren die overblijven ook dezelfde oppervlakte. Links blijven een vierkant met zijde aen een vierkant met zijde bover, met een gezamenlijke oppervlakte van {\displaystyle a^{2}+b^{2}}. Rechts resteert een vierkant met zijde c. Het vierkant met zijde {\displaystyle ac}heeft een oppervlakte van c^2. Hiermee is de stelling bewezen.

Voor mensen die van meer algebraïsche bewijzen houden, ziet het bewijs er als volgt uit: Telkens zijn er een korte en een lange zijde in elkaars verlengde geplaatst. De lengte en breedte van de zijden van het vierkant zijn beide {\displaystyle a+b}, dus de oppervlakte van het grote vierkant is {\displaystyle (a+b)^{2}}.

De oppervlakte is ook gelijk aan de som van de vier driehoeken {\displaystyle 4\times {\tfrac {1}{2}}ab}plus de oppervlakte van het binnenste vierkant, dat oppervlakte c^2heeft. Dus

{\displaystyle (a+b)^{2}=2ab+c^{2}}

Uitwerken van het kwadraat links geeft:

{\displaystyle a^{2}+2ab+b^{2}=2ab+c^{2}},

dus:

a^{2}+b^{2}=c^{2}

Bewijs met gelijkvormigheid

P triangle.svg

Een ander inzichtelijk bewijs maakt gebruik van een hulplijn. Hiertoe dient de hoogtelijn vanuit de rechte hoek C, die zijde AB snijdt in het punt D.

Het is nu snel in te zien dat driehoek {\displaystyle ACD} gelijkvormig is aan driehoek {\displaystyle ABC}. Immers, de hoeken bij A zijn dezelfde, en beide driehoeken hebben ook een rechte hoek, bij D resp. C.

Op dezelfde manier blijkt dat driehoek {\displaystyle CBD} gelijkvormig is aan driehoek {\displaystyle ABC}. Er dus drie gelijkvormige driehoeken. Wordt gekeken naar de verhoudingen van de lengtes van de zijden van de driehoeken, dan ziet men dat die gelijk zijn aan {\displaystyle a:b:c}, precies de schuine zijden van de drie driehoeken. Dat betekent dat de oppervlaktes van de driehoeken zich verhouden als {\displaystyle a^{2}:b^{2}:c^{2}}, de kwadraten van de verhoudingen van de zijden. Omdat duidelijk is dat {\displaystyle \mathrm {Opp} \,CBD+\mathrm {Opp} \,ACD=\mathrm {Opp} \,ABC}, geldt kennelijk voor een bepaald getal k dat {\displaystyle ka^{2}+kb^{2}=kc^{2}}. De stelling van Pythagoras volgt door deling door k.

Bewijzen zonder woorden

Hoewel geen formeel bewijs, is het bewijs zonder woorden een populaire manier om de geldigheid van een stelling te visualiseren zonder daarbij tekst te gebruiken. Ook van de stelling van Pythagoras zijn diverse bewijzen zonder woorden bekend, met name zogenaamde puzzelstukjesbewijzen. Enkele voorbeelden staan hieronder.

  • Animatie

  •  

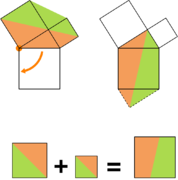
  • Pythagoras theorem leonardo da vinci.png

  •  

  • Puzzelstukjesbewijs

  •  

  • Puzzelstukjesbewijs

  •  

  • Animatie

  • Puzzelstukjesbewijs

Oefening

Hieronder staan verschillende tekeningen. Reken bij de tekeningen het ? uit.

Antwoorden

gegeven: BC=? AC=25 AB=65

formule: AB²=BC²+AC²

65²=BC²+25²

BC²=65²-25²=3600

BC²=3600

BC=√3600=60

 

gegeven: PQ=10 QR=20 PR=?

formule: PR²=PQ²+QR²

PR²=10²+20²=500

PR=√500=22,4

 

gegeven: KL=√5 MK=? ML=3

formule: ML²=KL²+MK²

3²=(√5)²+MK²

MK²=9-5=4

MK=√4=2

 

gegeven: FD=7 FE=? DE=9

formule: FD²+FE²=DE²

7²+FE²=9²

FE²=9²-7²=32

FE=√32=5,7

 

gegeven: JI=5 HI=8 HJ=?

formule: HJ²=HI²+JI²

HJ²=8²+5²=89

HJ=√89=9,4

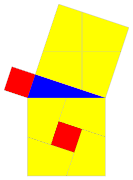
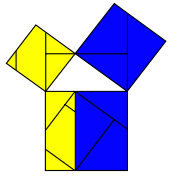
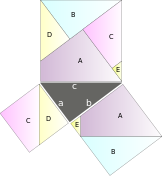
  • Het arrangement Stelling van Pythagoras is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.

    Auteur
    Hendrica de Hoop
    Laatst gewijzigd
    2018-11-07 16:11:32
    Licentie

    Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:

    • het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
    • het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
    • voor alle doeleinden, inclusief commerciële doeleinden.

    Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.

    Aanvullende informatie over dit lesmateriaal

    Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:

    Toelichting
    HAVO 2
    Eindgebruiker
    leerling/student
    Moeilijkheidsgraad
    gemiddeld
    Studiebelasting
    4 uur 0 minuten

  • Downloaden

    Het volledige arrangement is in de onderstaande formaten te downloaden.

    Metadata

    LTI

    Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI koppeling aan te gaan.

    Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.

    Arrangement

    IMSCC package

    Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.

    Voor developers

    Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op onze Developers Wiki.

  • Gebruik
    Weergave
  • Wikiwijs is een dienst van