Het arrangement H2 Berekenen en bewijzen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 29-03-2020 01:12:39
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
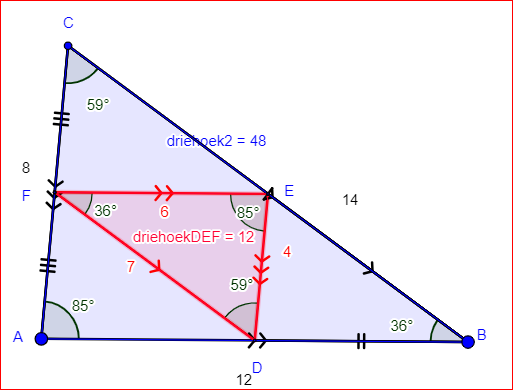
- Voorkennis van leerlingen: • H 2.1 Kruisproducten en parallelprojectie • H 2.2 Gelijkvormigheid • H2.3 Gelijkvormige driehoeken Deze les gaat over stelling en bewijzen middenparallel.
- Leerniveau
- VWO 3;
- Leerinhoud en doelen
- Vergelijkingen en ongelijkheden; Rekenen/wiskunde; Vormen en figuren; Redeneren in de (vlakke) meetkunde; Meten en meetkunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 2 uur 0 minuten
- Trefwoorden
- middenparallel en zwaartelijnen
Bronnen
| Bron | Type |
|---|---|
|
Gelijkvormigheid https://youtu.be/0Q3o-fq99zI |
Video |
|
https://www.youtube.com/watch?v=hie1iloKpZI&feature=youtu.be https://www.youtube.com/watch?v=hie1iloKpZI&feature=youtu.be |
Video |
|
Kennisclip https://screencast-o-matic.com/embed?sc=cFXXr5rctQ&v=5&ff=1 |
Video |
|
Geogebra applet https://www.geogebra.org/classic/sgatanmx |
Link |

 A =
A =