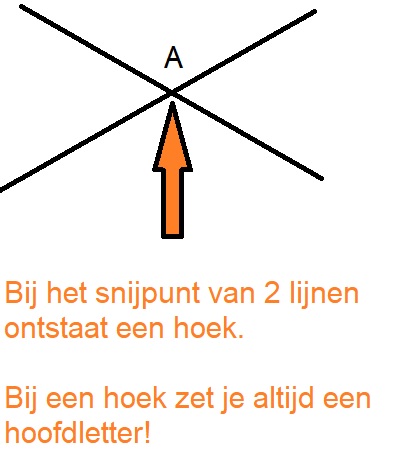
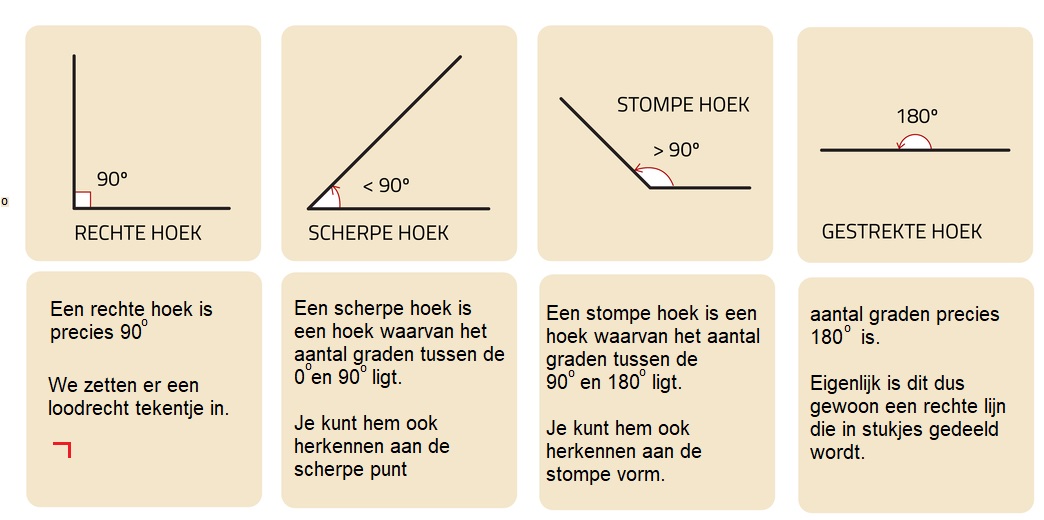
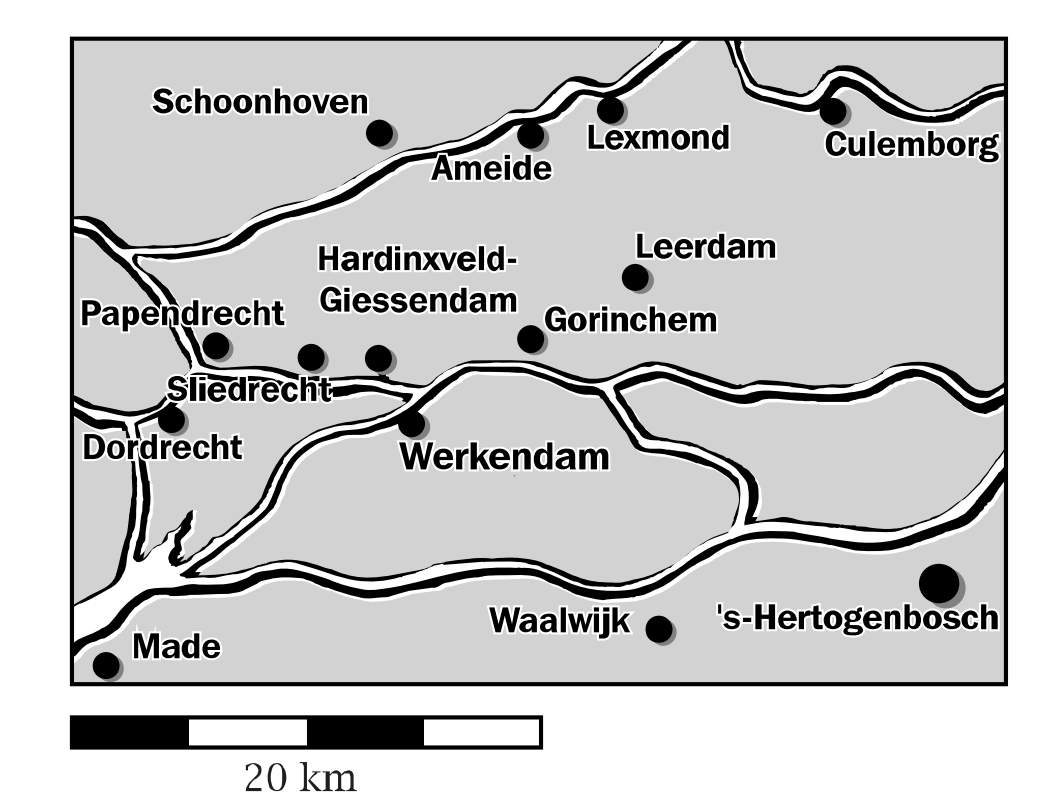
Het arrangement Verdieping Klas 1 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 16-04-2019 11:53:51
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Bronnen
| Bron | Type |
|---|---|
|
Verschillende soorten hoeken https://www.youtube.com/watch?v=_JJmiB4WNbI |
Video |
|
In deze video wordt voorgedaan hoe je met behulp van je geodriehoek hoeken kunt meten. https://www.youtube.com/watch?v=3uOMMN6xJwo |
Video |
|
Een tweede (nog duidelijker) filmpje over het meten van hoeken met je geodriehoek. https://www.youtube.com/watch?v=qrPIJ4z1fqE |
Video |
|
Hoeken tekenen met je geodriehoek https://www.youtube.com/watch?v=gp0fAVNzFiA |
Video |
|
Hoeken tekenen met je geodriehoek https://www.youtube.com/watch?v=ZxlnzsPF4eM |
Video |
|
De hoekjes van een driehoek bij elkaar leggen https://www.youtube.com/watch?v=6koMm3Qu0KU |
Video |
|
Hoekensom https://www.youtube.com/watch?v=sDoQ2VjS90A |
Video |
|
Hoe bereken je een hoek in een driehoek https://www.youtube.com/watch?v=CAFlamoi9ag |
Video |
|
Hoe bereken je de ontbrekende hoek? (in een driehoek) https://www.youtube.com/watch?v=-LIJcosuSU0 |
Video |
Gebruikte Wikiwijs Arrangementen
Wiskundesectie Juliana. (2018).
1H02.4 Schaallijnen
Wiskundesectie Juliana. (z.d.).
Hoeken meten, tekenen en berekenen
https://maken.wikiwijs.nl/135709/Hoeken_meten__tekenen_en_berekenen