Het arrangement Rekenen ontmoet Praktijk is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 12-01-2019 16:02:00
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Gebruikte Wikiwijs Arrangementen
Rekenen ontmoet Praktijk. (z.d.).
1 - Ruimtegebruik
Rekenen ontmoet Praktijk. (z.d.).
4 - Vakantie langs Europese hoofdsteden
https://maken.wikiwijs.nl/122127/4___Vakantie_langs_Europese_hoofdsteden
Rekenen ontmoet Praktijk. (z.d.).
5 - Het huishoudboekje
Rekenen ontmoet Praktijk. (z.d.).
6 - Boodschappenlijstje voor de cakes
https://maken.wikiwijs.nl/124157/6___Boodschappenlijstje_voor_de_cakes
Rekenen ontmoet Praktijk. (z.d.).
Breuken - Gelijknamigheid
Rekenen ontmoet Praktijk. (z.d.).
Breuken - Handigheidje mislukt?
https://maken.wikiwijs.nl/137386/Breuken___Handigheidje_mislukt_
Rekenen ontmoet Praktijk. (z.d.).
Vaardigheden student

 Rekenen is met de boeken, of via de website, niet altijd even leuk. Er zijn veel ‘saaie’ sommen en waarom we er zoveel van moeten maken is ook niet altijd duidelijk. Via deze opdracht ga daarom nu vanuit de praktijk aan het werk. Nu verneem je waarom al die ‘saaie’ sommetjes nodig waren en hoe ze je kunnen helpen in het uitvoeren van je werk. Nu kun je laten zien dat je zowel je vakleer als andere vaardigheden beheerst en je deze kunt gebruiken om goed te zijn in je werk.
Rekenen is met de boeken, of via de website, niet altijd even leuk. Er zijn veel ‘saaie’ sommen en waarom we er zoveel van moeten maken is ook niet altijd duidelijk. Via deze opdracht ga daarom nu vanuit de praktijk aan het werk. Nu verneem je waarom al die ‘saaie’ sommetjes nodig waren en hoe ze je kunnen helpen in het uitvoeren van je werk. Nu kun je laten zien dat je zowel je vakleer als andere vaardigheden beheerst en je deze kunt gebruiken om goed te zijn in je werk. In deze opdracht kies je een ruimte, bedenk je een functie hiervoor en ga je deze inrichten en onderhouden en dat allemaal voor een bepaald bedrag. Hiervoor moet je onderzoeken welke ruimte je wilt gebruiken en wat verschillende zaken kosten. De opdrachtgever wil één prijs en deze ga jij berekenen. Maar de opdrachtgever wil ook een ruimte die goed te gerbuiken is en daarvoor moet je de wensen en de eisen kennen.
In deze opdracht kies je een ruimte, bedenk je een functie hiervoor en ga je deze inrichten en onderhouden en dat allemaal voor een bepaald bedrag. Hiervoor moet je onderzoeken welke ruimte je wilt gebruiken en wat verschillende zaken kosten. De opdrachtgever wil één prijs en deze ga jij berekenen. Maar de opdrachtgever wil ook een ruimte die goed te gerbuiken is en daarvoor moet je de wensen en de eisen kennen. Zoek een ruimte binnen de school. Er kan gekozen worden uit de volgende lokalen: S1.420, S1.421, S1.330, S1.460, S2.540 en S2.160. Bedenk en geef argumenten hoe je deze ruimte gaat gebruiken, als kantoor, winkel, als studenten kamer of ,,.
Zoek een ruimte binnen de school. Er kan gekozen worden uit de volgende lokalen: S1.420, S1.421, S1.330, S1.460, S2.540 en S2.160. Bedenk en geef argumenten hoe je deze ruimte gaat gebruiken, als kantoor, winkel, als studenten kamer of ,,. Indien de ruimte gebruikt wordt als winkel, dan:
Indien de ruimte gebruikt wordt als winkel, dan:
 Indien je een andere functie kiest, die de goedkeuring van de docent heeft en waarbij er minimaal 4 deel opdrachten zijn,
Indien je een andere functie kiest, die de goedkeuring van de docent heeft en waarbij er minimaal 4 deel opdrachten zijn, De opdracht dient aan de volgende criteria te voldoen:
De opdracht dient aan de volgende criteria te voldoen: Voor deze opdracht kun je de kennis en theorie terugvinden in bijvoorbeeld:
Voor deze opdracht kun je de kennis en theorie terugvinden in bijvoorbeeld: Laatst ontving ik een foto van een goede vriend van me. Een lachwekkende foto waarvan er vele op het internet te vinden zijn.
Laatst ontving ik een foto van een goede vriend van me. Een lachwekkende foto waarvan er vele op het internet te vinden zijn.
 Gegeven krijg je namelijk wel 2 zaken:
Gegeven krijg je namelijk wel 2 zaken:
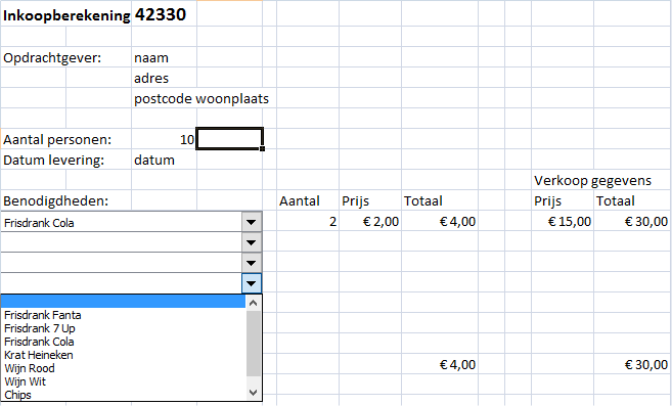 De cateraar hiervoor al eerder een rekenprogramma laten maken waarmee hij alleen maar het aantal gasten hoeft te weten.
De cateraar hiervoor al eerder een rekenprogramma laten maken waarmee hij alleen maar het aantal gasten hoeft te weten.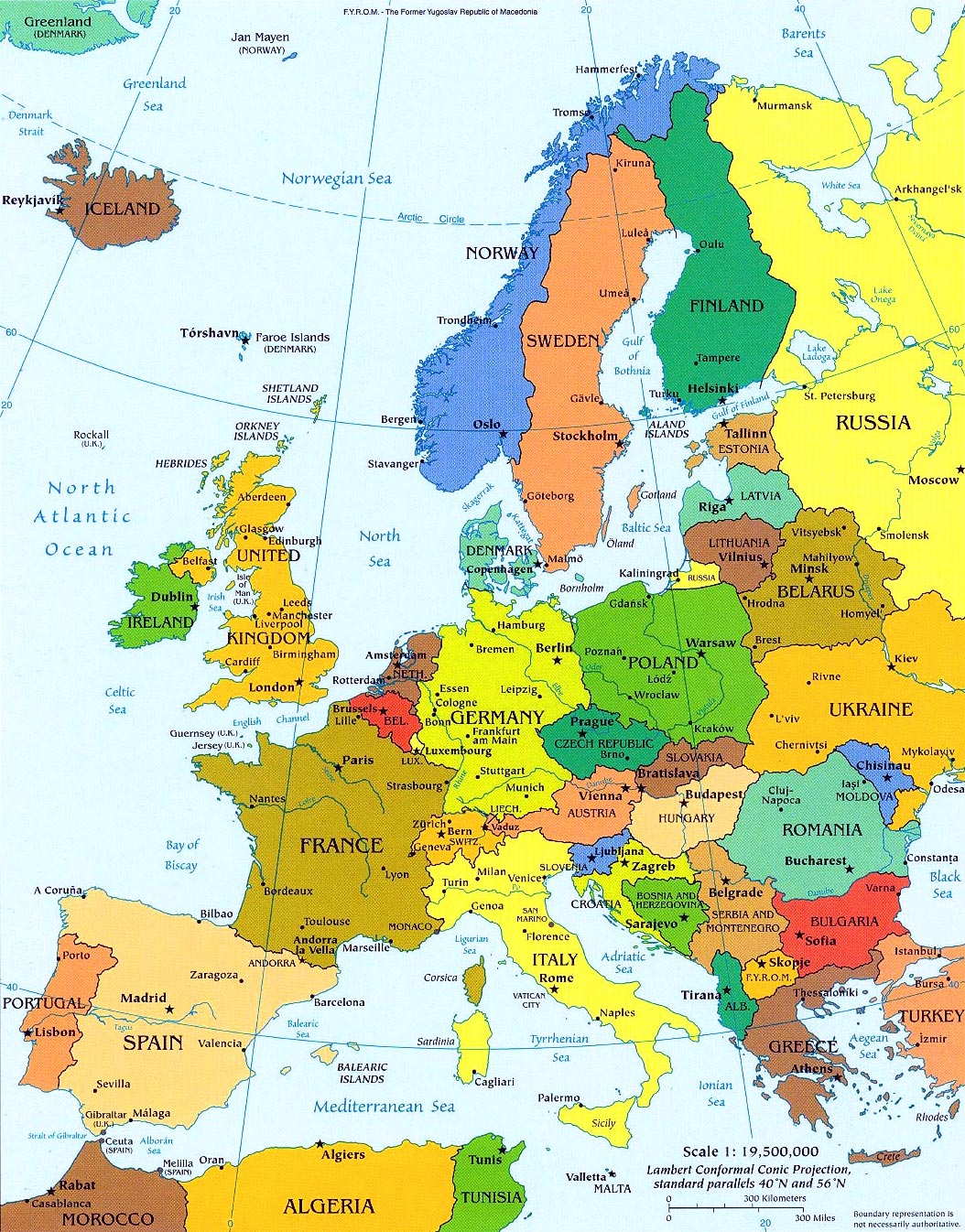 Zo tegen de zomervakantie aan komen de wilde plannen voor een grote vakantie weer boven drijven. Ga ik nu dit jaar of volgend jaar een rondreis maken door Europa, langs vele hoofdsteden? Ga ik dat in mijn 'uppie' doen of gaat we met z'n tweeen?
Zo tegen de zomervakantie aan komen de wilde plannen voor een grote vakantie weer boven drijven. Ga ik nu dit jaar of volgend jaar een rondreis maken door Europa, langs vele hoofdsteden? Ga ik dat in mijn 'uppie' doen of gaat we met z'n tweeen? Vakantie langs europese hoofdsteden
Vakantie langs europese hoofdsteden Tijdens het werken aan deze opdracht is het handig om:
Tijdens het werken aan deze opdracht is het handig om:

 Op het einde van elke maand zijn er telkens weer enkele van jullie die zich afvragen wat ze die week nog zullen en kunnen uitgaan en of de rekeningen wel allemaal betaald kunnen worden. De bankrekening lijkt immers de nul wel zeer snel te naderen. Toch dient er nog een cadeautje of brandstof gekocht worden voor de laatste dag van de maand zich aandient.
Op het einde van elke maand zijn er telkens weer enkele van jullie die zich afvragen wat ze die week nog zullen en kunnen uitgaan en of de rekeningen wel allemaal betaald kunnen worden. De bankrekening lijkt immers de nul wel zeer snel te naderen. Toch dient er nog een cadeautje of brandstof gekocht worden voor de laatste dag van de maand zich aandient. Binnen de opdracht 'huishoudboekje' komen verschillende vaardigheden aan de orde:
Binnen de opdracht 'huishoudboekje' komen verschillende vaardigheden aan de orde: Op een nieuw te openen Biologisch Centrum ben jij werkzaam en je krijgt de opdracht, om voor een receptie die binnenkort gehouden wordt, de cake te verzorgen bij het welkoms kopje koffie voor de gasten. Het idee is dat je als Biologisch Centrum dit zelf gaat maken. Gelukkig is er een een geschikte keuken en bijbehorende ovens en andere machinerien dus dat is gaat wel goed komen.
Op een nieuw te openen Biologisch Centrum ben jij werkzaam en je krijgt de opdracht, om voor een receptie die binnenkort gehouden wordt, de cake te verzorgen bij het welkoms kopje koffie voor de gasten. Het idee is dat je als Biologisch Centrum dit zelf gaat maken. Gelukkig is er een een geschikte keuken en bijbehorende ovens en andere machinerien dus dat is gaat wel goed komen. Voor deze opdracht ga je volgende onderdelen uitvoeren:
Voor deze opdracht ga je volgende onderdelen uitvoeren:


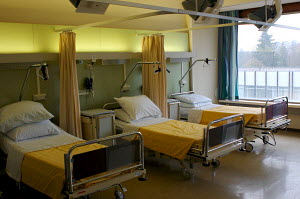 Op de verpleegzaal wordt een aantal keren per dag aan de patiënten medicatie verstrekt. Sommige patiënten halen hun medicijnen op afgesproken tijden op bij de verpleegkundigen. Bij de ziekere of bedlegerige mensen komt de verpleegkundige langs om de medicijnen te geven. En jij hebt nu 5 patiënten ‘op zaal liggen’:
Op de verpleegzaal wordt een aantal keren per dag aan de patiënten medicatie verstrekt. Sommige patiënten halen hun medicijnen op afgesproken tijden op bij de verpleegkundigen. Bij de ziekere of bedlegerige mensen komt de verpleegkundige langs om de medicijnen te geven. En jij hebt nu 5 patiënten ‘op zaal liggen’: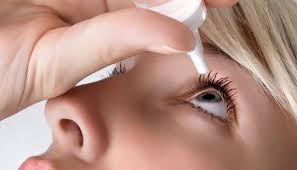 De oogarts schrijft voor dat meneer Brown in zijn linkeroog 2 oogdruppels krijgt. Je beschikt over oogdruppels 5 mg/ml (1 ml= 20 druppels). Meneer Brown wil precies weten hoeveel mg medicijn hij krijgt en vraagt je om dat voor hem uit te rekenen.
De oogarts schrijft voor dat meneer Brown in zijn linkeroog 2 oogdruppels krijgt. Je beschikt over oogdruppels 5 mg/ml (1 ml= 20 druppels). Meneer Brown wil precies weten hoeveel mg medicijn hij krijgt en vraagt je om dat voor hem uit te rekenen. Je krijgt een spoedopname: Meneer Puchalski (49 jaar oud 58 kg zwaar) heeft een overdosis paracetamol genomen. Op de Spoedeisende Hulp vertelt Meneer Puchalski aan de psychiater dat het leven voor hem vrijwel zinloos geworden is: hij is onlangs gescheiden, heeft daardoor schulden en ook zijn baan als verkoper van antiquarische boeken en prenten is hij kwijt geraakt. Hij weet niet meer hoe hij verder moet. Nadat door de SEH-verpleegkundige zijn maag is gespoeld is er geactiveerde kool en natriumsulfaat toegediend. Als antidotum werd op de SEH al een startdosis acetylcysteïne toegediend: 150 mg acetylcysteïne per kg lichaamsgewicht, in 15 minuten. Dat is bedoeld om beschadiging van de lever te voorkomen. Op de zaal moet je de man een vervolgdosis toedienen: 50 mg acetylcysteïne per kg lichaamsgewicht, in 500 ml infuusvloeistof (glucose 5%, met een inlooptijd van 4 uur). Het concentraat voor infusievloeistof bevat 200 mg/ml (25 ml (= 5 g). Je moet een aantal dingen weten alvorens je meneer Puchalski zijn medicatie kan geven. Je moet berekenen hoeveel mg acetylcysteïne je moet toedienen, hoeveel ml concentraat dat is, en wat de druppelsnelheid van het infuus moet zijn om de medicatie in 4 uur in te laten lopen.
Je krijgt een spoedopname: Meneer Puchalski (49 jaar oud 58 kg zwaar) heeft een overdosis paracetamol genomen. Op de Spoedeisende Hulp vertelt Meneer Puchalski aan de psychiater dat het leven voor hem vrijwel zinloos geworden is: hij is onlangs gescheiden, heeft daardoor schulden en ook zijn baan als verkoper van antiquarische boeken en prenten is hij kwijt geraakt. Hij weet niet meer hoe hij verder moet. Nadat door de SEH-verpleegkundige zijn maag is gespoeld is er geactiveerde kool en natriumsulfaat toegediend. Als antidotum werd op de SEH al een startdosis acetylcysteïne toegediend: 150 mg acetylcysteïne per kg lichaamsgewicht, in 15 minuten. Dat is bedoeld om beschadiging van de lever te voorkomen. Op de zaal moet je de man een vervolgdosis toedienen: 50 mg acetylcysteïne per kg lichaamsgewicht, in 500 ml infuusvloeistof (glucose 5%, met een inlooptijd van 4 uur). Het concentraat voor infusievloeistof bevat 200 mg/ml (25 ml (= 5 g). Je moet een aantal dingen weten alvorens je meneer Puchalski zijn medicatie kan geven. Je moet berekenen hoeveel mg acetylcysteïne je moet toedienen, hoeveel ml concentraat dat is, en wat de druppelsnelheid van het infuus moet zijn om de medicatie in 4 uur in te laten lopen. In de lessen Medisch rekenen heb je alle theorie gehad en zijn alle formules, omzettingen, tips en trucs voorbij gekomen. Maar soms kan het geen kwaad om dan toch nog eens even terug te kijken hoe zat het ook al weer.
In de lessen Medisch rekenen heb je alle theorie gehad en zijn alle formules, omzettingen, tips en trucs voorbij gekomen. Maar soms kan het geen kwaad om dan toch nog eens even terug te kijken hoe zat het ook al weer.


 Een zorgvrager heeft 1,5 l/min zuurstof nodig. Een cilinder van 10 liter met een druk van 150 bar kan genoeg zuurstof leveren voor hoeveel uur en hoeveel minuten?
Een zorgvrager heeft 1,5 l/min zuurstof nodig. Een cilinder van 10 liter met een druk van 150 bar kan genoeg zuurstof leveren voor hoeveel uur en hoeveel minuten? Mevrouw Van Peppel krijgt viermaal daags 180 ml sondevoeding. De voeding moet per keer in 45 minuten doorlopen. Op welke inloopsnelheid, ml per uur, moet de pomp worden ingesteld?
Mevrouw Van Peppel krijgt viermaal daags 180 ml sondevoeding. De voeding moet per keer in 45 minuten doorlopen. Op welke inloopsnelheid, ml per uur, moet de pomp worden ingesteld?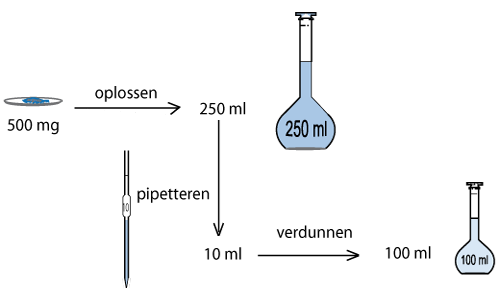 Een zorgvrager krijgt tussen 17:00 uur en 9:00 uur in totaal 2 liter sondevoeding. In één flacon zit 500 ml. Je moet de flacons omwisselen om de hoeveel uur?
Een zorgvrager krijgt tussen 17:00 uur en 9:00 uur in totaal 2 liter sondevoeding. In één flacon zit 500 ml. Je moet de flacons omwisselen om de hoeveel uur? In de eerste periode van de opleiding ga je in een groep de ouderavond organiseren. Deze avond is voor heel veel ouders een eerste echte kennismaking met jouw opleiding en daarom voor je ouders echt heel belangrijk.
In de eerste periode van de opleiding ga je in een groep de ouderavond organiseren. Deze avond is voor heel veel ouders een eerste echte kennismaking met jouw opleiding en daarom voor je ouders echt heel belangrijk. Voor deze opdracht ga je volgende onderdelen uitvoeren:
Voor deze opdracht ga je volgende onderdelen uitvoeren:
 Maar laten we eerst eens even beginnen met het begin. Zoals eerder genoemd leren we bij optellen en aftrekken de werkwijze van het ‘gelijknamig maken’. Dat betekent dat je de noemer van beide breuken gelijk maakt. Het eenvoudigst gaat dit door bij de eerste breuk, de teller (het bovenste deel van de breuk) te vermenigvuldigen met de noemer (het onderste deel van de breuk) van de andere breuk. En deze handeling doen we ook met de noemer van de eerste breuk en de noemer van de tweede breuk. Je hebt nu eigenlijk de eerste breuk vermenigvuldigd met ‘1’, dus de waarde van de oorspronkelijke breuk is niet gewijzigd. Maar laten we dit eens bekijken in een voorbeeld:
Maar laten we eerst eens even beginnen met het begin. Zoals eerder genoemd leren we bij optellen en aftrekken de werkwijze van het ‘gelijknamig maken’. Dat betekent dat je de noemer van beide breuken gelijk maakt. Het eenvoudigst gaat dit door bij de eerste breuk, de teller (het bovenste deel van de breuk) te vermenigvuldigen met de noemer (het onderste deel van de breuk) van de andere breuk. En deze handeling doen we ook met de noemer van de eerste breuk en de noemer van de tweede breuk. Je hebt nu eigenlijk de eerste breuk vermenigvuldigd met ‘1’, dus de waarde van de oorspronkelijke breuk is niet gewijzigd. Maar laten we dit eens bekijken in een voorbeeld: Voor het vermenigvuldigen leren we echter dat we ‘boven en boven’ en ‘onder en onder’ met elkaar mogen vermenigvuldigen en dan zijn we klaar. In dit geval laten we het vereenvoudigen voor nu even achterwege. In een voorbeeld uitgeschreven ziet het er dan zo uit:
Voor het vermenigvuldigen leren we echter dat we ‘boven en boven’ en ‘onder en onder’ met elkaar mogen vermenigvuldigen en dan zijn we klaar. In dit geval laten we het vereenvoudigen voor nu even achterwege. In een voorbeeld uitgeschreven ziet het er dan zo uit: Nu we alle 4 de basis-bewerkingen hebben besproken kunnen we voorzichtig concluderen dat we gelijknamigheid nodig zijn voor optellen en aftrekken en dat vermenigvuldigen en delen met breuken, met omkering, gelijk aan elkaar zijn.
Nu we alle 4 de basis-bewerkingen hebben besproken kunnen we voorzichtig concluderen dat we gelijknamigheid nodig zijn voor optellen en aftrekken en dat vermenigvuldigen en delen met breuken, met omkering, gelijk aan elkaar zijn. Goed met het bovenstaande hebben we dus bewezen dat we ook voor vermenigvuldigen en delen de breuken ook gelijknamig mogen maken. Hiermee kunnen we dus ook stellen dat we de breuken altijd eerst gelijknamig gaan maken en daarna de bewerking van optellen, aftrekken, vermenigvuldigen of delen gaan uitvoeren.
Goed met het bovenstaande hebben we dus bewezen dat we ook voor vermenigvuldigen en delen de breuken ook gelijknamig mogen maken. Hiermee kunnen we dus ook stellen dat we de breuken altijd eerst gelijknamig gaan maken en daarna de bewerking van optellen, aftrekken, vermenigvuldigen of delen gaan uitvoeren.
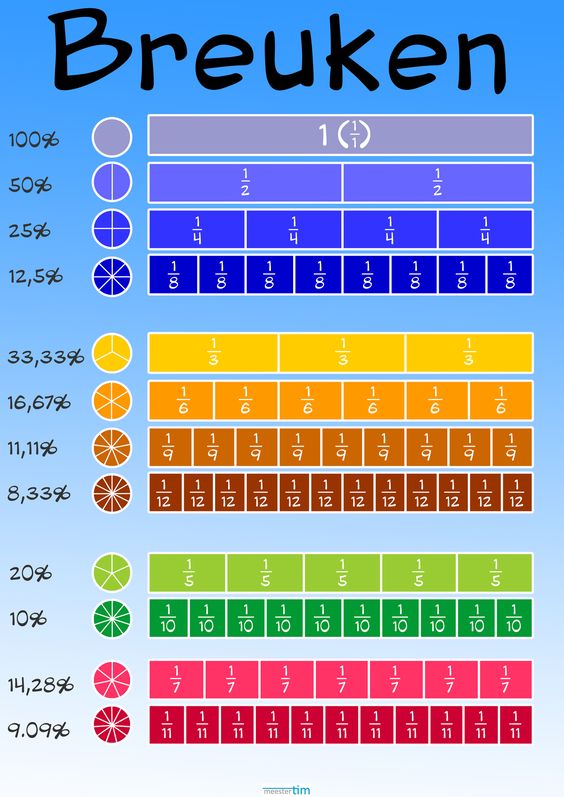 Laten we eens kijken naar het volgende sommetje met breuken:
Laten we eens kijken naar het volgende sommetje met breuken: 







 Bij een
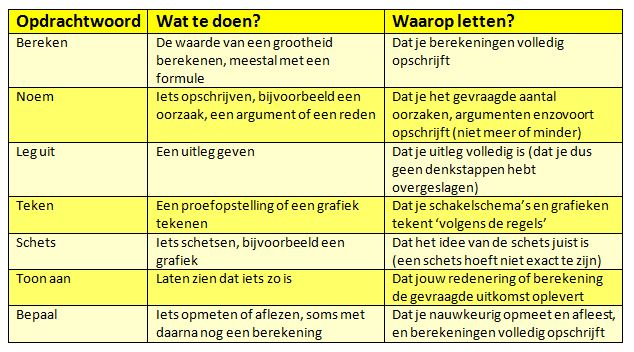
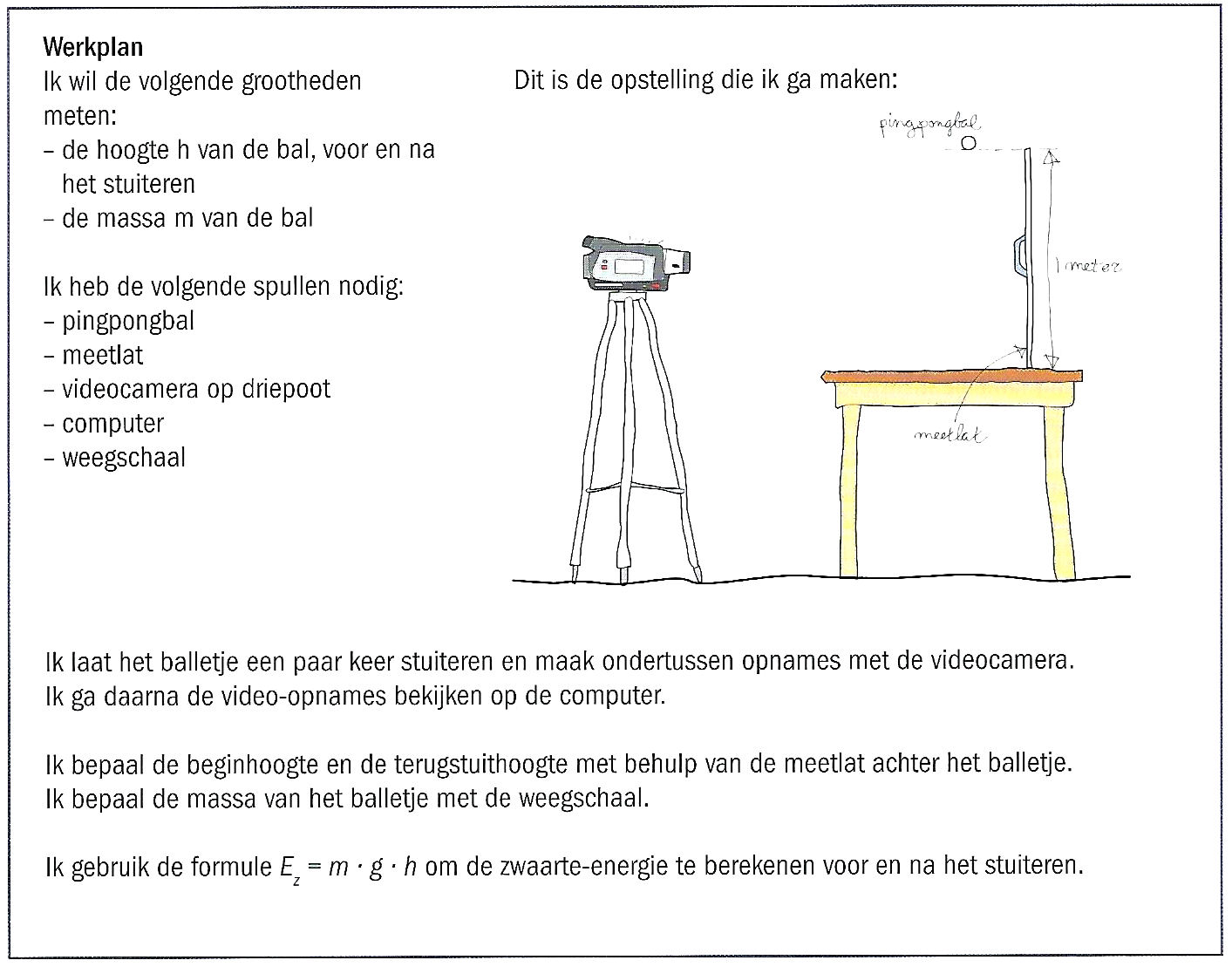
Bij een  Een aantal aanwijzingen:
Een aantal aanwijzingen: